Теоретическая механика (Голубева О.В.)
Теоретическая механика (Голубева О.В.)
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИЗА § 2. Вектор-функция Часть I. КИНЕМАТИКА § 1. Предмет теоретической механики и ее основные понятия § 2. Уравнение движения точки и ее траектория § 3. Скорость точки § 4.  Ускорение точки§ 5. Проекции ускорения на естественные оси § 6. Частные случаи движепия точки. Физический смысл тангенциального и нормального ускорения точки § 7. Уравнения движения точки в криволинейных координатах. Проекция скорости и ускорения на осн криволинейных координат ГЛАВА 2. КИНЕМАТИКА НЕСВОБОДНОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 2. Ограничения на скорость и ускорение, налагаемые геометрическими связями § 3. Число степеней свободы системы. Обобщенные координаты уравнения движения системы, обобщенные скорости ГЛАВА 3. КИНЕМАТИКА ТВЕРДОГО ТЕЛА ИЛИ НЕИЗМЕНЯЕМОЙ СРЕДЫ § 1. Уравнения движения абсолютно твердого тела § 2. Поступательное движение твердого тела § 3. Вращение твердого тела вокруг неподвижной оси § 4. Вращение тела около неподвижной точки. Теорема Даламбера § 5. Общий случай движения свободного твердого тела. Теорема Шаля Б. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ И ТВЕРДОГО ТЕЛА § 2.  Сложение скоростей§ 3. Сложение ускорений ГЛАВА 5. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 2. Сложение вращений § 3. Плоскопараллельное движение твердого тела § 4. Кривошипно-шатупный механизм Часть II. КИНЕТИКА § 1. Вектор силы § 2. Тяжелая масса тел § 3. Закон инерции. Инерциальные системы координат § 1. Основной закон механики (второй закон Ньютона). Инертная масса. Принцип независимости действия сил § 5. Закон равенства действия и противодействия (третий закон Ньютона) Б. ДИНАМИКА ТОЧКИ § 2. Характеристика сил § 3. Дифференциальные уравнения движения § 4. Определение уравнения движения точки по заданной силе § 5. Определение силы по заданному уравнению движения § 6. Интегрирование дифференциальных уравнений движения точки в случае сил частного вида ГЛАВА 8. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 1. Уравнение движелия материальной точки в неинерциальной системе координат § 2.  Координатные системы, связанные с Землей§ 3. Отклонение падающих тел от вертикали ГЛАВА 9. ДВИЖЕНИЕ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ § 1. Характерные особенности движения точки иод действием центральной силы § 3. Закон всемирного тяготения § 4. Задача двух тел § 5. Движение электрона в поле ионизированного атома (центральная отталкивающая сила) Б. СТАТИКА ГЛАВА 10. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Активные силы и силы реакции связей § 3. Система сходящихся сил § 4. Система параллельных сил § 5. Центр тяжести и центр масс § 6. Момент силы относительно точки и относительно оси § 7. Свойства пары сил § 8. Приведение произвольной системы сил § 9. Равновесие произвольной системы сил, действующих на твердое тело § 10. Раваовесне системы материальных точек ГЛАВА 11. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ И ИХ ПЕРВЫЕ ИНТЕГРАЛЫ § 2.  Принцип Даламбера. Основные уравнения диижения системы§ 3. Теорема о количестве движения системы § 4. Теорема импульсов § 5. Теорема о количестве движения центра инерции системы и примеры ее применения § 6. Теорема о кинетическом моменте ГЛАВА 12. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ § 1. Теорема о количестве движения в неинерциальной системе координат § 3. Законы сохранения § 4. Уравнения движения в расчетной системе координат Д. КОНСЕРВАТИВНЫЕ СИЛЫ ГЛАВА 13. РАБОТА СИЛЫ. ПОТЕНЦИАЛЬНОЕ ПОЛЕ § 2. Силовое поле и его частный случай — потенциальное поле § 3. Работа внутренних сил, действующих в системе ГЛАВА 14. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 1. Теорема о кинетической энергии и закон сохранения механической энергии точки § 2. Теорема о кинетической энергии системы § 3. Формула Кенига § 4. 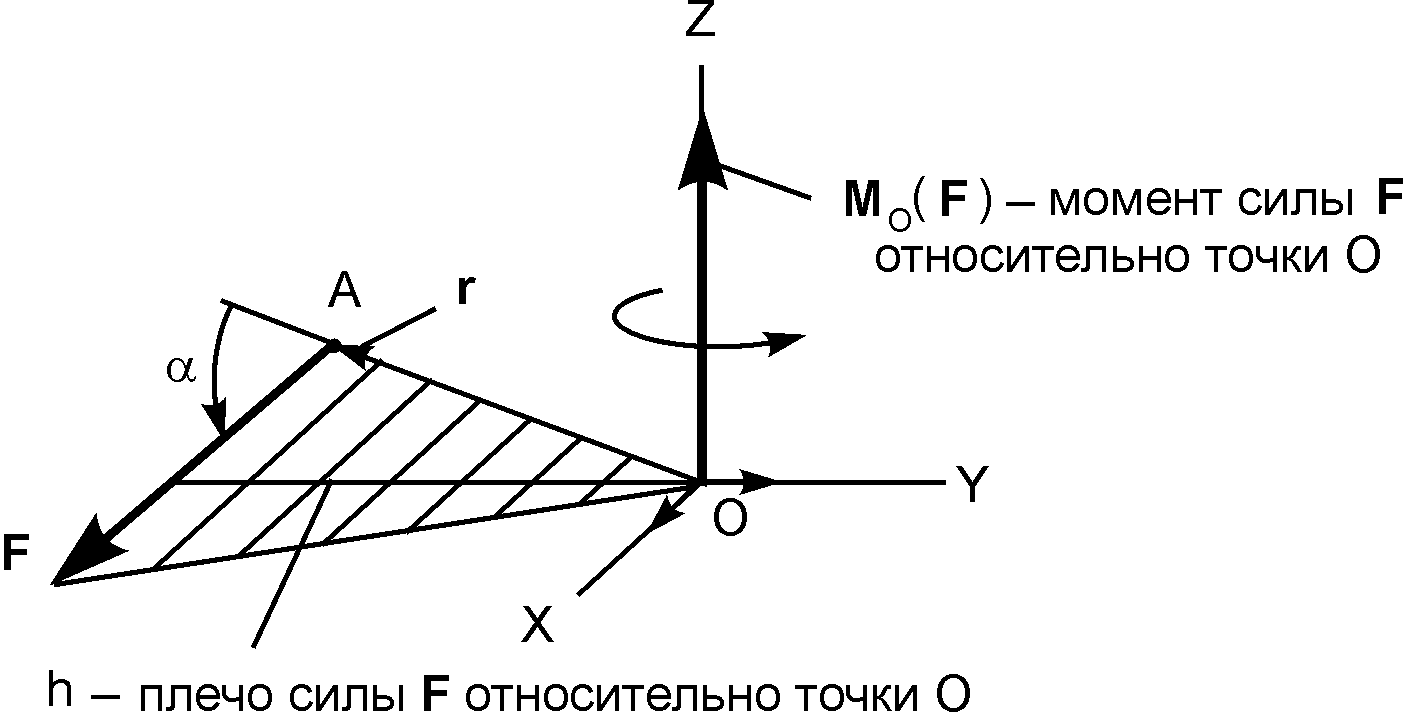 Е. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА § 1. Кинетический момент твердого тела в частных случаях его движения § 2. Вычисление моментов инерции относительно параллельных осей § 3. Эдлипсоид инерции ГЛАВА 16. ДИНАМИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 2. Вращение твердого тела вокруг неподвижной оси § 3. Физический и математический маятники ГЛАВА 17. ДИНАМИКА ТЕЛА, ВРАЩАЮЩЕГОСЯ ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА § 1. Кинематические уравнения Эйлера Углы Эйлера § 2. Динамические уравнения Эйлера § 3. Постановка задачи о движении твердого тела вокруг неподвижной точки § 5. Приближенная теория гироскопа § 6. Общий случай движения твердого тела Ж. ПРИМЕНЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ ДИНАМИКИ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ВОПРОСАМ МЕХАНИКИ ГЛАВА 18. ДВИЖЕНИЕ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ § 2. Примеры применения уравнения Мещерского. Задачи Циолковского ГЛАВА 19.  УДАР§ 1. Основное уравнение теории удара § 2. Гипотеза Ньютона § 3. Абсолютно упругий удар точки о сферу § 4. Прямое центральное соударение двух тел З. ДИНАМИКА СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ (АНАЛИТИЧЕСКАЯ МЕХАНИКА) ГЛАВА 20. ЗАДАЧА О ДВИЖЕНИИ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 3. Идеальные связи (основной постулат аналитической механики) § 4. Уравнения Лагранжа первого рода ГЛАВА 21. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА § 2. Уравнения Лагранжа второго рода § 3. Уравнения Лагранжа второго рода, как уравнения движения точки в 3n-мерном пространстве § 4. Уравнения Лагранжа второто рода для частных случаев сил, действующих на систему § 5. Первые интегралы уравнений движения ГЛАВА 22. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА § 2. Канонические уравнения Гамильтона 3. Первые интегралы канонических уравнений § 4. Скобки Пуассона § 5. Метод Рауса ГЛАВА 23. ОБЩИЕ ПРИНЦИПЫ МЕХАНИКИ  Принцип Лагранжа — Даламбера и принцип виртуальных перемещений Лагранжа§ 3. Вариационный интегральный принцип Гамильтона — Остроградского И. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ ГЛАВА 24. ПРЯМОЛИНЕЙНОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ § 2. Свободные колебания точки при наличии сопротивления среды § 3. Вынужденные колебания точки § 4. Резонанс ГЛАВА 25. ОБЩИЕ УРАВНЕНИЯ МАЛЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Устойчивое равновесие консервативной системы § 3. Уравнения малых колебаний механических систем ГЛАВА 26. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ § 2. Собственные колебания системы § 3. Главные координаты § 4. Вынужденные колебания системы с двумя степенями свободы § 5. Двойной математический маятник Часть III. УРАВНЕНИЯ МЕХАНИЧЕСКИХ ДВИЖЕНИИ ТОЧЕК СО СКОРОСТЯМИ, БЛИЗКИМИ К СКОРОСТИ СВЕТА (ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) ГЛАВА 27.  ВВЕДЕНИЕ В СПЕЦИАЛЬНУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ§ 2. Элементарные сведения об ортогональных преобразованиях ГЛАВА 28. СВОЙСТВА ПРОСТРАНСТВА И ВРЕМЕНИ ПРИ СКОРОСТЯХ ТОЧЕК, СРАВНИМЫХ СО СКОРОСТЬЮ СВЕТА (ПЕРВЫЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) § 1. Порвый закон Ньютона и свойства пространства и времени ньютонианской маханики § 2. Преобразования Лоренца § 3. Свойства пространства и времени при относительном движении координатных систем, сравнимых со скоростью света § 4. Преобразование скорости и ускорения (теорема сложения скоростей Эйнштейна) ГЛАВА 29. ВТОРОЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Второй закон Ньютона в специальной теории относительности § 3. Уравнение энергии в специальной теории относительности § 4. Закон взаимной связи массы и энергии ГЛАВА 30. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Уравнения движения механических систем ГЛАВА 31. РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ.  РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ§ 1. Релятивистские уравнения движения точки в криволинейных координатах § 2. Релятивистские уравнения движения связных механических систем |
Как правильно найти момент силы, формула, решение задач
Оглавление
Время чтения: 7 минут
264
Определение
Момент силы — это крутящий или вращательный момент, который является векторной величиной.
Чтобы определить, чему равен момент силы, нужно получить произведение вектора силы и радиус-вектора, который проводится к точке приложения силы от оси вращения. Поэтому величину можно назвать характеристикой вращательного воздействия силы на твердое тело.
Термины “крутящий” и “вращающий” моменты в данном случае не являются тождественными. Разница между ними состоит в том, что “вращающий” момент воспринимается как внешнее усилие, которое прикладывают к объекту.
Термин “крутящий” же рассматривается как внутреннее усилие, которое появляется при приложении конкретных нагрузок (что делает определение схожим с используемым при изучении сопротивления материалов).
Понятие «момент силы»
Физики воспринимают этот термин в качестве так называемой “вращающей силы”. В соответствии с системой СИ, измеряется данная величина в ньютон-метрах. Иногда в литературе можно также встретить понятие “момент пары сил” (такое определение, например, появляется в исследованиях Архимеда над рычагами).
При использовании простых примеров (например, при приложении силы к рычагу в перпендикулярном отношении к нему) величина рассчитывается как произведение расстояния до оси вращения рычага и непосредственно силы, которая на него воздействует.
Пример: На рычаг оказывает воздействие силы в 3 ньютона, которую прикладывают на расстоянии 2 м от оси вращения рычага. В результате момент силы будет равнозначен силе в 1 ньютон, прикладываемой на расстоянии 6 м по отношению к рычагу.
Как определить, чему равен момент силы
Формула
Точно определить момент действия силы частицы удастся, применив следующую векторную формулу:
\[\vec{\mathrm{M}}=\vec{\mathrm{r}} \vec{\mathrm{F}}\]
В данном случае \[\vec{\mathrm{r}}\] — это радиус вектора частицы, а
\[\vec{\mathrm{F}}\] — сила, воздействующая на эту частицу.
Важно помнить, что в физике энергия воспринимается как скалярная величина. В то же время момент силы считается (псевдо)векторной величиной. Поэтому совпадение размерностей указанных величин никогда не бывает случайным. Например, момент силы в 1 Н/м, приложенный через целый оборот, при выполнении механической работы сообщает энергию в 2 Дж. В математическом отображении эта формула момента силы будет выглядеть так:
\[\mathbf{E}=\mathbf{M} \boldsymbol{\theta}\], где:
- \[\mathbf{E}\] — это энергия;
- \[\mathbf{M}\] — это вращающийся момент;
- \[\boldsymbol{\theta}\] — это угол в радианах.
В современных условиях момент силы измеряется при помощи особых датчиков нагрузки, которые могут быть трех типов:
- оптического;
- тензометрического;
- индуктивного.
Применение специальной техники позволяет определить величину предельно точно и избавляет ученых от необходимости производить лишние расчеты.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Момент силы: формулы
Наиболее интересным в физике считается определение момента силы в поле. Для этого используется следующая формула:
\[\vec{M}=\vec{M_{1}} \vec{F}\]
Где:
\[\vec{M_{1}}\]- это момент рычага;
\[\vec{F}\]- это величина силы, действующей на тело.
У такой формулы момента силы в физике будет один недостаток. С ее помощью не удастся определить, в каком направлении направлен момент силы. Известной станет только его величина. Если сила окажется перпендикулярной вектору, тогда момент рычага окажется равен расстоянию от центра до точки, в которой была приложена сила. В таком случае момент силы достигнет максимального значения:
\[\vec{T}=\vec{r} \quad \vec{F}\]
Если сила совершает какое-либо действие на определенном расстоянии, она параллельно выполняет механическую работу относительно того же объекта.
В таком случае в физической практике считается, что и момент силы выполняет работу (при совершении действия через угловое расстояние).
\[\mathrm{P}=\mathrm{M} {\omega}\]
Международная система измерений предлагает определять мощность в Ваттах, при этом момент силы измеряется в радианах в секунду. Для определения величину угловой скорости используется единица “радианы в секунду”).
Как определяется момент действия нескольких сил
Если на тело действуют одновременно две равные по величине и противоположно направленные силы (не лежащие на одной и той же прямой), оно находится в состоянии равновесия. Такая ситуация связана с тем, что результирующий момент данных сил по отношению к любой из осей не обладает нулевым значением. Ведь обе силы направлены в одну сторону момента и являются парой сил.
Если тело закреплено на оси, оно будет вращаться под влиянием пары сил. Когда же пара сил прилагается по отношению к свободному телу, последнее начнет крутиться вокруг той оси, которая проходит через центр тяжести.
В соответствии с правилом моментов сил в физике, момент пары сил считается одинаковым по отношению к любой оси, перпендикулярной плоскости этой пары. При этом суммарный момент пары M всегда определяется как произведение плеча пары (то есть расстояния l между силами) и одной из этих сил F. Данный расчет производится независимо от типов отрезков, на которые разделяется положение оси.
\[\mathrm{M}=\mathrm{FL}_{1}+\mathrm{FL}-2=\mathrm{FL}_{1}+\mathrm{L}_{2}=\mathrm{FL}\]
В случае, если равнодействующая момент нескольких сил равняется нулю, он будет одинаковым по отношению ко всем параллельным друг другу осям. Именно поэтому воздействие всех сил на тело можно заменить действием только одной пары сил, имеющих точно такой же момент.
Что такое момент и как его рассчитать?
Когда я обучаю своих студентов-физиков, я хочу, чтобы они понимали основы концепции, а не только то, как подставлять числа в уравнение. Когда я изучал физику, мне хотелось, чтобы мои учителя больше опирались на приложения из реальной жизни, на то, что мы уже знаем о мире, чтобы помочь нам действительно получить его .
Я надеюсь, что этот пример понравится всем моим заядлым лыжникам.
Когда я был молод и учился кататься на лыжах, я боялся кресельных подъемников (немного до сих пор). Висеть высоко на открытом воздухе было страшно. Когда кресельный подъемник был полным, когда я сидел на нем со всей семьей — все казалось сбалансированным, меня там благополучно придавливало. Но если бы я был на кресельном подъемнике один, если бы я сел на один край, кресельный подъемник сильно бы наклонился в эту сторону.
Или, если бы я (маленький ребенок) сидел с папой (намного тяжелее ребенка), кресельный подъемник опрокинулся бы в его сторону.
За годы катания на кресельном подъемнике я понял, как мне удерживать кресельный подъемник в равновесии. Если бы я был один, я бы сидел посередине. Если бы я был со своим папой, он мог бы сидеть чуть не по центру с одной стороны, а я мог бы сесть полностью к одному краю с другой стороны. Это позволит кресельному подъемнику оставаться в горизонтальном положении.
Кто-нибудь из вас замечал такое, когда сидел на кресельном подъемнике с кем-то, кто намного легче или тяжелее вас?
Вот несколько правил, касающихся сидения на кресельном подъемнике. Подумайте, имеют ли они смысл для вас.
- Один человек, сидящий посередине, сделает кресельный подъемник горизонтальным.
- Более тяжелый человек будет опрокидывать кресельный подъемник сильнее, чем легкий, если он сидит на одинаковом расстоянии от центра.
- Есть способ достичь равновесия двумя людьми разного веса, сидящими на рассчитанном расстоянии от центра.
Это фундаментальное понятие физики называется моментом .
МОМЕНТ силы является мерой ее стремления заставить тело вращаться вокруг определенной точки или оси.
Когда я сижу на кресельном подъемнике, я создаю момент, который заставляет кресельный подъемник вращаться вокруг оси.
Как рассчитать момент?Момент равен приложенной силе, умноженной на расстояние от оси вращения:
Момент = Сила x Расстояние
Давайте рассмотрим пример: A взвешивание 2 фута от центра кресельного подъемника.
На каком расстоянии от центра на противоположной стороне кресельного подъемника должен сидеть ее отец (который весит 180 фунтов), чтобы кресельный подъемник был горизонтальным («уравновешенным»)? Сначала вычислите момент, создаваемый ребенком:
ПРИМЕЧАНИЕ. Мы можем смоделировать кресельный подъемник как невесомую балку = 120 ft-lbs
Если ребенок сидит слева от точки поворота, в какую сторону наклоняется кресельный подъемник?
Она поворачивает кресельный подъемник против часовой стрелки .
Правило: моменты против часовой стрелки считаются отрицательными значениями.Чтобы кресельный подъемник находился в равновесии, момент, действующий на ось со стороны Отца, должен быть равен и противоположен ребенку.
Ребенок создал момент -120 ft-lbs, поэтому ее отцу необходимо создать момент +120 ft-lbs.
120 ft-lbs = (180 фунтов)(x футов)
x = ⅔ футов = 8 дюймов.
С какой стороны от точки опоры должен сидеть Отец, чтобы уравновесить ребенка
С правой стороны!
Когда Отец сидит с правой стороны, он заставляет кресельный подъемник наклониться по часовой стрелке .
Правило: моменты по часовой стрелке считаются положительными величинами.Когда Отец сидит в 8 дюймах слева от оси вращения, он создает момент +120 ft-lbs вокруг оси. Равный и противоположный момент ребенку. Следовательно, кресельный подъемник находится в равновесии.
Какие еще приложения в реальной жизни, связанные с моментами, вы можете придумать?- Если гайку трудно открутить коротким ключом, поможет более длинный ключ. Это связано с тем, что на гайку будет действовать больший момент, когда та же сила будет приложена дальше от оси.
- Попробуйте толкнуть дверь очень близко к петле. Чем ближе к точке шарнира, тем сильнее придется давить. Если дверь очень тяжелая, толкните дверь в сторону, которая находится дальше всего от петли. Это еще одно реальное применение момента.
Это еще одно реальное применение момента.Физика может показаться абстрактной и запутанной, когда вы рисуете балки и диаграммы свободного тела. Но физика есть везде. Когда вы изучаете новую концепцию в физике, попросите своих наставников привести примеры из реальной жизни и объяснить, как теория применяется на практике!
Определение, Первая и Вторая, Сила, Уравнение
Почему дверные ручки всегда находятся на противоположной стороне дверных петель? Если вы попытаетесь толкнуть дверь рядом с петлей, а затем с противоположного конца, вы заметите большую разницу. Находясь рядом с петлей, трудно закрыть дверь; на дверной ручке, это довольно легко. Причина этого в том, что чем дальше от шарнира, тем сильнее эффект поворота.
Что вызывает эффект поворота?
Если объект неподвижен или находится в статическом равновесии, все силы, действующие на этот объект, уравновешивают друг друга. Но если они уравновешивают друг друга и общей силы нет, означает ли это, что объект находится в статическом равновесии?
Взгляните на следующую схему:
Рис.
1 – Две силы, действующие на объект в разных точках
В первом примере обе силы имеют одинаковую величину и действуют в одной и той же точке, но в противоположных направлениях направлении, в результате чего стержень остается неподвижным.
Во втором примере, поскольку силы не действуют в одной и той же точке, они создают вращательный эффект, известный как крутящий момент . В этом случае стержень начнет вращаться против часовой стрелки и, следовательно, не будет находиться в статическом равновесии.
Моменты
Величина поворотного эффекта, создаваемого силой, называется моментом силы . Это происходит, когда силы заставляют объект вращаться вокруг некоторой оси .
Момент силы рассчитывается следующим образом:
Момент = (Сила) · (Перпендикулярное расстояние от силы до оси вращения)
Моменты измеряются в ньютон-метрах, записывается Нм. Сила в ньютонах, расстояние в метрах.
То, что мы исследовали до сих пор, объясняет, почему дверные ручки расположены по другую сторону дверных петель, которые действуют как стержень.
Максимальное расстояние между силой, которую мы прикладываем к дверной ручке, и шарниром, приводит к большему моменту. Это облегчает открытие или закрытие двери. Тот же принцип применим к гаечным ключам с длинными рукоятками для увеличения величины момента, что облегчает затяжку болтов.
Груз массой 100 кг подвешен на расстоянии 30 м от оси, на которую опирается стальной стержень. Предполагая, что вес стержня пренебрежимо мал, каков крутящий момент относительно оси вращения?
Рис. 2. Масса 100 кг создает момент
Сначала нам нужно определить силу, создаваемую массой. Это его вес или его масса, умноженная на константу гравитационного ускорения. Это дает нам:
\(F = масса \cdot g = 100 \cdot 9,81 = 981 Н\)
Теперь у нас есть сила, приложенная к стержню, а перпендикулярное расстояние от силы до оси вращения было указано выше. Все, что нам тогда нужно сделать, это использовать момент силового уравнения следующим образом:
Момент = (Сила) · (Перпендикулярное расстояние от силы до оси вращения)
Пары
Уникальный случай моментов — это когда две параллельные силы, равные по величине, но противоположные по направлению, а также разделенные расстоянием d заставить объект вращаться.
Это известно как пара .
Пара не имеет равнодействующей силы; он производит только поворотный эффект.
Например, ваши руки производят пару на руле автомобиля, чтобы повернуть руль.
Рис. 3. Поворот рулевого колеса на примере пары
Момент пары рассчитывается с помощью следующего уравнения:
Пара = (величина одной силы) · (перпендикулярное расстояние между двумя силами)
Рассчитаем пару, создаваемую силами, действующими на этот стальной стержень длиной 1 м.
Рис. 4 – Две силы, действующие на стальной стержень и создающие пару
Все, что нам нужно сделать, это применить уравнение, используя приведенные выше значения:
\(Пара = F \cdot d = 15 \cdot 1 = 15 \пробел Нм\)
Принципы моментов
Моменты могут быть по часовой стрелке или против часовой стрелки.
Представьте себе двух детей, играющих на качелях, причем мальчик сидит слева, а девочка справа.
Вес мальчика слева создает момент против часовой стрелки, а вес девочки справа создает момент, который поворачивает качели по часовой стрелке.
Что означали бы два момента, созданные детьми, если бы качели были сбалансированы? Чтобы объект находился в равновесии — чтобы качели были сбалансированы — ни в одной точке не должно быть общего эффекта поворота. Таким образом, моменты по часовой стрелке и против часовой стрелки должны уравновешивать друг друга.
Это резюмируется принципом моментов . Объект находится в статическом равновесии, когда:
Сумма моментов по часовой стрелке = сумма моментов против часовой стрелки
Качели на следующей диаграмме уравновешены. Рассчитайте W, вес блока слева от оси, используя принцип моментов.
Рис. 5 – Различные силы, действующие на качели
Для расчета W применяем уравнение, складывая значения из диаграммы:
Сумма моментов против часовой стрелки = Сумма моментов по часовой стрелке
\(Вт \cdot 1.5 = (300 \cdot 1) + (550 \cdot 1.5)\)
\(Вт \cdot 1.5 = 300 + 825 = 1125 Нм\)
\(W = 750 Н\)
Моменты — ключевые выводы
- Момент — это вращательное действие силы.
