Момент силы — Студопедия
Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки — полюса) и относительно оси.
Если имеется материальная точка О, к которой приложена сила 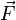 , то момент силы относительно этой точки равен векторному произведению радиус-вектора
, то момент силы относительно этой точки равен векторному произведению радиус-вектора 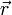 , соединяющего точку О и точку приложения силы, на вектор силы
, соединяющего точку О и точку приложения силы, на вектор силы 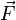 :
:
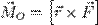 ., (Н•м).
., (Н•м).
 Момент силы
Момент силы
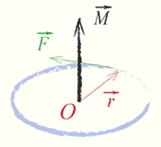
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).
Рис. 4
Модуль момента силы:
M =F• l =F •r •sin α,
где: M – момент силы (Ньютон •метр),
F – приложенная сила,
r – расстояние от центра вращения до места приложения силы,
l = r.sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,
α — угол, между вектором силы F и вектором положения r.
Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора
Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:
если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:
М1 + М2 + … + Мn = 0.
Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F
Рис. 5.
Моменты силы относительно точки и оси — Студопедия
Пусть имеются сила  , приложенная в точке какой-либо НМС, точка О и ось l. Тогда можно дать определения моментам силы относительно точки и оси и установить связь между ними.
, приложенная в точке какой-либо НМС, точка О и ось l. Тогда можно дать определения моментам силы относительно точки и оси и установить связь между ними.
1.3.1. Момент силы относительно точки
Определение: Моментом силы относительно точки называется вектор, приложенный в этой точке, равный по величине произведению величины силы на кратчайшее расстояние от точки до линии действия силы (называемое плечом), направленный перпендикулярно к плоскости, проходящей через точку и силу, по правилу правого винта, т. е. в ту сторону, откуда совершаемый силой поворот тела, относительно точки виден против хода часовой стрелки (рис. 6).
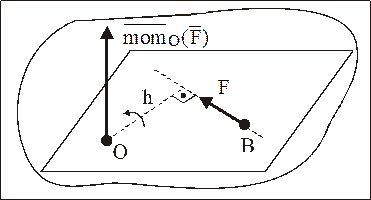
Рис. 6
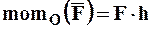
Введем в рассмотрение радиус-вектор , определяющий положение точки B – точки приложения силы
, определяющий положение точки B – точки приложения силы  (рис. 7).
(рис. 7).
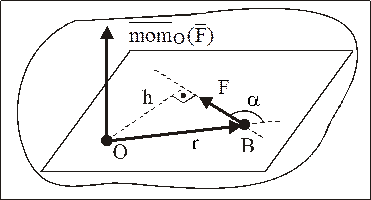
Рис. 7
При рассмотрении векторного произведения векторов 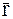 и
и 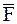 , оказывается, что
, оказывается, что
а) 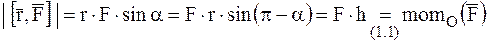
б) 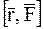
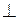 плоскости, в которой находятся
плоскости, в которой находятся 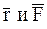 ;
;
в) 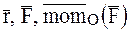 составляют правую тройку векторов, т. е. если смотреть с конца третьего вектора, поворот от первого ко второму вектору виден против хода часовой стрелки.
составляют правую тройку векторов, т. е. если смотреть с конца третьего вектора, поворот от первого ко второму вектору виден против хода часовой стрелки.
Таким образом, можно сделать следующий вывод:
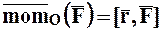
В случае плоской системы сил величину момента силы относительно точки, лежащей в плоскости действия сил, можно рассматривать как алгебраическую величину, равную взятому со знаком плюс или минус произведению модуля силы на плечо:
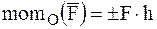 .
.
При этом величина момента берется со знаком плюс, если сила стремится осуществить поворот тела относительно точки против хода часовой стрелки и со знаком минус в противоположном случае (рис. 8).

Рис. 8
1.3.2. Момент силы относительно оси
Определение: Моментом силы относительно оси называется взятая со знаком плюс или минус величина момента проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси и плоскости:
 . (1.3)
. (1.3)
Момент берется со знаком плюс, если, смотря с конца положительного направления оси, видно, что проекция силы стремится осуществить поворот тела относительно оси против хода часовой стрелки. В противном случае момент берется со знаком минус (рис. 9).
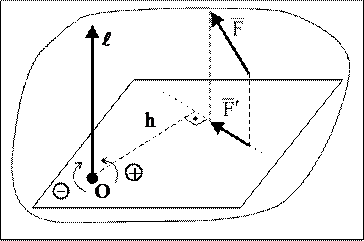
Рис. 9
Момент силы относительно оси не зависит от выбора плоскости, перпендикулярной оси.
Момент силы относительно оси равен нулю, если:
·  =0 , т.е. сила параллельна оси,
=0 , т.е. сила параллельна оси,
· h=0 , т.е. линия действия силы пересекает ось.
Момент силы — Студопедия
Рассмотрим движение некоторой материальной точки A относительно начала координат O (рис. 28). Точку О в этом случае называют полюсом. Обозначим буквой 
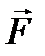 . Моментом силы
. Моментом силы 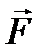 относительно точки О называется векторное произведение радиуса-вектора
относительно точки О называется векторное произведение радиуса-вектора 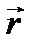 на силу
на силу 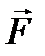 :
: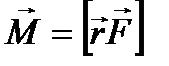 . (79)
. (79)
Векторы 
 равна M = r*F*sin(α), где α – угол между векторами
равна M = r*F*sin(α), где α – угол между векторами  и
и 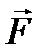 .
.Момент силы имеет размерность «сила*расстояние», и в системе СИ единицей момента силы является ньютон*метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы.
Если сила, действующая на точку A, равняется равнодействующей нескольких сил, например, двух 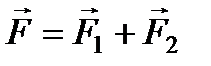 , то на основании известного свойства векторного произведения можно написать:
, то на основании известного свойства векторного произведения можно написать:
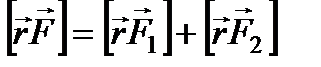 . (80)
. (80)
Это значит, что момент равнодействующей двух или нескольких сил относительно некоторого начала равен геометрической сумме моментов составляющих сил относительно того же начала.
Момент силы относительно оси. Если тело может вращаться относительно точки О произвольным образом, то под действием силы 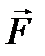
Если тело может вращаться только вокруг некоторой фиксированной оси, способность силы вращать тело вокруг этой оси характеризуется величиной, которая называется моментом силы относительно оси.
Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментом силы относительно оси.
Плечом силы относительно некоторой оси называется кратчайшее расстояние между осью и линией действия силы. Из рис. 28 следует, что это расстояние равно d = r*sin(α). Тогда момент силы относительно той же оси может быть определен как взятое с надлежащим знаком произведение перпендикулярной составляющей силы на соответствующее плечо (рис. 29):
Mz = Fп * d. (81)
На рисунках 28 и 29 плоскость П перпендикулярна оси z.
Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы d относительно точки О.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
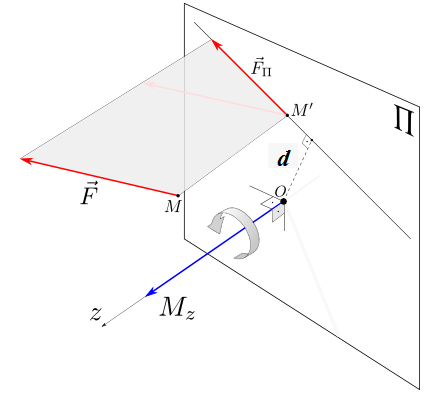
Рис. 29.
Момент силы F относительно оси z 
Суммарный момент внутренних сил. Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (рис. 30). Их моменты . относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы материальных точек, в частности для твердого тела, всегда равна нулю, это утверждение справедливо как для суммарного момента всех внутренних сил, взятого относительно любой точки, так и для суммарного момента этих сил, взятого относительно любой оси.
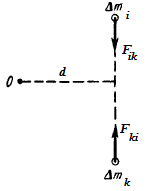
Рис. 30.
Суммарный момент сил взаимодействия двух элементарных масс 
Момент силы относительно центра [wiki.eduVdom.com]
Внимание! Этот раздел может иметь неточности в формулировках.
Вскоре он будет доработан.
Рассмотрим тело, которое закреплено в центре О и может поворачиваться вокруг оси, проходящей через точку О и перпендикулярной к плоскости чертежа. Приложим в точке А этого тела силу P и выясним, чем определяется вращательное действие этой силы (Рис.1).
Рис.1
Очевидно, что воздействие силы на тело будет зависеть не только от ее величины, но и от того, как она направлена, и в конечном итоге будет определяться ее моментом относительно центра О.
Определение 1. Моментом силы Р относительно центра О называется
взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть длину
перпендикуляра, опущенного из моментной точки на линию действия силы.
Правило знаков: момент силы считается положительным, если сила
стремится повернуть тело против хода часовой стрелки и отрицательным, если
она вращает тело по ходу часовой стрелки.
В соответствии с данным определением момент силы численно равен удвоенной площади треугольника OAB, построенного на векторе силы P с вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .
Отметим, что момент силы относительно точки О равен нулю, если линия действия силы проходит через моментную точку.
Рассмотренное определение момента силы подходит только для плоской системы сил. В общем случае для однозначного описания вращательного действия силы введем следующее определение.
Определение 2. Вектор-моментом силы Р относительно центра О
называется вектор, который:
приложен в моментной точке О перпендикулярно к плоскости треугольника, построенного на векторе силы с вершиной в моментной точке;
направлен по правилу право винта;
равен по модулю моменту силы Р относительно центра О (
Рис.1а).
Правило правого винта, известное также из курса физики как правило
буравчика, означает, что если смотреть навстречу вектор-моменту $\vec{М_0}(\vec{P})$ , мы
увидим вращение силой $\vec{P}$ плоскости своего действия, происходящим против хода
часовой стрелки.
Обозначим через $\vec{r}$ радиус-вектор точки приложения силы $\vec{P}$ и докажем, что справедлива следующая
Теорема 1. Вектор-момент силы $\vec{P}$ относительно центра О равен
векторному произведению радиус-вектора $\vec{r}$ и вектора силы $\vec{P}$ :
$$\vec{M_0}(\vec{P}) = ( \vec{r} \times \vec{P})$$
Напомним, что векторным произведением векторов $\vec{a}\text{ и }\vec{b}$ называется вектор $\vec{c}$ , который (Рис.2б):
Рис.2
перпендикулярен к векторам $\vec{a}\text{ и }\vec{b}$ ;
образует с ними
правую тройку векторов, то есть, направлен так, что, смотря навстречу этому вектору, мы увидим поворот от вектора $\vec{a}$ к вектору $\vec{b}$ на наименьший угол происходящим против хода часовой стрелки;равен по модулю удвоенной площади треугольника, построенного на этих векторах:
$$|\vec{c}| = |\vec{a} \times \vec{b}| = |\vec{a}|\cdot|\vec{b}|\cdot\sin(\vec{a},\,\vec{b})$$
Для доказательства теоремы отметим, во-первых, что вектор, равный векторному произведению векторов $\vec{r}\text{ и }\vec{P}$ будет коллинеарным вектору $\vec{M_0}(\vec{P})$.
Чтобы убедиться в этом, достаточно отложить эти векторы от одной точки (Рис.1в). Итак, $(\vec{r} \times \vec{P}) \uparrow \uparrow \vec{M_0}(\vec{P})$.
Во-вторых, модуль векторного произведения этих векторов будет равен:
$$|\vec{r} \times \vec{P}| = |\vec{r}|\cdot|\vec{P}|\cdot\sin(\vec{r},\,\vec{P}) = P \cdot d =|\vec{M_0}(\vec{P})|$$
, откуда и следует соотношение теоремы.
Следствием этой теоремы является:
Теорема Вариньона (о моменте равнодействующей сходящихся сил). Вектор-
момент равнодействующей системы сходящихся сил относительно произвольного
центра О равен геометрической сумме вектор-моментов всех сил системы
относительно этого центра:
$$\vec{M_0}(\vec{R}) = \sum_{i=1}^{i=n}\vec{M_{0\,\,i}}(\vec{P_i})$$
В самом деле, момент равнодействующей, с учетом теоремы 1 и аналитического определения равнодействующей сходящихся сил, будет равен:
$$ \vec{M_0}(\vec{R})= \vec{R}\times\vec{r} \,\,\,\;\;\text{ , т.к. } \vec{M_0}(\vec{P}) = ( \vec{r} \times \vec{P}) \\ \vec{R}\times\vec{r}= \vec{r}\times\sum_{i=1}^{i=n}\vec{P_i} \,\,\,\;\;\text{ , т.к. } (\vec{P_1}, \vec{P_2}, \dots, \vec{P_n}) \sim \vec{R} = \sum_{i=1}^{i=n} \vec{P_i} \\ \vec{r}\times\sum_{i=1}^{i=n}\vec{P_i} = \sum_{i=1}^{i=n}(\vec{r}\times\vec{P_i}) = \sum_{i=1}^{i=n}\vec{M_{0\,\,i}}(\vec{P_i}) $$
Для плоской системы сходящихся сил геометрическая сумма в теореме Вариньона переходит в алгебраическую:
$$M_0(R)=\sum_{i=1}^{i=n}M_{0\,\,i}(\vec{P_i})$$
Кинетика • Момент силы
Представьте, что вы в тренажерном зале делаете упражнения для укрепления грудных мышц или разгибателей колен на специальном мультипрессе. Вы устанавливаете нагрузку на 50 кг, но вскоре вы обнаружите, что сопротивление, которое вы чувствуете, также зависит от положения вашей ноги на руке при данном мультипрессе. Во время упражнения нагрузка в 50 кг иногда может показаться вам «половинной». Почему так получается, что мы можем поднимать тяжелые грузы с относительно небольшой силой?
Этот парадокс можно объяснить с помощью концепции момента силы.Момент силы — это стремление силы скручивать или вращать объект. Движения наших конечностей относительно суставов вызываются моментами силы, создаваемыми нашими мышцами. Благодаря мышцам, создающим моменты силы в наших суставах, мы можем двигаться.
Что такое момент силы?
Момент силы — это мера тенденции силы заставить тело вращаться.
Например, гимнаст на турнике начнет вращаться, только если он создаст соответствующий момент силы по отношению к турнику.Существует три типа ситуаций, в которых внешняя сила действует на свободное тело 52 :
- Центральная сила — внешняя сила, векторная линия которой 53 проходит через центр тяжести тела. Центральная сила вызывает только линейное движение. Это сила, которая действует на бобслей в прямой части трассы 54 .
- Эксцентрическая сила 55 — внешняя сила, векторная линия которой 56 не проходит через центр тяжести тела.Эксцентрическая сила вызывает изменения как линейного, так и вращательного движения. Сила, действующая на гимнаст в момент взлета в приземистом своде над лошадью является хорошим примером здесь.
- Пара сил — силы одинаковой величины, но противоположного направления, не лежащие на одной линии. Такие пары сил вызывают только изменения во вращательном движении. Результат этих двух сил равен нулю, поэтому согласно первому закону Ньютона эти силы не вызывают изменения линейного движения.
Момент определения силы
Величина момента силы, действующего вокруг точки 57 , прямо пропорциональна величине действующей силы и расстоянию этой точки от векторной линии силы, создающей момент.Расстояние между векторной линией силы и выбранной точкой называется плечом момента (рис. 15).
Рисунок 15 Схема свободного тела — прыжок с шестом. Синяя точка — это центр тяжести спортсмена. Черные стрелки обозначают силы реакции, через которые шест действует на руки спортсмена. Синие стрелки представляют плечи момента относительно оси вращения и центра тяжести.
Верно следующее: M = Fr , где M 58 — величина момента силы (Н · м), F — величина силы, создающей момент (Н), и r — плечо момента (м).
Момент силы как вектор определяется с помощью векторного произведения вектора положения r 59 и силы F :
Чтобы полностью описать момент силы, нам нужно знать величину, направление и точку приложения силы, которая производит импульс, и мы должны выбрать точку момента. Если вектор силы лежит в плоскости, перпендикулярной оси вращения тела, полезно выбрать в качестве точки момента точку пересечения этой плоскости и оси вращения.
Примеры использования момента силы в спорте
При гребле на байдарке или каноэ мы используем весло. Очень важно тщательно выбирать положение, в котором мы держим весло. Удерживание весла в различных положениях означает различные моменты силы при вождении и управлении лодкой. Поскольку точка вращения находится в том месте, где мы держим ракетку верхней рукой, чем ниже мы ставим нижнюю руку, тем больше момент силы. Практически это означает, что наши удары будут длиннее, но с более высоким вращающим эффектом при той же силе удара.Например, когда мы учим новичков грести, необходимо следить за тем, чтобы их нижняя рука была достаточно низкой, чтобы они могли управлять лодкой, несмотря на меньшее усилие.
В теннисе, гольфе, хоккее и т. Д. Момент силы зависит от того, как мы держим ракетку, клюшку для гольфа, хоккейную клюшку и т. Д. Правильный захват необходим. Но правильный хват может варьироваться в зависимости от потребностей конкретного спортсмена в конкретной ситуации. Момент силы также должен использоваться в видах спорта, где либо спортсмен, либо оборудование, которое он использует, вращаются.В боевых искусствах, таких как дзюдо или греко-римская борьба, спортсмены выбирают зацепы для создания максимально возможного момента силы.
Момент силы мышц
Вышеупомянутые примеры моментов силы в спорте были примерами внешних моментов силы, действующих на человеческое тело или спортивное снаряжение. Что заставляет наши руки и ноги вращаться вокруг суставов? Мышцы создают моменты силы, которые вращают наши руки и ноги. Мышцы создают силы, которые действуют на прикрепления, а затем и на скелет.На рис. 16 мы можем видеть силу, создаваемую двуглавой мышцей плеча на предплечье, когда положение локтевого сустава изменяется с полного разгибания на сгибание на 90 °. Всегда ли мышцы производят один и тот же момент силы во время этого движения? Способность двуглавой мышцы плеча создавать момент силы в локтевом суставе зависит от положения локтевого сустава. Момент плеча мышечной силы меняется в зависимости от взаимного положения отдельных сегментов сустава (рис. 16). Изменение угла сустава вызывает изменение моментного плеча мышечной силы.Этот факт частично объясняет, почему наши мышцы способны создавать значительно большие моменты силы в определенных положениях по сравнению с другими положениями, в которых моменты силы, создаваемые теми же мышцами, намного меньше.
Рисунок 16 Момент плеча мышечной силы двуглавой мышцы плеча уменьшается с r 1 до r 2 при разгибании в локтевом суставе. Центр вращения локтевого сустава отмечен белой точкой.Вставка двуглавой мышцы плеча отмечена черной точкой в положении 90 ° и синей точкой в положении 120 °. Стрелками отмечены силы, с помощью которых прикрепление двуглавой мышцы плеча действует на бугорки лучевой кости и на апоневроз двуглавой мышцы глубокой фасции на медиальном участке предплечья.
Силы и моменты силы в статическом равновесии
Чтобы тело оставалось в статическом равновесии, сумма внешних сил и сумма внешних силовых моментов, действующих на это тело, должны быть равны нулю.
Следовательно, должно выполняться следующее:
Оценка мышечных сил с помощью уравнений статического равновесия
Можем ли мы узнать силы, с помощью которых отдельные мышцы действуют на прикрепления, а затем и на кости, когда, например, мы поднимаем штангу? Представьте, что мы держим штангу весом 30 кг.Наш локтевой сустав согнут на 90 °, а предплечье параллельно полу. Если длина нашего предплечья 0,4 м, с какого момента штанга воздействует на наше предплечье по отношению к оси вращения (локтевому суставу)?
Штанга создаст момент силы, действующий на наше предплечье с величиной 118 Н · м по часовой стрелке с нашей точки зрения. Обозначим направление вращения по часовой стрелке как отрицательное. Чтобы удерживать штангу, сгибатели локтя должны создавать момент силы той же величины, что и у штанги, но с противоположным направлением — в нашем случае против часовой стрелки.Если сгибатели локтевого сустава зафиксированы на расстоянии примерно 0,03 м от оси локтевого сустава на предплечье, выполняется следующее:
Сгибатели локтя должны создавать силу почти 4000 Н, чтобы удерживать штангу весом 30 кг! Это означает, что наши мышцы должны создавать относительно большие силы для создания эффективных моментов в наших суставах, потому что их плечо момента часто довольно короткое. Хороший момент в том, что для создания эффективных моментов достаточно, чтобы наши мышцы лишь слегка сокращались (укорачивались).
Центр тяжести
Центр тяжести — это воображаемая точка тела, в которой, как можно предположить, сосредоточен общий вес тела. 60 . Понятие центра тяжести помогает нам представить движения спортсменов и их снаряжения. Он заменяет реальные движения человеческого тела, потому что человеческое тело имеет сложную форму и, кроме того, эта форма постоянно меняется во время движения. Такое упрощение сложного тела до одной точки помогает нам лучше понять реальные движения человеческого тела и других объектов.
Можно считать, что в центре тяжести сосредоточен общий вес тела, потому что это точка приложения гравитационной силы данного тела.
Центр тяжести — это точка, вокруг которой все гравитационные силы, действующие на все отдельные точки тела, идеально сбалансированы. Таким образом, центр тяжести является точкой равновесия. Что это означает? Наше тело, например, состоит из отдельных сегментов, таких как голова, плечо, предплечье, кисть, туловище, бедро, голень и ступня.Человеческое тело можно в упрощенном виде представить как модель из четырнадцати сегментов. Гравитационная сила действует на каждый из этих четырнадцати сегментов. Эти гравитационные силы, действующие на отдельные сегменты, создают моменты силы, векторная сумма которых по отношению к центру тяжести тела равна нулю. В центре тяжести наше тело находится в равновесии. Но ненулевые моменты гравитационной силы возникают по отношению ко всем другим точкам человеческого тела, поэтому человеческое тело (или любой объект) не находится в равновесии.
Центр тяжести — это точка, вокруг которой идеально сбалансирована сила тяжести элементов массы тела (например, сегментов человеческого тела).
Определение центра тяжести тела человека
Если нам известна сила тяжести, действующая на отдельные сегменты, и их положение относительно начала выбранной системы отсчета, мы можем вычислить центр тяжести как:
, где r T — вектор положения центра тяжести тела, r i — вектор положения сегмента i th , m i — масса сегмента i th , m — масса корпуса, а N — количество сегментов 61 .
Указанное выше соотношение можно переписать в координатную форму:
, где x T , y T , z T — координаты центра тяжести корпуса, а x i , y i , z i — координаты центров тяжести отдельных сегментов тела.
Как мы уже знаем, человеческое тело не является абсолютно твердым телом, и поэтому положение центра тяжести зависит от положения отдельных сегментов.Представим, что мы стоим в основной анатомической позиции. Сагиттальная плоскость делит тело на правую и левую части. Поскольку человеческое тело почти симметрично относительно сагиттальной плоскости, центр тяжести будет расположен очень близко к этой плоскости. Если мы поднимем правую руку, центр тяжести сместится вправо и вверх. Несмотря на то, что человеческое тело не симметрично в сагиттальном направлении, центр тяжести находится где-то во фронтальной плоскости, которая разделяет тело на переднюю и заднюю части.Эта плоскость проходит примерно через плечи и бедра, а затем чуть впереди лодыжек. Если вытянуть руки вперед, центр тяжести тоже сместится вперед. Оценить положение центра тяжести в вертикальной плоскости гораздо сложнее. В базовом анатомическом положении центр тяжести находится в области крестцовых позвонков с 3 rd по 4 крестца.
Рисунок 17 Центр тяжести человеческого тела при ходьбе (синий).
У женщин центр тяжести вертикально ниже, чем у мужчин, потому что их тела больше в области таза, но их плечи уже.Положение центра тяжести у женщин находится на относительной высоте 55% от общего роста, а у мужчин — 57%. У детей положение центра тяжести относительно выше, чем у взрослых, потому что у детей относительно большая голова и короче ноги, чем у взрослых.
Рисунок 18 Центр тяжести не обязательно должен находиться внутри человеческого тела. Центр тяжести гимнастки ниже отмечен синей точкой.
Понятие центра тяжести и его использование для повышения производительности
Теперь мы можем подумать о том, как движение сегментов нашего тела влияет на нашу моторику и производительность посредством изменения положения центра тяжести.Если мы подпрыгиваем в воздухе и теряем контакт с полом, на нас действует только сила гравитации, и мы превращаемся в снаряд. Под действием силы тяжести с момента взлета наш центр тяжести равномерно ускоряется вниз (9,81 м / с 2 ). В начале нашего прыжка наш центр тяжести имеет максимальную скорость и под действием силы тяжести постепенно замедляется, пока не остановится на максимальной высоте прыжка. Движение наших рук и ног не может влиять на движение центра тяжести, потому что мы не касаемся других тел и не можем создавать контактные силы.Результирующая сила, действующая на нас, по-прежнему остается всего лишь силой тяжести. На траекторию центра тяжести нашего тела не могут повлиять наши движущиеся руки и ноги, но движения отдельных рук и ног влияют друг на друга. Так, например, если мы сгибаем колени во время прыжка, высота рук уменьшается, так что центр тяжести все еще движется по той же траектории, определяемой с момента взлета 62 .
Баскетболисты, например, пытаясь заблокировать мяч, подпрыгивают, подняв только одну руку.Другая рука и обе ноги не согнуты и не двигаются относительно туловища. Волейболисты также прыгали выше всего, подняв только одну руку и вытянув ноги. Почему же тогда волейболисты, в отличие от баскетболистов, прыгают с поднятыми над головой руками? Ответ прост. Баскетболисты знают, куда направляется мяч, и пытаются заблокировать мяч только в том случае, если он направляется в корзину. Однако волейболисты не имеют возможности узнать, куда направится мяч после удара, и поэтому им лучше прыгать, подняв обе руки над головой, чтобы покрыть более широкую область над сеткой, хотя таким образом они не могут прыгать так высоко, как в противном случае они могли бы.
Когда мы смотрим на некоторые зрелищные прыжки баскетболистов, фигуристов, танцоров, гимнастов и т. Д., Мы можем увидеть, что они иногда кажутся подвешенными в воздухе. Это всего лишь эффект относительного движения отдельных сегментов тела друг к другу. Если, например, баскетболист, прыгающий под корзину, сгибает колени, траектория его центра тяжести остается параболической, но его руки и мяч дольше остаются на той же высоте. Этот факт создает иллюзию полета, потому что мяч в руках игрока не падает, хотя его центр тяжести падает.
Как положение центра тяжести влияет на устойчивость человеческого тела?
Стабильность тела — это мера его способности вернуться в положение равновесия после нарушения.
Во многих видах спорта и человеческой деятельности спортсмены или люди в целом не хотят терять равновесие из-за определенной позиции или положения. Они хотят быть в максимально стабильном положении. Борцы стараются сохранять максимально устойчивую позицию, чтобы их не опрокинули соперники.Биатлонистам, теннисистам, баскетболистам, лучникам — всем им нужна стабильная позиция, чтобы лучше всего проявлять свои способности. С другой стороны, в некоторых видах спорта успех определяется способностью очень быстро менять положение. Спринтерам на старте необходимо как можно скорее покинуть свои стартовые позиции. Горнолыжники, подающие теннисисты, пловцы на старте, футбольные вратари — все они должны иметь возможность менять свое положение как можно быстрее, когда наступает подходящий момент. Для этого создают не очень устойчивую подготовительную позицию.
Факторы, влияющие на стабильность
Устойчивости тел зависят от высоты центра тяжести над полом, размером зоны поддержки и массой тела.
Как мы можем объяснить с помощью механики, что именно эти три фактора влияют на стабильность? Мы знаем, что для сбалансированного тела верно то, что сумма всех моментов силы, действующих на это тело, должна быть равна нулю. Отсюда следует:
, где F — сила, пытающаяся вывести тело из равновесия, h — плечо момента, F G — сила тяжести, а b — его сила тяжести. момент руки.
Факторы в левой части уравнения минимизируют увеличение устойчивости, а факторы в правой части уравнения максимизируют увеличение устойчивости. Это означает, что чем выше гравитационная сила тела, тем выше момент силы в правой части уравнения и по этой причине также выше устойчивость тела. Удлинение плеча силы тяжести также увеличивает стабильность. Длина b — это горизонтальное расстояние медианы 63 от края (точки) поворота.Следовательно, устойчивость тела зависит от направления сил, которые пытаются его нарушить. Высота, на которой сила может воздействовать на тело, принимается как доля от общей высоты этого тела. Чем выше сила F, тем выше момент силы в правой части уравнения и, следовательно, шансы на сохранение устойчивости становятся меньше.
Тот факт, что высота центра тяжести влияет на устойчивость, лучше объясняется соотношением между работой и потенциальной энергией.Самая устойчивая стойка или положение человеческого тела — это положение с минимальной потенциальной энергией. Когда противник пытается помешать нам из сбалансированной позиции с минимальной потенциальной энергией, он / она должен выполнить больше работы, чем если бы мы были в позиции с большей потенциальной энергией. Наиболее устойчивыми считаются те положения тела человека, которые позволяют разместить центр тяжести ниже точки вращения. Гимнастка в висе на турнике — хороший тому пример. Если его потревожить из уравновешенного положения, он возвращается, не выполняя никакой работы.Это стабильное равновесие. С другой стороны, когда центр тяжести находится выше точки вращения, устойчивость ниже (рис. 19). Гимнастка, стоящая на руках, — хороший тому пример. Если его потревожить из сбалансированного положения, он, скорее всего, перевернется и не вернется в сбалансированное положение. Его потенциальная энергия была слишком велика, потому что его центр тяжести находился выше точки вращения. Это неустойчивое равновесие. В спорте тоже есть примеры безразличного равновесия. Это особая ситуация, когда ось вращения проходит через центр тяжести.Во время вращения потенциальная энергия тела не меняется. Если борец лежит на полу и расставляет руки и ноги так, что его центр тяжести находится почти на одном уровне с полом, можно говорить о безразличном равновесии.
Рисунок 19 Неустойчивое равновесие. Центр тяжести (синий) находится над точкой вращения.
Движение человека, центр тяжести и устойчивость
Человеческое тело не является твердым телом, и его форма может изменяться при движении рук, ног, головы и туловища.Поэтому люди могут контролировать свою стабильность, меняя положение тела.
Например, как мы начинаем шаг при ходьбе? Сначала мы наклоняемся вперед, пока наша середина не окажется перед нашей стопой. Потом теряем равновесие и начинаем падать. Падение прерывается другой ногой, и весь процесс повторяется снова. Поэтому мы можем описать ходьбу как серию контролируемых падений, приземлений и взлетов. Во многих видах спорта спортсмены стараются максимизировать свою стабильность в целом или только в одном конкретном направлении.В некоторых видах спорта мы стараемся в определенных ситуациях максимизировать подвижность (и минимизировать стабильность).
Если сила, которая пытается помешать нам, имеет определенное направление, мы должны использовать изменение основы нашей позиции, чтобы достичь большей стабильности. Например, при игре ударом справа теннисисты стараются расставить ноги далеко друг от друга в направлении летящего мяча и, таким образом, улучшить баланс между передней и задней сторонами (Рис. 20). Они стоят боком к мячу, и одна нога находится в направлении удара — их ступни не стоят рядом.Подобную технику используют боксеры и баскетболисты. Положение с одной ногой впереди очень удобно во многих спортивных ситуациях. Это позволяет уменьшить или увеличить импульс и силу удара в заданное время, но также дает большую стабильность.
Рисунок 20 Теннисисты на определенных этапах гребка используют специальное положение для максимальной устойчивости в направлении гребка.
В определенных ситуациях люди повышают устойчивость с помощью снаряжения.Люди с травмами ног часто используют костыли для повышения устойчивости. Лыжники повышают свою устойчивость спереди назад с помощью лыж. Чем длиннее лыжи, тем лучше устойчивость спереди и сзади. Вот почему у даунхиллеров лыжи длиннее, чем у слаломистов. Им нужна лучшая устойчивость спереди назад. Мы часто используем короткие лыжи для занятий фанкарвингом. Короткие лыжи помогают инструкторам определить, правильно ли занимают ученики базовое положение при спуске с горы. Если во время тренировки на коротких лыжах ученик начинает падать вперед или назад, это является признаком неправильного базового положения на лыжах с точки зрения устойчивости спереди назад.
Спринтеры на старте стараются занять позицию, которая позволила бы им двигаться вперед как можно быстрее. Центр тяжести спринтера находится перед носком передней ноги, вокруг которого будет вращаться тело во время первого шага. После сигнала спринтер поднимает руки и сразу начинает падать вперед. Его / ее останавливает сила его / ее ног. Пловцы так же начинают с позиции минимальной устойчивости.
52 Свободное тело имеет шесть степеней свободы — его движение не ограничено в пространстве.Zpět
53 Векторная линия проходит через начальную и конечную точки вектора силы. Zpět
54 Бобслей не является свободным телом, но, тем не менее, действие центральной силы вызывает только линейное движение. Zpět
55 Эксцентричность в данном случае означает тип силы, а не тип мышечного сокращения. Zpět
56 Векторная линия проходит через начальную и конечную точки вектора силы. Zpět
57 Точка, до которой определяется момент силы.Он может располагаться на оси вращения, вдали от нее или даже от самого тела. Zpět
58 На английском языке момент силы также называется крутящий момент и обозначается с большой буквы T . Zpět
59 Также называется радиус-вектором. Zpět
60 Это точка приложения результирующей гравитационной силы, состоящей из всех гравитационных сил, действующих на все элементы массы тела. Zpět
61 Если выбранными сегментами являются голова, туловище, левое и правое плечо, левое и правое предплечье, левая и правая рука, левое и правое бедро, левая и правая голень, а также левая и правая ступня, тогда N = 14.Zpět
62 Если сопротивление воздуха не принимается во внимание Zpět
63 Медиана — это линия, на которой лежит вектор гравитационной силы. Следовательно, он проходит через центр тяжести и находится вертикально. Zpět
,| пиропатрон | ссылка | DOI | |
|---|---|---|---|
| 1940Smy / Lew: 1219 | С. П. Смит, Г. Л. Льюис, А. Дж. Гроссман, Ф. Б. Дженнингс III «Дипольные моменты и структуры некоторых соединений серы, селена и фосфора» J. Am. Химреагент Soc. 1940, 62, 5, 1219-1223 | 10.1021 / ja01862a067 | |
| 1954Hro / Mye: 262 | HJ Hrotowski, RJ Myers «Микроволновые спектры, структура и дипольный момент стабильного пентаборана» J. Chem. Phys. 22, 262, 1954 | 10,1063 / 1,1740048 | |
| 1954Кис: 86 | П. Кислюк «Дипольные моменты, ядерное квадрупольное взаимодействие и связывающие орбитали в группе V — тригалогениды» Журнал химической физики 22 (1) стр. 86 1954 | 10.1063 / 1.1739863 | |
| 1955 Кра / Дай: 184 | J Kraitchman, BP Dailey «Микроволновый спектр этилфторида» J. Chem. Phys. 23, 184, 1955 | 10,1063 / 1,1740525 | |
| 1957Маг: 223 | Д.В. Магнусон «Микроволновый спектр и молекулярная структура трифторида брома» J. Chem. Phys. 27, 223, 1957 | 10,1063 / 1,1743675 | |
| 1959Cur: 1529 | RF Curl «Микроволновый спектр, барьер для внутреннего вращения и структура метилформиата» J.Химреагент Phys. 30 (6) 1529, 1959 | 10,1063 / 1,1730232 | |
| 1961Lau: 291 | VW Laurie «Микроволновый спектр цис-дифторэтилена. Структуры и дипольный момент фторэтиленов» J. Chem. Phys. 34, 291, 1961 | 10,1063 / 1,1731582 | |
| 1961 Лори: 1516 | VW Laurie «СВЧ-СПЕКТР ДИПОЛЬНОГО МОМЕНТА ИЗОБУТИЛЕНА, ВНУТРЕННИЙ БАРЬЕР, КОНФОРМАЦИЯ И СТРУКТУРА Равновесия» Дж.Химреагент Phys. 34 (5) 1516, 1961 | 10,1063 / 1,1701038 | |
| 1962 Его: 283 | E Hirota «Вращательная изомеризация и микроволновая спектроскопия. I. Микроволновый спектр нормального фторида пропила» J. Chem. Phys. 37, 283 (1962) | 10,1063 / 1,1701318 | |
| 1962 Лев: 276 | И. Н. Левин «Микроволновый спектр формальдоксима» Ж.Mol. Spect. 8, 276-284, 1962 | 10.1016 / 0022-2852 (62) | |
| 1962 г. | WM Tolles, WD Gwinn, «Структура и дипольный момент для SF4» J. Chem. Phys. 36 (5), 1119, 1962 год | 10,1063 / 1,1732702 | |
| 1963 Номер 456 | DR Lide «Микроволновый спектр и структура дифторамина» J. Chem. Phys. 38, 456, 1963 | 10.1063 / 1,1733680 | |
| 1963 Номер: 2382 | R Nelson «Микроволновый спектр, молекулярная структура и дипольный момент диметилфосфина» J. Chem. Phys. 39 (9) 2382, 1963 | 10,1063 / 1,1701456 | |
| 1964 Sas / Cur: 77 | KVL Sastry, RF Curl «СВЧ-СПЕКТР N-МЕТИЛМЕТИЛЕНИМИНА» J. Chem. Phys. 41 (1) 77, 1964 год | 10.1063 / 1.1725653 | |
| 1965 Хун / Леа: 1931 | RH Hunt, RA Leacock, CW Peters, KT Hecht «Внутреннее вращение в перекиси водорода: дальний инфракрасный спектр и определение тормозящего потенциала» J. Chem. Phys. 42, 1931, 1965 | 10,1063 / 1,1696228 | |
| 1966Bak / Chr: 883 | B Bak, JJ Christiansen, K Kuntsmann, L. Nygaard, J Rastrup-Andersen «Микроволновый спектр, молекулярная структура, барьер для внутреннего вращения и дипольный момент метилкетена» J.Химреагент Phys. 45 (1), 883, 1966 | 10,1063 / 1,1727700 | |
| 1966 Пчелка: 414 | JF Beecher «Микроволновый спектр, дипольный момент, структура и внутреннее вращение диметилселенида» J. Molecular Spectroscopy 4: 414-424 (1966) | 10.1016 / 0022-2852 (66) | |
| 1966 Хар / Кокс: 5049 | Хармой, М; Кокс, К. «Микроволновый спектр, дипольный момент и структура бицикло [1.1.0] бутан «. Журнал Американского химического общества. 88, 5049-5050 (1966) | 10.1021 / ja00973a066 | |
| 1967Coo / Kir: 4521 | RL Cook, WH Kirchhoff «Дальнейшие исследования микроволнового спектра NSF: оценка молекулярного силового поля, констант центробежных искажений и дипольного момента» J. Chem. Phys. 47 (11) 4521, 1967 | 10,1063 / 1,1701662 | |
| 1967 Кир: 1312 | WH Кирхгоф «Микроволновый спектр и дипольный момент пиразола» J.Am. Химреагент Soc. 89: 6 1312 (1967) | 10.1021 / ja00982a006 | |
| 1968 Bro / Bur: 415 | Р. Д. Браун, Ф. Р. Бёрден, П. Д. Годфри «Микроволновый спектр селенофена» J. Mol. Spect. 25, 415-421 (1968) | 10,1016 / с 0022-2852 (68) 80012-8 | |
| 1968 Для / Bea: 4671 | Р. Г. Форд, Р. А. Боде «Микроволновые спектры метилциклопропанов.II. Метилциклопропан | 10,1063 / 1,1668043 | |
| 1968 Лег / Мил: 1736 | AC Legon, DJ Millen «Микроволновый спектр, структура и дипольный момент нитрилфторида» J. Chem. Soc. А 1968, 1736, | 10,1039 / J19680001736 | |
| 1968Poc / Bal: 1072 | JM Pochan, JE Baldwin, WH Flygare «Микроволновый спектр, структура и дипольный момент в циклопропаноне» JACS 90: 4 1072, 1968 | 10.1021 / ja01006a049 | |
| 1968Tho / Dal: 2815 | Р. Томсон, Ф. У. Долби «Экспериментальное определение дипольных моментов состояния X (2 сигма +) и B (2 сигма +) молекулы CN» Canadian Journal of Physics 46, 2815 (1968) | 10.1139 / p68-652 | |
| 1969 Мир / Кор: 4118 | AM Mirri, C Corbelli, P Forti «Эффект Штарка и электродипольный момент h3Se» J.Химреагент Phys. 50, 4118, 1969 | 10,1063 / 1,1671680 | |
| 1969Rog / Schneider Electric: 397 | Роговский, Швендеман, Микроволновые спектры, барьеры для внутреннего вращения, константы квадрупольной связи и дипольные моменты цис- и транс-ацетальдоксима | 10,1063 / 1,1670810 | |
| 1969 То / Даль: 1155 | Р. Томсон, Ф. У. Долби «Экспериментальное определение дипольных моментов состояний X (1Σ) и A (1Π) молекулы BH» Canadian Journal of Physics, 1969, 47 (11): 1155-1158 | 10.1139 / стр69-144 | |
| 1970Kon / Hir: 97 | S Kondo, E Hirota «Микроволновый спектр и внутреннее вращение изопропилового спирта» J. Mol. Спекуляция 34, 97-107 (1970) | 10.1016 / 0022-2852 (70) | |
| 1971 Но / Coh: 4123 | SS Butcher, RA Cohen, TC Rounds «Микроволновый спектр 1,2-дифторэтана» J. Chem. Phys. 54, 1971, 4123 | 10.1063 / 1,1675477 | |
| 1971Byf / Автомобиль: 271 | CR Byfleet, A Carrington, DK Russell, «Электрические дипольные моменты двухатомных молекул с открытой оболочкой» Molecular Physics 1971, 20 (2), 271-277 | 10.1080 / 00268977100100251 | |
| (1971) Высшее / женское: 358 | C. Hirose, RF Curl Jr, «Микроволновый спектр, конформация и дипольный момент дивинилового эфира» J. Molecular Spectroscopy 38, 358-366 (1971) | 10.1016 / 0022-2852 (71) | -6|
| 1971Кри / Саэ: 4553 | LC Krisher, E. Saegebarth «МИКРОВОЛНОВЫЙ СПЕКТР УКСУСНОЙ КИСЛОТЫ, Ch4COOH И CD3COOH» J. Chem. Phys. 54 (11) 4553, 1971 | 10,1063 / 1,1674721 | |
| 1971 Лов / Джон: 41 | FJ Lovas, DR Johnson «Микроволновый спектр BF» J. Chem. Phys. 55 (1), 41, 1971 | 10.1063 / 1.1675537 | |
| 1971 Ола / Вир: 18 | П. Олави, И. Виртанен, П. Руостесуо «Дипольные моменты N-фенилзамещенных сульфонамидов» Suomen Kemistilehti B 44 (1) 18-22, 1971 | ||
| 1971Vau: 21 | WE Vaughan, Сборник литературы по диэлектрикам, т.33, 1969, 21 | ||
| 1972Fre / Kle: 1467 | С.М. Фройнд, В. Клемперер, Р.П. Мариэлла, Э. Хербст «РАДИОЧАСТОТНЫЙ СПЕКТР X 2II СОСТОЯНИЯ ЛИ-7-О-16» Дж.Химреагент Phys. 56 (4) 1467, 1972 | 10,1063 / 1,1677391 | |
| 1972Гра / Даг: 710 | J Graff, PG Dagdigian, L. Wharton «Электрический резонансный спектр NaLi» J. Chem. Phys. 57 (2), 710-714, 1972 | 10,1063 / 1,1678303 | |
| 1972Мур / Виль: 575 | Дж.Т. Мюррей, К. Уильямс, Т.Л. Уэтерли, «Микроволновый спектр и молекулярные константы SCl2» Bull.Am. Phys. Soc. 17, 575, 1972 г. | ||
| 1973 г., Ама / Хир: 417 | Т. Амано, Э. Хирота «Микроволновый спектр радикала SF» J. Mol. Спекуляция 45, 417-419 (1973) | 10.1016 / 0022-2852 (73) | |
| 1973 Дур / Ли: 2491 | JR Durig, YS Li, LA Carreira, JD Odom «Микроволновый спектр, структура, дипольный момент и барьер для внутреннего вращения фофин-борана» J.Am. Химреагент Soc. 95, 1973, 2491 | 10.1021 / ja00789a013 | |
| 1973То: 70 | CH Thomas «Микроволновый спектр, барьер для внутреннего вращения, структура и дипольный момент селенола метана» J. Chem. Phys. 59 (1), 70, 1973 | 10,1063 / 1,1679859 | |
| 1974 Хел / Хель (II / 6) | Hellwege, KH и AM Hellwege (ред.). Ландольт-Борнштейн: Группа II: Том 6 Молекулярные константы по данным микроволновой спектроскопии, спектроскопии молекулярного пучка и электронного спинового резонанса Springer-Verlag.Берлин. 1974. | 10.1007 / b19951 | |
| 1974Кью: 509 | R Kewley «Микроволновый спектр метоксиацетонитрила» Кан. J. Chem. 52, 509, 1974 | 10.1139 / v74-080 | |
| 1974 Отпуск / Загар: 241 | Р. Сугисаки, Т. Танака, Э. Хирота «Микроволновый спектр, структура, дипольный момент, константа квадрупольного взаимодействия и внутреннее движение тиоформамида» Дж.Mol. Spect. 49, 241-250 (1974) | 10.1016 / 0022-2852 (74) | -2|
| 1975Бит / Победа: 141 | J Bendtsen, M Winnewisser «Спектроскопические константы основного состояния и дипольный момент гидразойной кислоты, h24N3» Chem. Phys. Lett. 33 (1) 141, 1975 | 10.1016 / 0009-2614 (75) 85471-6 | |
| 1975 Бро / Бог: 445 | Р. Д. Браун, П. Д. Годфри, Дж. Стори «Микроволновый спектр мочевины» Дж.Molec. Spect. 58, 445-450 (1975) | 10.1016 / 0022-2852 (75) | -6 |
| 1975 Комплект / Мал: 179 | RW Kitchin, TB Malloy, RL Cook «Молекулярная конформация и дипольный момент тиана из микроволнового спектра» J. Mol. Спекуляция 57, 179–188, 1975 | 10.1016 / 0022-2852 (75) | -3 |
| 1975Sch / Qua: 3864 | Р.Э. Шмидт, CR Quade «Микроволновый спектр этилмеркаптана» J.Химреагент Phys. 62 (10), 3864-3874, 1975 | 10,1063 / 1,430307 | |
| 1976 Вел / Гер: 117 | Р. Веллингтон Дэвис, М.К.Л. Джерри «Микроволновый спектр, структура, константы хлор-ядерного квадрупольного взаимодействия, дипольный момент и константы центробежных искажений дихлорсилана» J. Mol. Спектроскопия. 60, 117-129, 1976 | 10.1016 / 0022-2852 (76) | -X |
| 1977 Alm / Cha: 483 | V Almond, SW Charles, JN MacDonald, NL Owen «Ethenethiol: the Infrared and Microwave Spectroscopic Study» J.C.S. Chem. Comm. 1997 (14) 483-484 | 10.1039 / c39770000483 | |
| 1977 Дос / сут: 1444 | K-F Dossel, DH Sutter «Вращательный спектр высокого разрешения силилбромида Sih4Br» Z. Naturforsch. 32а, 1444–1449 (1977) | 10.1515 / зна-1977-1217 | |
| 1977 Джон / Она: 866 | Х. Джонс, Дж. Шеридан, О. Л. Штифватер «Микроволновой спектр бромацетилена; rs-структура, дипольный момент, константы квадрупольного взаимодействия и состояния возбужденной вибрации» Zeitschrift für Naturforschung A.Том 32, выпуск 8, страницы 866–875 | 10.1515 / зна-1977-0811 | |
| 1977 Мех / Гри: 244 | SC Mehrotra, LL Griffin, CO Britt, JE Boggs «Микроволновый спектр, структура, дипольный момент и константы квадрупольного взаимодействия изопропиламина» J. Mol. Спекуляция 64, 244–251 (1977) | 10.1016 / 0022-2852 (77) | -8 |
| 1977 Сью / Джон: 239 | RD Suenram, DR Johnson «Микроволновый спектр нитрата хлора (ClNO3)» Journal of Molecular Spectroscopy 65, 239-248 (1977) | 10.1016 / 0022-2852 (77) | -6|
| 1978 Св. / Лов: 5117 | RD Suenram, FJ Lovas «Диоксиран. Его синтез, микроволновый спектр, структура и дипольный момент» J. Am. Химреагент Soc.100, 5117, 1978 | 10.1021 / ja00484a034 | |
| 1979Даг: 2328 | PJ Dagdigian «Дипольный момент основного состояния NaH» J. Chem. Phys. 71 (5) 2328, 1979 | 10.1063 / 1,438574 | |
| 1979Лар: 175 | Н.В. Ларсен «Спектры микроканалищ шести моно-13C замещенных фенолов и некоторых монодейтерированных разновидностей фенола. Полная структура замещения и абсолютный дипольный момент» J. Mol Struct. 51 (1979) 175-190 | 10.1016 / 0022-2860 (79) 80292-6 | |
| 1980Cox / Dux: 339 | AP Cox, G Duxbury, JA Hardy, Y Kawashima «Микроволновые спектры CF3Br и CF3I.Структуры и дипольные моменты «J.C.S Faraday II, 1980, 76, 339-350 | 10,1039 / f29807600339 | |
| 1981Dur / Li: 1564 | Во время, Ли, Во время, Спектры и структура малых кольцевых соединений. XLII. Микроволновый спектр 2,5-дигидротифена, J. Chem., Phys., Vol. 74, # 3, стр. 1564-1567 | 10,1063 / 1.441297 | |
| 1981Kro / Nix: 367 | HW Kroto, JF Nixon, K Ohno «СВЧ-СПЕКТР, СТРУКТУРА И ДИПОЛЬ-МОМЕНТ НЕСТАБИЛЬНОЙ МОЛЕКУЛЫ ФОСФЭТЕНА, Ch3 = PH» J.Mol. Spect. 90 (2) 367-373, 1981 | 10.1016 / 0022-2852 (81) | -X |
| 1981 Kuc / Sue: 2561 | Kuczkowski, Suenram, Lovas, Микроволновые спектры, структура и дипольный момент серной кислоты, J. Am. Химреагент Soc., Vol. 103, стр. 2561-2566 | 10.1021 / ja00400a013 | |
| 1981 Par / Buc: 465 | JE Parkin, PJ Buckley, CC Costain «Микроволновой спектр пиперидина: экваториальное и осевое основные состояния» J.Mol. Спекуляция 89, 465-483 (1981) | 10.1016 / 0022-2852 (81) | -0 |
| 1981 Сим / Bur: 533 | Н.П. Симмонс, А.Б. Бург, Р.А. Боде «Микроволновый спектр, Стурктру и дипольный момент тетраборана (10), B4h20» Неорг. Химреагент 1981, 20, 533-536 | 10.1021 / ic50216a044 | |
| 1982Chr / Gri: 1378 | Д. Кристен, Дж. Х. Гриффитс, Дж. Шеридан «Микроволновый спектр имидазола; полная структура и распределение электронов от ядерных тензоров квардупольного взаимодействия и ориентация дипольного момента» Z.Naturforsch. 37а, 1378-1385 (1982) | 10.1515 / зна-1981-1220 | |
| 1983 Лов / Сью: 316 | FL Lovas, RD Suenram, WJ Stevens «Продукты реакции разряда N2 и h3S: микроволновый спектр Nh3SH» J. Mol. Spect. 100, 316-331 (1983) | 10.1016 / 0022-2852 (83) | -9|
| 1983 Тан / Тан: 425 | К. Танака, Т. Танака «Лазерная штарк-спектроскопия на CO2 и N2O полосы nu1 радикала ClO2» Дж.Mol. Spect. 98, 425-452, 1983 | 10.1016 / 0022-2852 (83) | |
| 1983 То / Сью: 167 | LR Thorne, RD Suenram, FJ Lovas «Микроволновый спектр, торсионный барьер и структура Bh4Nh4» J. Chem. Phys. 1983, 78, 167-171 | 10,1063 / 1.444528 | |
| 1984 Гра / Губ | Грей К.Г., Габбинс К.Э. Теория молекулярных жидкостей.Том 1: Основы «Clarendon Press, Oxford 1984 | ||
| 1984 Род / Брат: 447 | М. Родлер, Р. Д. Браун, П. Д. Годфри, Л. М. Тэк «Генерация, микроволновый спектр и дипольный момент кетенимина» Chem. Phys. Lett. 110 (5) 447-451, 1984 | 10.1016 / 0009-2614 (84) 87068-2 | |
| 1984 Ям / Суг: 2315 | Яманучи, Суги, Такео, Мацумура, Кучицу, Молекулярная структура и конформация 1-хлорпропана по данным газовой дифракции и микроволновой спектроскопии, J.Phys. Chem., Vol. 88, стр. 2315-2320 | 10.1021 / j150655a026 | |
| 1986 Св. / Лов: 406 | RD Suenram, FJ Lovas «Микроволновый спектр и молекулярная конформация пероксинитриновой кислоты (HOONO2)» Journal of Molecular Spectroscopy 116, 406-421 (1986) | 10.1016 / 0022-2852 (86) | -0 |
| 1986Тыб / га: 353 | M Tyblewski, T-K Ha, A. Bauder «Микроволновый спектр, электрический дипольный момент, барьер внутреннего вращения и молекулярная структура метилгидродисульфида» J.Mol. Spect. 115, 353-365 (1986) | 10.1016 / 0022-2852 (86) | |
| 1987Ч / мин: 7020 | Д. Кристен, Р. Минквиц, Р. Насс «Микроволновый спектр, инверсия и молекулярная структура монофторамина, FNh3» J. Am. Химреагент Soc. 1987, 109, 7020-7024 | 10.1021 / ja00257a019 | |
| 1987 Эбе / Хан: 1948 | WL Ebenstein, C Hanning, SL Shostak, JS Muenter «Радиочастотные спектры хлорацетилена в v = 0 и v = 1 валентного колебания C-H» J.Химреагент Phys. 87, 1948 (1987) | 10,1063 / 1,453723 | |
| 1988 Кан / Ям: 89 | H Kanata, S Yamamoto, S Saito «Дипольный момент радикала PO, определенный с помощью микроволновой спектроскопии» J. Mol. Spect. 131, 89-95 (1988) | 10.1016 / 0022-2852 (88) | |
| 1989Бир / Выигрыш: 402 | М. Бирк, М. Винньюиссер «Вращательно-крутильный спектр карбодиимида: проба для необычной динамики» Дж.Mol. Spect. 135, 402-445 (1989) | 10.1016 / 0022-2852 (89) | -7|
| 1989 Ког / Так: 467 | Y Koga, H Takeo, S. Kondo, M Sugie, C. Matsumura, GA McRae, EA Cohen «Спектры вращения, молекулярная структура, дипольный момент и сверхтонкие константы HOBr и DOBr» J. Mol. Спекуляция 138, 467-481 (1989) | 10.1016 / 0022-2852 (89) | |
| 1989 Вог / Бау: 62 | B Vogelsanger, A Bauder «Чистый вращательный спектр и дипольный момент квадрициклана, определенные с помощью микроволновой спектроскопии с преобразованием Фурье» J.Mol. Spect. 136, 62-67 (1989) | 10.1016 / 0022-2852 (89) | -1|
| 1991 Дур / Фен: 1827 | JR Durig, FS Feng, A Wang, HV Phan «Конформационная стабильность, барьеры для внутреннего вращения, расчеты ab initio и определение колебаний 2-бутанона» Can. J. of Chem. 69 (11) 1845-1856, 1991 | 10.1139 / v91-268 | |
| 1991 Мэй / Мор: 3860 | CW Meyer, G Morrison «Дипольные моменты семи частично галогенированных этановых хладагентов» J.Phys. Химреагент 1991, 95, 3860-3866 | 10.1021 / j100162a077 | |
| 1992LBII / 19c | Численные данные Ландольта-Борнштейна и функциональные взаимосвязи в науке и технике, новая серия, II / 19c (1992) Spreinger-Verlag, Heidelberg | ||
| 1994Xu / Joh: 147 | Y Xu, JWC Johns, ARW McKellar «Инфракрасные спектры высокого разрешения формилфторида, HFCO» Дж.Mol. Spect. 168, 147–157 (1994) | 10.1006 / JMSP.1994.1267 | |
| 1995 Лов / Кав: 201 | FJ Lovas, Y Kawashima, JU Grabow, RD Suenram, GT Fraser, E Hirota «МИКРОВОЛНОВЫЕ СПЕКТРЫ, ГИПЕРТОНКАЯ СТРУКТУРА И ЭЛЕКТРИЧЕСКИЕ ДИПОЛЬНЫЕ МОМЕНТЫ ДЛЯ CONFORMERS-I И CONFORMER-II ГЛИЦИНА» Astrophysical Journal «Astrophysical Journal» (2) L20 455 -L204, 1995 | ||
| 1996 Модель / Номер: 1645 | G Modugno, P De Natale, M Bellini, M Inguscio, G Di Lonardo, L Fusina, J Vander Auwera «Точное измерение молекулярных дипольных моментов с помощью настраиваемого дальнего инфракрасного спектрометра Штарка: применение к HOCl» Дж.Оптик Soc. Am. B Том 13 № 8 1996 p 1645-1649 | 10.1364 / JOSAB.13.001645 | |
| 1997Bau / Bei: 7558 | А. Баудер, А. Бейл, Д. Лакхаус, Ф. Мюллер, М. Кряк «Комбинированное исследование бромхлорфторметана в инфракрасном и микроволновом диапазоне с высоким разрешением» J. Chem. Phys. 106 (18) 7558, 1997 | 10.1063 / 1.473759 | |
| 1998 Wei / Hai: 3134 | М.А. Вейбель, Т.Д. Хайн, Т.Дж. Кертисс «Гексапольные сверхзвуковые пучки реактивных радикалов: CF3, SiF3, SH, CH и C2H» J.Химреагент Phys. 108 (8) 3134, 1998 год | 10,1063 / 1,475711 | |
| 2000Fra / Xu: 6209 | GT Fraser, LH Xu, RD Suenram, CL Lugez «Вращательные спектры четырех из пяти конформеров 1-пентена» J. Chem. Phys. 112 (14) 6209-6217, 2000 | 10,1063 / 1,481220 | |
| 2001Plu / Sue: 3057 | DF Plusquellic, RD Suenram, B Mate, JO Jensen, AC Samuels «Конформационные структуры и дипольные моменты этилсульфида в газовой фазе» J.Химреагент Phys. 115 (7), 3057, 2001 | 10,1063 / 1,1385527 | |
| 2002 Дур / Джин: 1 | JR Durig, Y Jin, HV Phan, J Liu, DT Durig «Спектры в дальней инфракрасной области, конформационная стабильность, барьеры для внутреннего вращения, расчеты Ab Initio, структурные параметры r0 и вибрационное распределение этилметилового эфира» Структурная химия, 13 ( 1) 2002, 1 | 10.1023 / А: 1013410428690 | |
| 2005 Обозначение / Пс: 1708 | O Desyatnyk, L Pszczolkowski, S Thorwirth, TM Krygowski, Z Kisiel «Вращательные спектры, электрические дипольные моменты и молекулярные структуры анизола и бензальдегида» Phys.Химреагент Химреагент Phys. 7 (8) 1708-1715, 2005 | 10.1039 / b501041a | |
| 2007Caz / Puz: 112 | G Cazzoli, C. Puzzarini, A. Baldacci, A. Baldan «Определение молекулярного дипольного момента бромфторметана: микроволновые спектры Штарка и расчеты ab initio» J. Mol. Спекуляция 241 (2007) 112-115 | 10.1016 / j.jms.2006.11.004 | |
| 2008Woh / Schweiz: 119 | К. Вольфарт, М. Шнелл, Дж.У. Грабов, Дж. Куппер «Точный дипольный момент и квадрупольные константы взаимодействия бензонитрила» Дж.Mol. Спекуляция 247 (2008) 119-121 | 10.1016 / j.jms.2007.10.006 | |
| 2011 Кан / Ее: 173 | P Kania, M Hermanns, S. Brunken, HSP Muller, TF Giesen «Миллиметровая спектроскопия диоксида титана, TiO2» J. Mol. Спекуляция 268 (2011) 173-176 | 10.1016 / j.jms.2011.04.013 | |
| 2011Le / Ste: 9370 | A Le, TC Steimle «Оптическая штарковская спектроскопия полосы D 1PI — X 1Sg + (0,0) моногидрида скандия» J.Phys. Химреагент А 2011, 115, 9370-9376 | 10.1021 / jp110838j | |
| 2012 г., стандарт: 114309 | TC Steimle, F Wang, X Zhuang, Z Wang «Оптическая штарковская спектроскопия полосы 2 (60) A 1A» — X 1A ‘хлорметилена, HCCl «J. Chem. Phys. 136, 114309 (2012) | 10,1063 / 1,3694245 | |
| NISTdiatomic | База данных диатомовых спектров NIST (www.Physics.nist.gov/PhysRefData/MolSpec/Diatomic/index.html) | 10,18434 / T4T59X | |
| NIST углеводород | База данных спектров углеводородов NIST (http://www.physics.nist.gov/PhysRefData/MolSpec/Hydro/index.html) | 10.18434 / T4PC70 | |
| NIST Триатомный | База данных трехатомных спектров NIST (http: //www.physics.nist.gov / PhysRefData / MolSpec / Triatomic / index.html) | 10.18434 / T4DW2S | |
| NSRDS-NBS10 | Р. Д. Нельсон-младший, Д. Р. Лид, А. А. Мариотт «Избранные значения электрических дипольных моментов для молекул в газовой фазе» NSRDS-NBS10, 1967 | 10.6028 / NBS.NSRDS.10 | |
| веб-книга | NIST Chemistry Webbook (http: // webbook.nist.gov/chemistry) | 10.18434 / T4D303 |

