формулы, теорема Штейнера, пример решения задачи — OneKu

Содержание статьи:

• Общие сведения о физической величине
• Величина I для тел разной формы
• Теорема Штейнера и формула
• Уравнение моментов
• Пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫m(r² * dm) = ρ * ∫V(r² * dV).

Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Теорема Штейнера и формула

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = IO + M * h3.

Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r0 + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

Зачем придумали момент инерции, если есть масса

Скачать 315,44 Kb. Дата 05.04.2023 Размер 315,44 Kb. #210071

Связанные:
ФИЗИКА ЛАБА М2 (1)

Навигация по данной странице:

• 1.Дайте определение момента инерции материальной точки
• 2.Дайте определение момента инерции твердого тела
• 3. Что такое момент силы
• 4.Сформулируйте основной закон динамики вращательного движения
• 5. Сформулируйте теорему Штейнера
• 6. Запишите формулы для моментов инерции тел правильной геометрической формы 7. Дайте определение момента импульса
• 8.Сформулируйте закон сохранения момента импульса

Зачем придумали момент инерции, если есть масса(требует знать ответ) Масса и момент инерции являются двумя физическими величинами, которые описывают движение тела в пространстве. Масса описывает, как тело реагирует на силы, приложенные к нему, и позволяет определить его ускорение. Момент инерции, с другой стороны, описывает, как тело реагирует на изменение своей скорости вращения вокруг оси. 2 2.Дайте определение момента инерции твердого тела Момент инерции твердого тела — это физическая величина, которая определяет количество инертной массы тела, расположенной на определенном расстоянии от оси вращения. 3. Что такое момент силы? Момент силы — это физическая величина, которая описывает силу, действующую на тело и приводящую к его вращению. +, когда сила действует против часовой стрелки, -, если сила действует по часовой стрелке (в этом случае вектор радиуса направлен к точке приложения силы). 4.Сформулируйте основной закон динамики вращательного движения Основной закон динамики вращательного движения (второй закон Ньютона для вращения) гласит: момент силы, действующей на тело, равен произведению массы тела на ускорение его центра масс, умноженному на расстояние от оси вращения до линии действия силы: M = Iα 5. Сформулируйте теорему Штейнера Теорема Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельно данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния R между осями: I=Ic+m*R² 6. Запишите формулы для моментов инерции тел правильной геометрической формы 7. Дайте определение момента импульса Момент импульса — это физическая величина, которая описывает количество движения с учетом распределения массы относительно оси вращения. L = mvr=R*P 8.Сформулируйте закон сохранения момента импульса Закон сохранения момента импульса гласит, что при любых взаимодействиях тел, сумма моментов импульса этих тел остается постоянной, если на эти тела не действуют внешние моменты сил. Скачать 315,44 Kb. Поделитесь с Вашими друзьями:

---

База данных защищена авторским правом ©psihdocs.ru 2023
обратиться к администрации

Как рассчитать момент инерции различных форм и твердых тел

В физике при расчете момента инерции объекта необходимо учитывать не только массу объекта, но и распределение массы. Например, если два диска имеют одинаковую массу, но у одного вся масса приходится на ободок, а другой твердый, то диски будут иметь разные моменты инерции.

Вычисление моментов инерции довольно просто, если вам нужно исследовать только орбитальное движение небольших точечных объектов, где вся масса сосредоточена в одной конкретной точке на заданном радиусе р . Например, для мяча для гольфа, который вы вращаете на веревке, момент инерции зависит от радиуса круга, по которому вращается мяч:

I = мр ²

Здесь r — радиус окружности от центра вращения до точки, в которой сосредоточена вся масса мяча для гольфа.

Однако, когда вы входите в мир без мячей для гольфа, считывание чисел может стать немного затруднительным, потому что вы можете не знать, какой радиус использовать. Что делать, если вы крутите удочку? Вся масса стержня не сосредоточена на одном радиусе. Когда у вас есть протяженный объект, такой как стержень, каждая частица массы находится на другом радиусе.

У вас нет простого способа справиться с этим, поэтому вы должны суммировать вклад каждой частицы массы на каждом другом радиусе следующим образом:

Вы можете использовать эту концепцию суммирования моментов инерции всех элементов, чтобы получить сумму, чтобы вычислить момент инерции любого распределения массы. Вот пример использования двух точечных масс, который немного сложнее, чем одна точечная масса. Скажем, у вас есть два мяча для гольфа, и вы хотите узнать, каков их суммарный момент инерции. Если у вас есть мяч для гольфа с радиусом

r ₁ и еще один с радиусом r ₂ , общий момент инерции равен

Так как же найти момент инерции, скажем, диска, вращающегося вокруг оси, проходящей через его центр? Вы должны разбить диск на крошечные шарики и сложить их все вместе. Вы завершаете это, используя исчисление процесса интегрирования.

Формы, соответствующие моментам инерции в таблице.

Надежные физики уже выполнили эту задачу для многих стандартных форм; В следующей таблице приведен список объектов, с которыми вы, вероятно, столкнетесь, и их моменты инерции.

На рисунке изображены формы, которым соответствуют эти моменты инерции.

Эта статья из книги:

• Физика I для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе

Physics For Dummies и Physics Essentials For Dummies. Доктор Хольцнер получил докторскую степень в Корнелле.

Эту статью можно найти в категории:

• Физика,

10.3 Динамика вращательного движения: инерция вращения

Цели обучения Вращательная инерция и момент инерции

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Понимать взаимосвязь между силой, массой и ускорением
• Изучение поворотного эффекта силы
• Изучить аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

• 4. D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил действуют на вращающаяся система жестко связанных тел изменяет угловую скорость и момент импульса системы. (СП ​​1.2, 1.4)
• 4.D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные рассматриваются как вращающиеся по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП ​​3.2, 4.1, 5.1, 5.3)
• 5.E.2.1 Учащийся может описать или рассчитать угловой момент и инерцию вращения системы в терминах местоположения и скорости объектов, составляющих систему. Ожидается, что учащиеся будут делать качественные рассуждения с составными объектами. Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (П. 2.2)

Если вам когда-либо приходилось крутить велосипедное колесо или толкать карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 10.10. На самом деле, ваша интуиция надежно предсказывает многие из задействованных факторов. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.

Рисунок 10.10 Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.

Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу FF размером 12{F} {} к точке массой мм размером 12{m} {}, которая находится на расстояние rr size 12{r} {} от точки вращения, как показано на рисунке 10.11. Поскольку сила перпендикулярна rr размером 12{r} {}, ускорение a=Fma=Fm размера 12{a= {{F} над {m} } } {} получается в направлении FF размера 12{F } {}. Мы можем изменить это уравнение так, что F=maF=ma size 12{F= ital «ma»} {}, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a=rαa=rα size 12{a=rα} {}, и подставим это выражение в F=maF=ma size 12{F= ital «ma»} {}, что даст

10,40 F=mrα. F=mrα. size 12{F= ital «mr»α».»} {}

Вспомним, что крутящий момент – это вращающая способность силы. В этом случае, поскольку размер FF 12{«F»} {} перпендикулярен размеру RR 12{r} {}, крутящий момент просто τ=Frτ=Fr размер 12{τ=rα} {}. Итак, если мы умножим обе части приведенного выше уравнения на размер rr 12{r} {}, мы получим крутящий момент в левой части. То есть,

10,41 rF=mr2αrF=mr2α размер 12{ ital «rF»= ital «mr» rSup { размер 8{2} } α} {}

или

10,42 τ=mr2α.τ=mr2α. size 12{τ= ital «mr» rSup { size 8{2} } α.} {}

Последнее уравнение является вращательным аналогом второго закона Ньютона (F=maF=ma size 12{F= ital «ma»} {}), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} аналогичен массе или инерции. Величина mr2mr2 размером 12{ ital «mr» rSup { size 8{2} } } {} называется инерцией вращения или моментом инерции точки массой mm размером 12{m} {} расстоянием rr размером 12{r} {} от центра вращения.

Рис. 10.11 Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила FF размером 12{F} {} приложена к объекту перпендикулярно радиусу rr размером 12{r} {}, заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно размеру rr 12{r} {}.

Создание соединений: динамика вращательного движения

Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.

Инерция вращения и момент инерции

Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 10.11, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции II размер 12{I} {} объекта должен быть суммой mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} для всех точечных масс, из которых он состоит. То есть, I=∑mr2I=∑mr2 size 12{I= Sum {} ital «mr» rSup { size 8{2} } } {}. Здесь II размер 12{I} {} аналогичен мм размером 12{м}{} в поступательном движении. Из-за расстояния rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен MR2MR2 размер 12{ ital «MR» rSup { размер 8{2} } } {}, где Размер MM 12{M} {} — это его полная масса, а размер RR 12{R} {} — его радиус. Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс. Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{«кг» cdot «м» rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.

Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:

10,43 net τ=Iαnet τ=Iα размер 12{τ=Iα} {}

или

10,44 α=net τI,α=net τI, размер 12{α= { { ital «net»τ} над {I } } «,»} {}

где чистый размер ττ 12{τ} {} — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в τ=Iα, α=net τIτ=Iα, α=net τI size 12{τ=Iα,««`α= { { ital «net»τ} over {I} } } {} является вращательный аналог второго закона Ньютона и очень широко применим. Это уравнение действительно справедливо для любой крутящий момент, приложенный к любому объекту относительно любой оси .

Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса в обоих случаях одинакова, но момент инерции намного больше, когда дети находятся на краю.

Эксперимент на вынос

Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от одного до двенадцати, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. Вы можете свободно прибить круг к стене. Держите круг неподвижно и с цифрой 12, расположенной вверху, прикрепите кусок синей замазки, липкого материала, используемого для крепления постеров к стенам, к цифре три. Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое для числа три, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте вращать круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.

В каком направлении вращался круг, когда вы добавляли замазку в номер три, по часовой или против часовой стрелки? В каком из этих направлений была результирующая угловая скорость? Была ли угловая скорость постоянной? Что мы можем сказать о направлении по часовой стрелке или против часовой стрелки углового ускорения? Как можно изменить положение замазки, чтобы создать угловую скорость в противоположном направлении?

Стратегия решения задач по динамике вращения

1. Изучите ситуацию, чтобы определить, участвуют ли крутящий момент и масса во вращении . Нарисуйте тщательный набросок ситуации.
2. Определить интересующую систему .
3. Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
4. Применить сеть τ=Iα, α=net τI net τ=Iα, α=net τI size 12{τ=Iα,«`α= { { ital «net»τ} over {I} } } {}, вращательный эквивалент второго закона Ньютона, чтобы решить проблему . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
5. Как всегда, проверьте решение, чтобы убедиться, что оно разумно .

Выполнение соединений

В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.

Рисунок 10.12 Некоторые инерции вращения.

Пример 10.7 Расчет влияния распределения массы на карусель

Рассмотрим отца, толкающего карусель на детской площадке на рис. 10.13. Он прикладывает силу 250 Н к краю 50-килограммовой карусели, имеющей радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.

Рис. 10.13. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.

Стратегия

Угловое ускорение задается непосредственно выражением .

10,45 α=τIα=τI размер 12{α= {{τ} над {I} } } {}

Чтобы найти αα размера 12{α} {}, мы должны сначала вычислить крутящий момент ττ размера 12{τ } {}, который в обоих случаях одинаков, и момент инерции II величиной 12{I} {}, который во втором случае больше. Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что

10,46 τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м.τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=»rFsinθ»= \( 1 «.» «50м» \) \( «250Н» \) =»375Н» «.» «m.»} {}

Решение для (a)

Момент инерции твердого диска относительно этой оси на рисунке 10.12 равен

10.47 12MR2,12MR2, размер 12{ { {1} свыше {2} } итал. «MR» rSup {размер 8{2} } «,»} {}

где M=50 кгM=50 кг размер 12{M=»50″ «.» 0 итал. «кг»} {} и R=1,50 мR=1,50 м размер 12{R=1 «.» «50»м} {}, так что

10,48 I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2.I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2. размер 12{I=0 «.» 5 \( «50» «.» «0kg» \) \( 1 «.» «50m» \) rSup { size 8{2} } =»56″ «.» «25кг» «.» «m» rSup { size 8{2} } «.»} {}

Теперь, после подстановки известных значений, находим угловое ускорение равным

10,49 α=τI=375 Н⋅м56,25 кг⋅ m2=6,67рад2.α=τI=375 Н⋅м56,25 кг⋅м2=6,67рад2.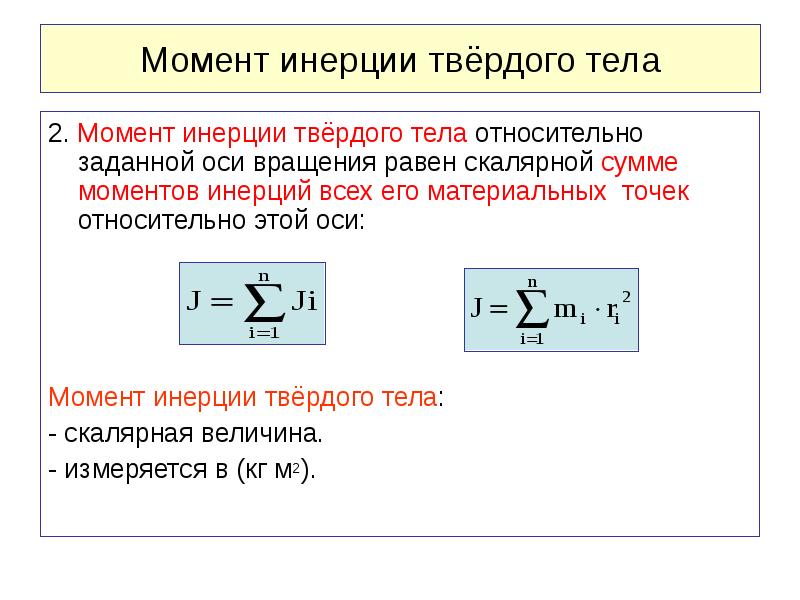 размер 12{α= {{τ} над {I} } = {{«375″`»N» «.» «м»} более {«56» «.» «25»`»кг» «.» «m» rSup {размер 8{2} } } } =6 «.» «67»` {{«rad»} over {s rSup {size 8{2} } } } «.»} {}

Решение для (b)

Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти общий момент инерции II размера 12{I} {}, мы сначала найдем момент инерции ребенка IcIc размера 12{I rSub { размер 8{c} } } {}, считая ребенка эквивалентным точке массы на расстоянии 1,25 м от оси. Тогда

10,50 Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. размер 12{I rSub { размер 8{c} } =»MR» rSup { размер 8{2} } = \(«18» «.» 0`»кг» \) \( 1 «.»»25″` м \) rSup {размер 8{2}} =»28» «.» «13»`»кг» «.» m rSup {размер 8{2} } «.»} {}

Суммарный момент инерции равен сумме моментов инерции карусели и ребенка относительно одной оси. Чтобы оправдать для себя эту сумму, изучите определение II размера 12{I}{}.

10,51 I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2 размер 12{I=»28″ «.» «13»`»кг» «.» m rSup {размер 8{2}} +»56″ «.» «25»`»кг» «.» m rSup { размер 8{2} } =»84″ «.» «38»`»кг» «.» m rSup { размер 8{2} } } {}

Подстановка известных значений в уравнение для размера αα 12{α} {} дает

10,52 α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2.α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2. размер 12{α= {{τ} над {I} } = {{«375N» «.» м} более {«84» «.» «38кг» «.» m rSup {размер 8{2} } } } =4 «.» «44» { {«rad»} over {s rSup { size 8{2} } } } «.»} {}

Обсуждение

Угловое ускорение меньше, когда ребенок на карусели круглый, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, а только 8,89.рад/с, когда на нем находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.

Создание соединений: воздействие нескольких сил на одну систему

Большой гончарный круг диаметром 60 см и массой 8 кг. Он приводится в действие двигателем мощностью 20 Н, воздействующим на внешний край. Также имеется тормоз, способный оказывать усилие 15 Н в радиусе 12 см от оси вращения, на нижней стороне.

Каково угловое ускорение при работе двигателя?

Крутящий момент находится по формуле τ = rF sin θ = (0,300 м)(20 Н) = 6 Н·мτ = rF sin θ = (0,300 м)(20 Н) = 6 Н·м.

Момент инерции рассчитывается как I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2.

Таким образом, угловое ускорение будет α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2.

Обратите внимание, что трение всегда действует в направлении, противоположном вращению, происходящему в данный момент в этой системе. Если гончар ошибается и включает одновременно и тормоз, и двигатель, сила трения тормоза создаст крутящий момент, противоположный крутящему моменту двигателя.

Крутящий момент от тормоза τ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н⋅мτ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н.

Таким образом, чистый крутящий момент равен 6 Н·м – 1,80 Н·м = 4,20 Н·м. 6 Н·м – 1,80 Н·м = 4,20 Н·м..

А угловое ускорение равно α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2.

Проверьте свое понимание

Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?

Решение

Нет.