формулы, теорема Штейнера, пример решения задачи — OneKu

Содержание статьи:

• Общие сведения о физической величине
• Величина I для тел разной формы
• Теорема Штейнера и формула
• Уравнение моментов
• Пример решения задачи

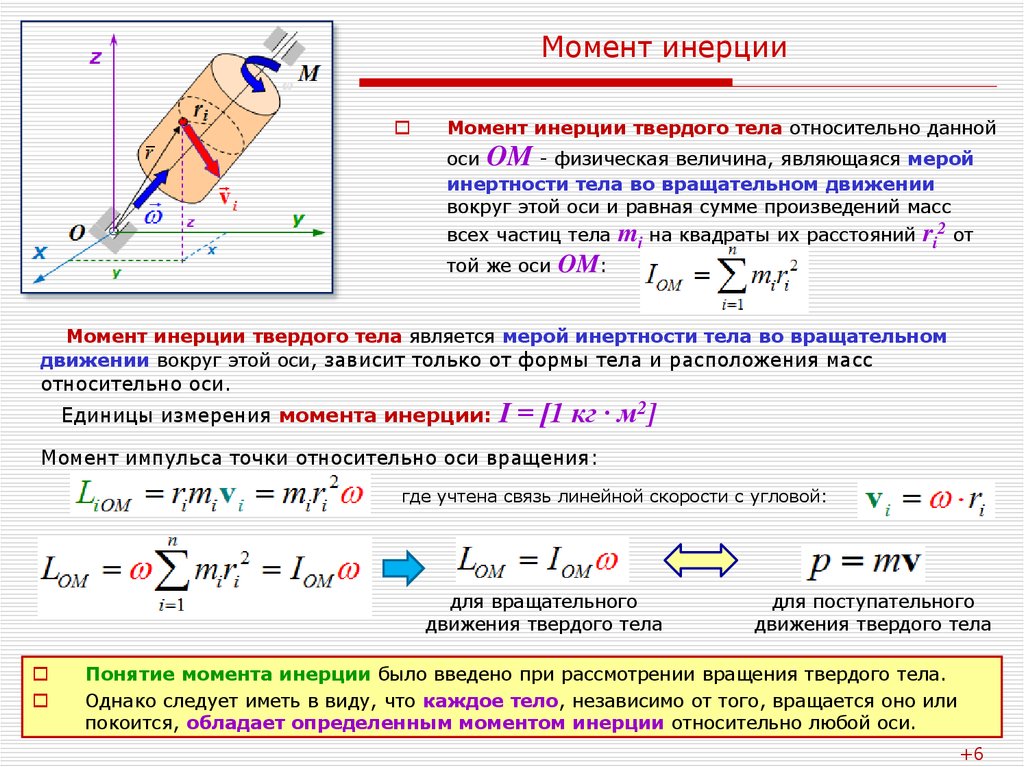
Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫m(r² * dm) = ρ * ∫V(r² * dV).

Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

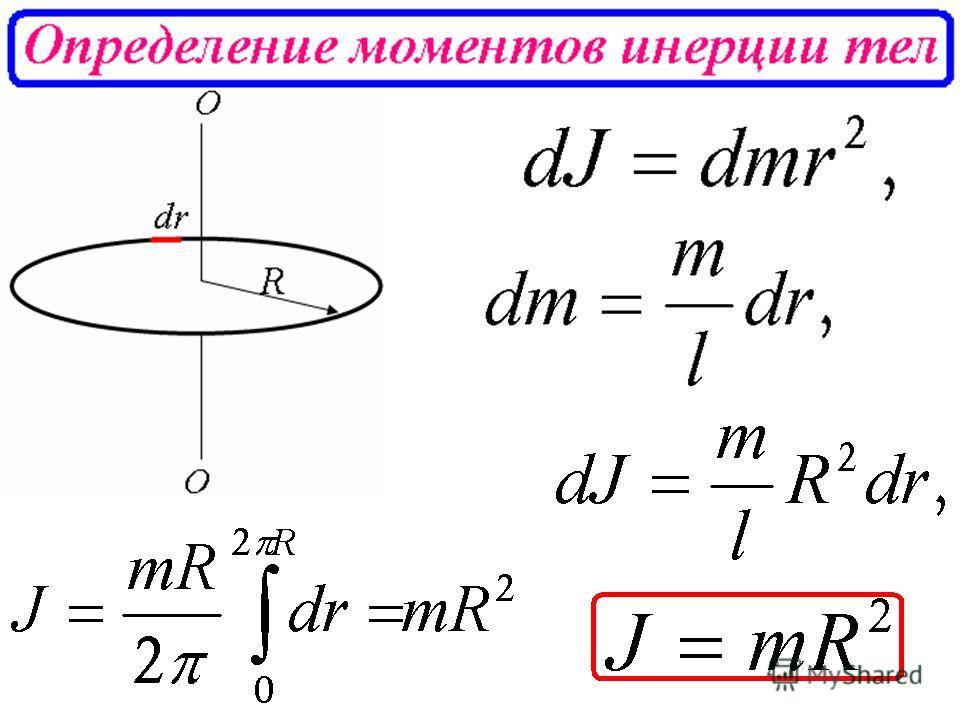
При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Теорема Штейнера и формула

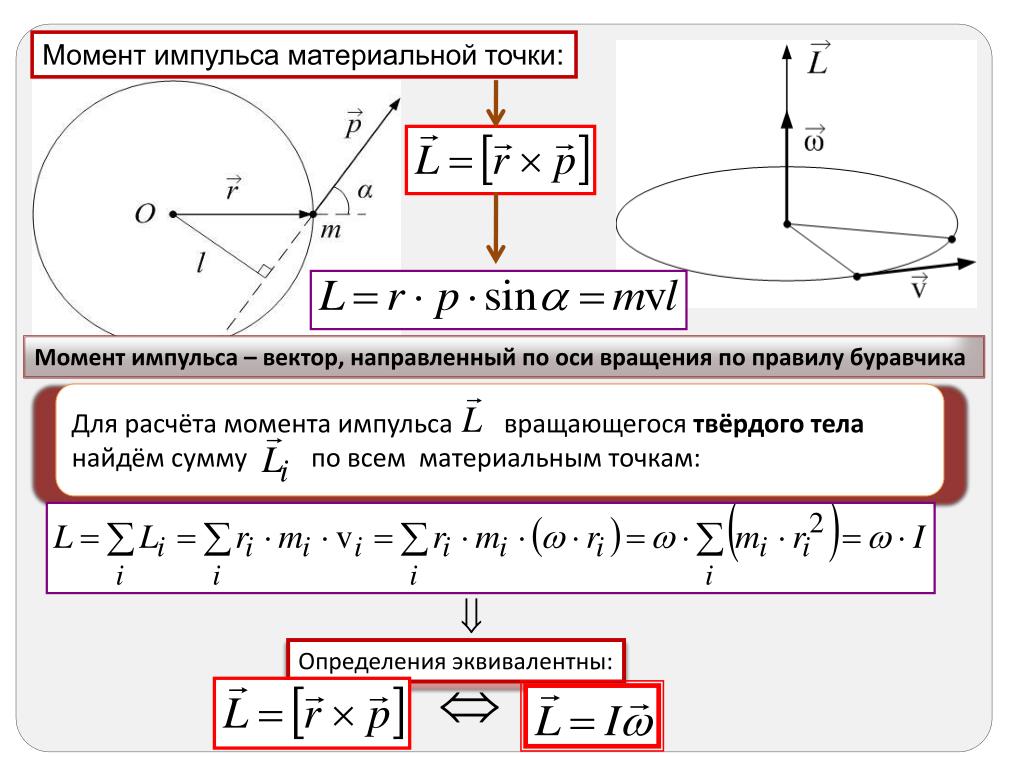
Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = IO + M * h3.

Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r0 + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

формулы, теорема Штейнера, пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫_m(r² * dm) = ρ * ∫_V(r² * dV).

Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину I_O тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром I_O и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = I_O + M * h².

Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r₀ + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = I_O + M * (L / 2)² = 1 / 12 * M * L² + M * L² / 4 = M * L² / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = I_O + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

Карта механики — Теорема о параллельных осях

В качестве альтернативы интегрированию моменты инерции площади и массы могут быть рассчитаны с помощью метода составных частей, подобно тому, как мы это делали с центроидами. В этом методе мы разобьем сложную форму на простые части, найдем моменты инерции для этих частей в таблице, отрегулируем моменты инерции для положения и, наконец, сложим скорректированные значения вместе, чтобы найти общий момент инерции. Этот метод известен как метод составных частей .

Ключевой частью этого процесса, которой не было в расчетах центроидов, является корректировка положения. Как обсуждалось на предыдущих страницах, площадь и моменты инерции масс зависят от выбранной оси вращения. Моменты инерции частей тела могут складываться только тогда, когда они взяты относительно одной и той же оси . Однако моменты инерции в таблице обычно указаны относительно центроида этой формы. Поскольку каждая часть имеет свою собственную координату центра тяжести, мы не можем просто сложить эти числа. Мы будем использовать что-то под названием Параллельная ось Теорема , чтобы настроить моменты инерции так, чтобы все они были взяты относительно некоторой стандартной оси или точки. Как только моменты инерции будут скорректированы с помощью теоремы о параллельных осях, мы можем сложить их вместе, используя метод составных частей.

Теорема о параллельных осях

Когда мы вычисляли момент инерции площади и массы с помощью интегрирования, одной из первых вещей, которые нам нужно было сделать, было выбрать точку или ось, относительно которой мы собирались измерять момент инерции. Затем мы измерили все расстояния от этой точки или оси, где расстояния были плечами моментов в наших интегралах моментов. Поскольку центр тяжести фигуры является геометрическим центром площади или объема, среднее расстояние до любой точки тела минимально.

Если мы выберем другую точку или ось для измерения момента инерции, то в среднем все расстояния в нашем интеграле моментов будут немного больше. В частности, чем дальше мы удаляемся от центроида, тем больше становятся средние расстояния.

Расстояния, используемые в наших интегралах моментов, зависят от выбранной точки или оси. Эти расстояния будут минимальными в центроиде и будут увеличиваться по мере того, как мы начинаем дальше от центроида.

Хотя это усложняет наш анализ, приятно то, что изменение момента инерции предсказуемо. Он всегда будет минимальным, если мы возьмем момент инерции относительно центроида или оси, проходящей через центроид (площадной момент инерции), и минимальным относительно оси, проходящей через центр тяжести (массовый момент инерции). Этот минимум, который мы будем называть I 9{2}\]

Этот процесс настройки с приведенными выше уравнениями является теоремой о параллельной оси . Термины площади или массы просто представляют собой площадь или массу части, на которую вы смотрите, в то время как расстояние (r) представляет собой расстояние, на которое мы перемещаем ось, вокруг которой мы измеряем момент инерции.

Это может быть расстояние по вертикали, расстояние по горизонтали или диагональ в зависимости от оси, вокруг которой находится момент или инерция.

Очень важно отметить, что теорема о параллельных осях верна только для I _c или I _G — в этой формуле нельзя использовать момент инерции относительно другой точки. Также ясно, что добавленный член всегда будет положительным (площадь, масса и квадрат расстояния не могут быть отрицательными). Это напоминание о том, что момент инерции относительно центра тяжести (момент площади) или центра тяжести (момент массы) является наименьшим моментом инерции для этого объекта — относительно любой другой оси момент инерции будет больше.

Расстояние (r) в теореме о параллельных осях представляет собой расстояние, на которое мы перемещаем ось, которую мы фиксируем в момент или намерение.

Допустим, мы пытаемся найти моменты инерции прямоугольника выше относительно точки P. Начнем с поиска I _xx , I _yy и J _zz относительно центра тяжести прямоугольника (C) в момент инерции табл.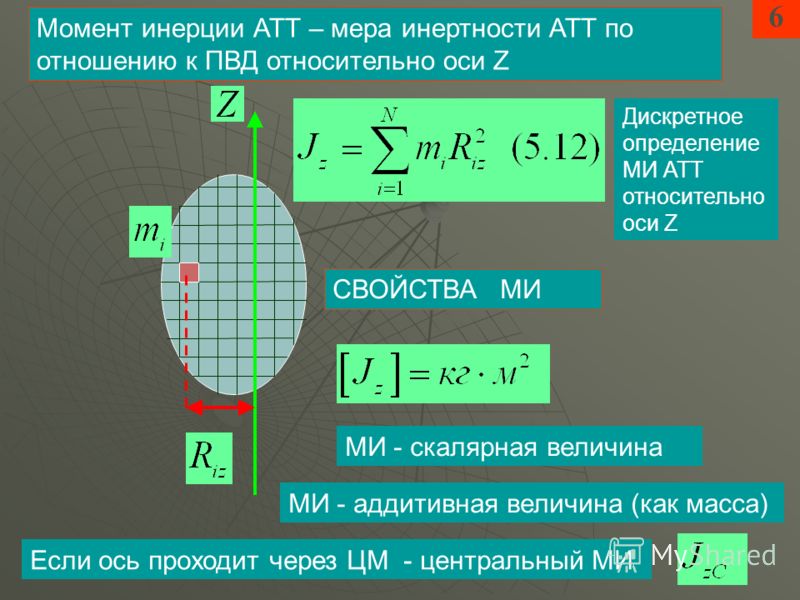 Затем мы добавили бы площадь, умноженную на квадрат расстояния, к каждому, чтобы найти скорректированные моменты инерции относительно P. Расстояние, на которое мы перемещаемся по оси x для I

xx , равно вертикальному расстоянию r _x , расстояние, на которое мы перемещаемся ось Y для I _yy — это расстояние по горизонтали r _y , а расстояние, на которое мы переместим ось z (которая указывает за пределы страницы) для J _zz , — это диагональ r _z .

Корректировка центра масс осуществляется по аналогичной логике, используя массу, умноженную на квадрат расстояния, где расстояние показывает, насколько далеко вы перемещаете ось вращения в трехмерном пространстве.

Использование метода составных частей для нахождения момента инерции

Чтобы найти момент инерции тела с помощью метода составных частей, вам нужно начать с разбиения площади или объема на простые формы. Убедитесь, что каждая отдельная форма доступна в таблице моментов инерции, и вы можете рассматривать отверстия или вырезы как отрицательную площадь или массу.

Начните с разбиения площади или объема на простые части и пронумеруйте их. Отверстия или вырезы будут считаться отрицательными областями или массами.

Далее вы создадите таблицу для отслеживания значений. Выделите строку для каждой части, которую вы пронумеровали ранее, и включите последнюю «итоговую» строку, которая будет использоваться для некоторых значений. Большая часть работы по методу составных частей заключается в заполнении этой таблицы. Столбцы будут немного отличаться в зависимости от того, что вы ищете, но обычно вам потребуется следующее.

Большая часть работы по методу составных частей будет вращаться вокруг заполнения таблицы, подобной этой. Эта таблица содержит строки и столбцы, необходимые для нахождения моментов инерции прямоугольной площади (I _xx и I _yy ) для этого составного тела.

• Площадь или масса каждой детали (площадь для моментов инерции площади или масса для моментов инерции масс). Помните, что вырезы должны быть перечислены как отрицательные области или массы.
• Центроид или положение центра масс (координаты X, Y и, возможно, Z). Большую часть времени мы будем находить момент инерции относительно центроида составной формы, и если он не указан вам явно, вам нужно будет найти его, прежде чем идти дальше. Подробнее об этом см. На странице «Центроиды и центр масс с помощью метода составных частей».
• Значения момента инерции относительно центроида каждой формы. Чтобы найти эти значения, вы подставите значения высоты, радиуса, массы и т. д. в формулы таблицы моментов инерции. Не используйте эти формулы вслепую, так как вам может понадобиться мысленно повернуть тело и, таким образом, поменять местами уравнения, если ориентация фигуры в таблице не совпадает с ориентацией фигуры на вашей диаграмме.
• Регулировочные расстояния (r) для каждой формы. Для этого значения вы захотите определить, как далеко перемещается ось x, ось y или z, чтобы пройти от центра тяжести детали до общего центра тяжести или точки, относительно которой вы берете момент инерции. Чтобы рассчитать эти значения в целом, вам нужно будет найти расстояния по горизонтали, вертикали или диагонали между центроидами частей и общими центроидами, которые вы указали ранее в таблице. См. раздел теоремы о параллельных осях на этой странице ранее для более подробной информации.
• Наконец, у вас будет столбец скорректированных моментов инерции. Возьмите первоначальный момент инерции относительно центроида, а затем просто добавьте площадь, умноженную на r в квадрате, или массу, умноженную на r в квадрате, для этого скорректированного значения.

Общий момент инерции вашего составного тела — это просто сумма всех скорректированных моментов инерции частей, которая будет суммой значений в последнем столбце (или столбцах, если вы находите моменты инерции относительно более чем одной оси).

Понимание момента инерции площади

Момент инерции площади , также называемый вторым моментом площади , является параметром, который определяет, какое сопротивление имеет форма (например, поперечное сечение балки).

на изгиб из-за своей геометрии.

https://www.youtube.com/watch?v=Bls5KnQOWkYВидео не может быть загружено, так как отключен JavaScript: понимание момента инерции площади (https://www.youtube.com/watch?v=Bls5KnQOWkY)

Рассмотрим тонкую доску, которая выдерживает нагрузку в 100 кг. Планка будет намного менее жесткой, когда нагрузка будет приложена к более длинному краю поперечного сечения. Это связано с тем, что сопротивление изгибу зависит от того, как материал поперечного сечения распределен относительно оси изгиба. Доска слева имеет больше материала, расположенного дальше от оси изгиба, что делает ее намного более жесткой. 94$. Он отражает, как площадь поперечного сечения распределяется относительно той или иной оси. Это не уникальное свойство поперечного сечения — оно меняется в зависимости от рассматриваемой оси изгиба.

Давайте сравним значения $I$, рассчитанные для нескольких различных сечений, для оси изгиба, показанной ниже:

Значения момента инерции площади (в мм ⁴ ) для трех форм материалы вдали от оси изгиба имеют большие моменты инерции – их труднее согнуть. Это одна из причин Двутавровая балка — такое широко используемое поперечное сечение для конструкционных применений — большая часть материала расположена далеко от оси изгиба, что делает ее очень эффективной при сопротивлении изгибу при использовании минимального количества материала.

Момент инерции площади против второго момента площади

Используются термины «секундный момент площади» и «момент инерции площади». Второй момент площади часто предпочтительнее, чтобы избежать путаницы с моментом инерции, который является совершенно другим параметром, описывающим сопротивление тела угловому ускорению, хотя и рассчитывается аналогичным образом. 92 dA}$$

Нижние индексы $x$ и $y$ указывают на то, что момент инерции площади соответствует изгибу вокруг осей $x$ и $y$ соответственно.

Приведенные выше уравнения можно использовать для расчета $I$ для любой произвольной формы.

Давайте рассмотрим пример того, как это уравнение можно применить для расчета $I$ для прямоугольного поперечного сечения.

Пример — прямоугольное сечение

Мы будем использовать приведенное выше уравнение для расчета $I$ для изгиба вокруг оси $x$ для следующего поперечного сечения: 93ч{12}$$

К счастью, вам не нужно выполнять этот процесс интегрирования всякий раз, когда вам нужно вычислить $I$ для поперечного сечения и оси изгиба. Если это довольно стандартная форма, вы можете просто найти уравнение, которое уже было получено для вашего конкретного поперечного сечения. Большинство учебников по сопротивлению материалов содержат таблицы, подобные приведенной ниже, в которых перечислены уравнения $I$ для обычных поперечных сечений.

Сечение		Площадь Момент инерции 92$$ Утверждается, что момент инерции площади вокруг любой оси $I_x$ может быть рассчитан из момента инерции площади относительно параллельной оси $I_{xc}$, проходящей через центр тяжести поперечного сечения, площадь поперечного сечения $A$ и расстояние между двумя осями $d$. Иллюстрация теоремы о параллельных осях, которую можно использовать для вычисления $I_x$ на основе $I_{xc}$, $d$ и площади поперечного сечения $A$. C — центр тяжести поперечного сечения. Центроид — это геометрический центр поперечного сечения или, другими словами, точка, в которой можно сбалансировать поперечное сечение на штифте. В справочных текстах обычно приводятся уравнения для $I$ для центроидальных осей, поэтому теорема о параллельных осях является мощным инструментом для распространения этих уравнений на любые другие параллельные оси. Сложение и вычитание моментов инерции площади Моменты инерции площади можно суммировать и вычитать для расчета значений составных сечений. На изображении ниже показано, как этот метод можно использовать для расчета $I_x$ для полого сечения. Пример расчета $I$ для составного поперечного сечения путем прибавления или вычитания При использовании этого метода необходимо убедиться, что значения $I$ для поперечных сечений компонентов ($I_{xA}$ и $I_{xB}$ ​​в приведенном выше примере) соответствуют правильной оси изгиба, иначе сначала вам нужно будет применить теорему о параллельной оси, чтобы получить значения $I$ для правильной оси. Применение момента инерции площади Момент инерции площади является важным параметром для любого применения, связанного с изгибом элемента конструкции, что означает, что он постоянно присутствует в 92}$$ Если вы хотите узнать больше об этих приложениях, ознакомьтесь со страницами , отклонение балки и , изгиб . Как показывают два приведенных выше примера, момент инерции площади часто появляется в уравнениях вместе с модулем Юнга $E$. Термин $EI$ получил название изгибной жесткости . $I$ представляет собой жесткость поперечного сечения балки из-за ее геометрии , а $E$ представляет собой жесткость поперечного сечения из-за материала . Жесткость на изгиб $EI$ представляет собой общую жесткость поперечного сечения. Полярный момент инерции В дополнение к расчету момента инерции площади для осей $x$ и $y$, находящихся в той же плоскости, что и поперечное сечение, мы также можем рассчитать момент инерции площади для оси это перпендикулярно поперечному сечению. Это называется полярным моментом инерции и обычно обозначается буквой $J$ или $I_z$. Он часто используется в задачах, связанных с деформацией кручения, которая является 9-й.2 dA}$$ $J$ учитывает, как площадь поперечного сечения распределяется радиально относительно оси вращения или кручения $z$. Член $\rho$ — это расстояние от оси $z$ (которая на изображении ниже направлена ​​за пределы экрана) до элемента dA. Полярный момент инерции рассчитывается на основе распределения площади поперечного сечения относительно оси кручения ($z$ на изображении выше) Как и в случае с $I_x$ и $I_y$, $\rho$ член в уравнении возведен в квадрат, а это означает, что наибольший вклад в значение $J$ вносят участки поперечного сечения, расположенные далеко от оси вращения. Вот почему трансмиссионные валы полые — центральная часть поперечного сечения не сильно влияет на сопротивление скручиванию, поэтому более эффективно использовать полые валы. Мы можем сделать интересное наблюдение: полярный момент инерции относительно оси, проходящей через определенную точку поперечного сечения, равен сумме площадных моментов инерции двух перпендикулярных осей, проходящих через одну и ту же точку. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника