Инерция — Википедия

Ине́рция (от лат. inertia — покой, бездеятельность, постоянство, неизменность) — свойство тела оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие внешних воздействий^[1][2], а также препятствовать изменению своей скорости (как по модулю, так и по направлению^[3]) при наличии внешних сил за счёт своей инертной массы.

Понятию «инерция» синонимично одно из значений понятия инертность^[1] (другие значения последнего не относятся к физике).

Количественно соотношение между воздействием на тело и изменением его движения даётся формулой второго закона Ньютона^[4]:

F→=ddt(mv→){\displaystyle {\vec {F}}={\frac {d}{dt}}(m{\vec {v}})}.

Здесь F→{\displaystyle {\vec {F}}} — сила, действующая на тело, m{\displaystyle m} — инертная масса, v→{\displaystyle {\vec {v}}} — скорость тела.

С понятием инерции связано понятие инерциальных систем отсчёта.

Существование инерциальных систем отсчёта в классической механике постулируется первым законом Нью́тона, который также называется зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Современная, более точная, формулировка закона:

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными.

В неинерциальных системах отсчёта закон инерции не выполняется. Тем не менее движение тел в неинерциальных системах отсчёта можно описывать теми же уравнениями движения, что и в инерциальных, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать силы инерции^[5][6].

Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте^[7]:

Никто не сможет сказать, почему [тело], приведенное в движение, где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там? Следовательно, ему необходимо или покоиться, или двигаться до бесконечности.

Однако в другом труде «Механика», приписываемом Аристотелю, утверждается^[8]:

Движущееся тело останавливается, если сила, его толкающая, прекращает своё действие.

Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.

Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку «аристотелевской физики». В своем труде «Беседы о двух новых науках» Галилей писал

[8]:

…скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно

Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то при движении по горизонтальной плоскости у тела нет причин ускоряться или замедляться — и оно должно пребывать в состоянии равномерного движения или покоя.

Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считали Аристотель и его последователи. Это открытие Галилея вошло в науку как

закон инерции. Однако, Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В 1638 году итальянец Балиани уточнил закон инерции, указав, что при полном отсутствии внешних воздействий естественной траекторией движения тела является прямая. В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.

Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведённой в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.

Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (другими примерами абстрактной модели служат абсолютно твёрдое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами, и соответствие реально наблюдаемого движения тел в таких системах результатам расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика.

Инертная масса — мера инертности тела в физике, показатель того, в большей или меньшей степени данное тело будет препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии внешних сил. Инертная масса фигурирует в выражении второго закона Ньютона, являющегося важнейшим законом классической механики.

Видеоурок: инерция

1. ↑ ^{1 2 3} Инерция // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
2. ↑ Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
3. ↑ Т.И.Трофимов. Физика. — Москва: «Академия», 2012.
4. ↑ Коноплёва Н. П. Об эволюции понятия инерции (Ньютон, Мах, Эйнштейн) // Эйнштейновский сборник 1975-1976. — М., Наука, 1978. — с. 216-244
5. ↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — С. 118—119.
6. ↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 292
7. ↑ Физика (Аристотель)/Книга 4/Глава 8
8. ↑ ^{1 2} Эйнштейн А., Инфельд Л. Эволюция физики. — М.: Наука, 1965. — С. 10-12.

• Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
• Спасский Б. И.. История физики. М., «Высшая школа», 1977.
• Кокарев С. С. Три лекции о законах Ньютона. Ярославль. Сб. трудов РНОЦ Логос, вып. 1, 45-72, 2006.

Ссылки новых исследований:

Инерция — это… Что такое Инерция?

Ине́рция (от лат. inertia — бездеятельность, косность) — свойство тел сохранять покой или равномерное прямолинейное движение, если внешние воздействия на него отсутствуют или взаимно скомпенсированы.

Формулировка

Существование явления инерции в классической механике постулируется Первым законом Нью́тона, который также называется Зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Современная формулировка закона:

Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными. Проявлением неинерциальности в них является возникновение фиктивных сил, называемых «силами инерции».

История

Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте^[1]:

Никто не сможет сказать, почему [тело], приведенное в движение, где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там? Следовательно, ему необходимо или покоиться, или двигаться до бесконечности.

Однако сам Аристотель считал, что пустота в природе не может существовать, и в другом его труде, «Механике», утверждается^[2]:

Движущееся тело останавливается, если сила, его толкающая, прекращает свое действие.

Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (сил трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.

Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку Аристотеля. В своем труде «Беседы о двух новых науках» он писал^[2]:

…скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно

Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то, при движении по горизонтальной плоскости, у тела нет причин ускоряться или замедляться, и оно должно пребывать в состоянии равномерного движения или покоя.

Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считал Аристотель и его последователи. Это открытие Галилея вошло в науку как Закон инерции. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.

Смежные понятия

Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведенной в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.

Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (примерами абстрактной модели служат абсолютно твердое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами, и соответствие реально наблюдаемого движения тел в таких системах с результатами расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика и ограничивается лишь величиной искривления пространства-времени, которое было предсказано в рамках общей теории относительности (1915 год) и впервые зафиксировано в 1919 году при исследовании отклонения света в гравитационном поле Солнца.

Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил. Мерой инертности в физике выступает инертная масса.

См. также

Литература

Примечания

Инертность — Википедия

Инертность — в общем случае бездеятельность, пассивность, вялость. Свойство по значению прил. инертный. Свойство быть в состоянии не делать ничего или почти ничего.

В химии инертными называются вещества, не являющихся химически активными.

Благородные газы были ранее известны как инертные газы из-за предполагаемого отсутствия участия в каких-либо химических реакциях. Причина этого заключается в том, что их крайняя электронная оболочка (валентная оболочка) полностью заполнена, так, что они имеют незначительную тенденцию к приобретению или потере электрона.^[1] В настоящее время известно, что эти газы реагируют с образованием химических соединений, например, тетрафторида ксенона. Поэтому они были переименованы в благородные газы. Тем не менее для проведения таких реакций требуется большое количество энергии, как правило подводимой в виде тепла, давления, или излучения, а также присутствие катализаторов. Полученные соединения инертных газов часто неустойчивы. Инертные среды, состоящие из газов, таких как аргон или гелий широко используются в химических реакционных камерах и контейнерах для хранения реагентов.

Термин инертный также может быть применён в относительном смысле, как не реакционно-способный. Например, молекулярный азот инертен в обычных условиях, существующих в двухатомных молекулах, N₂. Наличие сильной тройной ковалентной связи в N₂ молекулах делает его не реакционно-способным в нормальных условиях. Тем не менее, азот реагирует со щелочным металлом литием, образуя нитрид лития (Li₃N) даже в обычных условиях. При высоких давлениях и температурах и с нужным катализатором, азот становится более реактивным. Процесс Габера использует такие условия, для производства аммиака из азота воздуха. Инертная среда из азота широко используется для хранения чувствительных к кислороду или водно-чувствительных веществ, чтобы предотвратить нежелательные реакции этих веществ с кислородом или водой.

Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил.^[2] Упоминается в русскоязычной литературе, наряду с Инерцией, как синоним, но дается несколько различное определение. Ине́ртность (от лат. inertia — бездеятельность, косность.) — свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие или при взаимной компенсации внешних воздействий.^[3] Мерой инертности в поступательном движении является масса тела^[4]. Мерой инертности во вращательном движении является момент инерции^[5].

Федеральный закон США о Инсектицидах, Фунгицидах и Родентицидах (англ.)русск. делит ингредиенты в пестицидах на две группы: активные и инертные. Химически инертные, в этом контексте, это такие, которые не оказывают токсического влияния на определённые виды, для защиты которых предназначены пестициды, но это не исключает, что они всё ещё могут иметь биологическую активность на другие виды, в том числе, могут быть токсичны для человека. В частности, растворители, пропелленты, консерванты, кроме прочего, считаются инертными ингредиентами (англ.)русск.^[6] в пестицидах.^[7]

Начиная с 1997 года, Агентство по охране окружающей среды США рекомендовало производителям пестицидов маркировать неактивные ингредиенты как «прочие ингредиенты», а не «инертные», чтобы предотвратить дезинформацию общественности.^[7].

В русскоязычной литературе термин инертность используется в работах по пестицидам ^[8], биотехнологиям^[9], а также в официальных инструкциях препаратов, например «Агропол».

В алгебре, простой идеал дедекиндова кольца называют инертным, если он по-прежнему простой, при рассмотрении в расширении поля. Такой простой идеал, возможно, вместо разбиения простых идеалов на расширения Галуа (англ.)русск. имеет в результате другие простые идеалы, но, будучи инертным, остается практически неизменным.^[10][11]

В области оружия и взрывчатых веществ, инертный боеприпас — такой, в котором все энергетические материалы, такие как огнепроводный шнур, капсюль, и разрывные или зажигательные материалы в них были сняты или иным образом обезврежены. Инертные врывно-тупо-режущие боеприпасы используются в военной и военно-морской подготовке и используются для показа в музеях. См. также военный муляж (англ.)русск.. Как правило, американские и натовские инертные боеприпасы окрашены полностью в светло-голубой цвет, и/или на видных местах есть слово «INERT» нанесённое по трафарету. В российской армии такие боеприпасы маркируются белой полосой и/или надписью «ИНЕРТНО» или «ИНЕРТ».^[12] Регламентируются в Европейском соглашении о международной дорожной перевозке опасных грузов^[13]

1. ↑ Некрасов Б.В. Основы общей химии. — М.: Рипол Классик, 1965. — Т. 1. — 656 с. — ISBN 5458424085, 9785458424080.
2. ↑ Инертность // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1990. — Т. 2. — ISBN 5-85270-034-7.
3. ↑ Инерция // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1990. — Т. 2. — ISBN 5-85270-034-7.
4. ↑ Инертность // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2.
5. ↑ Момент инерции // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
6. ↑ EPA (2010), Inert Ingredients Eligible for FIFRA 25(b) Pesticide Products Last Updated December 20, 2010, Office of prevention, pesticides and toxic substances
7. ↑ ^{1 2} Inert ingredients in pesticide products. US Environmental Protection Agency, Office of Pesticide Programs.
8. ↑ к.б.н. Семенова А.Г.; к.б.н. Свирина Н.В. Современные препаративные формы пестицидов / УДК 632.95. — Санкт-Петербург: Санкт-Петербургский Государственный Аграрный Университет, 2010. — 15 с.
9. ↑ Хиггинс И., Бест Д., Джонс Дж. Биотехнология. Принципы и применение / пер. с англ. д-ра биол. н. Антонова А.С., под ред. акад. Баева А.А.. — М.: Мир (издательство), 1988. — 479 с. — ISBN 5-03-000058-5 0-623-01029-0.
10. ↑ Ленг С. Origins and early evolution of predation // Алгебраические числа, пер. с англ.. — М.: Мир, 1966. — 230 с.
11. ↑ Вейль Г. Алгебраическая теория чисел, пер. с англ.. — М.: Гос. изд. ин.лит., 1947. — 226 с. — ISBN 978-5-354-01363-0.
12. ↑ Веремеев Ю. Маркировка инженерных боеприпасов Советской Армии // Анатомия армии. — М.: Эксмо, Алгоритм, 2010. — Т. Инженерные войска. — 292 с. — ISBN 978-5-699-46005-2.
13. ↑ Организация Объединённых Наций. Европейское соглашение о международной дорожной перевозке опасных грузов. — Нью-Йорк и Женева: United Nations, 2010. — 689 с. — ISBN 978-92-1-439042-8.

Инерция. Видеоурок. Физика 7 Класс

Тема: Взаимодействие тел

Урок: Инерция

В 1632 году вышла книга итальянского ученого Галилео Галилея «Диалог о двух главнейших системах мира» – Птолемея и Коперника. В одном из разделов этой книги есть такие слова:

«Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то… движение его является равномерным и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца».

В этой фразе описывается физическое явление, которое называется инерцией.

 

Рис. 1

Галилей приводит различные примеры, в которых доказывает, что подобное движение было бы не только равномерным, но и прямолинейным. А это означает, что неизменным остается не только численное значение, но и направление скорости. Другими словами, в ходе такого движения постоянным остается вектор скорости.

Сформулируем закон инерции так, как он звучал во времена Галилея.

Тело сохраняет свою скорость постоянной, или покоится, если на него не действуют другие тела.

Подтвердить справедливость этого утверждения на опыте невозможно, так как невозможно создать такие идеальные условия, когда на тело не действуют никакие другие тела. А если условия приближены к идеальным, то только потому, что действие других тел скомпенсировано.

Телега будет находиться в состоянии покоя, пока на нее не подействует другое тело (лошадь).

 

Рис. 2. Телега будет находиться в покое, пока с ней не начнет взаимодействовать лошадь

Пуля будет находиться в стволе пистолета, пока на нее не подействуют пороховые газы.

 

Рис. 3. Пуля приходит в движение вследствие взаимодействия с пороховыми газами

В 1687 году английский ученый Исаак Ньютон предлагает свою интерпретацию закона инерции.

Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

 

Рис. 4

Немного позднее мы выясним, что сила – это физическая величина, описывающая действие одного тела на другое. Поэтому можно сказать:

«Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано».

Когда автобус начинает свое движение от остановки, пассажиры отклоняются назад. И наоборот, при резком торможении, стремясь сохранить свою прежнюю скорость, пассажиры отклоняются вперед. Бывает, что для того, чтобы уменьшить свою скорость до значения скорости автобуса, им приходится крепко держаться за сидения (то есть взаимодействовать с сидением для изменения своей скорости).

 

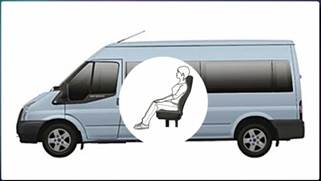
Рис. 5. При разгоне автобуса пассажиры наклоняются назад, при торможении – вперед

Когда лошадь внезапно останавливается, то неопытный наездник может перелететь через ее голову вперед.

 

Рис. 6. Резко остановившись, лошадь может сбросить неопытного наездника

То же бывает и с велосипедистом, при слишком резком нажатии на передний тормоз или при наезде на крупное препятствие.

 

Рис. 7. Наезд велосипеда на препятствие грозит падением через руль

Проведите такой простой опыт. Положите на стакан небольшую открытку, а на открытку положите монету.

 

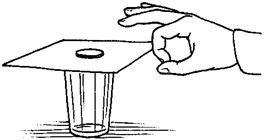
Рис. 8. Опыт со стаканом и монетой.

Если резким щелчком сбоку привести открытку в движение, то монета по инерции почти не сдвинется и упадет в стакан.

Все это – демонстрации явления инерции. 

Опыт, аналогичный описанному ниже, в свое время проводил Галилео Галилей.

С наклонной плоскости скатывается шарик и далее движется по гладкому горизонтальному столу. Поскольку стол гладкий, то скорость шарика изменяется очень медленно, его движение приближено к равномерному прямолинейному. Но если на пути движения шарика возникнет небольшое препятствие – тонкий слой песка, – характер движения изменится. Скорость шарика быстро уменьшится вплоть до полной остановки.

  

Рис. 9. Взаимодействие с песком изменяет скорость катящегося шарика

Сделаем вывод. Чем меньше действие одного тела на другое, тем медленнее изменяется скорость тела и тем ближе движение тела к равномерному прямолинейному.

Подведем итог нашего урока. Инерция (от латинского inertia – неподвижность, бездеятельность) это физическое явление, которое проявляется в том, что изменить скорость тела можно, только подействовав на него другим телом. В противном случае тело будет сохранять свою скорость, то есть двигаться равномерно и прямолинейно (или находиться в покое).

 

Список  литературы

1. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.

2. Перышкин А.В. Сборник задач по физике, 7 – 9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

3. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7 – 9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

                                     

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. YouTube (Источник).

2. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

3. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

 

Домашнее задание

Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7 – 9 классов №№ 175–187.

Доклады на тему » Инерция

Явление, которому посвящена наша сегодняшняя беседа, встречается в разных жизненных ситуациях. Мы с удовольствием его используем, учитываем и частенько ругаем.

Речь пойдет об инерции. Постараемся разобраться, что скрывается за этим названием.

Что же такое инерция

Наблюдая полёт копья, брошенного рукой атлета, падение всадника через голову споткнувшейся лошади; созерцая камни, веками неподвижно лежащими на одних и тех же местах — греческие мыслители задумывались, что общего в этих явлениях?

На пути их познания Аристотелем было введено понятие инерции, что дословно означает «бездействие». Эти размышления греческого философа об инерции получили продолжение в опытах Г. Галилея. Он делает вывод о том, что если на тело не действуют другие тела, то скорость тела не изменяется. Спустя несколько веков эти выводы дополнил и обобщил в своих трудах Исаак Ньютон.

Данная им формулировка явления инерции известна как I закон Ньютона.

«Инер­ция — это фи­зи­че­ское яв­ле­ние со­хра­не­ния ско­ро­сти тела по­сто­ян­ной, если на него не дей­ству­ют дру­гие тела или их дей­ствие ском­пен­си­ро­ва­но».

Это означает, что, благодаря инерции, тела, находящиеся в покое, продолжают покоиться, а движущиеся продолжают свое движение, пока на них не окажут воздействие внешние силы.

Например, автомобиль может находиться в покое в двух случаях, если на горизонтальном участке дороги его двигатель выключен, либо его двигатель включен, но силы сопротивления уравновесили силу тяги двигателя, т. е. скомпенсировали её.

Теперь вернемся к нашему всаднику, перелетающему через голову споткнувшейся лошади. Лошадь, споткнувшись, резко теряет скорость, а невезучий всадник… по инерции продолжает движение.

По этой же причине при ДТП водитель, пренебрегающий ремнями безопасности, получает удар о лобовое стекло.

Почему, поскользнувшись при ходьбе, мы падаем назад? Тело по инерции сохраняет прежнюю скорость, а ноги на скользком участке быстренько «убегают» вперед.

Формула силы инерции

Количественной характеристикой явления инерции является сила инерции.

Для расчета этой силы используют формулу:

F_ин= — ma

где:

• F_ин — сила инерции;
• m — масса тела;
• a — ускорение.

Знак минус указывает на то, что сила инерции противодействует силе, вызвавшей изменение скорости тела.

Понятие инертности в физике

Итак, инерция — это физическое явление. С ним тесно связано еще одно понятие — инертность. Под инертностью в физике понимают свойства тел противодействовать мгновенному изменению направления или скорости движения.

Любое тело не может мгновенно изменить свою скорость, однако, одни тела это делают быстрее, другие — медленнее. Для остановки гружёного и порожнего самосвалов, движущихся с одинаковой скоростью, требуется разное время.

Это происходит потому, что тело с большей массой более инертно, и ему на изменение скорости требуется больше времени. То есть мерой инертности в физике является масса тела.

Инертные люди, инертные газы

Термин «инертный» широко используется в химии. Он относится к химическим элементам, которые при обычных условиях не вступают в химические реакции. Например, благородные газы аргон, ксенон и др.

Этот термин может быть применен и к поведению человека. Инертные люди отличаются равнодушием к окружающему миру. Они противятся любым переменам, как в их собственной судьбе, так и в работе. Они ленивы и безынициативны.

Инертность вращающихся объектов

Все приведенные ранее примеры относились к поступательно движущимся телам. А как же быть с вращающимися объектами? Скажем, с вентилятором, с маховиком в двигателе внутреннего сгорания или детской игрушке. Ведь после выключения электрического вентилятора его лопасти ещё некоторое время по инерции продолжают крутиться.

Насколько тела инертны во время вращения определяет момент инерции. Он зависит от массы тела, его геометрических размеров и расстояния до оси вращения. Изменение этого расстояния влияет на скорость вращения тела. Это используют спортсмены — фигуристы, поражая зрителей продолжительным вращением с изменением скорости.

Специальные расчёты позволяют определить оптимальные размеры механизма и допустимую скорость вращения, чтобы не допустить разрыва вращающихся частей.

Т.е. момент инерции во вращательном движении играет ту же роль, что и масса при поступательном движении. Но в отличие от массы момент инерции можно изменять, как это делают фигуристы — то широко разводя руки, то прижимают их к груди.

Инерция вокруг нас

Именно это явление используют:

• для сбрасывания ртутного столбика в медицинском термометре и выбивания пыли из ковров;
• для продолжения движения после разбега на коньках, лыжах, велосипеде;
• для экономии горючего при езде на автомобиле;
• в принципе работы артиллерийских детонаторов и т. д.

Это лишь небольшая часть из всех применений инерции. Но не следует забывать о возможной опасности, которую таит это явление природы. Надпись на заднем борту грузовика «Водитель, сохраняй дистанцию», напоминает, что транспорт мгновенно остановить нельзя.

И при торможении впереди едущего автомобиля, следующая за ним машина, остановиться мгновенно не может. По этой же причине категорически запрещено перебегать дорогу перед движущимся транспортом.

Теперь вы легко ответите на вопрос, почему при торможении автомобилей обязательно включается задний красный свет, почему при повороте водитель обязательно сбрасывает скорость.

В спортзале и на катке, в цирке и в мастерской — инерция сопровождает нас всюду. Присмотритесь.

Автор: Драчёва Светлана Семёновна

---

Если это сообщение тебе пригодилось, буда рада видеть тебя в группе ВКонтакте. А ещё — спасибо, если ты нажмёшь на одну из кнопочек «лайков»:

---

Вы можете оставить комментарий к докладу.

Сила инерции — Википедия

Наблюдатель, вращающийся вместе с каруселью, может объяснить отклонение кресел на аттракционе действием центробежной силы инерции

Си́ла ине́рции (также инерционная сила) — многозначное понятие, применяемое в механике по отношению к трём различным физическим величинам. Одна из них — «даламберова сила инерции»^[⇨] — вводится в инерциальных системах отсчёта для получения формальной возможности записи уравнений динамики в виде более простых уравнений статики. Другая — «эйлерова сила инерции»^[⇨] — используется при рассмотрении движения тел в неинерциальных системах отсчёта^[1][2]. Наконец, третья — «ньютонова сила инерции»^[⇨] — сила противодействия, рассматриваемая в связи с третьим законом Ньютона^[3].

Общим для всех трёх величин является их векторный характер и размерность силы. Кроме того, первые две величины объединяет возможность их использования в уравнениях движения, по форме совпадающих с уравнением второго закона Ньютона^[1][4][5], а также их пропорциональность массе тел^[6][4][5].

Русский термин «сила инерции» произошёл от французского словосочетания фр. force d’inertie. Термин применяется для описания трёх различных векторных физических величин, имеющих размерность силы:

• величин, которые вводят при описании движения тел в неинерциальных система отсчёта — «эйлеровы силы инерции»;
• величины, используемой в принципе Д’Аламбера — «даламберова сила инерции»;
• силы-противодействия из третьего закона Ньютона — «ньютонова сила инерции».

Определения «эйлерова», «даламберова» и «ньютонова» предложены академиком А. Ю. Ишлинским^[7][8]. Они используются в литературе, хотя и не получили пока повсеместного распространения. В дальнейшем мы будем придерживаться данной терминологии, как позволяющей сделать изложение более сжатым и ясным.

Эйлерова сила инерции в общем случае складывается из нескольких составляющих различного происхождения, которым также присвоены специальные наименования («переносная», «кориолисова» и др.). Более детально об этом говорится в соответствующем разделе ниже.

В других языках используемые названия сил инерции более явно указывают на их особые свойства: в немецком нем. Scheinkraft^[9] («мнимая», «кажущаяся», «видимая», «ложная», «фиктивная» сила), в английском англ. pseudo force^[10](«псевдосила») или англ. fictitious force («фиктивная сила»). Реже в английском используются названия «сила д’Аламбера» (англ. d’Alembert force^[11]) и «инерционная сила» (англ. inertial force^[12]). В литературе, издаваемой на русском языке, по отношению к эйлеровой и даламберовой силам также используют аналогичные характеристики, называя эти силы «фиктивными»^[13], «кажущимися»^[14], «воображаемыми»^[8] или «псевдосилами»^[15].

Одновременно с этим в литературе иногда подчёркивают реальность сил инерции^[16][17], противопоставляя значение данного термина значению термина фиктивность. При этом, однако, различные авторы вкладывают в эти слова различный смысл, и силы инерции оказываются реальными или фиктивными не в силу отличий в понимании их основных свойств, а в зависимости от избранных определений. Такое употребление терминологии некоторые авторы считают неудачным и рекомендуют просто избегать его в учебном процессе^[18][19].

Хотя дискуссия по поводу терминологии ещё не закончена, имеющиеся разногласия не влияют на математическую формулировку уравнений движения с участием сил инерции и не приводят к возникновению каких-либо недоразумений при использовании уравнений на практике.

В классической механике представления о силах и их свойствах основываются на законах Ньютона и неразрывно связаны с понятием «инерциальная система отсчёта». Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила, эти физические величины силами в смысле, принятом в механике, не являются^[20][15].

Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта^[21]. Соответственно, понятие силы оказывается определённым только для таких систем отсчёта^[22].

Уравнение второго закона Ньютона, связывающее ускорение a→{\displaystyle {\vec {a}}} и массу m{\displaystyle m} материальной точки с действующей на неё силой F→{\displaystyle {\vec {F}}}, записывается в виде

a→=F→m.{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}}.}

Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.

Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.

Учёт содержания всех законов Ньютона приводит к заключению о том, что силы, о которых идёт речь в классической механике, обладают неотъемлемыми свойствами:

• сила есть мера механического действия на данное материальное тело других тел.^[23]

• в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова^[24][25].

• любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результат взаимодействия тел^[26].

Никакие другие силы в классической механике в рассмотрение не вводятся и не используются^[22][27]. Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается^[26][28].

Некоторые авторы используют термин «сила инерции» для обозначения силы-противодействия из третьего закона Ньютона. Понятие было введено Ньютоном в его «Математических началах натуральной философии»^[29]: «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому врожденная сила могла бы быть весьма вразумительно названа силою инерции. Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко — и как сопротивление, и как напор.», а собственно термин «сила инерции» был, по словам Эйлера, впервые употреблён в этом значении Кеплером(^[29], со ссылкой на Е. Л. Николаи).

Для обозначения этой силы-противодействия (действующей на ускоряющее тело со стороны ускоряемого тела^[29]) некоторые авторы предлагают использовать термин «ньютонова сила инерции» во избежание путаницы с фиктивными силами, применяемыми при вычислениях в неинерциальных системах отсчёта и при использовании принципа д’Аламбера.

Отголоском мистических и теологических взглядов Ньютона^[30] является применённая им терминология при описании силы инерции: «врождённая сила материи», «сопротивление». Такой подход к описанию ньютоновской силы инерции хотя и сохранился в современном обиходе^[где?], однако является нежелательным, поскольку вызывает ассоциации с некой способностью тела сопротивляться изменениям, волевым усилием сохранить параметры движения. Максвелл заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким он становится не сам по себе, а лишь после добавления сахара^[29].

Уравнение движения материальной точки в инерциальной системе координат (ИСО), представляющее собой уравнение 2-го закона Ньютона

ma0=F,{\displaystyle m\mathbf {{a}_{0}} =\mathbf {F} ,}

в неинерциальной системе отсчёта (НСО) приобретает четыре дополнительных члена с размерностью силы — так называемые «силы инерции»^[31], иногда называемые «эйлеровыми»:

ma=F−mdVdt+m[rdΩdt]+2m[vΩ]+m[Ω[rΩ]],{\displaystyle m\mathbf {a} =\mathbf {F} -m{\frac {d\mathbf {V} }{dt}}+m[\mathbf {r} {\frac {d\mathbf {\Omega } }{dt}}]+2m[\mathbf {v} \mathbf {\Omega } ]+m[\mathbf {\Omega } [\mathbf {r} \mathbf {\Omega } ]],}

где:

Классификация[править | править код]

Четыре дополнительных члена в уравнении движения принято рассматривать как отдельные силы инерции, которые получили собственные названия:

1. −mdVdt{\displaystyle -m{\frac {d\mathbf {V} }{dt}}} называется поступательной силой инерции. Сила связана с линейным ускорением НСО^[32] и противонаправлена ему;
2. m[rdΩdt]{\displaystyle m[\mathbf {r} {\frac {d\mathbf {\Omega } }{dt}}]} называется вращательной силой инерции. Сила связана с угловым ускорением НСО^[32];
3. m[Ω[rΩ]]{\displaystyle m[\mathbf {\Omega } [\mathbf {r} \mathbf {\Omega } ]]} называется центробежной силой. Сила связана с вращением НСО и потому проявляется и в случае равномерного вращения^[33];
4. 2m[vΩ]{\displaystyle 2m[\mathbf {v} \mathbf {\Omega } ]} называется силой Кориолиса^[34].

Первые три силы, не связанные сдвижением точки, объединяются термином «переносные силы инерции»^[32].

Примеры использования[править | править код]

В некоторых случаях при расчётах удобно использовать неинерциальную систему отсчёта, например:

• движение подвижных деталей автомобиля удобно описывать в системе координат, связанных с автомобилем. В случае ускорения автомобиля эта система становится неинерциальной;
• движение тела по круговой траектории иногда удобно описывать в системе координат, связанной с этим телом. Такая система координат неинерциальна из-за центростремительного ускорения.

В неинерциальных системах отсчёта стандартные формулировки законов Ньютона неприменимы. Так при ускорении автомобиля, в системе координат, связанной с корпусом автомобиля, незакреплённые предметы внутри получают ускорение в отсутствие какой-либо силы, прикладываемой непосредственно к ним; а при движении тела по орбите, в связанной с телом неинерциальной системе координат тело покоится, хотя на него действует ничем не сбалансированная сила гравитации, выступавшая в качестве центростремительной в той инерциальной системе координат, в которой наблюдалось вращение по орбите.

Для восстановления возможности применения в этих случаях привычных формулировок законов Ньютона и связанных с ними уравнений движения для каждого рассматриваемого тела оказывается удобно ввести фиктивную силу — силу инерции — пропорциональную массе этого тела и величине ускорения системы координат, и противонаправленную вектору этого ускорения.

С использованием этой фиктивной силы появляется возможность краткого описания реально наблюдаемых эффектов в неинерциальной системе отсчёта (в разгоняющемся автомомбиле): «почему при разгоне автомобиля пассажира прижимает к спинке сиденья?» — «на тело пассажира действует сила инерции». В инерциальной системе координат, связанной с дорогой, сила инерции для объяснения происходящего не требуется: тело пассажира в ней ускоряется (вместе с автомобилем), и это ускорение производит сила, с которой сиденье действует на пассажира.

Сила инерции на поверхности Земли[править | править код]

В инерциальной системе отсчёта (наблюдатель вне Земли) тело, находящееся на поверхности Земли, испытывает центростремительное ускорение ac{\displaystyle a_{c}}, по величине совпадающее с ускорением точек поверхности Земли, вызванным её суточным вращением. Это ускорение, в соответствии со вторым законом Ньютона, определяется воздействующей на тело центростремительной силой c{\displaystyle c} (зелёный вектор). Последняя складывается из силы гравитационного притяжения к центру Земли g0{\displaystyle g_{0}} (красный вектор) и силы реакции опоры b{\displaystyle b} (чёрный вектор)^[35]. Таким образом, уравнение второго закона Ньютона для рассматриваемого тела в случае инерциальной системы отсчёта имеет вид mac=c{\displaystyle ma_{c}=c} или, что то же самое, mac=g0+b{\displaystyle ma_{c}=g_{0}+b}.

Для наблюдателя, вращающегося вместе с Землёй, тело неподвижно, хотя на него действуют в точности те же силы, что и в предыдущем случае: сила гравитации g0{\displaystyle g_{0}} и реакция опоры b{\displaystyle b}. Противоречия здесь не возникает, поскольку в неинерциальной системе отсчёта, каковой является вращающаяся Земля, применять второй закон Ньютона в обычной форме неправомерно. Вместе с тем в неинерциальной системе отсчёта возможно ввести в рассмотрение силы инерции. В данном случае единственной силой инерции является центробежная сила a{\displaystyle a} (синий вектор), равная произведению массы тела на его ускорение в инерциальной системе отсчёта, взятому со знаком минус, то есть −mac{\displaystyle -ma_{c}}. После введения этой силы уравнение движения тела, приведённое выше, преобразуется в уравнение равновесия тела, имеющее вид g0+a+b=0{\displaystyle g_{0}+a+b=0}.

Сумму сил гравитации g0{\displaystyle g_{0}} и центробежной силы инерции a{\displaystyle a} называют силой тяжести g{\displaystyle g} (жёлтый вектор)^[36]. С учётом этого последнее уравнение можно записать в виде g+b=0{\displaystyle g+b=0} и утверждать, что действия силы тяжести и силы реакции опоры компенсируют друг друга. Отметим также, что относительное значение центробежной силы невелико: на экваторе, где такое значение максимально, её вклад в силу тяжести составляет ~0,3 %^[37]. Соответственно, невелики и отклонения векторов g{\displaystyle g} и b{\displaystyle b} от радиального направления.

Общий подход к нахождению сил инерции[править | править код]

Сравнивая движение тела в инерциальной и неинерциальной СО, можно прийти к следующему выводу^[29]:

Пусть F1→{\displaystyle {\vec {F_{1}}}} есть сумма всех сил, действующих на тело в неподвижной (первой) системе координат, которая вызывает его ускорение a1→{\displaystyle {\vec {a_{1}}}}. Эта сумма находится путём измерения ускорения тела в этой системе, если известна его масса.

Аналогично, F2→{\displaystyle {\vec {F_{2}}}} есть сумма сил, измеренная в неинерциальной системе координат (второй), вызывающая ускорение a2→{\displaystyle {\vec {a_{2}}}}, в общем случае отличающаяся от a1→{\displaystyle {\vec {a_{1}}}} вследствие ускоренного движения второй СО относительно первой.

Тогда сила инерции в неинерциальной системе координат будет определяться разницей:

Fi2→=F2→−F1→{\displaystyle {\vec {F_{i_{2}}}}={\vec {F_{2}}}-{\vec {F_{1}}}} (19)

или:

Fi2→=m(a2→−a1→){\displaystyle {\vec {F_{i_{2}}}}=m({\vec {a_{2}}}-{\vec {a_{1}}})} (20)^[29]

В частности, если тело покоится в неинерциальной системе, то есть a2→=0{\displaystyle {\vec {a_{2}}}=0}, то

Fi2→=−F1→{\displaystyle {\vec {F_{i_{2}}}}=-{\vec {F_{1}}}} (21)^[29].

Работа сил инерции[править | править код]

В классической физике силы инерции встречаются в двух различных ситуациях в зависимости от системы отсчёта, в которой производится наблюдение^[29]. Это — сила, приложенная к связи при наблюдении в инерциальной СО, или сила, приложенная к рассматриваемому телу, при наблюдении в неинерциальной системе отсчёта. Обе эти силы могут совершать работу. Исключением является сила Кориолиса, которая работы не совершает, поскольку всегда направлена перпендикулярно вектору скорости. В то же время сила Кориолиса может изменить траекторию движения тела и, тем самым, способствовать совершению работы другими силами (такими, как сила трения). Примером этому может служить эффект Бэра.

Кроме того, в некоторых случаях бывает целесообразно разделить действующую силу Кориолиса на две составляющие, каждая из которых совершает работу. Суммарная работа, производимая этими составляющими, равна нулю, но такое представление может оказаться полезным при анализе процессов перераспределения энергии в рассматриваемой системе^[38].

При теоретическом рассмотрении, когда искусственно сводят динамическую задачу движения к задаче статики, вводят третий вид сил, называемый силами Даламбера, которые работы не совершают ввиду неподвижности тел, на которые эти силы действуют.

Эквивалентность сил инерции и гравитации[править | править код]

Согласно принципу эквивалентности сил гравитации и инерции локально невозможно отличить, какая сила действует на данное тело — гравитационная сила или сила инерции. Различие между силами гравитации и силами инерции классической механики заключается в невозможности устранения сил гравитации в конечной области пространства-времени переходом к какой-либо системе отсчёта^{[источник не указан 15 дней]}. В этом смысле глобальные или даже конечные инерциальные системы отсчёта в общей теории относительности в общем случае отсутствуют.

В принципе д’Аламбера в рассмотрение вводятся подлинно отсутствующие в природе силы инерции, которые невозможно измерить никакой физической аппаратурой.

Эти силы вводятся ради использования искусственного математического приёма, основанного на применении принципа Д’Аламбера в формулировке Лагранжа, где задача на движение с помощью введения сил инерции формально сводится к проблеме равновесия^[29].

1. ↑ ^{1 2} Тарг С. М. Сила инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. ↑ Сила инерции — статья из Большой советской энциклопедии. 
3. ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—15. — 320 с.
4. ↑ ^{1 2} Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М., Наука, 1987. — Тираж 233000 экз. — с. 119—120
5. ↑ ^{1 2} Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М., Наука, 1975. — Тираж 350000 экз. — с. 291—292
6. ↑ Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике.- М., Наука, 1988. — Тираж 300000 экз. — с. 33
7. ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—18. — 320 с.
8. ↑ ^{1 2} Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3—8.
9. ↑ Walter Greiner Klassische Mechanik II. Wissenschaftlicher Verlag Harri Deutsch GmbH. Frankfurt am Main. 2008 ISBN 978-3-8171-1828-1
10. ↑ ^Richard Phillips Feynman, Leighton R. B. & Sands M. L. (2006). The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. Vol. I, section 12-5. ISBN 0-8053-9049-9. https://books.google.com/books?id=zUt7AAAACAAJ& <=intitle:Feynman+intitle:Lectures+intitle: on+intitle:Physics&lr=&as_brr=0.
11. ↑ ^Cornelius Lanczos (1986). The Variational Principles of Mechanics. New York: Courier Dover Publications. p. 100. ISBN 0-486-65067-7. https://books.google.com/books?id=ZWoYYr8wk2IC&pg=PA103&dq=%22Euler+force%22&lr=&as_brr=0&sig=UV46Q9NIrYWwn5EmYpPv-LPuZd0#PPA100,M1.
12. ↑ ^ Max Born & Günther Leibfried (1962). Einstein’s Theory of Relativity. New York: Courier Dover Publications. pp. 76-78. ISBN 0-486-60769-0. https://books.google.com/books?id=Afeff9XNwgoC&pg=PA76&dq=%22inertial+forces%22&lr=&as_brr=0&sig=0kiN27BqUqHaZ9CkPdqLIjr-Nnw#PPA77,M1.
13. ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
14. ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
15. ↑ ^{1 2} Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
16. ↑ Седов Л. И. Об основных моделях механики. М.: МГУ, 1992. Стр 17.; Седов Л. И. Очерки, связанные с основами механики и физики. М.: Знание, 1983. Стр 19.
17. ↑ Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1979. Стр 393. (в 3-е изд. 2003. Стр.393)
18. ↑ [1]. Вестник высшей школы. Советская наука, 1987. С. 248.
19. ↑ А. Ишлинский при переиздании своей работы удалил эти термины («Классическая механика и силы инерции», 1987, с. 279): … термин «реальная сила» и «фиктивная сила» понимались по-разному. Считаю, что лучше не спорить на эту тему и от упомянутых слов вообще отказаться.
20. ↑ «„Силы инерции“ — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
21. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 182. — 416 с. — ISBN 5-06-003117-9.
22. ↑ ^{1 2} Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 19. — 46 с.
23. ↑ Тарг С. М. Сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
24. ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 16. — 368 с. — ISBN 5-93972-051-X.
25. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 84. — 560 с. — ISBN 5-9221-0225-7.
26. ↑ ^{1 2} Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 59—60. — 546 p. — ISBN 0-07-035048-5.
27. ↑ Встречается утверждение, что применительно к силе Лоренца сказанное не верно и требует дополнительного уточнения (Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132). Согласно другой точке зрения, «в электродинамике силы противодействия силам Лоренца приложены к электромагнитному полю (подстрочное примечание: Стоит отметить, что ещё недавно некоторые видные учёные считали, что сила Лоренца вообще не удовлетворяет закону действия и противодействия…) как к физическому объекту, претерпевающему соответствующее влияние» (Седов, Очерки, с. 17).
28. ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 8. — 320 с.
29. ↑ ^{1 2 3 4 5 6 7 8 9} Хайкин, Семён Эммануилович. Силы инерции и невесомость. — 1. — М., «Наука». Главная редакция физико-математической литературы. 1967 г..— С. 129—130, 188—189. — 312 с.
30. ↑ Ньютон: Физика в контексте Теологии (рус.). snob.ru. Дата обращения 24 января 2020.
31. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 362. — 560 с. — ISBN 5-9221-0225-7.
32. ↑ ^{1 2 3} Егоров Г. В. О силах инерции // Вестник БГУ. 2013. № 1.
33. ↑ Ландавшиц, 1988, с. 165—166.
34. ↑ Ландавшиц, 1988, с. 165.
35. ↑ Китайгородский А. И. Введение в физику. М:Изд.-во «Наука», гл.ред.физико-математической литературы.1973
36. ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
37. ↑ Грушинский Н. П. Основы гравиметрии. — М.: «Наука», 1983. — С. 34. — 351 с.
38. ↑ Krigel A. M. The theory of the index cycle in the general circulation of the atmosphere // Geophys. Astrophys. Fluid Dynamics.— 1980.— 16.— p. 1-18.

Инерции закон — это… Что такое Инерции закон?



Инерции закон

Зако́н ине́рции (Первый закон Нью́тона): свободное тело, на которое не действуют силы со стороны других тел, находится в состоянии покоя или равномерного прямолинейного движения (понятие скорости здесь применяется к центру масс тела в случае непоступательного движения). Иными словами, телам свойственна ине́рция (от лат. inertia — «бездеятельность», «косность»), то есть явление сохранения скорости, если внешние воздействия на них скомпенсированы.

Первый закон Ньютона с точки зрения современных представлений можно сформулировать так: существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на него внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО).

Явлением инерции также является возникновение фиктивных сил инерции в неинерциальных системах отсчета.

Впервые закон инерции был сформулирован Галилео Галилеем, который после множества опытов заключил, что для движения свободного тела с постоянной скоростью не нужно какой-либо внешней причины. До этого общепринятой была иная точка зрения (восходящая к Аристотелю): свободное тело находится в состоянии покоя, а для движения с постоянной скоростью необходимо приложение постоянной силы.

Впоследствии Ньютон сформулировал закон инерции в качестве первого из трёх своих знаменитых законов.

Принцип относительности Галилея: во всех инерциальных системах отсчета все физические процессы протекают одинаково(если условия для всех тел одинаковы). В системе отсчета, приведенной в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчета (условно — «покоящейся») все процессы протекают точно так же, как и в покоящейся системе.

Следует отметить что понятие инерциальной системы отсчета — абстрактная модель (некий идеальный объект рассматриваемый вместо реального объекта. Примерами абстрактной модели служат абсолютно твердое тело или невесомая нить), реальные системы отсчета всегда связаны с каким-либо объектом и соответствие реально наблюдаемого движения тел в таких системах с результатами расчетов будет неполным.

См. также

Литература

Ссылки

Wikimedia Foundation. 2010.

• Инерциальная система отсчета
• Инерции сила

Смотреть что такое «Инерции закон» в других словарях:

• ИНЕРЦИИ ЗАКОН — один из осн. законов механики, согласно к рому при отсутствии внеш. воздействий (сил) или когда действующие силы взаимно уравновешены тело сохраняет неизменным состояние своего движения или покоя относительно инерциальной системы отсчёта. В… …   Физическая энциклопедия

• ИНЕРЦИИ ЗАКОН — см. Ньютона законы …   Большой Энциклопедический словарь

• инерции закон — см. Ньютона законы. * * * ИНЕРЦИИ ЗАКОН ИНЕРЦИИ ЗАКОН, см. Ньютона законы (см. НЬЮТОНА ЗАКОНЫ) …   Энциклопедический словарь

• ИНЕРЦИИ ЗАКОН — квадратичных форм теорема, утверждающая, что при любом способе приведения квадратичной формы с действительными коэффициентами к сумме квадратов посредством линейной замены переменных где Q невырожденная матрица с действительными коэффициентами,… …   Математическая энциклопедия

• ИНЕРЦИИ ЗАКОН — первый закон Ньютона (см. Ньютона законы механики) …   Большой энциклопедический политехнический словарь

• ИНЕРЦИИ ЗАКОН — первый Ньютона закон …   Естествознание. Энциклопедический словарь

• Инерции закон —         один из основных законов механики, согласно которому при отсутствии внешних воздействий (сил) или когда действующие силы взаимно уравновешены, тело сохраняет неизменным состояние своего движения или покоя относительно инерциальной системы …   Большая советская энциклопедия

• Закон инерции — в физике  первый закон Ньютона. см. статью Инерция Закон инерции в математике  см. раздел «Свойства» в статье «Квадратичная форма» (закон инерции Сильвестра) …   Википедия

• ЗАКОН ИНЕРЦИИ — см …   Большая политехническая энциклопедия

• Инерции сила — Сила инерции  фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем. В математических вычислениях введения этой силы происходит путём преобразования… …   Википедия

Книги

• Аналитическое Естествознание, Панченков А.Н.. Монография – итоговый документ пятидесятилетних исследований автора, посвященных Природе и Действительности. Ее цель: создание современного научного Миропонимания в виде аксиоматической… Подробнее  Купить за 1222 руб
• Живая материя. Фундаментальная физика с литературными вставками, А. И. Заказчиков. Успехи формализованного описания явлений природы, блестящим примером которых является закон всемирного тяготения, превратили формализм как бы в достаточную ступень научного познания, снизили… Подробнее  Купить за 440 грн (только Украина)
• Живая материя. Фундаментальная физика с литературными вставками, Заказчиков А.И.. Успехи формализованного описания явлений природы, блестящим примером которых является закон всемирного тяготения, превратили формализм как бы в достаточную ступень научного познания, снизили… Подробнее  Купить за 340 руб

Другие книги по запросу «Инерции закон» >>