Индуктивность — определение термина

Термин и определение

параметр, определяющий энергию магнитного поля участка электрической цепи и численно равный отношению величины потокосцепления этого участка к величине протекающего по нему тока.

Еще термины по предмету «Электроника, электротехника, радиотехника»

Плотность энергии электромагнитного поля (Electromagnetic energy density)

физическая величина, равная отношению энергии электромагнитного поля в некотором объеме к этому объему.

Пробой p-n перехода

явление резкого увеличения дифференциальной проводимости p-n перехода при достижении обратным напряжением (током) критического для данного прибора значения; необратимые изменения в переходе не являются необходимым следствием пробоя.

Сокет (Socket)

то же, что колодка, контактирующее устройство-гнездо, в которое устанавливается микросхема с возможностью простой ее замены.

Похожие

• Индуктивный
• Индуктивные выводы
• Переходная индуктивность
• Индуктивное мышление
• Обучение индуктивное
• Индуктивное определение
• Взаимная индуктивность
• Динамическая индуктивность
• Дифференциальная индуктивность
• Индуктивная катушка
• Индуктивная связь
• Индуктивное сопротивление
• Индуктивный элемент
• Катушка индуктивности
• Собственная индуктивность
• Индуктивный уровнемер
• Индуктивная логика
• Индуктивное умозаключение
• Индуктивный вывод
• Индуктивность переменного тока

Смотреть больше терминов

Научные статьи на тему «Индуктивность»

. -$, является индуктивный…
Стабилизация будет осуществляться в результате действия индуктивного

эффекта заместителей….
В толуоле метильная группа имеет положительный индуктивный эффект, поэтому, по сравнению с бензолом,…
Индуктивное влияние фенильных групп на кислотность Индуктивный эффект может выражаться в системе с пирамидальной…
Чаще всего это индуктивный эффект и эффект сопряжения.

Статья от экспертов

Рассматривается электрическая колебательная система, состоящая из однородных элементов – двух катушек индуктивности. Показана возможность возникновения в такой системе свободных гармонических колебаний.

Научный журнал

Creative Commons

Общая характеристика индуктивных заключений Определение 1 Индуктивные умозаключения – это умозаключения. ..
Пример индуктивного заключения: в ходе проведения физических опытов была обнаружена хорошая электропроводность…
Перечисленные проводники – металлы, что позволило сделать индуктивное обобщение об электропроводности…
В качестве посылок индуктивного умозаключения используются суждения, фиксирующие полученную опытным путем…

Индуктивные выводы в познании в первую очередь реализуют функцию генерализации – обеспечивают получение

Статья от экспертов

Тайваньская фирма Yageo выпускает широкий ассортимент пассивных компонентов. Большой интерес представляют индуктивные элементы, о которых и пойдет речь в этой статье.

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

Привет! Рады, что термин оказался полезен 🤩

Для копирования текста подпишись на Telegram bot. Удобный поиск по учебным материалам в твоем телефоне

Подписаться и скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Подписчики нашего бота Edu24_bot получают определение прямо в телеграмм! Просто перейди по ссылке ниже

Скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Определение индуктивности катушки (Лабораторная работа № 11)

Лабораторная работа 11

Определение индуктивности катушки

Цель работы: изучение явления электромагнитной индукции.

Задание 1. Определить индуктивность катушки без сердечника.

Задание 2. Определить индуктивность катушки с железным сердечником.

Приборы и принадлежности: исследуемая катушка, сердечник из трансформаторной стали, вольтметр, амперметр, источник переменного тока –  (лабораторный автотрансформатор).

Теория метода

Закон Ома для квазистационарных токов (токи частотой до ) имеет вид

,                                                       (1)

где  – напряжение в цепи переменного тока;  – сопротивление в цепи переменного тока ;  – омическое или активное сопротивление;  – индуктивное сопротивление;  – емкостное сопротивление.

Для цепи с сосредоточенными и

.                                                    (2)

Из выражения (2) можно найти индуктивность катушки

,                                                   (3)

где  – круговая (циклическая) частота – число колебаний тока (или его изменений) в  секунд;  – промышленная частота переменного тока
(50 Гц).

Если катушку включить в цепь переменного тока, то в ней возникает ЭДС самоиндукции

ℰ,                                                      (4)

где  – коэффициент пропорциональности между ℰ и изменением тока во времени  или индуктивность катушки.

Так как по правилу Ленца индукционный ток  направлен против возрастания тока в цепи , то из-за уменьшения тока возникает кажущееся сопротивление индуктивности (реактивное сопротивление) (рис. 1)

.                                                        (5)

Рис. 1. Электрическая схема цепи

Выполнение работы

Задание 1. Определение индуктивности катушки без сердечника

1. Проверьте электрическую цепь по схеме рис. 1. ЛАТР (лабораторный автотрансформатор) должен быть выведен на «0» (вращением ручки ЛАТРа против часовой стрелки).

2. Катушка должна быть без сердечника. Замкните ключ  и, плавно вращая ручку ЛАТРа по часовой стрелке, подайте напряжение на катушку величиной 50 В. Снимите показания амперметра. Подавая затем 60 В и 70 В, снимите     показания амперметра и занесите все в табл. 1.

Таблица 1

Номер опыта	Наименование показателей
	,	,	,	,	,	,	,	, %
Катушка без сердечника
1
2
3
Сердечник в катушку введен
1
2
3

Задание 2. Определение индуктивности катушки с железным сердечником

1. Выведите  на «0». Введите сердечник в катушку и произведите измерения согласно п. 2 задания 1. Все данные занесите в табл. 1.

Данные одной из обмоток катушки индуктивности:  = 1200 витков,      = 14 Ом.

Zи L рассчитайте по (2) и (3). Результаты занесите в табл. 1.

Рассчитайте ошибки методом среднего арифметического для задания 1 и задания 2.

Сделайте выводы по результатам работы.

Контрольные вопросы

1. В чем заключается явление электромагнитной индукции? Как читается правило Ленца? На основании какого закона возникает индуктивный ток?

2. Дайте понятие индуктивности. Единицы измерения.

3. В чем заключается явление самоиндукции?

4. Почему при включении катушки с  (омическое сопротивление)
в цепь переменного тока ее сопротивление возрастает и обозначается
буквой ?

5. Закон Ома для цепи переменного тока.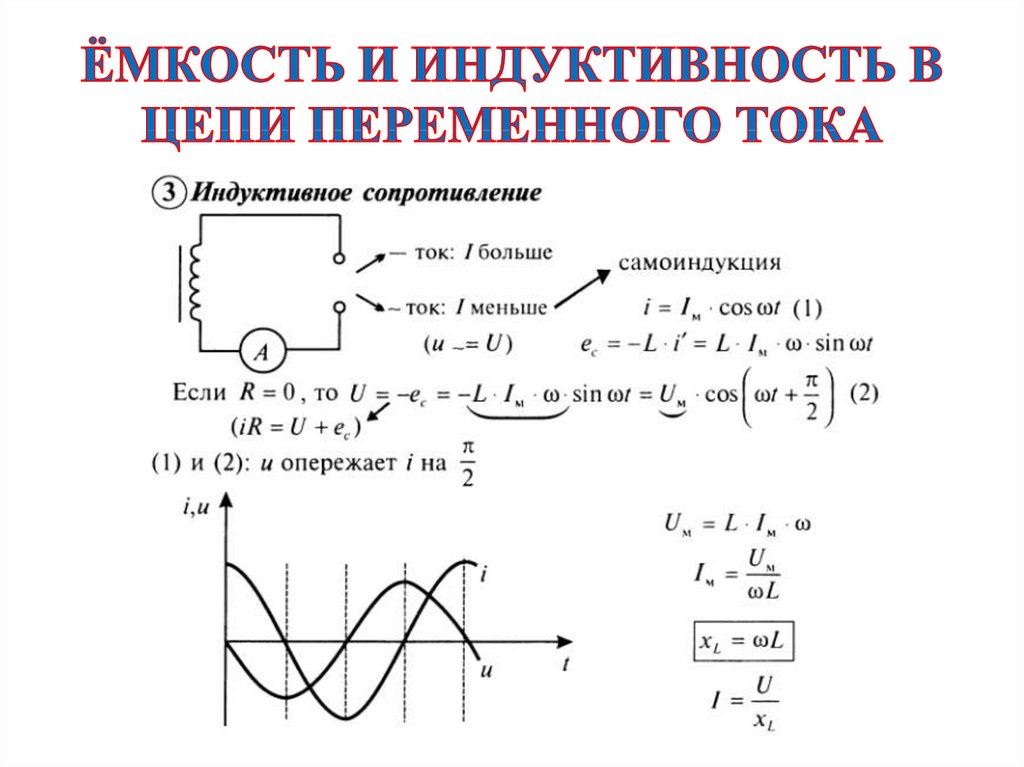

6. Векторная диаграмма напряжений. Что из нее можно извлечь?

7. Реактивные сопротивления ( и ) называют «кажущимися»
сопротивлениями. Причина такого названия.

8. Линейная частота  и как она связана с периодом колебаний и круговой или циклической частотой ?

9. Что значит омическое, или активное сопротивление?

Библиографический список

1. Савельев И. В. Курс общей физики / И. В. Савельев. – М. : Наука, 1982. – Т. 2. – Гл. XIII. – С. 181–15, 188–191. (Электромагнитная индукция.
§ 60. Явление электромагнитной индукции. § 61. Электродвижущая сила
индукции. § 64. Явление самоиндукции).

2. Грабовский Р. И. Курс физики / Р. И. Грабовский. – М. : Высш. шк., 2002. – Гл. XV. – С. 353-362. (Электрическая индукция и переменный
ток. §103. Электромагнитная индукция. Закон Фарадея. Правило Ленца.
§ 104. Взаимная индукция и самоиндукция).

3. Поцелуйко А. А. Общая физика : курс лекций для студентов торгово-экономических вузов / А. А. Поцелуйко; Краснояр. гос. торг.-экон. ин-т. – Красноярск, 2005. – Раздел 3.– С. 148–152. (Электромагнитная индукция.     Лекция 31).

23.9 Индуктивность – Колледж физики 2e

Цели обучения

К концу этого раздела вы сможете:

• Расчет индуктивности катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Катушки индуктивности

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью.

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 23.37, где простые катушки наводят друг в друге ЭДС.

Рисунок 23.37 Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2E2 индуцируемая» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока ΔI/ΔtΔI/Δt как на причине индукции. Изменение тока I1I1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС2ЭДС2 в другом. Мы выражаем это в виде уравнения как

ЭДС2=-MΔI1Δt, ЭДС2=-MΔI1Δt,

23,34

, где MM определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность ММ, тем эффективнее связь. Например, катушки на рис. 23.37 имеют малый ММ по сравнению с катушками трансформатора на рис. 23.27. Единицы измерения ММ: (В⋅с)/A=Ω⋅с(В⋅с)/A=Ω⋅с, что называется генри (H) в честь Джозефа Генри. То есть 1 H=1Ω⋅s1 H=1Ω⋅s.

Природа здесь симметрична. Если мы изменим ток I2I2 в катушке 2, мы индуцируем ЭДС1ЭДС1 в катушке 1, которая определяется как

, где ММ — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью MM .

Большая взаимная индуктивность MM может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность MM — это встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 23.38.)

Рисунок 23.38 Нагревательные катушки электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока ΔIΔI через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

ЭДС=-LΔIΔt, ЭДС=-LΔIΔt,

23,36

, где LL — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется индуктором и обозначается символом на рис. 23.39.

Рисунок 23.39

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность LL устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой LL и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшой LL, например, за счет встречной обмотки катушек, как показано на рис. 23.38.

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L=1,0 HL=1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная формулой ЭДС=-L(ΔI/Δt)ЭДС=-L(ΔI/Δt), будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться по формуле ЭДС=-L(ΔI/Δt)=(1,0 Гн)[(10 А)/(1,0 мс)]=10 000 ВЭДС=-L(ΔI/Δt)=(1,0 Гн)[ (10 А)/(1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение имеет то же направление, что и ток, и препятствует его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Такое большое наведенное напряжение может быть использовано. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 23.40.)

Рисунок 23.40 Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать LL для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Так что в этом тексте индуктивность LL обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как ЭДС=−N(ΔΦ/Δt) э.д.с.=−N(ΔΦ/Δt) и, по определению самоиндукции, как ЭДС=−L( ΔI/Δt) э.д.с.=-L(ΔI/Δt). Приравнивая эти выходы

ЭДС=-NΔΦΔt=-LΔIΔt.ЭДС=-NΔΦΔt=-LΔIΔt.

23,37

Решение для LL дает

L=NΔΦΔI.L=NΔΦΔI.

23,38

Это уравнение для собственной индуктивности LL устройства всегда справедливо. Это означает, что собственная индуктивность LL зависит от того, насколько эффективно ток создает поток; тем эффективнее, чем больше ΔΦΔΦ/ ΔIΔI.

Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь соленоида AA фиксирована, изменение потока равно ΔΦ=Δ(BA)=AΔBΔΦ=Δ(BA)=AΔB. Найти ΔBΔB, заметим, что магнитное поле соленоида определяется выражением B=μ0nI=μ0NIℓB=μ0nI=μ0NIℓ. (Здесь n=N/ℓn=N/ℓ, где NN – количество витков и ℓℓ — длина соленоида.) Изменяется только ток, так что ΔΦ=AΔB=μ0NAΔIℓΔΦ=AΔB=μ0NAΔIℓ. Замена ΔΦΔΦ в L=NΔΦΔIL=NΔΦΔI дает

L=NΔΦΔI=Nμ0NAΔIℓΔI.L=NΔΦΔI=Nμ0NAΔIℓΔI.

23,39

Это упрощается до

L=μ0N2Aℓ(соленоид).L=μ0N2Aℓ(соленоид).

23,40

Самоиндукция соленоида с площадью поперечного сечения AA и длиной ℓℓ. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 23,7

Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.

Стратегия

Это прямое применение L=μ0N2AℓL=μ0N2Aℓ, поскольку известны все величины в уравнении, кроме LL.

Решение

Используйте следующее выражение для собственной индуктивности соленоида:

L=μ0N2Aℓ.L=μ0N2Aℓ.

23,41

Площадь поперечного сечения в этом примере равна A=πr2=(3,14…)(0,0200 м)2=1,26×10−3 м2A=πr2=(3,14…)(0,0200 м)2= 1,26×10−3 м2, NN принимается равным 200, а длина ℓℓ составляет 0,100 м. Мы знаем, что проницаемость свободного пространства равна µ0=4π×10−7T⋅м/Aµ0=4π×10−7T⋅м/A. Подставляя их в выражение для ЛЛ дает

L=(4π×10−7 Т⋅м/А)(200)2(1,26×10−3 м2)0,100 м=0,632 мH.L=(4π×10−7 Т⋅м/А)(200 )2(1,26×10-3 м2)0,100 м=0,632 мГн.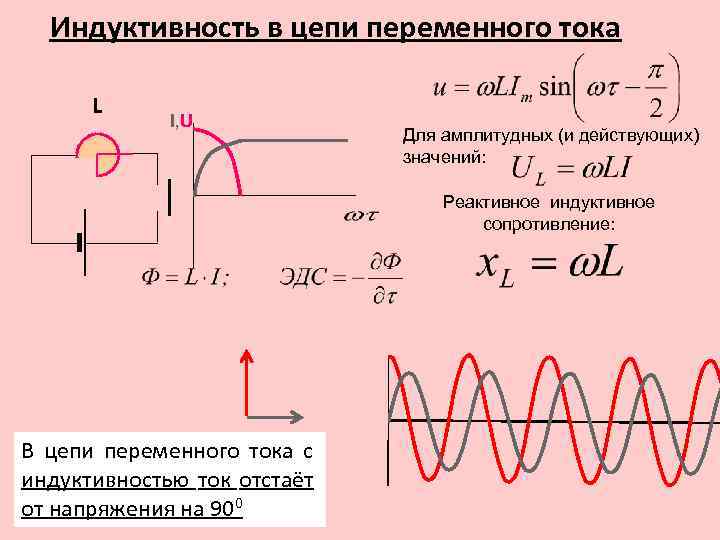

23,42

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных приложений индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. См. рисунок 23.41.

Рисунок 23.41 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: shankar s/Flickr)

Энергия, хранящаяся в индукторе

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что энергия, запасенная в катушке индуктивности EindEind, равна

Eind=12LI2.Eind=12LI2.

23,43

Это выражение похоже на выражение для энергии, запасенной в конденсаторе.

Пример 23,8

Расчет энергии, запасенной в поле соленоида

Сколько энергии сохраняется в катушке индуктивности 0,632 мГн из предыдущего примера, когда через нее протекает ток 30,0 А?

Стратегия

Энергия задается уравнением Eind=12LI2Eind=12LI2, и все величины, кроме EindEind, известны.

Решение

Подстановка значения LL, найденного в предыдущем примере, и заданного тока в Eind=12LI2Eind=12LI2 дает

Eind=12LI2=0,5(0,632×10−3 H)(30,0 A)2=0,284 Дж. Eind=12LI2=0,5(0,632×10−3 H)(30,0 A)2=0,284 Дж.

23,44

Обсуждение

Этого количества энергии, безусловно, достаточно, чтобы вызвать искру при внезапном отключении тока. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

Определение, формула, типы и применение

Индуктивность — это свойство проводника, намотанного в виде катушки, которое сопротивляется любому изменению тока, протекающего через него. Согласно закону электромагнитной индукции Фарадея, при изменении тока в катушке возникает ЭДС (электродвижущая сила). Величина ЭДС пропорциональна скорости изменения тока. Константа пропорциональности — это индуктивность.

Индуктивность

Формула индуктивности

Индуктивность ( L ) рассчитывается из отношения ЭДС индукции ( ε ) и величина скорости изменения тока ( ΔI/Δt ).

\[ L = \frac{\epsilon}{|\frac{\Delta I}{\Delta t}|} \]

Для измерения индуктивности мы используем в электрической цепи устройство, называемое катушкой индуктивности. Единицей индуктивности в СИ является Генри или H, названная в честь американского ученого Джозефа Генри. Он открыл электромагнитную индукцию примерно в 1831 году.

Индуктивность и форма индукторов

Индуктивность разработана таким образом, чтобы использовать преимущества индуктивности, принимая форму катушки. Эта форма приводит к более сильному магнитному полю, чем то, которое создается прямым проводом.

Некоторые катушки индуктивности состоят из одного провода и свернуты в самонесущую катушку. Другие катушки индуктивности состоят из проволоки, намотанной в катушку вокруг длинного сплошного сердечника, круглого сердечника или прямоугольного сердечника из мягкого железа. Сердечник из мягкого железа подавляет рост тока более эффективно, чем воздух, увеличивая индуктивность.

Типы индуктивности

Существует два способа использования индуктивности в электрической цепи.

1. Самоиндукция

Если ЭДС индуцируется в той же катушке, что и протекающий ток, это называется самоиндукцией. Примером устройства, в котором возникает самоиндукция, является дроссель. Символ L обозначает его.

Собственная индуктивность

Уравнение

Собственная индуктивность L может быть найдена через поток φ , число витков катушки N и ток I .

\[ L = \frac{N\phi}{I} \]

Используя приведенное выше уравнение, можно рассчитать самоиндукцию для соленоида и тора.

1. Соленоид

Следующее уравнение дает самоиндукцию соленоида.

92 a} {2 \ pi r} \]

, где

N : количество поворотов

A : область поперечного сечения

R : радиус

μ _{: радиус}

μ _{: радиус}

μ _{: радиус}

μ _{: радиус}

μ _{: радиус}

μ _{: радиус}

μ _{: радиус}

μ _. : Проницаемость воздуха

Самоиндукция тороидальной катушки

Предположим, катушка намотана на сплошной сердечник, а не на полый. В этом случае воздухопроницаемость заменяется проницаемостью материала сердцевины и обозначается μ .

2. Взаимная индуктивность

Если ЭДС создается в другой катушке, расположенной рядом с первой, это называется взаимной индуктивностью. Взаимная индуктивность возникает в трансформаторе, генераторе и двигателе. Обозначается символом M .

Уравнение взаимной индуктивности

Предположим, что вторая катушка имеет N ₂ , а поток проходит через нее из -за тока I ₁ в первой катушке φ 288888888888888 2101288888888. Следующее уравнение дает взаимную индуктивность.

\[ M = \frac{N_2 \phi_{21}}{I_1} \]

На основании вышеприведенного уравнения можно рассчитать взаимную индуктивность для различного расположения катушек.

Взаимная индуктивность между катушкой и соленоидом

Следующее уравнение дает взаимную индуктивность катушки, намотанной на соленоид.

\[ M = \frac{\mu_o N_1N_2 A}{d} \]

Где

N ₁ : Количество витков соленоида

N ₂ : Число витков катушки

A : Площадь поперечного сечения соленоида

d : Длина соленоида

1. Длина катушки : обратно пропорциональна длине катушки. При увеличении длины катушки индуктивность уменьшается, и наоборот.

2. Площадь поперечного сечения катушки : Прямо пропорциональна площади поперечного сечения катушки. Чем больше площадь катушки, тем выше индуктивность.

3. Количество витков : Прямо пропорционально количеству витков в квадрате. Следовательно, чем больше число витков, тем выше индуктивность.

4. Проницаемость сердечника : Проницаемость материала сердечника позволяет формировать магнитное поле внутри сердечника. Индуктивность прямо пропорциональна магнитной проницаемости. Чем выше проницаемость, тем выше будет индуктивность.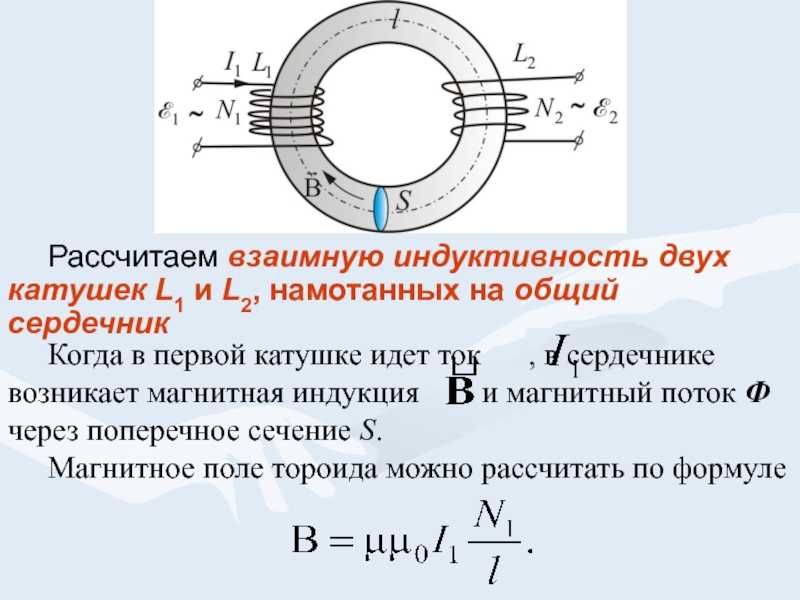

Использование и применение

• Для замедления скачков тока путем временного накопления электрической энергии в электромагнитном поле и высвобождения ее в цепь
• Для подавления или блокирования высокочастотных помех в электрической цепи
• Для накопления и передачи энергии в преобразователи мощности, такие как постоянный или переменный ток в постоянный
• Для выбора желаемой частоты в настроенной цепи, такой как LC-цепь
• Для согласования импеданса источника питания с импедансом электрической нагрузки, известной как согласование импеданса
• To amplify the current in a proximity sensor

What is the Difference Between Self-inductance and Mutual Inductance

	Self-inductance	Mutual Inductance
Definition	Магнитный поток в одной катушке создает ЭДС, противодействующую току	Магнитный поток связывает пару катушек, и в обеих катушках создается ЭДС, которая противодействует току в другой катушке
Что происходит	ЭДС индукции противодействует нарастанию/падению тока, когда ток в катушке увеличивается/уменьшается	ЭДС индукции во второй катушке противодействует нарастанию/падению тока в первой катушке, когда ток увеличивается/уменьшается
Где это происходит	Это происходит в одной катушке, как дроссель	Это происходит в паре катушек в трансформаторе, генераторе и двигателе
Символ	L	M

различие между собой и мутоил. Как найти эквивалентную индуктивность последовательно соединенных катушек индуктивности?

Ответ. Когда катушки индуктивности соединены последовательно, эквивалентная индуктивность представляет собой сумму отдельных индуктивностей.

Q.2. Как общая индуктивность соотносится с отдельными индуктивностями при параллельном соединении катушек индуктивности?

Ответ. Когда катушки индуктивности соединены параллельно, общая индуктивность меньше индуктивности любой из параллельных катушек индуктивности.

Q.3. В чем разница между индуктивностью и емкостью?

Ответ. Основное различие между индуктивностью и емкостью заключается в том, что индуктивность — это свойство проводника с током, который создает магнитное поле вокруг проводника. С другой стороны, емкость — это свойство устройства, которое может удерживать и накапливать электрические заряды.