Как рассчитать плотность тока?
Электричество стало неотъемлемой частью нашей современной жизни. Нам нужно электричество, чтобы осветить темную комнату и привести в действие все наши приборы, такие как вентиляторы, смесители, кондиционеры, телевизоры и т. д. На самом деле мы не можем представить мир без электричества. Электричество называют формой энергии, возникающей из-за потока электронов. Есть два вида электричества, а именно статическое электричество и электричество тока. Поскольку использование электроэнергии в настоящее время увеличивается, она производится в больших количествах и хранится. Ток определяется как скорость потока заряда от отрицательных точек к положительным точкам в электрической цепи. Измеряется в амперах (А) и обозначается буквой (I). Существует два вида тока, а именно, переменный ток и постоянный ток.
Плотность тока В физике плотность тока или плотность электрического тока связана с электромагнетизмом и определяется как мера тока, протекающего через единицу площади поперечного сечения. Электрический ток (I) — это макроскопическая величина, и мы определяем соответствующую микроскопическую величину, называемую плотностью тока. Плотность тока имеет как величину, так и направление, поскольку это векторная величина. В случае постоянного тока ток протекает равномерно по всему проводнику, даже если площадь поперечного сечения различается. С помощью плотности тока мы можем рассчитать количество тока, протекающего в заданном участке проводника. Он обозначается буквой «J», а его единица СИ — А/м 9.0009 2 .
Электрический ток (I) — это макроскопическая величина, и мы определяем соответствующую микроскопическую величину, называемую плотностью тока. Плотность тока имеет как величину, так и направление, поскольку это векторная величина. В случае постоянного тока ток протекает равномерно по всему проводнику, даже если площадь поперечного сечения различается. С помощью плотности тока мы можем рассчитать количество тока, протекающего в заданном участке проводника. Он обозначается буквой «J», а его единица СИ — А/м 9.0009 2 .
Рассмотрим проводящий провод и подключим оба конца провода к батарее. Теперь будет создаваться электрическое поле, которое приводит к потоку электронов через проводник. Теперь, если σ — электропроводность проводящего провода, то плотность тока прямо пропорциональна напряженности электрического поля.
Плотность тока (Дж) = σ E
Где σ — электрическая проводимость,
E — электрическое поле.
Формула плотности тока:
Плотность тока (Дж) = I/A площадь сечения проводника.
Размерная формула плотности тока M 0 L -2 T 0 I 1 , где M — масса, L — длина, T — время, I — ток.
Решенные проблемыЗадача 1: Рассчитать плотность тока, если по медному проводу с площадью поперечного сечения 20 м 2 протекает ток силой 60 А.
Решение:
Данные,
Ток, протекающий по проводу (I) = 60 A
Площадь поперечного сечения провода (A) = 20 м 2
9002 Мы знаем, что ,Плотность тока (Дж) = I/A
Дж = (60)/(20)
Дж = 3 А/м 2
Отсюда плотность тока 3 А/м 2 .
Задача 2. Определить плотность тока, если по медному проводу диаметром 3 мм протекает ток силой 5 А.
Решение:
Данные данные,
Ток, протекающий через проволоку (I) = 5A
Диаметр провода = 3 мм
⇒ Радиус = 3/2 = 1,5 мм = 0,0015 м
.
поперечного сечения провода = πr 2
A = 3.14 × (0.0015) 2
A = 0.000007065 m 2
We know that,
Current density (J) = I/A
J = 5/0.000007065
J = 7,07 × 10 5 А/м 2
Таким образом, плотность тока равна 7,07 × 10 5 А/м 2 .
Задача 3. Найти ток, протекающий по металлической проволоке, если площадь ее поперечного сечения 15 м 2 и плотность тока 5 А/м 2 .
Решение:
Данные данные,
Площадь поперечного сечения (A) = 15 M 2
Плотность тока (J) = 5 A/M 2
Мы знаем,
Плотность тока (Дж) = I/A
5 = I/15
I= 5 × 15 = 75 А
Следовательно, сила тока, протекающего по проводу, равна 75 А.
Задача 4. Найти площадь поперечного сечения провода при протекании тока по проводу 4 мА и плотности его тока 0,25 А/м 2 .
Решение:
Данные,
Ток, протекающий по проводу (I) = 4 мА = 0,004 А
Плотность тока (Дж) = I/A
0,25 = 0,004/A
A = 0,004/0,25
A = 0,016 м 2 = 16 мм 2
03 площадь поперечного сечения, провод 16 мм 2 .
Задача 5. Определить плотность тока, если по проводнику с площадью поперечного сечения 17 м 9 протекает ток силой 85 А.0009 2 .
Решение:
Данные,
Ток, протекающий по проводу (I) = 85 A
Площадь поперечного сечения провода (A) = 17 м2
Мы знаем, что, Плотность тока (Дж) = I/A
Дж = 85/17
Дж = 5 А/м 2
Следовательно, плотность тока равна 5 А/м 2 .
Задача 6: Каково определение плотности тока и ее единица измерения СИ?
Решение:
В физике плотность тока или плотность электрического тока определяется как мера тока, протекающего через единицу площади поперечного сечения.
Он обозначается буквой «J», а единицей измерения в системе СИ является ампер на квадратный метр (А/м 2 ).
Как анализировать схемы — основы схем
Прежде чем мы углубимся в обсуждение анализа схем, давайте сначала определим схему или электронную схему.
Электронная схема представляет собой систему, состоящую из электронных компонентов, таких как резисторы, транзисторы, конденсаторы, катушки индуктивности, диоды и многих других, соединенных проводами, по которым может протекать электрический ток. Создание схем — это использование электричества для создания полезных устройств для нашей повседневной жизни.
Итак, что такое анализ цепи? Это математический анализ электрической или электронной цепи. Это процесс изучения и анализа электрических величин посредством расчетов. С помощью этого анализа мы можем найти неизвестные элементы цепи, такие как напряжение, ток, сопротивление, импеданс, мощность и т. д., по ее компоненту. При анализе цепей нам необходимо понимать электрические величины, отношения, теоремы и некоторые основные законы.
Есть два важных закона, которые нам необходимо усвоить для анализа цепей. Это основные сетевые законы, а именно: (1) KCL или закон тока Кирхгофа и (2) KVL или закон напряжения Кирхгофа.
Что такое KCL?
Текущий закон Кирхгофа (KCL) также известен как первый закон Кирхгофа, правило точек Кирхгофа или правило соединения Кирхгофа (или узловое правило). Это один из фундаментальных законов, используемых для анализа цепей. В нем говорится, что общий ток, входящий в соединение или узел, равен току, выходящему из узла, поскольку ток в узле не теряется 9.0269 . Другими словами, KCL утверждает, что алгебраическая сумма всех токов, входящих и исходящих из узла, должна быть равна нулю . Густав Кирхгоф основывал свою идею на законе сохранения заряда.
Математически это может быть выражено как:
Поскольку KCL также называется узловым правилом, мы можем связать его с анализом узлового напряжения. Мы можем выполнить узловой анализ с помощью KCL. Узловой анализ или метод анализа узлового напряжения определяет напряжение (разность потенциалов) между «узлами» в электрической цепи с точки зрения токов ветвей. Метод анализа узловых напряжений решает неизвестные напряжения в узлах схемы с помощью системы уравнений KCL.
Метод анализа узловых напряжений решает неизвестные напряжения в узлах схемы с помощью системы уравнений KCL.
Как использовать анализ узлового напряжения
Для иллюстрации рассмотрим схему ниже.
Во-первых, давайте вспомним Текущий Закон Кирхгофа, который может быть выражен как:
Из рисунка видно, что есть два узла, V1 и V2. Напомним, что узел — это место, где соединены две или более ветвей. Эти узлы представляют собой неизвестные напряжения узлов, которые нам нужно найти. Ниже схемы находится эталонный узел, где нулевое напряжение. Для каждого узла должно быть уравнение. Поскольку у нас есть два узла, нам понадобятся два уравнения.
Чтобы применить KCL к V 1 и V 2 , нам нужно знать направления каждого тока. Но сначала нам нужно обратиться к источникам.
Для источника питания 20 В обратите внимание, что ток выходит из положительной клеммы и идет к V 1 . Для источника тока мы уже знаем его текущее направление на основе символа на схеме; ток идет к V 2 .
Помните, что ток течет от высокого потенциала к низкому, а опорный узел имеет 0 В. Следовательно, мы можем сказать, что это низкий потенциал, что означает, что ток течет от V1 и V2 к эталонному узлу.
Теперь, для тока в ответвлении с резистором 4 Ом, мы можем просто предположить, что ток течет от V 1 до V 2 .
Чтобы получить уравнения тока для каждого элемента, нам нужно применить закон Ома, который гласит, что ток равен разнице между высоким и низким потенциалом, деленной на сопротивление. Это выражается как:
Чтобы упростить задачу, нам нужно назначить полярность резисторам в соответствии с направлением тока. Нам также нужно назначить токи, протекающие по каждой ветви:
i 1 = ветвь резистора 2 Ом
i 2 = ветвь резистора 4 Ом
i 3 = ветвь резистора 10 Ом
i 4 = ветвь резистора 20 Ом3 применит KCL к каждому узлу. Выразите каждый ток через V 1 и V 2 , используя закон Ома.
Затем мы можем написать узловые уравнения. А так как у нас два узла, то нужно написать два уравнения. Для простоты предположим, что токи, входящие в узел, положительны, а токи, выходящие из узла, отрицательны.
@node 1 or V 1 : i 1 – i 3 – i 2 = 0
@node 2 or V 2 : i 2 – i 4 + 4 = 0
Выражая эти два уравнения через V 1 и V 2 , мы имеем:
@node 1,
@node 2,
два неизвестных, мы можем начать решать.
Для первого уравнения упростите:
Для второго уравнения упростите:
Примените сокращение для двух уравнений.
Подставьте значение в любое из двух уравнений, чтобы получить V 2 .
Для проверки:
Теперь, когда у нас есть значения V 1 и V 2 , мы можем найти ток, протекающий по каждой ветви.
Что такое КВЛ?
Вторым фундаментальным законом анализа цепей является закон Кирхгофа о напряжении или KVL. Это также называется вторым законом Кирхгофа или правилом петли (или сетки) Кирхгофа. КВЛ утверждает, что направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю . Проще говоря, в нем говорится, что алгебраическая сумма всех напряжений в контуре должна быть равна нулю .
Математически это может быть выражено как:
Поскольку KVL также называется правилом сетки, мы можем связать его с текущим анализом сетки. Мы можем выполнить анализ сетки с помощью KVL.
Анализ сетки или анализ тока сетки используется для решения схемы с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений. Это особенно полезно, если вам нужно решить ее без калькулятора. Это хорошо организованный метод решения схемы, но для анализа сети с помощью анализа сетки нам необходимо выполнить определенные условия. Анализ сетки применим только к схемам или сетям планировщика, которые проще и не имеют перекрестных проводов.
Анализ сетки применим только к схемам или сетям планировщика, которые проще и не имеют перекрестных проводов.
Как использовать анализ тока сетки
Сетка — это одиночный замкнутый контур, указанный в цепи. Чтобы проиллюстрировать анализ тока сетки, давайте рассмотрим схему ниже.
Вспоминая KVL, мы выражаем его в следующем уравнении:
Из рисунка видно, что две сетки назначены как сетка 1 и сетка 2. . Напряжение, возникающее от положительного (+) к отрицательному (-), является положительным, а напряжение, возникающее от отрицательного (-) к положительному (+), является отрицательным.
Теперь давайте назначим потоки сетки в каждой сетке. Для сетки 1 у нас есть i
Затем смотрим текущее направление в каждой ветке.
Затем примените KVL к каждому из мешей. А так как в КВЛ сумма напряжений в замкнутом контуре равна нулю, то нужно найти напряжение на каждом элементе. Мы будем использовать закон Ома: V=IR.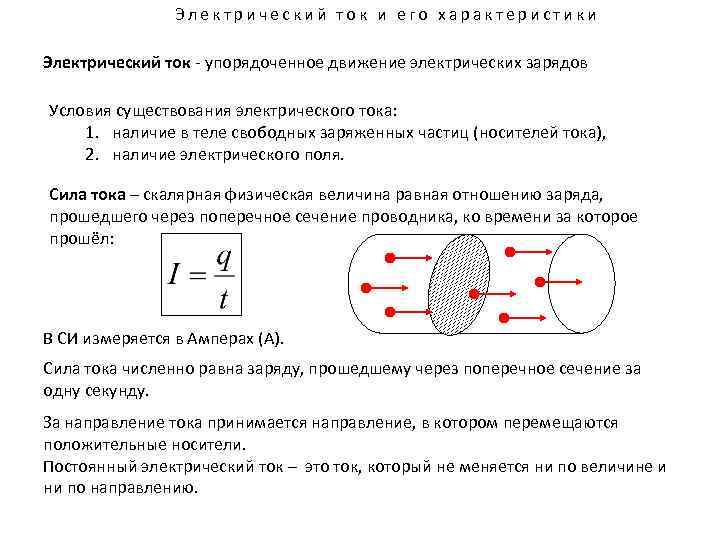
Итак, если у нас есть резистор сопротивлением 1 Ом, по закону Ома напряжение равно 2i 1 . Для ветки с резистором 6 Ом напряжение находится между сеткой 1 и сеткой 2. Мы должны назначить ток i
Глядя на узел, мы имеем:
Применяя KCL, мы можем получить i 3 через i 1 и i 2 по:
Затем мы можем написать уравнения сетки.
@mesh 1 или I 1 :
@mesh 2 или I 2 :
, выражая I 3 , используя I 1 и I 2 , У нас есть:
Теперь. два уравнения для двух сеток, мы можем начать решать.
Подставив i 2 в уравнение 1, мы получим:
Для проверки подставим полученные значения в любое из двух уравнений сетки.
Теперь, когда у нас есть значения i1 и i2, мы можем найти падение напряжения на каждом резисторе.
Используя закон Ома, мы можем просто найти падение напряжения путем подстановки.



 поперечного сечения провода = πr 2
поперечного сечения провода = πr 2 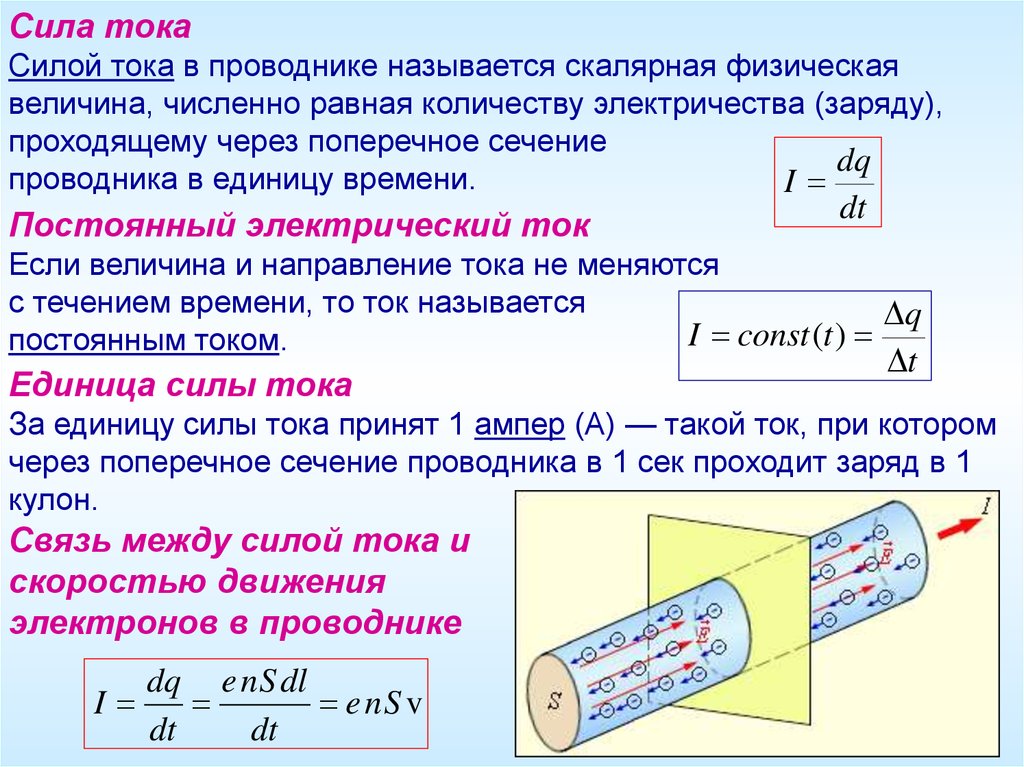 Он обозначается буквой «J», а единицей измерения в системе СИ является ампер на квадратный метр (А/м 2 ).
Он обозначается буквой «J», а единицей измерения в системе СИ является ампер на квадратный метр (А/м 2 ).