Электродвижущая сила индукции

Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.

Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.

Электромагнитная индукция

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.

Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:

1. Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
2. Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.

Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.

Закон Фарадея

Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).

Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:

$\left|Ɛ_{i} \right|=\frac{dФ}{dt}\left( 1 \right)$.

где $Ф$ — поток магнитной индукции.

Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.

Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:

Определение 1

Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 2 \right)$.

где под $\frac{dФ}{dt}$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.

Минус в формуле (2) указывает на то, что:

• При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($\frac{dФ}{dt}>0)$, ЭДС индукции меньше нуля ($Ɛ_i
• При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.

Замечание 1

Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.

Закон Фарадея справедлив при:

1. произвольных перемещениях замкнутого проводящего контура;
2. при любых его деформациях;
3. изменениях магнитного поля.

ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).

$\left[ Ɛ_{i} \right]=\left[ \frac{dФ}{dt} \right]=\frac{Вб}{с}$=В.

Значение закона Фарадея

Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.

Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.

Природа электродвижущей силы индукции

Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.

Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ

Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $\vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:

$\vec{F}_{L}=q\left( \vec{v}\times \vec{B} \right)\left( 3 \right)$.

где$ \vec{B}$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($\vec n$) к площади контура указана на рис.1.

Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:

$\vec{E}=\frac{\vec{F}_{L}}{q}=\vec{v}\times \vec{B}\left( 4 \right)$.

Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:

$\left( Ɛ_{i} \right)_{21}=\int\limits_1^2 \vec{E} d\vec{l}=\int\limits_1^2\left( \vec{v}\times \vec{B} \right) d\vec{l}\left( 5 \right)$.

В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:

$\left( Ɛ_{i} \right)_{DG}=\int\limits_G^D {vBdl=vBl\, \left( 6 \right).} $

На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.

$Ɛ_{i}=\int\limits_{AGDCA} {\vec{E}d\vec{l}=vBl\, \left( 7 \right).} $

Скорость перемещения проводника выразим как:

$v=\frac{dx}{dt}\left( 8 \right)$.

где $x$ — координата контактов проводника в точках $D$ и $G$ направляющими проводниками:

$Ɛ_{i}=Bl\frac{dx}{dt}\left( 9 \right)$.

Учитывая, что:

$Ф=-xlB$ (10),

где $Ф$ — поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $\vec B$ и $ d\vec S$ противоположны,

окончательно имеем:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 11 \right)$.

Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.

Электромагнитная индукция

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.

Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

ЭДС индукции

Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{\mathcal E}}_i$). Величина ${{\mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($\frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:

Знак потока $Ф$ и знак ${{\mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{\mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($\overrightarrow{n}$) $\frac{dФ}{dt} >0,\ {{\mathcal E}}_i

Рисунок 1.

Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1\frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.

В гауссовой системе формула (1) принимает вид:

где $с$ — скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{\mathcal E}}_i$ измеряется в СГСЭ — единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:

Среднее значение ЭДС индукции может быть определено как:

Поток сцепления

Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{\mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:

Величину $\Psi$, равную:

называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:

В сложном контуре ${{\mathcal E}}_i$ вычисляют как:

Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея — Максвелла).

Частные случаи применения закона электромагнитной индукции

1. Если проводник длины $l\ $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:

где $\alpha $ — угол между направлением скорости и вектором магнитной индукции.

1. ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $\omega$ в однородном магнитном поле с индукцией $В$ и она равна:

где $\omega t$ — мгновенное значение угла между вектором магнитной индукции ($\overrightarrow{B}$) и вектором нормали к плоскости рамки ($\overrightarrow{n}$).

Пример 1

Задание: Найдите мгновенное значение ЭДС индукции рамки, которое соответствует углу поворота рамки $\alpha ,$ площадь рамки, равна $S$, она содержит $N$ витков. Рамка вращается в постоянном магнитном поле с индукцией $B$. Частота вращения рамки равна $n$.

Решение:

За основу решения задачи примем уравнение Фарадея — Максвелла:

\[{{\mathcal E}}_i=-\frac{d \Psi}{dt}\ \left(1.1\right),\]

где потокосцепление можно определить как:

\[\Psi=NФ\ \left(1.2\right),\]

где $N$ — количество витков, которые пронизывает магнитный поток $Ф$. Соответственно (1.1) примет вид:

\[{{\mathcal E}}_i=-N\frac{dФ}{dt}\ \left(1.3\right).\]

Если рамку вращать, то магнитный поток изменяется в соответствии с законом:

\[Ф=BScos\omega t\left(1.4\right),\]

где $\omega $ — угловая частота вращения. Подставим выражение (1.4) в (1.3), получим:

\[{{\mathcal E}}_i=NBS\omega sin\omega t\left(1.5\right).\]

Связь угловой частоты и часты вращения, определим как:

\[\omega =2\pi n\ \left(1.6\right),\] \[\omega t=\alpha \left(1.7\right).\]

Подставим выражения (1.6), (1.7) в формулу (1.5) получим:

\[{{\mathcal E}}_i=2\pi nNBSsin\alpha .\]

Ответ: ${{\mathcal E}}_i=2\pi nNBSsin\alpha .$

Пример 2

Задание: Определите среднее ЭДС индукции ($\left\langle {{\mathcal E}}_i\right\rangle )$, если магнитный поток, который пронизывает контур, изменяется от $Ф_1=40Вб$ до $Ф_2=0Вб$ в течении промежутка времени равного $2 с$.

Решение:

За основу решения примем формулу, определяющую среднюю ЭДС индукции:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{\Delta Ф}{\Delta t}\left(2.1\right).\]

Проведем вычисления:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{0-40}{2}=20\ \left(В\right).\]

Ответ: $\left\langle {{\mathcal E}}_i\right\rangle =20 В$.

Что такое электромагнитная индукция? | HomeElectronics

Всем доброго времени суток. В прошлых статьях я рассказал о магнитном поле в веществе, а так же магнитных цепях и методах их расчёта. Данная статья посвящена такому явлению, как ЭДС индукции, в каких случаях она возникает, а так же затрону понятие индуктивности, как основного параметра характеризующего возникновение магнитного потока при возникновении электрического поля в проводнике.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Как возникает ЭДС индукции и индукционный ток?

Как я говорил в предыдущих статьях вокруг проводника, по которому протекает электрический ток, возникает электромагнитное поле. Данное магнитное поле я рассмотрел здесь и здесь. Однако существует и обратное явление, которое называется электромагнитная индукция. Данное явление открыл английский физик М. Фарадей.

Для рассмотрения данного явления рассмотрим следующий рисунок

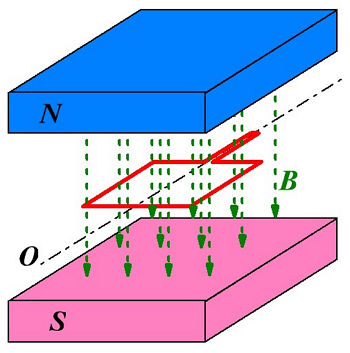
Рисунок, иллюстрирующий электромагнитную индукцию.

На данном рисунке показана рамка из проводника, помещённая в электрическое поле с индукцией В. Если данную рамку двигать вверх-вниз по направлению магнитных силовых линий или влево – вправо перпендикулярно силовым линиям, то магнитный поток Φ пронизывающий рамку буден практически постоянным. Если же вращать рамку вокруг оси О, то за некоторый промежуток времени ∆t  магнитный поток изменится на некоторую величину ∆Φ и в результате в рамке появится ЭДС индукции Е_i и потечёт ток I, называемым индукционным током.

Чему равно ЭДС индукции?

Для определения величины возникающей ЭДС рассмотрим контур помещенный в однородное магнитное поле с индукцией В, по данному контуру свободно может перемещаться проводник длиной l.

 

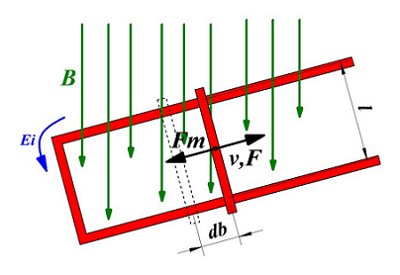
Возникновение ЭДС индукции в прямолинейном проводнике.

Под действием силы F проводник начинает двигаться со скоростью v. За некоторое время ∆t проводник пройдёт путь db. Таким образом, затрачиваемая работа на перемещение проводника составит

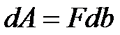
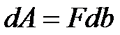
Так как проводник состоит из заряженных частиц – электронов и протонов, то они также движутся вместе с проводником. Как известно на движущуюся заряженную частицу действует сила Лоренца, которая перпендикулярна к направлению движения частицы и к вектору магнитной индукции В, то есть электроны начинают двигаться вдоль проводника приводя  к возникновению электрического тока в нём.

Однако на проводник с током в магнитном поле действует некоторая сила F_т, которая в соответствии с правилом левой руки будет противоположна действию силы F, за счёт которой проводник движется. Так как проводник движется равномерно, то есть с постоянной скоростью, то силы  F_т и F равны по абсолютному значению

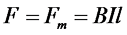
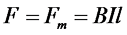
где В – индукция магнитного поля,

I – сила тока в проводника, возникающая по действием ЭДС индукции,

l – длина проводника.

Так как путь db пройденный проводником зависит от скорости v и времени t, то работа, затрачиваемая на перемещения проводника, в магнитном поле составит

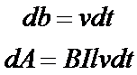
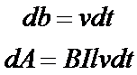
При перемещении проводника в магнитном поле практически вся затрачиваемая на эту работу механическая энергия переходит в электрическую энергию, то есть

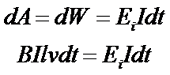
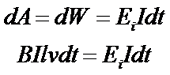
Таким образом, преобразовав последнее выражение, получим значение ЭДС индукции при движении прямолинейного проводника в магнитном поле

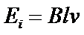
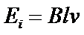
где В – индукция магнитного поля,

l – длина проводника,

v – скорость перемещения проводника.

Данное выражение соответствует движению проводника перпендикулярно линиям магнитной индукции. Если происходит движение под некоторым углом к линиям магнитной индукции, то выражение приобретает вид

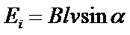
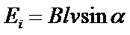
На практике достаточно трудно посчитать скорость перемещения проводника, поэтому преобразуем выражение к следующему виду

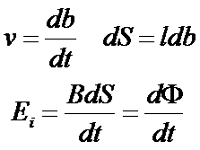
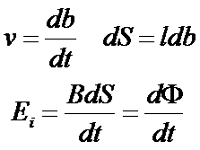
где dS – площадка, которую пересекает проводник при своём движении,

dΦ – магнитный поток пронизывающий площадку dS.

Таким образом, ЭДС индукции равна скорости изменения магнитного потока, который пронизывает контур.

Для обозначения направления движения тока в контуре вводят знак «–», который указывает, что ток в контуре направлен против положительного обхода контура. Таким образом

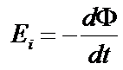
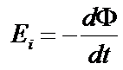
Зачастую в магнитном поле движется контур, состоящий из множества витков провода, поэтому ЭДС индукции будет иметь вид

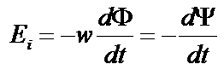
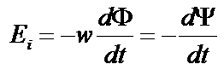
где w – количество витков в контуре,

dΨ = wdΦ – элементарное потокосцепление.

Перефразируя предыдущее определение, ЭДС индукции в контуре равна скорости изменения потокосцепления этого контура.

Что такое ЭДС самоидукции? Индуктивность 

Как известно вокруг проводника с током существует магнитное поле. Так как индукция магнитного поля пропорциональна силе тока протекающего через проводник, а магнитный поток пропорционален магнитной индукции, следовательно, магнитный поток пропорционален силе тока, протекающей через проводник.

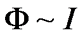
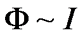
Таким образом, при изменении силы тока происходит изменение магнитного потока (или потокосцепления). Однако в соответствие с законом электромагнитной индукции, изменение потокосцепления приводит к возникновению в проводнике ЭДС индукции.

Данное явление (возникновение ЭДС) в проводнике при изменении проходящего по нему тока называется самоиндукцией. Возникающая вследствие самоиндукции ЭДС называется ЭДС самоиндукции Е_L, которая равна

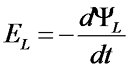
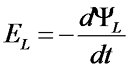
где dΨ_L – изменение потокосцепления.

Следовательно между электрическим током в проводнике и потокосцеплением, возникающего вокруг проводника магнитного поля существует некоторый коэффициент пропорциональности связывающий их. Таким коэффициентом является индуктивность – обозначается L (имеет старое название коэффициент самоиндукции)

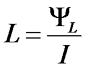
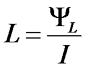
Величина индуктивности характеризует способность электрической цепи создавать потокосцепление (магнитный поток) при протекании по ней электрического тока. Единицей индуктивности является Генри (обозначается Гн)

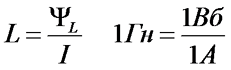
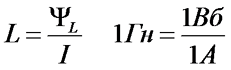
Таким образом, индуктивность зависит от геометрических размеров проводника с током и от магнитных свойств магнитной цепи, через которую замыкается магнитный поток, создаваемый проводником с током.

В следующей статье я расскажу, как рассчитать индуктивность различных по форме проводников с током.

 

Что такое взаимная индукция? Взаимная индуктивность

 

Для разъяснения понятия взаимной индукции рассмотрим две катушки К1 и К2 расположенные близко друг от друга

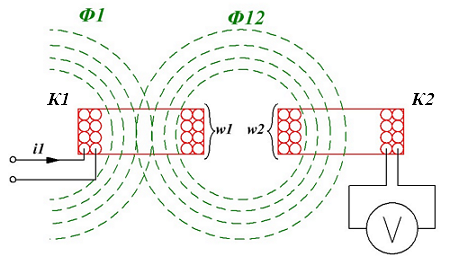
Взаимная индукция двух катушек расположенных рядом.

Если по одной из катушек пропускать электрический ток i1, то вокруг данной катушки возникнет магнитное поле с потоком Φ1, часть магнитных силовых линий которого будет пересекать и вторую катушку, вокруг которой образуется магнитный поток Φ12. Таким образом, при изменении тока i1в первой катушке будет изменяться магнитный поток Φ1, а, следовательно, и магнитный поток Φ12, пересекающий вторую катушку, что непременно приведёт к изменению электрического тока во второй катушке и соответственно возникновению ЭДС.

Таким образом, возникновение ЭДС в контуре под действием изменяющегося тока в близкорасположенном соседней катушке, имеет название взаимной индукции.

Как было сказано выше, явление самоиндукции в количественной форме выражается индуктивностью L, аналогично и взаимная индукция определяется физической величиной называемой взаимной индуктивностью М (имеет размерность Генри – «Гн»). Данная величина определяется отношением потокосцепления во вторичной катушке Ψ₁₂  к току в первичной катушке i₁

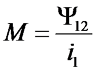
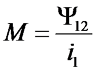
Однако, определить взаимную индукцию можно и обратным способом, то есть пропуская ток i₂ через вторичную катушку. В этом случае будет создаваться магнитный поток Φ2, часть которого Φ21 будет пронизывать первичную катушку, тогда взаимная индукция будет определяться следующим выражением

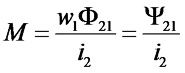
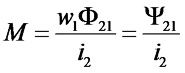
Так же как и в случае с самоиндукцией, ЭДС взаимной индукции во вторичной катушке будет зависеть от скорости изменения магнитного потока или потокосцепления

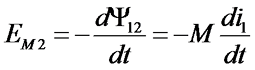
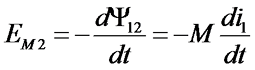
Взаимная индуктивность М имеет зависимость от индуктивности двух катушек и определяется согласно следующему выражению

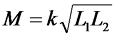
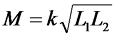
где k – коэффициент связи, зависящий от степени индуктивной связи между катушками;

L₁ – индуктивность первой катушки;

L₂ – индуктивность второй катушки.

Коэффициент индуктивной связи k определяется следующим выражением

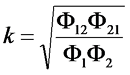
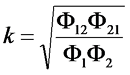
Из данного выражения видно, что коэффициент связи всегда будет меньше единицы, так как Φ₁₂< Φ₁ и Φ₂₁< Φ₂.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

ЭДС индукции в движущихся проводниках

ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции () появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.

Закон Фарадея для электромагнитной индукции

Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:

   

Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:

   

Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.

ЭДС индукции в движущемся проводнике

Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.

Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие .

ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.

Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:

   

где , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:

   

где – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:

   

где v – скорость движения подвижной стороны рамки по оси X.

Если угол между направлением вектора магнитной индукции () и вектором скорости движения проводника () составляет угол , то модуль ЭДС в проводнике можно вычислить при помощи формулы:

   

Примеры решения задач

Величина и направление ЭДС индукции — КиберПедия

Величина ЭДС индукции зависит от количества силовых линий поля, пересекающих проводник в единицу времени, т. е. от скорости движения проводника в поле.

Величина индуктированной ЭДС находится в прямой зависимости от скорости движения проводника в магнитном поле.

Величина индуктированной ЭДС зависит также и от длины той части проводника, которая пересекается силовыми линиями поля. Чем большая часть проводника пересекается силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец, чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС возникает в проводнике, пересекающем это поле.

Итак, величина ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо пропорциональна индукции магнитного поля, длине проводника и скорости его перемещения.

Зависимость эта выражается формулой Е = Blv,

где Е — ЭДС индукции; В — магнитная индукция; I — длина проводника; v — скорость движения проводника.

Следует твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС индукции возникает только в том случае, если этот проводник пересекается магнитными силовыми линиями поля. Если же проводник перемещается вдоль силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой ЭДС в нем не индуктируется

Направление индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую сторону движется проводник. Для определения направления индуктированной ЭДС существует правило правой руки.

 

2. Как известно, электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальная задача была блестяще решена М.Фарадеем. Фарадея посетило великое прозрение: электрическое поле возбуждается лишь при изменении магнитного поля. Самого по себе присутствия магнитного поля недостаточно. Сегодня эффект возникновения электрического поля при изменении магнитного физики называют явлением

электромагнитной индукцией. Оно заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного

Повторяя свои опыты и анализируя результаты, Фарадей вскоре пришел к выводу, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром…

 

В первоначальной формулировке закон электромагнитной индукции Фарадея гласил, что при изменении магнитного потока, проходящего через контур, по проводящему контуру протекает электрический заряд, пропорциональный изменению магнитного потока, который возбуждается без всякого внешнего источника питания типа электрической батареи. Не будучи до конца удовлетворенным формулировкой, в которой фигурировала столь трудноизмеримая величина, как электрический заряд, Фарадей вскоре объединил свой закон с законом Ома и получил формулу (иногда ее принято называть вторым законом электромагнитной индукции Фарадея) для определения электродвижущей силы, возникающей в результате изменения магнитного потока через контур.

Закон фарадея электромагнитной индукции выражается следующей формулой:

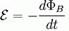
Где 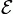— это электродвижущая сила, действующая вдоль произвольно выбранного контура;
Φ_B — магнитный поток через поверхность, натянутую на этот контур.

Согласно правилу Ленца в формуле стоит знак «-» (минус). Правило Ленца гласит: индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Или ещё можно сформулировать так :направление индуктированной э. д. с. всегда таково, что вызванный ею ток и его магнитное поле имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктированную э. д. с

Изменить магнитный поток через контур можно тремя способами:

• изменить площадь контура;
• изменить интенсивность магнитного поля;
• изменить взаимную ориентацию магнитного поля и плоскости, в которой лежит контур.

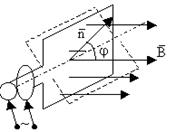3.Рассмотрим прямоугольную рамку, вращающуюся в однородном магнитном поле с угловой скоростью ω.
Магнитный поток, пронизывающий контур равен

Ф=BScosφ=cosωt
т.к. угол поворота φ=ωt при равномерном вращении.

При вращении магнитный поток Ф периодически изменяется, т.е. в контуре возникает периодически изменяющаяся э.д.с. индукции. Согласно закону Фарадея

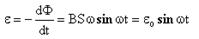
где ε₀=BSω — амплитуда э.д.с.
Переменная э.д.с. создает в контуре переменный ток.

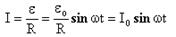
где I₀ — амплитуда тока, R — сопротивление рамки.

Переменный ток характеризуется амплитудой I₀, круговой частотой ω, фазой ωt. Помимо этих величин вводится период тока T и частота ν.
ω=2πν=2π/T
э.д.с. и ток изменяются синфазно.

В промышленных генераторах рамки соединены последовательно, т.е. э.д.с.
ε=NBSωsinωt, ε≈10⁴B — переменная.

 

3.Рассмотрим прямоугольную рамку, вращающуюся в однородном магнитном поле с угловой скоростью ω.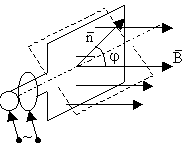
Магнитный поток, пронизывающий контур равен

Ф=BScosφ=cosωt
т.к. угол поворота φ=ωt при равномерном вращении.

При вращении магнитный поток Ф периодически изменяется, т.е. в контуре возникает периодически изменяющаяся э.д.с. индукции. Согласно закону Фарадея

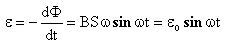
где ε₀=BSω — амплитуда э.д.с.
Переменная э.д.с. создает в контуре переменный ток.

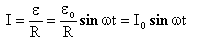
где I₀ — амплитуда тока, R — сопротивление рамки.

Переменный ток характеризуется амплитудой I₀, круговой частотой ω, фазой ωt. Помимо этих величин вводится период тока T и частота ν.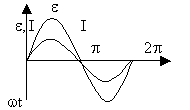
ω=2πν=2π/T
э.д.с. и ток изменяются синфазно.

В промышленных генераторах рамки соединены последовательно, т.е. э.д.с.
ε=NBSωsinωt, ε≈10⁴B — переменная.

5. стр 45 6642(1.,2.(3. не обязательно!)Трансформатор под. номером4.

7. методичка 53(07) стр. 74-78.Стр 74 со слов:если в магнитное поле с индукцией…стр.75 До слов:тоесть любое вещество-магнетик.Тут же со слов:основной макроскопической величиной…и до конца страницы.Стр 78 сло слов Намагниченность j магнетика… и до слов для парамагнетиковX>=1

4.ЭДС индукции, возникающая в самом же контуре называется ЭДС самоиндукции, а само явление – самоиндукция.

Явление самоиндукции:

Ток I, текущий в любом контуре создает магнитный поток Ψ, пронизывающего этот же контур. При изменении I, будет изменятся Ψ , следовательно в контуре будет наводится ЭДС индукции.

Т.к. магнитная индукция В пропорциональна току I (В = μμ0nI), следовательно

Ψ = LI,