Лекция 02. Теория булевых функций. Булева алгебра

Определение.

Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (Аксиомы булевой алгебры). Названия операций пока не введены.

1. X & Y = Y&X, X V Y = Y V X – коммутативность.

2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.

3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.

4. Поглощение – X & X = X, X V X = X.

5. Свойства констант

X & 0 = 0

X & I = X, где I – аналог универсального множества.

6. Инвальтивность (X*)* = X

7. Дополнимость X V X* = I, X & X* = 0.

8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y

Булева алгебра всех подмножеств данного множества.

U = {a1, a2… an)

[U] = N

[P(U)] = 2n

Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, Множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.

Oбъединение эквивалентно V, пересечение — &, дополнение — *, пустое множество – 0, а универсальное – I.

Все аксиомы булевой алгебры справедливы в операциях над множествами.

Булева алгебра характеристических векторов.

Пусть A <= U, A <- P(U) a- характеристический вектор этого подмножества.

AA = {a, a2 ..an)

N = [P(U)]

Ai = 1, если ai <- A (принадлежит).

Ai = 0, если ai не принадлежит A.

U = {1 2 3 4 5 6 7 8 9}

A = {2 4 6 8}

B = {1 2 7}

AA = {0 1 0 1 0 1 0 1 0}

AB = {1 1 0 0 0 0 1 0 0}

Или

AA = 010101010 – скобки не нужны

AA= 110000100

Характеристические векторы размерностью n называются булевыми векторами.

Они располагаются в вершинах n – мерного булева куба.

Номером булевого вектора является число в двоичном представлении, которым он является

1101 – номер.

Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (если они отличаются только одной координатой).

Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bn.

Булев куб размерности 1

Булев куб размерности 2

Булев куб размерности 3

0 – нулевой вектор.

I – вектор из одних единиц.

Отрицание

X = 0 Y = 0

_ _

Х = 1 Y= 1

Для размерности n операции над векторами производятся покоординатно.

Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.

Утверждение

Между множеством всех подмножеств множества U и булевым кубом Bn, где n= =[U] можно установить взаимное соответствие, при котором операции объединения множества соответствует операции логического сложения (их характеристических векторов), операции пересечения множеств соответствует операция логического умножения их характеристических векторов, а операции дополнения – операция отрицания.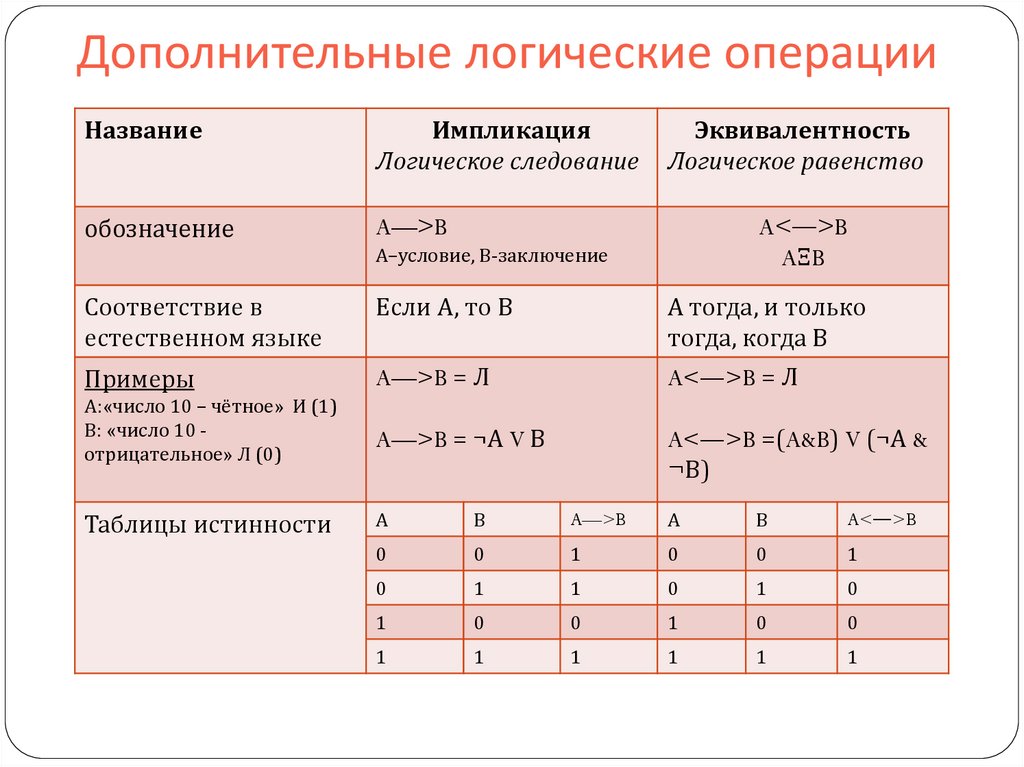 Пустому множеству соответствует нулевой вектор, а универсальному – единичный.

Следствие

Множество всех характеристических векторов является булевой алгеброй.

Булева алгебра высказываний (алгебра логики)

Высказыванием об элементах множества U называется любое утверждение об элементах множества U, которое для каждого элемента либо истинно, либо ложно.

U = {1 2 3 4 5 6 7 8 9}

A = «число четное»

B = «число, меньшее пяти»

Множеством истинности высказывания называется совокупность всех элементов, для которых это высказывание истинно.

SA = {2 4 6 8}

SB = {1 2 3 4}

Высказывание, для которого множество истинности пусто, называется тождественно ложным, а для которого SB = U называется тождественно истинным.

Высказывания, для которых множества истинности совпадают, называются тождественными или равносильными.

Равносильные высказывания объединим в один класс Р. В. и не будем их разделять, т. к. все они имеют одно и то же множество истинности.

Операции над высказываниями

Дизъюнкция высказываний (V, ИЛИ, OR)

Дизъюнкция высказываний – высказывание, истинное тогда, когда истинно хотя бы одно из высказываний.

Конъюнкция высказываний (&, И, AND).

Конъюнкцией высказываний называется высказывание, истинное тогда и только тогда, когда истинны все высказывания.

Отрицание высказываний (- над буквой, НЕ, NOT).

Отрицанием высказывания называется высказывание, истинное только тогда, когда исходное высказывание ложно.

A B	A & B	A V B	Not A
Л Л	Л	Л	И
Л И	Л	И	И
И Л	Л	И	Л
И И	И	И	Л

Л – ложно.

И – истинно.

Утверждение (основа всей алгебры логики)

Между множеством всех классов эквивалентных высказываний об элементах множества U и множеством P(U) можно установить взаимно однозначное соответствие, при котором операция дизъюнкции высказываний соответствует операции объединения множеств истинности, а конъюнкция соответствует операции пересечения. Операция отрицания соответствует операции дополнения.

Следствие. Множество классов эквивалентных высказываний является булевой алгеброй.

Теорема

Существуют 3 булевых алгебры:

1. P(U)

2. Bn

3. Множество классов эквивалентных высказываний.

Три булевых алгебры являются изоморфными, если между их элементами можно установить такое однозначное соответствие, при котором операции сохраняются.

Договоримся конъюнкцию обозначать точкой (как знак умножения в алгебре чисел). Конъюнкция выполняется раньше дизъюнкции (аналог выполнения операций сложения и умножения в алгебре чисел).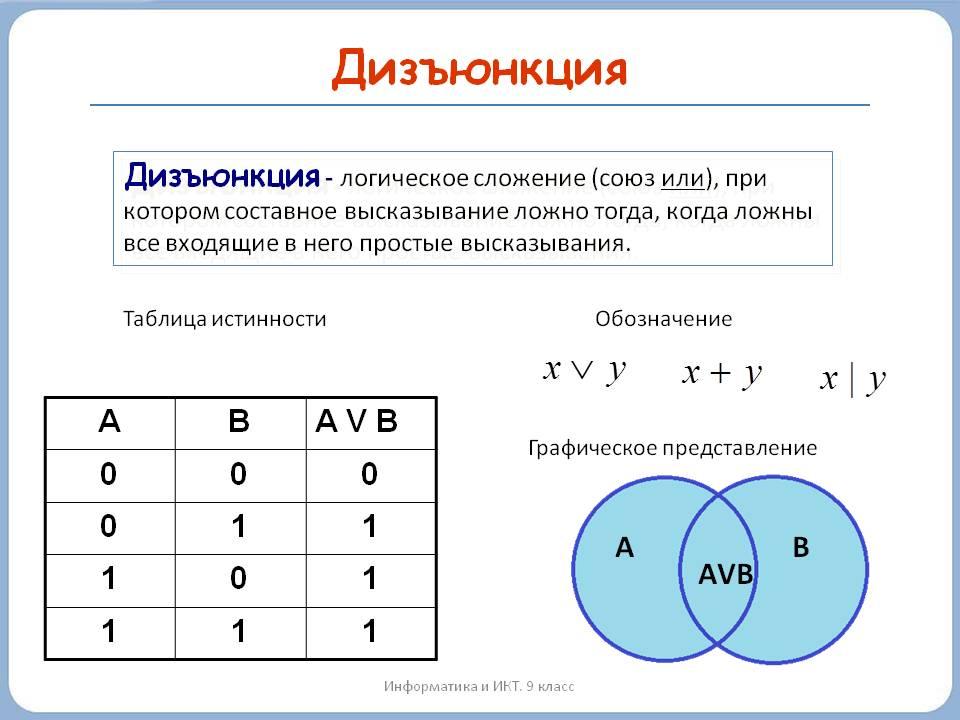

< Предыдущая		Следующая >

Математика — Алгебра Логики

Закон двойного отрицания.

Этот закон не имеет отношения к закону «отрицания отрицания» в диалектике. В булевой алгебре он гласит, что если два раза подряд применить операцию отрицания, то получится исходная величина:

~(~x) = x

Обратные операции.

Формулы обратных операций позволяют убирать знак отрицания в формулах вида ~(x # y) путем замены некоторой операции # на другую операцию:

~(x & y) = x | y
~(x | y) = x & y

~(x > y) = x y
~(x y) = x > y
~(x y
~(x y) = x
~(x y) = x y
~(x y) = x y
~(x y) = x y
~(x y) = x y
(Напоминание программистам: | — это штрих Шеффера, а не побитовое «или»)

Коммутативные операции.

Коммутативными называют операции, которые позволяют переставлять местами свои операнды, не меняя операцию. По схеме: x + y = y + x, где + — некоторая операция.

x & y = y & x
x y = y x
x y = y x
x y = y x
x y = y x
x | y = y | x

Остальные операции также позволяют переставлять операнды, но с заменой на другую операцию:

x > y = y
x y = y x

Как видите, и в булевой алгебре операции сложения () и умножения (&) позволяют переставлять свои слагаемые.

Можно использовать простое мнемоническое правило: при перестановке операндов логической операции местами надо повернуть знак операции вокруг веритикальной оси. Если получится другой знак логической операции, взять его. Если получится тот же знак, взять его. Если получится несуществующий знак (для операции &), то оставить прежний знак.

Ассоциативные операции.

Ассоциативными называют операции, которые можно выполнять в произвольном порядке. По схеме: (x + y) + z = x + (y + z), где + — некоторая операция. Здесь приведена программа на языке C, позволяющая увидеть таблицу истинности всех 16 бинарных логических операций и проверить их ассоциативность путем перебора вариантов.

Проверка показывает ассоциативность всего лишь для 4 операций «&», «», «», «» из 10 нетривиальных.

(x & y) & z = x & (y & z)
(x y) z = x (y z)
(x y) z = x (y z)
(x y) z = x (y z)

Из комутативности и ассоциативности этих четырех операций следует, что если мы имеем много переменных подряд, соединенных такой операцией, то переменные можно переставлять в любом порядке, а значит скобки для указания порядка не обязательны:

(a & b) & (c & d) = a & d & c & b.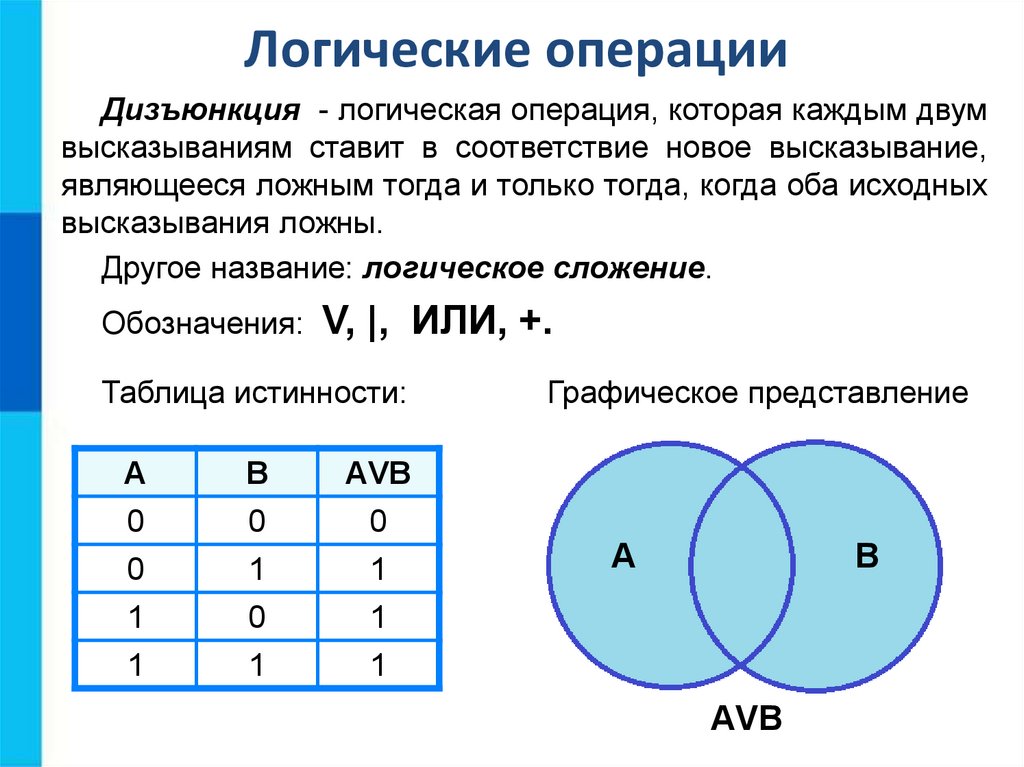

Дистрибутивные операции.

Дистрибутивной называют пару операций, для которых работает схема раскрытия скобок, характерная для сложения и умножения в арифметике:

x * (y + z) = (x * y) + (x * z) и
(x + y) * z = (x * z) + (y * z),
где * и + — некоторые логические операции.

Первую схему будем называть левой дистрибутивностью, вторую схему — правой дистрибутивностью, а если срабатывают обе схемы, то будем говорить о полной дистрибутивности или просто дистрибутивности.

Здесь приведена программа на языке C, позволяющая проверить дистрибутивность для всех возможных комбинаций бинарных логических операций путем перебора вариантов. Она автоматически пропускает тривиальные операции и составляет правила дистрибутивности.

Результаты программы выглядят так.

Из полученных правил наибольший практический интерес представляют:
x & (y z) = (x & y) (x & z)

(x y) & z = (x & z) (y & z)
x (y & z) = (x y) & (x z)
(x & y) z = (x z) & (y z)
x & (y z) = (x & y) (x & z)
(x y) & z = (x & z) (y & z)

Как видите, дистрибутивность между логическим умножением и сложением в алгебре логики такая же как в обычной алгебре (где она называется «распределительным законом»).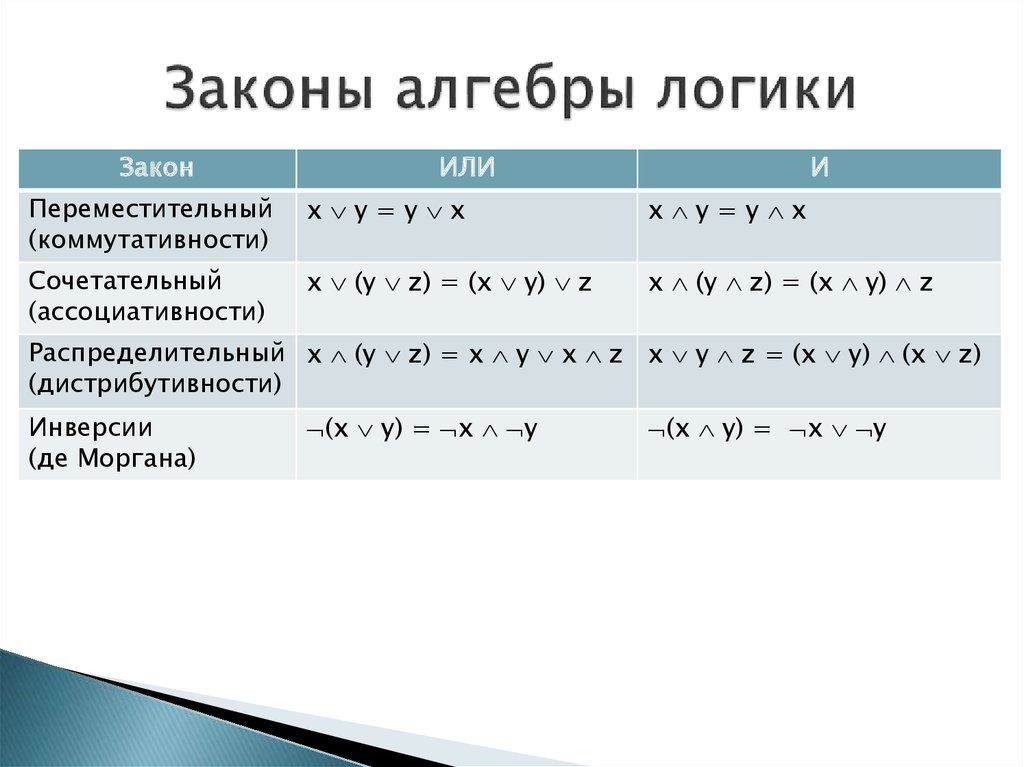 Обратите внимание, что и для операций «» и «&» можно раскрывать скобки таким же способом. Причем обе операции оказываются равноправны: можно раскрывать скобки когда в них стоит «&», а вне скобок — «», а можно и в обратной ситуации — когда внутри скобок стоит «».

Законы поглощения.

Формула вида x # 0 (где # — некоторая бинарная операция) представляет собой функцию от одной переменной. Мы знаем все 4 функции от одной переменной, поэтому всякую такую формулу можно упростить до одной из этих 4 функций: 0, 1, x или ~x.

То же самое рассуждение применимо и к формулам вида: x # 1, x # x, x # ~x, 1 # x, 0 # x, ~x # x. В результате для каждой такой формулы получается закон поглощения, который позволяет избавиться от лишних знаков операций и переменных.

Как обычно, поручим нудную работу по перебору вариантов компьютеру.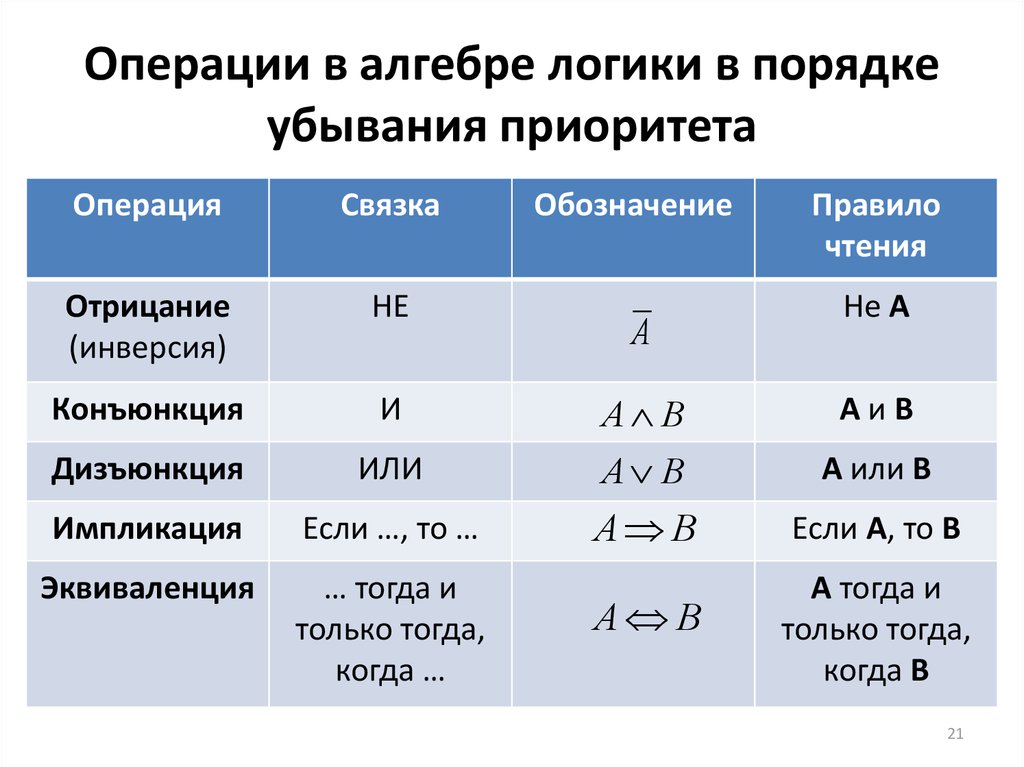 Здесь приведена программа на языке C, позволяющая получить список всех правил поглощения сразу в виде web-странички.

Цветом выделены законы поглощения, используемые чаще всего.

Закон исключенного третьего.

Это — один из законов поглощения:

x ~x = 1

В булевой алгебре этот закон оспорить невозможно, так как достаточно подставить значения x = 0, 1 и убедиться в наличии равенства в обоих случаях. Применение этого закона на практике, например в психологике, накладывает дополнительные ограничения, описанные в первой главе. Что, впрочем, справедливо и для осталных законов булевой алгебры.

Я специально останавливаюсь на этом законе потому, что в некоторых логических системах (интуиционистская логика, конструктивная логика), которые построены на иных принципах, чем булева алгебра, в этих системах закон исключенного третьего не действует. Что неудивительно, ведь в тех системах совсем другие границы применимости.

Законы Де Моргана.

~(x & y) = ~x ~y

~(x y) = ~x & ~y

Эти равенства удобны для избавления от лишних скобок.

Формулы для импликации.

x y = (x y) & (x y)
x y = y x
x y = ~x y
x y = ~y ~x

---

[предыдущая глава]  [оглавление]  [следующая глава]

---

Булева алгебра — 1. Операторы и основы

Булева алгебра!

Это действительно логично.

Введение

Мы начнем с рассмотрения того, что такое булева алгебра, а затем рассмотрим некоторые из основных строительных блоков, также называемых операторами. На данном этапе это может показаться немного абстрактным, но как только вы проработаете этот раздел и следующий, он начнет обретать немного больше смысла.

Булева алгебра

Булева алгебра — это способ формального определения или описания конкретной ситуации или процедуры. Мы используем переменных для представления элементов нашей ситуации или процедуры. Переменные могут принимать одно из двух значений. Традиционно это будет True и False . Так, например, у нас может быть переменная X , и мы можем указать, идет ли дождь на улице или нет. Значение X будет следующим:

• True , если на улице идет дождь.
• Ложь , если на улице нет дождя.

Вы должны помнить, что хотя многие вещи в реальном мире существуют в спектре, в булевой алгебре все сводится к черному и белому. Таким образом, у нас может быть, например, небольшой дождь, постоянный дождь или сильный дождь. Однако в булевой алгебре либо идет дождь, либо нет. Это может показаться немного ограничивающим, но такое упрощение вещей на самом деле оказывается весьма мощным.

Можно заменить True и False другими значениями. При работе с компьютером часто бывает, что True и False заменяются на 9.0013 1 и 0 . При работе с физическими цепями мы можем заменить True и False на наличие или отсутствие напряжения.

Таким образом, булева алгебра полезна для описания процесса, а затем для создания механизмов, которые могут выполнять эти процессы. Имейте это в виду, когда будете работать над следующими несколькими разделами. Это то, к чему мы движемся.

Основные операции

Выше мы видели, что переменные могут использоваться для представления текущего состояния элементов, которые нас интересуют. Операции позволяют нам затем определить отношения между этими переменными. Есть три основных операции. Они часто используются в логических выражениях, но также используются для создания более сложных операций. Вы, вероятно, обнаружите, что на самом деле использовали эти операции довольно часто, просто вы никогда раньше не думали о них формально.

Результат операции аналогичен переменным, только может быть либо True , либо False .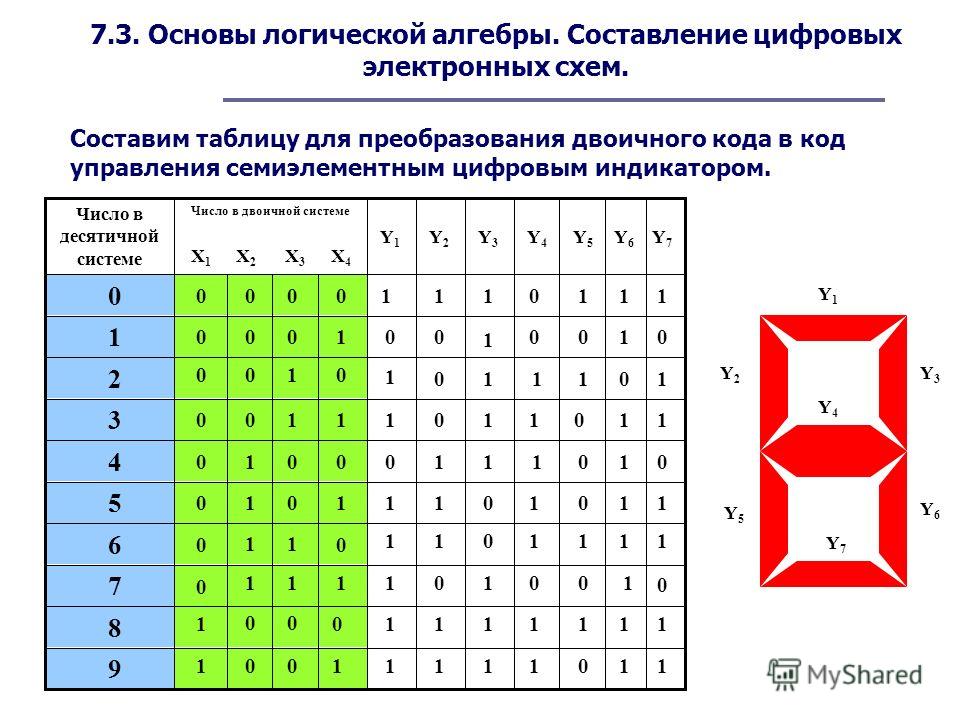

Я решил всегда писать операции БОЛЬШИМИ БУКВАМИ. Поэтому их легко идентифицировать как операции. Многие люди следуют этому соглашению, но это не обязательно. Не стесняйтесь использовать любой метод, который вам больше подходит.

И

Первая операция — это И , и на простом английском языке она означает почти то же самое. Так, например, я могу заявить: «Если на улице солнечно И Я закончил свою работу, тогда я пойду на пробежку». Чтобы представить это в булевой алгебре, я могу сказать, что:

• x представляет, солнечно на улице или нет.
• y показывает, выполнил я свою работу или нет.
• z показывает, иду ли я на пробежку или нет.

А я бы написал так:

x AND y = z

Здесь это представлено визуально. Заштрихованная область представляет собой область, которая представляет И .

А теперь мы представим это с помощью так называемой таблицы истинности . В таблице истинности перечислены все возможные комбинации входных данных для выражения (в данном случае одной операции) и то, каким должен быть результат или вывод.

Ложь	Ложь	Ложь
Правда	Ложь	Ложь
Ложь	Правда	Ложь
Правда	Правда	Правда

ИЛИ

ИЛИ тоже самое, что и в простом английском языке. Это означает, что если любая из двух переменных равна True , то результатом будет True . Так, например, я мог бы сказать, что «Я вернусь домой с работы раньше, если я уйду рано ИЛИ , пробки хорошие».

Вот ИЛИ представлен визуально:

И снова таблица истинности:

Ложь	Ложь	Ложь
Правда	Ложь	Правда
Ложь	Правда	Правда
Правда	Правда	Правда

Обратите внимание, что И является ложным для всех, кроме True и True, в то время как ИЛИ является истинным для всех, кроме False и False. Это наблюдение пригодится нам в дальнейшем. На самом деле есть много сокращений и выгодных преимуществ, которые можно получить от поиска подобных шаблонов, поэтому следите за ними.

Not

Not очень похоже на то, как мы используем его в простом английском языке. Он имеет тонкое отличие при использовании в булевой алгебре. Обычно я могу сказать что-то вроде «Я съем десерт, если не наелся». Я также мог бы сказать: «Я съем десерт, если я все еще голоден», что имеет то же значение, но использует противоположное значение. Так , а не фактически приводит к переворачиванию значения переменной. Если:

• переменная d в настоящее время имеет значение True , то
• выражение не d имеет результат False

Представлено визуально:

И как таблица истинности:

True	Ложь
Ложь	Правда

Производные операции

Вышеуказанные три операции являются строительными блоками практически для всего остального, что мы можем делать в булевой алгебре.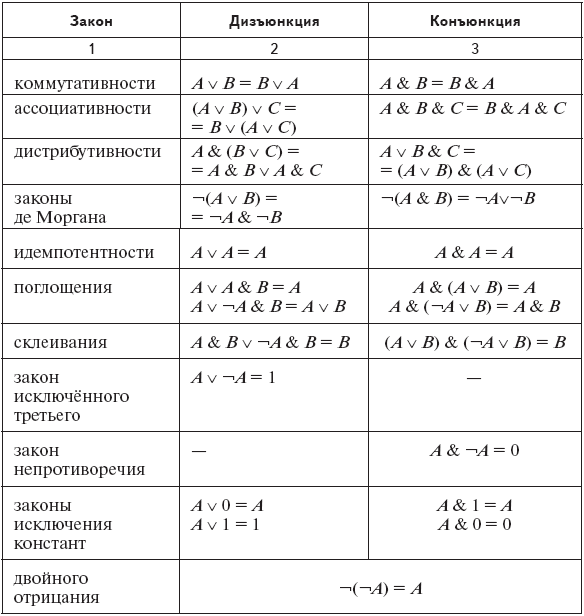 Теперь мы представим так называемые производные операции . По сути, это ярлыки для часто используемых комбинаций основных операций. Как мы узнаем позже, некоторые из этих производных операций очень полезны, когда мы хотим выполнять вычисления и другие вещи.

Исключающее ИЛИ или Исключающее ИЛИ

С помощью операции ИЛИ мы увидели, что пока одна из переменных равна True , результатом будет True . Это также было правдой, если оба они были правдой. С помощью операции XOR мы теперь говорим, что результат будет True, только если одна из двух переменных имеет значение True. То есть одно из них истинно, но истинно только одно из них. Мы можем построить эту операцию из основных операций, например:

g XOR p эквивалентно (g OR p) AND NOT(g AND p)

Когда в выражении используются скобки ( ) , это означает, что мы сначала оцениваем эту часть выражения перед другими частями.

Давайте рассмотрим пример, чтобы лучше понять, что происходит.

Если g истинно, а p ложно, то:

Подставляя g и p вместо этих значений, мы получаем: набор скобок (верно или неверно) AND NOT(True AND False) оценивается как True, поэтому давайте заменим его в выражении, и мы получим:

True AND NOT(True AND False)

Следующий набор скобок True AND NOT (True AND False) оценивается как False, поэтому давайте заменим его в выражении, что даст нам:

True AND NOT( False )

NOT(False) оценивается как True, поэтому мы можем применить это к выражению, и в итоге мы получим :

Правда и True

И конечный результат True .

Визуально XOR выглядит так:

XOR как таблица истинности:

Ложь	Ложь	Ложь
Правда	Ложь	Правда
Ложь	Правда	Правда
Правда	Правда	Ложь

И-НЕ или НЕ-И

НЕ-И фактически противоположно тому, что есть И.

r NAND S эквивалентно NOT(r AND s)

Визуально это выглядит так:

NAND как таблица истинности:

Ложь	Ложь	Правда
Правда	Ложь	Правда
Ложь	Правда	Правда
Правда	Правда	Ложь

ИЛИ или НЕ ИЛИ

ИЛИ фактически противоположно ИЛИ.

b NOR k эквивалентно NOT(b OR k)

Визуально это выглядит так:

NOR как таблица истинности:

Ложь	Ложь	Правда
Правда	Ложь	Ложь
Ложь	Правда	Ложь
Правда	Правда	Ложь

Сводка

Переменная

Элемент в логическом выражении.

Основные операторы

И, ИЛИ и НЕ.

Производные операторы

XOR, NAND и NOR

Выражение

Результат объединения переменных и операторов.

Только два значения

В булевой алгебре существует только два возможных значения. Обычно True и False, но могут быть и другие значения, например 0 и 1.

Действия

Теперь давайте оценим некоторые выражения.

• :
• :
• :

Джордж Буль | Факты, биография, смерть, образование и книги

Джордж Буль

Смотреть все медиа

Дата рождения:

2 ноября 1815 г. Линкольн Англия

Умер:

8 декабря 1864 г. (49 лет) Ирландия

Предметы изучения:

Булева алгебра формальная система

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

См. посвящение математика Джорджа Буля к двухсотлетию со дня его рождения из Университетского колледжа Корка, Ирландия.

См. все видео к этой статье. 8, 1864, Ballintemple, графство Корк, Ирландия), английский математик, который помог создать современную символическую логику и чья алгебра логики, теперь называемая булевой алгеброй, лежит в основе проектирования цифровых компьютерных схем.

Первые уроки математики Буль получил от своего отца, ремесленника, который также научил его делать оптические приборы. Однако, помимо помощи отца и нескольких лет в местных школах, Буль был математиком-самоучкой. Когда бизнес его отца пришел в упадок, Джорджу пришлось работать, чтобы прокормить семью. С 16 лет он преподавал в деревенских школах в Западном райдинге Йоркшира, а в 20 лет открыл собственную школу в Линкольне. В свободное время он читал математические журналы в Институте механики Линкольна. Там же он прочитал книгу Исаака Ньютона «9».0509 Principia , Traité de mécanique céleste Пьера-Симона Лапласа и Аналитическая механика Жозефа-Луи Лагранжа и начали решать сложные задачи по алгебре.

Викторина «Британника»

Числа и математика

Буль представил поток оригинальных статей в новый Кембриджский математический журнал , начиная с 1841 года с его «Исследований по теории аналитических преобразований». Эти статьи были посвящены дифференциальным уравнениям и алгебраической проблеме линейного преобразования с упором на концепцию инвариантности. В 1844 г. в важной газете 9-го0509 Philosophical Transactions of the Royal Society , «Об общем методе анализа», за которую он был награжден первой золотой медалью Королевского общества по математике, он обсуждал, как можно объединить методы алгебры и исчисления. Вскоре Буль увидел, что его алгебра может применяться и в логике.

Развивая новые идеи о логическом методе и будучи уверенным в символических рассуждениях, которые он вывел из своих математических исследований, он опубликовал в 1847 году брошюру «Математический анализ логики», представляющую собой эссе по исчислению дедуктивных рассуждений , в котором он убедительно доказывал, что логика должна быть связана с математикой, а не с философией.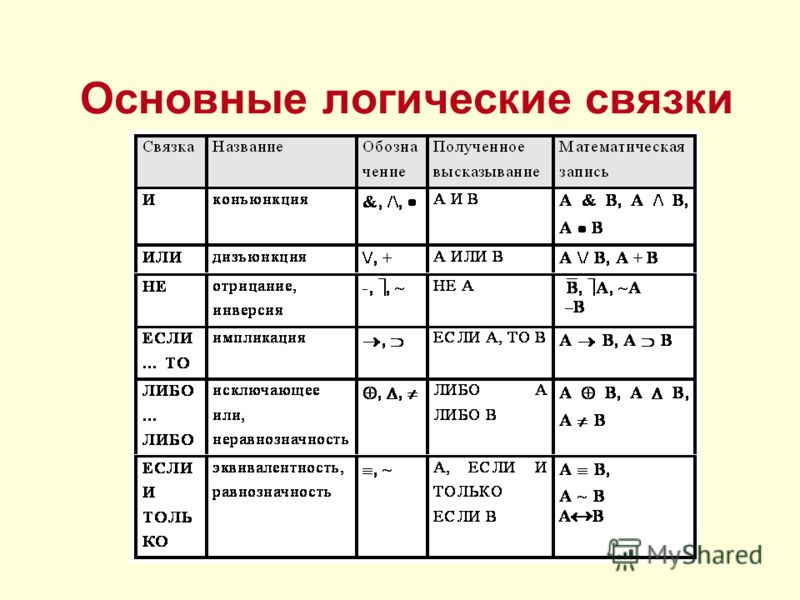 Он завоевал восхищение английского логика Августа Де Моргана, опубликовавшего в том же году «Formal Logic ». На основании своих публикаций Буль в 1849 году был назначен профессором математики в Королевском колледже графства Корк (ныне Университетский колледж Корка), хотя у него не было университетской степени. В 1854 году он опубликовал «Исследование законов мышления, на которых основаны математические теории логики и вероятностей».0510, который он считал зрелым изложением своих идей. В следующем году он женился на Мэри Эверест, племяннице сэра Джорджа Эвереста, в честь которого названа гора. У Булей было пять дочерей.

Один из первых англичан, написавших о логике, Буль указал на аналогию между алгебраическими символами и теми, которые могут представлять логические формы и силлогизмы, показав, как символы количества можно отделить от символов действия. С Буля в 1847 и 1854 годах началась алгебра логики, или то, что сейчас называется булевой алгеброй. Оригинальный и замечательный общий символический метод логического вывода Буля, полностью изложенный в Laws of Thought (1854) позволяет, учитывая любые предложения, включающие любое количество терминов, делать выводы, которые логически содержатся в посылках.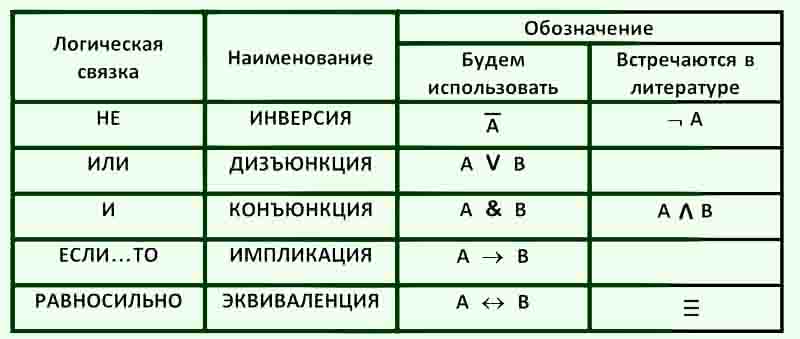 Заумные рассуждения Буля привели к приложениям, о которых он и не мечтал, — например, телефонная коммутация и электронные компьютеры используют двоичные числа и логические элементы, построенные и работающие на основе булевой логики. Он также попытался использовать общий метод вероятностей, который позволил бы по заданным вероятностям любой системы событий определить последующую вероятность любого другого события, логически связанного с данными событиями.

В 1857 году Буль был избран членом Королевского общества. Влиятельный Трактат о дифференциальных уравнениях появился в 1859 году, а в следующем году за ним последовало его продолжение, Трактат о исчислении конечных разностей . Эти работы, которые использовались в качестве учебников в течение многих лет, воплощают в себе развитие наиболее важных открытий Буля.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Буль заболел пневмонией, пройдя три мили от своего дома до Королевского колледжа во время ливня 24 ноября 1864 года.