Делитель тока, калькулятор, пример
Делитель тока — это простейшая линейная электрическая цепь, позволяющая разделять и использовать только часть от подаваемого в цепь тока. Простейший делитель тока — это два резистора, соединенных параллельно.
В данном обзоре мы рассмотрим, как работает и где применяется делитель тока. Также будет представлен онлайн калькулятор и программа, где можно просчитать токи на каждом параллельном участке цепи с резистором.
Как работает делитель тока
Принцип действия делителя тока основан на первом Законе Кирхгофа, согласно которому сумма всех токов втекающих в узел равна сумме всех токов вытекающих из узла. Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа.
Если рассматривать простую электрическую цепь с одним источником питания, то здесь для понимания деления тока достаточно воспользоваться правилом параллельного соединения резисторов. И именно им мы и будем пользоваться далее.
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Рассмотрим простую схему с источником постоянного тока и двумя параллельно соединенными резисторами:
Что происходит в такой цепи? В первую очередь отметим, что напряжение источника питания и номиналы резисторов приведены условно, и они больше подходят для переменного напряжения, которое далее в примерах и будет участвовать. Также, возвращаясь к постоянному току, следует не путать условное направление тока от «+» к «-» от направления движения носителей электрического заряда (электронов) от «-» к «+».
В цепи с напряжением 220 В и суммарным сопротивлением от двух резисторов 30 и 20 Ом сила тока 18,3 А. При этом ток доходя до места параллельного соединения разделяется и проходит по двум путям, имеющим разные сопротивления. На синем пути с резистором 30 Ом сила тока 7,3 А. На зеленом пути с резистором 20 Ом сила тока 11 А.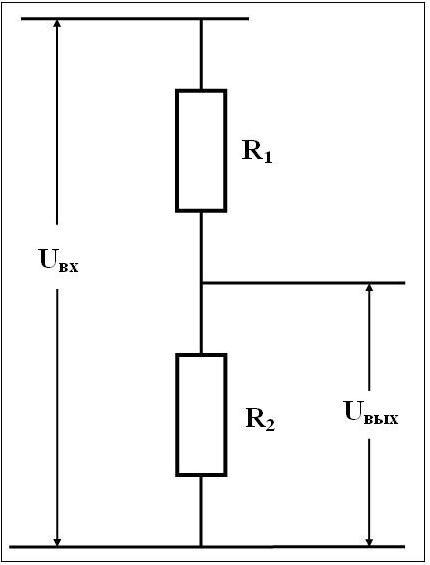 То есть на том пути, где сопротивление больше электроны замедляются и сила тока меньше. На пути, где сопротивление меньше, электроны движутся быстрее — соответственно и сила тока на этом отрезке больше. Пройдя участок с параллельным соединением ток опять сливается и по одному пути возвращается к источнику питания с силой 18,3 А (сумма сил тока на двух предыдущих участках 7,3 + 11).
То есть на том пути, где сопротивление больше электроны замедляются и сила тока меньше. На пути, где сопротивление меньше, электроны движутся быстрее — соответственно и сила тока на этом отрезке больше. Пройдя участок с параллельным соединением ток опять сливается и по одному пути возвращается к источнику питания с силой 18,3 А (сумма сил тока на двух предыдущих участках 7,3 + 11).
В рассмотренном примере для анализа делителя тока была использована программа Multisim, которая просчитывает с помощью соответствующих приборов силу тока на каждом участке цепи с учетом напряжения источника питания и сопротивления резисторов. Стоит отметить, что в составе делителя тока может быть любое количество резисторов. Помимо параллельного соединения в цепи может быть и последовательное соединение резисторов. Полученное смешанное соединение также легко просчитывается в программе.
Все расчеты в цепи с делителем тока можно произвести и самостоятельно с использованием соответствующих формул. Далее мы приведем онлайн калькулятор делителя тока и рассмотрим пример расчета.
Калькулятор делителя тока онлайн
Представленный онлайн-калькулятор позволяет рассчитать силу тока при использовании последовательных резистивных делителей на любом участке цепи. Для расчета необходимо ввести общую силу тока цепи и значения сопротивлений резисторов на параллельном участке. Калькулятор делителя тока поддерживает до 10 резисторов одновременно.
Калькулятор делителя тока на резисторах:
| Сила тока источника, А | |
| Резистор | Сила тока на участке резистора, А |
Делитель тока — расчет по формулам
Для примера возьмем схожую с рассмотренной ранее схему. На параллельном участке три резистора 30, 20 и 10 Ом. Напряжение источника питания 220 В. Программа Multisim просчитала силу тока на каждом участке.
На параллельном участке три резистора 30, 20 и 10 Ом. Напряжение источника питания 220 В. Программа Multisim просчитала силу тока на каждом участке.
Нам же нужно рассчитать силу тока на разных участках самостоятельно. Исходные данные следующие:
- R1 = 30 Ом, R2 = 20 Ом, R3 = 10 Ом.
- В первом случае известно только напряжение источника питания U1 = 220 В (вольтметр V1).
- Во втором случае известна только общая сила тока в цепи I4 = 40,333 А.
Требуется определить силу тока I1, I2, I3 (амперметры U1, U2, U3) на участках с резисторами R1, R2, R3.
Решение:
- Если неизвестно напряжение источника питания, то в первую очередь нужно определить сумму сопротивлений всех резисторов, соединенных параллельно. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1+I2+I3+…+In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей.
 Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением: - Зная общую силу тока цепи и общее сопротивление, находим напряжение. U = I×R = 40,333×5,45 ≈ 219,8 ≈ 220 В.
- При параллельном соединении резисторов напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания. Соответственно I1 = U/R1; I2 = U/R2; I3 = U/R3.
- I1 = 220/30 = 7,333 A
- I2 = 220/20 = 11 A.
- I1 = 220/10 = 22 A.
Особенности делителя тока
Выделим основные особенности делителя тока, состоящего из параллельно соединенных резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.

- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Где применяется делитель тока
Делитель тока очень часто встречается в электротехнике. Важно не путать делитель тока с делителем напряжения, так как после анализа общедоступных источников была выявлена противоречивая информация даже в википедии.
Цитирование из википедии: «Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.
Важно понимать, что напряжение во всей цепи одинаково для каждого резистора. И сила тока на участке резистора зависит только от его сопротивления. Поэтому, если рассмотреть пример с вентилятором, изменяя сопротивление другого резистора, мы не можем изменить силу тока, проходящую через вентилятор. Мощность останется прежней. Чтобы изменить силу тока и соответственно мощность, вместе с вентилятором должна быть последовательно соединена нагрузка, а не параллельно.
Последовательное соединение — это делитель напряжения. Параллельное соединение — это делитель тока. Информацию из википедии трудно назвать неверной, но она не полная. Там не хватает уточнения, что для подключения устройства с номинальным током меньшим, чем протекающий в цепи, нужно совмещать делитель тока с делителем напряжения.
Вернемся к примерам использования делителя тока. Цепи делителей тока находят применение в измерительных схемах, где требуется, чтобы часть измеряемого тока проходила через чувствительный прибор. Используя формулу делителя тока, можно подобрать подходящий шунтирующий резистор таким образом, чтобы через измерительный прибор всегда проходила точно заданная доля общего тока:
Теперь обратимся к примерам делителя тока, которые буквально рядом с каждым. Любой частный дом или квартира — это параллельное соединение, соответственно и делитель тока. Совокупность всех повторных заземлителей нейтрали трансформатора — это тоже делитель тока.
Расчет делителя напряжения с шунтом. Делитель напряжения
Делитель тока – устройство позволяющее поделить ток в цепи на две составные части, с целью использования одной из них.
Принцип действия делителя тока основан на первом законе Кирхгофа – сумма токов сходящихся в узле равна нулю. Если провести аналогию с водой, то его можно представить как русло реки, которое разветвляется на два более маленьких оттока.
Для нахождения токов I 1 и I 2 воспользуемся законом Ома , но для начала найдем эквивалентное сопротивление для параллельного соединения.
Делители тока применяются в измерительных устройствах, например при измерении больших токов. С помощью добавочного сопротивления –
Выведем коэффициент деления (шунтирования) n . Будем считать, что параметры с индексом 1 принадлежат амперметру (прибору), а параметры с индексом 2 – шунту. Параметры без индексов общие.
Рассмотрим пример.
Из формулы для коэффициента шунтирования, выразим R ш
Еще один пример
Каким станет новый предел измерения амперметра, после его шунтирования сопротивлением в 10 Ом, если старый предел был равен 0,5 А? Сопротивление измерительного механизма амперметра – 25 Ом.
Посчитаем коэффициент шунтирования
Тогда новый предел измерения амперметра
Дели́тель напряже́ния — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .
Энциклопедичный YouTube
1 / 5
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} .
 Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{ U 1 = I R 1 U 2 = I R 2 {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}\end{array}}\right.}
Разделив выражение для на выражение для в итоге получаем:
U 1 U 2 = R 1 R 2 {\displaystyle {\frac {U_{1}}{U_{2}}}={\frac {R_{1}}{R_{2}}}} Таким образом, отношение напряжений U 1 {\displaystyle U_{1}} и U 2 {\displaystyle U_{2}} в точности равно отношению сопротивлений R 1 {\displaystyle R_{1}} и R 2 {\displaystyle R_{2}} .
Далее
U 1 = R 1 R 2 U 2 {\displaystyle U_{1}={\frac {R_{1}}{R_{2}}}U_{2}}
U 1 + U 2 = R 1 R 2 U 2 + U 2 {\displaystyle U_{1}+U_{2}={\frac {R_{1}}{R_{2}}}U_{2}+U_{2}}
U = (R 1 R 2 + 1) U 2 {\displaystyle U=\left({\frac {R_{1}}{R_{2}}}+1\right)U_{2}}
Т. е.
е.
U = (R 1 + R 2 R 2) U 2 {\displaystyle U=\left({\frac {R_{1}+R_{2}}{R_{2}}}\right)U_{2}}
Откуда:
U 2 = U R 2 R 1 + R 2 {\displaystyle U_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}}Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму . Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} .
 Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр , а в качестве нелинейного — параметрический стабилизатор напряжения .
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ . В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на
Представьте, что течёт река, и вдруг ширина её русла резко уменьшается, через некоторое расстояние ширина русла снова увеличивается.
 Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.

Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам).
 Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в , или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в .
Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в , или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в .Изобразим цепь делителя тока:
На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.
Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов:
Выведем закон Ома для этой цепи. Его можно записать в следующем виде:
Преобразовывая указанные формулы так, как нам удобно, мы можем определить:
1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2 :
Пример: Определить значения I1 и I1 делителя тока, если значение общего тока Iобщ = 0,6А, сопротивление R1 =100 Ом, а R2 = 20 Ом.

I1 = 0,6 * 20 / (100 + 20) = 0,1 А; По формуле (18) вычисляем: I2 = 0,6 * 100 / (100 + 20) = 0,5 А; Не забывайте, что резисторы поглощают мощность, поэтому её необходимо рассчитать, (формула3):
P = I * I * R
Определим рассеиваемую мощность резисторов по формуле (3):
Для резистора R1: P = 0,1 * 0,1 * 100 = 1 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт;
Для резистора R2: P = 0,5 * 0,5 * 20 = 5 Вт; по правилу (1) выбираем резистор мощностью P = 10 Вт.
2. Расчитать шунт R2 в цепи измерительного прибора, при известных: внутреннем сопротивлении R1 , максимальном токе обмотки катушки прибора I1 и максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:
Пример: Полное отклонение стрелки миллиамперметра при значении I1 = 1 мА, внутреннее сопротивление катушки прибора R1 = 200 Ом.
 Рассчитайте шунт R2 , чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.
Рассчитайте шунт R2 , чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.Решение: По формуле (17) вычисляем: R2 = 0,001 * 200 / (1 – 0,001) = 0,2 Ом; Рассчитаем поглощаемую (рассеиваемую) мощность R2 (формула 3): P = I2 * I2 * R2 , где I2 = Iобщ — I1 = 999 мА, P = 0,999 * 0,999 * 0,2 = 0,199 Вт; по правилу (1) выбираем резистор мощностью P = 0,25 Вт
Для достижения точности в измерительных цепях, выбирают высокоточные резисторы, кроме того, используют их последовательное и параллельное соединение.
Как и в случае с делителем напряжения, Вы спросите: Если это делитель, должен быть коэффициент деления? Да он есть, но в определении необходимых величин, пользоваться им крайне неудобно, поэтому не буду ломать голову ни себе, ни Вам.
Делитель напряжения на резисторах
В электронике существует множество схем, требующих регулировки и оптимизации напряжения на различных участках. Для решения этой задачи чаще всего используется делитель напряжения на резисторах, зарекомендовавший себя наиболее эффективным устройством. Данные приборы используются в самых разных конструкциях, начиная от простейших настенных светильников, и заканчивая сложными схемами в платах управления.
Для решения этой задачи чаще всего используется делитель напряжения на резисторах, зарекомендовавший себя наиболее эффективным устройством. Данные приборы используются в самых разных конструкциях, начиная от простейших настенных светильников, и заканчивая сложными схемами в платах управления.
Делитель напряжения это устройство, осуществляющее регулировку выходного напряжения по отношению значения входного напряжения, в соответствии с коэффициентом передачи. То есть, из большего значения получается меньшее, а само напряжение бывает постоянным или переменным. Самая простая схема делителя напряжения состоит как минимум из двух сопротивлений. Если их сопротивления равны между собой, то и падения напряжения будут одинаковыми. Поэтому, по закону Ома напряжение на выходе прибора будет ровно в два раза ниже, чем на входе. В других случаях для расчетов падения напряжений используются формулы.
Как работает делитель напряжения
Основной функцией делителя напряжения в электрических цепях является снижение напряжения и получение нескольких его значений с фиксированными показателями на различных участках. Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.
Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.
Простейший делитель представляется в виде двух участков цепи, называемых плечами. Верхним плечом считается участок между нулевой точкой и положительным напряжением, а нижним участок между нулевой точкой и минусом. После того как определены исходные данные, можно сделать самый простой расчет делителя напряжения.
В качестве примера рассматриваются два резистора, соединенные последовательно. К ним подается напряжение U, которое может быть переменными или постоянным. После этого в действие вступает закон Ома, когда при последовательном соединении резисторов, общее сопротивление составит сумму их номиналов. В виде формы это будет выглядеть следующим образом: I = U/Rобщ, в которой Rобщ = R1+R2. Следовательно, I = U/(R1+R2).
Сила тока при последовательно соединенных резисторов, будет одинаковой на всех участках цепи. Если у каждого резистора имеется собственное значение сопротивления, то по закону Ома у них образуются совершенно разные напряжения.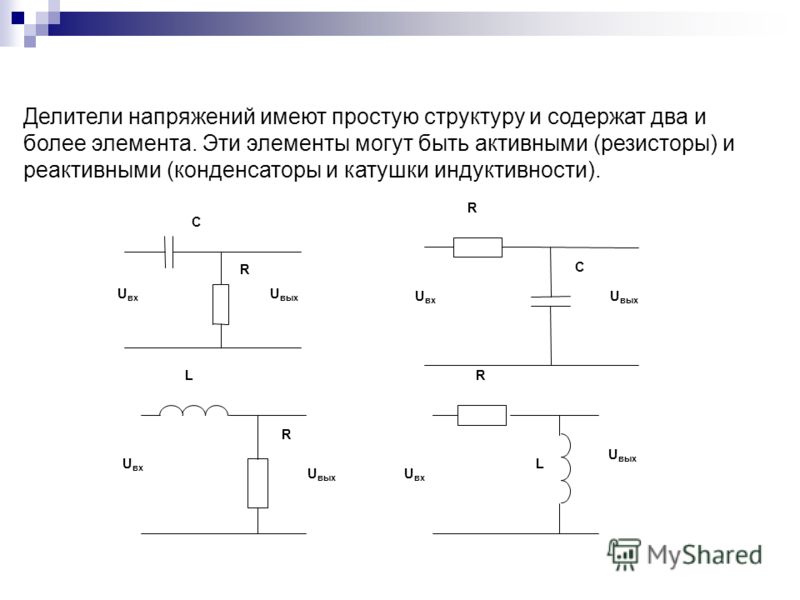 Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2).
Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2).
Для того, чтобы найти значения напряжений U1 и U2, необходимо выполнить такие действия: U1 = U x R1/(R1+R2) и U2 = U x R2/(R1+R2). Если правые части каждого уравнения сложить друг с другом, то в результате получится значение входящего напряжения U, состоящее из суммы напряжений U1 и U2, то есть U = U1 + U2. Это значит, что сумма падений напряжений на всех последовательно соединенных резисторах, будет равна напряжению источника питания, то есть входящему напряжению. Таким образом, данное выражение есть ни что иное, как формула делителя напряжения. Практически получается, что входящее напряжение U оказалось разделенным на два напряжения с собственными значениями U1 и U2.
Во многих случаях необходимо, чтобы процесс разделения напряжения осуществлялся плавно. С этой целью был изобретен прибор переменный резистор. Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.
Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.
Расчет резистивного делителя напряжения
Сделать расчеты делителя, состоящего из более чем трех резисторов можно по специальным формулам. Существуют методики, позволяющие выводить формулы для схем, содержащих от четырех и более резисторов. В примерных расчетах будет использоваться источник питания с напряжением 12 вольт. Необходимо получить разные значение напряжения: U1 = 1В, U2 = 3В, U3 = 5В, U1 = 7В.
На представленном рисунке номера резисторов, расположенных в определенном порядке, соответствуют создаваемым падениям напряжения. Для того чтобы получить требуемые значения напряжения понадобится пять резисторов. Их сопротивления и нужно будет определить.
Их сопротивления и нужно будет определить.
Прежде чем рассчитать делитель напряжения на резисторах, необходимо задать его общее сопротивление. Его значение будет находиться в промежутке между 1 кОм и 100 кОм. Могут быть заданы и другие параметры, однако следует учитывать, что при малых значениях сопротивления, на делителе произойдет рост тепловых потерь, а при слишком больших значения полученного напряжения будут неточными из-за подключенной нагрузки. Поэтому при расчетах рекомендуется использовать значение в пределах 12 кОм.
Итогом будут следующие формулы для каждого резистора:
- R1 = U1Rдел/Uпит,
- R2 = U2Rдел/Uпит — R1,
- RЗ = U3Rдел/Uпит-(R1+R2),
- R4 = U4Rдел/Uпит — (R1+R2+RЗ).
Остается лишь определить сопротивление дополнительного, пятого резистора:
- Rдоп = Rдел-(R1+R2+RЗ+R4).
Если в указанные формулы подставить исходные данные, то сопротивления резисторов будут иметь следующие значения: R1 = 1 кОм, R2 = 2 кОм, R3 = 2 кОм, R4 = 2 кОм, Rдоп = 5 кОм. Полученные значения резисторов №№ 1,2,3,4 совпадают с номиналами, расположенными в ряду Е24. Для дополнительного резистора в этом ряду нет точного номинала, поэтому ему подойдет сопротивление, максимально приближенное к расчетному 5,1 кОм.
Полученные значения резисторов №№ 1,2,3,4 совпадают с номиналами, расположенными в ряду Е24. Для дополнительного резистора в этом ряду нет точного номинала, поэтому ему подойдет сопротивление, максимально приближенное к расчетному 5,1 кОм.
С целью получения более реальных значений напряжений, соответствующие заданным значениям, каждый резистор, используемый в делителе, необходимо заранее проверить омметром. В этом случае точные данные позволят получить результаты, в которых отклонение от номинала составит не более 1%. Данные формулы могут использоваться при расчетах делителей, включающих в схему любое количество резисторов.
Применение резисторных делителей напряжения
Каждый резисторный делитель получил широкое практическое применение в различных электронных схемах. Типичным примером является потенциометр, который является переменным резистором, входящим в состав регулируемого делителя напряжения. Он состоит из резистора и скользящего контакта, разделяющего этот резистор на две части и передвигающегося между ними.
Другим вариантом, где применяется резистивный делитель напряжения, являются резистивные датчики, устанавливаемые в различные устройства. Типичным примером служит фоторезистор, изменяющий сопротивление, пропорционально количеству света, падающему на него. Кроме того, эти элементы используются и в других приборах датчиках давления, ускорения, термисторах и других аналогичных устройствах.
Расчет делителя напряжения на резисторах онлайн при помощи калькулятора
| |||||||||||
| |||||||||||
Как «поделить» АЦП правильно / Хабр
Довольно часто в устройствах применяются активные датчики (терморезисторы, тензорезисторы, фоторезисторы, времярезисторы, счастьерезисторы и прочее).
Чтобы измерять соответствующую величину, датчик включают в цепь делителя в одно из его плеч.
Так рекомендуют поступать практически везде, особенно там, где точность не так важна как стоимость. В интернете множество уроков для ардуинщиков о считывании температуры именно при помощи терморезистора. Так поступают и в более серьезных приложениях.
Для примера ниже я представил часть схемы из драйвера VESC 4.2, который измеряет температуру ключей.
О величине резистора во втором плече все высказываются по-разному. Кто-то связывает величину только с ограничением тока на нагрев термистора.
Где-то существуют прикидки и советы.
Но я не нашел конкретных указаний по типу: «Сделай так, потому что так-то и так-то».
Инженерный подход не дает мне спать спокойно. Место для прикидки в жизни есть, но порой встает вопрос: «А почему именно такое сопротивление?»
Интерес подогрел спор с коллегой. Что же, вызов принят.
Сразу скажу, что расчет выполнялся в программе SMath Studio. Прикладываю исходник. Вы можете использовать его в своих расчетах.
Прикладываю исходник. Вы можете использовать его в своих расчетах.
Постановка задачи
Необходимо ввести только диапазон изменения сопротивления, а формула должна возвратить оптимальное сопротивление второго плеча. Критерий оптимальности – максимальный размах напряжения на выходе.
Решение
Вариантов схем включения может быть две: либо изменяющееся сопротивление находится в лапах АЦП, либо наоборот.
С точки зрения оптимальности выбора значения не имеет, куда поставить резистор с изменяющимся сопротивлением, так как важно общее изменение сопротивления в цепи и как следствие тока, и как следствие падения напряжение, и не важно на каком плече.
Но далее идет рассмотрение именно первого варианта.
Напряжение на входе АЦП зависит от сопротивления постоянного резистора и пределов изменения переменного:
где – сопротивление постоянного резистора;
– самое большое сопротивление изменяющегося резистора;
– самое маленькое сопротивление изменяющегося резистора;
– напряжение питания.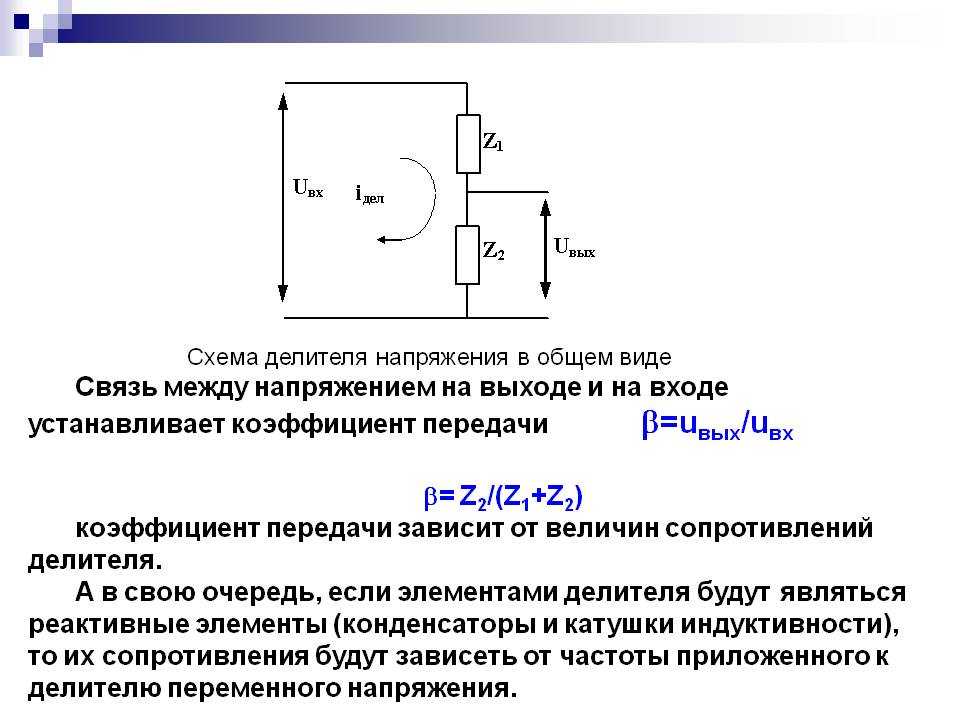
Если построить график зависимости этого напряжения от сопротивления постоянного резистора, то можно увидеть ярко выраженный пик, а это именно то, что нам нужно (график построен для случая питающего напряжения в 1 В при использовании NTC термистора в широком диапазоне температур).
Если надо найти максимум функции, то мы берем производную. (Входное напряжение я намеренно приравнял к нулю, так как здесь важны соотношения сопротивлений).
Корни нам подскажет либо листок бумаги, либо компьютерная алгебра (благодарность GarryC за пинок в сторону символьных вычислений):
Естественно, нам больше подойдет сопротивление больше нуля. Так как сроки поставки резисторов с отрицательным сопротивлением слишком большие.
Бывает, что считать числа сложно, но хочется покачать свое мышление навскидку. Бывает, люди навскидку считают децибелы, а все диву даются их уму. На самом деле они знают несколько секретов того как это делать.
Выделим и мы несколько правил для умничанья в дальнейшем. По графику такие прикидки делать легче. Как раз ниже он и представлен (но он лишь демонстрирует зависимость, описанную ранее).
По графику такие прикидки делать легче. Как раз ниже он и представлен (но он лишь демонстрирует зависимость, описанную ранее).
1 правило: Если изменение сопротивление незначительно, то постоянное сопротивление должно быть примерно равным среднему изменяющемуся. Но и изменение напряжения будет ничтожно. Используй лучше мостовую схему.
2 правило: Если сопротивление изменяется в разы, то постоянное сопротивление должно быть меньше максимально возможного у изменяемого.
3 правило: Чем больше изменяется сопротивление в изменяемом резисторе, тем меньше должно быть сопротивление постоянного относительно максимума изменяемого.
Например, при разнице между граничными заключениями сопротивления изменяемого резистора в 10 раз рекомендуемое сопротивление постоянного должно быть примерно в три раза меньше максимального, а в случае изменения в 50 раз постоянный резистор уже должен составлять 0,14 от максимального в диапазоне изменения переменного резистора.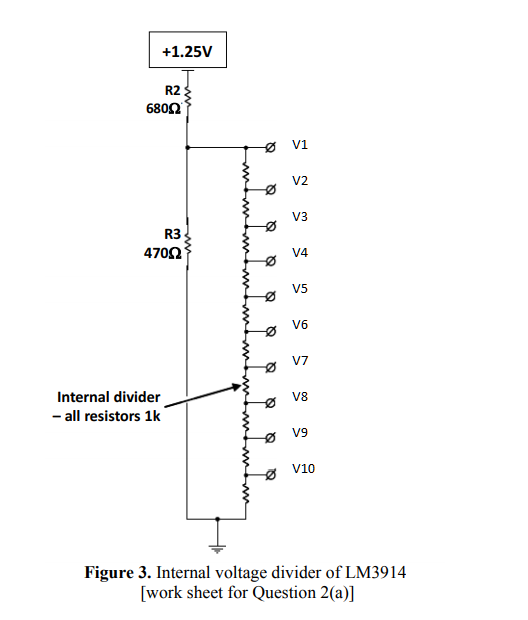
Если кто-то выделил дополнительные правила или не согласен с имеющимся, делитесь, и мы сделаем наш мир более грамотным.
Если совсем не охота вникать, но хочется поставить в свой arduino проект «осознанный» делитель, то можно воспользоваться готовым ответом.
Какой резистор ставить в паре с NTC термистором на 10 кОм с В = 3950.
Ниже я представил таблицу, в которой показаны различные диапазоны измеряемых температур и соответственное сопротивление второго плеча.
| Диапазон изменения сопротивления, градусов целься | Применение | Рекомендуемое сопротивление второго плеча, кОм | Процент использования динамического диапазона АЦП, % |
|---|---|---|---|
| 0..+125 | Мониторинг температуры внутри устройств в помещении | 3,3 | 81 |
| -50…+125 | Максималка для данного термистора | 18 | 96 |
-20. .+50 .+50 |
Температура на улице | 20 | 68 |
Если есть еще распространенные применения, то пишите, добавлю еще.
Надеюсь, теперь вы сможете оценить правильность используемого вами делителя. Конечно, все советы по выбору значения этого резистора, которые я упоминал ранее, верны. Но здорово осознавать то, что ты сделал все оптимально.
Расчет понижающих DC-DC преобразователей на микросхемах 34063 (топология Buck) + online-калькулятор — radiohlam.ru
Рассмотрим типовую схему понижающего DC/DC конвертера на микросхемах 34063:
Выводы микросхемы:
- SWC (switch collector) — коллектор выходного транзистора
- SWE (switch emitter) — эмиттер выходного транзистора
- Tc (timing capacitor) — вход для подключения времязадающего конденсатора
- GND — земля (общий провод)
- CII (comparator inverting input) — инвертирующий вход компаратора
- Vcc — питание
- Ipk — вход схемы ограничения максимального тока
- DRC (driver collector) — коллектор драйвера выходного транзистора (в качестве драйвера выходного транзистора также используется биполярный транзистор)
Элементы:
L1 — дроссель.
С1 — времязадающий конденсатор, он определяет частоту преобразования. Максимальная частота преобразования для микросхем 34063 составляет порядка 100-150 кГц.
R2, R1 — делитель напряжения для схемы компаратора. На неинвертирующий вход компаратора подается напряжение 1,25 В от внутреннего регулятора, а на инвертирующий вход — с делителя напряжения. Когда напряжение с делителя становится равным напряжению от внутреннего регулятора — компаратор переключает выходной транзистор.
C2, С3 — соответственно, выходной и входной фильтры. Емкость выходного фильтра определяет величину пульсаций выходного напряжения. Если в процессе расчетов получается, что для заданной величины пульсаций требуется очень большая емкость, можно расчет сделать для бо’льших пульсаций, а потом использовать дополнительный LC-фильтр. Емкость С3 обычно берут 100 … 470 мкФ.
Rsc — токочувствительный резистор. Он нужен для схемы ограничения тока. Максимальный ток выходного транзистора для MC34063 = 1.5А, для AP34063 = 1.6А. Если пиковый переключаемый ток будет превышать эти значения, то микросхема может сгореть. Если точно известно, что пиковый ток даже близко не подходит к максимальным значениям, то этот резистор можно не ставить.
Он нужен для схемы ограничения тока. Максимальный ток выходного транзистора для MC34063 = 1.5А, для AP34063 = 1.6А. Если пиковый переключаемый ток будет превышать эти значения, то микросхема может сгореть. Если точно известно, что пиковый ток даже близко не подходит к максимальным значениям, то этот резистор можно не ставить.
Порядок расчёта:
- Выбирают номинальные входное и выходное напряжения: Vin, Vout и максимальный выходной ток Iout.
- Выбирают минимальное входное напряжение Vin(min) и минимальную рабочую частоту fmin при выбранных Vin и Iout.
- Рассчитывают значение (ton+toff)max по формуле (ton+toff)max=1/fmin, ton(max) — максимальное время, когда выходной транзистор открыт, toff(max) — максимальное время, когда выходной транзистор закрыт.

- Рассчитывают отношение ton/toff по формуле ton/toff=(Vout+VF)/(Vin(min)-Vsat-Vout), где VF — падение напряжения на выходном фильтре, Vsat — падение напряжения на выходном транзисторе (когда он находится в полностью открытом состоянии) при заданном токе. Vsat определяется по графикам, приведенным в документации на микросхему (или на транзистор, если схема с внешним транзистором).Из формулы видно, что чем больше Vin, Vout и чем больше они отличаются друг от друга — тем меньшее влияние на конечный результат оказывают VF и Vsat, так что если вам не нужен суперточный расчет, то я бы посоветовал, уже при Vout=5 В, смело брать VF=0, Vsat=1,2 В (обычный, средненький биполярный танзистор) и не заморачиваться.

- Зная ton/toff и (ton+toff)max решают систему уравнений и находят ton(max).
- Находят емкость времязадающего конденсатора С1 по формуле: C1 = 4.5*10-5*ton(max).
- Находят пиковый ток через выходной транзистор: IPK(switch)=2*Iout. Если он получился больше максимального тока выходного транзистора (1,5 …1,6 А), то преобразователь с такими параметрами невозможен. Нужно либо пересчитать схему на меньший выходной ток (Iout), либо использовать схему с внешним транзистором.
- Рассчитывают Rsc по формуле: Rsc=0,3/IPK(switch).
- Рассчитывают минимальную емкость конденсатора выходного фильтра:
- С2=IPK(switch)*(ton+toff)max/8Vripple(p-p), где Vripple(p-p) — максимальная величина пульсаций выходного напряжения.
 Берется максимальная ёмкость из ближайших к расчётному стандартных значений.
Берется максимальная ёмкость из ближайших к расчётному стандартных значений. - Рассчитывают минимальную индуктивность дросселя:
L1(min)=ton(max)*(Vin(min)-Vsat-Vout)/IPK(switch). Если получаются слишком большие C2 и L1, можно попробовать повысить частоту преобразования и повторить расчет. Чем выше частота преобразования — тем ниже минимальная емкость выходного конденсатора и минимальная индуктивность дросселя. - Сопротивления делителя рассчитываются из соотношения Vout=1,25*(1+R2/R1).
Online-калькулятор для расчёта понижающего преобразователя:
(для правильности расчётов используйте в качестве десятичной точки точку, а не запятую)
1) Исходные данные:
(если вы не знаете значения Vsat , Vf , Vripple(p-p) , то расчёт будет сделан для Vsat=1.2 В, Vf=0 В, Vripple(p-p)=50 мВ)
Vin(min)=В; Vout=В; Iout=А; f=кГц;
Vsat=В; Vf=В Vripple(p-p)=мВ;
2) Расчётные данные:
(ton+toff)max=мкс; ton/toff=; ton(max)=мкс; IPK=А;
Rsc=Ом; C1=нФ; С2(min)=мкФ; Lmin=мкГн;
Готовые схемы для самостоятельного изготовления преобразователей
Описание принципов функционирования микросхем импульсных регуляторов серии 34063
Резистивный делитель онлайн.
 Делители напряжения и тока
Делители напряжения и токаПри проектировании электрических цепей возникают случаи, когда необходимо уменьшить величину напряжения (разделить его на несколько частей) и только часть подавать на нагрузку. Для этих целей используют делители напряжения . Они основаны на втором законе Кирхгофа .
Самая простая схема — резистивный делитель напряжения. Последовательно с подключаются два сопротивления R1 и R2.
При последовательном подключении сопротивлений через них протекает одинаковый ток I.
В результате, согласно закону Ома , напряжения на резисторах делится пропорционально их номиналу.
Подключаем нагрузку параллельно к R1 или к R2. В результате на нагрузке будет напряжение равное U R2 .
Примеры применения делителя напряжения
- Как делитель напряжения. Представьте, что у Вас есть лампочка, которая может работать только от 6 вольт и есть батарейка на 9 вольт. В этом случае при подключении лампочки к батарейке, лампочка сгорит.
 Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах.
Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах. - Датчик параметр — напряжение. Сопротивление резистивных элементов зависит от многих параметров, например температура. Помещаем одно из сопротивлений в среду с изменяющейся температурой. В результате при изменении температуры будет изменяться сопротивление одного из делителей напряжения. Изменяется ток через делитель. Согласно закону Ома входное напряжение перераспределяется между двумя сопротивлениями.
- Усилитель напряжения. Делитель напряжения может использоваться для усиления входного напряжения. Это возможно, если динамическое сопротивление одного из элементов делителя отрицательное, например на участке вольт-амперной характеристики туннельного диода.
Ограничения при использовании резистивных делителей напряжения
- Номинал сопротивлений делителя напряжения на резисторах должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки, подключаемой к делителю.
 В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения.
В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения. - Малые значения сопротивлений, являющихся делителем напряжения, приводят к большим потерям активной мощности . Через делитель протекают большие токи. Необходимо подбирать сопротивления, чтобы они не перегорали и могли рассеять такую величину отдаваемой энергии в окружающую среду.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины , нагревательные элементы, индукционные печи.
- Снижение КПД схемы за счет потерь на активных элементах делителя напряжения.
- Для получения точных результатов в делителе напряжения необходимо использовать прецизионные (высокоточные) сопротивления.
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Что такое делитель напряжения? Формулировка проста — это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно потребителей. Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
На самом деле примеров много.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два — это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин — это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
). Можно представить как два участка цепи, называемые плечами , сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним , а другое — верхним . Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах . Сопротивление может быть как активным , так и реактивным .
Резистивный делитель напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
Для каждого резистора:
Разделив выражение для на выражение для в итоге получаем:
Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .
Используя равенство
, в котором , а
И, выражая из него соотношение для тока:
Получим формулу, связывающую выходное () и входное () напряжение делителя:
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму . Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .
Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр , а в качестве нелинейного — параметрический стабилизатор напряжения .
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ . В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.
В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а — отрицательно, например как на участке вольт-амперной характеристики туннельного диода
Ограничения в применении резистивных делителей напряжения
- Номинал сопротивлений делителя должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки.
- Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
Примечания
Ссылки
Wikimedia Foundation
. 2010
.
2010
.
Смотреть что такое «Делитель напряжения» в других словарях:
делитель напряжения — делитель напряжения Преобразующее устройство, состоящее из плеч высокого и низкого напряжения, таких, что напряжение входа прикладывается ко всему устройству, а напряжение выхода снимается с плеча низкого напряжения. [МЭС… … Справочник технического переводчика
Большой Энциклопедический словарь
Устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. Используется в радио и… … Энциклопедический словарь
делитель напряжения — įtampos dalytuvas statusas T sritis automatika atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Automatikos terminų žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель… …
atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель… …
делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas, sudarytas iš rezistorių, induktyvumo ričių, kondensatorių, transformatorių arba iš šių elementų derinio taip, kad tarp dviejų šio įtaiso taškų susidarytų… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis chemija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider rus. делитель напряжения … Chemijos terminų aiškinamasis žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis fizika atitikmenys: angl. voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Fizikos terminų žodynas
Электротехническое устройство для деления напряжения постоянного или переменное тока на части. Любой Д. н. состоит из активных или реактивных электрических сопротивлений. Обычно Д. н. применяют для измерения напряжения. При низких… … Большая советская энциклопедия
Любой Д. н. состоит из активных или реактивных электрических сопротивлений. Обычно Д. н. применяют для измерения напряжения. При низких… … Большая советская энциклопедия
Электротехническое устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. При… … Энциклопедия техники
В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:
U вых = U вх х (R2 / R1 + R2)
Рис. 1. Делитель напряжения
Пример.
С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 1.
1.
Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.
Следовательно, R2 / (R1 +R2) R2 = 0,2
R2 = 0 ,2R1 + 0,2R2 .
R1 = 4R2
Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).
Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.
Для получения заданного значения напряжения следует применять высокоточные резисторы.
Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U
вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U
выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.
Важно помнить о том, что с уменьшением сопротивлений резисторов R1
и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.
Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов Rl и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)
Пример. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 3) .
Рис. 2 Делитель тока
Рис. 3.
Коэффициент деления тока определяется соотношением:
I вых / I вх = 1/10 = 0,1 = R1 / R2 + R1 , R2 = 100 Ом.
Отсюда,
0,1R1 + 0,1R2 = R1
0,1R1 + 10 = R1
R1 = 10/0 ,9 = 11,1 Ом
Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это .
Заметим еще раз, что на рис. 3 сопротивление R2 — это .
Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.
Устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.
Принципиальная схема делителя напряжения
В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?
Расчёт делителя напряжения
Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.
Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:
Rобщ = R1 + R2 = 400 + 500 = 900 Ом
По закону Ома находим силу тока, протекающего через резисторы:
I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА
Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):
Uвых = I * R2 = 0. 01А * 500 Ом = 5В
01А * 500 Ом = 5В
Или упрощая цепочку вычислений:
Uвых = Uвх * (R2 / (R1+R2))
Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:
R1 = (Uвх-Uвых)/Iд+Iн
R2 = Uвых / Iд
Здесь Iд и Iн — ток делителя и ток нагрузки соответственно. В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:
R1 = (Uвх-Uвых) * 100
R2 = Uвых * 100
P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.
Проверяем:
Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:
R1 = (9-5) * 100 = 400 Ом
R2 = 5 * 100 = 500 Ом
Всё сходится!
Применение делителя напряжений
В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление. На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.
Калькулятор делителя напряжения| Простобесплатные инструменты
Калькулятор делителя напряжения: вычисляет падение напряжения на каждой резисторной нагрузке при последовательном соединении.
Введите общее напряжение питания и нажмите кнопку Calculate :
Введите общее напряжение В T =
Вольт [В]
Введите сопротивление первой нагрузки R 1 =
Ом [Ом]
Введите сопротивление второй нагрузки R 2 =
Ом [Ом]
Введите сопротивление третьей нагрузки (опционально) R 3 =
Ом [Ом]
Падение напряжения R1 В 1 =
Вольт [В]
Падение напряжения R2 В 2 =
Вольт [В]
Падение напряжения R3 В 3 =
Вольт [В]
Правило делителя напряжения
Для цепи постоянного тока с источником постоянного напряжения В T и резисторы последовательно, падение напряжения V i в резисторе R i определяется по формуле:
Делитель напряжения »
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций. для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация пароля или калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 9 Инструменты Текст Онлайн-инструменты
- Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Бесплатные онлайн-калькуляторы и инструменты для электротехники
- Бесплатные онлайн финансовые калькуляторы и инструменты
- Бесплатные онлайн калькуляторы оценок и инструменты
- Бесплатные онлайн калькуляторы освещения и инструменты
- Бесплатные онлайн математические калькуляторы и инструменты
- Бесплатные онлайн калькуляторы и инструменты для проводов
- Бесплатные онлайн детские калькуляторы и инструменты
- Бесплатные онлайн-калькуляторы кузова и инструменты
- Ампер в кВА бесплатный онлайн калькулятор0089
- Ампер в вольт бесплатный онлайн калькулятор
- Ампер в ватт бесплатный онлайн калькулятор
- Счет за электричество бесплатный онлайн калькулятор
- Электрон вольт в вольт бесплатный онлайн калькулятор
- Бесплатный онлайн калькулятор потребления энергии
- Бесплатный онлайн калькулятор стоимости энергии 90888 90 джоулей 90 s
- Киловатт-часы в Киловатты онлайн калькулятор
- Киловатт-часы в Киловатты онлайн калькулятор
- кВА в ампер калькулятор
- кВА в киловатт калькулятор
- кВА в ватт онлайн калькулятор
- кВт в ВА калькулятор онлайн0088 Закон Ома калькулятор онлайн калькулятор
- Делитель напряжения онлайн калькулятор
- Падение напряжения онлайн калькулятор
- Вольт в ампер калькулятор онлайн
- Вольт в электрон-вольт бесплатный онлайн калькулятор
- Вольт в Джоули калькулятор онлайн
- Вольт в киловатты онлайн калькулятор
- Вольт в ватт калькулятор онлайн
- Вт в ВА бесплатный онлайн калькулятор
- Вт в вольт бесплатный онлайн калькулятор
- Вт-вольт-ампер-ом бесплатный онлайн-калькулятор
- Втч в мАч бесплатный онлайн-калькулятор
- Калибр провода бесплатный онлайн-калькулятор
И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Нашли ошибку? Дайте нам знать!
Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.
Ой! Что-то пошло не так, обновите страницу и повторите попытку.
Идентификатор страницы: 40
Калькулятор делителя напряженияCAF иллюстрирует теорему о максимальной передаче мощности Пэт использует калькулятор, чтобы проиллюстрировать «Теорему о максимальной передаче мощности», которая утверждает, что интерфейс с согласованным импедансом передает наибольшую мощность от источника к нагрузке.
 Обучающее видео прилагается.
Обучающее видео прилагается. VDivider — калькулятор делителя напряжения. Это последнее дополнение к бесплатному приложению CAFViewer для Windows. Это площадка для изучения работы аналоговых аудиоинтерфейсов всех типов, позволяющая пользователю развить интуицию в отношении того, как эти интерфейсы работают.
В этой статье я буду использовать VDivider для анализа интерфейса усилитель-громкоговоритель и сделать некоторые универсальные выводы. Во-первых, некоторые соглашения: в этой статье все напряжения являются среднеквадратичными, все импедансы резистивными, а все мощности рассчитаны на непрерывную синусоиду. Вот условности. Не стесняйтесь следовать в VDivider. Для тех из вас, кто предпочитает смотреть видео, а не читать статью, просто переходите к концу.
Оптимизация передачи мощности
Теорема о максимальной передаче мощности (и закон Якоби) утверждает, что интерфейс с согласованным импедансом передает наибольшую мощность от источника к нагрузке. В этом случае половина доступной мощности от источника (Вт S ) поступает в нагрузку (Вт L ). Хотя оптимизация передачи мощности интуитивно кажется желательной целью, особенно для усилителя мощности, она приводит к КПД всего 50%, поскольку половина W S рассеивается внутри источника. Это нормально, если вы собираетесь жарить бекон на усилителе, но не в том случае, если вы пытаетесь воспроизвести звук через громкоговоритель, используя минимально возможный ток, потребляемый от сети. Воспользуемся программой VDivide (рис. 1) для доказательства теоремы.
В этом случае половина доступной мощности от источника (Вт S ) поступает в нагрузку (Вт L ). Хотя оптимизация передачи мощности интуитивно кажется желательной целью, особенно для усилителя мощности, она приводит к КПД всего 50%, поскольку половина W S рассеивается внутри источника. Это нормально, если вы собираетесь жарить бекон на усилителе, но не в том случае, если вы пытаетесь воспроизвести звук через громкоговоритель, используя минимально возможный ток, потребляемый от сети. Воспользуемся программой VDivide (рис. 1) для доказательства теоремы.
Рисунок 1 – В согласованном интерфейсе R С = Р Л . Это передает 1/2 мощности источника (Вт S = 60 Вт) на нагрузку (Вт L = 30 Вт).
В VDivide я выбрал предустановку Ldspk Low-Z и изменил R S на 8 Ом, сопоставив его импеданс со значением по умолчанию R L = 8 Ом. Напряжение источника установлено на 31 В, значение, при котором W S = 60 Вт. Обратите внимание, что W L = 30 Вт, что составляет 1/2 от W S . Можно ли получить в нагрузку более 30 Вт? Физика говорит «нет», но давайте все же попробуем. Я установил ток источника I S на 15 А чтобы не кончились пока экспериментируем. Хороший источник питания имеет больший ток, чем требуется при фактическом использовании.
Обратите внимание, что W L = 30 Вт, что составляет 1/2 от W S . Можно ли получить в нагрузку более 30 Вт? Физика говорит «нет», но давайте все же попробуем. Я установил ток источника I S на 15 А чтобы не кончились пока экспериментируем. Хороший источник питания имеет больший ток, чем требуется при фактическом использовании.
Если удвоить сопротивление R L до 16 Ом, мощность W L упадет до 27 Вт, что составляет менее 30 Вт. Теперь передаваемая мощность составляет <50 % (рис. 2).
Рисунок 2. Удвоение импеданса нагрузки до 16 Ом снижает мощность W L до 27 Вт.
передача меньше, чем 30 Вт, создаваемые согласованным условием.
Рисунок 3. Уменьшение вдвое импеданса нагрузки до 4 Ом снижает мощность нагрузки до 27 Вт.
Есть три важных вывода.
- 1. Максимальная передача мощности (50 %) происходит, когда R L = R S .
 Получить большую мощность, чем у W L , произведенного с согласованным интерфейсом (30 Вт), просто невозможно. Это подтверждает теорему о максимальной передаче мощности и закон Якоби. Они были формализованы в 1840 году, так что это не новая разработка.
Получить большую мощность, чем у W L , произведенного с согласованным интерфейсом (30 Вт), просто невозможно. Это подтверждает теорему о максимальной передаче мощности и закон Якоби. Они были формализованы в 1840 году, так что это не новая разработка. - 2. Когда R L увеличивается, мощность передачи снижается, но эффективность передачи увеличивается. При R L = 16 Ом, W S = 40 Вт и W L = 27 Вт. Получаем меньше W S , но больше , чем 1/2 из них поступает в нагрузки (рис. 1)! Получается, что передача эффективности может быть увеличена, если мы готовы принять сокращение W S . Это большое дело. Это означает, что мы можем пожертвовать передачей мощности ради эффективности, если захотим получать от источника меньше энергии, чем та, которая производится в условиях согласования импеданса. Я вернусь к этому позже.
- 3. На напряжение на нагрузке E L влияет значение R L .
 В этом примере оно колеблется между 10 В (при 4 Ом) и 21 В (при 16 Ом). Это большая проблема, если вы используете громкоговоритель с типичной для американских горок кривой импеданса. Используя согласованный интерфейс, усилитель не может сохранить форму входного сигнала на своем выходе при работе нагрузки с частотно-зависимым импедансом (например, практически любой реальный громкоговоритель ). Это и есть определение «низкой точности».
В этом примере оно колеблется между 10 В (при 4 Ом) и 21 В (при 16 Ом). Это большая проблема, если вы используете громкоговоритель с типичной для американских горок кривой импеданса. Используя согласованный интерфейс, усилитель не может сохранить форму входного сигнала на своем выходе при работе нагрузки с частотно-зависимым импедансом (например, практически любой реальный громкоговоритель ). Это и есть определение «низкой точности».
- 1. Максимальная передача мощности (50 %) происходит, когда R L = R S .
Повторим упражнение с новыми начальными значениями. Сначала это может показаться странным, но оставайтесь со мной.
На рис. 4 я ввел R S = 0,1 Ом и R L = 0,1 Ом. Это согласованный интерфейс с использованием R S , типичный для современных усилителей. Напряжение источника E S установлено равным 30 В – удобное значение. «Перегрузка!» условие возникает из-за того, что калькулятор потребляет только 15 А, а этому усилителю пришлось бы потреблять колоссальные 149 А. А гонять эту нагрузку! Это нормально, потому что это гипотетический усилитель, который обеспечивает эталонное состояние. Усилитель, который может управлять нагрузкой 0,1 Ом, не имел реального применения, по крайней мере, в аудио.
А гонять эту нагрузку! Это нормально, потому что это гипотетический усилитель, который обеспечивает эталонное состояние. Усилитель, который может управлять нагрузкой 0,1 Ом, не имел реального применения, по крайней мере, в аудио.
Максимальная мощность W L , которую может выдать этот усилитель, составляет 2206 Вт, что составляет половину от 4455 Вт W S , что доказывает, что мы подключены для максимальной передачи мощности при эффективности 50%. Закон Якоби выполняется.
Рисунок 4 – Согласованный интерфейс с типичным выходным сопротивлением усилителя.
В первом примере мы обнаружили, что если мы готовы принять более низкое значение W L , чем у согласованного интерфейса, эффективность передачи может быть увеличена. Я сказал, что это важно, и вот почему.
На рис. 5 сопротивление R L увеличено до 8 Ом. Мощность W S (значительно) снижается до 111 Вт, но эффективность передачи возрастает с 50 % почти до 100 %, при этом 110 Вт подается на нагрузку и только 1 Вт рассеивается внутри усилителя. Это отличная сделка, тем более что этому усилителю требуется всего около 4 А вместо (теоретических) 149 А.A.
Это отличная сделка, тем более что этому усилителю требуется всего около 4 А вместо (теоретических) 149 А.A.
Рисунок 5. Увеличение R L до 8 Ом приводит к оптимизированному по напряжению интерфейсу с почти 100% эффективностью передачи.
За счет оптимизации передачи напряжения вместо передачи мощности напряжение нагрузки E L стабильно, как скала, поскольку R L варьируется. Этому усилителю все равно, что делает кривая импеданса громкоговорителя.
Окончательное решение в этой конструкции усилителя — выбрать реалистичный источник тока I S . 15 А позволит 2-омную нагрузку управлять синусоидой (рис. 6), но также увеличит размер, вес и цену усилителя. Более скромный номинал 4 Ом (рис. 7) позволяет I S должен быть уменьшен примерно до 8 А. Теперь у нас есть солидный усилитель мощностью 100 Вт при 8 Ом, который должен правильно раскачать любой 8-омный громкоговоритель без падения напряжения. Это источник постоянного напряжения, который выдает мощность в зависимости от частоты, определяемую кривой импеданса громкоговорителя.
Рис. 6. Для управления нагрузкой 2 Ом потребуется около 15 А тока источника.
Рис. 7. Нагрузка 4 Ом вдвое снижает потребляемый ток источника примерно до 8 А.
ЗаключениеСогласование полного сопротивления обеспечивает передачу максимальной мощности от источника к нагрузке. Поскольку R S не часто указывается для современных усилителей, многие предполагают, что интерфейс усилителя-громкоговорителя совпадает. Нет, это не так. За счет преобразования R L >> R S эффективность передачи резко возрастает за счет достижения максимальной теоретической передачи мощности. Это хорошая сделка, которой занимаются все современные твердотельные усилители.
Еще добавлю, что КПД, о котором идет речь в этой статье, относится к передаче звуковой мощности в нагрузку. Этот термин также используется для описания преобразования мощности электросети в мощность звука, что не рассматривалось в этой статье. pb
pb
Вы предпочитаете смотреть, а не читать? Вот видео.
Калькулятор делителя напряжения | Electronics Engineering
Калькулятор делителя напряжения | Электронная инженерия- ОБЩИЕ СВЕДЕНИЯ
- ГРАЖДАНСКАЯ
- ОПТИЧЕСКИЙ
- ПЛАСТИК
- ХИМИЧЕСКИЙ
- КЕРАМИКА
- МЕХАНИЧЕСКИЙ
- ЭЛЕКТРОНИКА
- ЭЛЕКТРИЧЕСКИЙ
- МЕТАЛЛУРГИЯ
- НЕФТЬ/ГАЗ
- ФИЗИКА
В электронике делитель напряжения (также известный как делитель потенциала) представляет собой пассивную линейную схему, которая создает выходное напряжение (Vout), которое составляет часть его входного напряжения (Vin). Деление напряжения является результатом распределения входного напряжения между компонентами делителя. Простым примером делителя напряжения являются два последовательно соединенных резистора, при этом входное напряжение прикладывается к паре резисторов, а выходное напряжение возникает в результате соединения между ними. Резистивные делители напряжения обычно используются для создания опорных напряжений или для уменьшения величины напряжения, чтобы его можно было измерить, а также могут использоваться в качестве аттенюаторов сигналов на низких частотах. Для постоянного тока и относительно низких частот делитель напряжения может быть достаточно точным, если он состоит только из резисторов, где требуется частотная характеристика в широком диапазоне (например, в пробнике осциллографа), делитель напряжения может иметь добавленные емкостные элементы для компенсации нагрузки. емкость. При передаче электроэнергии для измерения высокого напряжения используется емкостный делитель напряжения. Общий случай Делитель напряжения относительно земли создается путем последовательного соединения двух электрических импедансов, как показано на рисунке 1. Входное напряжение прикладывается к последовательным импедансам Z1 и Z2, а выходное напряжение представляет собой напряжение к Z2. Z1 и Z2 могут состоять из любой комбинации элементов, таких как резисторы, катушки индуктивности и конденсаторы.
Резистивные делители напряжения обычно используются для создания опорных напряжений или для уменьшения величины напряжения, чтобы его можно было измерить, а также могут использоваться в качестве аттенюаторов сигналов на низких частотах. Для постоянного тока и относительно низких частот делитель напряжения может быть достаточно точным, если он состоит только из резисторов, где требуется частотная характеристика в широком диапазоне (например, в пробнике осциллографа), делитель напряжения может иметь добавленные емкостные элементы для компенсации нагрузки. емкость. При передаче электроэнергии для измерения высокого напряжения используется емкостный делитель напряжения. Общий случай Делитель напряжения относительно земли создается путем последовательного соединения двух электрических импедансов, как показано на рисунке 1. Входное напряжение прикладывается к последовательным импедансам Z1 и Z2, а выходное напряжение представляет собой напряжение к Z2. Z1 и Z2 могут состоять из любой комбинации элементов, таких как резисторы, катушки индуктивности и конденсаторы. Если ток в выходном проводе равен нулю, то соотношение между входным напряжением Vin и выходным напряжением Vout будет следующим: V о ты т знак равно Z 2 Z 1 + Z 2 V я п {\ displaystyle V _ {\ mathrm {out} } = {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}} \ cdot V _ {\ mathrm {in}}} Доказательство (с использованием закона Ома): V i n = I ( Z 1 + Z 2 ) {\ displaystyle V _ {\ mathrm {in}} = I \ cdot (Z_ {1} + Z_ {2})} V о ты т знак равно я Z 2 {\ displaystyle V _ {\ mathrm {out}} = I \ cdot Z_ {2}} я знак равно V я п Z 1 + Z 2 {\ displaystyle I = {\ frac {V _ {\ mathrm {in}}} {Z_ {1} + Z_ {2}}}} V о ты т знак равно V я п Z 2 Z 1 + Z 2 {\ displaystyle V _ {\ mathrm {out}} = V _ {\ mathrm {in}} \ cdot {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}}} Передаточная функция (также известная как отношение напряжения делителя) этой схемы: H = V o u t V я п знак равно Z 2 Z 1 + Z 2 {\ displaystyle H = {\ frac {V _ {\ mathrm {out}}} {V _ {\ mathrm {in}}}} = {\ frac {Z_ {2}} { Z_{1}+Z_{2}}}} В целом эта передаточная функция представляет собой сложную рациональную функцию частоты.
Если ток в выходном проводе равен нулю, то соотношение между входным напряжением Vin и выходным напряжением Vout будет следующим: V о ты т знак равно Z 2 Z 1 + Z 2 V я п {\ displaystyle V _ {\ mathrm {out} } = {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}} \ cdot V _ {\ mathrm {in}}} Доказательство (с использованием закона Ома): V i n = I ( Z 1 + Z 2 ) {\ displaystyle V _ {\ mathrm {in}} = I \ cdot (Z_ {1} + Z_ {2})} V о ты т знак равно я Z 2 {\ displaystyle V _ {\ mathrm {out}} = I \ cdot Z_ {2}} я знак равно V я п Z 1 + Z 2 {\ displaystyle I = {\ frac {V _ {\ mathrm {in}}} {Z_ {1} + Z_ {2}}}} V о ты т знак равно V я п Z 2 Z 1 + Z 2 {\ displaystyle V _ {\ mathrm {out}} = V _ {\ mathrm {in}} \ cdot {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}}} Передаточная функция (также известная как отношение напряжения делителя) этой схемы: H = V o u t V я п знак равно Z 2 Z 1 + Z 2 {\ displaystyle H = {\ frac {V _ {\ mathrm {out}}} {V _ {\ mathrm {in}}}} = {\ frac {Z_ {2}} { Z_{1}+Z_{2}}}} В целом эта передаточная функция представляет собой сложную рациональную функцию частоты.


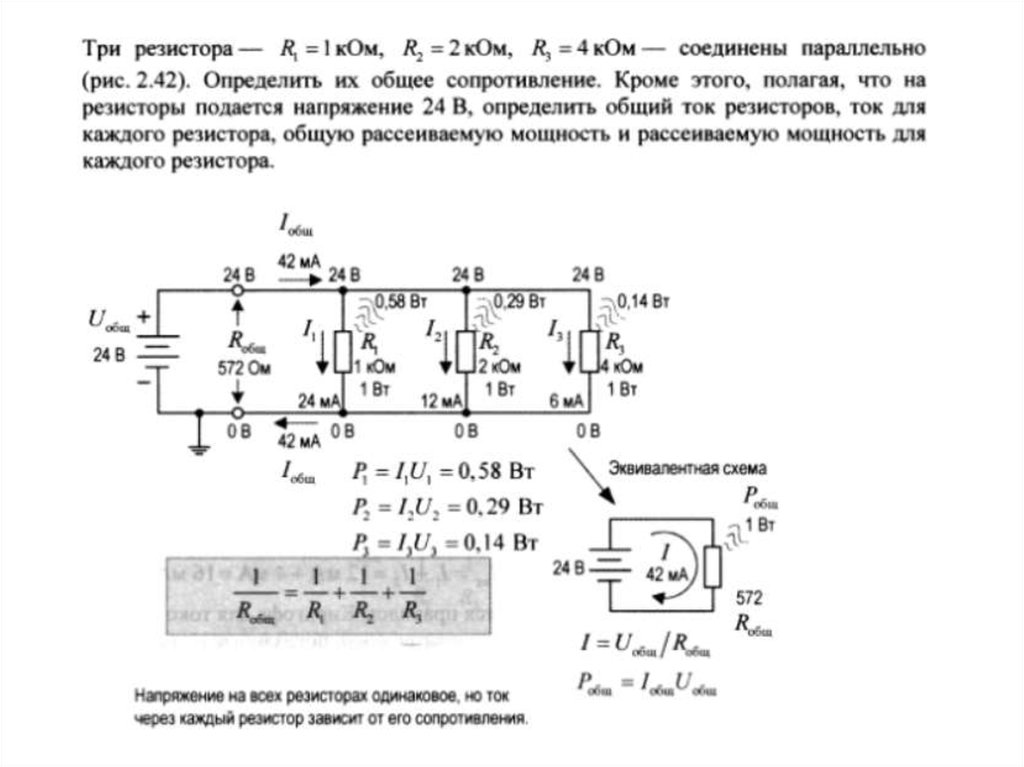 Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением: 
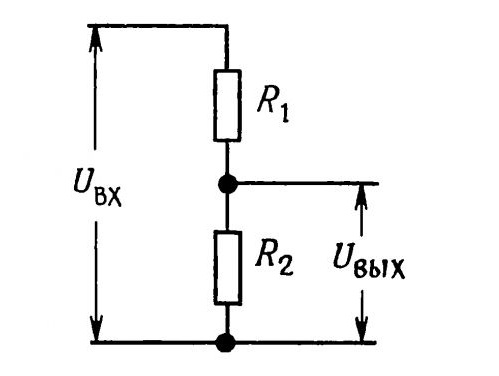 Последовательное соединение — это делитель напряжения. Параллельное соединение — это делитель тока. Информацию из википедии трудно назвать неверной, но она не полная. Там не хватает уточнения, что для подключения устройства с номинальным током меньшим, чем протекающий в цепи, нужно совмещать делитель тока с делителем напряжения.
Последовательное соединение — это делитель напряжения. Параллельное соединение — это делитель тока. Информацию из википедии трудно назвать неверной, но она не полная. Там не хватает уточнения, что для подключения устройства с номинальным током меньшим, чем протекающий в цепи, нужно совмещать делитель тока с делителем напряжения. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков): е.
е.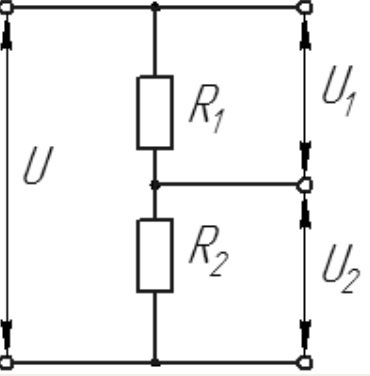 Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность. Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
 Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в , или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в .
Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в , или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в .
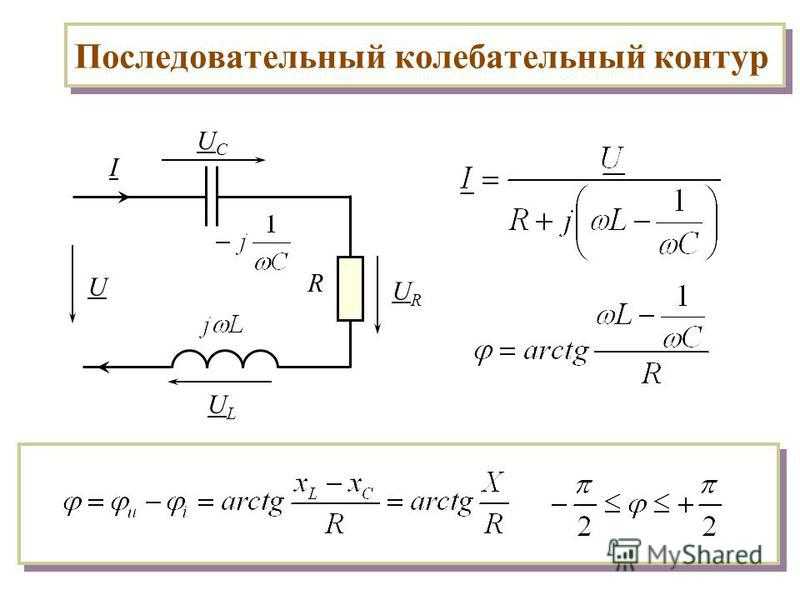 Рассчитайте шунт R2 , чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.
Рассчитайте шунт R2 , чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.