Векторное произведение векторов калькулятор
Результатом векторного произведения двух векторов будет являться вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
;
}
Задайте координаты второго вектора
b̅ =
{
;
;
}
Векторное произведение векторов
Векторным произведением двух векторов a и b в трехмерном евклидовом пространстве – называется вектор c. Модуль вектора c, численно равен площади параллелограмма OABQ, построенного на векторах

Векторное произведение векторов a и b обозначается как: [a b], [a, b], a × b, a ∧ b
Параллелограмм OABQНаправление получившегося вектора c будет перпендикулярно плоскости параллелограмма OABQ.
В правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (aybz — byaz) — j̅ (axbz — b
Формула для координат векторного произведения вычисляется из определителя третьего порядка, где первая строка – векторы i, j, k (i = (1 0 0), j(0 1 0), k = (0 0 1)), а вторая и третья строки – координаты векторов a и b:
[a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axbax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то в правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] =
i̅
((By — Ay)(Dz — Cz) — (D
Векторное произведение не обладает переместительным свойством, поэтому при перестановке множителей векторное произведение изменит знак: b × a = -(a × b)
Векторное произведение равно нулю, когда векторы
 е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.
е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.В левом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (azby — bzay) + j̅ (axbz — bxaz) + k̅ (aybx — byax)
Примеры векторного произведения векторов
Пример 1. Найдем векторное произведение векторов. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
N̅ = [AB × CD] =
= i̅i̅ j̅ k̅ ABx ABy ABz CDx CDy CDz
— j̅ABy ABz CD CDz
+ k̅ABx ABz CDx CDz
= i̅ AByCDz — i̅ ABzCDy — j̅ ABxCDz + j̅ ABzCDx + k̅ ABxCDy — k̅ AByCDx = ABx ABy CDx CDy
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0.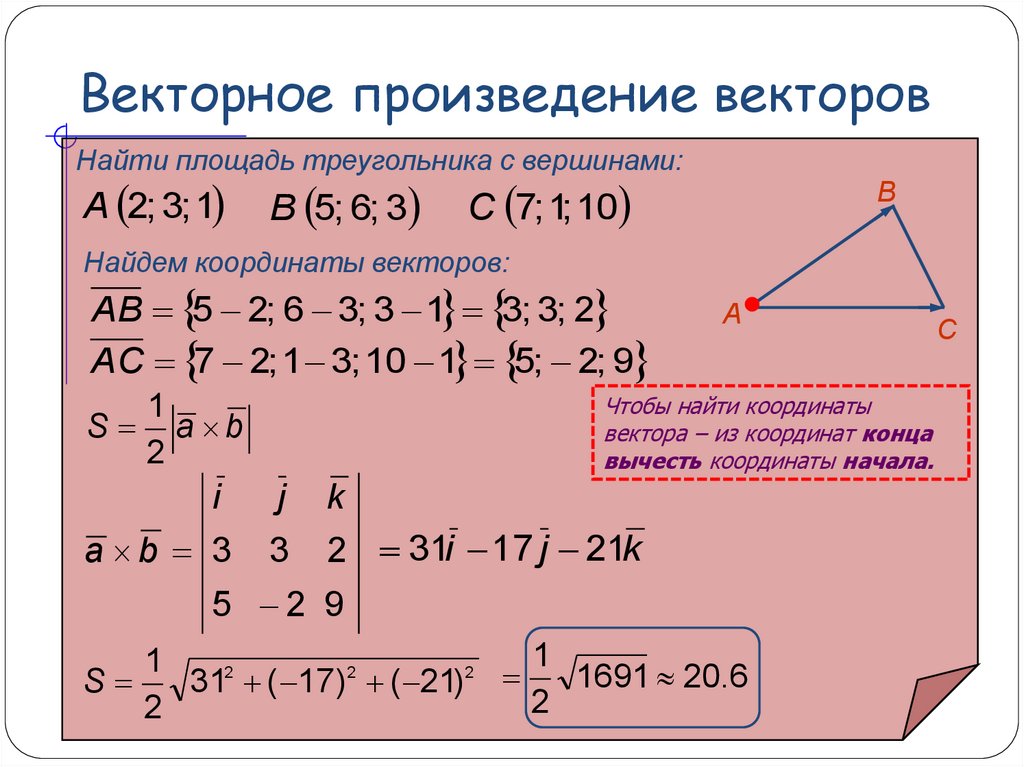 2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx
ABx = -8
ABy = -1/5
ABz = -275/4
CDx = 7
CDy = 6
CDz = 7
N̅ = [AB × CD] = i̅ (-1/5 ⋅ 7 — 6 ⋅ (-275/4)) — j̅ (-8 ⋅ 7 — 7 ⋅ (-275/4)) + k̅ (-8 ⋅ 6 — 7 ⋅ (-1/5)) = i̅ (-7/5 — (-825/2)) — j̅ (-56 — (-1925/4)) + k̅ (-48 — (-7/5)) = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = [AB × CD] = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = {4111/10 ; -1701/4 ; -233/5}
N̅ = {411.1 ; -425.25 ; -46.6}
Пример 2.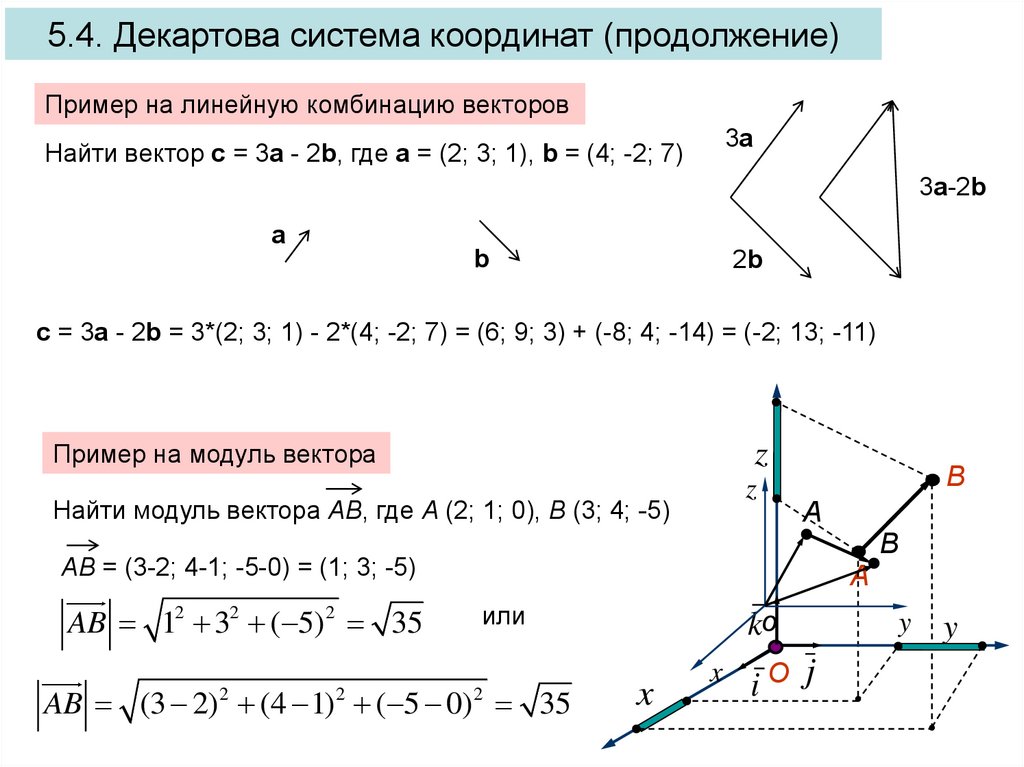 Найдем векторное произведение векторов.
Найдем векторное произведение векторов.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)
N̅ = [a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
ax = 5
ay = 1
az = 7
bx = 2
by = 4
bz = 6
N̅ = [a × b] = i̅ (1 ⋅ 6 — 4 ⋅ 7) — j̅ (5 ⋅ 6 — 2 ⋅ 7) + k̅ (5 ⋅ 4 — 2 ⋅ 1) = i̅ (6 — 28) — j̅ (30 — 14) + k̅ (20 — 2) = -22i̅ -16j̅ +18k̅
N̅ = [a × b] = -22i̅ -16j̅ +18k̅
N̅ = {-22 ; -16 ; 18}
Как найти векторное произведение векторов? Ответ на webmath.
 ru
ruСодержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение $[\bar{a}, \bar{b}]$ двух векторов, заданных своими координатами $\bar{a}=\left(a_{x} ; a_{y} ; a_{z}\right)$ и $\bar{b}=\left(b_{x} ; b_{y} ; b_{z}\right)$ соответственно, необходимо вычислить следующий определитель
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Задание. Найти векторное произведение векторов $\bar{a}=(1 ; 0 ; 0)$ и $\bar{b}=(0 ; 1 ; 0)$
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Подставляя координаты заданных векторов, получим:
$$[\bar{a}, \bar{b}]=\left|\begin{array}{lll}\bar{i} & \bar{j} & \bar{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{array}\right|$$
Раскладываем определитель по первой строке:
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{array}\right|=$$ $$=\bar{i} \cdot\left|\begin{array}{cc}0 & 0 \\ 1 & 0\end{array}\right|-\bar{j} \cdot\left|\begin{array}{cc}1 & 0 \\ 0 & 0\end{array}\right|+\bar{k} \cdot\left|\begin{array}{cc}1 & 0 \\ 0 & 1\end{array}\right|=$$ $$=0 \cdot \bar{i}-0 \cdot \bar{j}+1 \cdot k$$
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[\bar{a}, \bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[\bar{a}, \bar{b}]=(0 ; 0 ; 1)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы $\bar{a}=(5 ; 3 ;-4)$ и $\bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения $[\bar{a}, \bar{b}]$
Решение. Координаты векторного произведения $[\bar{a}, \bar{b}]$ вычисляются по формуле
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Подставляя координаты заданных векторов, получим:
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ 5 & 3 & -4 \\ 6 & 7 & -8\end{array}\right|$$
Раскладываем полученный определитель по первой строке:
$$=\bar{i} \cdot\left|\begin{array}{cc}3 & -4 \\ 7 & -8\end{array}\right|-\bar{j} \cdot\left|\begin{array}{cc}5 & -4 \\ 6 & -8\end{array}\right|+\bar{k} \cdot\left|\begin{array}{cc}5 & 3 \\ 6 & 7\end{array}\right|=$$ $$=[3 \cdot(-8)-7 \cdot(-4)] \cdot \bar{i}-[5 \cdot(-8)-6 \cdot(-4)] \cdot \bar{j}+$$ $$+[5 \cdot 7-6 \cdot 3] \cdot \bar{k}=(-24+28) \bar{i}-(-40+24) \bar{j}+(35-18) \bar{k}=$$ $$=4 \cdot \bar{i}+16 \cdot \bar{j}+17 \cdot \bar{k}$$
Тогда
$$[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$
$[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.
Калькулятор перекрестного произведения — векторный расчет
Перекрестное произведение, онлайн-исчисление
Резюме:
Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн из их координат.
cross_product online
Описание:
Калькулятор перекрестного произведения может выполнять расчеты, указав шагов расчета 9vec(v)` образуют прямую ортогональную ссылку. Расчет векторного произведения двух векторов онлайн выполняется очень быстро с помощью калькулятора векторного произведения ,
просто введите координаты двух векторов, а затем нажмите кнопку, позволяющую выполнить расчет векторного произведения. cross_product(vector;vector) В этом примере показано, как использовать калькулятор перекрестного произведения: cross_product(`[1;1;1];[5;5;6]`), возвращает [1;-1;0] Расчет онлайн с помощью cross_product (калькулятор перекрестного произведения) См. также Список связанных калькуляторов: Прочие ресурсы Форма представления первого вектора: По координатам По точкам Форма представления второго вектора: По координатам По точкам Первый вектор Второй вектор Заполните форму калькулятора и нажмите кнопку «Рассчитать», чтобы получить результат здесь Решение: — Расчет векторного произведения онлайн
 Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0]. Синтаксис:
Примеры:
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Калькулятор перекрестного произведения — векторное умножение с шагами
РЕЗУЛЬТАТЫ
Оставьте свой отзыв!
Худший Бедный Средний Хороший Супер
Содержание:
| 1 | Калькулятор векторного произведения двух векторов |
| 2 | Что такое векторное произведение |
| 3 | Formula of Vector Multiplication Calculator |
| 4 | How to do Cross-Product |
| 5 | Cross-Product of Two Vectors |
| 6 | How to use Cross Product Калькулятор |
| 7 | Метод координат и метод начальных точек |
| 8 | Скалярное произведение против векторного произведения |
Калькулятор векторов двух векторов0022
Затрудняетесь вычислить сумму двух траекторий? Не беспокойтесь, вы в правильном месте! Наш калькулятор перекрестного произведения поможет вам в этом. Просто введите значения в этот инструмент, и все готово!
Просто введите значения в этот инструмент, и все готово!
Что такое кросс-произведение
Чтобы понять это, давайте сначала разберемся с вектором: это математический инструмент с четко определенными величиной и направлением. Он используется в физике, математике, технике и информатике.
Кросс-произведение (не путать со скалярным произведением), проще говоря, — это бинарная операция над двумя траекториями в трехмерном пространстве. Он представлен знаком «х» (читай: крест). Рассмотрим два линейно самоопределяющихся из них, «a» и «b»; перекрестное произведение этих двух векторов будет траекторией, перпендикулярной как a, так и b.
Калькулятор формулы векторного умножения
Опять же, давайте рассмотрим «a x b», где «x» является результатом векторного умножения.
Итак, формула выглядит так:
C=a×b=∣a∣∣b∣sin(θ)n\mathbf{C = a \times b = |a| |б| sin(\theta) n}C=a×b=∣a∣∣b∣sin(θ)n
Где,
C=?C=?C=?
a – первый вектор,
b – вторая траектория,
θ – угол между обоими указанными векторами,
n – результирующая третья линия пути, перпендикулярная как a, так и b.
Как сделать кросс-произведение
Если вы знаете, как вычислять умножения, то это становится довольно просто. Все, что вам нужно сделать, это использовать приведенную выше формулу калькулятора векторного умножения, и все готово. Кроме того, как вы, возможно, уже знаете, результатом двух линий пути является третий маршрут, который находится под прямым углом к обоим предыдущим векторам.
Однако здесь уместно отметить, что когда обе траектории ‘a’ и ‘b’ указывают в одном и том же или противоположном направлении, длина третьей линии пути равна 0. Однако, когда и ‘a’, и ‘b’ ‘b’ расположены под прямым углом друг к другу, длина третьего максимальна.
Определим «a» и «b» с координатами ax, ay и az и bx, by и bz соответственно. Теперь, естественно, предположим, что результирующий вектор ‘c’ идет с координатами cx, cy и cz.
Рассмотрим значения двух векторов:
a=(4,5,6)a = (4,5,6)a=(4,5,6)
b=(7,8,9)b = (7,8,9)b=(7,8,9)
c=?c =?c=?
Давайте применим формулу перекрестного произведения и выясним!
cx=aybz−azby=5×9−6×8=45−48=−3\mathbf{cx = aybz — azby} = 5\times9 — 6\times8 = 45 — 48 = -3cx=aybz-azby =5×9−6×8=45−48=−3
cy=azbx−axbz=6∗7−4∗9=42−36=6\mathbf{cy = azbx — axbz} = 6*7 — 4*9 = 42 — 36 = 6cy=azbx−axbz=6∗7−4∗9=42−36=6
cz=axby−aybx=4∗8−5∗7=32−35=−3\mathbf{cz = axby — aybx} = 4*8 — 5*7 = 32 — 35 = -3cz=axby-aybx=4∗8−5∗7=32−35=−3
Ваш ответ = −3,6,−3 -3,6,-3−3,6,−3
Или, если вам не интересно заниматься всей математикой, вы можете просто использовать наш калькулятор перекрестного умножения и автоматически получить ответ за долю секунды.
Перекрестное произведение двух векторов
Два вектора ‘a’ и ‘b’ подчиняются приведенным ниже правилам:
(ya)xb=y(axb)=ax(yb)(ya) x b=y (a x b)=a x (yb)(ya )xb=y(axb)=ax(yb),
a x (b+c)=a × б+а × c
(b+c) × а=б &раз; а+с &раз; a
Где c — значение суммы, а y — коэффициент масштабирования. Мы можем использовать эти свойства, чтобы придумать формулу для результата умножения по отношению к компонентам.
Как использовать Калькулятор перекрестного произведения
Возвращаясь к нашей цифровой штуковине, вы можете определить результаты траектории с помощью нашего калькулятора векторного умножения. Он чрезвычайно прост в использовании. Есть два способа определить ответ. Либо вы можете использовать метод координат или метод начальных точек.
Оба варианта представлены в нашем декартовом калькуляторе произведений. Вы можете выбрать любой из этих двух вариантов для вычисления векторного векторного произведения.
Метод координат и метод начальных точек
- В методе координат вы должны ввести координаты (x, y, z) для единичных траекторий, траекторию продукта которых вы хотите определить, и это все.
- С другой стороны, при подходе к начальным точкам вы должны ввести начальные точки, а также конечные точки обеих линий траектории, чтобы получить ответ.
Все, что вам нужно сделать, это просто выполнить шаги, указанные ниже, чтобы использовать этот калькулятор векторного перекрестного произведения:
- Введите значения (координаты или начальные точки) двух траекторий
- Нажмите «Рассчитать», чтобы найти отвечать.
Скалярное произведение и перекрестное произведение
Люди часто задаются вопросом «Скалярное произведение такое же, как перекрестное произведение?» эти двое — полные противоположности. Умножение точек по своей природе масштабируется, и масштабирование не определяется конкретным направлением, в то время как вектор, с другой стороны, описывается конкретным направлением.

