Резистор

16 декабря 2022 — Admin

Главная / Теория

Резистор — один из самых простых электронных компонентов. Вместе с тем, без резисторов не обходится практически ни одна схема. Казалось бы, что важного он делает — только сопротивляется току, и больше ничего? Но не всё так просто. В этой статье собраны все базовые знания о резисторах, необходимые электронщику.

Содержание статьи:

• Общие сведения о резисторах
• Закон Ома
• Как измерить сопротивление
• Параллельное и последовательное соединение резисторов
• Применение: делители напряжения и тока
• Рассеиваемая мощность
• Устройство резистора
• Паразитные характеристики
• Переменные и подстроечные резисторы
• Другие типы резисторов

Общие сведения

Резистор, или сопротивление, относятся к пассивным компонентам электрических цепей. Пассивный — значит, не привносящий в цепь дополнительную энергию. В отличие от, например, транзистора — который способен усиливать слабый сигнал, добавляя к нему энергию от более мощного источника питания.

Резистор оказывает сопротивление идущему через него току. В качестве механической аналогии можно представить трубу с водой. Резистор — сужение на этой трубе, замедляющее поток. Из-за сужения по трубе будет проходить меньше воды в единицу времени.

Сужение в трубе, замедляющее поток

Резистор обозначается на схеме вытянутым прямоугольником, с двумя выводами. Обычно каждому резистору присваивается буква R с порядковым номером. Иногда в зарубежной литературе можно встретить обозначение ломаной линией.

Два варианта обозначения резистора на схемах

Резистор и закон Ома

Главная характеристика резистора — его сопротивление. Оно измеряется в Омах. А ток, проходящий через резистор, зависит от приложенного напряжения. Перечисленные величины  связаны законом Ома. При этом в случае идеального резистора ток линейно зависит от напряжения, то есть резистор обладает линейной вольт-амперной характеристикой:

Вольт-амперные характеристики двух резисторов и закон Ома

Как измерить сопротивление резистора

В лаборатории радиолюбителя для измерения сопротивлений должен быть омметр.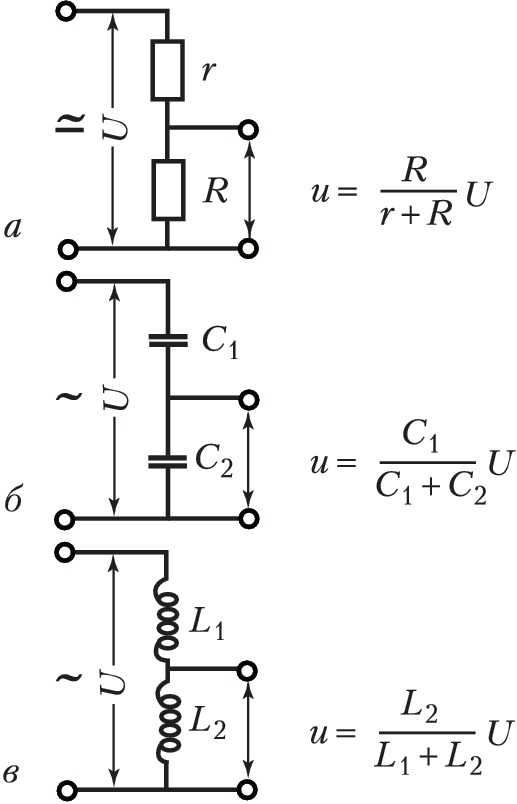 Обычно, эта функция входит в состав комбинированных приборов, мультиметров. Между тем, принцип измерения сопротивления основан всё на том же законе Ома: омметр прикладывает к тестируемому резистору небольшое напряжение и замеряет ток, после чего вычисляет сопротивление.

Измерение сопротивления с помощью мультиметра. В данном примере взят резистор 20 кОм.

Кстати, об этом нужно помнить, тыкая омметром в схемы: на схему попадает небольшое напряжение, которое для чувствительных деталей может оказаться фатальным.

Параллельное и последовательное соединение резисторов

Резисторы нужны в схеме, чтобы упрявлять токами и напряжениями. Но сначала нужно разобраться, как они взаимодействуют между собой и с другими элементами схемы.

Если соединить несколько резисторов последовательно, через каждый из них будет течь одинаковый ток. Это логично: сколько зарядов вошло в цепь, столько же должно выйти на другом конце, закон сохранения заряда. А вот напряжение (потенциал) распределяется по-разному. Чем выше сопротивление резистора, тем больше на нём падение напряжения — нужно большее усилие, чтобы протолкнуть через большое сопротивление заряды.

При этом, если просуммировать потенциал на всех резисторах, сумма будет равна напряжению, приложенному к концам цепи. Отсюда выводится формула суммарного сопротивления цепочки из последовательных резисторов: оно равно сумме сопротивлений всех резисторов.

Последовательное соединение резисторов

При параллельном соединении резисторов картина иная. Здесь фиксировано напряжение — оно одинаковое на каждом резисторе. А вот ток будет разный — он потечёт туда, где ему легче пройти. Опять же, применяя несложные рассуждения и используя закон Ома, выводится формула общего сопротивления параллельно соединённых резисторов.

Параллельное соединение резисторов

Более сложные, смешанные соединения резисторов разбиваются на небольшие блоки, и так последовательно, от меньших к большим блокам считается общее сопротивление:

Сложное соединение резисторов. Сначала считаем блок R1,R2 (параллельные), потом к этому блоку добавляем последовательно R3, наконец, считаем параллельно R1,R2,R3 и R4. Если каждое сопротивление по 10 Ом, общее сопротивление получается 6 Ом.

Нужно добавить, что иногда разбить на блоки невозможно. В этом случаи применяются более сложный метод расчёта — правила Кирхгофа.

Применение резисторов в схемах

Итак, как же с помощью резисторов управляют напряжениями и токами? Допустим, стоит задача ограничить напряжение на нагрузке. Под «нагрузкой» здесь может пониматься любой элемент или узел схемы, на котором мы хотим получить заданное напряжение или заданный ток.  Это могут быть и лампочка, и светодиод, и следующий каскад усилителя и т. д.

Самое простое — поставить последовательно с нагрузкой гасящий резистор. Как мы обсуждали выше, в этом случае напряжение распределится между элементами в соответствии с сопротивлением каждого. То есть, получается делитель напряжения.

Схема делителя напряжения, когда нагрузка является элементом делителя.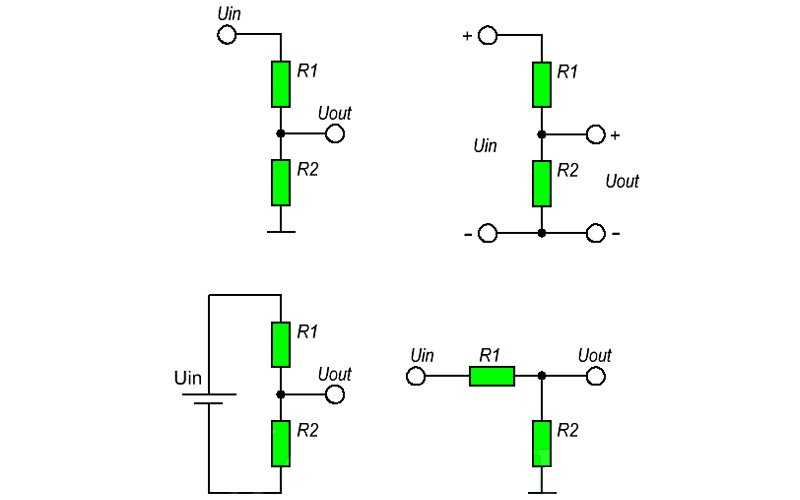

А что делать, если сопротивление нагрузки очень велико или не постоянно? В этом случае ставят два последовательных резистора, образующих плечи делителя. А нагрузка снимает напряжение с одного из них. Подчеркну, что всегда нужно помнить про сопротивление нагрузки. Оно должно быть достаточно большим, чтобы им можно было пренебречь при расчёте делителя.

Схема делителя напряжения, когда нагрузка подключена параллельно нижнему плечу делителя

Если последовательное соединение резисторов является делителем напряжения, нетрудно догадаться, что паралелльное соединение — делитель тока. На рисунке приведён способ ограничить ток через нагрузку — поставить параллельно ей резистор, так называемый шунт. Который будет отвевлять на себя часть тока, обратно пропорциональную его сопротивлению.

Схема делителя тока

Мощность резистора

Резистор сопротивляется проходящему току. Значит, он отбирает у тока часть энергии. И куда она девается? Переходит в тепло.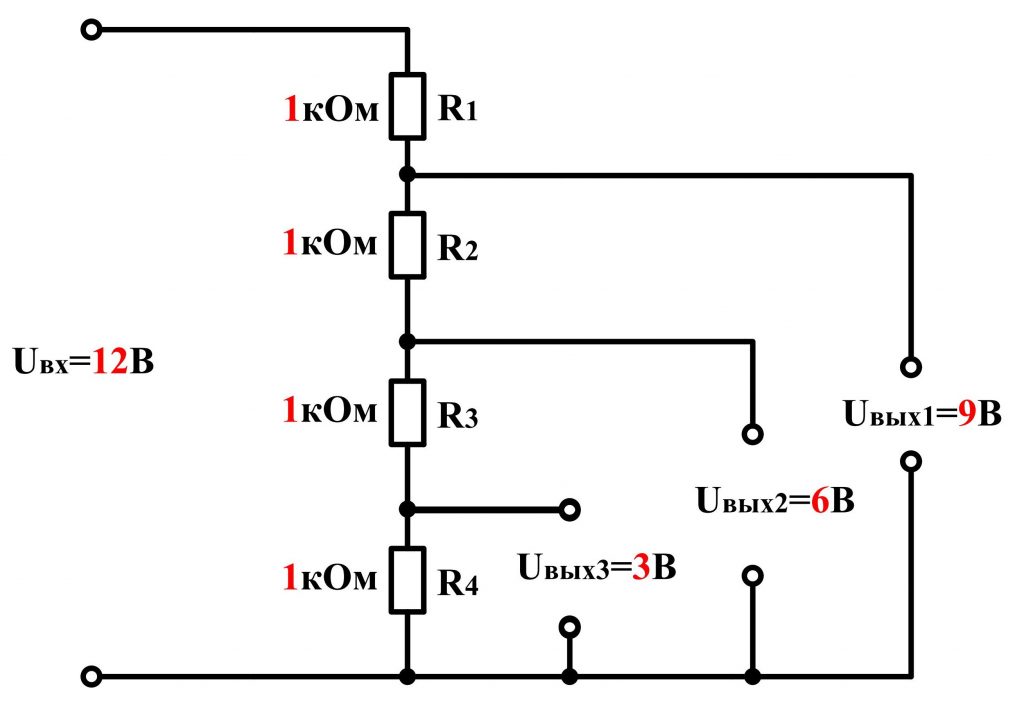 Мощность, рассеиваемая на резисторе, считается по формуле P = U*I. Поскольку U, I и R связаны законом Ома, можно записать несколько вариантов этой формулы, выражая мощность через U и R, или через R и I. Кстати, на сайте есть онлайн-калькулятор мощности и закона Ома.

Так вот, если ток через резистор слишком велик, из-за большой рассеиваемой мощности резистор перегреется и выйдет из строя, в буквальном смысле, сгорит. В этом случае нужно взять резистор такого же номинала, но рассчитанный на бОльшую мощность рассеивания. Более мощные резисторы и физически большего размера, чтобы увеличить площадь рассеивания тепловой энергии.

Там, где это важно (где ожидаются сравнительно большие токи), на схемах указывают, на какую мощность должен быть рассчитан резистор, с помощью следующих обозначений:

Допустимая мощность рассеивания резистора

Устройство резисторов

Из школьного курса физики мы знаем, что сопротивление проводника определяется его удельным сопротивлением, длинной и сечением.

Формула сопротивления проводника

В начале статьи приводилась механическая аналогия резистора, как сужения трубы. Это работает и в элекрике: если уменьшить сечение проводника, его сопротивление увеличится.

Поэтому, резисторы делают из тонкой проволоки, из тонких плёнок разных металлов и сплавов, из композитных материалов. При этом, чтобы увеличить эффективную длину, в резистивном слое нарезают различного вида спирали и канавки:

Очень условно показано устройство резистора. Слева: на поверхности цилиндрической основы резистора слой токопроводящего материала, в котором нарезаны канавки для увеличения сопротивления. Справа: плёночный вариант.

Паразитные характеристики

Но, такой подход, кроме плюсов, даёт ещё и некоторые минусы. Дело в том, что реальный резистор, в отличие от идеального, обладает не только сопротивлением, но и некоторой индуктивностью и ёмкостью. То есть схема реального резистора выглядит примерно так:

Схема замещения резистора

Ёмкость и индуктивность — паразитные характеристики резистора, они искажают его функции в схеме. И само по себе устройство резистора может являться причиной этих паразитных свойств. Спиральные канавки в резистивном слое — чем не витки катушки индуктивности? А между близко расположенными участками проводящего слоя возникает ёмкость.

Хотя эти индуктивность и ёмкость небольшие по величине, но в некоторых ситуациях (например, на высоких частотах) способны вносить заметные искажения.

Поэтому, при изготовлении резисторов применяют различные ухищрения, чтобы снизить паразитные характеристики. Например, нарезают канавки хитрым рисунком. Впрочем, эта тема уже выходит за рамки данной статьи.

Переменные и подстроечные резисторы

Иногда в схеме необходимы резисторы с переменным сопротивлением. Они являются элементами настройки и управления.

Различают переменные резисторы (обычно их ручку выводят на панель управления) и подстроечные (которые регулируются отвёрткой на плате и к которым нет доступа, пока не разобрать корпус устройства). Вот как они выглядят:

Переменные и подстроечные резисторы

У них три вывода.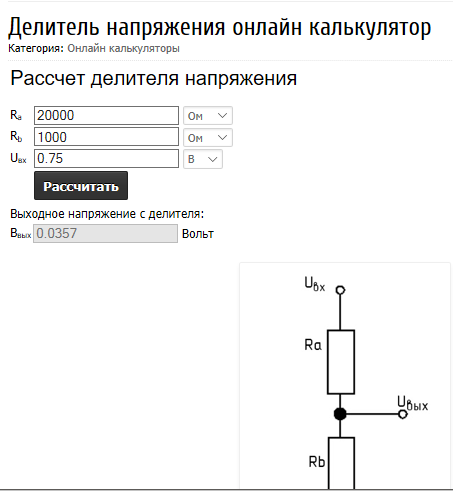 Между двумя крайними постоянное сопротивление. А средний «скользит» между ними. Таким образом, получается готовый делитель напряжения, с регулируемым сопротивлением плечей.

Если средний вывод соединить с одним из крайних — получится реостат, резистор с переменным сопротивлением.

Другие типы резисторов

В заключение остаётся упомянуть некоторые специфичные типы резисторов. Например, теримистор. Его сопротивление зависит от температуры, и этот тип резисторов широко используется в электронных термометрах и схемах контроля температуры.

Или, фоторезистор. Его сопротивление зависит от освещённости.

Варисторы — уменьшают своё сопротивление при росте приложенного напряжения. Могут использоваться в схемах защиты и стабилизаторах.

Поделиться в соцсетях:

Расчет резисторного делителя напряжения

: Онлайн калькулятор

Делитель напряжения — это простой и удобный способ получить нужное напряжение в определенной точке цепи.

Он используется в цепях обратной связи для измерения выходных параметров, когда на выходе десятки вольт, а измерительный вход микросхемы рассчитан на единицы или доли вольт и для многих других целей. Самый простой вариант на основе резисторов, их может быть 2 и больше.

Давайте разберемся, как рассчитать этот элемент цепочки. Сделать это можно вручную или воспользоваться следующим онлайн-калькулятором, рассчитывающим делитель напряжения на резисторах:

Главное, о чем нельзя забывать, это то, что ток делителя должен быть на 1 и более порядков выше входного тока нагрузки . Это необходимо для минимизации перепадов напряжения и сохранения стабильности выходных параметров. После этого приступайте к расчету тока и напряжения.

Если ваш делитель состоит из двух элементов, то ток через него рассчитывается по формуле:

I = Uвх / (R1 + R2) = Uвх / Rобщ

Или сопротивление для заданного тока:

Rобщ = Uвх/I

Мы знаем R общее для заданного I, входного напряжения и сколько нам нужно получить на выходе. Рассчитываем сопротивление:

R2 = Uвых * Rобщ/Uвх

Тогда:

R1 = Rобщ-R2

Если вам нужно определить параметры цепи по известным сопротивлениям и входному напряжению — вычислите выход по формуле:

Uвых = Uвх * R2 / R1 + R2

Итак, зная напряжение на выходе , его можно рассчитать на входе:

Uвх = (Uвых * R1 + R2)/R2

Это основной метод расчета резистивного делителя, также он может быть емкостным или индуктивным. В этом случае вместо активного сопротивления R в расчетах появляется реактивное сопротивление Xc или Xl.

Для регулировки выходного напряжения резисторного делителя вместо нижнего сопротивления устанавливается подстроечный или переменный резистор. Расчеты ничем не отличаются — используют максимальное значение на переменном резисторе. Также можно ограничить минимальное выходное напряжение, установив константу последовательно с переменной, тогда минимальное вычисляется без учета переменной.

Эту схему удобно использовать, если у вас есть резисторы с большим допуском, и вам нужно получить точные выходные параметры.

Сэкономить время можно воспользовавшись онлайн калькулятором, в нем можно рассчитать номиналы элементов с учетом желаемого выходного и входного напряжения. Использование калькулятора сэкономит ваше время, если вам нужно рассчитать большую цепь или вы запутались и не можете сообразить, как рассчитать резистивный делитель с нагрузкой.

Учтите, что элементы нужно подбирать не только по номиналу, но и по мощности, так как при большом токе нагрузки нужно рассчитывать схему на большие токи. Результаты расчетов онлайн-калькулятора укажут, сколько ватт необходимо резистора.

Опубликовано: 15.08.2018 Обновлено: 15.08.2018 Пока без коментариев

ac-thevenin-calculator — Googlesuche0003

suchoptionen

AC Теорема Тевенина — Гиперфизика

гиперфизика. phy-astr.gsu.edu ›electric ›acthev

Чтобы заменить сеть ее эквивалентом Тевенина, вычислите напряжение Тевенина: выход сформированного делителя напряжения через Z1 и Z3. Импеданс Thevenin равен …

AC Задача эквивалентной цепи Thevenin — YouTube

www.youtube.com › смотреть

23.01.2016 · Получить полный курс на MathTutorDVD.com. На этом уроке ученик научится считать…
Dauer: 20:47
Прислан: 23.01.2016

Анализ электрических цепей переменного тока: Теорема Тевенина — YouTube

www.youtube.com › смотреть

04.05.2020 · Теорема Тевенина позволяет преобразовать любой одиночный линейный порт двусторонняя сеть в …
Dauer: 14:20
Прислан: 04.05.2020

Простые эквивалентные цепи переменного тока Тевенина и Нортона — Wira Electrical

wiraelectrical.com › Цепи переменного тока

цепи переменного тока так же, как и цепи постоянного тока. · Эквивалентная схема Нортона изображена на рисунке.

Ähnliche Fragen

Как рассчитать тевениновый эквивалент цепи переменного тока?

Можно ли применять Thevenin для AC?

Применима ли теорема Нортона к источнику переменного тока?

Как рассчитать VTh в Thevenin?

Калькулятор напряжения Thevenin (без триггера) — все PE

www.everythingpe.com › Калькуляторы

Этот калькулятор предназначен для расчета напряжения Thevenin трехфазного мостового выпрямителя. Просто введите значение и нажмите «Рассчитать». все, что есть у PE …

Пример теоремы Тевенина с решением для цепи переменного тока цепь слева от клемм x-y в сети на рис. 1.

THÉVENIN AND NORTON ЭКВИВАЛЕНТНЫЕ ЦЕПИ — TINA

www.tina.com › thevenin-and-norton-equivalent-circ… ЭКВИВАЛЕНТНЫЕ ЦЕПИ: Добро пожаловать на наш бесплатный интернет-курс по цепям переменного/постоянного тока с использованием программного обеспечения для моделирования цепей TINA.

ac thevenin калькулятор — Gallarate Sposi

gallaratesposi.