Однофазный переменный ток основные понятия: Однофазные электрические цепи переменного тока – 11. Электрические цепи однофазного переменного тока. Основные определения — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Однофазные электрические цепи переменного тока

Основные понятия и определения

Широкое применение в электрических цепях находят периодические ЭДС, напряжения и токи.

Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые промежутки времени Т, называемые периодом.

На практике подавляющее большинство промышленных источников переменного тока (генераторы электростанций) создают ЭДС, изменяющуюся по синусоидальному закону.

Преимущества такого закона:

а) простота получения;

б) напряжение легко трансформируется;

в) синусоидальная функция является единственной, которая в процессе интегрирования и дифференцирования не меняет своей формы и в процессе передачи и преобразования (в процессе трансформации) напряжения временная зависимость остается неизменной, т.е. синусоидальной.

Любая периодическая величина, изменяющаяся по синусоидальному закону, имеет ряд характерных параметров:

период — Т [c];

2) частота — f [Гц] .

Величина обратная периоду называется частотой:

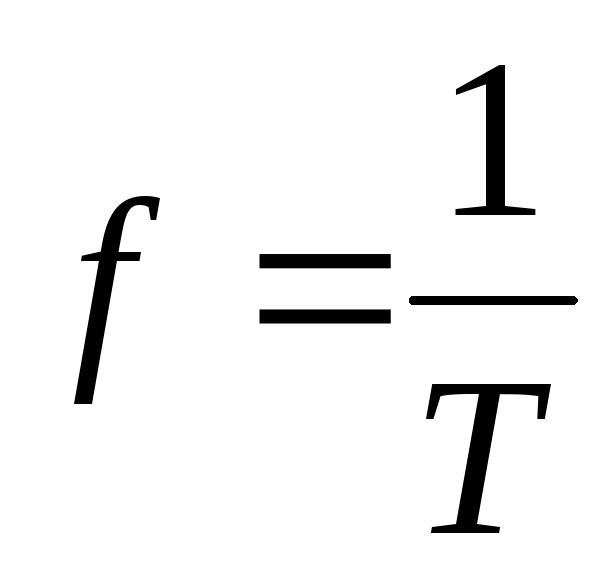Частота для всех электроустановок строго нормируется:

— для наземных систем — 50 (60)Гц;

— в авиации — 400Гц;

— космические летательные аппараты — 1000Гц.

Увеличение частоты позволяет уменьшить габариты электроустановок.

3) Циклическая частота — ω=2πf.

Для частоты 50Гц циклическая частота ω=2*3,14*50=314рад/с или 1/с.

4) Мгновенное значение — значение периодически изменяющейся величины в рассматриваемый момент времени.

Мгновенные значения обозначают — e, i, u.

5) Амплитудное значение

Максимальное значение или амплитуду ЭДС, напряжения и тока обозначают — E_m, U_m, I_m.

6) Действующее значение

Действующее значение ЭДС, напряжения и тока обозначают — E, U, I.

Для количественной оценки синусоидального тока, который в течение времени непрерывно, периодически изменяется, используют значение постоянного тока, эквивалентное значению переменного тока по совершаемой работе. Такое значение будет действующим для синусоидального тока.

Действующим (или эффективным)значением

синусоидального тока называют такое значение постоянного тока, при протекании которого в одном и том же резисторе с сопротивлением R за время одного периода Т выделятся столько же тепла, сколько при прохождении синусоидальнего тока.

При синусоидальном токе:

i=I_msinωt

количество теплоты, выделяемое в резисторе R за время Т равно:

а при постоянном токе

Согласно определению Q_≈=Q_—, тогда

, .

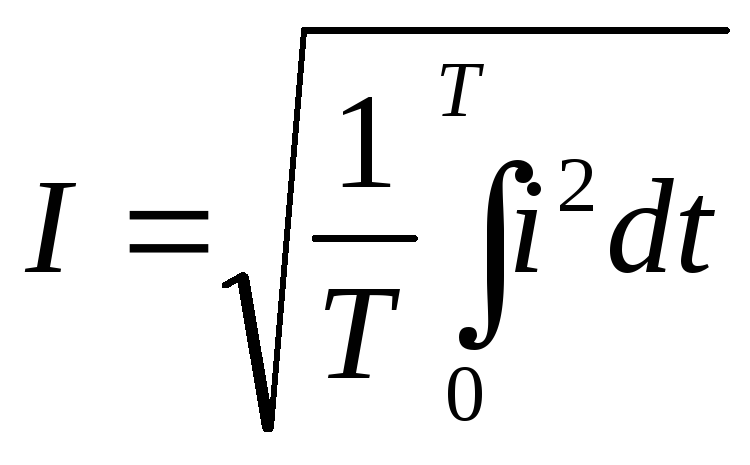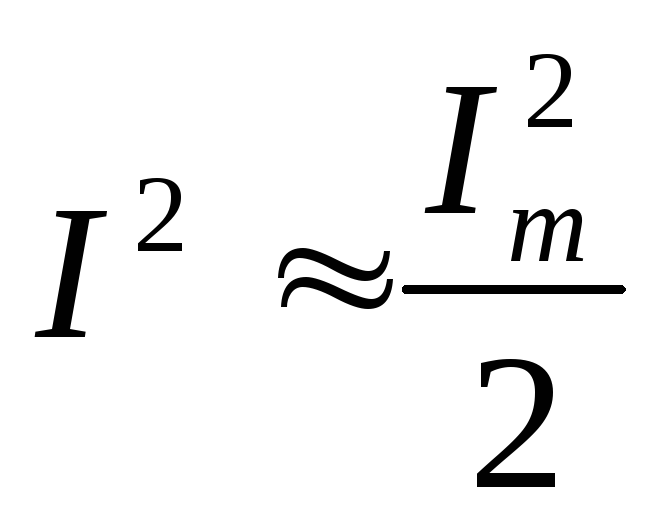Таким образом действующее значение синусоидального тока I является его среднеквадратичным значением за период Т

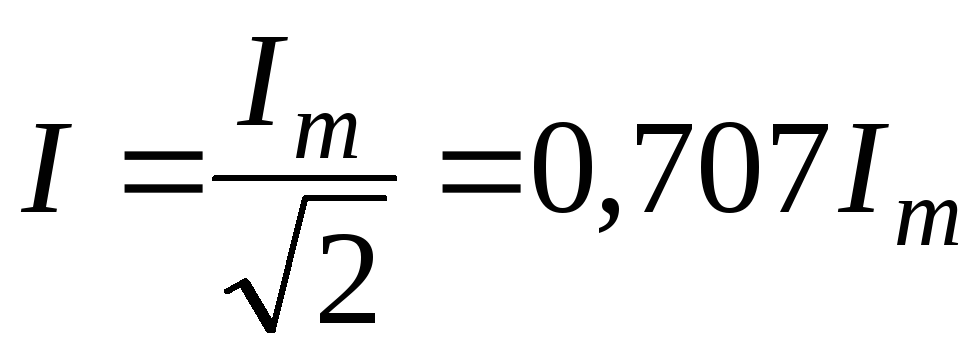
Действующее значение переменного тока обозначается как постоянный ток и в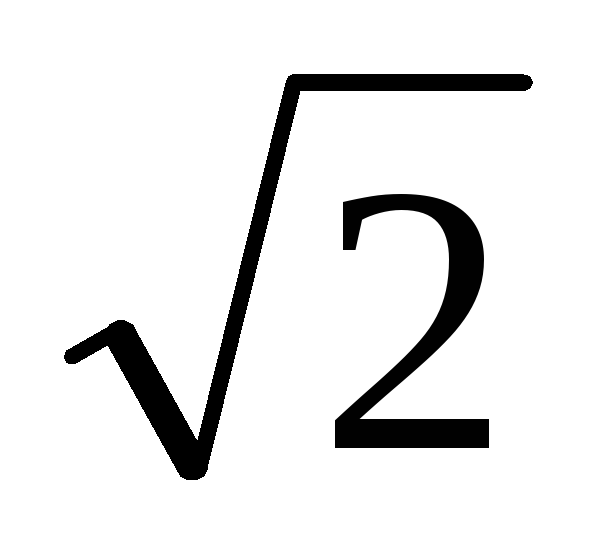

раз меньше чем его амплитуда.

Аналогично

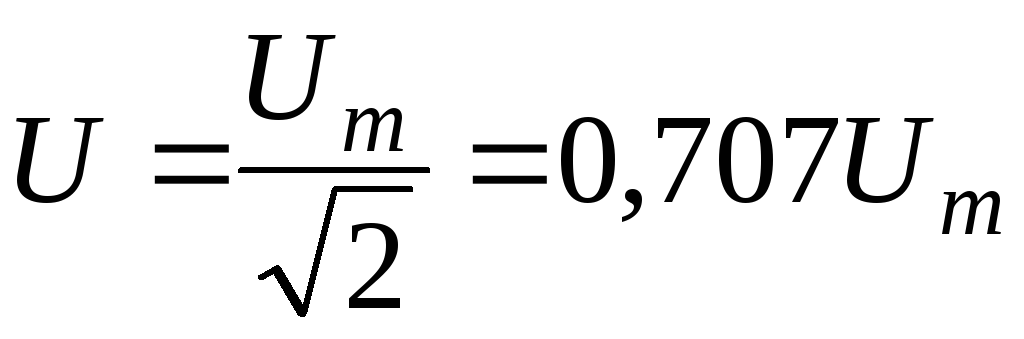Большинство электроизмерительных приборов работают на тепловом или электродинамическом эффекте, поэтому они всегда показывают действующее значение. Основные расчеты электроцепей синусоидального тока проводятся по действующим значениям. Для несинусоидальных величин эти соотношения будут другими.

Среднее значение

Среднее значение синусоидальной величины это ее среднеарифметическое значение. Однако, если определять среднее значение синусоидальной величины за период Т, то оно будет равно нулю, так как положительная и отрицательная полуволны синусоидальной кривой совпадают по форме. Поэтому среднее значение определяют за полпериода.

За среднее значение синусоидального тока принимают такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе:

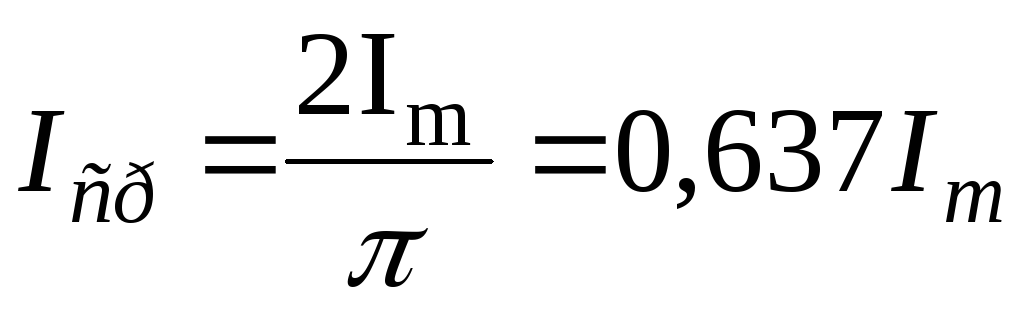
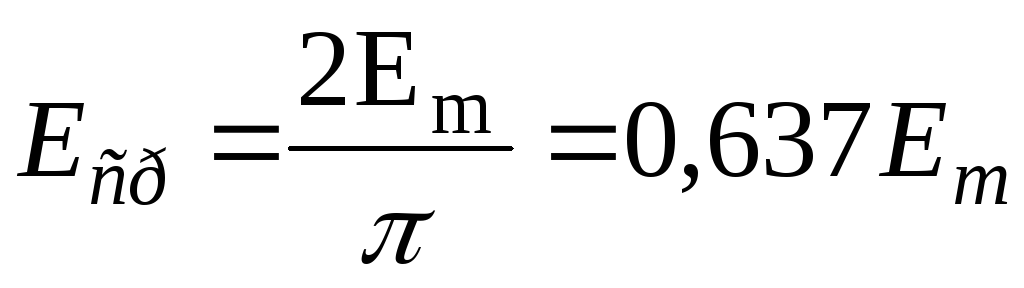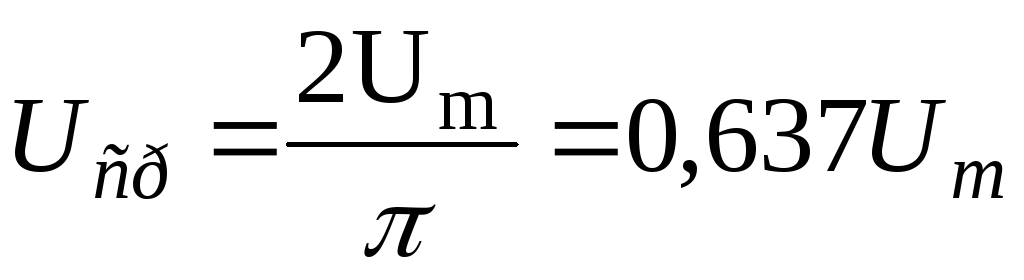Таким образом, среднее значение меньше действующего.

Изображение синусоидальных величин в прямоугольных координатах

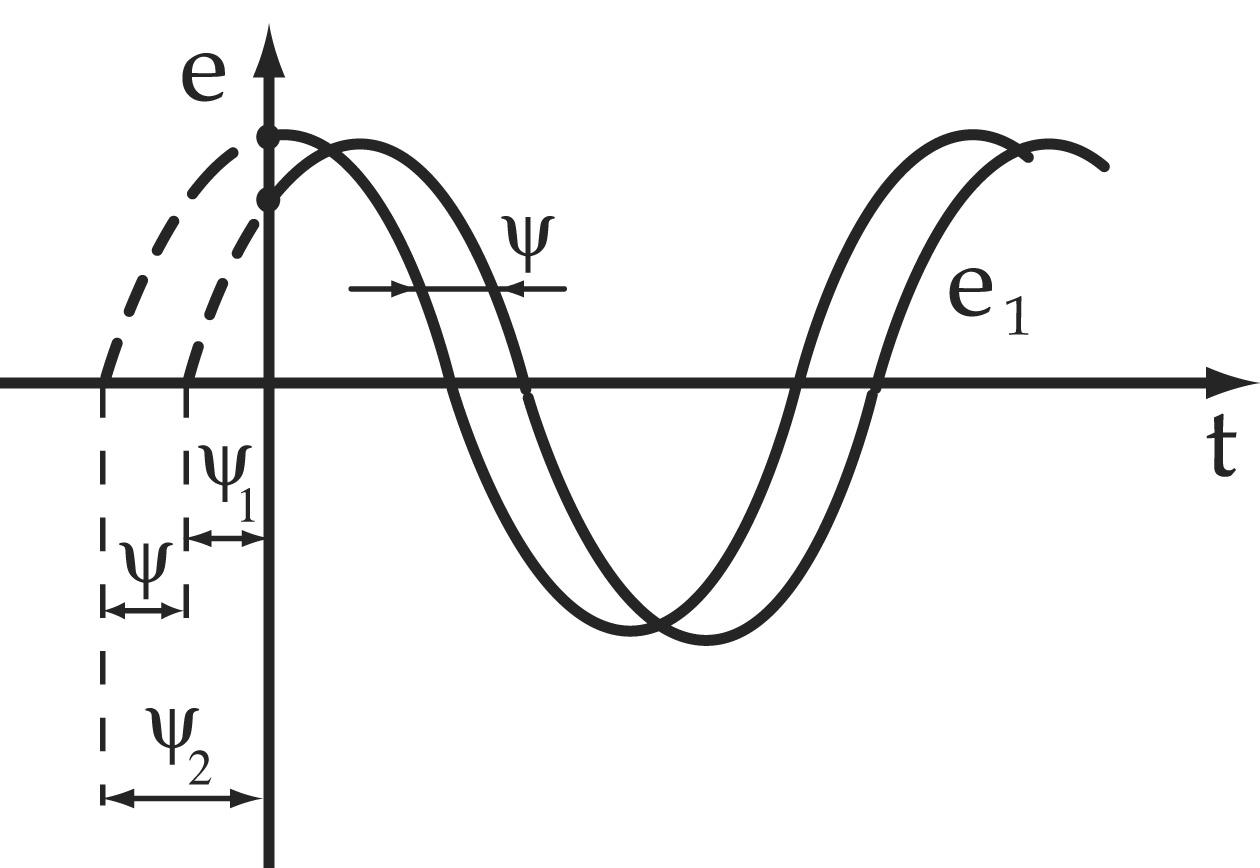
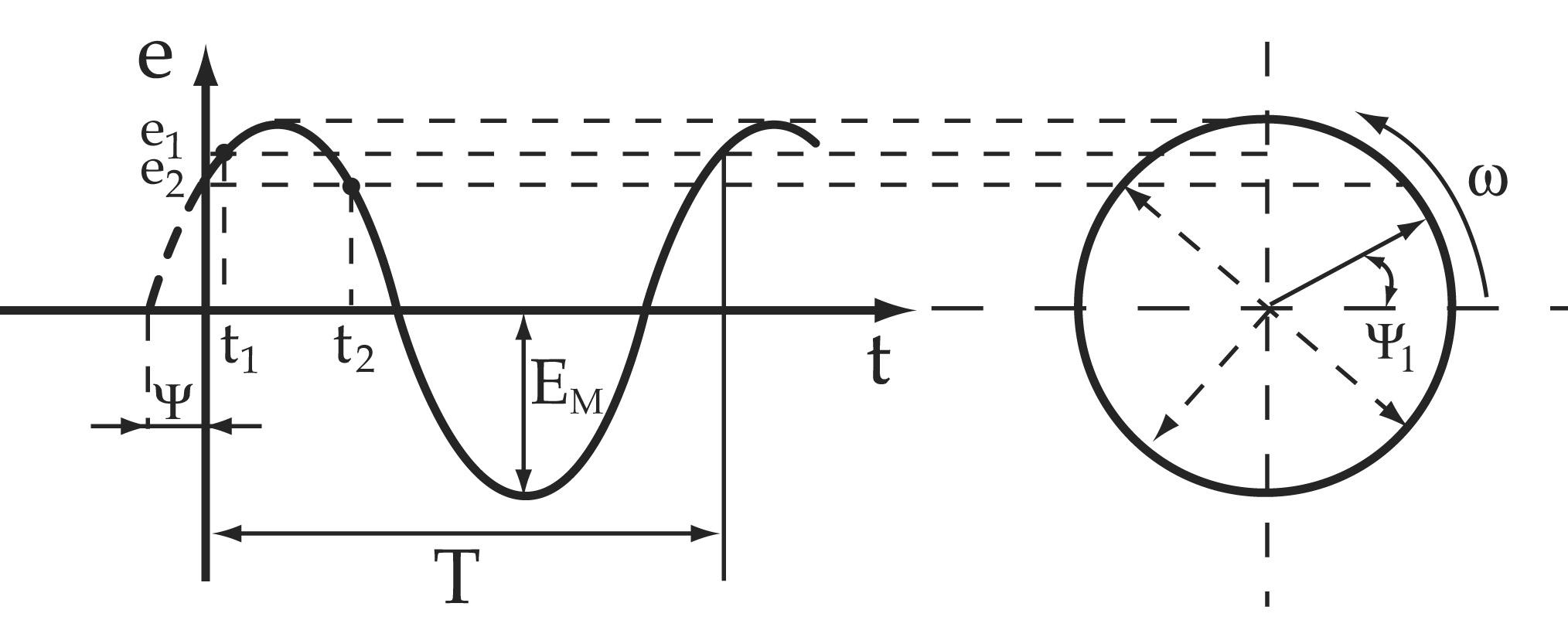
В общем случае синусоидальные величины (рис.1), могут быть записаны:

e=E_msin(ωt+ψ_e)

u=U_msin(ωt+

ψ_u),

i=I_msin(ωt+ψ_i),

где e,u,i — мгновенные значения ЭДС, напряжения и тока;

E_m,U_m,I_m — амплитуды ЭДС, напряжения и тока.

(ωt+ψ_e) — фазовый угол;

ψ_e, ψ_u, ψ_i — начальные фазы ЭДС, тока и напряжения.

На практике чаще имеют место случаи, когда электрические величины не совпадают по фазе.

Из рис. 1 видно, что напряжение опережает ток на угол ψ_u-ψ_i . Разность фазовых углов называется разностью или сдвигом фаз.

φ=ψ_u-ψ_i — разность фаз между напряжением и током.

При этом пользуются правилом: начальные фазы расположенные по левую сторону от начала координат имеют положительные значения, а по правую отрицательные.

Если угол φ >0, то ток отстает от напряжения по фазе. Если φ<0, то ток опережает напряжение по фазе.

При сложении двух синусоидальных величин (одинаковой частоты), изображенных в прямоугольных координатах, необходимо сложить ординаты для ряда значений угла

ωt и по точкам построить суммарную синусоиду. Получается новая амплитуда, новый фазовый сдвиг, причем:

I_m≠I_m₁ + I_m₂;

φ_i≠ φ_i₁+ φ_i₂.

Такой расчет является трудоемким и имеет недостаточную точность.

екторное изображение синусоидальных величин

Рис.2

Наиболее просто складывать синусоидальные величины, представив их вращающимися векторами (рис.3).

Рис.3

В плоскости с осями ОX и ОY рассмотрим вращающийся с постоянной скоростью, равной угловой частоте ω, вектор ОА, длина которого равна амплитуде синусоидальной ЭДС, т.е.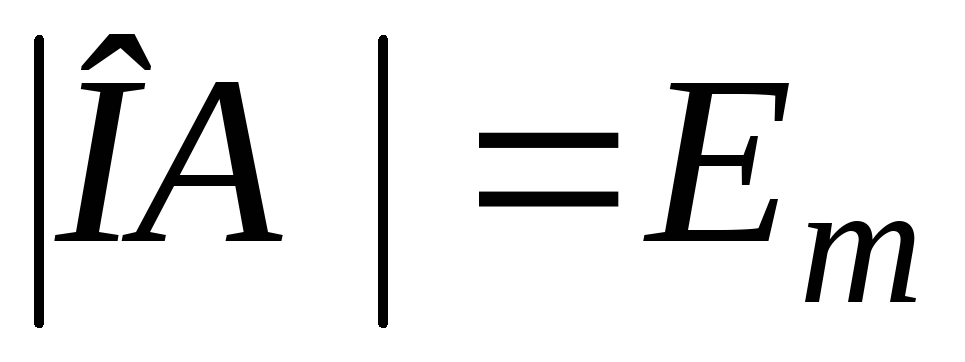

Мгновенное значение ЭДС описывается известным соотношением:

e=E_msin(ωt+ψ_e).

За положительное направление вращения принимают направление против часовой стрелки, а угол поворота отсчитывают от оси ОX. В начальном положении (при t=0) вектор ОА повернут по отношению к оси OX на угол ψ_e

Построим проекцию вектора ОА на ось OY, которые изменяются по мере поворота вектора на угол ωt по отношению к начальному положению. В начальном положении (при t=0) проекция ОА₀= E_msinψ_e=e₀, т.е. равна мгновенному значению ЭДС при t=0.

Через некоторое время (t=t₁) вектор ОА будет повернут на угол ωt₁ и составлять с осью ОX угол (ωt₁+ψ_e). Проекция его на ось OY :

ОА₁= E_msin(ωt₁+ψ_e)=e₁, т.е. равна мгновенному значению ЭДС при t=t₁.

При t=t₂ вектор ОА совпадает с осью OY и его проекция ОА₂= E_m= e₂. При дальнейшем вращении вектора АО его проекции на ось YO начнут уменьшаться, затем станут отрицательными и т.д.

Таким образом, проекции на ось OY вектора, вращающегося с постоянной скоростью ω и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидальному закону, т.е. представляют собой мгновенные значения синусоидальной ЭДС. Следовательно, справедливо и обратное: если имеем синусоидальную величину. то ее можно представить вращающимся вектором.

Правила построения векторных диаграмм

Любую синусоидально изменяющуюся во времени величину (ЭДС, напряжение, ток) можно представить в виде вращающегося вектора, длина которого равна амплитуде, а угловая скорость угловой частоте этой синусоидальной величины.
Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины и откладываем от положительного направления оси O в сторону, противоположную вращению часовой стрелки.
В одних и тех же осях можно представить векторы всех ЭДС, действующих в данной цепи, напряжений на всех участках данной цепи и токов во всех ее ветвях (в заданных масштабах).
Так как синусоидальные величины имеют одинаковую частоту, то изображающие их векторы вращаются с одинаковой скоростью. Их взаимное положение на плоскости, относительно друг друга, остается неизменным. Поэтому на практике векторы не вращают, а строят их, соблюдая углы между векторами (углы сдвига фаз).
Отказавшись от вращения вектора можно строить векторы не только максимальных, но и действующих значений.
Вектора можно складывать, по правилу параллелограмма, получив при этом суммарный вектор (рис. 4).

Рис.4

В связи с отсутствием необходимости вращения нас интересует только взаимное расположение векторов, один из которых можно строить по направления оси OX, остальные вектора направляются относительно этого вектора (рис.5).

Например, если к элементам электрической цепи подается переменное напряжение u=U_msin(ωt+ψ_u), то возникнет переменный ток i=I_msin(ωt-ψ_i). В этом случае ток отстает от напряжения по фазе на угол φ=ψ_u-ψ_i. Начальные фазы ψ_u и ψ_i на векторной диаграмме не изображают, так как взаимное положение векторов определяется полностью разностью фаз — φ. Принимаем начальную фазу тока равную нолю (ψ_i=0), тогда начальная фаза напряжения ψ_u равна сдвигу фаз — φ.

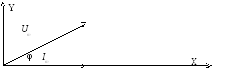
Рис.5

Графический метод расчета является грубым неточным. На практике переходят к точным математическим методам расчета на основе теории комплексных чисел.

Понятия о комплексных числах

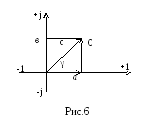
Комплексная плоскость — прямоугольная системе координат, на которой по одной оси откладываются вещественные числа +1, на другой (перпедикулярной) — мнимые числа +j.

Здесь j= — мнимая единица.

Действия с мнимой единицей:

1) j²=-1; 2)

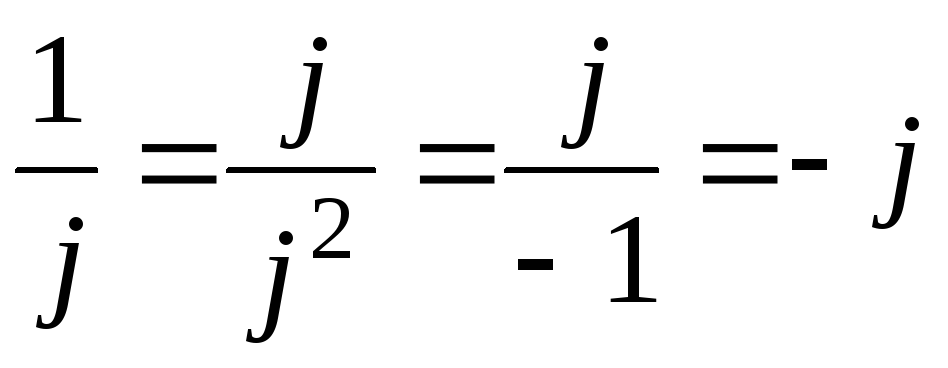
Любую точку на комплексной плоскости можно охарактеризовать комплексным числом. Известно, что комплексное число С имеет вещественную Re и мнимую Im составляющие.

Алгебраическая форма записи комплексного числа:

С=а+jв,

где а= Аcosα – реальная часть комплексного числа,

в= Аsinα – мнимая часть, γ=arctg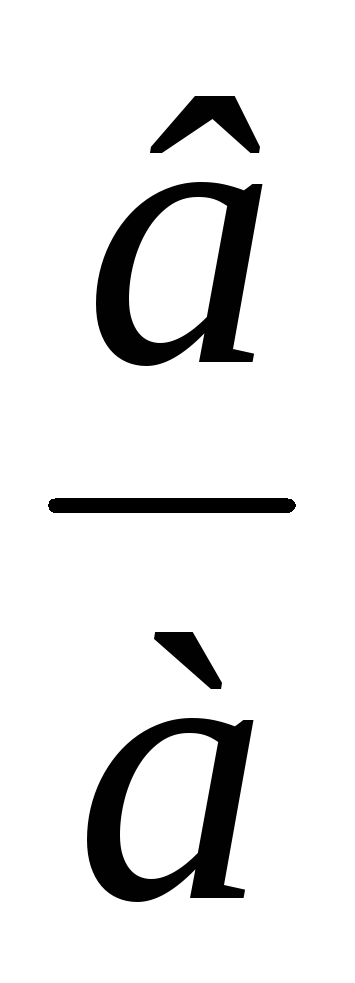 — фаза,

с=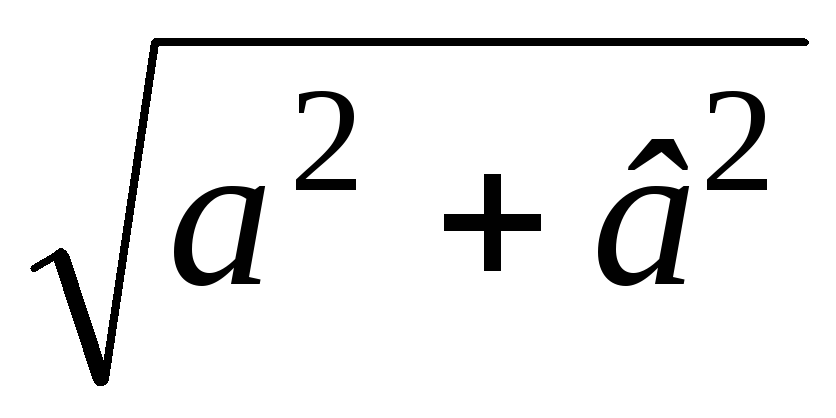 — модуль комплексного числа.

Тригонометрическая форма записи комплексного числа:

С=с(cosγ+jsinγ).

Показательная форма записи комплексного числа:

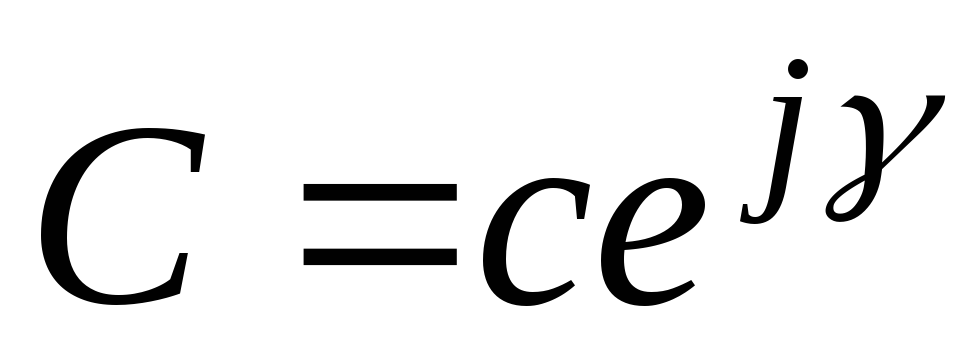, где 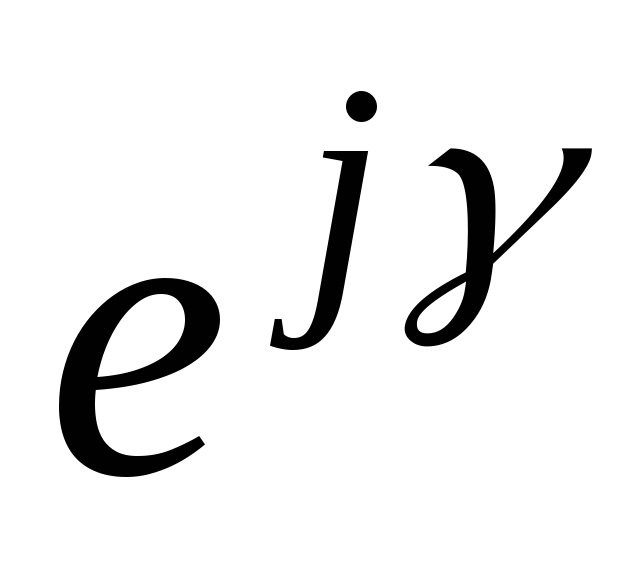— оператор поворота (поворотный множитель).

cosγ + jsinγ = 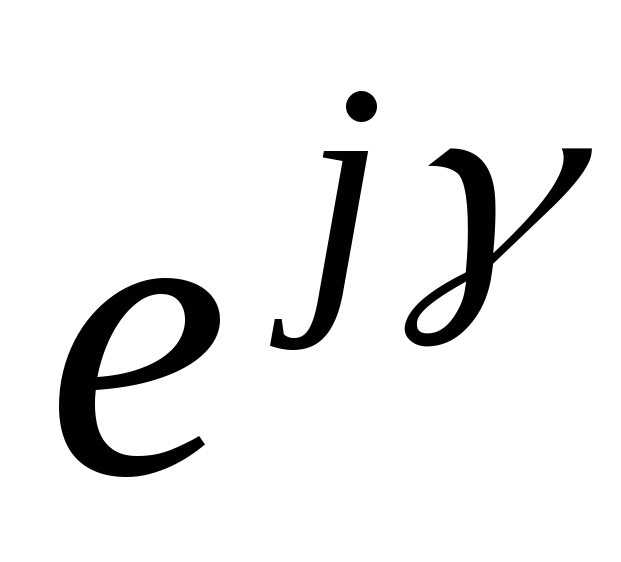— формула Эйлера.

Частные случаи:

Для γ= π/2 ;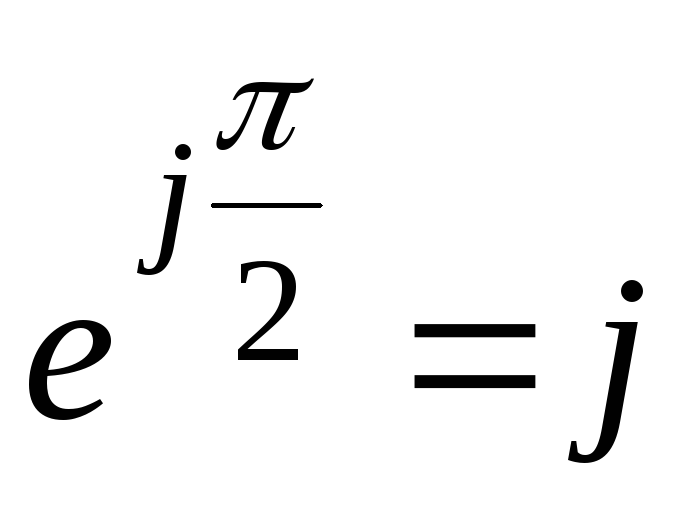

γ= -π/2 ;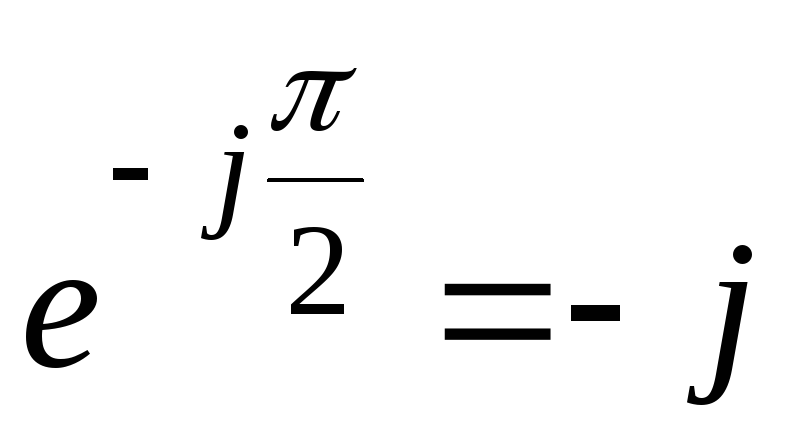

γ= π .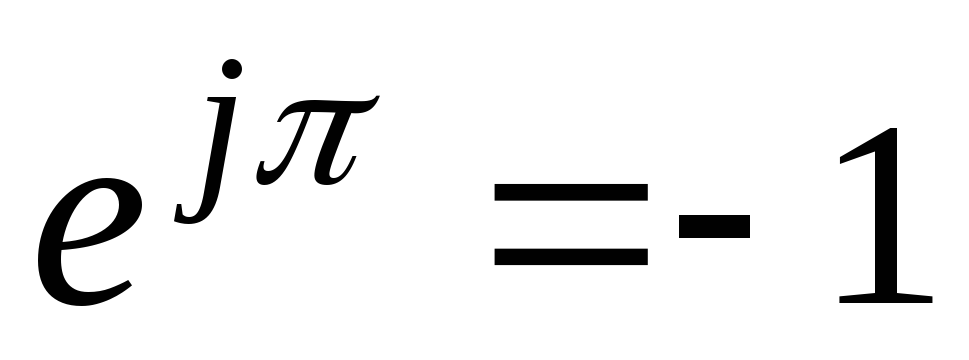

Тригонометрическая форма записи служит для перехода из алгебраической формы в показательную и наоборот.

11. Электрические цепи однофазного переменного тока. Основные определения

Переменным называется электрический ток, величина и направление которого изменяются во времени. Область применения переменного тока намного шире, чем постоянного. Это объясняется тем, что напряжение переменного тока можно легко понижать или повышать с помощью трансформатора, практически в любых пределах. Переменный ток легче транспортировать на большие расстояния. Но физические процессы, происходящие в цепях переменного тока, сложнее, чем в цепях постоянного тока из-за наличия переменных магнитных и электрических полей. Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i. Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени

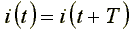Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом. Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными. Мгновенное значение синусоидального тока определяется по формуле

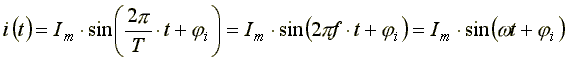
где I_m — максимальное, или амплитудное, значение тока. Аргумент синусоидальной функции 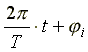называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.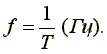— частотой50 Гц. Величину 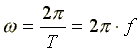называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c. Если у синусоидальных токов начальные фазы при одинаковых частотах одинаковы, говорят, что эти токи совпадают по фазе. Если неодинаковы по фазе, говорят, что токи сдвинуты по фазе. Сдвиг фаз двух синусоидальных токов измеряется разностью начальных фаз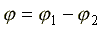Действующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока (для синусоиды)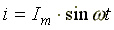

Аналогично определяются действующие значения ЭДС и напряжений

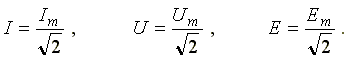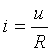Действующие значения переменного тока, напряжения, ЭДС меньше максимальных в √2 раз. Законы Ома и Кирхгофа справедливы для мгновенных значений токов и напряжений. Закон Ома для мгновенных значений: . Законы Кирхгофа для мгновенных значений: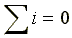. 6.2)

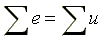12. Изображения синусоидальных функций времени в векторной форме

При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими. Задача упрощается, если представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию 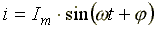. Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону. Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени 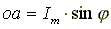. Когда отрезок повернется на угол α₁, проекция его 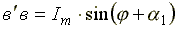. Откладывая углы α₁, α₂, … на горизонтальной оси, а проекции отрезка прямой — на вертикальной оси, получим ряд точек синусоиды (рис. 6.1).

Пусть даны два синусоидальных тока: 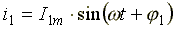и

. Нужно сложить эти токи и получить результирующий ток: 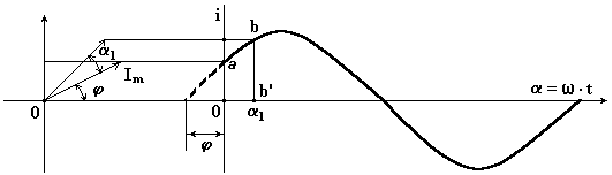Представим синусоидальные токи i₁ и i₂ в виде двух радиус — векторов, длина которых равна в соответствующем масштабе I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ₁ и φ₂ относительно горизонтальной оси. Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 6.2). Векторная диаграмма — это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.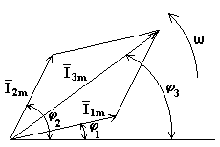

Необходимо отметить, что напряжение, ток и ЭДС — это скалярные, а не векторные величины. Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус — векторов, вращающихся с одинаковой угловой скоростью. Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, бессмысленно.

Рис. 6.2 Положительным считается направление вращения векторов против часовой стрелки. Векторные диаграммы используются для качественного анализа электрических цепей, а также при решении некоторых электротехнических задач.

При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам. Комплексное число может быть представлено в виде радиус — вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.6.3).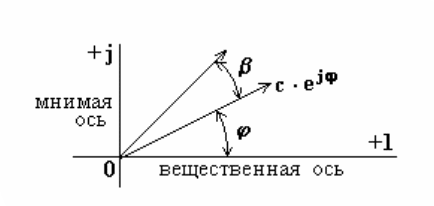

Умножим комплексное число на множитель 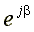.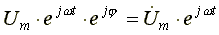— комплексную функцию времени для напряжения.— комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.

Мгновенное синусоидальное напряжение (ток, ЭДС) является мнимой частью соответствующей комплексной функции времени.

13.Сопротивление в цепи синусоидального тока

Если напряжение 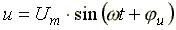подключить к сопротивлению R, то через него протекает ток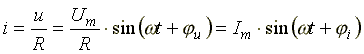Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе. Формула (6.7) в комплексной форме записи имеет вид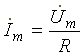гдеи— комплексные амплитуды тока и напряжения. Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению. Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением. Рис.6.4 Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

Переменный (синусоидальный) ток и основные характеризующие его величины.

Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

В быту для электроснабжения переменяется переменный, синусоидальный ток.

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):

Рисунок 1
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
амплитуду тока обозначают lm;
амплитуду напряжения Um.
Период Т— это время, за которое совершается одно полное колебание.
Частота f равна числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с^-1)
f = 1/T
Угловая частота ω (омега) (единица угловой частоты — рад/с или с^-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Обратите внимание! При обозначении величин на схемах или в расчетах важен регистр букв, то есть заглавные буквы (E,I,U…) или строчные (e, i ,u…). Так как строчными буквами принято обозначать мгновенное значение, а заглавными могут обозначаться действующее значение величины (подробнее о действующем значении в следующей статье).
Основные характеристики (параметры) переменного тока
Переменные синусоидальные напряжение и ток обычно представляют в алгебраической форме в виде записи:i = I_m Sin( ωt + Ψ_i)
u = U_m· Sin( ωt +Ψ_u ) , где i , u – мгновенные значения функции,
I_m, U_m, – амплитудные значения функции,

( ωt +Ψ_i) – аргумент или фаза функции, Ψ_i , Ψ_u – начальные фаз,
Т [с] — период — длительность полного цикла изменения синусоидальной величины.
ω = 2πf [рад/с] — угловая частота — скорость изменения аргумента функции,
f =1 /Т [с^-1] или [Гц] — циклическая частота — число периодов в единицу времени (промышленная частота f = 50 Гц),
Начальная фаза функции – Ψ _i_{,
и, е}– это значение аргумента функции в нулевой момент времени (t = 0).
Сдвиг фаз (в электротехнике) – это разность начальных фаз напряжений и тока : φ = Ψ_и – Ψ_i .
Величина и знак сдвига фаз не зависит от выбора момента времени, а определяется характером электрической цепи (активным, индуктивным, ёмкостным или смешанным).
Действующее значение переменного тока
Для сравнения теплового, механического и др. эффектов действия переменного и постоянного тока вводится понятие — действующее значение переменного тока ( I ) (а также напряжения — U и ЭДС — E ).
Из условия равенства тепловыделения при протекании постоянного и переменного тока получены следующие соотношения между действующими и амплитудными значениями синусоидальных величин: I = I _m/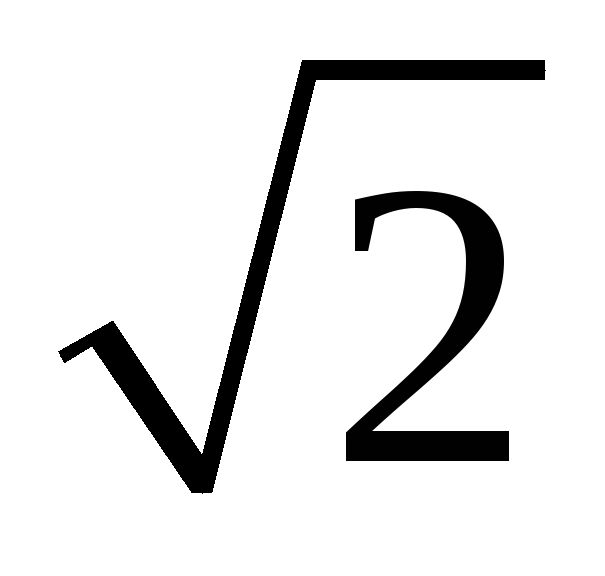, U _m/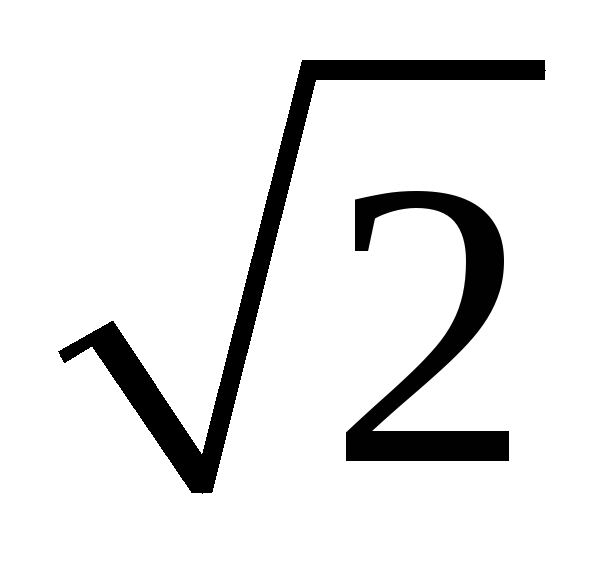, E = E _m/.
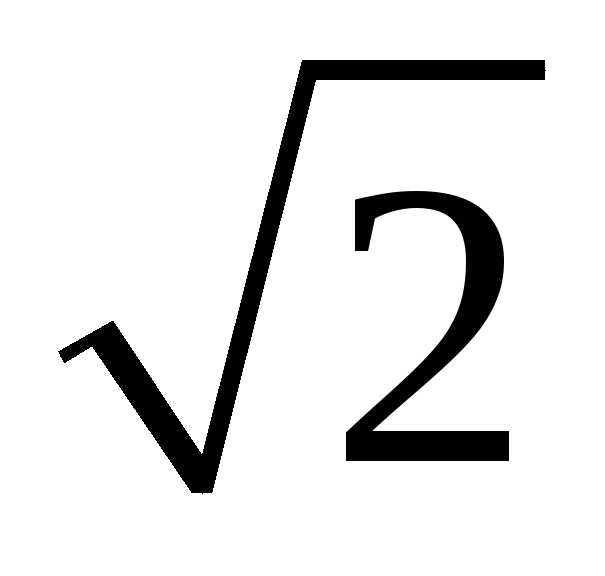Действующее значение переменного тока (напряжения, ЭДС) меньше амплитудного значения в 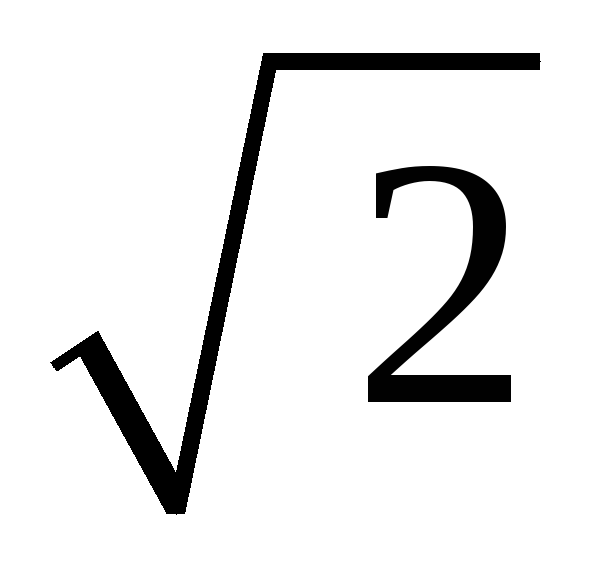раза. Все измерительные приборы, если это специально не оговорено, показывают действующие значения.
7. Метод векторных диаграмм. Основные характеристики переменного тока. Применение комплексного метода для анализа электрических цепей переменного тока (алгебраическая, тригонометрическая и показательная форма).
В электротехнике переменного тока для расчета и анализа электрических цепей широко используются так называемые векторные диаграммы.
Метод векторных диаграмм основан на том, что любая электрическая синусоидальная величина (i, u, e) может быть представлена на плоскости в виде векторной диаграммы, т.е. в виде вращающегося против часовой стрелки радиус-вектора, модуль которого равен амплитуде функции, а угловая скорость ω равна угловой частоте функции (ω = 2π f).

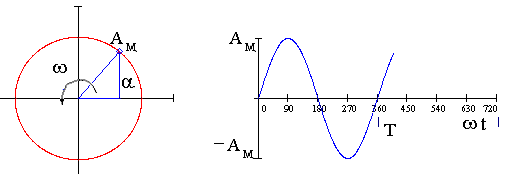
1. Мгновенное значение — (i, u, e) на векторной диаграмме определяется как проекция радиус-вектора на ось ординат.
2. Начальная фаза — Ψ на векторной диаграмме определяется углом между радиус-вектором и осью абсцисс.
3. Сдвиг фаз —  на векторной диаграмме определяется углом между векторами напряжения U и тока I .
Применение комплексных чисел для анализа цепей переменного тока
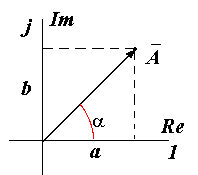
Комплексное число – это сумма действительного и мнимого чисел, например, Ā = а + j b,
где a и b — действительные числа, j = 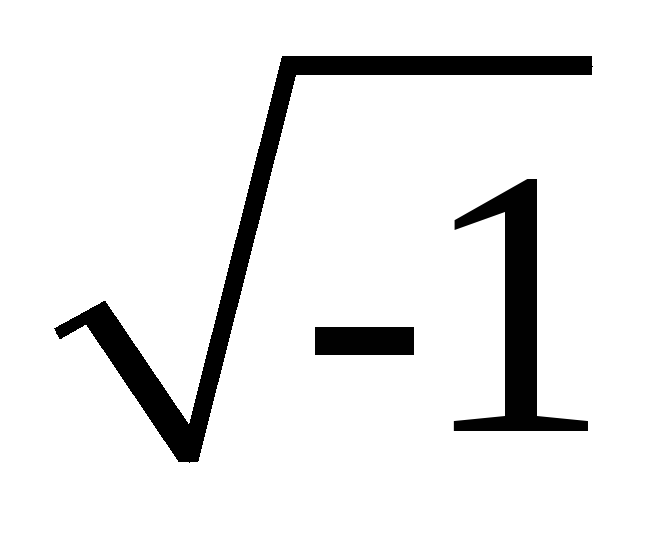— мнимая единица.
На комплексной плоскости в координатах (+1 , +j ) комплексное число Ā может быть представлено либо точкой с координатами ( a , b), либо вектором Ā, проведенным из начала координат в эту точку, и фазовым углом α .

В электротехнике любая синусоидальная величина (i, u, e) может быть представлена на комплексной плоскости в виде вращающегося против часовой стрелки вектора, например, напряжения Ū_m.
Для удобства расчетов в электротехнике используют различные формы представления электрических величин в комплексном виде:
1. Алгебраическая форма: Ū_m = U_m ₍_R_e₎+ j U_m₍_Im₎;
— удобна при сложении и вычитании комплексных величин.
2. Тригонометрическая форма:
Ū_m = U_m Cos ( ωt +Ψ_u)+ j U_mSin ( ωt +Ψ_u) ;
— используется для перехода от алгебраической формы записи к операторной и наоборот.
3. Операторная или показательная форма основана на использовании формулы Эйлера Cos α + j Sin α = e^j^α и удобна при умножении и делении комплексных величин: Ū_m = U_me ^j⁽^ωt⁺^Ψu⁾.
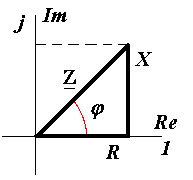
В качестве характеристики (параметра) элемента (участка) электрической цепи вводится понятие – комплексное сопротивление:
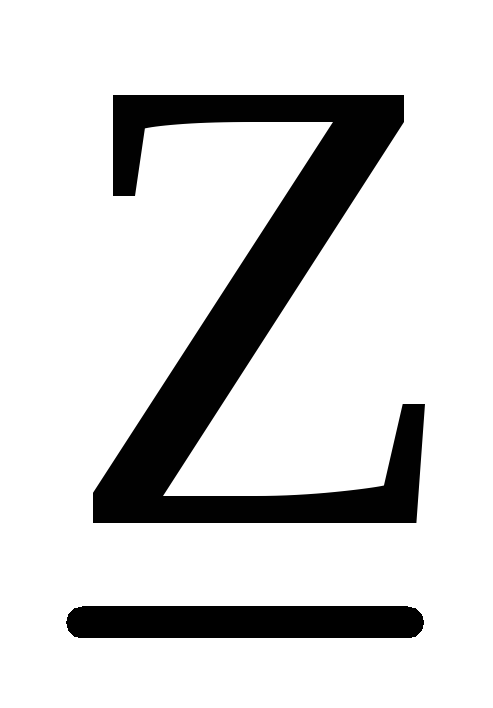= Ū /Ī = (U /I) e ^j⁽^Ψu^—^Ψi⁾= Ze ^j^φ= Z   ,
или в тригонометрической форме : 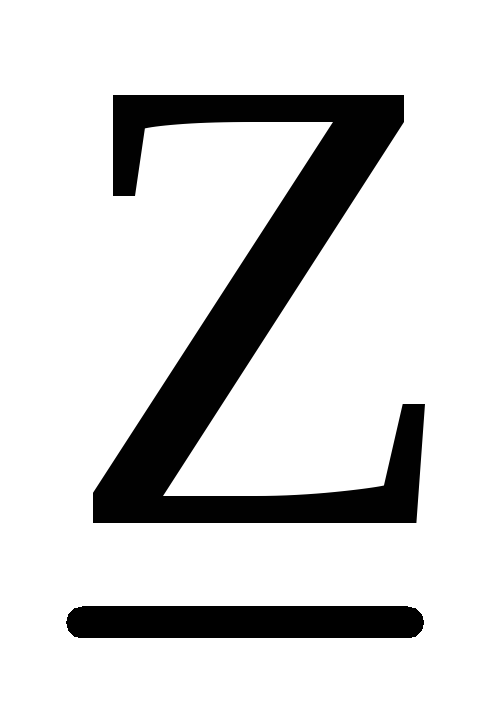= Z Cos  + j Z Sin  , где Z= || = U /I – модуль комплексного сопротивления или полное сопротивление.
Z Cos  = R — действительная составляющая комплексного сопротивления называется активным сопротивлением,
Z Sin  = Х — мнимая составляющая комплексного сопротивления называется реактивным сопротивлением.
Комплексное сопротивление элемента (участка) электрической цепи можно представить в алгебраической форме: = R + j X и на комплексной плоскости в виде прямоугольного треугольника сопротивлений:
8. Электрическая цепь переменного тока. Характеристики идеальных и реальных элементов цепи переменного тока. Условно-графические обозначения. Понятие об активной, реактивной и полной мощностях.
Понятие об активной, реактивной и полной мощностях.
В цепях переменного тока в связи с периодическим изменением электрического тока энергия электрических и магнитных полей периодически изменяется и между этими полями и источником электрической энергии происходит обратимый периодический процесс обмена электрической энергией. Скорость такого обратимого процесса обмена электрической энергией между источником и электрической цепью характеризуется понятием реактивная мощность Q [ ВАр], (Вольт-Ампер реактивный).
Одновременно в электрической цепи переменного тока происходит необратимый процесс преобразования электрической энергии в тепло, свет и другие виды энергии, т.е. в работу. Скорость такого необратимого процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт], (Ватт).
Таким образом, в общем случае в цепи переменного тока одновременно происходят два процесса: процесс преобразования электрической энергии в другие виды (в работу) и процесс обратимого периодического обмена энергией между источником и цепью. Эти два одновременно протекающих процесса, накладываясь друг на друга, создают в цепи сложный единый энергетический процесс, для характеристики которого вводится понятие полная мощность S [ВА], (Вольт-Ампер).

Полученные энергетические соотношения могут быть условно представлены на плоскости в геометрической форме — в виде прямоугольного треугольника — треугольника мощностей, из которого могут быть получены дополнительные формулы, необходимые для выполнения электротехнических расчетов.
Для удобства анализа работы и расчета цепей переменного тока вводят упрощения и используют условные идеализированные электрические схемы – схемы замещения, которые составляют из так называемых идеальных электрических элементов и которые с достаточным для практических целей приближением отображают электрофизические закономерности реальной электрической цепи.
Идеальный электрический элемент — это участок условной идеальной электрической цепи (схемы замещения), выделенный условно-графическим обозначением (УГО) и буквенно-цифровым обозначением (БЦО), в котором происходит только один энергетический процесс.
Для раздельного отображения процессов преобразования и обмена электрической энергией на электрической схеме замещения используются активный и реактивный элементы.
Активный (резистивный) R— элемент (идеальный резистор) — это элемент схемы замещения, в котором происходит процесс необратимого преобразования электрической энергии в другие виды, т.е. в работу как полезную, так и включающую различного рода потери. В активном элементе по определению отсутствуют переменные электромагнитные поля, поэтому в нем не происходит обмена электрической энергией.
Скорость процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт].
R [Ом] — сопротивление активного (резистивного) элемента (активное сопротивление).
Реактивный Х- элемент — это элемент схемы замещения, в котором происходит процесс обратимого периодического обмена электрической энергии между электрическим полем (ёмкостный элемент) и переменным магнитным полем (индуктивный элемент). Реактивные элементы (ёмкостный и индуктивный) можно рассматривать как аккумуляторы электрической энергии, которая запасается в них в виде энергии электрического или магнитного поля. Скорость периодического процесса обмена электрической энергией между электромагнитными полями характеризуется понятием реактивная мощность Q [ВАр].
Индуктивный L — элемент (идеальная катушка) обладает свойством периодически запасать электрическую энергию в виде энергии переменного магнитного поля и характеризуется понятием индуктивность: L = ddi [Гн] , где:  w магнитное потокосцепление катушки, w — число витков обмотки, - магнитный поток катушки.
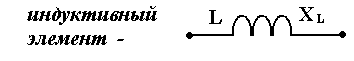X _L[Ом] — сопротивление индуктивного элемента
Преобразования электрической энергии в индуктивном элементе не происходит Р = 0, поэтому индуктивный элемент активным сопротивлением не обладает, т. е. R = 0.
Ёмкостный С — элемент (идеальный конденсатор) обладает свойством периодически запасать электрическую энергию в виде энергии переменного электрического поля и характеризуется понятием ёмкость: С = dq/ du [Фарада],[Ф], где: q — электрический заряд конденсатора, u – напряжение на зажимах конденсатора.

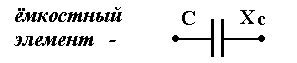
X_C [Ом] — сопротивление ёмкостного элемента (ёмкостное сопротивление).
Преобразования электрической энергии в ёмкостном элементе (по определению) не происходит Р = 0 , поэтому ёмкостный элемент (идеальный конденсатор) активным (резистивным) сопротивлением не обладает, т. е. R = 0.
В общем случае в любом реальном электротехническом устройстве — потребителе электрической энергии (Z), включенном в сеть переменного тока, одновременно происходят оба энергетических процесса — преобразование и периодический обмен электрической энергии. Поэтому такой реальный элемент Z на схеме замещения можно представить как комбинированный, т.е. состоящий из двух идеальных элементов: активного — R и реактивного – Х (индуктивного — Lили ёмкостного – C ).
Реальный элемент: Z [ R , X ]  Z { R , L } или Z { R , C }.
Для характеристики любого реального элемента цепи переменного тока обычно используют такие параметры как: R [Ом], L [Гн] или X_L[Ом], С [Ф] или Х_С[Ом].
Таким образом, схема замещения реальной цепи переменного тока может характеризоваться либо одним параметром (R, L, C) в случае идеализированной реальной цепи, либо комбинацией этих параметров при различных способах соединения резистивного R и реактивного Х элементов.

Действующее и среднее значения переменного тока
Действующее значение переменного тока численно равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет за время, равное 1 периоду, одинаковое количество тепла. Все приборы показывают действующее значение .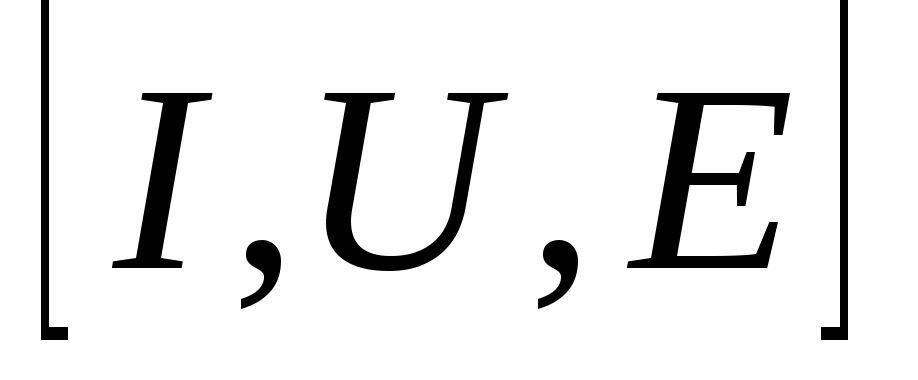
Если левые части уравнения равны, то и правые будут тоже равны. Приравняв правые части и выполнив операцию интегрирования, получим:

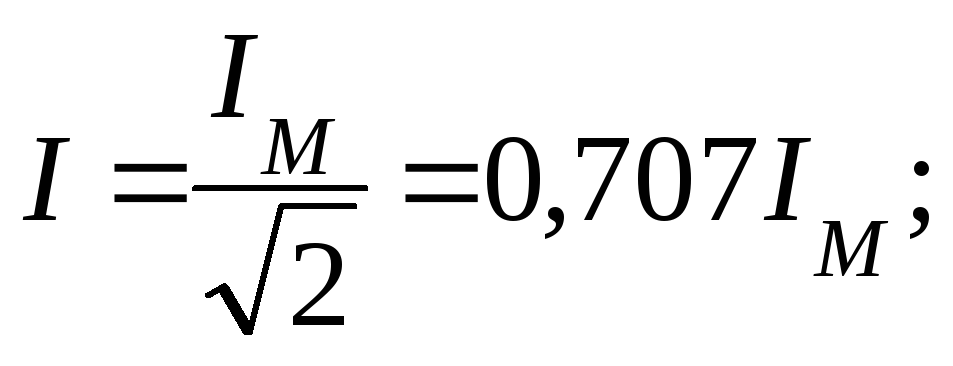
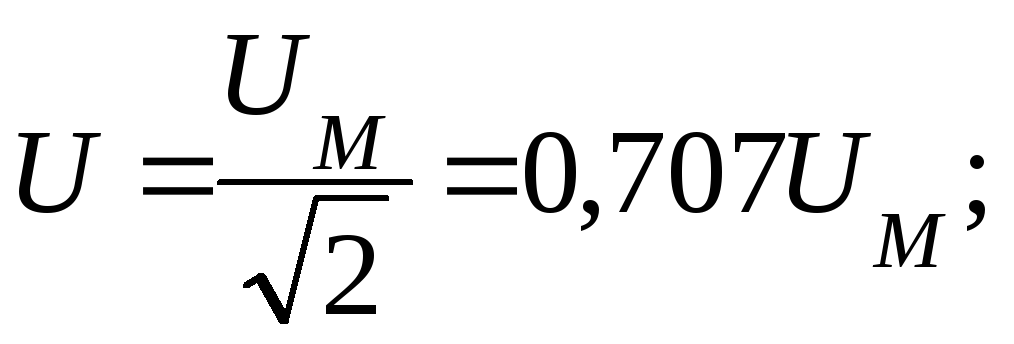
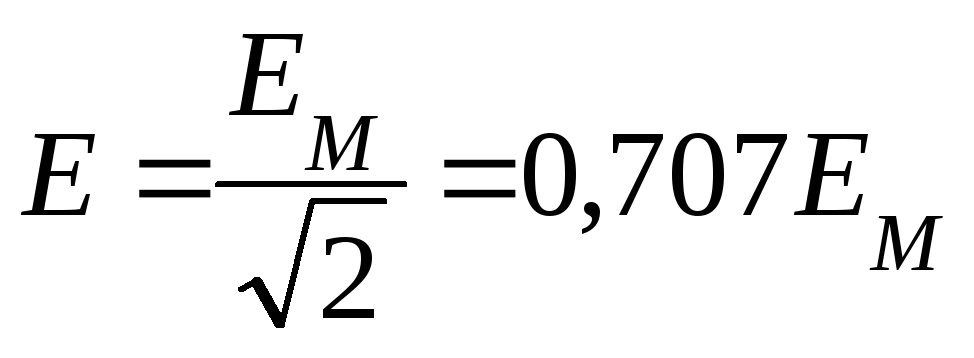
Среднее арифметическое значение переменного тока определяется в течении полупериода; если через поперечное сечение проводника в течении 1 полупериода будет протекать один и тот же заряд при постоянном и переменном токе, то такое значение постоянного тока будет равно среднему значению переменного тока .

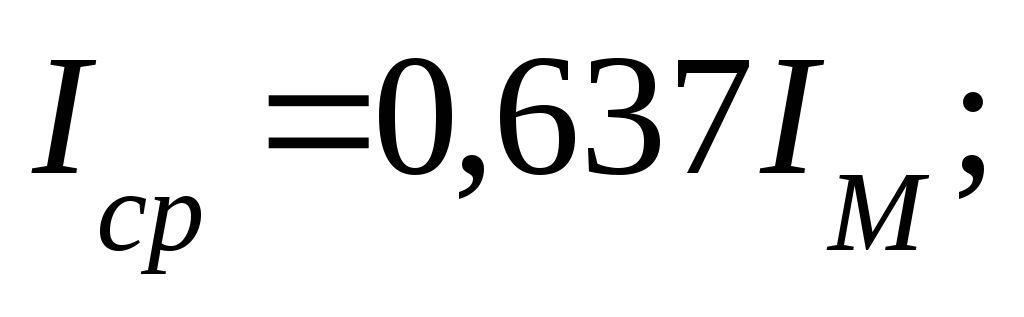
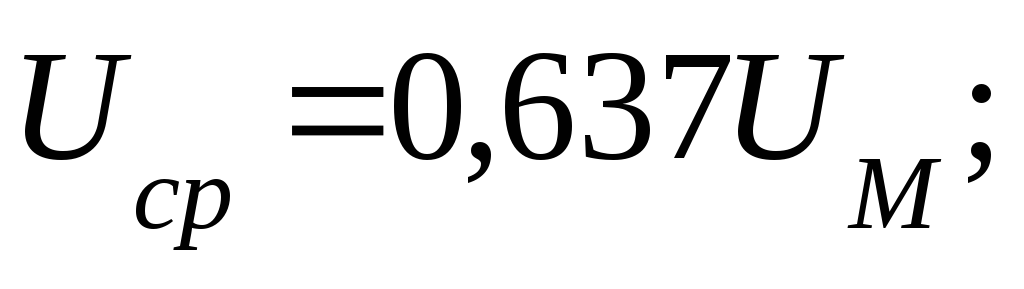
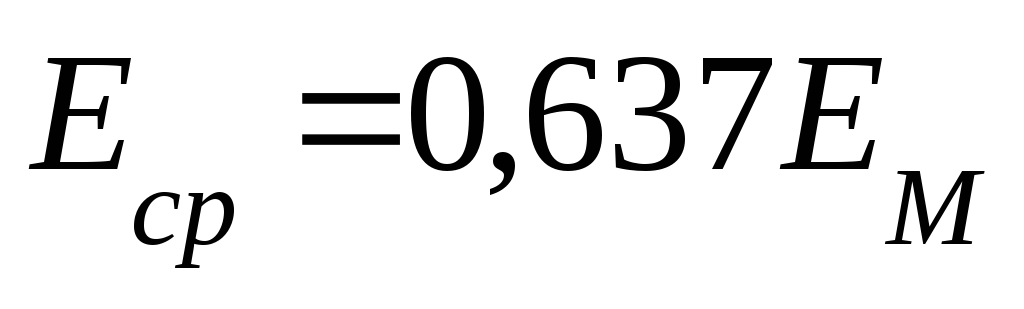
Среднее значение тока за период равно нулю.
Коэффициенты формы и амплитуды
Отношение действующего значения переменного тока (напряжения или ЭДС) к среднему значению называется коэффициентом формы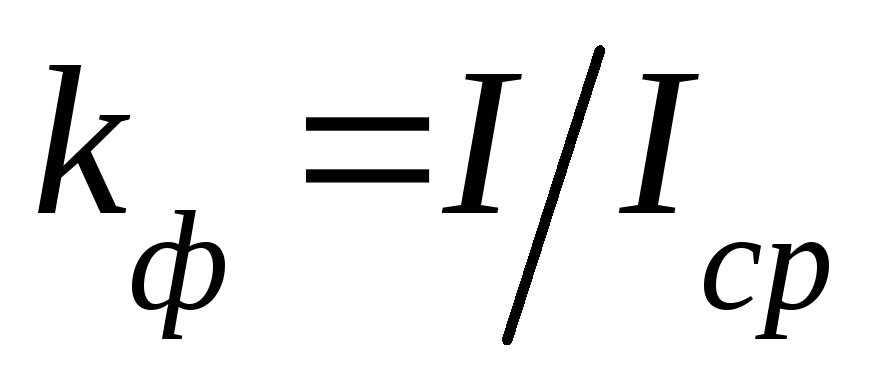, а отношение амплитудного значения к действующему –коэффициентом амплитуды.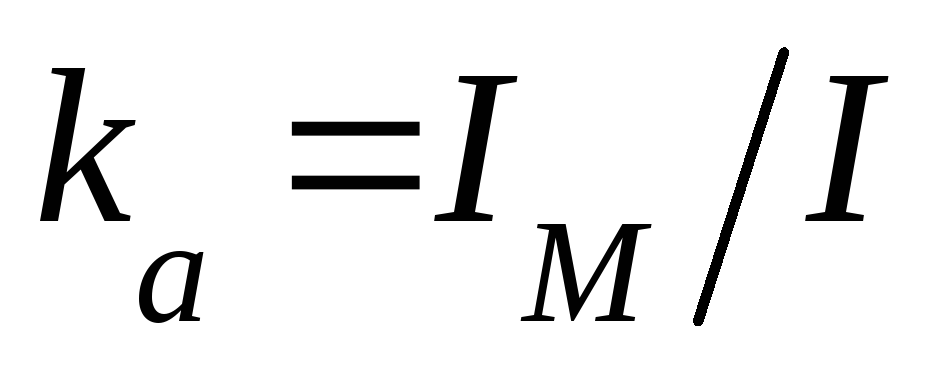
Для синусоидального ток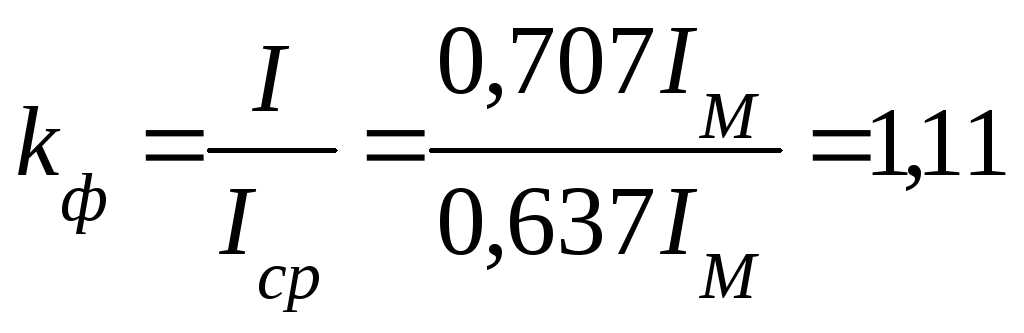а:
, а .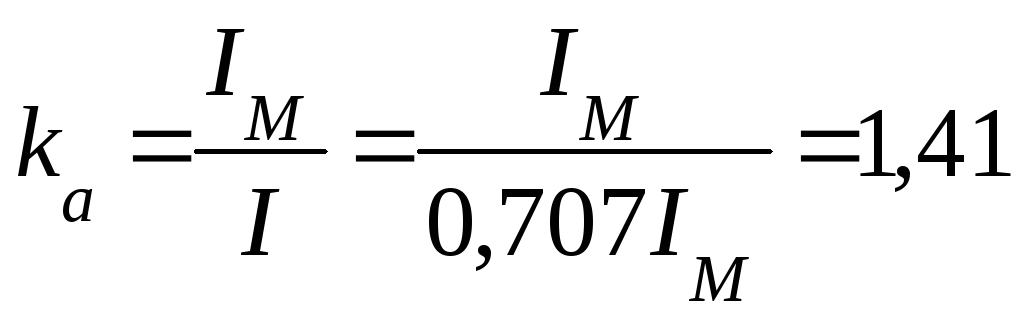
Для кривых, имеющих более острую форму, чем синусоида: ;.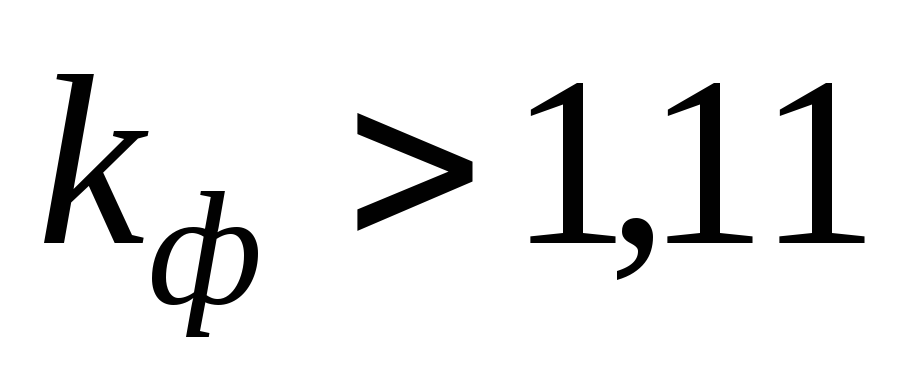
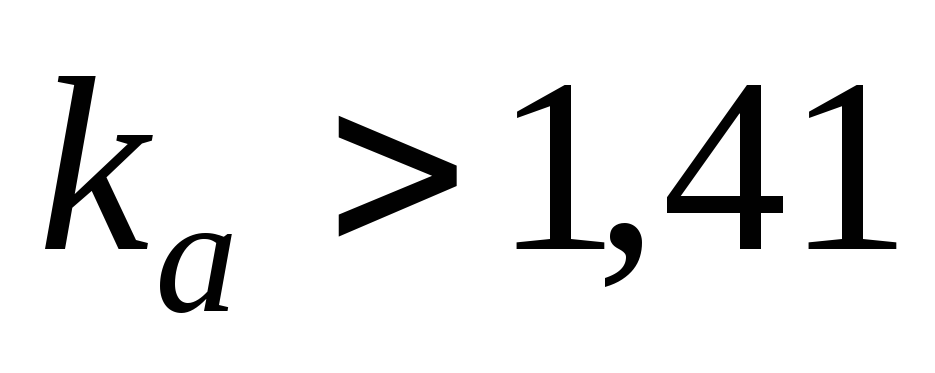Начальная фаза. Сдвиг фаз
Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды.
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени ЭДС витка будет:

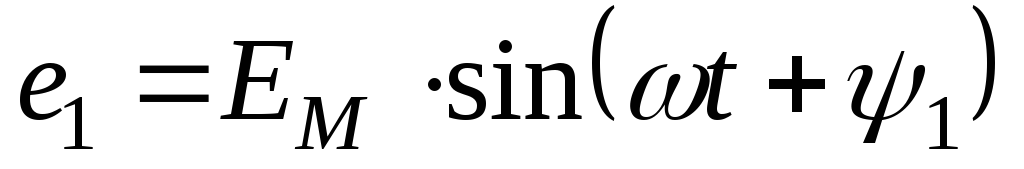
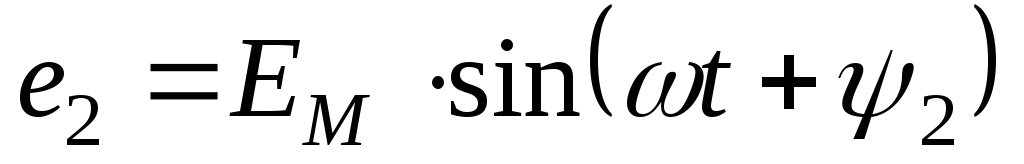
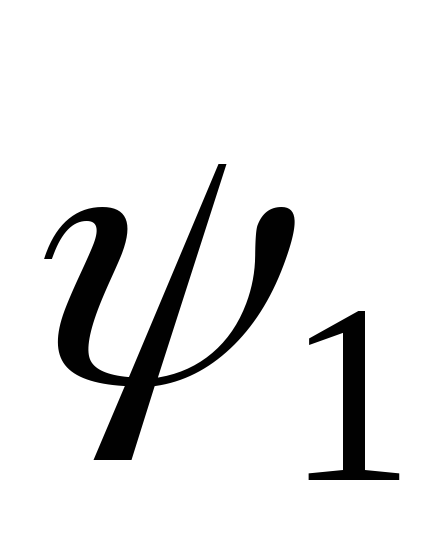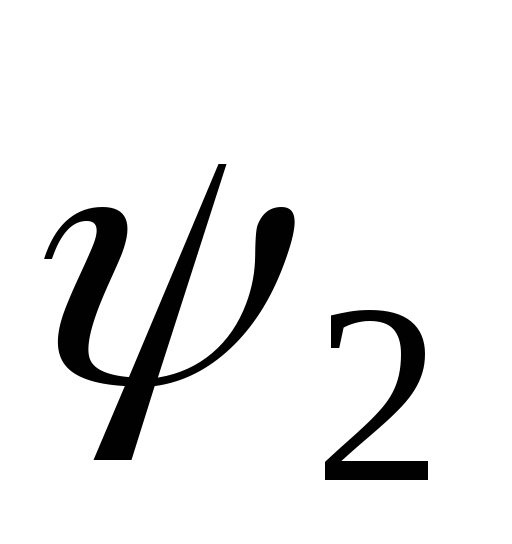В этих выражениях углы иназываютсяфазными, илифазой. Углыиназываютсяначальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз

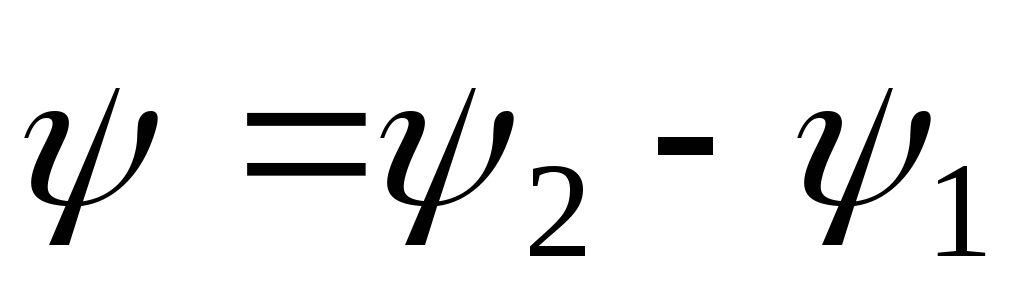
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:

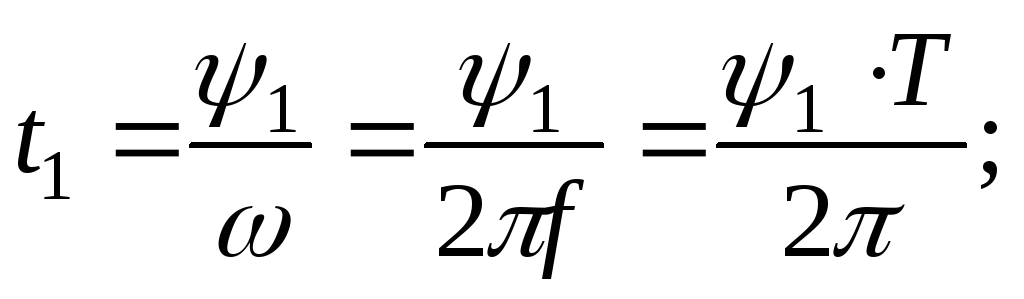
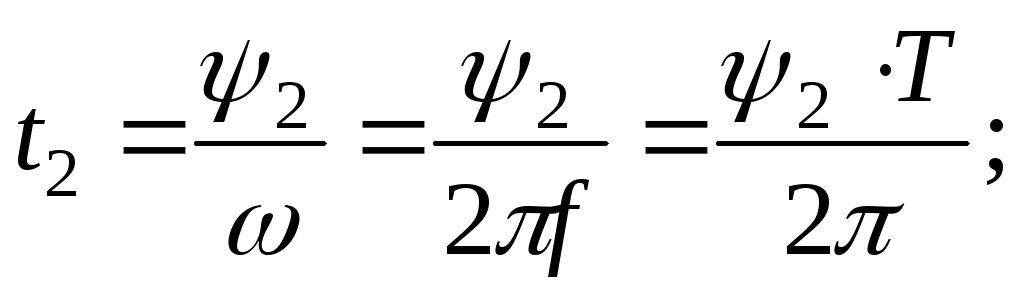
Если угол сдвига фаз составляет 180⁰, то такие ЭДС находятся в противофазе
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.

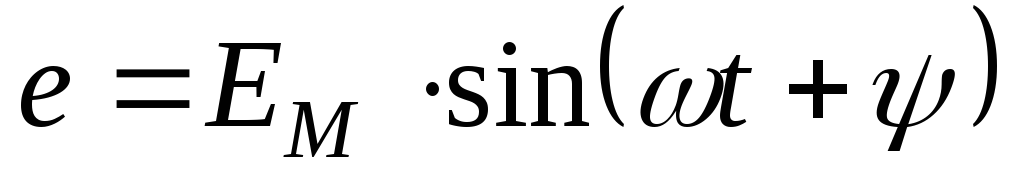
Любая синусоидальная величина характеризуется:
амплитудой;
угловой частотой;
начальной фазой.

При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин

.

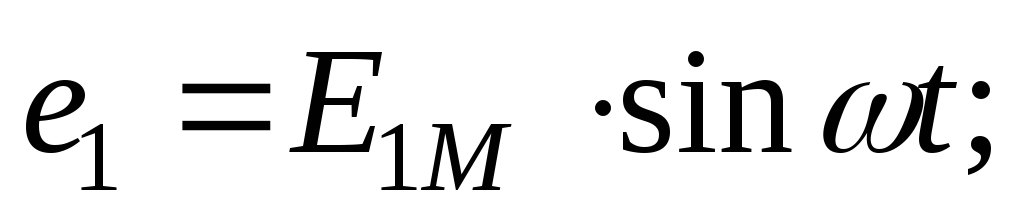
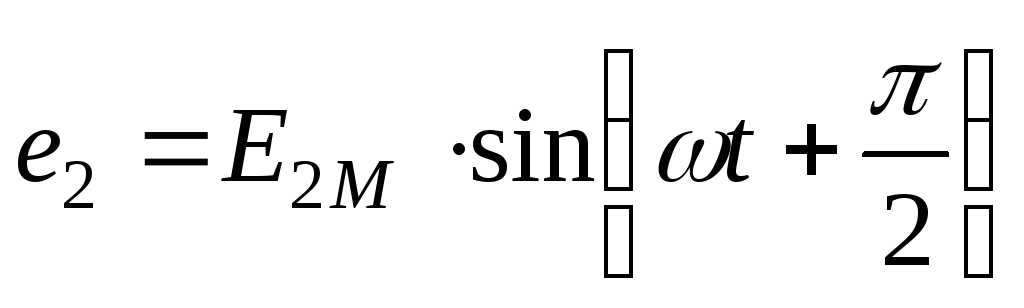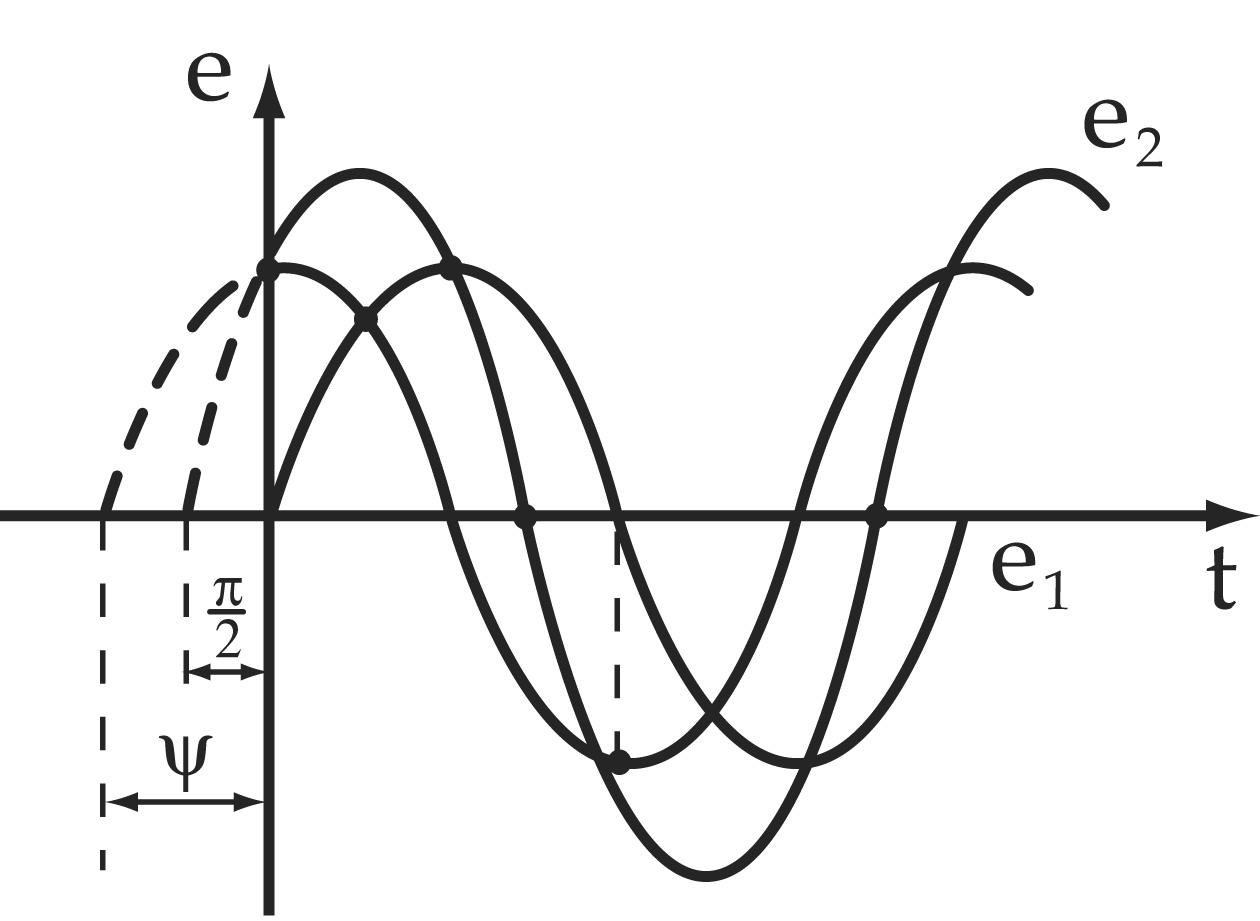
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
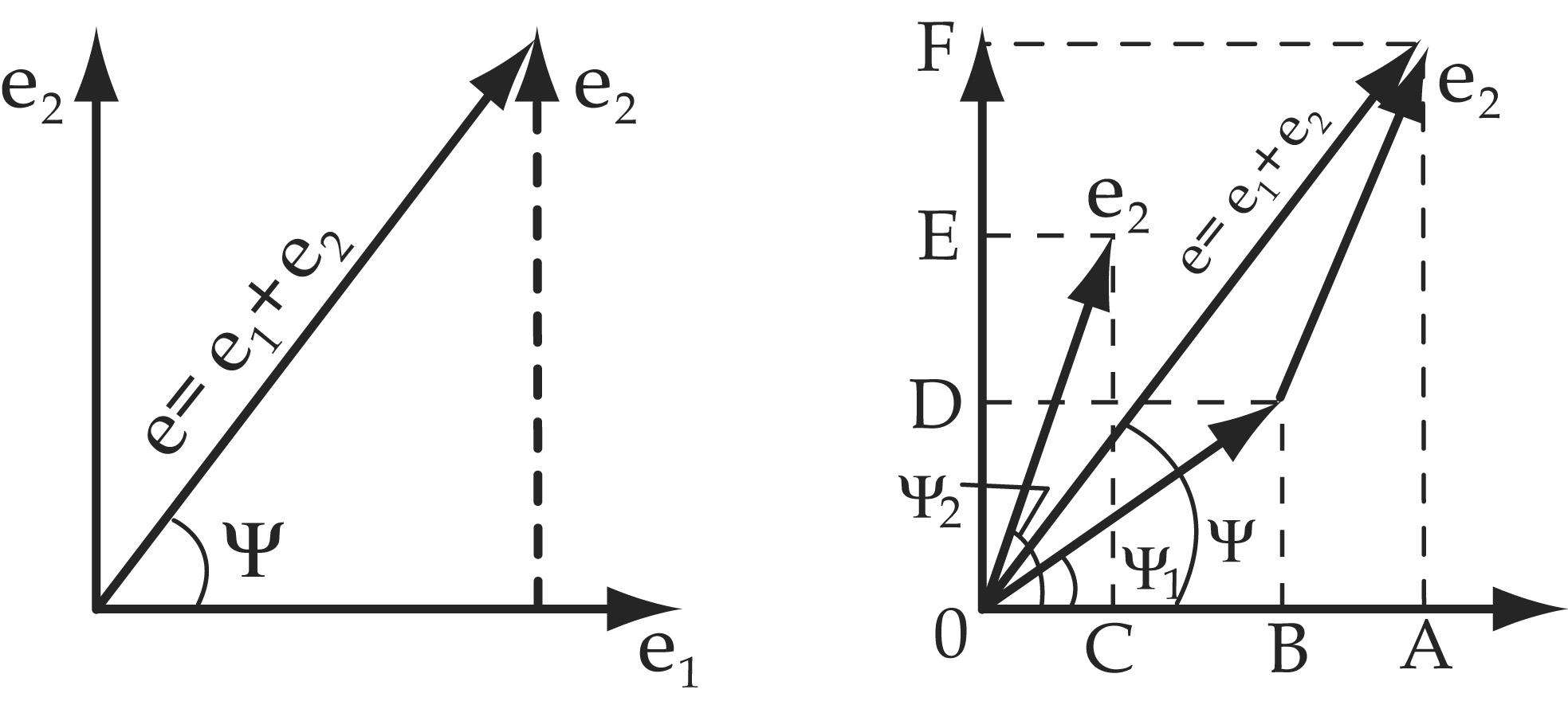
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.

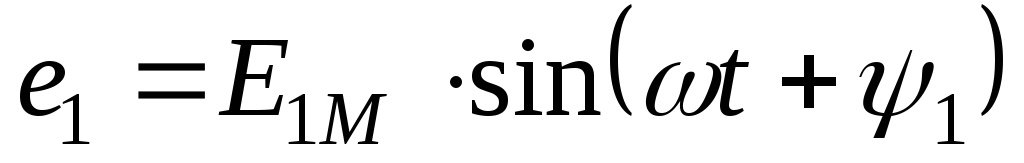
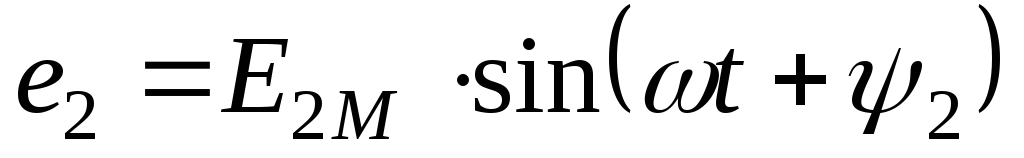
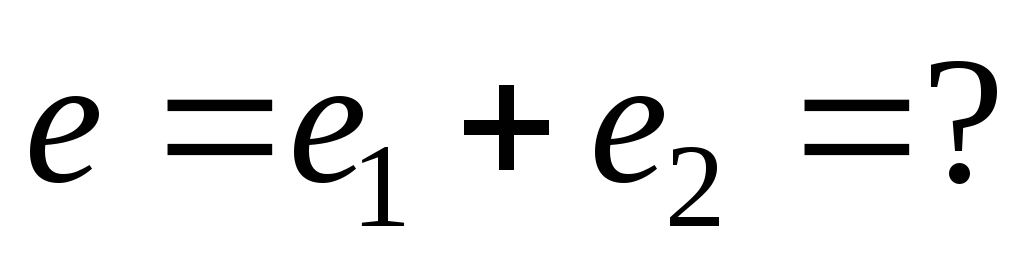
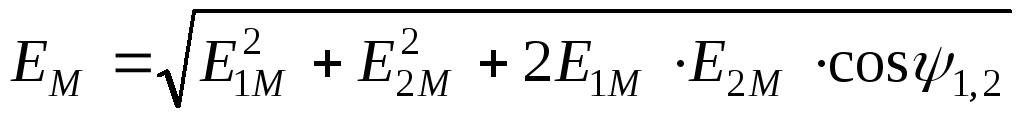
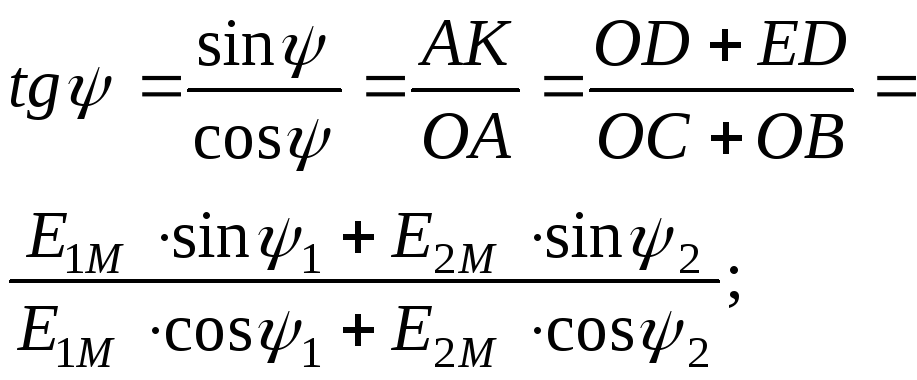
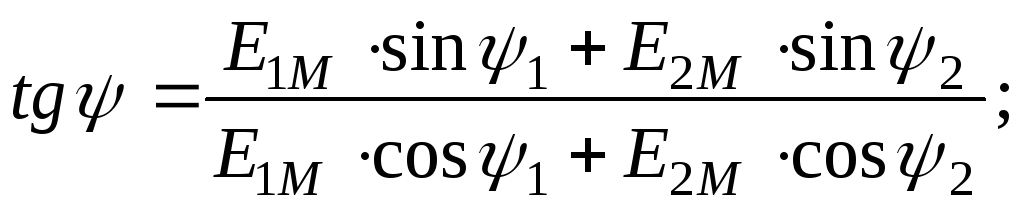
Трёхфазный переменный ток
Трёхфазный переменный ток
Подробности
Категория: Электротехника
Трехфазная система переменного тока

Электростанции вырабатывают трехфазный переменный ток. Генератор трехфазного тока представляет собой как бы три объединенных вместе генератора переменного тока, работающих так, чтобы сила тока (и напряжение) изменялась у них не одновременно, а с отставанием на 1/3 периода. Это осуществляется за счет смещения катушек генераторов на 120° одна относительно другой (рис. справа).

Каждая часть обмотки генератора называется фазой. Поэтому генераторы, которые имеют обмотку, состоящую из трех частей, называют трехфазными.

Следует отметить, что термин «фаза» в электротехнике имеет два значения: 1) как величина, которая совместно с амплитудой определяет состояние колебательного процесса в данный момент времени; 2) в смысле наименования части электрической цепи переменного тока (например, часть обмотки электрической машины).

Некоторое наглядное представление о возникновении трехфазного тока дает установка, изображенная на рис. слева.
Три катушки от школьного разборного трансформатора с сердечниками размещаются по окружности под углом 120° по отношению друг к другу. Каждая катушка соединена с демонстрационным гальванометром. В центре окружности на оси укрепляется прямой магнит. Если вращать магнит, то в каждой из трех цепей «катушка — гальванометр» возникает переменный ток. При медленном вращении магнита можно заметить, что наибольшее и наименьшее значения токов и их направления будут в каждый момент во всех трех цепях различными.

Таким образом, трехфазный ток представляет совместное действие трех переменных токов одинаковой частоты, но сдвинутых по фазе на 1/3 периода относительно друг друга.
Каждая обмотка генератора может соединяться со своим потребителем, образуя несвязанную трехфазную систему. Выигрыша от такого соединения нет никакого по отношению к трем отдельным генераторам переменного тока, так как передача электрической энергии осуществляется с помощью шести проводов (рис. справа).

На практике получили два других способа соединения обмоток трехфазного генератора. Первый способ соединения получил название звезды (рис. слева, а), а второй — треугольника (рис. б).

При соединении звездой концы (или начала) всех трех фаз соединяются в один общий узел, а от начал (или концов) идут провода к потребителям. Эти провода называются линейными проводами. Общую точку, в которой соединяются концы фаз генератора (или потребителя), называют нулевой точкой, или нейтралью. Провод, соединяющий нулевые точки генератора и потребителя, называют нулевым проводом. Нулевой провод применяется в том случае, если в сети создается неравномерная нагрузка на фазы. Он позволяет уравнять напряжения в фазах потребителя.

Нулевой провод, как правило, применяется в осветительных сетях. Даже при наличии одинакового количества ламп равной мощности во всех трех фазах равномерная нагрузка не сохраняется, так как лампы могут включаться, выключаться не одновременно во всех фазах, могут перегорать, и тогда равномерность нагрузки фаз будет нарушена. Поэтому для осветительной сети применяется соединение в звезду, которая имеет четыре провода (рис. справа) вместо шести при несвязанной трехфазной системе.

При соединении в звезду различают два вида напряжения: фазное и линейное. Напряжение между каждым линейным и нулевым проводом равно напряжению между зажимами соответствующей фазы генератора и называется фазным (U_ф), а напряжение между двумя линейными проводами — линейным напряжением (U_л).
Между фазными и линейными напряжениями можно установить соотношение:
U_л = √3 ^.U_ф ≈ 1,73 ^.U_ф,
если рассмотреть треугольник напряжения (рис. слева).

Действительно,

Ил= ^ч-Т^-г-Т^-сойШ^ Сф-л/2 + 2-со5б0° = л/3 -Ц,

На практике широкое распространение получили трехфазные цепи с нейтральными проводами при напряжениях U_Л = 380 В; U_Ф = 220 В.

Поскольку в нулевом проводе при симметричной нагрузке сила тока равна нулю, то ток в линейном проводе равен току в фазе.
При неравномерной нагрузке фаз по нулевому проводу проходит уравнительный ток относительно малой величины. Поэтому сечение этого провода должно быть значительно меньше, чем у линейного провода. В этом можно убедиться, если включить четыре амперметра в линейные и нулевой провода. В качестве нагрузки удобно использовать обычные электрические лампочки (рис. справа).

При одинаковой нагрузке в фазах ток в нулевом проводе равен нулю и надобность в этом проводе отпадает (например, равномерную нагрузку создают электродвигатели). В этом случае производят соединение в «треугольник», которое представляет собой последовательное соединение друг с другом начал и концов катушек генератора. Нулевой провод в этом случае отсутствует.
При соединении обмоток генератора и потребителей «треугольником» фазные и линейные напряжения равны между собой,
т.е. U_Л = U_Ф, а линейный ток в √3 раз больше фазного тока I_Л = √3^.I_Ф
Соединение треугольником применяется как при осветительной, так и при силовой нагрузке. Например, в школьной мастерской станки можно включать в звезду или треугольник. Выбор того или иного способа соединения определяется величиной напряжения сети и номинальным напряжением приемников электрической энергии.
Принципиально можно соединять треугольником и фазы генератора, но обычно этого не делают. Дело в том, что для создания заданного линейного напряжения каждая фаза генератора при соединении треугольником должна быть рассчитана на напряжение, в раз большее, чем в случае соединения звездой. Более высокое напряжение в фазе генератора требует увеличения числа витков и усиленной изоляции для обмоточного провода, что увеличивает размеры и стоимость машин. Поэтому фазы трехфазных генераторов почти всегда соединяют звездой. Двигатели же иногда в момент пуска включают звездой, а затем переключают на треугольник.