Параллельное соединение конденсаторов – общая емкость, заряд, формула кратко
4.8
Средняя оценка: 4.8
Всего получено оценок: 46.
Обновлено 20 Ноября, 2020
4.8
Средняя оценка: 4.8
Всего получено оценок: 46.
Обновлено 20 Ноября, 2020
Компоненты электрической цепи могут быть соединены различными способами, чаще всего используется параллельное и последовательное соединение. Рассмотрим работу параллельно соединенных конденсаторов.
Виды соединений в электрической цепи
Любая электрическая цепь состоит из одного или нескольких источников тока и одного или нескольких потребителей. Все эти компоненты связаны между собой проводниками.
Как бы ни сложна была электрическая цепь, в ней всегда можно выделить узлы и звенья:
- узел — это точка, в которой сходятся три и более проводника;
- звено — это участок цепи между двумя соседними узлами.
Каждое звено может быть простым проводником, может состоять из одного потребителя, а может содержать несколько потребителей, соединенных «цепочкой», один за другим.
Если несколько звеньев подключаются к одним и тем же двум узлам, такое соединение называется параллельным.
Если три и более звена соединяются так, что некоторые звенья будут соединены параллельно, а некоторые — последовательно, то такое соединение называется смешанным.
Рис. 1. Виды соединений в электрической цепи.Параллельное соединение конденсаторов
При параллельном соединении к двум выводам звена подключается каждый из соединенных конденсаторов. Получается, что при подключении к внешней цепи электрический ток будет поступать сразу на все конденсаторы. Произведем расчет емкости такой батареи конденсаторов.
Напомним, что емкость конденсатора показывает, насколько легко сообщить конденсатору заряд, и равна отношению заряда к напряжению на обкладках:
$$C={q\over U}$$
Если сообщить батарее конденсаторов некоторый заряд, то по закону сохранения этот заряд может лишь распределиться между конденсаторами, однако суммарно он останется прежним:
$$q_{общ}=q_1+q_2+…+q_n$$
При параллельном соединении конденсаторов напряжение на каждом из них будет одинаково.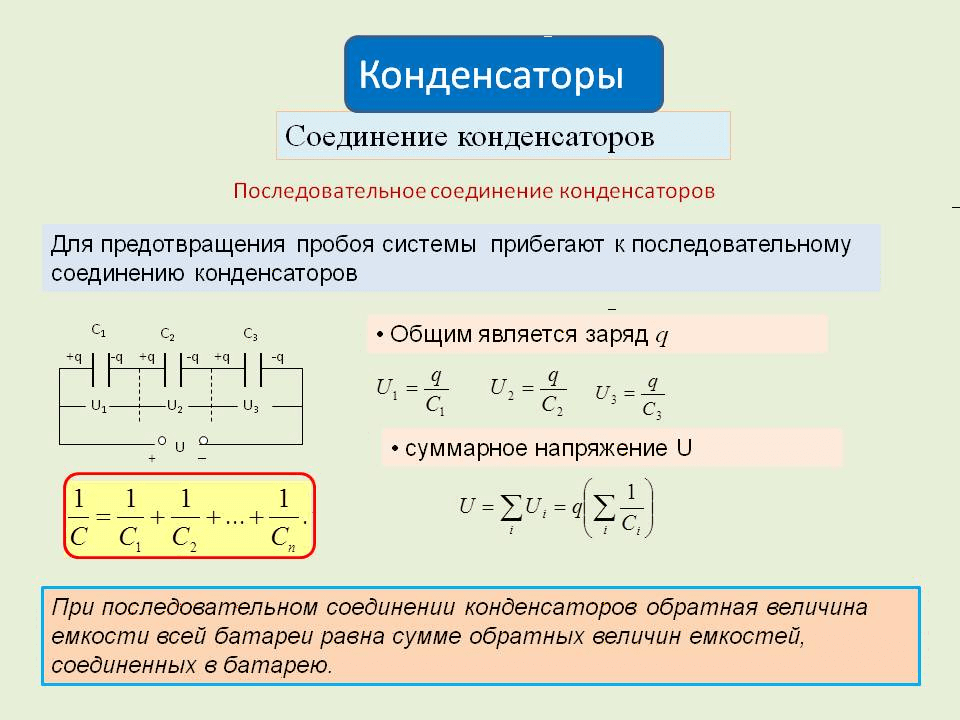
Действительно, если на каком-то из конденсаторов напряжение было бы больше, то заряд из этого конденсатора сразу же перешел бы к другому, тем самым уменьшив напряжение на первом и увеличив на втором.
Таким образом, общая емкость батареи конденсаторов равна:
$$C_{общ}={q_1+q_2+…+q_n\over U}={q_1\over U}+{q_2\over U}+…+{q_n\over U}$$
Каждый компонент полученной суммы равен отношению заряда на одном из конденсаторов к напряжению на нем, а это — емкость данного конденсатора. Заменяя каждую дробь на соответствующую емкость, получаем формулу для определения общей емкости параллельно соединенных конденсаторов:
$$C_{общ}=C_1+C_2+…+Cn$$
При параллельном соединении конденсаторов общая емкость батареи равна сумме емкостей отдельных элементов.
Рис. 2. Параллельное соединение конденсаторов.Использование параллельного соединения конденсаторов
Основная причина состоит в том, что выпускаемые номиналы конденсаторов имеют не любые значения.
Например, конденсаторы емкостью 7 мкФ не выпускаются. Однако выпускаются конденсаторы емкостью 6,8 мкФ и 0,2 мкФ. Соединив их параллельно, можно получить требуемые 7 мкФ.
Существует еще одна причина использования параллельного соединения конденсаторов — их неидеальность. Например, у больших конденсаторов имеется заметная на высоких частотах паразитная индуктивность. Из-за этого высокочастотная составляющая сигнала, которая в идеале должна легко проходить через большую емкость конденсатора, не проходит через него. Поэтому в этом случае параллельно конденсатору большой емкости ставится еще один, малой емкости, но имеющий очень малую паразитную индуктивность, которой можно пренебречь. В результате высокочастотная составляющая будет проходить через него.
Что мы узнали?
Общая емкость конденсаторов при параллельном соединении равна сумме емкостей отдельных конденсаторов. Такое соединение используется чаще всего для того, чтобы получить номиналы, не выпускающиеся промышленностью.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.8
Средняя оценка: 4.8
Всего получено оценок: 46.
А какая ваша оценка?
Параллельное соединение конденсаторов — Без Сменки
29 июня, 2022
1 мин
Физ 🔬
В электрических цепях применяются различные способы соединения конденсаторов. Сегодня мы рассмотрим параллельное.
✍️ Если группа конденсаторов включена в цепь так, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным.
Главное замечание: общая ёмкость конденсаторов при ПАРАЛЛЕЛЬНОМ соединении равна сумме ёмкостей всех соединённых конденсаторов.
Общие формулы найдёшь на картинке 👇
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.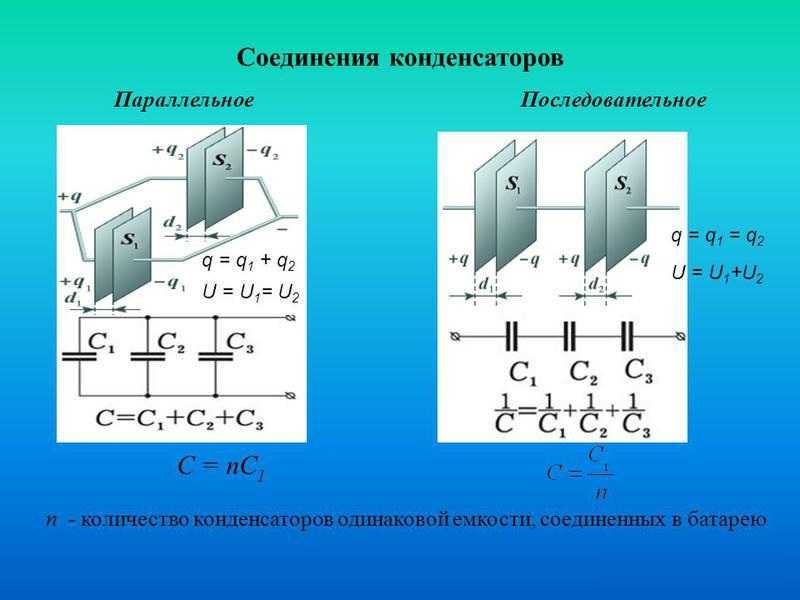
Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
40 подписчиков
+ Подписаться
Редакция Без Сменки
01 июля, 2022
1 мин
Хим 🧪
Анилин
🔹 ОБЩИЕ СВЕДЕНИЯ
Анилин (С₆H₅NH₂), он же фениламин — ароматический амин.
🔹 ФИЗИЧЕСКИЕ СВОЙСТВА
…
Редакция Без Сменки
07 июня, 2022
1 мин
Англ 🇬🇧
Идиомы на тему «время»
❤️ Donkey’s ears/years — долгие годы, долгое время, целая вечность. Эта фраза используется, когда…
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Пищеварительные ферменты
Пищеварительные ферменты — их много, но достаточно знать пять основных, и вы без труда опишете…
Редакция Без Сменки
29 июня, 2022
1 мин
Гео 🌍 Решение задач ✏️
ЗАДАНИЕ 17 | изобары
II тип — изобары
📚 Теория для задания:
• Изобары — линии на карте, соединяющие точки с.
..
Редакция Без Сменки
20 апреля, 2022
1 мин
Ист 🤴
Все русско-турецкие войны
Русско-турецкие войны…. Порой кажется, будто их целый миллиард, и запомнить все невозможно,…
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Вопрос Видео: Нахождение общей емкости последовательно и параллельно соединенных конденсаторов
Стенограмма видео
Цепь на схеме содержит конденсаторы, соединенные последовательно и параллельно. Какова общая емкость цепи? Дайте свой ответ с точностью до микрофарад.
На схеме, которую нам дали, показана цепь, в которой ячейка подключена к комбинации конденсаторов. Мы видим, что эта схема имеет две параллельные ветви с включенными конденсаторами.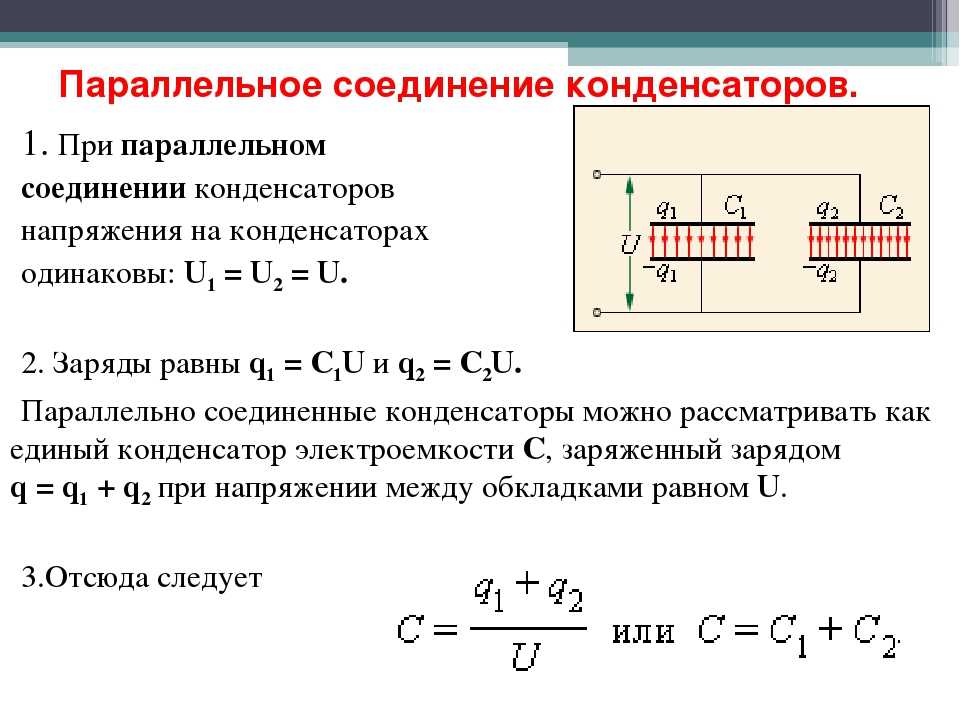
Вот эта ветвь посередине, которую мы обозначим как ветвь А. И мы видим, что на ней есть конденсаторы. Есть один с емкостью 75 мкФ и другой с емкостью 55 мкФ. Затем есть вот эта ветвь, которую мы обозначим как ветвь B. И она содержит только один конденсатор на 35 мкФ.
Нас просят найти общую емкость цепи. А для этого нам нужно будет вспомнить, как мы соединяем конденсаторы последовательно и параллельно. При последовательном соединении нескольких конденсаторов обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. То есть, если мы соединим последовательно кучу конденсаторов с емкостями 𝐶 один, 𝐶 два, 𝐶 три и так далее, то один сверх общей емкости 𝐶 нижний индекс Т будет равен единице больше 𝐶 один плюс один больше 𝐶 два плюс один больше 𝐶 три и так далее.
Между тем, если у нас есть несколько конденсаторов, соединенных параллельно, то мы просто добавляем отдельные емкости, чтобы получить общую емкость. На нашей диаграмме видно, что ветвь, обозначенная буквой А, состоит из двух последовательно соединенных конденсаторов.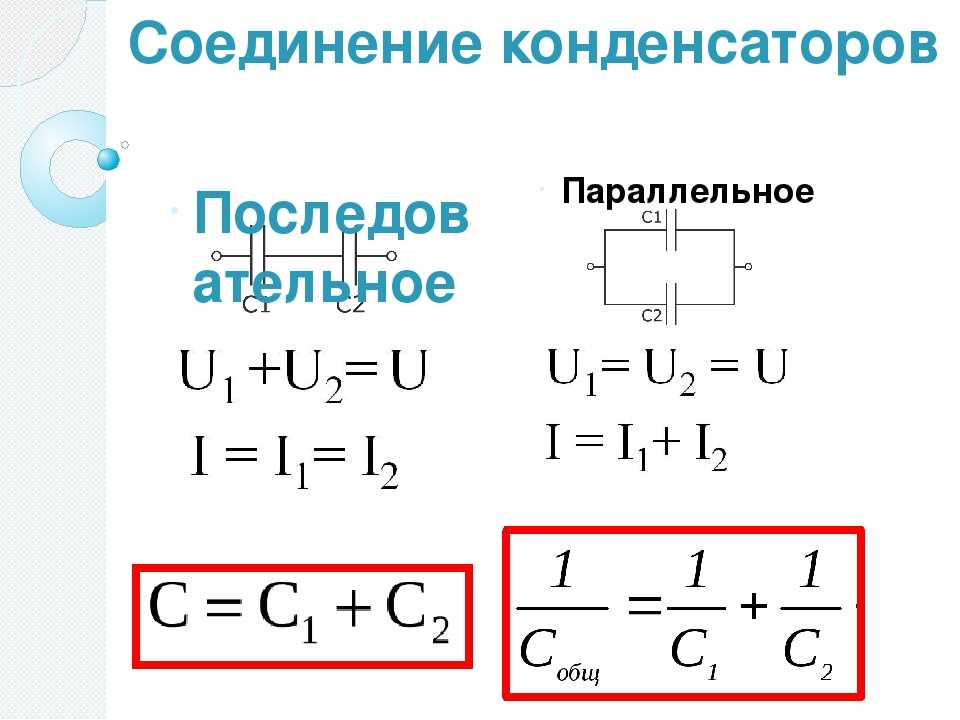
Обозначим общую емкость этой ветви, так что это общая емкость этих двух последовательно соединенных конденсаторов, как 𝐶 нижний индекс A. Мы также обозначим эту емкость 75 мкФ как 𝐶 один, а эту емкость 55 мкФ как 𝐶 два. Тогда из нашего общего выражения для конденсаторов, соединенных последовательно, мы знаем, что один над 𝐶 нижним индексом A равен одному над 𝐶 одним плюс один над 𝐶 двумя.
Поскольку мы знаем значения как 𝐶 единицы, так и 𝐶 двойки, мы можем использовать это уравнение, чтобы найти значение 𝐶 нижнего индекса A. Для этого мы хотим сделать 𝐶 нижний индекс A предметом уравнения . Мы начнем с умножения обеих частей уравнения на 𝐶 нижний индекс A, 𝐶 один и 𝐶 два. Раскрыв скобки в правой части, мы можем переписать уравнение следующим образом. В этой дроби слева индекс 𝐶 A в числителе сокращается с индексом 𝐶 A в знаменателе. В этой первой дроби справа 𝐶 в числителе и знаменателе сокращаются. И в этой второй дроби справа две 𝐶 в числителе и знаменателе сокращаются.
Как только мы избавимся от отмененных терминов, мы получим вот это выражение.
Затем мы можем вынести индекс 𝐶 A, который появляется в обоих терминах справа. Последний шаг, который нам нужно сделать, чтобы получить 𝐶 индекс A как субъект этого уравнения, — это разделить обе части на 𝐶 один плюс 𝐶 два, так что справа 𝐶 один плюс 𝐶 два в числителе сокращается с единицей в знаменатель. Если мы затем напишем уравнение наоборот, мы получим, что 𝐶 Нижний индекс A равен 𝐶 один раз 𝐶 два, деленное на 𝐶 один плюс 𝐶 два.
Итак, это уравнение говорит нам, как рассчитать общую емкость 𝐶 индекс А двух конденсаторов, 𝐶 одного и 𝐶 двух, соединенных последовательно.
Давайте теперь освободим место, чтобы мы могли подставить наши значения 𝐶 один и 𝐶 два из этой схемы. Подставив сюда 𝐶 единица равна 75 мкФ и 𝐶 двойка равна 55 мкФ, получим такое выражение для 𝐶 индекса А. В числителе имеем 75 мкФ умножить на 55 мкФ. И это получается как 4125 единиц микрофарад в квадрате. Затем в знаменателе у нас есть 75 микрофарад плюс 55 микрофарад, что дает 130 микрофарад.
С точки зрения единиц, мы можем сократить один из двух множителей микрофарад из числителя с микрофарадами из знаменателя.
Это оставляет нам единицы для 𝐶 нижнего индекса A микрофарад. Тогда вычисление выражения дает результат с точностью до двух знаков после запятой 31,73 мкФ. Итак, мы нашли значение индекса 𝐶 A, которое представляет собой емкость ветви, которую мы обозначили как A на нашей принципиальной схеме. Так как ветвь В содержит всего один конденсатор, то мы знаем, что его емкость как раз равна этой величине 35 мкФ. Обозначим это как 𝐶 индекс B.
Теперь у нас есть две параллельные ветви. Это ветвь A и ветвь B. И мы знаем емкость каждой ветви. Это наши значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B. Если мы теперь освободим место на доске, то сможем использовать наше общее выражение для конденсаторов, соединенных параллельно, чтобы найти общую емкость этих двух ветвей. .
Это общее выражение говорит нам, что для конденсаторов, соединенных параллельно, мы просто добавляем отдельные емкости. В нашем случае это значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B. Таким образом, общая емкость 𝐶 нижнего индекса T равна 𝐶 нижнему индексу A плюс 𝐶 нижнему индексу B.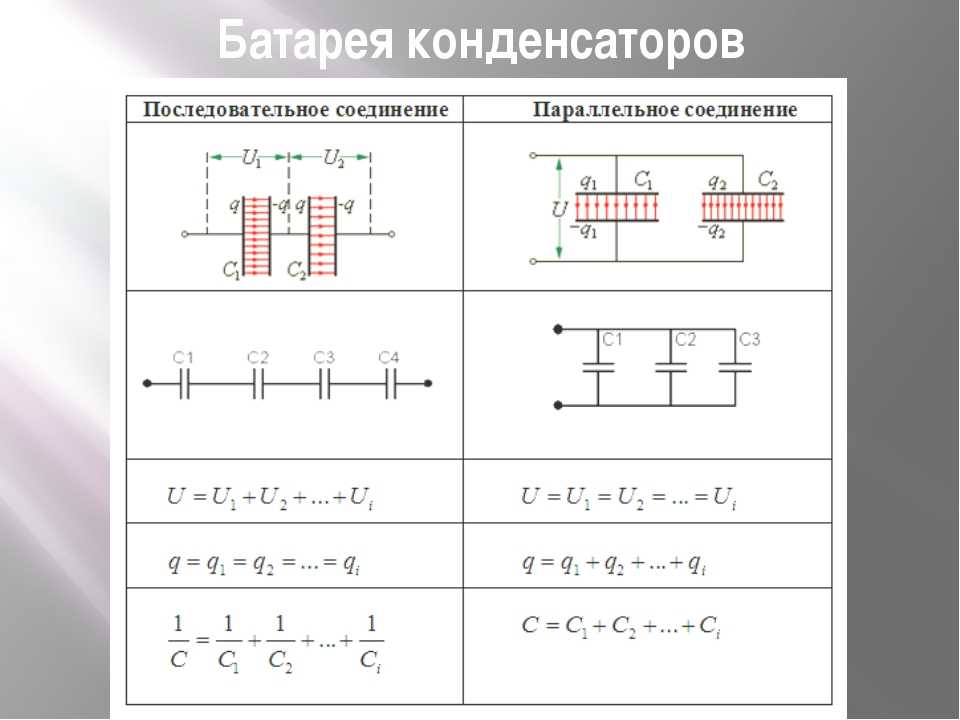
Затем мы можем подставить наши значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B. и оцените сумму, чтобы получить значение общей емкости 𝐶 индекс T.
В вопросе нас просят дать ответ с точностью до микрофарад. Округлив до микрофарад, получим наш ответ для полной емкости цепи как 67 мкФ.
Конденсаторы последовательно и параллельно — конденсаторы
Конденсаторы
Конденсаторы могут быть соединены последовательно или параллельно, чтобы получить результирующее значение, которое может быть либо сумма отдельных значений (параллельно) или значение меньше, чем у наименьшей емкости (последовательно).
Конденсаторы серии
Цепь, состоящая из нескольких последовательно соединенных конденсаторов, в некоторых отношениях похожа на одну.
несколько последовательно соединенных резисторов. В последовательной емкостной цепи один и тот же ток смещения
протекает через каждую часть цепи, и приложенное напряжение будет делиться на отдельные конденсаторы.
На рисунке ниже показана схема, содержащая источник и три последовательных конденсатора.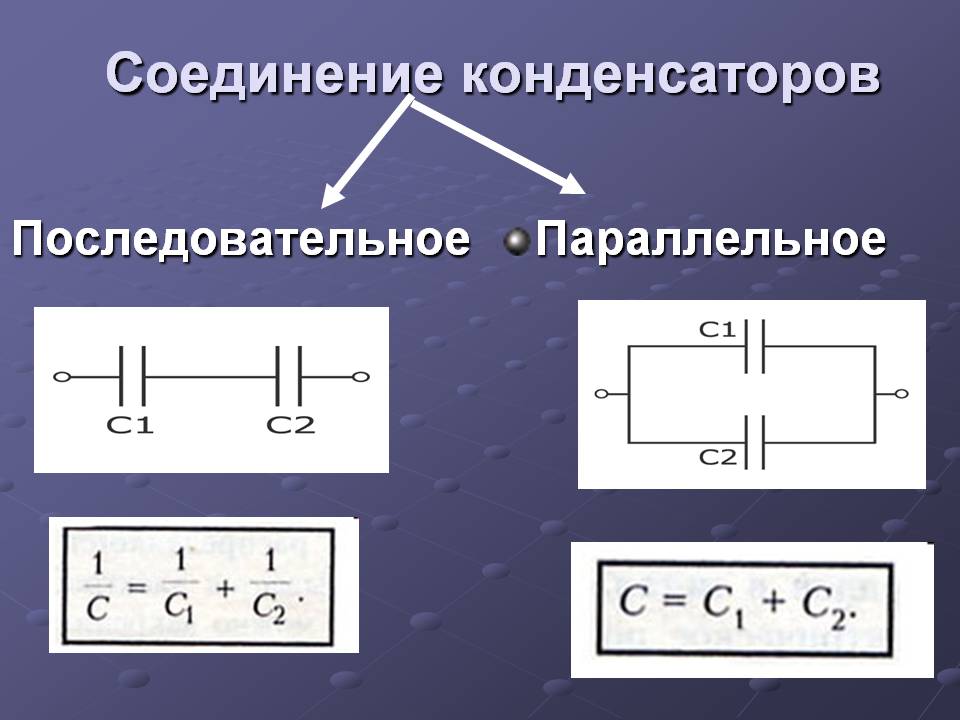
Конденсаторы последовательно.
Сумма напряжений на конденсаторе должна равняться напряжению источника (закон напряжения Кирхгофа).
Заряды на всех конденсаторах должны быть одинаковыми, так как конденсаторы соединены последовательно и любые движение заряда в одной части цепи должно происходить во всех частях последовательной цепи. Решение уравнения C = Q / V для напряжения через емкость и заряд ( V = Q / C ), для каждого из рядов получены следующие результаты конденсаторов и суммарной емкости ( C т )
Подставив эти результаты в приведенное выше уравнение закона Кирхгофа для напряжения
Разделив обе части приведенного выше уравнения на общий множитель Q
Взяв обратную величину обеих сторон и предполагая любое количество конденсаторов
Это уравнение является общим уравнением, используемым для расчета общей емкости конденсаторов.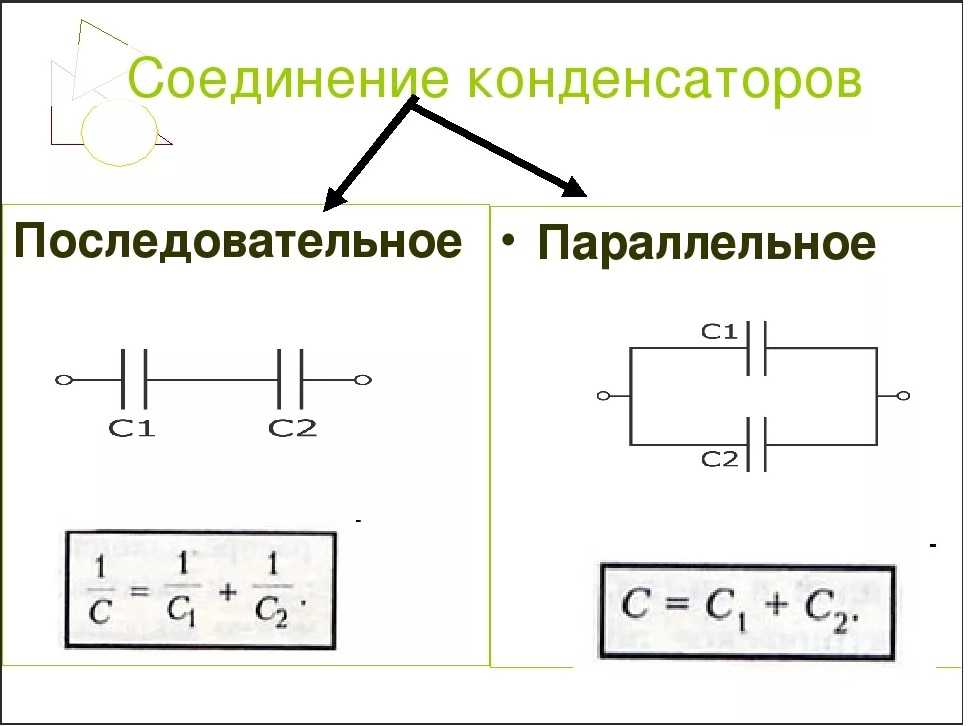
соединены последовательно. Обратите внимание на сходство между этим уравнением и тем, которое использовалось для нахождения эквивалента.
сопротивление параллельных резисторов. Если в цепи всего два конденсатора, произведение превышает
можно использовать формулу суммы
Из приведенных выше формул должно быть видно, что суммарная емкость конденсаторов при последовательном соединении меньше емкости любого из отдельных конденсаторов.
Пример:
Определите общую емкость последовательной цепи, содержащей три конденсатора, номиналы которых
составляют 10 нФ, 0,25 мкФ и 50 нФ соответственно.
Решение:
Общая емкость 8 нФ немного меньше самого маленького конденсатора (10 нФ).
Параллельные конденсаторы
При параллельном соединении конденсаторов (см. рисунок ниже) одна пластина каждого конденсатора подключается напрямую.
к одной клемме источника, а другая пластина каждого конденсатора подключена к
другой терминал источника.
На рисунке ниже все отрицательные пластины конденсаторов
соединены вместе, и все положительные пластины соединены вместе.
Суммарная (эквивалентная) емкость Кл t , следовательно, выступает как емкость с пластиной
площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее,
емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов
увеличивает площадь пластины и тем самым увеличивает общую емкость.
Параллельное подключение конденсаторов.
Полную емкость можно рассчитать математически. Применяя уравнение C = Q / V на каждый конденсатор и на общую емкость
Общий заряд Q t есть сумма зарядов на каждом конденсаторе
Из уравнения C = Q / V следует, что Q = C V , а если заряд записывается в этой форме и подставляется в приведенное выше уравнение, это уравнение приводит к
Разделив обе части приведенного выше уравнения на общий множитель В и приняв любое количество конденсаторов
Это уравнение математически утверждает, что общая емкость ряда конденсаторов
параллельно сумма отдельных емкостей.
