4.1.2.2. Обозначения, представляющие собой или содержащие элементы, способные ввести в заблуждение относительно товара, его свойств и качества \ КонсультантПлюс

• Главная
• Документы
• 4.1.2.2. Обозначения, представляющие собой или содержащие элементы, способные ввести в заблуждение относительно товара, его свойств и качества

Документ утратил силу или отменен. Подробнее см. Справку

Приказ Роспатента от 24.07.2018 N 128 «Об утверждении Руководства по осуществлению административных процедур и действий в рамках предоставления государственной услуги по государственной регистрации товарного знака, знака обслуживания, коллективного…

4.1.2.2. Обозначения, представляющие собой или содержащие элементы, способные ввести в заблуждение относительно товара, его свойств и качества

В ходе проведения экспертизы обозначения, заявленного на регистрацию в качестве товарного знака, необходимо оценить, содержит ли оно элементы, способные порождать в сознании потребителей представление об определенном виде товара и/или услуги, его свойствах и качестве.

В том случае, когда обозначение содержит указание на конкретный вид, свойства и качество товаров и/или услуг и заявляется на регистрацию в отношении широкого перечня товаров и/или услуг, оно может ввести потребителя в заблуждение относительно вида, свойств и качества товаров и/или услуг. В сознании потребителя может сложиться представление о виде, свойствах и качестве товаров и/или услуг, не соответствующих их настоящему виду, свойствам или качеству.

Примеры:

1. На регистрацию в качестве товарного знака заявлено комбинированное обозначение (изображение обозначения приведено ниже) со словесными элементами «CAMEL», «NATURAL WOOL» и изобразительным элементом в виде стилизованного верблюда, в отношении товаров 22 класса МКТУ «шерсть верблюжья; шерсть для набивки; шерсть древесная; шерсть овечья».

В данном случае экспертиза признала бы заявленное обозначение способным ввести потребителя в заблуждение относительно вида товара и состава сырья в отношении части вышеуказанных товаров 22 класса МКТУ, таких как «шерсть древесная; шерсть овечья».

2. На регистрацию в качестве товарного знака заявлено обозначение, включающее изобразительный элемент в виде стилизованной головы свиньи (изображение обозначения приведено ниже), в отношении товаров 29 класса МКТУ «29 — консервы мясные, а именно говядина тушеная, свинина тушеная, конина тушеная».

В данном случае экспертиза признала бы заявленное обозначение способным ввести потребителя в заблуждение относительно вида товара и состава сырья в отношении части вышеуказанных товаров 29 класса МКТУ, таких как «консервы мясные, а именно говядина тушеная, конина тушеная».

3. На регистрацию в качестве знака обслуживания заявлено комбинированное обозначение (изображение обозначения приведено ниже), содержащее словесный элемент «Частная пивоварня», указывающий на определенный вид и назначение услуг.

Перечень товаров и/или услуг, в отношении которых испрашивается регистрация, включает помимо товаров 32 класса МКТУ «пиво; сусло пивное» следующие услуги:

35 класс — «оценка леса на корню, оценка шерсти»;

36 класс — «обмен денег; оценка произведений искусства; услуги банковские»;

39 класс — «прокат инвалидных кресел; подъем затонувших судов».

В этом случае экспертиза признала бы заявленное обозначение в отношении всех перечисленных выше услуг способным ввести потребителя в заблуждении относительно вида и назначения услуг, т.к. эти услуги не оказываются пивоварнями.

Следует отметить, что заявленные обозначения, содержащие в своем составе натуралистические изображения товаров и (или) натуралистические изображения ингредиентов этих товаров, могут рассматриваться экспертизой как элементы, указывающие на вид товаров и/или услуг и/или состав сырья. Поэтому подобные обозначения по отношению к некоторым заявленным товарам также могут ввести потребителя в заблуждение относительно вида товара, сырья и т.п.

Например, приведенное ниже обозначение, содержащее натуралистическое изображение ананаса, может рассматриваться как способное ввести потребителя в заблуждение в отношении состава сырья, указанного в перечне товара «овощные консервы», т.к. ананас относится не к овощам, а к фруктам.

В то же время обозначение, содержащее натуралистические изображения фруктов — яблока и банана, размещенное на нижеприведенном рисунке, может рассматриваться как фантазийное в отношении товара «краски акварельные».

При включении в состав заявленных обозначений, элементов, символизирующих определенную область деятельности или отрасль хозяйства, экспертизе следует оценить эти элементы с точки зрения их способности порождать в сознании потребителей представление об определенном виде товаров и/или услуг, его свойствах и качестве, не соответствующих действительности.

Например, включение в состав заявленного обозначения общепринятого медицинского символа «чаша со змеей» в отношении таких товаров, как «алкогольные напитки», «кондитерские изделия», будет вводить потребителя в заблуждение относительно свойства и назначения товара.

4.1.2.1. Обозначения, представляющие собой или содержащие элементы, являющиеся ложными 4.1.2.3. Обозначения, представляющие собой или содержащие элементы, способные ввести в заблуждение относительно изготовителя

Что обозначают буквы на коробке автомат и обозначение типов коробок передач

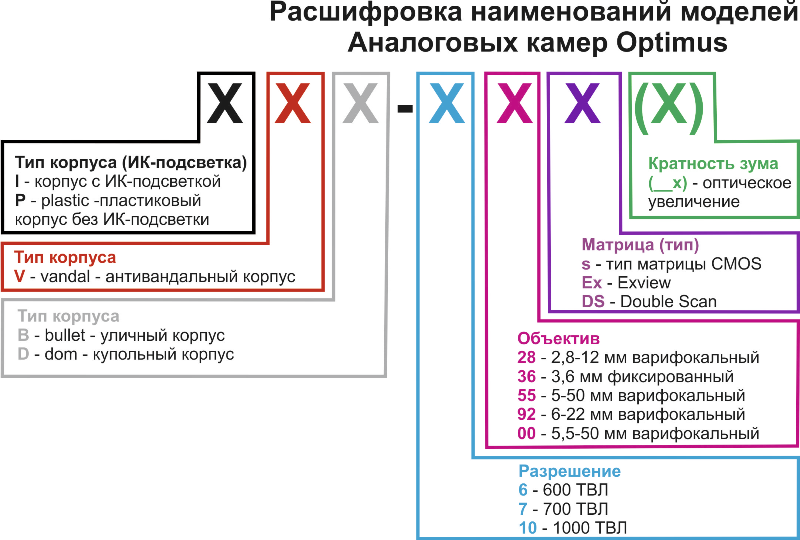
Принцип работы — не единственное, что отличает классическую механическую коробку передач в автомобилях от автоматической. На селекторе последней размещаются буквы и знаки, обозначающие то или иное действие. Они не всегда идентичны на разных моделях АКПП, так как производители используют разные варианты маркировки для различных режимов.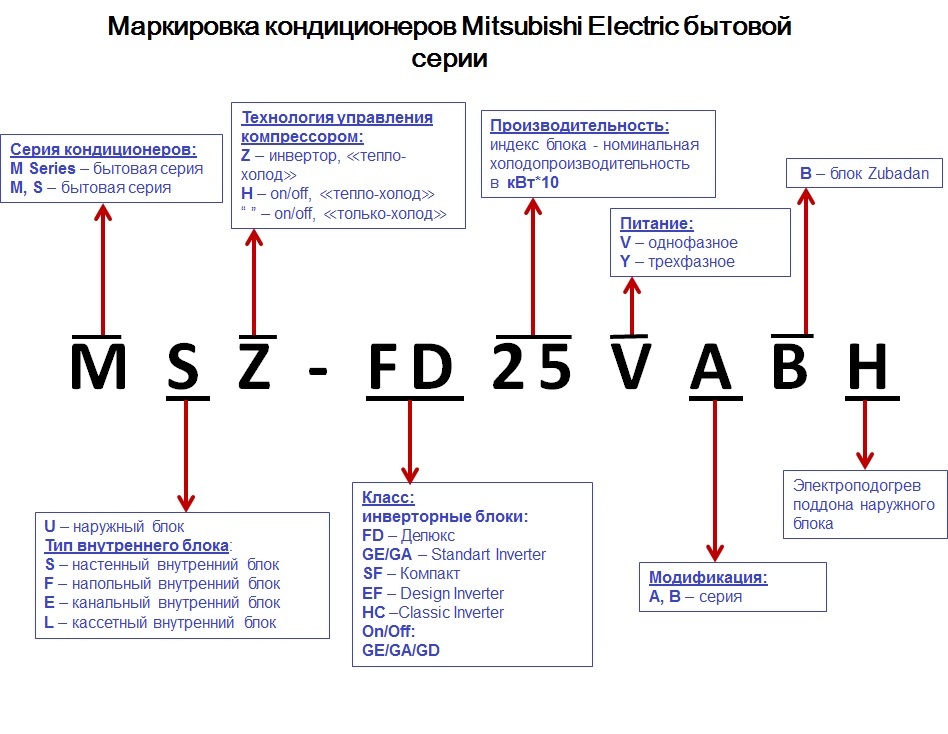

Кроме стандартного набора, в некоторых машинах-автоматах предусматриваются дополнительные функции. Давайте разберемся в обозначениях символов, встречающихся на современных моделях автоматических коробок передач.

Основные обозначения на АКПП

В процессе управления автомобилем водитель постоянно взаимодействует с селектором коробки-автомат. С помощью рычага он переключает режимы, меняя направление, скорость и другие особенности движения авто. Каждое положение элемента соответствует определенной букве, цифре или слову. Они дают понять, как именно коробка передач будет работать после переключения.

Основные режимы коробки-автомат:

• «P». Соответствует слову Parking, переводит коробку в режим парковки. Действие блокирует ведущие колеса машины крюкообразной деталью, которая встает между зубцами шестерни. Чтобы крюк не сломался, активировать режим можно только после полной остановки авто с использованием тормоза. В ином случае коробку придется ремонтировать.
• «R». Обозначение кроется в слове Reverse, которое соответствует заднему ходу. При активации данного режима нужно выжимать тормоз. Если же переход в R осуществляется с D, то между ними нужно соблюсти недолгую паузу в N. Если этого не делать, детали АКПП будут подвержены более быстрому износу.
• «N». Это нейтральная передача — Neutral. Здесь колеса не блокируются, но и усилие на них не передается. Режим наиболее востребован при неисправностях авто, поэтому чаще всего применяется при буксировке или погрузке на эвакуатор.
• «D». Буква взята из английского слова Drive. Режим необходим для движения машины вперед. При включении нужно воспользоваться педалью тормоза. Если осуществляется переход с R, его рациональнее делать, минуя нейтральный N.
• «A». Соответствует автоматическому режиму Automate. Полностью идентичен D, просто в одних моделях указывается одна буква, в других другая.
• «L». На английском звучит как Low, что характеризует пониженную передачу. Необходим при движении на крутом подъеме или спуске, в условиях бездорожья. Чем выше передаточное число коробки передач, тем проще управлять загруженным автомобилем в плохих условиях.

• «B». Звучит на английском как Bottom, соответствует режиму L на автомате. Обычно встречается на гибридах, где торможение осуществляется мотором. Особенно актуален на горных серпантинах и во время спуска с крутых горок. Способствует более быстрому заряду батарей.
• «M». Переводит коробку передач в ручной режим, так как обозначает слово Manual («ручной»). Используя знаки «+» и «-», можно вести машину-автомат как механику, переключая передачи вниз и вверх.
• «S». Произносится, как Sport — включает спортивный режим, при котором повышаются обороты двигателя во время старта и обгона. Как результат, существенно увеличивается нагрузка на трансмиссию, резину, двигатель, сжигается больше топлива. Поэтому злоупотреблять режимом S на автомате не рекомендуется.
• «OD». Соответствует словосочетанию Over Drive. Как и в предыдущем режиме, переключив коробку передач в OD, обороты двигателя повышаются. Это необходимо для резкого ускорения и обгона.
• «W». Многие коробки-автомат предусматривают режим Winter, то есть зимний. Его стоит активировать, чтобы избежать пробуксовки на льду. Благодаря ему, машина трогается с места сразу на второй передаче.
• Кнопка «Hold». Чаще монтируется непосредственно на рычаге КПП, иногда выносится на приборную панель. Соответствует зимнему режиму.
• «E». Обозначение режима Economic заключается в экономии топлива. Переключения коробки передач происходят на малых оборотах, за счет чего езда становится более динамичной. Ездить в таком режиме на постоянной основе не рекомендуется, так как тонкие каналы двигателя не будут прочищаться, и возникнет «масляное голодание». 
• «2». Если переключить рычаг коробки-автомат в этот режим, авто будет двигаться вперед не выше, чем на второй передаче. Если активация происходит из режима D, использовать тормоз необязательно.
• «3». Аналогичен предыдущему режиму, но означает движение не выше, чем на третьей передаче.

Обозначение типов коробок передач

Разные типы коробок-автомат имеют отличные друг от друга названия, которые заключаются в легко узнаваемых аббревиатурах. Зная, что означают буквы, можно понять из мануала к автомобилю, какой КПП он оснащен и на что она способна. В современных машинах встречаются:

• CVT или Continuous Variable Transmission, или попросту «вариатор». Здесь предусмотрена бесступенчатое переключение передач. Коробки работают очень плавно, но степень их надежности несколько ниже обычных автоматов.
• DSG, или Direct Shift Gearbox. Эта КПП роботизирована, и имеет два сцепления. В ее основе лежит механическая КПП, усовершенствованная электромодулем управления и сервоприводами, с помощью которых сменяются передачи.
• AT или автоматическая коробка. Представляет собой классическую гидромеханическую конструкцию. Она очень надежна, так как проверена временем.
• MTA или Manual Transmission Shifted Automatically, или «робот». Название говорит само за себя — такая КПП полностью роботизирована. Педали сцепления в ней нет.

Что означают те или иные буквы можно узнать как у производителя, продавца, так и в открытых источниках в Сети. Не стоит действовать наугад при управлении новым авто. Лучше детально ознакомиться с возможностями имеющейся КПП, чтобы в дальнейшем корректно использовать ее на 100%.

Возможно вам будет интересно:

• Правила проезда кольца

  Пересечение перекрестка с круговым движением вызывает сложности не только у новичков, но и у водителей с большим стажем. Далеко не все знают правила, в соответствии с которыми нужно проезжать «кольцо». Многие действуют интуитивно или повторяют ошибки других, копируя их маневры. Перекрестки такого типа считаются малоопасными, однако количество ДТП на них в последнее время стремительно растет. Как же избежать проблем на дороге?

• Можно ли купить машину без прав

  Согласно действующему законодательству, приобрести и оформить автомобиль может любой человек, в том числе тот, у которого нет водительского удостоверения. Такая ситуация может возникнуть, если машина передается в наследство, транспортное средство используется для инвестиций или попросту возникло желание купить авто для близкого. В данном случае автомобиль рассматривается как имущество, поэтому никаких проблем с его регистрацией возникнуть не может. Однако, нужно учесть важный нюанс — для перемещения авто с места на место понадобится водитель. Рассмотрим детальнее, как оформить машину на человека без действующих прав.

• Как получить права в другом городе

  В соответствии с недавними изменениями в Правилах дорожного движения, теперь можно получить права в другом городе. Раньше это можно было сделать только в подразделении ГИБДД того, населенного пункта, где есть прописка. Сложнее всего приходилось студентам, военнослужащим и тем, кто часто вынужден находиться в командировках. Теперь же есть возможно пройти обучение в одном городе, а получить заветный документ в другом. Важно только учесть нюансы.

• На что обратить внимание при выборе автошколы?

  Сегодня наличие автомобиля – это норма жизни. С ростом количества авто на дорогах, растет и количество новых автошкол. Каждая школа предлагает свою программу обучения, лояльные условия оплаты, различные акции, то есть делают все, что бы заманить к себе клиента. Но как среди такого количества автошкол, сделать верный и безошибочный выбор. Давайте попробуем разобраться вместе. Обучение в любой автошколе состоит из теории, обучении езды на специальном тренажере, обучению езды на автодроме и вождению в городе. Остановимся на каждом из этих этапов.

Исчисление

. Как мне интерпретировать «d» в производной нотации?

Обозначение $dx$ действительно означало разные вещи на протяжении многих лет и означает разные вещи в разных контекстах даже сегодня.

Лейбниц изобрел обозначение $\frac{dy}{dx}$ в 17 веке, по-видимому, потому, что оно согласовывалось с понятием исчисления, в котором «бесконечно малое» изменение $x$ приводило к «бесконечно малому» изменению $y,$ и что между этими двумя «бесконечно малыми» суммами существует четко определенное соотношение. Обозначение предположительно на самом деле было это соотношение.

На какое-то время у математиков возникли проблемы с бесконечно малыми. Робинсон, наконец, понял, как правильно их делать примерно в 1960 году, но тем временем люди использовали исчисление в течение сотен лет и придумали эпсилон-дельта определение для производных. При таком определении $\frac{dy}{dx}$ было (в лучшем случае) оператором дифференцирования $\frac{d}{dx}$, примененным к функции $y$, а часть $dx$ сама по себе не имела смысла.

Люди часто используют обозначение $dx$ как часть интеграла, $\int f(x)\,dx,$, где это помогает нам отслеживать переменную интегрирования. Но в других местах пишут $\int f$, что означает то же самое.

Символ $dx$ также встречается в дифференциальных формах, где он действует как базисный вектор. В этом контексте это действительно математический объект, имеющий значение, стоящее само по себе вне какой-либо другой математической формулы.

Таким образом, значение этого символа (и даже означает ли он что-либо самостоятельное) зависит от

• того, кто его пишет и
• , где они это пишут. 2$ и, следовательно, $du = 2x\,dx$ для U-подстановки в интеграле.

  Нотация обладает замечательной мнемонической силой. Хотя технически неправильно сокращать $dx$ в «знаменателе» с $dx$ в «числителе», на практике это работает очень хорошо, по крайней мере, в исчислении функций с одной переменной. Подумайте, когда не следует рассматривать dy/dx как дробь в исчислении с одной переменной? и его ответы.

  Поскольку вы сталкиваетесь с этим в прикладной математике, где часто вы узнаете, как решать задачи, не понимая, почему решения гарантированно верны, я бы рассматривал $dx$ и $dy$ как формальные обозначения, знаки отсортируйте это (если вы будете отслеживать их в соответствии с правилами, которые вам показали) позволит получить ваши результаты, чтобы выйти правильно. Я не думаю, что будет очень полезно пытаться создавать математические объекты, которые $dx$ и $dy$ могут представлять, когда эти символы стоят сами по себе. 9x y \,dx$ — это просто сокращенный способ записи левой части этого уравнения. Я считаю сокращенную запись немного нестандартной и, возможно, даже назовем это «злоупотреблением обозначениями» — то, что удобно писать но на самом деле не является строго правильным обозначением. (Но я готов быть поправленным в этом пункте: может быть, если у вас есть правильное определение дифференциалов $dx$ и $dy$ и интегрирования по подынтегральному выражению, в котором эти дифференциалы появляются, сокращенная запись столь же верна и правильно, как обычное обозначение функции одной переменной.)

  В любом случае, в конце мы имеем лишь несколько обычных интегралов от функций одной переменной (если правильно определить функции). Я думаю, вы можете решить эту проблему, применив интегрирование по частям несколько раз; если я прав, есть трюк с отменой, позволяющий вам оставить один из интегралов как есть. (На самом деле вам никогда не придется его вычислять.)

  исчисление — d/dx Обозначение Объяснение, пожалуйста?

  спросил 9 лет, 1 месяц назад

  Изменено 6 месяцев назад

  Просмотрено 8к раз

  $\begingroup$

  Я умею выводить, умею интегрировать. Я знаю, что делать, когда вижу $\frac{d}{dx}$ и тому подобное, но что это на самом деле означает? Я знаю, что это означает что-то вроде получения в терминах $x$, но в чем разница между $\frac{dy}{dx}$ и $\frac{d}{dx}$?

  Если бы кто-нибудь мог дать мне объяснение с точки зрения непрофессионала, это было бы очень полезно, так как это всегда ставило меня в тупик.

  В общем, что означает этот $d$?

  • исчисление

  $\endgroup$

  3

  $\begingroup$

  Если у вас есть функция $f$ с независимой переменной $x$, то $$ \frac{d}{dx} f(x) $$ означает производную от $f$ по $x$. Мы также иногда пишем это как $f'(x)$. Теперь, если у вас есть такая функция, как $$ f (х) = ах, $$ тогда производная $$ f'(x) = а. $$ Это понятно, потому что при написании $f(x)$ мы указали, что функция $f$ является функцией переменной $x$. Если бы я вместо этого сказал вам, что $$ у = топор $$ и я просто попросил вас найти производную, что бы вы сделали? Вероятно, вы снова просто скажете, что производная равна $a$. Но в этой ситуации на самом деле непонятно, что является переменной, а что константой. И поэтому мы можем написать $$ \frac{dy}{dx} \quad\text{or}\quad \frac{d}{dx}y $$ чтобы указать, что мы рассматриваем $y$ как функцию переменной $x$, и мы рассматриваем $a$ как константу (в случае функций с несколькими переменными мы действительно должны рассматривать частные производные в этом случае). Теперь вы также можете написать $$ \ гидроразрыв {dy} {da} $$ и в этом случае вы говорите, что $a$ является переменной. Таким образом, нотация $\frac{d}{dx}$ очень полезна, когда у вас есть выражения, в которых есть несколько букв.

  Так что же такое $\frac{d}{dx}$? Вы можете рассматривать это как оператор , который принимает в качестве «входа» (дифференцируемую) функцию и «выводит» функцию.

  $\endgroup$

  1

  $\begingroup$

  $\dfrac{dy}{dx} = \dfrac{d(y)}{dx} = \dfrac{d}{dx}(y)$. 2y’$ часто используется в дифференциальных уравнениях как сокращение для замены более длинного выражения $\dfrac{dy}{dx}$.

  $\endgroup$

  $\begingroup$

  $\dfrac{d}{dx}$ — это то, что аналитики назвали бы оператором, что означает, что вы даете ему элемент определенного векторного пространства, а он дает вам другой элемент в этом векторном пространстве. Так что же такое векторное пространство? Ну, векторное пространство — это любая коллекция объектов, которые удовлетворяют определенным аксиомам (например, вы можете сложить два из этих объектов вместе, чтобы получить еще один объект в коллекции, вы можете умножить объект на число, чтобы получить другой объект в коллекции, каждый объект имеет отрицательное значение и т. д.). Векторные пространства в некотором роде являются обобщением действительных чисел.

  Не говоря уже об этом, как это связано с $\dfrac{d}{dx}$? Ну, вы можете посмотреть на $\dfrac{d}{dx}f$ для некоторой функции $f$.