Обобщенный закон Ома.

Закон Ома выражаемый формулой, определяет зависимость между током и напряжением на пассивном участке электрической цепи.

Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).

Из формулы 15 следует:

_a-_b=I(R₁+R₂)- E₁+E₂ (16)

На положительное напряжение на участке a – b Uab=_a-_b

Следовательно, Uab= I(R₁+R₂)- E₁+E₂ (17)

(18)

Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.

Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».

Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.

Пример № 1 построения потенциальной диаграммы:

Построить потенциальную диаграмму для одноконтурной схемы:

E₁=25В; E₂=5В; E₃=20В; E₄=35В,

R₁=8 Ом; R₂=24 Ом; R₃=40 Ом; R₄=4 Ом,

r₁=2 Ом; r₂=6 Ом; r₃=2 Ом; r₄=4 Ом.

Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r

1— r₄) за их пределы; обозначим точки контура.

Рис.2

2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:

3. За базисную точку примем точку a. Найдем потенциалы остальных точек:

_b= _a– IR_{1 =} — 4В _e= _d– IR_{2 =} 8В

_c= _b– Ir_{1 =} — 5В _f= _e+ E_{2 =} 13В

_d= _c+ E_{1 =} 20В _q= _f– Ir_{2 =} 10В

_k= _q– IR_{3 =} — 10В _n= _m– IR_{4 =} — 33В

_e = _k – E_{3 =} — 30В _o = _n – Ir_{4 =} — 35В

_m = _e

– Ir_{3 =} — 31В _a = _o + E_{4 =} 0

4. В системе координат строим потенциальную диаграмму:

Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.

Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.

Первый закон Кирхгофа:

Алгебраическая сумма токов в узле равна нулю:

_i = 0 (19)

Где i — число ветвей, сходящихся в данном узле.

Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.

Рис.17. Иллюстрация к первому закону Кирхгофа.

Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:

Nуp = Nу – 1,

Где Nу – число узлов в рассматриваемой цепи.

Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.

Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».

Тогда уравнение по первому закону Кирхгофа запишется так:

I₁ – I₂ + I₃ – I₄ = 0.

Уравнения, составленные по первому закону Кирхгофа, называются узловыми.

Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.

Второй закон Кирхгофа:

Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:

 Ui =  Ei

 IiRi=Ei(20)

Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.

**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:

Nуp = Nb – Nу + 1 – Nэ.д.с.

Где Nb – число ветвей электрической цепи;

Nу — число узлов;

Nэ.д.с. — число идеальных источников э.д.с.

Рис.18. Иллюстрация ко второму закону Кирхгофа.

Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:

1. произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).

2. э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».

Например, для контура рис.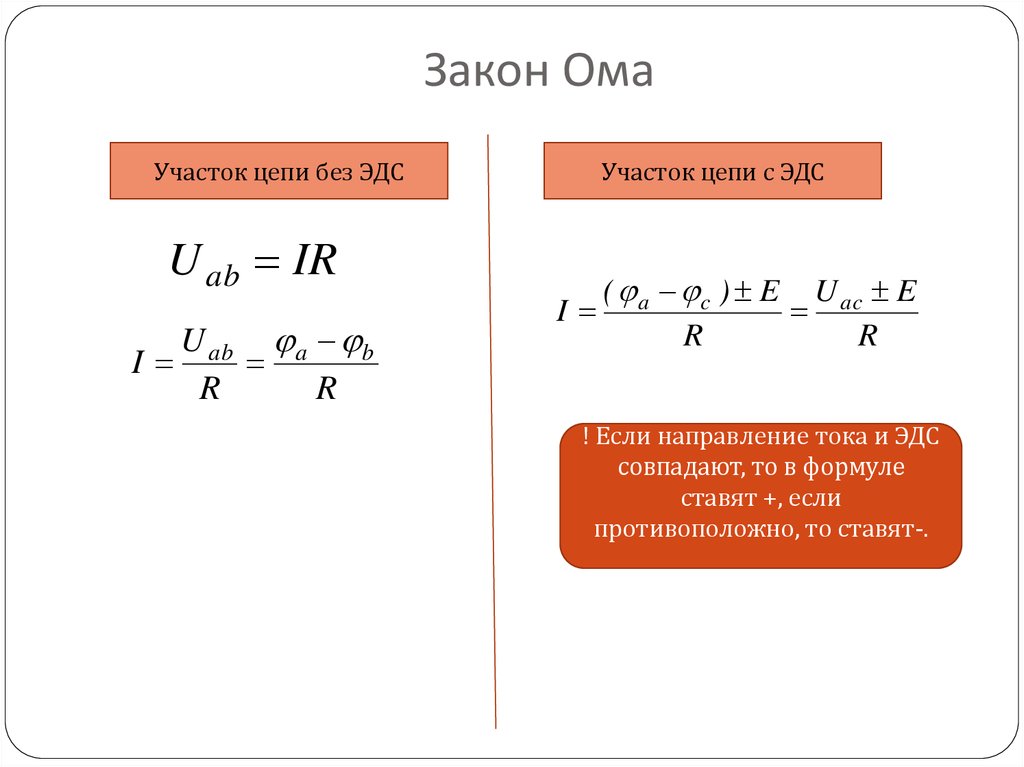 18, второй закон Кирхгофа запишется следующим образом:

U₁ – U₂ + U₃ = E₁ – E₃ – E₄ (21)

Уравнение (20) можно переписать в виде:

 (Ui – Ei) = 0 (22)

Где (U – E) – напряжение на ветви.

Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:

Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.

Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.

Задача №1.

В схеме рис.1 заданы токи I₁ и I₃, сопротивления и э.д.с. Определить токи I₄, I₅, I₆ ; напряжение между точками a и b, если I₁ = 10мA, I₃ = -20 мA, R₄ = 5kОм, E₅ = 20B, R₅ = 3kОм, E₆ = 40B, R₆ = 2kОм.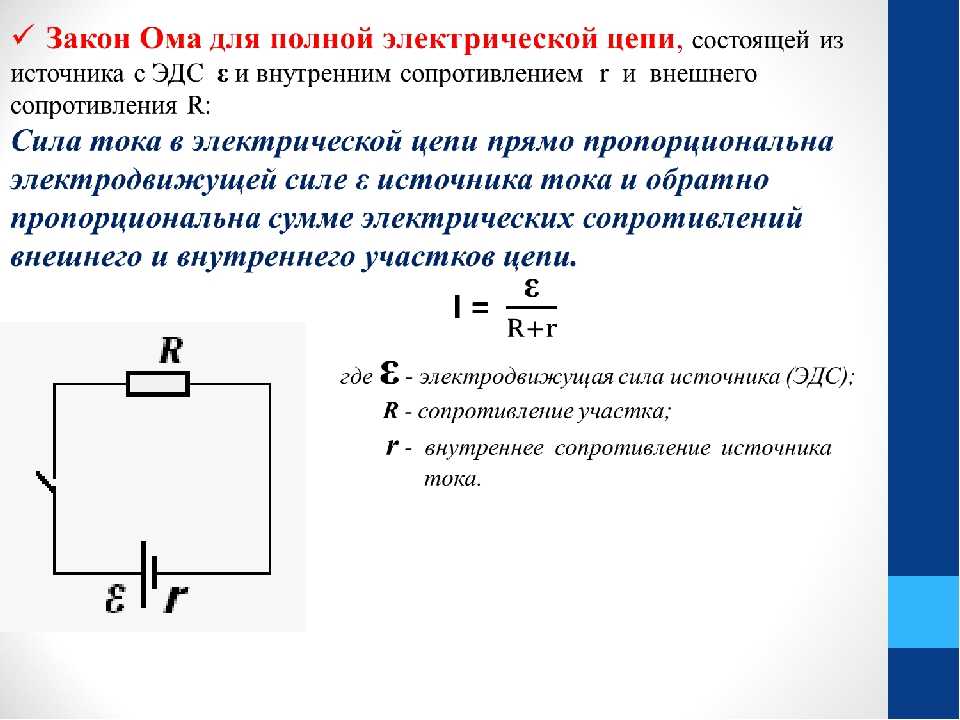

.

Рис.1

Решение:

1. Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.

В результате решения получаем: I₆ = 0; I₄ = 10мA; I₅ = -10мA

2. зададим направление напряжения между точками a и b от точки «a» к точке «b» — U_ab. Это напряжение найдем из уравнения по второму закону Кирхгофа:

I₄R₄ + U_ab

+ I₆R₆ = 0

U_ab = — 50B.

Задача №2.

Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.

Дано: I₁ = 20мA; I₂ = 10мA

R₁ = 5kОм, R₃ = 4kОм, R₄ = 6kОм, R₅ = 2kОм, R₆ = 4kОм.

Рис.2

Решение:

Число узловых уравнений – 3, число контурных уравнений – 1.

Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.

В данной цепи известны токи ветвей I₁ и I₂. Неизвестные токи I₃, I₄, I₅, I₆.

Решая систему, получаем: I₃ = 13,75 мA; I₄ = -3,75мA; I₅ = 6,25мA; I₆ = 16,25мA.

Закон Ома для участка цепи. (Лекция 11)

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1.

Лекция 11. Закон Ома11.1
. Закон Ома для неоднородного участка це
пи.
11.2
. Закон Ома в дифференциальной форме.
11.3
. Работа и мощность. Закон Джоуля–Ленца.
11.4. КПД источника тока.
11.5. Закон Кирхгофа.
900igr.net

2. 11.1. Закон Ома для неоднородного участка цепи

Один из основных законов
электродинамики был открыт в
1822 г. немецким учителем физики
Георгом Омом.
• Он установил, что сила тока в
проводнике пропорциональна
разности потенциалов:
φ1 φ 2
I
R
• Георг Симон Ом (1787 – 1854) –
немецкий физик.
• В 1826 г. Ом открыл свой основной
закон электрической цепи. Этот закон
не сразу нашел признание в науке, а
лишь после того, как Э. X. Ленц,
Б. С. Якоби, К. Гаусс, Г. Кирхгоф и
другие ученые положили его в основу
своих исследований.
• Именем Ома была названа единица
электрического сопротивления (Ом).
• Ом вел также исследования в области
акустики, оптики и кристаллооптики.
• Рассмотрим неоднородный участок
цепи, участок, содержащий источник ЭДС
(т.е. участок, где действуют неэлектрические
силы).
E
• Напряженность
поля в любой точке
цепи равна векторной сумме поля
кулоновских сил и поля сторонних сил:
E E q E ст .
• Величина, численно равная работе по
переносу единичного положительного
заряда суммарным полем кулоновских
и сторонних сил на участке цепи (1 –
2), называется напряжением на этом
участке U12
2
2
U12
E q d l E ст d l
1
1
• т.к.
E q d l dφ
2
E qd l φ1 φ 2
, или
, тогда
1
U 12 (φ1 φ 2 ) E12 .
(11.1.2)
• Напряжение на концах участка цепи
совпадает с разностью потенциалов
только в случае, если на этом участке нет
ЭДС, т.е. на однородном участке цепи.
• Запишем обобщенный закон Ома для
участка цепи содержащей источник ЭДС:
(11.1.3)
IR12 (φ1 φ 2 ) E12 .
• Обобщенный закон Ома выражает
закон сохранения энергии
применительно к участку цепи
постоянного тока.
• Он в равной мере справедлив как
для пассивных участков (не
содержащих ЭДС), так и для
активных.
• В электротехнике часто используют
термин падение напряжения –
изменение напряжения вследствие
переноса заряда через сопротивление
U IR.
• В замкнутой цепи: φ1 φ 2
;
E
I
,
IR
E
или
Σ
RΣ
где RΣ R r; r – внутреннее сопротивление
активного участка цепи
• Тогда закон Ома для замкнутого участка
цепи, содержащего источник ЭДС запишется
в виде
E
I
.
R r
(11.1.1)
•Закон Ома для замкнутого участка
цепи, содержащего источник ЭДС
E
I
.
R r

12. 11.2. Закон Ома в дифференциальной форме

• Закон Ома в интегральной форме для
однородного участка цепи (не
содержащего ЭДС)
U
(11.2.1)
I
R
• Для однородного линейного проводника
выразим R через ρ:
(11.2.2)
l
R ρ
S
• ρ – удельное объемное сопротивление; [ρ] =
[Ом·м].
jи Eв бесконечно
• Найдем связь между
малом объеме проводника – закон Ома в
дифференциальной форме.
• В изотропном проводнике (в данном случае с
постоянным сопротивлением) носители
зарядов движутся в направлении действия
силы, т.е. вектор плотности тока j и вектор
напряженности
поля коллинеарны
E
• Исходя из закона Ома (11.2.1), имеем:
U Edl EdS
I
R ρ dl
ρ
dS
• А мы знаем, что j dI 1 E . Отсюда
dS ρ
• можно записать
(11.2.3)
j σE
• это запись закона Ома в
дифференциальной форме.
• Здесь
– удельная
σ 1/ ρ
электропроводность.
• Плотность тока можно выразить через
заряд электрона е, количество
зарядов
n
и дрейфовую скорость υ :
j enυ
• Обозначим
υ
b
E
, тогда
j enbE
υ bE
(11.2.4)
;
• Теперь, если удельную
электропроводность σ выразить через
е, n и b:
σ enb,
то вновь получим выражение закона
Ома в дифференциальной форме:
j σE

18.

11.3. Работа и мощность тока. Закон Джоуля – Ленца• Рассмотрим произвольный участок цепи, к
концам которого приложено напряжение U.
За время dt через каждое сечение
проводника проходит заряд
dq Idt.
• При этом силы электрического поля,
действующего на данном участке,
совершают работу: dA Udq UIdt.
• Общая работа:
A IUt
• Разделив работу на время, получим выражение
для мощности:
dA
(11.3.1)
N
dt
UI .
• Полезно вспомнить и другие формулы для
мощности и работы:
2
N RI ;
(11.3.2)
(11.3.3)
2
A RI t.
• В 1841 г. манчестерский пивовар Джеймс Джоуль и
в 1843 г. петербургский академик Эмилий Ленц
установили закон теплового действия
электрического тока.
• Джоуль Джеймс Пресскотт (1818 – 1889) –
английский физик, один из первооткрывателей
закона сохранения энергии. Первые уроки по
физике ему давал Дж. Дальтон, под влиянием
которого Джоуль начал свои эксперименты.
Работы посвящены электромагнетизму,
кинетической теории газов.
• Ленц Эмилий Христианович (1804 – 1865) –
русский физик. Основные работы в области
электромагнетизма. В 1833 г. установил
правило определения электродвижущей силы
индукции (закон Ленца), а в 1842 г.
(независимо от Дж. Джоуля) – закон теплового
действия электрического тока (закон ДжоуляЛенца). Открыл обратимость электрических
машин. Изучал зависимость сопротивление
металлов от температуры. Работы относятся
также к геофизике.
• При протекании тока, в проводнике
выделяется количество теплоты:
(11.3.4)
2
Q RI t.
• Если ток изменяется со временем:
2
Q RI dt
2
1 – Ленца в
• Это закон Джоуля
интегральной форме.
• Отсюда видно, что нагревание происходит
за счет работы, совершаемой силами
поля над зарядом.
• Соотношение (11.3.4) имеет интегральный
характер и относится ко всему проводнику с
сопротивлением R, по которому течет ток I.
• Получим закон Джоуля-Ленца в локальной дифференциальной форме, характеризуя
тепловыделение в произвольной точке.
• Тепловая мощность тока в элементе
проводника Δl, сечением ΔS, объемом
ΔV Δl ΔS равна:
2
ΔW I R IΔφ jΔSEΔl j EΔV
Удельная мощность тока
ΔW
ω
jE
ΔV
Согласно закону
Ома в дифференциальной
форме j σE
, получим
закон Джоуля — Ленца в дифференциальной
форме, характеризующий плотность
выделенной энергии.
ω σE
Так как выделенная теплота равна работе сил
электрического поля
A IUt
то мы можем записать для мощности тока:
(11.3.2)
2
W UI RI
• Мощность, выделенная в единице
объема проводника .
ω ρj
2
• Приведенные формулы справедливы
для однородного участка цепи и для
неоднородного.
11.4. КПД источника тока
•Рассмотрим элементарную электрическую
цепь, содержащую источник ЭДС с
внутренним сопротивлением r, и внешним
сопротивлением R
• КПД всегда определяем как отношение
полезной работы к затраченной:
Aп N п UI U
η
.
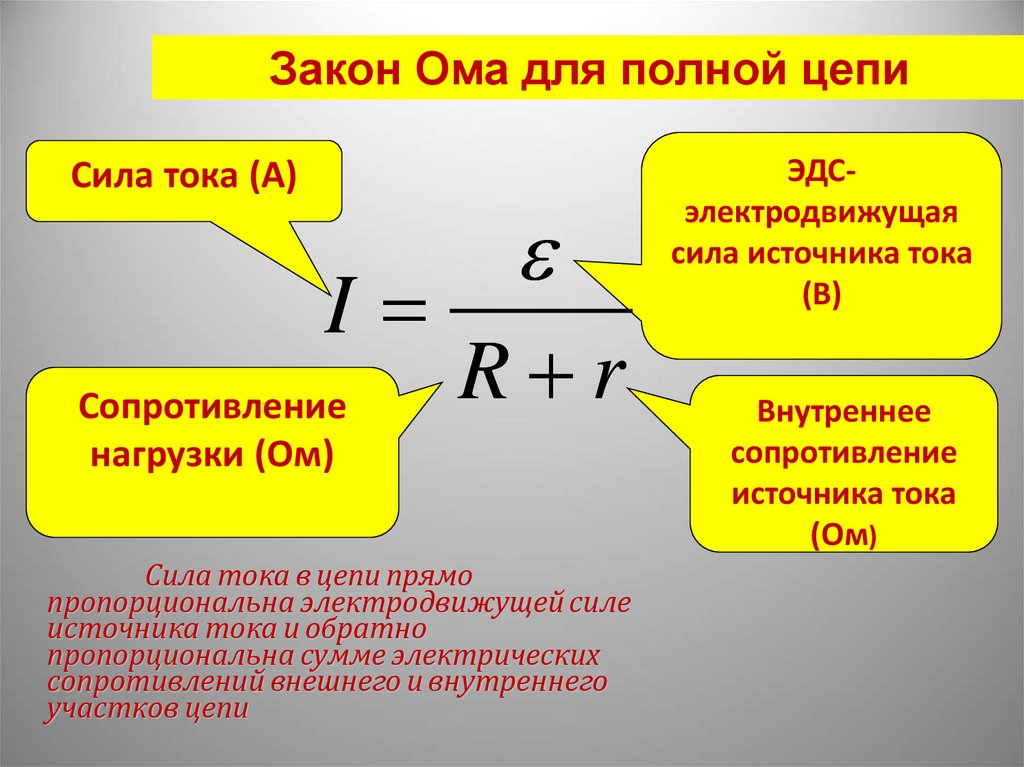
Aз N з E I E
(11.4.1)
• Полезная работа – мощность, выделяемая
на внешнем сопротивлении R в единицу
времени.
• По закону Ома имеем:
U IR,
E (R r)I ,
тогда
U
IR
R
η
E I (R r) R r
• Таким образом, имеем, что при
R ,
η 1, но при этом ток в цепи мал и
полезная мощность мала.
• Вот парадокс – мы всегда стремимся к
повышенному КПД, а в данном случае нам
это не приносит пользы.
• Найдем условия, при которых полезная
мощность будет максимальна.
• Для этого нужно, чтобы
dN п
0.
dR
E
Nп I R
R r
2
2
R
2
E R
r R
2
dN п E R r 2 r R E R
0
4
dR
R r
2
E
2
2
2
R r 2R 0
Это возможно при R = r
• В выражении (11.4.2) , E 0 , R r 0
следовательно, должно быть равно нулю
выражение в квадратных скобках, т.е. r = R.
• При этом условии выделяемая мощность
максимальна, а КПД равен 50%.

32.

11.5. Правила Кирхгофа для разветвленных цепей • Расчет разветвленных цепей с
помощью закона Ома довольно сложен.
• Эта задача решается более просто с
помощью двух правил немецкого
физика Г. Кирхгофа (1424 – 1443).
• Первое правило Кирхгофа
утверждает, что алгебраическая
сумма токов, сходящихся в любом узле
цепи равна нулю:
u
11.5.1)
I 0.
r 1
k
(узел – любой участок
цепи, где сходятся более
двух проводников)
• В случае установившегося постоянного тока
в цепи ни в одной точке проводника, ни на
одном из его участков не должны
накапливаться электрические заряды
Токи, сходящиеся к
узлу, считаются
положительными:
I1 I 2 I 3 0.
• Второе правило Кирхгофа
(обобщение закона Ома для
разветвленной цепи).
φ 2 φ 3 E1 I1 R1 ;
φ 3 φ1 E2 I 2 R2 ;
φ1 φ 2 E3 I 3 R3 .
Складывая получим:
I k Rk E k .
k
k
• В любом замкнутом контуре
электрической цепи алгебраическая
сумма произведения тока на
сопротивление равна алгебраической
сумме ЭДС, действующих в этом же
контуре.
I k Rk E k .
k
k
• Обход контуров осуществляется по
часовой стрелке, если направление обхода
совпадает с направлением тока, то ток
берется со знаком «плюс».
ВОТ И ЛЕКЦИИ КОНЕЦ,
А КТО СЛУШАЛ
–
МОЛОДЕЦ!!!

English     Русский Правила

14.10: Обобщенный импеданс — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5845

• Джереми Татум
• Университет Виктории

В главе 13 мы рассмотрели синусоидально изменяющееся напряжение, приложенное к последовательно соединенным индуктивности, сопротивлению и емкости. Уравнение, определяющее связь между напряжением и током, имеет вид

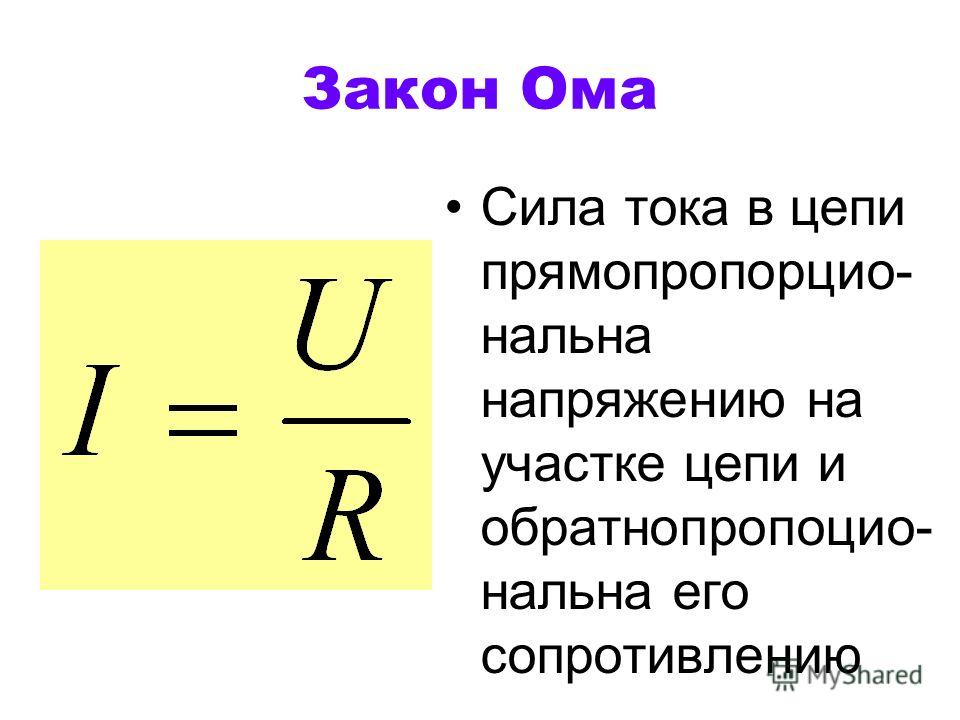. 2\), а оператор \(d/dt\), или «точка», эквивалентен умножению на \(j\omega\). Таким образом, уравнение \ref{14.10.2} эквивалентно 92I+ jRC\omega I + I.\label{14.10.3}\]

То есть \[V=[R+jL\omega + 1/jC\omega]I.\label{14.10.4}\]

Комплексное выражение в скобках — это уже знакомое импеданс Z , и мы можем записать

\[V=ИЗ.\метка{14.10.5}\]

Но что, если \(V\) не меняется по синусоиде ? Предположим, что \(V\) изменяется каким-то другим образом, может быть, даже не периодически? Это может включать, как один из возможных примеров, ситуацию, когда \(V\) постоянна и вообще не меняется со временем. Но независимо от того, \(V\) меняется со временем, уравнение \ref{14.10.2} остается в силе, за исключением того, что, если изменение во времени не является синусоидальным, мы не можем заменить \(j\omega\) на \(d/dt\). Мы столкнулись с необходимостью решить дифференциальное уравнение \ref{14.10.2}.

Но мы только что изучили новый изящный способ решения дифференциальных уравнений этого типа. Мы можем использовать преобразование Лапласа для каждой части уравнения. Таким образом,

\[C\bar{\dot V} = LC \bar{\ddot I} + RC \bar{\dot I} + \bar{I}.\label{14.10.6}\] 92\bar{I} — sI_0 — \dot I_0) + RC(s\bar{I} — I_0) + \bar{I}.\label{14.10.7}\]

Предположим, что в \(t=0\) \(V_0\) и \(I_0\) равны нулю, т.е. до \(t=0\) переключатель был разомкнут, и мы замыкаем переключиться на \(t=0\). Кроме того, поскольку цепь содержит индуктивность, ток не может измениться мгновенно, а поскольку она содержит емкость, напряжение не может измениться мгновенно, поэтому уравнение принимает вид

.

\[\bar{V} = (R+Ls+1/Cs)\bar{I}.\label{14.10.8}\]

Это так независимо от формы изменения \(V\): оно может быть синусоидальным, оно может быть постоянным, а может быть иным. Это обобщенный закон Ома . Обобщенный импеданс цепи равен \(R+Ls+\frac{1}{Cs}\). Напомним, что при комплексной обработке установившегося синусоидального напряжения комплексный импеданс был равен \(R+jL\omega+\frac{1}{jCw}\).

Чтобы узнать, как изменяется ток, все, что нам нужно сделать, это выполнить обратное преобразование Лапласа

\[\bar{I}=\frac{\bar{V}}{R+Ls+1/(Cs)}.\label{14.10.9}\]

В следующих разделах мы рассмотрим несколько примеров.

---

Эта страница под названием 14.10: Generalized Impedance распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джереми Татум

   Лицензия

   CC BY-NC

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. импеданс
   2. источник@http://orca. phys.uvic.ca/~tatum/elmag.html

Общее определение закона Ома

спросил 5 лет, 3 месяца назад

Изменено 5 лет, 3 месяца назад

Просмотрено 2к раз

\$\начало группы\$

В последнее время возникли разногласия по поводу того, следует ли диод закону Ома или нет: Действительно ли диод следует закону Ома?

В частности, такие вещи, как

Однако правда в том, что сопротивление диода меняется в зависимости от приложенного тока и/или напряжения.

и

В законе Ома конкретно указано, что R остается постоянным. Если вы попытаетесь рассчитать R из V/I, глядя на кривую IV диодов, вы увидите, что по мере увеличения напряжения «R» будет меняться.

также исторически: Почему светодиоды не подчиняются закону Ома?

[светодиоды] действуют [по закону Ома] — просто у них нет «фиксированного» сопротивления

Кажется, что основное разногласие сводится к тому, что на самом деле представляет собой определение «Закона Ома». Поскольку я не смог найти здесь вопрос, посвященный этому, я решил задать его.

Ниже приведены четыре определения закона Ома, взятые из различных вводных источников по материалу. Я не смог найти ничего в более продвинутых текстах, вероятно, потому, что они настолько просты, что их не стоит включать. Поэтому мой вопрос: что из этого правильно, если есть. Если нет, то каково правильное определение общего случая «закона Ома»?

Закон Ома гласит, что напряжение v на резисторе прямо пропорционально току i, протекающему через резистор. Ом определил константу пропорциональности резистора как сопротивление R. (Сопротивление — это свойство материала, которое может изменяться при изменении внутренних или внешних условий элемента, например, при изменении температуры. )

Чарльз К. Александр «Основы электрических цепей», 4-е изд.

Закон Ома утверждает, что ток, проходящий через устройство, всегда прямо пропорционален разности потенциалов, приложенной к устройству. (Это утверждение верно только в определенных ситуациях, однако по историческим причинам употребляется термин «закон».) Устройство […], которое оказывается резистором на 1000 Ом, — подчиняется закону Ома. Устройство […], которое называется диодом с p-n переходом — не

Холлидей и Резник «Расширенные основы физики», 10-е изд.

Закон Ома гласит, что ток в проводнике между двумя точками прямо пропорционален напряжению в этих двух точках. Вводя константу пропорциональности, сопротивление,

Википедия

Хорошо известное соотношение, описывающее соотношение между напряжением и током через сопротивление устройства, выраженное математически как V=IR. Эта формула говорит, что напряжение на устройстве равно току через устройство, умноженному на сопротивление.

electronics.stackexchange.com описание тега закона Ома

• закон ома

\$\конечная группа\$

5

\$\начало группы\$

Несмотря на все переводы и неверные толкования, существует только одно определение теории Ома, оригинал, написанный самим великим человеком.

В нем есть ответы на нелинейные части, которые явно включены и рассматриваются в отдельном специальном приложении.

См. мой дополненный ответ здесь, который включает ссылки на статью Ома.

Дело в том, что Ом просто сформулировал, как только он установится в стабильное состояние , напряжение в цепи равно сумме тока, умноженной на сопротивления частей.

^{смоделируйте эту схему – Схема создана с помощью CircuitLab}

\$E = I.R1 + I.R2 + I.R3\$

Приведенная выше формула верна независимо от того, является ли R3 диодом или нет.

Далее говорится, что если сопротивление какой-либо части нелинейно и зависит от стимула, необходимо подождать, пока цепь не сбалансируется, чтобы вышеуказанное продолжало оставаться верным.

Проблема в том, что люди, как правило, читают о «Законе Ома» больше, чем есть на самом деле, или не понимают его достаточно полно, или, что еще хуже, распространяют упрощенную версию, не передавая квалификации, что это подмножество работы Ома. Но, я думаю, это то, что происходит, когда вы пытаетесь сжать буклет на 280 страниц в один абзац.

В частности, упомянутое в статье понятие о том, что изменение I изменит E линейно, часто не цитируется. В документе конкретно указано, что конкретная экстраполяция Закона верна только для линейных частей, любое изменение возбуждения требует перебалансировки цепи с различными значениями R.

Таким образом, полезность закона Ома в цепи с нелинейными компонентами сильно ограничена.

\$\конечная группа\$

15

\$\начало группы\$

1) диоды являются нелинейными устройствами, что означает, что если вы удвоите напряжение, ток удвоится , а не .

Закон Ома применяется только к линейным устройствам (сопротивлениям), поэтому он не может относиться к поведению диода.

2) Все четыре верны. Почему вы считаете, что что-то из этого неверно? Все они описывают:

\$V = I * R \$

Где

\$V\$ = напряжение

\$I\$ = ток

\$R\$ = номинал резистора, имеющего это напряжение \$V\$ на его клеммах и ток \$I\$, протекающий через него.

Это закон Ома, и все четыре утверждения описывают его.

\$\конечная группа\$

9

\$\начало группы\$

Поэтому мой вопрос: какой из них правильный, если есть. Если нет, то каково правильное определение общего случая «закона Ома»?

Я посмотрю на вопрос немного по-другому.

Кривая IV устройства – кривая зависимости тока от напряжения – представляет собой график зависимости тока, протекающего через устройство, от напряжения на нем.

Рис. 1. ВАХ для различных резисторов. Линии можно продлить через 0, 0, чтобы показать взаимосвязь при отрицательных напряжениях и токах.

Как показано на рисунке, наклон ВАХ для резистора является постоянным при условии, что влияние температуры и т. д. не является значительным.

Рис. 2. Типичные ВАХ для различных цветов светодиодов.

Светодиоды и диоды вообще имеют нелинейную зависимость между током и напряжением. Однако они сопротивляются потоку тока и, следовательно, имеют сопротивление. Просто он меняется в зависимости от тока (или напряжения). например, красный светодиод на рисунке 2 пропускает 40 мА при 2,0 В. Его сопротивление в этих условиях составляет \$ R = \frac {V}{I} = \frac {2}{40m} = 50 \\Omega \$. При 100 мА сопротивление будет \$ R = \frac {V}{I} = \frac {2,5}{100м} = 25 \\Omega \$.

---

Мой ответ на ваш вопрос заключается в том, что все определения говорят об одном и том же немного по-разному.

1. «Закон Ома гласит, что напряжение v на резисторе прямо пропорционально току i, протекающему через резистор.» [Так \$V\propto I\$.]
2. «Закон Ома — это утверждение, что ток через устройство всегда прямо пропорционален разности потенциалов, приложенной к устройству». [Так что \$ I \propto V \$. Это то же самое, что и 1, просто поменяно местами слева направо.]
3. «Закон Ома гласит, что ток в проводнике между двумя точками прямо пропорционален напряжению в двух точках». [Итак, снова \$ I \propto V \$. Это точно так же, как 2.]
4. «Напряжение и ток через сопротивление устройства, выраженные математически как V = IR». [Это то же самое, что и 1, но с константой R, исключающей ‘\$ \propto \$’.]

Источник: LEDnique.

\$\конечная группа\$

\$\начало группы\$

Сопротивление устройства определяется как отношение напряжения к току.

Закон Ома предназначен для применения только в том случае, если это соотношение остается достаточно постоянным.

Иногда это так, как для типичного коммерческого резистора, и для него стоит указать цифру. Например, типичный дешевый резистор 10k может продаваться с допуском 1% и температурой 200 ppm, что означает, что его сопротивление при 25C находится в пределах 1% от 10k, и оно не будет изменяться более чем на 0,2% при изменении температуры на каждые 10 градусов.

Иногда сопротивление менее постоянно, как у лампы накаливания с вольфрамовой нитью, которая изменяет сопротивление в 10 раз между холодным и горячим.

Иногда устройство настолько нелинейно, что нецелесообразно указывать какое-либо значение сопротивления, например диод, ток которого может измениться в 1 миллион раз при изменении напряжения с 0,6 В до 0,7 В.

Иногда для диодов мы все еще можем указать сопротивление наклона, которое является отношением изменения напряжения для изменить тока, измеренного вокруг некоторого заданного тока.

Все диоды изготовлены из резистивных материалов, что означает, что при больших токах остаточное сопротивление материала будет преобладать в крутизне сопротивления.

\$\конечная группа\$

\$\начало группы\$

Если вы приложите постоянное напряжение (В) к устройству и измерите результирующий постоянный ток (I) через него, тогда сопротивление устройства в этой конкретной рабочей точке будет равно R=V/I. Но это НЕ закон Ома. Закон Ома требует, чтобы рассматриваемое устройство обеспечивало постоянное отношение V/I в заданном рабочем диапазоне. Таким образом, если график V/I не является линией, закон Ома не может быть применен.

\$\конечная группа\$

3

\$\начало группы\$

Хотя закон Ома предполагает фиксированное значение R для ряда условий, я покажу вам, что его также можно использовать для любой электронной аналоговой части, включая нелинейные, но только если вы понимаете ограничения, при которых существует линейное значение импеданса.

Я неоднократно писал о линейном объемном сопротивлении диодов или ESR как о важной переменной процесса во ВСЕХ диодах и биполярных транзисторах. ВЫ МОЖЕТЕ ПРИМЕНИТЬ ЗАКОН ОМА к этому ПАРАМЕТРУ. \$ESR=\Delta V /\Delta I\$ «но только при насыщении» или когда R динамическое < ESR. Закон Ома полезен только для линейных фиксированных R, которые включают в себя объемное R диодов, DCR катушек индуктивности и ESR конденсаторов. Исходя из этого параметра, пределы рассеиваемой мощности влияют на максимальный ток любого устройства.

Таким образом, правила использования закона Ома являются фиксированными линейными R, но это может быть применено к нелинейным устройствам, даже с большими температурными коэффициентами, такими как электрические лампочки, в течение короткого периода времени. Подобно оценке импульсного тока в вольфрамовой лампе R_cold ~ 10% R_hot, таким образом, импульс Pd в 10 раз превышает установившееся состояние. Таким образом, ограничения для использования закона Ома на любом нелинейном устройстве должны быть хорошо поняты и определены, и предполагается, что вы их поймете. (в конечном итоге)

---

(мин-макс) @Imax и по номинальной кривой VI можно измерить тангенс в ограниченном рабочем диапазоне, чтобы оценить объемное линейное сопротивление.

для более подробной информации

Эта линейная характеристика становится доминирующей только тогда, когда переход находится в состоянии насыщения, а динамическое сопротивление ниже объемного (линейного) сопротивления, когда можно применить закон Ома. Это часто находится в диапазоне от 30% до 100% номинального тока, но пользователи могут учитывать, где они работают, чтобы вычислить влияние нагрева или источника напряжения на ток.

Несмотря на то, что все диоды логарифмические, они становятся линейными, когда динамическое R< ESR.

Важно понимать, что закон Ома для увеличения рассеиваемой мощности применяется к «массовому» сопротивлению всех активных и пассивных устройств с. например в дросселях это называется DCR, в шапках это спецификация с использованием %D.