Билет №8

1. Алгебра логики. Логические константы, логические переменные, логические операции, логические функции.

1. Контроль работы цифрового автомата.

1) Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными. В алгебре логики используют алгебраические методы для решения логических задач.

Объектами алгебры логики являются высказывания.

Высказывание – это повествовательное предложение, содержание которого можно определить как истинное или ложное. Истинному значению высказывания ставится в соответствие 1(TRUE), ложному 0(FALSE).

Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение 1 при любых условиях. Такое высказывание называется тавтологией (логическая константа 1).

Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение 0 при любых условиях (логическая константа 0).

Такое высказывание называется противоречием.

Логические константы — это логическое высказывание (выражение) может быть либо истинно, либо ложно. Истине соответствует константа True, значению «ложь» — константа False

Логическая переменная — это переменная, принимающая только логические значения: «истина» или «ложь», которые в ЭВМ могут быть представлены в виде 1 и 0. В языках программирования эти значения обычно обозначаются 1, true, т или 0, false, F, соответственно. Л. п. вводятся в программу с помощью описания переменной, в котором указываются идентификатор (имя) переменной и ключевое слово, определяющее логический тип. В качестве ключевых слов в описаниях Л. п. применяются: logical — в Фортране и Boolean — в Паскале. См. описание переменной

Основные логические операции.

• Инверсия – логическое отрицание. Обозначается: или ¬х. Читается «не х».

• Высказывание истинно при ложном х и ложно при истинном х.

• Конъюнкция – логическое умножение. Обозначается символами: (или знак операции может быть вообще опущен), х₁ и х₂.

• Дизъюнкция – логическое сложение. Обозначается: х₁ ٧х₂, х₁ + х₂, х₁ или х₂.

Остальные операции выражаются через первые три операции: инверсию, конъюнкцию, дизъюнкцию.

• Импликация – логическое следование. Обозначается: х₁ х₂. Высказывание х₁ -> x₂ истинно только тогда, когда правый операнд является истинным, а левый операнд ложным.

• Эквивалентность(равносильность, необходимо и достаточно). Обозначается: символами . Высказывание истинно тогда и только тогда, когда операнды равны.

• Сложение по модулю 2(исключающее или). Обозначается символом .

• Высказывание истинно тогда и только тогда, когда операнды не равны.

• Коимпликация – отрицание импликации ( )

• Штрих Шеффера – отрицание конъюнкции (x₁ / x₂)

• Стрелка пирса – (отрицание дизъюнкции) (x₁ ↓ x₂)

Порядок выполнения операций задаётся круглыми скобками. При отсутствии скобок порядок выполнения операций следующий: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.

Составное высказывание (формула алгебры логики, логическое выражение) состоит из нескольких высказываний, соединённых логическими операциями. Исходные высказывания могут быть логическими переменными или логическими константами.

Логические функции:

f (x₁, x₂, … x_n)

Логические функции от n переменных называется функция, принимающая значение истина или ложь на любых наборах переменных x₁ … x_n, где каждая x_iпринимая значение либо истина, либо ложь.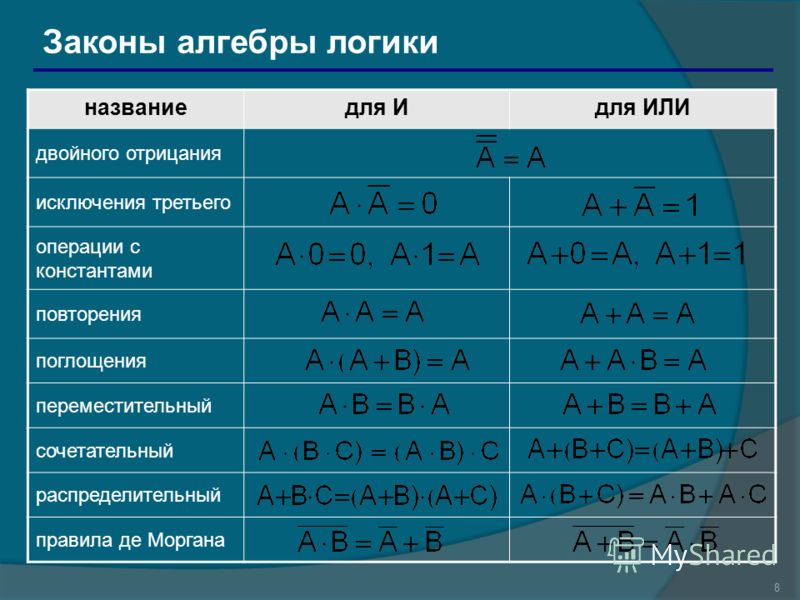 n.

2) При работе ЦА могут произойти те или иные сбои, приводящие к искажению информации. Поэтому при проектировании ЦА должны предусматриваться средства, позволяющие контролировать, выявлять и исправлять возникающие ошибки. Решение всех задач контроля становится возможным только при наличии определенной избыточности информации, которая сопровождает основную информацию. Иначе говоря, при представлении числа в каком-либо коде, необходимо предусмотреть в этом коде дополнительные (контрольные) разряды.

Систематический код – это код, содержащий в себе информационные и контрольные разряды. В контрольные разряды записывается некоторая информация об исходном числе, поэтому систематический код обладает избыточностью.

При этом абсолютная избыточность будет выражаться количеством контрольных разрядов –

k, а относительная избыточность – , где m – количество информационных разрядов.

Понятие корректирующей способности кода связывают с возможностью обнаружения и исправления ошибки.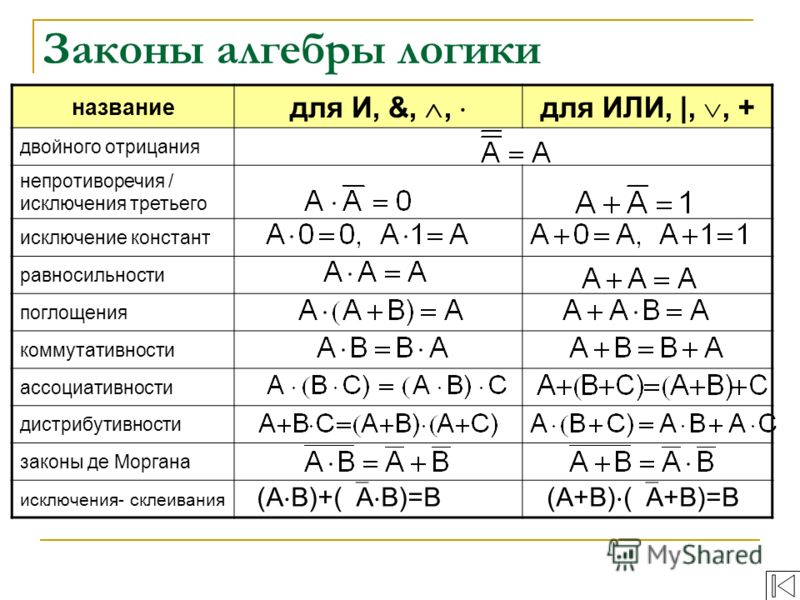 Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Корректирующая способность кода связана понятием кодового расстояния.

Кодовое расстояние (Хемингово расстояние) d для кодовых комбинаций A и B определяется как вес такой третьей комбинации, которая получается сложением исходных комбинаций по модулю 2. Вес кодовой комбинации V – это количество единиц содержащихся в кодовой комбинации.

Например, A=100111001 и B=011011100. Отсюда веса кодовых комбинаций будут равны: V(A)=5, V(B)=5. Кодовая комбинация C=A+B=111100101, вес этой кодовой комбинации равен V(C)=6. Таким образом кодовое расстояние для A и B – d(A,B)=V(C)=6.

В любой позиционной системе счисления минимальное кодовое расстояние равно 1. В теории кодирования показано, что систематический код обладает способностью обнаружения ошибки только тогда, когда код расстояния для него больше или равен 2t. Следовательно, , где t – кратность обнаруживаемых ошибок. Это означает, что между соседними кодовыми комбинациями должна существовать, по крайней мере одна кодовая комбинация.

Алгебра высказываний

Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.). Объектами алгебры логики являются высказывания.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:

А = {Аристотель — основоположник логики}

В= {На яблонях растут бананы}.

Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А= 1,В= 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.

Логическая операция КОНЪЮНКЦИЯ (логическое умножение):

 в естественном языке соответствует союзу и;

 в алгебре высказываний обозначение &;

 в языках программирования обозначение And.

Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств

АиВсоответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

 

 

Таблица истинности	Диаграмма Эйлера-Венна
А В А&В 0 0 0 0 1 0 1 0 0 1 1 1

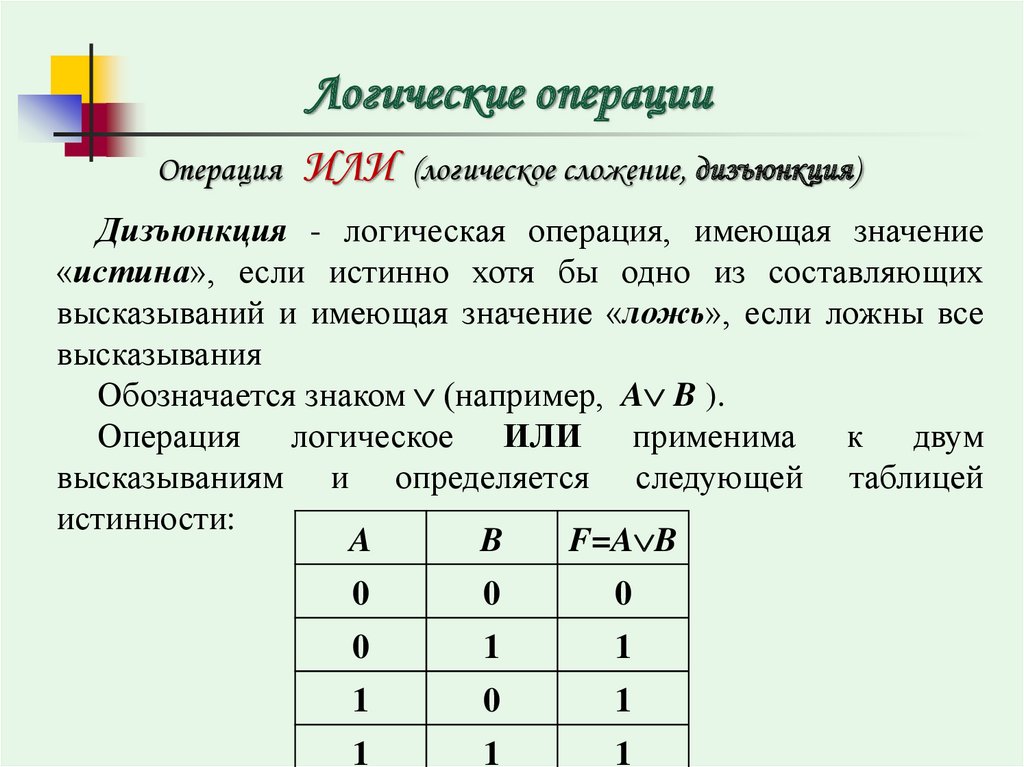
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):

 в естественном языке соответствует союзу или;

 обозначение ;

 в языках программирования обозначение Or.

Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множествАиВсоответствует множество, состоящее из элементов, принадлежащих либо множествуА, либо множествуВ.

Таблица истинности	Диаграмма Эйлера-Венна
А В А В 0 0 0 0 1 1 1 0 1 1 1 1

Логическая операция ИНВЕРСИЯ (отрицание):

 в естественном языке соответствует словам неверно, что.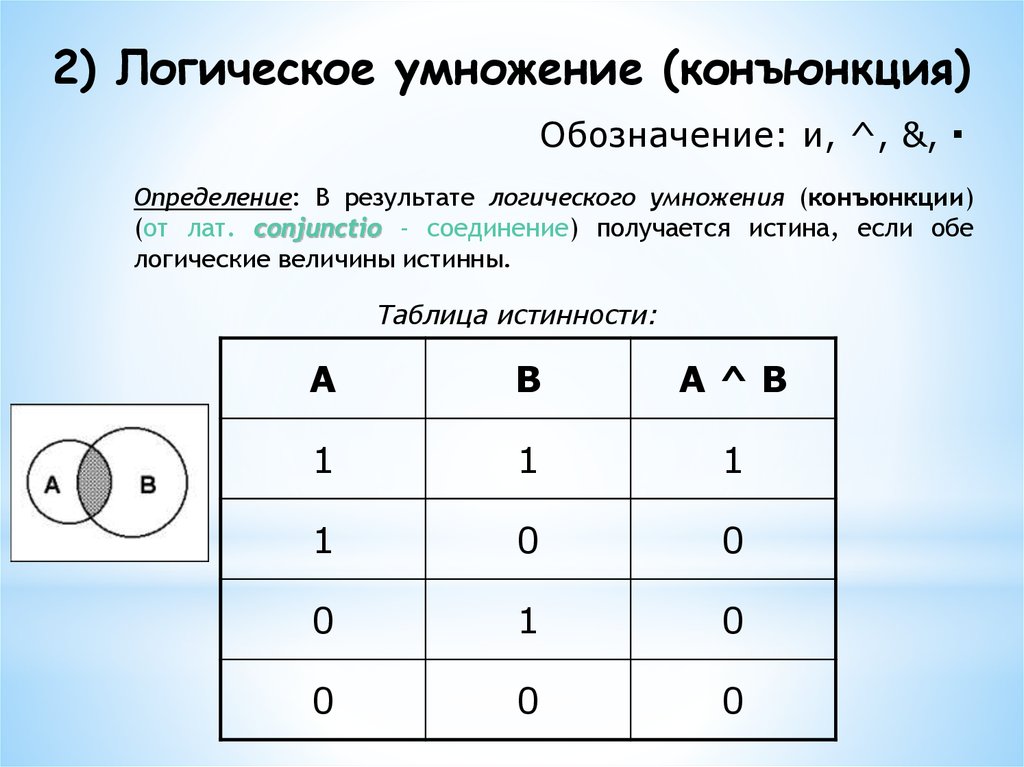 ..и частицене;

 обозначение ;

 в языках программирования обозначение Not;

Отрицание — это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множестваАсоответствует множество, дополняющее его до универсального множества.

Таблица истинности	Диаграмма Эйлера-Венна
A 0 1 1 0

Логическая операция ИМПЛИКАЦИЯ (логическое следование):

 в естественном языке соответствует обороту если . .., то …;

 обозначение .

Импликация — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

А	В	А В
0	0	1
0	1	1
1	0	0
1	1	1

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):

 в естественном языке соответствует оборотам речи тогда и только тогда;в том и только в том случае;

 обозначения ,~.

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:

А	В	АВ
0	0	1
0	1	0
1	0	0
1	1	1

Логические операции имеют следующий приоритет:действия в скобках, инверсия, &,,,.

Пример.Какие из высказыванийА, В, Сдолжны быть истинны и какие ложны, чтобы было ложно логическое выражение ((AВ) & В)С.

Импликация ложна на единственном наборе логических значений (1, 0). Значит, ((AВ)&В) = 1,С= 0.

Конъюнкция истинна на единственном наборе логических значений (1, 1). Значит, (AВ) = 1 иВ= 1.

Дизъюнкции истинна при наборах логических значений (0, 1) и (1, 1).

Следовательно, существуют два набора логических значений, удовлетворяющих условию задачи: (А= 0,В= 1,С= 0) и (А= 1,В= 1,С = 0).

 

Булева алгебра — Философская энциклопедия Routledge

Доступ к полному содержанию доступен только для членов учреждений, купивших доступ. Если вы принадлежите к такому учреждению, войдите в систему или узнайте больше о том, как сделать заказ.

---

Поделиться

Загрузка контента

Нам не удалось загрузить контент

Печать

Содержание

• Резюме статьи

• содержимое заблокировано

  1

  Основные факты

• содержимое заблокировано

  2

  Важные типы булевой алгебры

• содержание заблокировано

  3

  Булевы алгебры как алгебры истинностных значений

• содержимое заблокировано

  Библиография

Тематический

• К
• Белл, Дж. Л.

doi

10.4324/9780415249126-Y081-1

DOI: 10.4324/9780415249126-Y081-1
Версия: V1, опубликовано онлайн: 1998
. /статьи/тематические/булева-алгебра/v-1

---

Булева алгебра, или алгебра логики, была разработана английским математиком Джорджем Булем (1815–1864 гг.) и представляет собой первое успешное применение алгебраических методов к логике.

Похоже, Буль имел в виду несколько интерпретаций своей системы. В своей более ранней работе он думает о каждом из основных символов своей «алгебры» как об обозначении умственной операции по выбору только объектов, обладающих некоторым заданным атрибутом или включенных в некоторый данный класс; позже он понимает эти символы как обозначающие сами атрибуты или классы. В каждой из этих интерпретаций базовые символы понимаются как способные к комбинированию при определенных операциях: «умножение», соответствующее соединению признаков или пересечению классов; «дополнение», соответствующее (исключительной) дизъюнкции или (непересекающемуся) объединению; и «вычитание», соответствующее «исключению» или разнице. Он также признает, что предлагаемые им алгебраические законы выполняются, если основные символы интерпретируются как принимающие только числовые значения 0 и 1.

Идеи Буля с тех пор претерпели широкое развитие, и возникшая в результате концепция булевой алгебры теперь играет центральную роль в математической логике, теории вероятностей и компьютерном дизайне.

Поделиться

Загрузка контента

Нам не удалось загрузить контент

Печать

Ссылка на эту статью:
Белл, Дж.Л. Булева алгебра, 1998, doi:10.4324/9780415249126-Y081-1. Философская энциклопедия Рутледжа, Тейлор и Фрэнсис, https://www.rep.routledge.com/articles/thematic/boolean-алгебра/v-1.
Copyright © 1998-2023 Рутледж.

Похожие запросы

Темы

• Логика
• Философия математики

Связанные статьи

• Буль, Джордж (1815–1864 гг.) Альперин, Теодор

---

Подпишитесь на рассылку новостей

• Подпишитесь на рассылку новостей
• фейсбук
• твиттер

© 2023 Informa UK Limited, компания Informa Group

логика в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Логика

– Наоборот, – продолжал Труляля, – если бы это было так, то могло бы быть; и если бы это было так, то это было бы; но как это не так, это не так. Это логика».

(Льюис Кэрролл, Зазеркалье )

Контекст

Фундамент

Фундамент

Основа всего

• математическая логика

• система дедукции, естественная дедукция, последовательное исчисление, лямбда-исчисление, суждение

• теория типов, теория простых типов, теория зависимых типов

• коллекция, объект, тип, термин, набор, элемент

• равенство, оценочное равенство, типовое равенство

• Вселенная

  , проблемы с размером

• логика высшего порядка

 теория множеств

теория множеств

• основы теории множеств
  • пропозициональная логика
  • логика первого порядка
  • типизированная логика предиката
  • отношение членства
  • пропозициональное равенство
  • набор, элемент, функция, отношение
  • вселенная, маленький набор, большой набор
• теория набора материалов
  • отношение принадлежности, пропозициональное равенство, аксиома экстенсиональности
  • структура спаривания, аксиома спаривания
  • структура объединения, аксиома объединения
  • структура набора мощности, аксиома набора мощности
  • структура натуральных чисел, аксиома бесконечности
• презентаций по теории множеств
  • теория множеств первого порядка
  • теория несортированных множеств
  • просто отсортированная теория множеств
    • односортная теория множеств
    • теория двухсортных множеств
    • теория трехсортных множеств
  • теория зависимо отсортированных множеств
  • структурно представленная теория множеств
• структурализм в теории множеств
  • теория множества материалов
    • ЗФК
    • ЗФА
    • Теория множеств Мостовского
    • Новые фундаменты
  • структурная теория множеств
    • категориальная теория множеств
      • ETCS
        • полностью формальный ETCS
        • ETCS с элементами
        • Trimble на ETCS I
        • Trimble на ETCS II
        • Trimble на ETCS III
      • структурный ZFC
    • аллегорическая теория множеств
      • ПОЯВКА
• теория набора классов
  Класс
  • , соответствующий класс
  • универсальный класс, вселенная
  • категория классов
  Категория
  • со структурой классов
• конструктивная теория множеств
• алгебраическая теория множеств

Основополагающие аксиомы

основополагающая аксиома

• основные конструкции:

  • аксиома декартовых произведений
  • аксиома непересекающихся объединений
  • аксиома пустого множества
  • аксиома полноты
  • аксиома функциональных множеств
  • аксиома силовых множеств
  • аксиома частных множеств

• материальных аксиомы:

  • аксиома экстенсиональности
  • аксиома основания
  • аксиома антиосновы
  • Аксиома Мостовского
  • аксиома спаривания
  • аксиома транзитивного замыкания
  • аксиома союза

• структурных аксиомы:

  • аксиома материализации

• тип теоретических аксиом:

  • аксиомы усечения множества
    • уникальность доказательств личности
    • аксиома К
    • граница разделения
    • равенство отражение
    • аксиома локализации типа окружности
  • аксиом теории гомотопического типа:
    • аксиома однолистности
    • Принцип Уайтхеда

• аксиомы выбора:

  • аксиома выбора
  • аксиома счетного выбора
  • аксиома зависимого выбора
  • аксиома исключенного третьего
  • аксиома существования
  • аксиома множественного выбора
  • Аксиома Маркова
  • аксиома презентации
  • аксиома выбора малой мощности
  • аксиома малых нарушений выбора
  • аксиома слабо инициальных множеств покрытий

• больших кардинальных аксиомы:

  • аксиома бесконечности
  • аксиома вселенных
  • аксиома регулярного расширения
  • недоступный кардинал
  • измеримое кардинальное число
  • элементарное вложение
  • сверхкомпактный кардинал
  • Принцип Вопенки

• сильные аксиомы

  • аксиома разделения
  • аксиома замены

• далее

  • Принцип отражения

• аксиома пространств неравенств

Удаление аксиом

• конструктивная математика
• предикативной математики

Изменить эту боковую панель

(0,1)(0,1)-Теория категорий

(0,1)-категория теория : логика, теория порядка

(0,1)-категория

• связь между предзаказами и (0,1)-категориями

• proset, частично упорядоченный набор (направленный набор, общий порядок, линейный порядок)

  • верх, правда,

  • нижняя, ложная

  • монотонная функция

  • следствие

  • Фильтр

    , интервал

• решетка, полурешетка

  • встречаются, логическое соединение и

  • соединение, логическое разделение или

  • компактный элемент

• решетка подобъектов

• полная решетка, алгебраическая решетка

• дистрибутивная решетка, полностью дистрибутивная решетка, каноническое расширение

• гипердоктрина

  • первый порядок, логический, когерентный, тройной

(0,1)-топос

• Алгебра Гейтинга

  • обычный элемент

  • Булева алгебра

• Фрейм

  , локаль

Теоремы

• Каменная двойственность

Теория типов

естественная дедукция метаязык, практические основы

• решение

• гипотетическое решение, последовательное

  • антецеденты⊢\vdashconsequent, потомки

1. правило формирования типа
2. правило введения термина
3. правило устранения термина
4. правило вычисления

теория типов (зависимая, интенсиональная, наблюдательная теория типов, теория гомотопических типов)

• исчисление конструкций

синтаксис объектный язык

• теория,

  аксиома

• предложение/тип (предложения как типы)

• определение/корректура/программа (корректура как программа)

• Теорема

вычислительный тринитаризм =
предложения как типы + программы как доказательства + теория типов отношений/теория категорий

6 изоморфизмов 9 изоморфизмов. усеченный объект

logic	set theory (internal logic of)	category theory	type theory
proposition	set	object	type
predicate	family of sets	display morphism	зависимый тип
доказательство	элемент	обобщенный элемент	терм/программа
правило разреза		composition of classifying morphisms / pullback of display maps	substitution
introduction rule for implication		counit for hom-tensor adjunction	lambda
elimination rule for implication		unit for hom-tensor присоединение	приложение
устранение разреза для импликации		одно из зигзагообразных тождеств для гомин-тензорного присоединения	beta reduction
identity elimination for implication		the other zigzag identity for hom-tensor adjunction	eta conversion
true	singleton	terminal object/(-2)-truncated object	h-level 0-type/unit type
false	пустой набор	начальный объект	пустой тип
предложение, истинностное значение	subsingleton	subterminal object/(-1)-truncated object	h-proposition, mere proposition
logical conjunction	cartesian product	product	product type
disjunction	disjoint union (support of)	побочный продукт ((-1)-усечение)	тип суммы (тип скобки)
импликация	набор функций (в субсинглтон)	внутренний hom (в субтерминальный объект)	Тип функции (в H-пропозицию)
Отрицание	Функциональный набор в пустой набор	Внутренний HOM в начальный объект	Тип функции в пустой тип
	Univers субсинглетонов)	зависимый продукт (семейства субтерминальных объектов)	тип зависимого продукта (семейства h-предложений)
экзистенциальная квантификация	индексированное непересекающееся объединение (поддержка)	зависимая сумма ((-1)-усечение)	зависимый тип суммы (тип скобки)
логическая эквивалентность	множество биекций	объект тип
	опорный набор	опорный объект/(-1)-усечение	пропозициональное усечение/скобка тип
		n-образ 9-усечения в терминальный объект0676	N-модальности ncruncation
Равенство	h-level 2-type/set/h-set
set	set с отношением эквивалентности	internal 0-groupoid	Bishop set/setoid с его псевдоэквивалентным отношением фактическое отношение эквивалентности
	equivalence class/quotient set	quotient	quotient type
induction		colimit	inductive type, W-type, M-type
higher induction		higher colimit	высший индуктивный тип
—		0-усеченный высший копредел	частный индуктивный тип
коиндукция		limit	coinductive type
	preset		type without identity types
	set of truth values ​​	subobject classifier	type of propositions
domain of discourse	universe	object классификатор	универсум типов
модальность		оператор замыкания, (идемпотентная) монада	теория модальных типов, монада (в информатике)
linear logic		(symmetric, closed) monoidal category	linear type theory/quantum computation
proof net		string diagram	quantum circuit
(absence of) contraction rule		(отсутствие) диагонали	теорема о запрете клонирования
		синтетическая математика	встроенный язык программирования предметной области

гомотопические уровни

• теория типов

• 2-типовая теория, 2-категориальная логика

• теория гомотопических типов, теория гомотопических типов — содержание

  • гомотопический тип

  • однолистность, экстенсиональность функций, внутренняя логика (∞,1)-топоса

  • когезионная теория гомотопических типов

  • направленная теория гомотопических типов

  • Методы HoTT для гомотопистов

семантика

• внутренняя логика, категориальная семантика

  • показать карту

• внутренняя логика топоса

  • Язык Митчелла-Бенабу

  • Семантика Крипке-Джояла

• внутренняя логика (∞,1)-топоса

  • теоретико-типовая модель категории

Изменить эту боковую панель

• Идея
• Математическая логика
• Классические подполя
• Категориальная логика
• Записи по логике
• Связанные понятия
• Каталожные номера
• Общий
• По категориальной логике
• Логика в естественных языках

Идея

Традиционно как дисциплина логика изучает правильные методы рассуждения. Логики в основном изучали дедукцию, процесс перехода от посылок к заключению таким образом, что истинность первого требует истинности последнего. Другими словами, дедуктивная логика изучает, что значит аргумент быть действительный . Вторая ветвь логики изучает индукцию, рассуждая о том, как оценить правдоподобие общих предложений на основе наблюдений за их примерами. Это часто делалось с точки зрения теории вероятностей, особенно байесовской.

Некоторые философы, в частности Чарльз Пирс, считали, что существует третья разновидность рассуждений для изучения логики, а именно абдукция. Это процесс, посредством которого делают вывод об истинности объяснения, исходя из его способности объяснить наблюдаемое. Поэтому его иногда также называют вывод к лучшему объяснению . По крайней мере, некоторые аспекты этого также могут быть изучены с использованием байесовской вероятности.

Дедуктивная логика развита лучше всего. На протяжении веков лечение силлогизма было в авангарде дисциплины.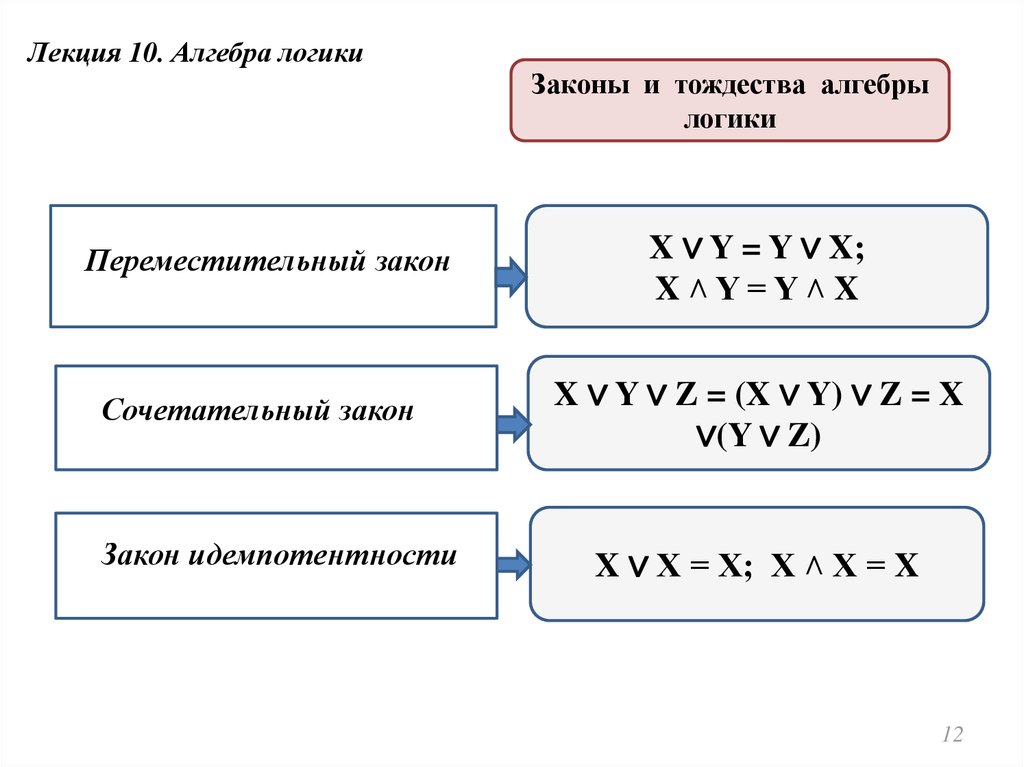 Однако в девятнадцатом веке, вызванная в основном потребностями математики, в частности необходимостью обращаться с отношениями и кванторами, возникла новая логика, известная сегодня как логика предикатов.

Как мы сказали выше, логика традиционно связана с правильных методов рассуждения, а философы (и другие) многое предписывающе сказали о логике. Однако можно изучать и логику описательно , принимая ее за изучение методов рассуждения, не пытаясь определить, правильны ли эти методы. Можно изучать конструктивную логику или субструктурную логику, не говоря о том, что ее следует принять. Также психологи изучают, как люди на самом деле быстро рассуждают в ситуациях без полной информации, например, с помощью быстрого и экономного подхода.

Логика — это особый метод рассуждения. Есть несколько способов формализовать логику как математический объект; см. Математическая логика ниже.

Математическая логика

Математическая логика или Символическая логика — это изучение логики и основ математики как формальных систем или с их помощью — теорий — таких как логика первого порядка или теория типов.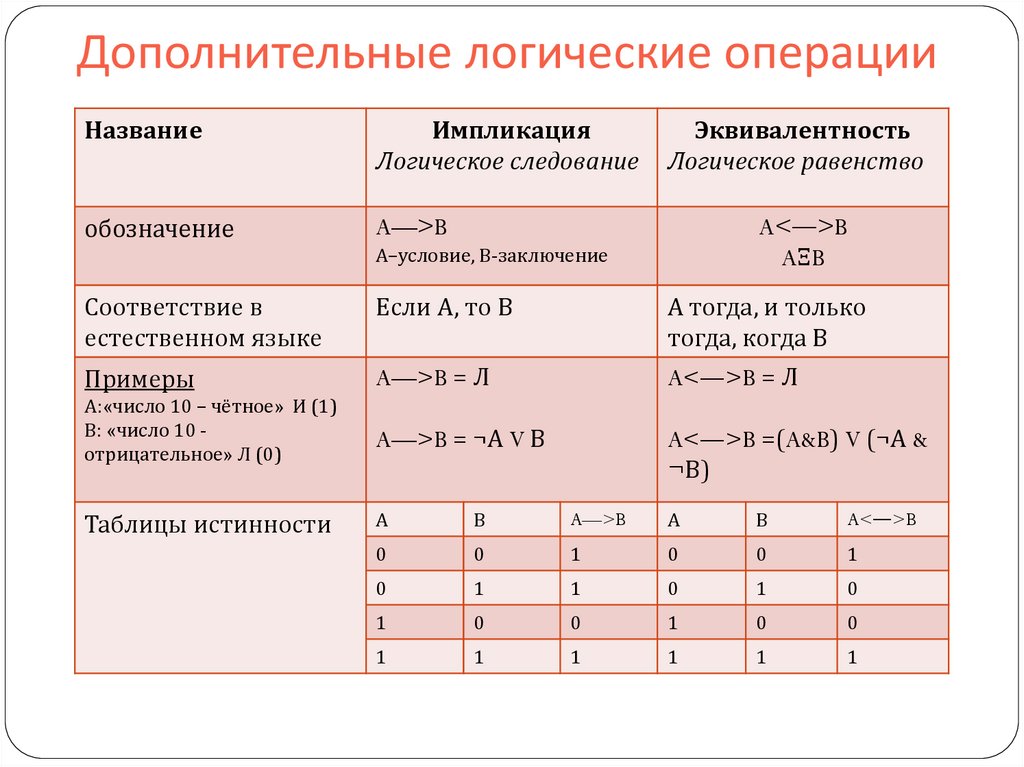

Классические подполя

Классические подполя математической логики

• теория множеств

• теория моделей,

• теория рекурсии

• теория доказательств

Категориальная логика

Путем конвергенции и объединения понятий, которые были названы вычислительным тринитаризмом , математическая логика эквивалентно воплощена в

1. теория типов

2. теория категорий

3. теория программирования

Логическая теория, которая определяется и специфицирует данную категорию 𝒞\mathcal{C} – называется ее внутренней логикой , см. там более подробную информацию, а также см. внутренний язык, синтаксическую категорию. – тот самый

• , типы которых являются объектами AA из 𝒞\mathcal{C};

• , контекстами которых являются категории срезов 𝒞/A\mathcal{C}_{/A};

• , чьи предложения в контексте являются (-1)-усеченными объектами ϕ\phi из 𝒞/A\mathcal{C}_{/A};

• , чьи доказательства A⊢PhiIsTrue:ϕA \vdash PhiIsTrue : \phi являются обобщенными элементами ϕ\phi.

Следовательно, чистая математическая логика в смысле изучения предложений отождествляется с теорией (0,1)-категории: в ней концентрируются только на (-1)-усеченных объектах. Настоящая теория категорий, которая касается 0-усеченных объектов, является домом для логики и теории множеств, или, скорее, теории типов, где 0-усеченные объекты являются множествами/типами/h-множествами.

Например,

• пределы и копределы, экспоненты и классификаторы объектов относятся к теории типов;

• , а их (-1)-усечение в следующем порядке: пересечения/(и), союзы(или), импликации и классификаторы подобъектов принадлежат логике.

В общем, теория (∞,1)-категории, которая касается неусеченных объектов, является домом для логики и типов с конструктивным понятием равенства, тождественных типов в теории гомотопических типов.

См. также теория категориальных моделей .

Записи по логике

• аксиома выбора

• Булева алгебра

• Булева алгебра с операторами

• логический домен

• логическая функция

• логическая функция

• классическая логика

• конструктивная математика

• контекст

• логика зависимости

• равенство

• принцип эквивалентности

• исключен средний

• геометрическая логика

• Алгебра Гейтинга

• логика высшего порядка

• внутренняя логика

• интуиционистская логика

• линейная логика

• логичность и инвариантность

• минимальная логика

• модальная логика

• сопряженная логика

  • алгебраические модели для модальной логики
    • алгебра замыканий
    • монадическая алгебра
    • темпоральная алгебра
  • стрелочная логика
  • эпистемическая логика
    • логика К(м)
    • логика Т(м)
    • логика S4(m)
    • логика S5(m)
  • фрейм (модальная логика)
  • геометрические модели для модальной логики
  • теория модальных типов
  • временная логика

• отрицание

• Закон Пирса

• предикат

• логика предиката

• предикативная математика

• пропозициональная логика

• отношение

• командная логика

• истинное значение

• тип

• теория типов

• математическая логика

• логических символа?

• теория типов, логика

• 2-типовая теория, 2-логика

• (∞,1)-теория, (∞,1)-логика

• объективная и субъективная логика

логическая эквивалентность \phantom{A}¬\not6

-\фантом{-}символ-\фантом{-}	—\фантом{-}в логике-\фантом{-}
А\фантом{А}∈\in	А \phantom{A}отношение элементов
A\phantom{A}:\,:	A\phantom{A}отношение типов
A\phantom{A}==	A\phantom{A }равенство
А\фантом{А}⊢\vdashA\фантом{А}	А\фантом{А}поведение / секвентА\фантом{А}
А\фантом{А}⊤\topA\ фантом{А}	A\phantom{A}true / topA\phantom{A}
A\phantom{A}⊥\botA\phantom{A}	A\phantom{A}false / bottomA\phantom{A}
A\phantom{A}⇒\Rightarrow	A\phantom{A}импликация
A\phantom{A}⇔\Leftrightarrow	A\phantom{A} 9071 65	A\phantom{A}отрицание
A\phantom{A}≠\neq	A\phantom{A}отрицание равенства/отдельностиA\phantom{A}
A\phantom{A}∉\notin	A\phantom{A}отрицательное отношение элемента A\phantom{A}
A\phantom{A}¬¬\not \not	A \фантом{А}отрицание отрицанияА\фантом{А}
А\фантом{А}∃\существует	А\фантом{А}квантификация существованияА\фантом{А}
А\фантом{А }∀\forall	A\phantom{A}всеобщая квантификацияA\phantom{A}
A\phantom{A}∧\wedge	A\phantom{A}логическая конъюнкция
A\phantom{A}∨\vee	A\phantom{A}logical disjunction
symbol	in type theory (propositions as types)
A\phantom{A}→\to	A\phantom{A}тип функции (импликация)
A\phantom{A}×\times	A\phantom{A}тип произведения (союз)
A\phantom{A}++	A\phantom{A}тип суммы (дизъюнкция)
A\phantom{A}00	A\phantom{A}пустой тип (ложь)
A\phantom{A}11	A\phantom{A}тип устройства (true)	16
A\phantom{A}==	A\phantom{A}тождественный тип (равенство)
A\phantom{A}≃\simeq	A\phantom{A}эквивалентность типов (логическая эквивалентность )
A\phantom{A}∑\sum	A\phantom{A}зависимый тип суммы (квантор существования)
A\phantom{A}∏\prod	A\phantom{A}dependent product type (universal quantifier) ​​
symbol	in linear logic
A\ phantom{A}⊸\multimapA\phantom{A}	A\phantom{A}линейная импликацияA\phantom{A}
A\phantom{A}⊗\otimesA\phantom{A}	A\phantom {A}множительная конъюнкцияA\phantom{A}
A\phantom{A}⊕\oplusA\phantom{A}	А\фантом{А}аддитивная дизъюнкцияА\фантом{А}
А\фантом{А}&\&А\фантом{А}	А\фантом{А}аддитивная конъюнкцияА\фантом{А}
A\phantom{A}⅋\invampA\phantom{A}	A\phantom{A}мультипликативная дизъюнкцияA\phantom{A}
A\phantom{A}!\;!A\phantom{A }	A\phantom{A}экспоненциальная конъюнкцияA\phantom{A}

Ссылки

Общее

На протяжении веков логика была аристотелевской логикой вывода силлогизма. В 19

• Hegel, Wissenschaft der Logik ( Science of Logic )
оказала влияние идея объективной логики как метафизики.

Эта «старая логика» подверглась известной критике

• Бертран Рассел, Логика как сущность философии , 1914

в противовес «новой логике» Пеано и Фреге, современной логике предикатов.

Учебники по математической логике:

• Дэвид Гильберт, Вильгельм Аккерманн, 9 лет0145 Основы теоретической логики , 4-е изд. Спрингер Гейдельберг 1959 [1928]

• Джон Лейн Белл, М. Маховер, Курс математической логики , Северная Голландия, Амстердам, 1977 г. (гл. 10, §5) (ISBN: 9780720428445)

• Жан-Ив Жирар (перевод и приложение Пола Тейлора и Ива Лафона), Proofs and Types , Cambridge University Press (1989) [ISBN:978-0-521-37181-0, веб-страница, pdf]

• Open Logic Project, Текст открытой логики (pdf)

По категориальной логике

• Уильям Лоувер, Смежность в основаниях , Dialectica 23 (1969), 281-296

• Уильям Лоувер Равенство в гипердоктринах и схема понимания как присоединенный функтор . В A. Heller, ed., Proc. Нью-Йорк Симп. по приложениям категориальной алгебры , стр. 1–14. АМС, 1970. (pdf)

• Пьер Картье, Логика, категории и faisceaux , Семинар Бурбаки, 20 (1977-1978), Exp. № 513, 24 с. (нумдам)

• Иоахим Ламбек, Филип Дж. Скотт, Введение в категориальную логику высшего порядка , Cambridge Studies in Advanced Mathematics 7 (1986) (ISBN: 0-521-24665-2)

• Джим Ламбек, Фил Скотт, Размышления о категориальных основаниях математики (pdf)

• Saunders MacLane, Ieke Moerdijk, Пучки в геометрии и логике

• Барт Джейкобс, Категориальная логика и теория типов , (1999) Elsevier

• Джон Белл, Развитие категориальной логики (pdf)

• Жан-Пьер Маркиз, Гонсало Рейес, (2009) История категориальной логики 1963-1977 (pdf, pdf)

• Жан-Ив Жирар, Лекции по логике , Европейское математическое общество 2011

• Джейкоб Лурье, Категориальная логика , Конспект лекций 2018 (веб)

• Майкл Маккай и Гонсало Рейес, Категориальная логика первого порядка: теоретико-модельные методы в теории топосов и родственных категорий , Конспект лекций по математике.