Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ).

Нормальное напряжение — отношение составляющей силы, действующей перпендикулярно данному сечению, к площади этого сечения. Измеряется в кг/мм

 в зависимости от знака различают сжимающие и растягивающие нормальные напряжения. Последние играют решающую роль в процессах хрупкого разрушения. Если на площадках действуют только нормальные напряжения (без касательных), то объемное (трехосное) напряженное состояние может быть охарактеризовано тремя величинами, напр. в цилиндрическом стержне — осевым, окружным и радиальным нормальным напряжением.

Понятие о схемах главных нормальных напряжениях.

Главными называют нормальные напряжения на площадках выделенного элемента с нулевыми касательными напряжениями.

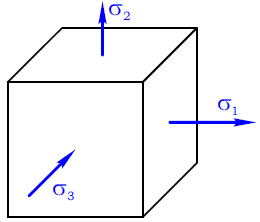
Для любого случая нагружения бруса всегда можно найти такое положение мысленно выделенного в нем элемента, на гранях которого касательные напряжения будут отсутствовать (т.е. τ=0)

Площадки (грани элемента) на которых касательные напряжения равны нулю называются главными.

Таким образом, главные – это нормальные напряжения на главных площадках.

Обозначение главных напряжений

Главные напряжения принято обозначать буквой σ с индексом 1, 2 и 3.

При этом наибольшее, с учетом знака, напряжение обозначается как σ1 а наименьшее соответственно σ3.

Другими словами, главное напряжение, расположенное на числовой оси правее других – σ1, а то, которое левее всех σ3.

Например, для случая объемного напряженного состояния:

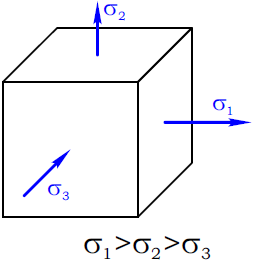
При плоском напряженном состоянии:

1. Когда оба напряжения растягивающие

2. По одной грани напряжение растягивающее, по другой сжимающее

3. Оба напряжения сжимающие.

При линейном напряженном состоянии единственное напряжение всегда обозначается как σ1 или просто σ.

Механическое напряжение — Википедия

Материал из Википедии — свободной энциклопедии

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение  — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

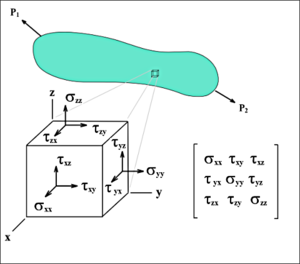
Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

Механическое напряжение — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Напряжение.

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

Механическое напряжение — Википедия. Что такое Механическое напряжение

Материал из Википедии — свободной энциклопедии

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

Механическое напряжение — Википедия. Что такое Механическое напряжение

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

Нормальное механическое напряжение Википедия

Механическое напряжение — мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

где:

• Q — механическое напряжение;
• F — сила, возникшая в теле при деформации;
• S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

Механическое напряжение — Википедия. Что такое Механическое напряжение Материал из Википедии — свободной энциклопедии

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q = F S {\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ {\displaystyle \sigma } ).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ {\displaystyle \tau } ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σ i j {\displaystyle \sigma _{ij}} равны отношению компоненты силы Δ F i {\displaystyle \Delta F_{i}} , действующей на элементарную площадку Δ S {\displaystyle \Delta S} , к её площади:

σ i j = Δ F i Δ S j . {\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под Δ S j {\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n → {\displaystyle {\vec {n}}} и её площади Δ S {\displaystyle \Delta S} :

Δ S → = n → Δ S . {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S {\displaystyle S} (в отсутствие объёмных сил):

F i = ∮ S ⁡ σ i j d S j {\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

См. также

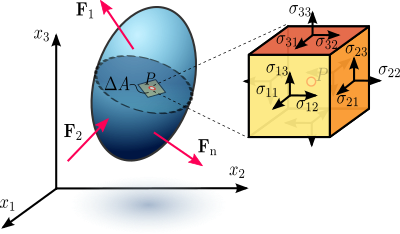Стресс (механика) — Простая английская Википедия, бесплатная энциклопедия Рисунок 1.1 Напряжение в нагруженном теле деформируемого материала, принятое как континуум. 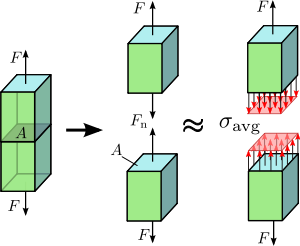Рисунок 1.2. Осевое напряжение в призматическом стержне с осевой нагрузкой. 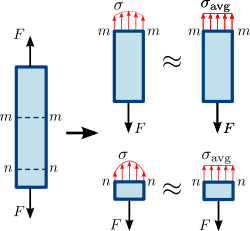Рис. 1.3 Нормальное напряжение в призматической (прямой элемент с одинаковой площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, средний нормальный стресс σ v грамм {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!} может быть использован.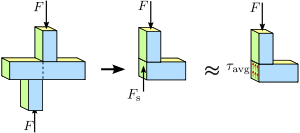 Рис. 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τ v грамм {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} разумное приближение. ^[1]

Стресс — это сила на единицу площади тела, которая стремится изменить его форму. ^[2]

Стресс — это мера внутренних сил в теле между его частицами. ^[2] Эти внутренние силы являются реакцией на внешние силы, воздействующие на тело, которые вызывают его отделение, сжатие или скольжение. ^[2] Внешние силы — это поверхностные силы или силы тела. Напряжение — это средняя сила на единицу площади, которую частица тела оказывает на смежную частицу, через воображаемую поверхность, которая разделяет их.

Формула для одноосного нормального напряжения:

σ знак равно F {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

, где σ — напряжение, F — сила, а A — площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь — в квадратных метрах. Это означает, что напряжение равно ньютонам на квадратный метр, или Н / м ² . Однако у стресса есть своя единица СИ, называемая паскалем. 1 паскаль (символ Па) равен 1 Н / м ² . В имперских единицах напряжение измеряется в фунт-силах на квадратный дюйм, которое часто сокращается до «фунтов на квадратный дюйм». Размерность напряжения такая же, как у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как континуум.Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела. (Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к постоянному изменению формы или разрушению конструкции, если материал недостаточно прочен.

Некоторые модели механики сплошных сред рассматривают силу как нечто, что может измениться. Другие модели смотрят на деформацию вещества и твердых тел, потому что характеристики вещества и твердого тела являются трехмерными.Каждый подход может дать разные результаты. Классические модели механики сплошных сред предполагают среднюю силу и не включают в себя «геометрические факторы». (Геометрия тела может быть важна для того, как распределяется стресс и как накапливается энергия при приложении внешней силы.)

В некоторых ситуациях напряжение внутри объекта может быть описано одним числом или одним вектором (число и направление). Три таких простых стрессовых ситуаций представляют собой одноосное нормальное напряжение , простое напряжение сдвига и изотропное нормальное напряжение . ^[3]

Одноосный нормальный стресс [изменить | изменить источник]

Растягивающее напряжение (или растяжение) — это напряженное состояние, приводящее к расширению; то есть длина материала имеет тенденцию к увеличению в направлении растяжения. Объем материала остается постоянным. Когда равные и противоположные силы применяются к телу, то напряжение, вызванное этой силой, называется растягивающим напряжением.

Следовательно, в одноосном материале длина увеличивается в направлении растягивающего напряжения, а два других направления уменьшаются в размерах.При одноосном растяжении растягивающее напряжение индуцируется растягивающими силами. Растягивающее напряжение противоположно сжимающему напряжению.

Конструктивными элементами, находящимися в прямом натяжении, являются канаты, грунтовые анкеры и гвозди, болты и т. Д. Балки, подверженные изгибающим моментам, могут включать в себя растягивающее напряжение, а также сжимающее напряжение и / или напряжение сдвига.

Растягивающее напряжение может увеличиваться до достижения предела прочности при растяжении, а именно предельного состояния , напряжения.

Все реальные объекты занимают трехмерное пространство.Однако, если два измерения очень велики или очень малы по сравнению с другими, объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. Одномерные объекты включают кусок проволоки, загруженный на концах и видимый сбоку, и металлический лист, загруженный на лицевой стороне и просматриваемый вблизи и через поперечное сечение.

1. ↑ Вальтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
2. 000 ^{2.0 2,1 2,2} Daintith, John, ed. (2005). Физический словарь (пятое издание). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
3. ↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжения в инженерном проектировании». 3-е издание, CRC Press, 634 стр. ISBN 9781574447132

• Ameen, Mohammed (2005). Вычислительная упругость: теория упругости и методы конечных и граничных элементов .Alpha Science Int’l Ltd. С. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
• Атанакович, Теодор М .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. стр. 1-46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
• Чедвик, Питер (1999). Механика сплошных сред: краткая теория и проблемы . Доверные книги по физике (2-е изд.). Dover Publications. стр. 90-106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
• Чакрабарти, J. (2006). Теория пластичности (3-е изд.). Butterworth-Heinemann. стр. 17-32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
• Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошных сред . Alpha Science Int’l Ltd. С. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
• Чэнь, Вай-Фа; Хан, Да-Цзянь (2007). Пластик для инженеров-строителей .J. Ross Publishing. стр. 46-71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
• Фунг Юань-чэн; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced в области технических наук. Мир Научный. стр. 66-96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
• Hamrock, Bernard (2005). Основы элементов машин . McGraw-Hill. стр. 58-59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
• Хельмстад, Кит Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. стр. 103-130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
• Irgens, Fridtjov (2008). Механика сплошной среды . Springer. стр. 42-81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
• Джегер, Джон Конрад; Кук, Н.G.W, & Zimmerman, R.W. (2007). Основы горной механики (Четвертое изд.). Wiley-Blackwell. стр. 9-41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
• Люблинер, Джейкоб (2008). Теория пластичности (пересмотренное издание) (PDF). Dover Publications. ISBN 0486462900 . CS1 maint: ref = harv (ссылка)
• Mase, George E. (1970). Механика сплошных сред . McGraw-Hill.стр. 44-76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
• Mase, G. Thomas; Джордж Э. Мэйс (1999). Механика сплошных сред для инженеров (Второе издание). CRC Press. стр. 47-102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
• Прагер, Уильям (2004). Введение в механику континуума . Dover Publications. стр. 43-61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
• Смит, Дональд Рэй; Truesdell, Clifford (1993). Введение в механику сплошных сред — после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
• Wu, Han-Chin (2005). Механика сплошных сред и пластика . CRC Press. стр. 45-78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

,

Механика материалов: изгиб — нормальное напряжение »Механика тонких конструкций

---

Моментов Зоны

Чтобы рассчитать напряжение (и, следовательно, напряжение), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки, и как рассчитать второй момент площади для данного поперечного сечения.

Давайте начнем с воображения произвольного поперечного сечения — что-то не круглое, не прямоугольное и т. Д.

На изображении выше, произвольная форма имеет площадь, обозначенную A . Мы можем взглянуть на небольшую дифференциальную область dA , которая существует на некотором расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующим формулам:

Первый момент площади — это интеграл длины по площади — это означает, что в нем будут указаны единицы измерения длины [L ³ ]. Это важно, потому что это помогает нам определить центр тяжести объекта.Центроид определяется как «среднее положение области x (или y )». Математически это утверждение выглядит так:

Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она ​​позволяет нам разбивать сложную фигуру на простые фигуры с известными областями и известными местоположениями центроидов. В большинстве инженерных сооружений имеется хотя бы одна ось симметрии — и это позволяет нам значительно упростить поиск центроида. Центроид должен быть расположен на оси симметрии .Например:

Для поперечного сечения слева мы знаем, что центроид должен находиться на оси симметрии, поэтому нам нужно найти центроид только по оси и . Поперечное сечение справа еще проще — поскольку центроид должен располагаться по осям симметрии, он должен находиться в центре объекта.

Теперь, когда мы знаем, как определить местонахождение центроида, мы можем обратить наше внимание на второй момент области. Как вы помните из предыдущего раздела о кручении, это определяется как:

И, наконец, иногда нам нужно будет определить второй момент области вокруг произвольной оси x или y — тот, который не соответствует центроиду.В этом случае мы можем использовать теорему о параллельной оси для ее вычисления. В этом случае мы используем второй момент площади относительно центроида, плюс термин, который включает расстояния между двумя осями.

Это уравнение называется теорема о параллельной оси . Это будет очень полезно на протяжении всего этого курса. Как описано во вводном видео к этому разделу, может быть легко вычислить второй момент площади для простой формы. Для более сложных фигур нам нужно будет рассчитать I путем вычисления отдельных I для каждой простой формы и объединения их вместе, используя теорему параллельной оси.

Диаграммы сдвига и момента

Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции. Эти поперечных нагрузок будут вызывать изгибающий момент М , который вызывает нормальное напряжение , и усилие сдвига В , которое индуцирует напряжения сдвига . Эти силы могут и будут изменяться по длине балки, и мы будем использовать диаграмм сдвига и момента (диаграмма V-M) , чтобы извлечь наиболее важные значения.Построение этих диаграмм должно быть вам знакомо по статикам , но мы рассмотрим их здесь. При рассмотрении поперечно нагруженного луча необходимо учитывать два важных момента:

1. Как загружается луч?

• точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…

1. Как поддерживается луч?

• просто поддерживаемый, консольный, нависающий, статически неопределенный…

Знание нагрузок и опор позволит вам построить качественную диаграмму V-M , а затем статический анализ свободного тела поможет определить количественное описание кривых .Давайте начнем с напоминания о наших условных обозначениях .

Эти условные обозначения должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает луч таким образом, что он изгибается в «улыбку» или в U-образную форму, он является положительным. Лучший способ вспомнить эти диаграммы — проработать пример. Начните с этой консольной балки — отсюда вы можете пройти через более сложные нагрузки.

Нормальное напряжение при изгибе

Во многих отношениях изгиб и кручение очень похожи.Результаты изгиба из пары, или изгибающий момент М , который применяется. Как и при кручении, в чистом изгибе в материале есть ось, где напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение больше не является равномерным по поперечному сечению конструкции — оно меняется. Давайте начнем с рассмотрения того, как ось z изгибает конструкцию. В этом случае мы не будем ограничиваться круговыми сечениями — на рисунке ниже мы рассмотрим призматическое сечение.

Прежде чем мы углубимся в математику за изгибом, давайте попробуем почувствовать это концептуально. Возможно, лучший способ увидеть, что происходит, это наложить изогнутый луч поверх оригинального, прямого луча.

Теперь вы можете заметить, что нижняя поверхность балки стала длиннее, а поверхность балки стала короче. Кроме того, вдоль центра балки длина не изменилась вообще — соответствует нейтральной оси. Чтобы повторить это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под давлением.Нечто более тонкое, но все еще наблюдаемое на вышеупомянутом наложенном изображении, заключается в том, что смещение луча изменяется линейно от вершины до низа, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и при кручении — напряжение варьировалось линейно от центра к центру. Мы можем посмотреть на это распределение напряжений через поперечное сечение балки немного более четко:

Теперь мы можем найти математическую связь между приложенным моментом и напряжением в балке.Мы уже упоминали, что луч деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или вдоль толщины луча). Таким образом, деформация будет иметь максимальное напряжение при y = -c (поскольку y = 0 находится на нейтральной оси, в данном случае это центр балки), и будет иметь максимальное сжатие при y = c , Мы можем записать это математически так:

Теперь, это говорит нам кое-что о напряжении, что мы можем сказать о максимальных значениях напряжения? Что ж, давайте начнем с умножения обеих сторон уравнения на E , модуль упругости Юнга.Теперь наше уравнение выглядит так:

Используя закон Гука, мы можем связать эти величины с фигурными скобками под напряжением в направлении x и максимальным напряжением. Что дает нам это уравнение для напряжения в направлении х-:

Наш последний шаг в этом процессе — понять, как изгибающий момент связан со стрессом. Для этого напомним, что момент — это сила, умноженная на расстояние. Если мы можем только представить, глядя на очень маленький элемент в пучке, дифференциальный элемент, то мы можем записать это математически как:

Поскольку у нас есть дифференциалы в нашем уравнении, мы можем определить момент M , действующий по площади поперечного сечения балки, путем интегрирования обеих сторон уравнения.И, если мы вспомним наше определение напряжения как силы на площадь, мы можем написать:

Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент области вокруг оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается как I (помните, что в цилиндрических координатах он обозначается как J ). Теперь мы можем наконец выписать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке по оси и , как:

Важно отметить, что индексы в этом уравнении и направлении вдоль сечения (здесь оно измеряется по и ) все будет меняться в зависимости от характера проблемы, т.е.е. направление момента — на какую ось изгибается луч? Мы основали нашу запись на шоу изогнутых лучей на первом изображении этого урока.

Помните, в начале раздела, когда я упоминал, что изгиб и кручение на самом деле были очень похожи? На самом деле мы видим это очень явно в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвига при кручении) равно парам / моменту ( М для изгиба и Т для кручения), умноженному на местоположение вдоль поперечного сечения , , поскольку напряжение не является равномерным вдоль поперечного сечения (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все это делится на второй момент области поперечного сечения.

Резюме

В этом уроке мы узнали о моментах из области и диаграмм моментов сдвига . Из первого момента области сечения мы можем вычислить центроида . Мы узнали, как вычислить второй момент для области в декартовых и полярных координатах, и узнали, как теорема параллельной оси позволяет нам получить второй момент площади относительно центроида объекта — это полезно для разбиения сложного сечения на несколько простых форм и объединение их вместе.Мы пересмотрели концепцию диаграмм сдвига и момента из статики. Эти диаграммы будут важны для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, которая, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. Как напряжение, так и деформация изменяются вдоль поперечного сечения балки, при этом одна поверхность натянута, а другая — сжата. Плоскость, проходящая через центроид, образует нейтральную ось — вдоль нейтральной оси нет напряжения или деформации.Напряжение является функцией приложенного момента и второго момента площади относительно оси, в которой находится момент.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат автору (авторам) и не обязательно отражают точку зрения Национального Научный фонд.

,

Механика материалов: деформация »Механика тонких конструкций

---

штамм

Пока что мы сосредоточились на напряжении внутри структурных элементов. Когда вы прикладываете стресс к объекту, он деформирует . Подумайте о резинке: вы натягиваете ее, и она становится длиннее — она ​​ тянется . Деформация — это мера растяжения объекта, а — деформация — это отношение деформации к исходной длине.Думайте о растяжении как о -процентном удлинении — насколько больше (или меньше) объект при его загрузке.

Как и стресс, существует два типа деформации, которые может испытывать структура: 1. Нормальная деформация и 2. Сдвиговая деформация . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она оказывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, она оказывает напряжение сдвига.

Рассмотрим шток под одноосным натяжением.При этом натяжение стержня удлиняется до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к исходной длине стержня.

Напряжение — это безразмерной меры того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация возникает, когда удлинение объекта является реакцией на нормальное напряжение (то есть перпендикулярно поверхности), и обозначается греческой буквой epsilon. Положительное значение соответствует деформации при растяжении , а отрицательное — при сжатии .Деформация сдвига возникает, когда деформация объекта является реакцией на напряжение сдвига (то есть параллельно поверхности) и обозначается греческой буквой гамма .

Механическое поведение материалов

Очевидно, что стресс и напряжение связаны между собой. Напряжение и деформация связаны между собой конституционным законом , и мы можем определить их соотношение экспериментально, измерив, какое напряжение требуется для растяжения материала. Это измерение может быть выполнено с использованием теста на растяжение . В простейшем случае, чем больше вы натягиваете объект, тем больше он деформируется, и при малых значениях деформации это соотношение является линейным. Эта линейная, упругая связь между напряжением и деформацией известна как закон Гука . Если вы построите график зависимости напряжения от деформации, то для небольших деформаций этот график будет линейным, а наклон линии будет являться свойством материала, известного как , модуль упругости Юнга . Это значение может значительно варьироваться от 1 кПа для Jello до 100 ГПа для стали.Для большинства конструкционных материалов линейная область диаграммы напряжение-деформация имеет место только для очень малых деформаций (<0,1%). В этом курсе мы сосредоточимся только на материалах с линейной упругостью , (т.е. они следуют закону Гука) и с изотропией (они ведут себя одинаково, независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простые соотношения для деформации материала.

Интуитивно, этот экзамен имеет смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или более толстому материалу, получите меньшую деформацию.Если структура меняет форму, или материал, или загружается по-разному в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип суперпозиции .

Обобщенный закон Гука

На последнем уроке мы начали изучать взаимосвязь стресса и напряжения — по закону Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили только о стрессе или напряжении в одном направлении.В этом уроке мы рассмотрим обобщенный закон Гука для однородных, изотропных и упругих материалов, подвергающихся воздействию сил более чем на одну ось.

Перво-наперво, даже просто потянув (или толкнув) большинство материалов в в одном направлении, фактически вызывает деформацию в во всех трех ортогональных направлениях . Давайте вернемся к этой первой иллюстрации напряжения. На этот раз мы учтем тот факт, что натяжение объекта в осевом направлении заставляет его сжимать в поперечном направлении в поперечных направлениях:

Таким образом, натяжение в направлении x приводит к его сжатию в направлениях и и z .Это свойство материала известно как коэффициент Пуассона , и оно обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это как уравнение:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также не имеет единиц. Коэффициент Пуассона является материальным свойством . Коэффициент Пуассона может варьироваться от -1 до 0.5. Для большинства конструкционных материалов, например, сталь или алюминий имеют коэффициент Пуассона около 0,3, а каучуки имеют коэффициент Пуассона около 0,5, которые называются «несжимаемыми». Несжимаемое означает просто, что любое количество, которое вы сжимаете в одном направлении, будет увеличиваться на столько же в других направлениях — следовательно, его объем не изменится.

В последнее десятилетие было проведено несколько очень интересных исследований по созданию структурированных материалов , которые используют геометрию и упругие неустойчивости (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона.Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип может быть применен и в 3D для создания расширяемых / складных оболочек:

Благодаря коэффициенту Пуассона мы получили уравнение, которое связывает деформацию в направлении и или z с деформацией в направлении z. Мы можем, в свою очередь, связать это со стрессом по закону Гука.Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, сигма _y = сигма _z = 0. Выпишем деформации в направлении y и z с точки зрения напряжения в направлении x .

Помните, до этого момента мы рассматривали только одноосную деформацию . В действительности, конструкции могут одновременно загружаться в нескольких направлениях, вызывая напряжение в этих направлениях.Полезный способ понять это — представить очень маленький «куб» материала внутри объекта. Этот куб может иметь напряжений , которые нормальны к каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое справедливо для нормальных напряжений в направлениях и и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях .Итак, теперь мы включаем эту идею в закон Гука и записываем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем на самом деле: деформация в каждом направлении (или, каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь мы приводим уравнения для того, как объект изменит форму в трех ортогональных направлениях. Хорошо, если объект меняет форму во всех трех направлениях, это означает, что он изменит свой объем на .Простую меру для этого изменения объема можно найти, сложив три нормальных компонента напряжения:

Теперь, когда у нас есть уравнение для изменения объема, или , , в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, который вызывает расширение, известен как гидростатический стресс. Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Таким образом, в случае гидростатического давления мы можем уменьшить наше окончательное уравнение для расширения до следующего:

Это последнее соотношение важно, потому что оно является определяющим для того, как объем материала изменяется под гидростатическим давлением.Префактор p может быть переписан как материала модуля , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой того, как материал меняет объем под заданным давлением — если коэффициент Пуассона для материала равен 0,5?

закон Гука в сдвиге

В предыдущем разделе мы разработали отношения между нормальным стрессом и нормальным напряжением.Теперь мы должны поговорить о сдвиге. Давайте вернемся к этому воображаемому кубу материала. В дополнение к внешним силам, вызывающим напряжения, которые являются нормальными для каждой поверхности куба, эти силы могут вызывать напряжения, параллельные каждой поверхности куба. И, как мы знаем, напряжения, параллельные поперечному сечению, составляют касательных напряжений

Теперь этот кубик материала выглядит намного сложнее, но на самом деле он не так уж и плох. На каждой поверхности есть два напряжения сдвига, и индексы сообщают вам, в каком направлении они указывают и с какой поверхностью они параллельны.Например, возьмите правильное лицо куба. Напряжения, нормальные для этого лица, являются нормальными напряжениями в направлении x . Эта поверхность параллельна двум напряжениям, одно из которых направлено в направлении и (обозначено тау _xy ), а другое направлено в направлении z (обозначено тау _xz ). Чтобы куб находился в равновесии, тау _xy = тау _yx (в противном случае куб вращался бы). Следовательно, в настоящее время существует шести напряжений (сигма _x , сигма, сигмаз, тау _xy, тау _, тау _xz ), которые характеризуют состояние напряжения в однородном, изотропном, упругом материале.

Итак, как эти напряжения сдвига относятся к деформации сдвига? Закон Гука в сдвиге выглядит очень похоже на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорциональность между сдвиговым напряжением и сдвиговым напряжением известна как модуль сдвига материала. Это уравнение в его общем виде, но мы можем переписать его более явно с точки зрения его компонентов: x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, упругих материалов.

В нашем обобщенном законе Гука мы имеем шесть компонентов напряжения и деформации и три свойства материала. Естественный вопрос: как эти три свойства материала связаны друг с другом? Это соотношение задается следующим уравнением:

Резюме

Мы представили понятие напряжения в этой лекции. Напряжение — это деформация материала от напряжения. Это просто отношение изменения длины к исходной длине.Деформации, которые применяются перпендикулярно поперечному сечению, представляют собой нормальных деформаций , в то время как деформации, применяемые параллельно поперечному сечению, представляют собой деформаций сдвига . Для линейных упругих материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под воздействием внешней нагрузки.

Кроме того, мы узнали о многоосевой нагрузке в этом разделе.В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона — соотношение между поперечным и осевым деформациями. Деформации, возникающие в трех ортогональных направлениях, могут дать нам меру расширения материала в ответ на многоосную нагрузку. В частности, материал может обычно изменять объем в ответ на изменения внешнего давления или гидростатического напряжения .Это привело к определению устойчивости материалов к изменению объема при гидростатическом напряжении — объемный модуль . Осмотрев воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие в норме и параллельные каждой грани куба. Это дало нам шесть напряжений и шесть штаммов (три нормальных и три сдвига), которые мы связали друг с другом, используя обобщенный закон Гука для однородных , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны с тремя свойствами материала: модуль упругости Юнга , модуль сдвига и коэффициент Пуассона .

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат автору (авторам) и не обязательно отражают точку зрения Национального Научный фонд.

,

Стресс | физика | Britannica

Стресс , в области физических наук и инженерии, сила на единицу площади в материалах, возникающая из-за приложенных извне сил, неравномерного нагрева или постоянной деформации и позволяющая точно описать и предсказать поведение упругости, пластичности и текучести. Напряжение выражается как отношение силы, деленной на площадь.

Подробнее на эту тему

рок: стресс и напряжение

Когда напряжение σ (сила на единицу площади) применяется к материалу, такому как камень, материал испытывает изменение размера, объема или…

Есть много видов стресса. Нормальное напряжение возникает от сил, которые перпендикулярны площади поперечного сечения материала, в то время как напряжение сдвига возникает от сил, которые параллельны и лежат в плоскости области поперечного сечения. Если стержень, имеющий площадь поперечного сечения 4 квадратных дюйма (26 квадратных см), вытягивают в длину силой 40000 фунтов (180 000 ньютонов) на каждом конце, нормальное напряжение внутри стержня равно 40000 фунтов, деленных на 4 квадратных дюйма. дюймов, или 10000 фунтов на квадратный дюйм (фунтов на квадратный дюйм; 7000 ньютонов на квадратный см).Это специфическое нормальное напряжение, возникающее в результате растяжения, называется растягивающим напряжением. Если две силы поменялись местами, чтобы сжимать стержень вдоль его длины, нормальное напряжение называется сжимающим напряжением. Если силы везде перпендикулярны всем поверхностям материала, как в случае объекта, погруженного в жидкость, которая может быть сжата сама, нормальное напряжение называется гидростатическим давлением или просто давлением. Напряжение под поверхностью Земли, которое сжимает горные тела до больших плотностей, называется литостатическим давлением.

Напряжение сдвига в твердых телах возникает в результате таких действий, как скручивание металлического стержня вокруг продольной оси, как при затягивании винта. Напряжение сдвига в жидкостях является результатом таких действий, как поток жидкостей и газов по трубам, скольжение металлической поверхности по жидкой смазке и прохождение самолета через воздух. Напряжения сдвига, пусть и небольшие, применяемые к истинным жидкостям, вызывают непрерывную деформацию или течение, когда слои жидкости движутся друг над другом с разными скоростями, как отдельные карты в колоде карт, которая распространяется.Для напряжения сдвига, см. Также модуль сдвига.

Реакция на напряжения в упругих твердых телах приводит к тому, что они возвращаются к своей первоначальной форме после снятия приложенных сил. Предел текучести, отмечающий переход от упругого к пластическому поведению, представляет собой минимальное напряжение, при котором твердое тело будет подвергаться постоянной деформации или пластическому течению без значительного увеличения нагрузки или внешней силы. Земля демонстрирует упругую реакцию на напряжения, вызванные землетрясениями, в том, как она распространяет сейсмические волны, тогда как она подвергается пластической деформации под поверхностью под большим литостатическим давлением.

Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской. Подпишитесь сегодня ,