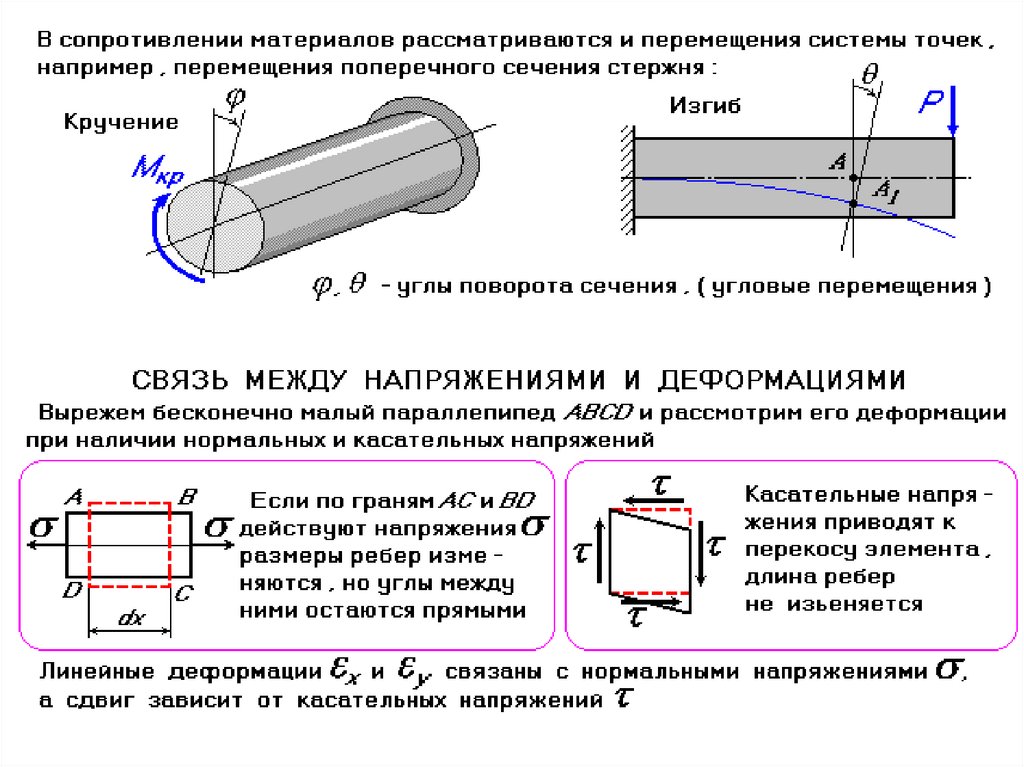
Механическое напряжение.
25. Модель строения твердых тел. Виды кристаллических структур.
Виды кристаллических структур.
В зависимости от характера сил взаимодействия и природы частиц, находящихся в узлах кристаллической решетки, различают 4 типа кристаллических решеток.
атомные кристаллы. В узлах кристаллической решетки находятся нейтральные атомы. Между ними существует связь, имеющая электрический характер. Эта связь осуществляется электронными парами, причем от каждого атома в ней участвует только только по одному электрону. Число связй, в которых может участвовать атом, определяется его валентностью. Примерами атомных кристаллов является графит, алмаз, кремний, германий.
Ионные кристаллы. В узлах кристаллической решетки этих кристаллов находятся ионы разных знаков. Связь между ними обусловлена электрическими силами взаимодействия между разноименными ионами.
Металлические кристаллы.

Молекулярные кристаллы. В узлах кристаллической решетки находятся молекулы, ориентированные определенным образом. Между молекулами действуют силы притяжения, характерные для взаимодействия молекул. К молекулярным кристаллам относятся нафталин, парафин, сухой лед, лед.
26. Механические свойства твердых тел. Виды деформаций. Механическое напряжение. Закон Гука.
Механические свойства твердых тел:
Деформация и напряжение Модуль упругости Диаграмма растяжения Дефекты в кристаллах
Деформацию сжатия и растяжения можно характеризовать абсолютным удлинением Δl , равным разности длин образца до растяжения l0 и после него l :
.
Абсолютное удлинение при растяжении положительно, при сжатии имеет отрицательное значение.
Отношение абсолютного удлинения к длине образца называется относительным удлинением :
. (30.1)
При деформации тела возникают силы упругости. Физическая величина, равная отношению модуля силы упругости к площади сечения тела, называется механическим напряжением :
. (30.2)
За единицу механического напряжения в СИ принят паскалъ (Па). .
Модуль упругости. При малых деформациях напряжение прямо пропорционально относительному удлинению:
. (30.3)
Коэффициент пропорциональности Е в уравнении (30.3) называется модулем упругости.Модуль упругости одинаков для образцов любой формы и размеров, изготовленных из одного материала:
. (30.4)
Из формулы (30.4) следует, что
. (30.5)
Сравнив
выражение (30. 5) с законом Гука, получим,
что жесткость k стержня
пропорциональна произведению модуля
Юнга на площадь поперечного сечения
стержня и обратно пропорциональна его
длине.
5) с законом Гука, получим,
что жесткость k стержня
пропорциональна произведению модуля
Юнга на площадь поперечного сечения
стержня и обратно пропорциональна его
длине.
Диаграмма растяжения.
Закон Гука выполняется при небольших деформациях. Максимальное напряжение , при котором еще выполняется закон Гука, называется пределом пропорциональности. За пределом пропорциональности напряжение перестает быть пропорциональным относительному удлинению; до некоторого напряжения после снятия нагрузки размеры тела восстанавливаются полностью. Такая деформация называется упругой. Максимальное напряжение , при котором деформация еще остается упругой, называется пределом упругости
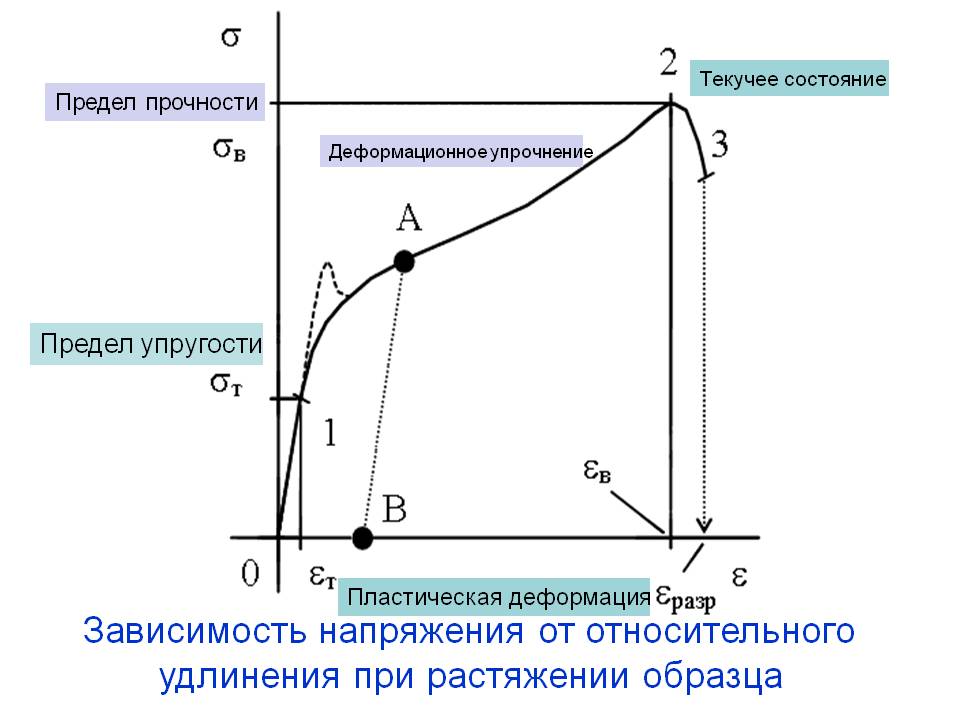
При напряжениях, превышающих предел упругости , образец после снятия нагрузки не восстанавливает свою форму или первоначальные размеры. Такие деформации называются остаточными или пластическими.
В области пластической деформации деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала.
Материалы, у котерых область текучести значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называются хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.
Дефекты в кристаллах. Способы повышения прочности твердых тел. Кристаллическими телами являются все металлические изделия — стальные каркасы зданий и мостов, рельсы железных дорог, линии электропередач, станки, машины, поезда, самолеты.
Одной
из важнейших задач науки и техники
является создание прочных и надежных
машин, станков и зданий с минимальной
затратой металлов и других материалов.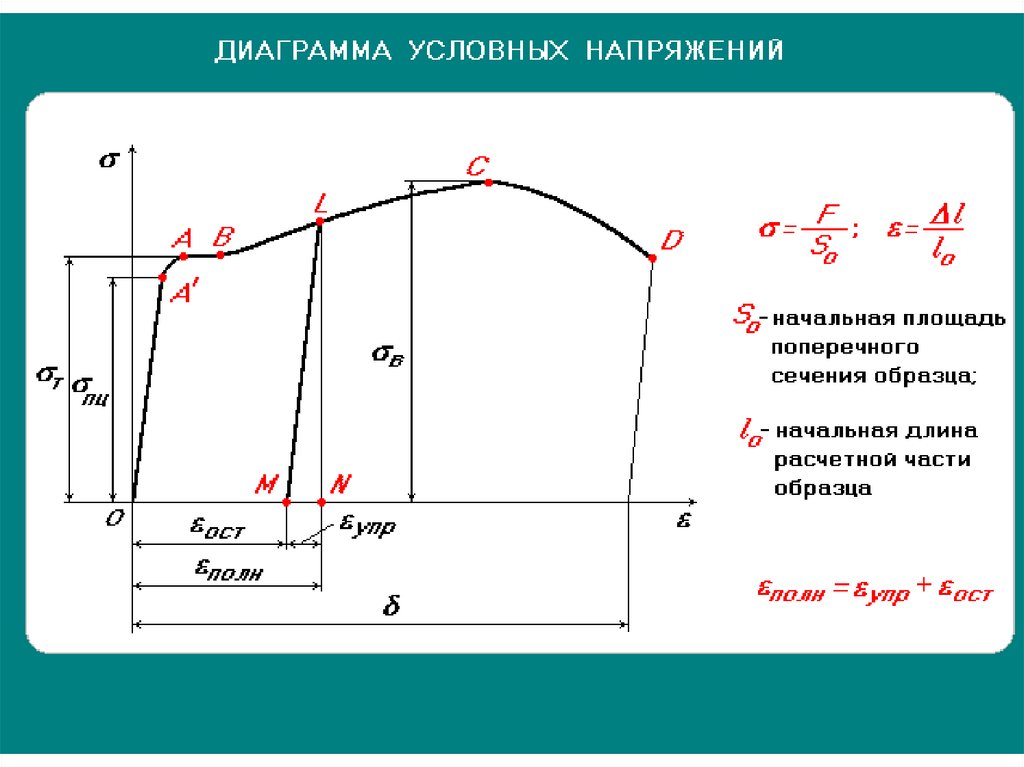
Сравнение реальной прочности кристаллов со значениями, полученными на основании теоретических расчетов, обнаруживает весьма существенные расхождения. Теоретический предел прочности в десятки и даже в сотни раз превосходит значения, получаемые при испытаниях реальных образцов.
Оказалось, что причина расхождения теории и эксперимента заключается в наличии внутренних и поверхностных дефектов в строении кристаллических решеток.
Самые простые дефекты в идеальной кристаллической решетке — точечные дефекты — возникают при замещении собственного атома чужеродным, внедрении атома в пространство между узлами решетки или при отсутствии атома в одном из узлов кристаллической решетки .
Другой вид дефектов — линейные дефекты — возникает при нарушениях в порядке расположения атомных плоскостей в кристаллах. Пример такого нарушения в структуре кристалла представлен на рисунке 104.
Деформация
и разрушение кристалла с линейным
дефектом облегчаются потому, что вместо
одновременного разрыва всех связей
между атомами двух плоскостей становится
возможным поочередный разрыв небольшого
числа связей между атомами с постепенным
перемещением дефекта в кристалле.
Для получения кристаллических материалов с высокой прочностью нужно выращивать монокристаллы без дефектов. Это очень сложная задача, и поэтому в практике этот путь пока широкого распространения не получил.
Большинство
современных методов упрочнения материалов
основано на другом способе. Для упрочнения
кристалла с дефектами в решетке можно
создать условия, при которых перемещение
дефектов в кристалле затрудняется.
Препятствием для перемещения дефектов
в кристалле могут служить другие дефекты,
специально созданные в кристаллической
решетке. Так, для увеличения прочности
стали применяется легирование стали —
введение в расплав небольших добавок
хрома, вольфрама и других элементов.
Внедрение атомов чужеродных элементов
в решетку кристаллов железа затрудняет
перемещение линейных дефектов при
деформации кристаллов, прочность стали
повышается при этом примерно в три раза.
Дополнительные дефекты в кристаллической
решетке создаются при протяжке,
дробеструйной обработке металлов.
Недеформируемых тел в природе не существует.
Деформация — изменение формы или объема тела под действием внешних сил. Деформация может быть упругая или неупругая.
Упругая деформация — деформация, при которой после прекращения действия силы размеры и форма тела восстанавливаются.
1. Линейная:
а) Растяжение (тросы подъемных кранов, канатных дорог, буксирные тросы)
б) Сжатие (колонны, стены, фундаменты зданий).
2. Сд <SMILE>id=420 alt=’:Лопну от смеха:'</SMILE> <SMILE>id=420 alt=’:Лопну от смеха:'</SMILE>виг (заклепки, болты, соед. металлические конструкции, процесс разрезания ножницами бумаги).
3. Кручение (завинчивание
гаек, работа валов машин, сверление
металлов и т.
4. Изгиб (формально деформация растяжения и сжатия, различная в разных частях тела. Нейтральный слой — слой, не подвергающийся ни растяжению, ни сжатию, при изгибе.)
Деформацию растяжения и сжатия можно охарактеризовать абсолютной деформацией ℓ, равной разности длин образца после растяжения ℓ и до него ℓ0: ℓ = ℓ – ℓ0
ℓ = ℓ – ℓ0
Отношение абсолютной деформации ℓ к первоначальной длине образцаℓo называют относительной деформацией:
Механическое
напряжение — мера внутренних сил,
возникающих в деформируемом теле под
влиянием внешних воздействий.
Механическое
напряжение в точке тела измеряется
отношением:
—
упругой силы, возникающей в теле при
деформации; к
—
площади малого элемента сечения,
перпендикулярного к этой силе. В
системе СИ механическое напряжение
измеряется в паскалях.
Различают
две составляющие вектора механического
напряжения:
—
нормальное механическое напряжение,
направленное по нормали к сечению; и
—
касательное механическое напряжение
в плоскости сечения.
В
системе СИ механическое напряжение
измеряется в паскалях.
Различают
две составляющие вектора механического
напряжения:
—
нормальное механическое напряжение,
направленное по нормали к сечению; и
—
касательное механическое напряжение
в плоскости сечения.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь F — сила натяжения стержня, Δl — абсолютное удлинение (сжатие) стержня, а kназывается коэффициентом упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как
Величина E называется Модулем
упругости первого рода или модулем
Юнга и
является механической характеристикой
материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов вещества.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности, связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
27. Плавление и кристаллизация. Теплота плавления.
Плавление и кристаллизация.
Плавлением
называют процесс перехода вещества из
твердого кристаллического состояния
в жидкое. Плавление происходит при
постоянной температуре с поглощением
тепла. Постоянство температуры объясняется
тем, что при плавлении вся подводимая
теплота идет на разупорядочение
регулярного пространственного
расположения атомов (молекул) в
кристаллической решетке. При этом
среднее расстояние между атомами и,
следовательно, силы взаимодействия
изменяется незначительно. Для большинства
кристаллов (кроме воды, и некоторых
сплавов) температура плавления растет
с увеличением внешнего давления, так
как для отдаления атомов друг от друга
при большем давлении требуется большая
энергия тепловых движений, т. е. Более
высокая температура.
При этом
среднее расстояние между атомами и,
следовательно, силы взаимодействия
изменяется незначительно. Для большинства
кристаллов (кроме воды, и некоторых
сплавов) температура плавления растет
с увеличением внешнего давления, так
как для отдаления атомов друг от друга
при большем давлении требуется большая
энергия тепловых движений, т. е. Более
высокая температура.
Кристаллизация — процесс фазового перехода вещества из жидкого состояния в твёрдое кристаллическое с образованием кристаллов.
Фазой называется однородная часть термодинамической системы отделённая от других частей системы(других фаз) поверхностью раздела, при переходе через которую химический состав, структура и свойства вещества изменяются скачками.
Или Кристаллизация — это процесс выделения твёрдой фазы в виде кристаллов из растворов или расплавов, в химической промышленности процесс кристаллизации используется для получения веществ в чистом виде.
Кристаллизация
начинается при достижении некоторого
предельного условия, например,
переохлаждения жидкости или пересыщения
пара, когда практически мгновенно
возникает множество мелких
кристалликов — центров
кристаллизации. Кристаллики растут, присоединяя атомы или
молекулы из жидкости или пара. Рост
граней кристалла происходит послойно,
края незавершённых атомных слоев
(ступени) при росте движутся вдоль грани.
Зависимость скорости роста от условий
кристаллизации приводит к разнообразию
форм роста и структуры кристаллов
(многогранные, пластинчатые, игольчатые,
скелетные, дендритные и
другие формы, карандашные структуры
и т. д.). В процессе кристаллизации
неизбежно возникают различные дефекты.
Кристаллики растут, присоединяя атомы или
молекулы из жидкости или пара. Рост
граней кристалла происходит послойно,
края незавершённых атомных слоев
(ступени) при росте движутся вдоль грани.
Зависимость скорости роста от условий
кристаллизации приводит к разнообразию
форм роста и структуры кристаллов
(многогранные, пластинчатые, игольчатые,
скелетные, дендритные и
другие формы, карандашные структуры
и т. д.). В процессе кристаллизации
неизбежно возникают различные дефекты.
Удельная теплота плавления.
Удельная теплота плавления— количество теплоты, которое необходимо сообщить одной единице массы кристаллического вещества в равновесном изобарно-изотермическом процессе, чтобы перевести его из твёрдого (кристаллического) состояния в жидкое (то же количество теплоты выделяется при кристаллизации вещества).
Теплота плавления — частный случай теплоты фазового перехода I рода.
Различают удельную теплоту плавления (Дж/кг) и молярную (Дж/моль)..
Удельная
теплота плавления обозначается
буквой (греческая
буква лямбда)
Формула расчёта удельной теплоты
плавления: ,
где —
удельная теплота плавления, — количество
теплоты, полученное веществом при
плавлении (или выделившееся при
кристаллизации), —
масса плавящегося (кристаллизующегося)
вещества.
28. Основы термодинамики. Внутренняя энергия. Распределение энергии по степеням свободы.
Начала термодинамики — совокупность аксиом, лежащих в основе термодинамики. Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически.
Необходимость начал термодинамики связана с тем, что термодинамика описывает макроскопические параметры систем без конкретных предположений относительно их микроскопического устройства. Вопросами внутреннего устройства занимается статистическая физика.
Начала термодинамики независимы, то есть ни одно из них не может быть выведено из других начал.
| Главная Учебные курсы Сопротивление материалов Напряжения и деформации Напряжения Мерой интенсивности внутренних сил, распределенных по сечениям, служат напряжения – усилия, приходящиеся на единицу площади сечения. Выделим в окрестности точки B малую площадку . Рис. 3.1. Среднее напряжение на площадке Величина pm называется средним напряжением. Она характеризует среднюю интенсивность внутренних сил. Уменьшая размеры площади, в пределе получим
Величина p называется истинным напряжением или просто напряжением в данной точке данного сечения. Единица напряжения – паскаль, 1 Па = 1 Н/м2. Так как реальные значения напряжений будут выражаться очень большими числами, то следует применять кратные значения единиц, например МПа (мегапаскаль) 1 МПа= 106 Н/м2. Напряжения, как и силы, являются векторными величинами. В каждой точке сечения тела полное напряжение p можно разложить на две составляющие (рис. 3.2): 1) составляющую, нормальную к плоскости сечения. Эта составляющая называется нормальным напряжением и обозначается σ ; 2) составляющую, лежащую(в плоскости сечения. Эта составляющая обозначается τ и называется касательным напряжением. У нормального напряжения ставится индекс, указывающий какой координатной оси параллельно данное напряжение. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначения касательных напряжений имеют два индекса: первый из них указывает, какой оси параллельна нормаль к площадке действия данного напряжения, а второй – какой оси параллельно само напряжение. Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальное напряжение возникает, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц материала по плоскости сечения. Рис. 3.2. Разложение вектора полного напряжения Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечно малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. Вычислим сумму моментов всех элементарных сил, действующих на элемент (рис.3.3), относительно координатных осей, так, например, для оси x с учетом равновесия элемента, имеем:
Повторяя указанные действия для других осей, получим закон парности касательных напряжений:
который формулируется следующим образом: составляющие касательных напряжений на двух взаимно перпендикулярных площадках, перпендикулярные общему ребру, равны по величине и противоположны по знаку, то есть либо обе направлены к ребру либо обе направлены от ребра. Рис. 3.3. Система напряжений в точке Напряжения Следующая Версия для печати |
определение, формула, единицы измерения :: SYL.
 ru
ru
Для длинных и кудрявых: 10 модных стрижек, на которые стоит обратить внимание
Когда лучшее время для вечернего ухода за кожей, чтобы старания пошли на пользу
Плохо пахнет обувь: что можно сделать, чтобы избавить ее от неприятных запахов
14 и 20 воздержимся: каледарь благоприятнх дней для стрижки в октябре 2022
Как создавать луки на все случаи с мешковатыми джинсами дамам в любом возраст
Модно и за ним просто ухаживать: в тренде по-прежнему боб длиной до челюсти
Имитация стрижки боб: как изменить свой образ на один вечер не обрезая волосы
Без погреба и холодильника: как сохранить домашний урожай яблок до весны
Куртки-рубашки на осень 2022: тенденции и самые актуальные модели в образах
Яркая оранжевая подводка с подиума обещает стать главным трендом осени
Автор Сенюкович Станислав
Степень изменения формы тела при деформации зависит не только от природы вещества, но и такой физической величиной, как механическое напряжение.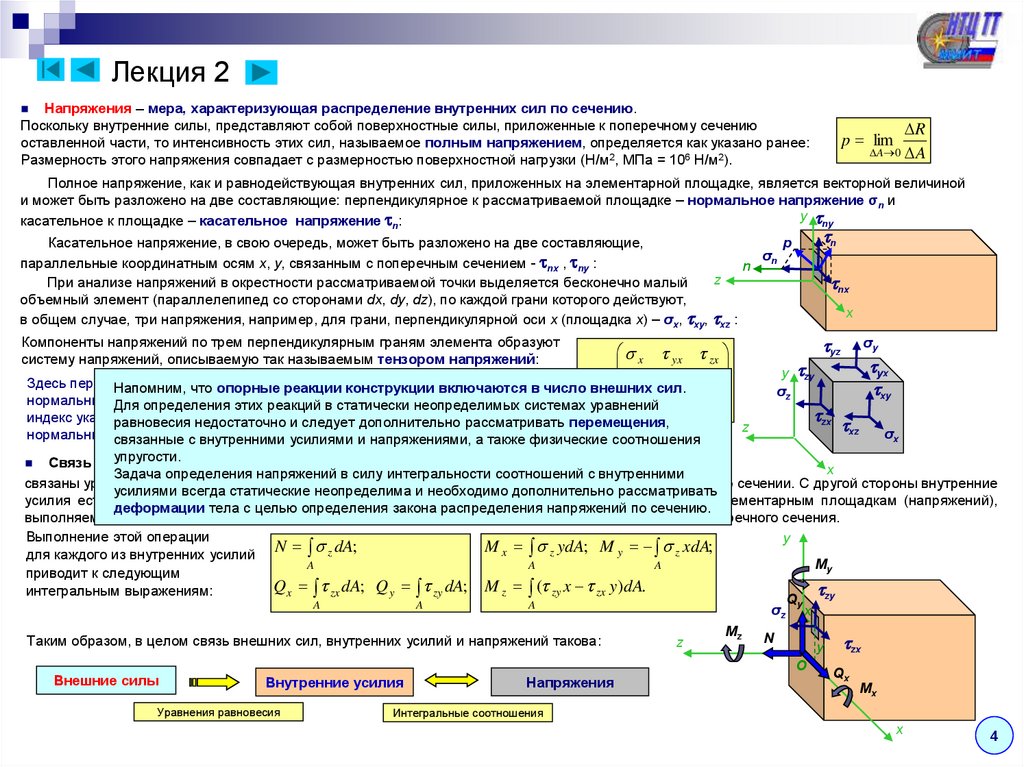 Если рассматривать атомную кристаллическую решетку такого вещества, можно отметить постоянное взаимодействие молекул друг с другом. Это состояние напрямую влияет на величину механического напряжения.
Если рассматривать атомную кристаллическую решетку такого вещества, можно отметить постоянное взаимодействие молекул друг с другом. Это состояние напрямую влияет на величину механического напряжения.
Что такое деформация? Виды деформации
Явление, при котором происходит изменение формы тела под действием какой-либо внешней силы, называется деформацией. Ее природа заключается в движении молекул вещества или целых слоев кристаллической решетки, что приводит к возникновению так называемых дефектов. Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение.
Выделяют несколько видов изменения формы тела:
- Деформация растяжения, когда внешняя сила воздействует вдоль всего тела. Имеет прикладное значение при изготовлении веревок, тросов и строительных материалов;
- Деформация сжатия. В этом случае вектор действия внешней силы совпадает с продольной осью тела, однако он направлен в сторону центра этого тела.
 Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;
Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности; - Деформация сдвига возникает под действием внешней силы, которая направлена перпендикулярно продольной оси и вызывает движение различных плоскостей тела относительно друг друга;
- Деформация изгиба характеризуется искривлением главной оси тела, например, когда имеется две точки опоры. Сила, которую может выдержать тот или иной предмет, а также механическое напряжение играют большую роль при создании строительных материалов;
- Деформация кручения возникает при повороте тела вокруг его продольной оси. Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.
Упругая и пластическая деформация
Механическое напряжение, которое зависит от природы вещества, влияет на способность тела восстанавливать свою первоначальную форму после возникновения дефекта в кристаллической решетке. По этому признаку выделяют упругую и пластическую деформацию.
По этому признаку выделяют упругую и пластическую деформацию.
При пластической деформации тело после воздействия внешней силы не способно восстановить прежнюю форму. Например, пластилин при надавливании на него пальцем сохраняет образовавшуюся ямку.
Упругая деформация характерна для тех веществ, которые способны восстанавливать свою первоначальную форму после воздействия на них внешней силы. Примером может служить та же пружина, которая при любом описанном выше виде деформации возвращается в первоначальное состояние.
Механическое напряжение: формула и определение
Величина механического напряжения характеризуется внутренними силами молекул, которые направлены против давления и деформации тела, на единицу площади.
Различают два вида напряжения:
- Нормальное напряжение приложено на единицу площади сечения, параллельного главной оси тела.
- Касательное механическое напряжение приложено на единицу площади сечения любой другой плоскости сечения.

Для математического вычисления механического напряжения используется формула: Q=F/S.
Единицы механического напряжения
Величина Q в СИ измеряется в паскалях (Па) и зависит от внутренней силы сопротивления деформации, а также площади тела. Сейчас можно встретить и другие единицы измерения механического напряжения. Среди них атмосфера, торр, бар, физическая и техническая атмосфера, метр водяного столба, миллиметр (дюйм) ртутного столба, фунт-сила на квадратный дюйм и т. д.
Похожие статьи
- Регулятор напряжения генератора: схема, проверка
- Основные механические свойства твердых тел
- Сервопривод — что это такое? Устройство, подключение, принцип работы, назначение
- Устройство защиты многофункциональное УЗМ-51М: схема подключения, инструкция и особенности
- Динамо-машина своими руками для велосипеда, для зарядки телефона: устройство
- Основные механические свойства материалов и их применение
- Основные свойства жидкостей
Также читайте
Сопротивление материалов | Механика материалов
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Сопротивление материалов , также известный как механика материалов , ориентирован на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки.
Стресс и напряжение
Когда сила приложена к элементу конструкции, этот элемент будет испытывать как напряжение, так и деформацию в результате действия силы. Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила/дюйм 2 (psi) для обычных единиц США и Н/м 2 (Па) для единиц СИ:
где F — приложенная сила, а A — площадь поперечного сечения, на которое действует сила. Приложенная сила заставит элемент конструкции деформироваться на некоторую длину пропорционально его жесткости.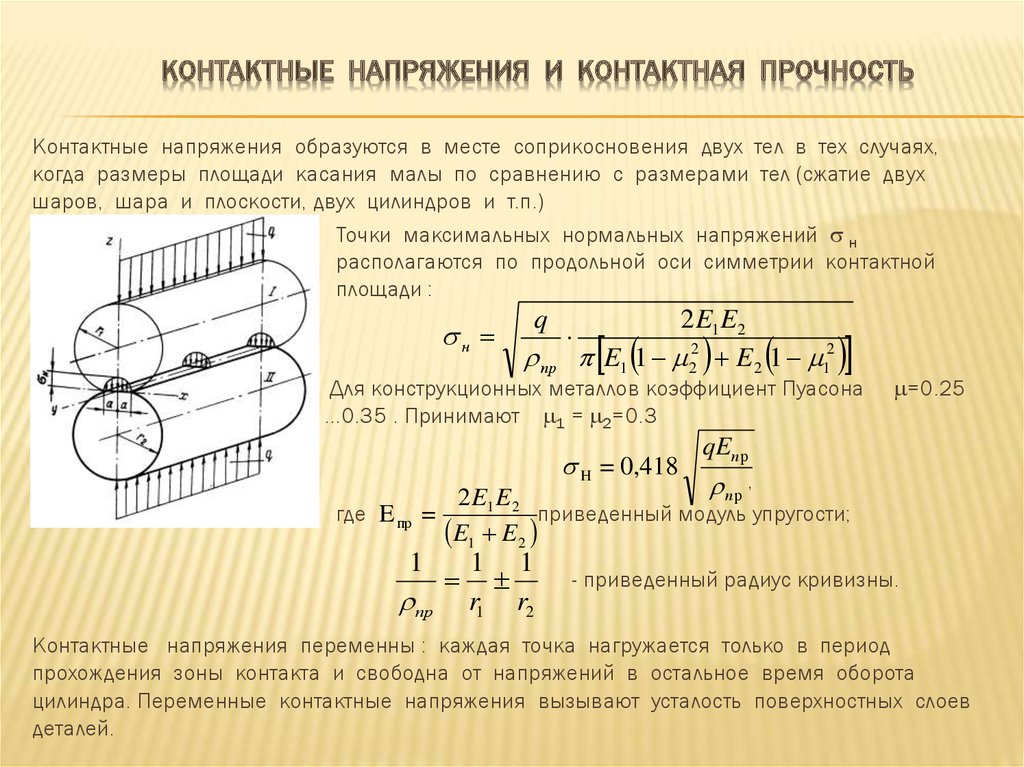 Деформация – это отношение деформации к исходной длине детали:
Деформация – это отношение деформации к исходной длине детали:
где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними).
Существуют различные типы нагрузки, которые приводят к различным типам напряжения, как указано в таблице ниже:
| Тип загрузки | Тип напряжения | Иллюстрация |
|---|---|---|
| Осевая сила |
| |
| Сила сдвига | Напряжение поперечного сдвига | |
| Изгибающий момент | Напряжение при изгибе | |
| Торсион | Напряжение кручения |
Осевое напряжение и напряжение изгиба являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно площади, противодействующей силе. Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.
Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.
| Нормальное напряжение | |
|---|---|
| Осевое напряжение: | |
| Напряжение при изгибе: | |
| Напряжение сдвига | |
|---|---|
| Поперечное напряжение: | |
| Напряжение при кручении: | |
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — сила, а A — площадь поперечного сечения элемента. В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c – центральный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения кручения T — это кручение, r — радиус, а J — полярный момент инерции поперечного сечения.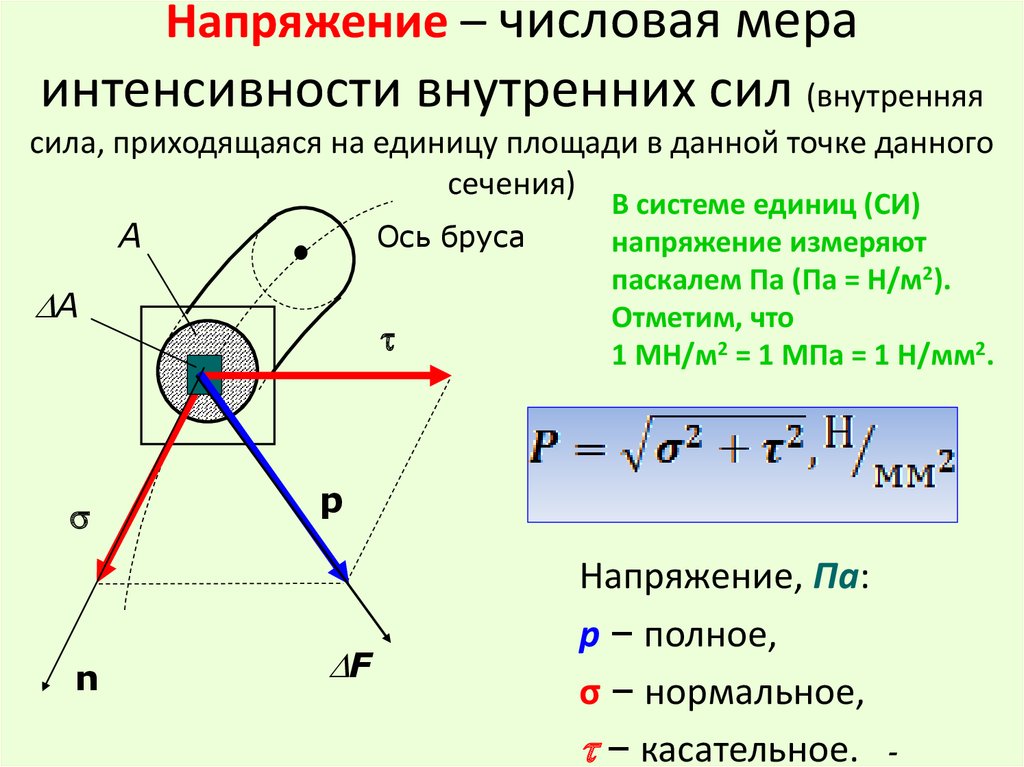
В случае осевого напряжения на прямолинейном участке напряжение распределяется равномерно по всей площади. В случае касательного напряжения распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F/A, и это среднее напряжение сдвига обычно используется при расчете напряжения. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и напряжения кручения максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.
Так же, как первичными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига . В случае нормальной деформации деформация нормальна к области, воспринимающей силу:
В случае деформации поперечного сдвига деформация параллельна площади, несущей силу:
где γ – деформация сдвига (безразмерная), а ϕ — деформированный угол в радианах.
В случае деформации кручения элемент скручивается на угол ϕ вокруг своей оси. Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется по формуле:
где ϕ — угол закручивания, r — радиус стержня, а L — длина.
Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:
где ρ — радиальное расстояние от оси стержня.
Закон Гука
Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, где кривая является линейной).
Нормальный стресс и деформация связаны:
σ = E ϵ
где E — модуль упругости материала, σ — нормальное напряжение, ϵ это нормальное напряжение.
Касательное напряжение и деформация связаны соотношением:
τ = G γ
где G — модуль сдвига материала, τ — касательное напряжение, γ — сдвиговая деформация. Модуль упругости и модуль сдвига связаны соотношением:
Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Закон Гука аналогичен уравнению силы пружины, F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно изменить, чтобы получить деформацию (удлинение) материала:
| Осевое удлинение (от нормального напряжения) | ||
| Угол закручивания (от напряжения сдвига/кручения) |
Энергия деформации
Когда к элементу конструкции прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина. Энергия деформации (т. е. количество потенциальной энергии, накопленной в результате деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и выражается в дюймо-фунтах в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах предела упругости, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F дл | (площадь под кривой нагрузки-прогиба) |
| В пределах эластичности: | (площадь под кривой нагрузки-прогиба) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределе упругости. Первое уравнение основано на площади под кривой отклонения нагрузки. Второе уравнение основано на уравнении потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Более подробную информацию об энергии деформации можно найти здесь.
Жесткость
Жесткость, обычно называемая жесткостью пружины, представляет собой усилие, необходимое для деформации элемента конструкции на единицу длины. Все конструкции можно рассматривать как наборы пружин, а силы и деформации в конструкции связаны уравнением пружины:
F = k δ макс.
где k — жесткость, F — приложенная сила и δ max — максимальный прогиб элемента.
Если прогиб известен, то жесткость элемента можно найти, решив k = F/δ max . Однако максимальное отклонение обычно неизвестно, поэтому жесткость необходимо рассчитывать другими способами. Таблицы прогиба балки можно использовать для общих случаев. Два наиболее полезных уравнения жесткости, которые нужно знать, — это уравнения жесткости для балки с осевой нагрузкой и для консольной балки с торцевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
| Жесткость [фунт-сила/дюйм] | Макс. отклонение [дюйм] | Иллюстрация | |
|---|---|---|---|
| Балка с осевой нагрузкой: | |||
| Консольная балка с торцевой нагрузкой: |
Крутильный эквивалент уравнения пружины:
T = k ϕ
Особый интерес представляет жесткость вала при нагрузке на кручение:
| Жесткость [дюйм*фунт-сила/рад] | Максимальное отклонение [рад] | Иллюстрация | |
|---|---|---|---|
| Вал с торсионной нагрузкой: |
Конструкция с несколькими путями нагрузки
Если в конструкции имеется несколько путей прохождения нагрузки (т. е. в конструкции есть несколько элементов, которые распределяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.
е. в конструкции есть несколько элементов, которые распределяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.
| Пружины параллельно | Пружины серии | |||
|---|---|---|---|---|
| Иллюстрация: | ||||
| Эквивалент жесткости конструкции: | k eq = k 1 + к 2 + к 3 + … | |||
| Сила в отдельном члене: | F 1 = k eq δ tot = F app | |||
| Прогиб отдельного элемента: | ||||
| Общая сила в конструкции: | Ф to = F 1 + F 2 + F 3 + . .. .. | F to = F 1 = F 2 = F 3 = … | ||
| Общий прогиб конструкции: | δ tot = δ 1 = δ 2 = δ 3 = … | δ to = δ 1 + δ 2 + δ 3 + … |
Если элементы на пути нагрузки нельзя рассматривать просто как пружины, соединенные последовательно или как пружины, соединенные параллельно, а скорее они представляют собой комбинацию пружин, соединенных последовательно и параллельно, то проблему необходимо будет решать итеративно. Найдите подгруппу стержней, которые либо чисто последовательно, либо параллельно, и используйте предоставленные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одну пружину с рассчитанными жесткостью, силой и прогибом, и эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Концентрация стресса
Можно представить, что силы и напряжения протекают через материал, как показано на рисунке ниже. Когда геометрия материала изменяется, линии потока перемещаются ближе или дальше друг от друга, чтобы приспособиться. Если в материале есть разрыв, такой как отверстие или выемка, напряжение должно течь вокруг разрыва, и линии потока будут собираться вблизи этого разрыва. Эта внезапная упаковка линий потока вызывает резкий скачок напряжения — это пиковое напряжение называется концентрация стресса . Элемент, вызывающий концентрацию напряжений, называется концентраторами напряжений .
Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в непосредственной близости от несплошности, рассчитайте номинальное напряжение в этой области, а затем масштабируйте его с помощью соответствующего коэффициента концентрации напряжения:
σ макс. = K σ ном.
где о max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, а K — коэффициент концентрации напряжения. При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше следует использовать наименьшую площадь в основании скругления.
Многие справочники содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрий. Двумя наиболее полными наборами факторов концентрации стресса являются факторы концентрации стресса Петерсона и формулы Рорка для стресса и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации напряжений.
Концентрация напряжения будет рассеиваться по мере удаления от источника напряжения. Принцип Сен-Венана — это общее практическое правило, согласно которому расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.
Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах локальная текучесть позволит перераспределить напряжения и уменьшит напряжение вокруг райзера. По этой причине коэффициенты концентрации напряжений обычно не применяются к конструктивным элементам, изготовленным из пластичных материалов. Коэффициенты концентрации напряжения также обычно не применяются при наличии избыточного пути нагрузки, и в этом случае текучесть одного элемента позволит перераспределить силы на элементы на других путях нагрузки. Примером этого является шаблон болтов. Если один болт начнет прогибаться, то другие болты в схеме примут на себя большую нагрузку.
Комбинированные напряжения
В любой точке нагруженного материала общее напряженное состояние можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью касательными напряжениями (по два в каждом направлении):
Нижние индексы нормальных напряжений σ указывают направление нормальных напряжений. Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Обычно напряжения в одном направлении равны нулю, так что полное напряженное состояние возникает в одной плоскости, как показано на рисунке ниже. Это называется плоскостное напряжение . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Поверхностные напряжения обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и напряжение кручения максимальны на поверхности.
На рисунке выше σ x и σ y — нормальные напряжения, τ — касательное напряжение. Напряжения уравновешиваются так, что точка находится в статическом равновесии. Поскольку все напряжения сдвига равны по величине, индексы для простоты опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y . )
)
Надлежащие соглашения о знаках показаны на рисунке. При нормальном напряжении растягивающее напряжение положительно, а сжимающее отрицательно. Для касательного напряжения направление по часовой стрелке является положительным, а против часовой стрелки — отрицательным.
Если напряжения на рисунке выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ по отношению к горизонтали, как показано на рисунке ниже. Приведенные ниже уравнения преобразования дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.
| Нормальное напряжение: | |
| Напряжение сдвига: |
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.
В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимальны и минимальны. Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
| Углы главных напряжений: | |
| Углы предельного напряжения сдвига: |
Приведенные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и предельных касательных напряжений:
| Главные напряжения: | |
| Экстремальные напряжения сдвига: |
Углы, под которыми возникают главные напряжения, составляют 90 ° друг от друга. Главные напряжения всегда сопровождаются нулевым касательным напряжением. Углы, под которыми возникают предельные касательные напряжения, составляют 45 ° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ x + σ y ) / 2.
Углы, под которыми возникают предельные касательные напряжения, составляют 45 ° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ x + σ y ) / 2.
Пара полезных отношений:
| σ 1 +плюс; σ 2 = σ x +плюс; о г | Сумма нормальных напряжений постоянна. |
| Максимальное касательное напряжение равно половине разности главных напряжений. |
Круг Мора
Круг Мора — это способ визуализации напряженного состояния в точке нагруженного материала. Это дает интуитивное представление об уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы главные напряжения, экстремальные касательные напряжения и углы, под которыми эти напряжения возникают. Пример круга Мора показан на рисунке ниже:
Пример круга Мора показан на рисунке ниже:
Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:
Поместите точки на круге, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты ( σ x , −τ ), а напряжения на грани y будут иметь координаты ( σ y , τ ). Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты ( σ 1 , 0 ), а минимальное главное напряжение будет иметь координаты ( σ 2 , 0 ). Поместите точки на окружность для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 2 ).
Все точки будут лежать на периметре окружности. Окружность имеет радиус, равный величине предельных касательных напряжений:
Окружность имеет радиус, равный величине предельных касательных напряжений:
Напряженное состояние на x и y гранях напрягаемого элемента представлено черной линией в круге Мора, соединяющей точки ( σ x , −τ ) и ( σ y , τ ). Эта линия в круге Мора соответствует невращенному элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек в конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента. Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, очки за 9Грань 0006 x и грань y отстоят друг от друга на 180 градусов на круге Мора, но только на 90 градусов на элементе напряжения.
Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в нагруженном элементе и как меняется напряженное состояние в зависимости от угла поворота, см. прилагаемый калькулятор круга Мора.
Приложения
Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:
- Балки
- Столбцы
- Болтовые соединения
- Подъемные проушины
- Сосуды под давлением
- Валы
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции. Предел текучести материала обычно выбирают в качестве предела прочности, с которым сравнивают расчетные напряжения.
Коэффициент безопасности , FS, рассчитывается как:
где σ фактическое — расчетное напряжение в конструкции, а σ предел — максимальный предел напряжения, обычно прочность материала, такая как предел текучести (S ty). Коэффициент безопасности показывает, насколько фактическое напряжение ниже предельного напряжения.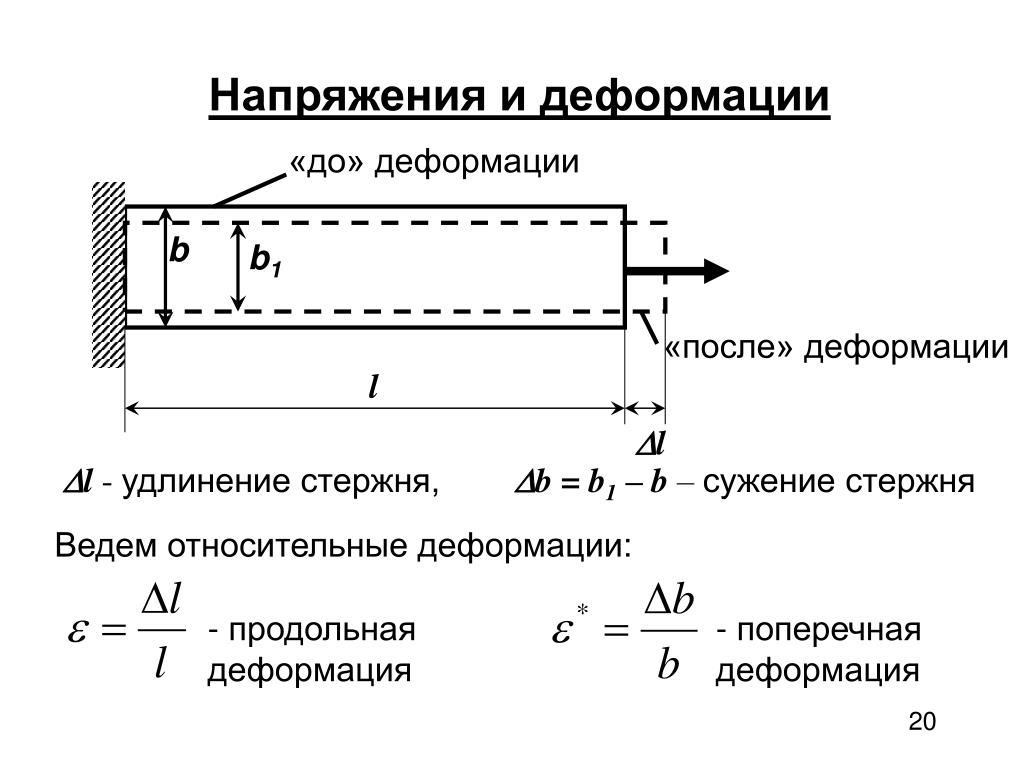 Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию. Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10.
Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию. Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10.
Запас прочности рассчитывается как:
В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы безопасности обычно представляются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции в 1,5 раза превышает фактическое напряжение, запас составляет 50 % (MS = 0,5).
Например, если предельное напряжение конструкции в 1,5 раза превышает фактическое напряжение, запас составляет 50 % (MS = 0,5).
При сообщении коэффициентов безопасности и пределов безопасности иногда требуемый коэффициент безопасности будет «запекаться» в сообщаемых факторах. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, чтобы FS req = 2. Для достижения необходимого коэффициента запаса прочности сообщаемые значения FS и MS рассчитываются как:
Обратите внимание, что при включении требуемого запаса прочности, FS req , сообщаемые FS и MS на самом деле представляют собой запасы по отношению к FS req , а не по отношению к напряжению.
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице прочности материалов. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Каталожные номера
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е издание.

- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е издание.
- Гир, Джеймс М., «Механика материалов», 6-е издание.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е издание.
- Пилки, Уолтер Д. и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
- «Формулы Рорка для стресса и напряжения», 8-е издание.
Определение уравнения напряжения — Прочность (механика) материалов
Напряжение — прочность (механика) материалов
Механика материалов
Когда металл подвергается нагрузке (силе), он деформируется или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Если нагрузка мала, искажение, вероятно, исчезнет при снятии нагрузки. Интенсивность или степень искажения известна как деформация . Если после снятия нагрузки искривление исчезает и металл возвращается к своим первоначальным размерам, деформация называется упругой деформацией . Если искажение исчезает, а металл остается искривленным, тип деформации называется 9.0006 пластиковый штамм . Более подробно деформация будет рассмотрена в следующей главе. Когда к металлу прикладывается нагрузка, сама атомная структура напрягается, сжимаясь, искривляясь или растягиваясь в процессе. Атомы, составляющие металл, располагаются в определенном геометрическом порядке, характерном для этого конкретного металла или сплава, и удерживаются в этом порядке за счет межатомных сил. При таком расположении атомы находятся в состоянии минимальной энергии и имеют тенденцию оставаться в этом расположении. Над металлом должна быть совершена работа (то есть должна быть добавлена энергия), чтобы исказить структуру атомов. (Работа равна произведению силы на расстояние, на которое перемещается сила.)
Если искажение исчезает, а металл остается искривленным, тип деформации называется 9.0006 пластиковый штамм . Более подробно деформация будет рассмотрена в следующей главе. Когда к металлу прикладывается нагрузка, сама атомная структура напрягается, сжимаясь, искривляясь или растягиваясь в процессе. Атомы, составляющие металл, располагаются в определенном геометрическом порядке, характерном для этого конкретного металла или сплава, и удерживаются в этом порядке за счет межатомных сил. При таком расположении атомы находятся в состоянии минимальной энергии и имеют тенденцию оставаться в этом расположении. Над металлом должна быть совершена работа (то есть должна быть добавлена энергия), чтобы исказить структуру атомов. (Работа равна произведению силы на расстояние, на которое перемещается сила.)
Напряжение – это внутреннее сопротивление или противодействующая сила материала искажающему воздействию внешней силы или нагрузки. Эти противодействующие силы стремятся вернуть атомы в их нормальное положение. Полное развиваемое сопротивление равно внешней нагрузке. Это сопротивление известно как стресс .
Полное развиваемое сопротивление равно внешней нагрузке. Это сопротивление известно как стресс .
Хотя невозможно измерить интенсивность этого напряжения, можно измерить внешнюю нагрузку и площадь, к которой она приложена. Напряжение (s) можно приравнять нагрузке на единицу площади или силе (F), приложенной к площади поперечного сечения (A) перпендикулярно силе, как показано в уравнении ниже 9.0003
Где:
s = напряжение (psi или фунты силы на дюйм 2 )
F = приложенная сила (фунты силы)
A = площадь поперечного сечения (дюймы 2 )
Виды стресса
Напряжения возникают в любом материале, который подвергается нагрузке или любой приложенной силе. Существует много типов напряжений, но все они в целом могут быть отнесены к одной из шести категорий: остаточные напряжения, структурные напряжения, напряжения давления, напряжения течения, термические напряжения и усталостные напряжения.
Остаточное напряжение
Остаточное напряжение возникает в результате производственных процессов, которые оставляют напряжения в материале. Сварка оставляет остаточные напряжения в свариваемых металлах.
Структурное напряжение
Структурное напряжение – это напряжение, возникающее в элементах конструкции из-за веса, который они поддерживают. Веса обеспечивают нагрузки. Эти напряжения возникают в фундаментах и каркасах зданий, а также в деталях машин.
Давление
Давление — это напряжение, возникающее в сосудах, содержащих материалы под давлением. Нагружение обеспечивается той же силой, что и давление.
Напряжения течения
Напряжения течения возникают, когда масса текущей жидкости создает динамическое давление на стенку трубопровода. Сила удара жидкости о стенку действует как нагрузка. Этот тип напряжения может применяться нестационарным образом, когда скорость потока колеблется. Гидравлический удар является примером нестационарного напряжения потока.
Этот тип напряжения может применяться нестационарным образом, когда скорость потока колеблется. Гидравлический удар является примером нестационарного напряжения потока.
Термическое напряжение
Термическое напряжение возникает всякий раз, когда в материале присутствуют температурные градиенты. Различные температуры вызывают различные расширения и подвергают материалы внутреннему напряжению. Этот вид напряжения особенно заметен в механизмах, работающих при высоких температурах и охлаждаемых холодной жидкостью.
Усталостное напряжение
Усталостное напряжение возникает из-за циклического приложения напряжения. Напряжения могут быть вызваны вибрацией или термоциклированием.
Значение всех напряжений увеличивается, когда поддерживающие их материалы имеют дефекты. Дефекты, как правило, добавляют дополнительную нагрузку на материал. Кроме того, при циклических или нестационарных нагрузках напряжения могут более сильно воздействовать на материал. Дополнительные напряжения, связанные с дефектами и циклическими нагрузками, могут превышать напряжения, необходимые для разрушения материала. Интенсивность напряжений в теле детали выражается одним из трех основных видов внутренней нагрузки. Они известны как растяжение, сжатие и сдвиг. Рисунок 1 иллюстрирует различные типы стресса.
Дополнительные напряжения, связанные с дефектами и циклическими нагрузками, могут превышать напряжения, необходимые для разрушения материала. Интенсивность напряжений в теле детали выражается одним из трех основных видов внутренней нагрузки. Они известны как растяжение, сжатие и сдвиг. Рисунок 1 иллюстрирует различные типы стресса.
Математически существует только два типа внутренней нагрузки, потому что напряжение растяжения и сжатия можно рассматривать как положительную и отрицательную версии одного и того же типа нормальной нагрузки.
Однако в механическом проектировании реакция компонентов на эти два состояния может быть настолько разной, что лучше и безопаснее рассматривать их как отдельные типы.
Как показано на рисунке 1, плоскость растягивающего или сжимающего напряжения лежит перпендикулярно оси действия силы, от которой оно исходит. Плоскость касательного напряжения лежит в плоскости системы сил, от которой оно исходит.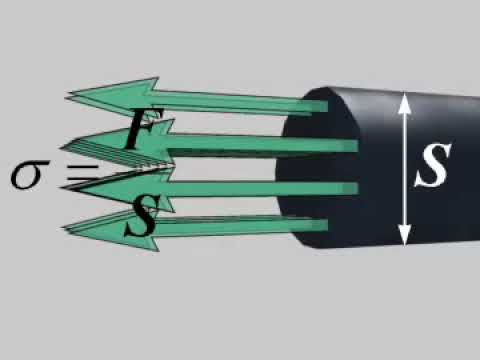 Очень важно сохранять эти различия совершенно ясными как в уме, так и в способе выражения.
Очень важно сохранять эти различия совершенно ясными как в уме, так и в способе выражения.
Растягивающее напряжение
Растягивающее напряжение — это тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться, как показано на рис. 1(а).
Напряжение сжатия
Напряжение сжатия является противоположностью напряжения растяжения. Соседние части материала имеют тенденцию прижиматься друг к другу через типичную плоскость напряжения, как показано на рисунке 1 (b).
Напряжение сдвига
Напряжение сдвига возникает, когда две части материала стремятся скользить друг относительно друга в любой типичной плоскости сдвига при приложении силы, параллельной этой плоскости, как показано на рис. 1(c).
Оценка механических свойств производится путем рассмотрения трех основных типов напряжения. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями.
Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями.
Сокращенные обозначения следующие.
Для растягивающих напряжений: «+S N » (или «S N «) или «s» (сигма)
Для сжимающих напряжений: «-S N » или «-s» (минус сигма) )
Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью . Например, металлы и жидкости несжимаемы, а газы и пары сжимаемы. Касательное напряжение равно силе, деленной на площадь поверхности, параллельной направлению действия силы, как показано на рисунке 1(c) выше.
Два вида напряжения могут одновременно присутствовать в одной плоскости при условии, что одно из напряжений является напряжением сдвига. При определенных условиях в материале могут одновременно присутствовать разные сочетания видов основных напряжений. Примером может служить корпус реактора во время работы. Стенка испытывает растягивающие напряжения в различных местах из-за температуры и давления жидкости, воздействующей на стенку. Сжимающее напряжение прикладывается снаружи в других местах на стенке из-за внешнего давления, температуры и сжатия опор, связанных с сосудом. В этом случае главными напряжениями считаются растягивающие и сжимающие напряжения. Если присутствует, напряжение сдвига будет действовать под углом 45° к основному напряжению.
Примером может служить корпус реактора во время работы. Стенка испытывает растягивающие напряжения в различных местах из-за температуры и давления жидкости, воздействующей на стенку. Сжимающее напряжение прикладывается снаружи в других местах на стенке из-за внешнего давления, температуры и сжатия опор, связанных с сосудом. В этом случае главными напряжениями считаются растягивающие и сжимающие напряжения. Если присутствует, напряжение сдвига будет действовать под углом 45° к основному напряжению.
Механический стресс как общий знаменатель между хроническим воспалением, раком и болезнью Альцгеймера
1. Jacobs CR, Huang H, Kwon RY. Введение в клеточную механику и механобиологию. Нью-Йорк, штат Нью-Йорк: Garland Science; (2012). [Google Scholar]
2. Бринкманн П., Фробин В., Лейвсет Г. Скелетно-мышечная биомеханика. Штутгарт. Нью-Йорк, штат Нью-Йорк: Thieme Medical Publishers Inc.; (2013). [Google Scholar]
3. Хэмилл О.П., Мартинак Б. Молекулярные основы механотрансдукции в живых клетках. Physiol Rev (2001) 81 (2): 685–740. [PubMed] [Академия Google]
Physiol Rev (2001) 81 (2): 685–740. [PubMed] [Академия Google]
4. Kim D-H, Wong PK, Park J, Levchenko A, Sun Y. Микроинженерные платформы для клеточной механобиологии. Annu Rev Biomed Eng (2009) 11: 203–33. 10.1146/annurev-bioeng-061008-124915 [PubMed] [CrossRef] [Google Scholar]
5. Eyckmans J, Boudou T, Yu X, Chen CS. Автостопщик по механобиологии. Dev Cell (2011) 21 (1): 35–47. 10.1016/j.devcel.2011.06.015 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
6. Thompson DW. Формы клеток. В: Боннер Дж. Т., редактор. О росте и форме. Кембридж: Издательство Кембриджского университета; (1942). 368 стр. [Google Scholar]
7. Модесто К., Сенгупта П.П. Механика миокарда при кардиомиопатиях. Prog Cardiovasc Dis (2014) 57 (1): 111–24. 10.1016/j.pcad.2014.03.003 [PubMed] [CrossRef] [Google Scholar]
8. Robicsek F, Thubrikar MJ. Механический стресс как причина порока аортального клапана. Презентация нового протеза корня аорты. Acta Chir Belg (2002) 102 (1): 1–6. [PubMed] [Google Scholar]
[PubMed] [Google Scholar]
9. Heo KS, Fujiwara K, Abe J. Напряжение сдвига и атеросклероз. Mol Cells (2014) 37(6):435–40. 10.14348/molcells.2014.0078 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
10. Visser AW, de Mutsert R, le Cessie S, den Heijer M, Rosendaal FR, Kloppenburg M, et al. Относительный вклад механического стресса и системных процессов в различные типы остеоартрита: исследование NEO. Энн Реум Дис (2014). 10.1136/annrheumdis-2013-205012 [PubMed] [CrossRef] [Google Scholar]
11. Michael R, Barraquer RI, Willekens B, van Marle J, Vrensen GFJM. Морфология возрастной клиновидной кортикальной катаракты: случай механического стресса. Vision Res (2008) 48 (4): 626–34. 10.1016/j.visres.2007.12.005 [PubMed] [CrossRef] [Google Scholar]
12. Бленноу К., де Леон М.Дж., Зеттерберг Х. Болезнь Альцгеймера. Ланцет (2006) 368 (9533): 387–403. 10.1016/S0140-6736(06)69113-7 [PubMed] [CrossRef] [Google Scholar]
13. Waring SC, Rosenberg RN. Полногеномные ассоциативные исследования болезни Альцгеймера. Arch Neurol (2008) 65 (3): 329–34. 10.1001/archneur.65.3.329 [PubMed] [CrossRef] [Google Scholar]
Полногеномные ассоциативные исследования болезни Альцгеймера. Arch Neurol (2008) 65 (3): 329–34. 10.1001/archneur.65.3.329 [PubMed] [CrossRef] [Google Scholar]
14. Selkoe DJ. Превращение клеточной биологии в терапевтические достижения при болезни Альцгеймера. Nature (1999) 399 (6738 Приложение): A23–31. 10.1038/19866 [PubMed] [CrossRef] [Google Scholar]
15. Шварц Л. Рак – Между гликолизом и физическими ограничениями: между гликолизом и физическими ограничениями. Берлин Гейдельберг: Springer Science & Business Media; (2004). 172 стр. [Google Scholar]
16. Гримбл РФ. Воспалительная реакция у пожилых людей. Curr Opin Clin Nutr Metab Care (2003) 6 (1): 21–9. 10.1097/00075197-200301000-00005 [PubMed] [CrossRef] [Google Scholar]
17. Greig NH, Mattson MP, Perry T, Chan SL, Giordano T, Sambamurti K, et al.
Новые терапевтические стратегии и кандидаты в лекарства для лечения нейродегенеративных заболеваний: ингибиторы p53 и TNF-альфа, а также агонисты рецептора GLP-1.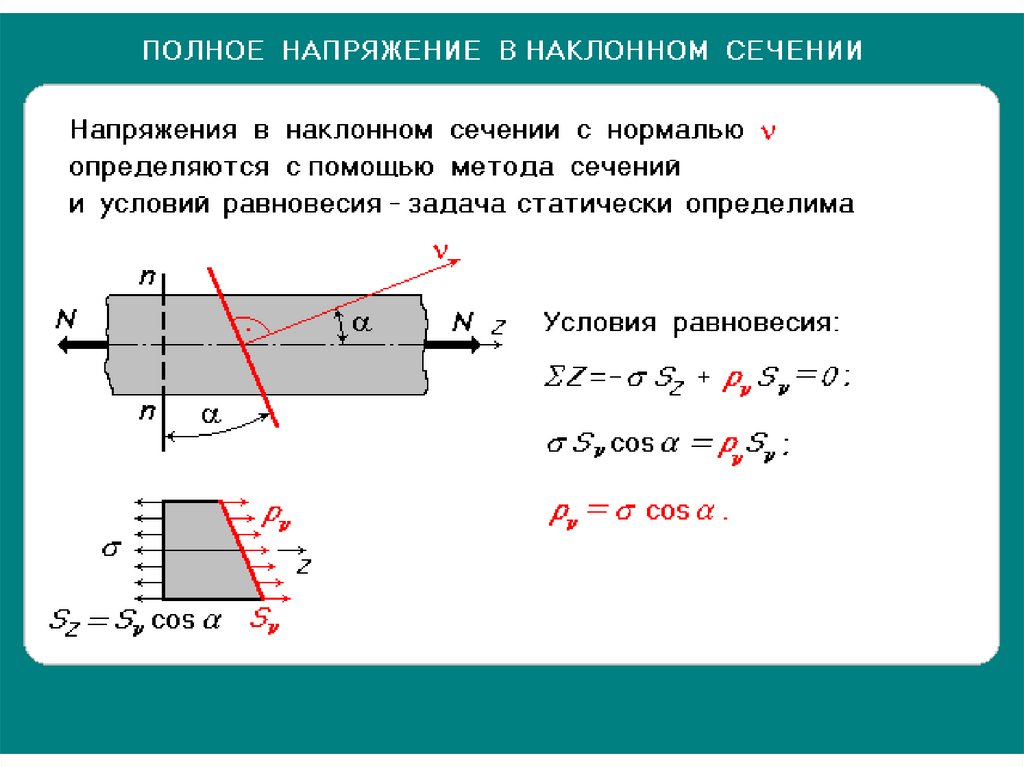 Энн Н.Ю. Академия наук (2004) 1035:290–315. 10.1196/annals.1332.018 [PubMed] [CrossRef] [Google Scholar]
Энн Н.Ю. Академия наук (2004) 1035:290–315. 10.1196/annals.1332.018 [PubMed] [CrossRef] [Google Scholar]
18. ДеВита В., Лоуренс Т., Розенберг С., ДеПиньо Р., Вайнберг Р. Рак печени. В: ДеВита Хеллман. редакторы. Рак Розенберга: принципы и практика онкологии. 9-е изд. Североамериканское издание. Филадельфия, Пенсильвания: LWW; (2011). 2800 р. [Google Scholar]
19. Подольский ДИК. Заболевания, связанные с алкоголем, и цирроз печени. Принципы внутренней медицины Харрисона. 13-е изд. Нью-Йорк: Макгроу Хилл; (1994). п. 1483–1499 гг.5. [Google Scholar]
20. Szekely CA, Town T, Zandi PP. НПВП для химиопрофилактики болезни Альцгеймера. Subcell Biochem (2007) 42: 229–48. 10.1007/1-4020-5688-5_11 [PubMed] [CrossRef] [Google Scholar]
21. Rothwell PM. Аспирин в профилактике спорадического колоректального рака: текущие клинические данные и общий баланс рисков и преимуществ. Недавние результаты Cancer Res (2013) 191: 121–42. 10.1007/978-3-642-30331-9_7 [PubMed] [CrossRef] [Google Scholar]
22.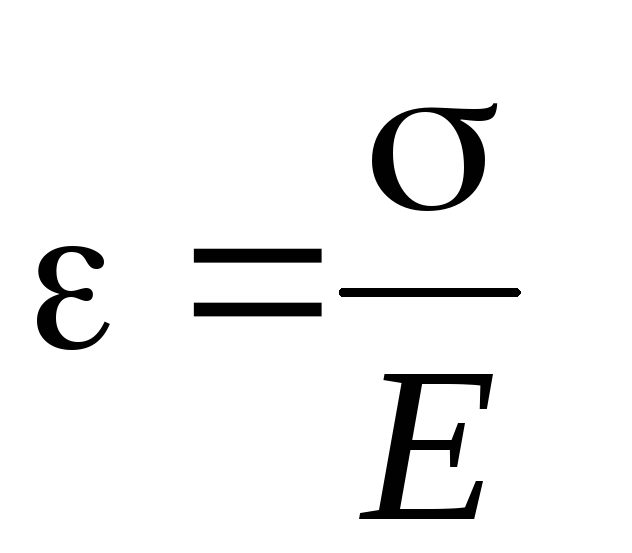 Schwartz L, Guais A, Pooya M, Abolhassani M. Является ли воспаление следствием внеклеточной гиперосмолярности?
J Inflamm (Лондон) (2009)) 6:21. 10.1186/1476-9255-6-21 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Schwartz L, Guais A, Pooya M, Abolhassani M. Является ли воспаление следствием внеклеточной гиперосмолярности?
J Inflamm (Лондон) (2009)) 6:21. 10.1186/1476-9255-6-21 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
23. Abolhassani M, Wertz X, Pooya M, Chaumet-Riffaud P, Guais A, Schwartz L. Причины гиперосмолярности воспаление за счет метилирования протеинфосфатазы 2А. Inflamm Res (2008) 57 (9): 419–29. 10.1007/s00011-007-7213-0 [PubMed] [CrossRef] [Google Scholar]
24. Schwartz L, Abolhassani M, Pooya M, Steyaert J-M, Wertz X, Israël M, et al. Гиперосмотический стресс способствует воспалению толстой кишки у мышей за счет метилирования протеинфосфатазы 2А. Am J Physiol Gastrointest Liver Physiol (2008) 295(5):G934–41. 10.1152/ajpgi..2008 [PubMed] [CrossRef] [Google Scholar]
25. Schwartz L, Balosso J, Baillet F, Brun B, Amman JP, Sasco AJ. Рак: роль внеклеточного заболевания. Медицинские гипотезы (2002) 58 (4): 340–6. 10.1054/mehy.2001. 1539 [PubMed] [CrossRef] [Google Scholar]
1539 [PubMed] [CrossRef] [Google Scholar]
26. Johnson FE, Zhou M, Collins BT, Huang JS. Механическая деформация вызывает пролиферацию клеток колоректальной карциномы человека. Int J Oncol (2000) 16(3):617–22. [PubMed] [Академия Google]
27. Helmlinger G, Netti PA, Lichtenbeld HC, Melder RJ, Jain RK. Солидный стресс тормозит рост многоклеточных опухолевых сфероидов. Nat Biotechnol (1997) 15(8):778–83. 10.1038/nbt0897-778 [PubMed] [CrossRef] [Google Scholar]
28. Флери В., Шварц Л. Численное исследование влияния потери клеточной полярности на инвазивность и геометрию рака. Фракталы (2003) 11 (04): 397–414. 10.1142/S0218348X0300204X [CrossRef] [Google Scholar]
29. Locke D. Щелевые соединения в нормальной и неопластической молочной железе. Джей Патол (1998) 186(4):343–9. 10.1002/(SICI)1096-9896(199812)186:4<343::AID-PATh289>3.3.CO;2-O [PubMed] [CrossRef] [Google Scholar]
30. Lingle WL, Lutz WH, Ingle JN, Maihle NJ, Солсбери JL. Гипертрофия центросом в опухолях молочной железы человека: значение для стабильности генома и клеточной полярности.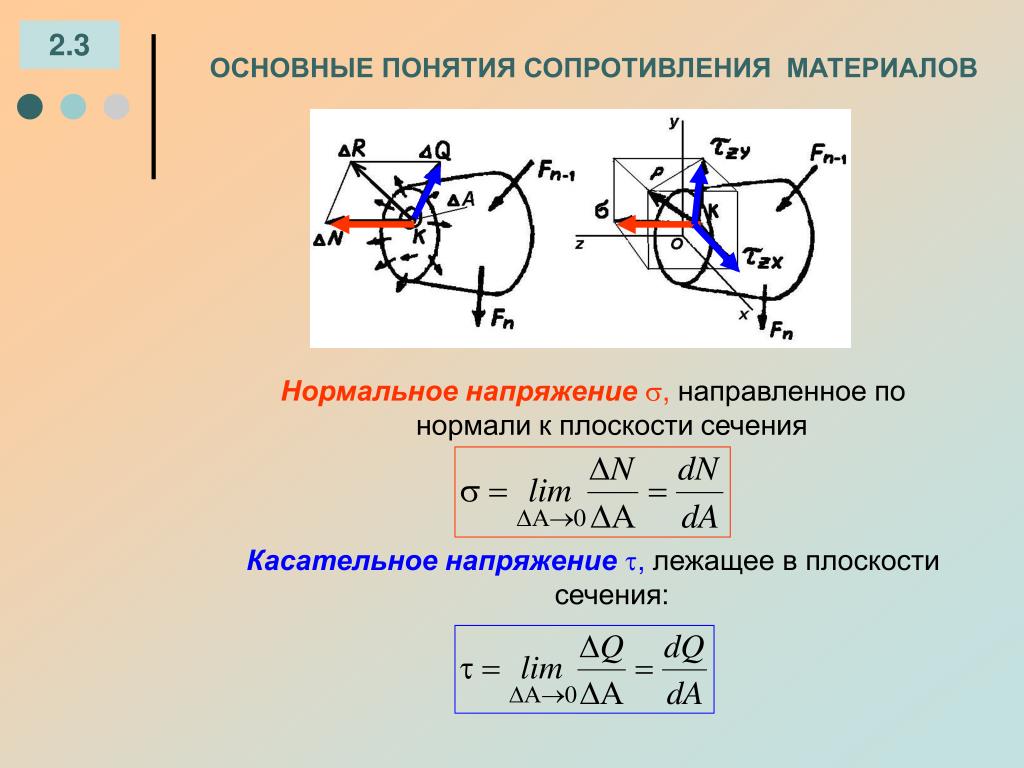 Proc Natl Acad Sci U S A (1998) 95(6):2950–5. 10.1073/pnas.95.6.2950 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Proc Natl Acad Sci U S A (1998) 95(6):2950–5. 10.1073/pnas.95.6.2950 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
31. Peters WS, Tomos AD. История натяжения тканей. Энн Бот (1996) 77(6):657–65. 10.1093/aob/77.6.657 [PubMed] [CrossRef] [Google Scholar]
32. Silverberg G, Mayo M, Saul T, Fellmann J, McGuire D. Повышенное давление спинномозговой жидкости у пациентов с болезнью Альцгеймера. Анализ спинномозговой жидкости (2006) 3:7. 10.1186/1743-8454-3-7 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
33. Wostyn P. Внутричерепное давление и болезнь Альцгеймера: гипотеза. Медицинские гипотезы (1994) 43 (4): 219–22. 10.1016/0306-9877(94)-8 [PubMed] [CrossRef] [Google Scholar]
34. Wostyn P. Может ли хроническое повышенное внутричерепное давление или воздействие повторяющихся прерывистых повышений внутричерепного давления повышать риск болезни Альцгеймера? Медицинские гипотезы (2004) 62 (6): 925–30. 10.1016/j.mehy.2004.01.013 [PubMed] [CrossRef] [Google Scholar]
35. Wostyn P, Audenaert K, De Deyn PP. Изменения, связанные с болезнью Альцгеймера, при заболеваниях, характеризующихся повышением внутричерепного или внутриглазного давления. Clin Neurol Neurosurge (2008) 110 (2): 101–9. 10.1016/j.clineuro.2007.10.011 [PubMed] [CrossRef] [Google Scholar]
Wostyn P, Audenaert K, De Deyn PP. Изменения, связанные с болезнью Альцгеймера, при заболеваниях, характеризующихся повышением внутричерепного или внутриглазного давления. Clin Neurol Neurosurge (2008) 110 (2): 101–9. 10.1016/j.clineuro.2007.10.011 [PubMed] [CrossRef] [Google Scholar]
36. Востин П., Оденарт К., Де Дейн П.П. Болезнь Альцгеймера: церебральная глаукома? Медицинские гипотезы (2010) 74 (6): 973–7. 10.1016/j.mehy.2009.12.019 [PubMed] [CrossRef] [Google Scholar]
37. Бейтман Г.А. Роль измененного импеданса в патофизиологии нормотензивной гидроцефалии, болезни Альцгеймера и сирингомиелии. Медицинские гипотезы (2004) 63 (6): 980–5. 10.1016/j.mehy.2004.04.019 [PubMed] [CrossRef] [Google Scholar]
38. El Sankari S, Gondry-Jouet C, Fichten A, Godefroy O, Serot JM, Deramond H, et al.
Цереброспинальная жидкость и кровоток при легких когнитивных нарушениях и болезни Альцгеймера: дифференциальный диагноз с идиопатической нормотензивной гидроцефалией. Жидкости Барьеры ЦНС. (2011) 8(1):12. 10.1186/2045-8118-8-12 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
(2011) 8(1):12. 10.1186/2045-8118-8-12 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
39. Бейтман Г.А. Пульсовая энцефалопатия: спектральная гипотеза, включающая болезнь Альцгеймера, сосудистую деменцию и гидроцефалию нормального давления. Медицинские гипотезы (2004) 62 (2): 182–7. 10.1016/S0306-9877(03)00330-X [PubMed] [CrossRef] [Google Scholar]
40. Bateman GA, Levi CR, Schofield P, Wang Y, Lovett EC. Венозные проявления пульсовой энцефалопатии: дисфункция виндкесселя при нормальном старении и старческом слабоумии. Нейрорадиология (2008) 50(6):491–7. 10.1007/s00234-008-0374-x [PubMed] [CrossRef] [Google Scholar]
41. Нагаи К., Акисита М., Мачида А., Сонохара К., Они М., Тоба К. Корреляция между скоростью пульсовой волны и когнитивной функцией при несосудистой деменции. J Am Geriatr Soc (2004) 52 (6): 1037–8. 10.1111/j.1532-5415.2004.52277_15.x [PubMed] [CrossRef] [Google Scholar]
42. Barz H, Schreiber A, Barz U. Импульсы и волны давления вызывают возбуждение и проводимость в нервной системе. Медицинские гипотезы (2013) 81 (5): 768–72. 10.1016/j.mehy.2013.07.049 [PubMed] [CrossRef] [Google Scholar]
Медицинские гипотезы (2013) 81 (5): 768–72. 10.1016/j.mehy.2013.07.049 [PubMed] [CrossRef] [Google Scholar]
43. Хачия Н.С., Кодзука Ю., Канеко К. Механический стресс и образование белковых агрегатов при нейродегенеративных заболеваниях. Медицинские гипотезы (2008) 70 (5): 1034–7. 10.1016/j.mehy.2007.06.043 [PubMed] [CrossRef] [Google Scholar]
44. Chetelat G. Болезнь Альцгеймера: aβ-независимые процессы – переосмысление доклинической БА. Nat Rev Neurol (2013) 9 (3): 123–4. 10.1038/nrneurol.2013.21 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
45. Xu Z, Paparcone R, Buehler MJ. Амилоидные фибриллы абета (1-40) болезни Альцгеймера имеют механические свойства, зависящие от размера. Биофиз Дж (2010) 98(10):2053–62. 10.1016/j.bpj.2009.12.4317 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
46. Lazarus C, Soheilypour M, Mofrad MRK. Торсионное поведение пучков аксональных микротрубочек. Биофиз J (2015) 109 (2): 231–9. 10.1016/j.bpj. 2015.06.029 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2015.06.029 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
47. Kristen AV, Schnabel PA, Winter B, Helmke BM, Longerich T, Hardt S, et al. Высокая распространенность амилоида в 150 хирургически удаленных сердечных клапанах — сравнение гистологических и клинических данных выявляет корреляцию с атеровоспалительными состояниями. Сердечно-сосудистый патол (2010) 19(4): 228–35. 10.1016/j.carpath.2009.04.005 [PubMed] [CrossRef] [Google Scholar]
48. Niggemeyer O, Steinhagen J, Fuerst M, Zustin J, Rüther W. Отложение амилоида при ревматоидном артрите тазобедренного сустава. Rheumatol Int (2012) 32(9):2645–51. 10.1007/s00296-011-2005-9 [PubMed] [CrossRef] [Google Scholar]
49. Varongchayakul N, Johnson S, Quabili T, Cappello J, Ghandehari H, Solares SDJ, et al. Прямое наблюдение за зародышеобразованием амилоида при наномеханическом растяжении. АСУ Нано (2013) 7(9)): 7734–43. 10.1021/nn402322k [PubMed] [CrossRef] [Google Scholar]
50. Solar M, Buehler MJ. Деформационное поведение и механические свойства нанопроволок амилоидного белка. J Mech Behav Biomed Mater (2013) 19:43–9. 10.1016/j.jmbbm.2012.10.007 [PubMed] [CrossRef] [Google Scholar]
Деформационное поведение и механические свойства нанопроволок амилоидного белка. J Mech Behav Biomed Mater (2013) 19:43–9. 10.1016/j.jmbbm.2012.10.007 [PubMed] [CrossRef] [Google Scholar]
51. Pannuzzo M, Milardi D, Raudino A, Karttunen M, La Rosa C. Аналитическая модель и многомасштабное моделирование агрегации пептида Aβ в липидах мембраны: к единому описанию конформационных переходов, олигомеризации и повреждения мембран. Phys Chem Chem Phys (2013) 15 (23): 8940–51. 10.1039/c3cp44539a [PubMed] [CrossRef] [Google Scholar]
52. Чаухан Н.Б. Хронические нейродегенеративные последствия черепно-мозговой травмы. Restor Neurol Neurosci (2014) 32(2):337–65. 10.3233/RNN-130354 [PubMed] [CrossRef] [Google Scholar]
53. Stein TD, Alvarez VE, McKee AC. Хроническая травматическая энцефалопатия: спектр нейропатологических изменений после повторных травм головного мозга у спортсменов и военнослужащих. Альцгеймер Res Ther (2014) 6 (1): 4. 10.1186/alzrt234 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
54. Gatson JW, Warren V, Abdelfattah K, Wolf S, Hynan LS, Moore C, et al.
Обнаружение β-амилоидных олигомеров как предиктор неврологического исхода после черепно-мозговой травмы. Дж. Нейросург (2013) 118(6):1336–42. 10.3171/2013.2.JNS121771 [PubMed] [CrossRef] [Google Scholar]
Gatson JW, Warren V, Abdelfattah K, Wolf S, Hynan LS, Moore C, et al.
Обнаружение β-амилоидных олигомеров как предиктор неврологического исхода после черепно-мозговой травмы. Дж. Нейросург (2013) 118(6):1336–42. 10.3171/2013.2.JNS121771 [PubMed] [CrossRef] [Google Scholar]
55. Kanayama G, Takeda M, Niigawa H, Ikura Y, Tamii H, Taniguchi N, et al. Влияние повторяющихся легких травм головного мозга на белок цитоскелета и поведение. Methods Find Exp Clin Pharmacol (1996) 18(2):105–15. [PubMed] [Академия Google]
56. Кейн М.Дж., Ангоа-Перес М., Бриггс Д.И., Виано Д.К., Крайпке К.В., Кун Д.М. Мышиная модель повторяющейся легкой черепно-мозговой травмы человека. J Neurosci Methods (2012) 203(1):41–9. 10.1016/j.jneumeth.2011.09.003 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
57. Kucewicz JC, Dunmire B, Leotta DF, Panagiotides H, Paun M, Beach KW. Функциональная визуализация пульсации тканей головного мозга при зрительной стимуляции. Ультразвуковая медицинская биология (2007) 33 (5): 681–90. 10.1016/j.ultrasmedbio.2006.11.008 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
10.1016/j.ultrasmedbio.2006.11.008 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
58. Linninger AA, Xenos M, Sweetman B, Ponkshe S, Guo X, Penn R. Математическая модель динамики крови, спинномозговой жидкости и головного мозга. J Math Biol (2009) 59 (6): 729–59. 10.1007/s00285-009-0250-2 [PubMed] [CrossRef] [Google Scholar]
59. Savolainen S, Paljärvi L, Vapalahti M. Распространенность болезни Альцгеймера у пациентов, обследованных по поводу гидроцефалии с предполагаемым нормальным давлением: клиническое и невропатологическое исследование . Acta Neurochir (Вена) (1999) 141 (8): 849–53. 10.1007/s007010050386 [PubMed] [CrossRef] [Google Scholar]
60. Bech RA, Waldemar G, Gjerris F, Klinken L, Juhler M. Эффекты шунтирования у пациентов с идиопатической гидроцефалией нормального давления; корреляция с результатами церебральной и лептоменингеальной биопсии. Acta Neurochir (Вена) (1999) 141 (6): 633–9. 10.1007/s007010050353 [PubMed] [CrossRef] [Google Scholar]
61. Golomb J, Wisoff J, Miller DC, Boksay I, Kluger A, Weiner H, et al.
Коморбидность болезни Альцгеймера при нормотензивной гидроцефалии: распространенность и шунтирующий ответ. J Neurol Neurosurg Psychiatry (2000) 68(6):778–81. 10.1136/jnnp.68.6.778 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Golomb J, Wisoff J, Miller DC, Boksay I, Kluger A, Weiner H, et al.
Коморбидность болезни Альцгеймера при нормотензивной гидроцефалии: распространенность и шунтирующий ответ. J Neurol Neurosurg Psychiatry (2000) 68(6):778–81. 10.1136/jnnp.68.6.778 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
62. Кабрал Д., Бич Т.Г., Веддерс Л., Сью Л.И., Якобсон С., Майерс К. и соавт. Частота патологии болезни Альцгеймера на аутопсии у больных с клинической нормотензивной гидроцефалией. Демент Альцгеймера (2011) 7 (5): 509–13. 10.1016/j.jalz.2010.12.008 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
63. Streitberger K-J, Wiener E, Hoffmann J, Freimann FB, Klatt D, Braun J, et al. Прижизненные вязкоупругие свойства головного мозга при нормотензивной гидроцефалии. ЯМР Биомед (2011) 24 (4): 385–92. 10.1002/nbm.1602 [PubMed] [CrossRef] [Google Scholar]
64. Silverberg GD, Mayo M, Saul T, Rubenstein E, McGuire D. Болезнь Альцгеймера, нормотензивная гидроцефалия и старческие изменения ликвороциркуляции физиология: гипотеза.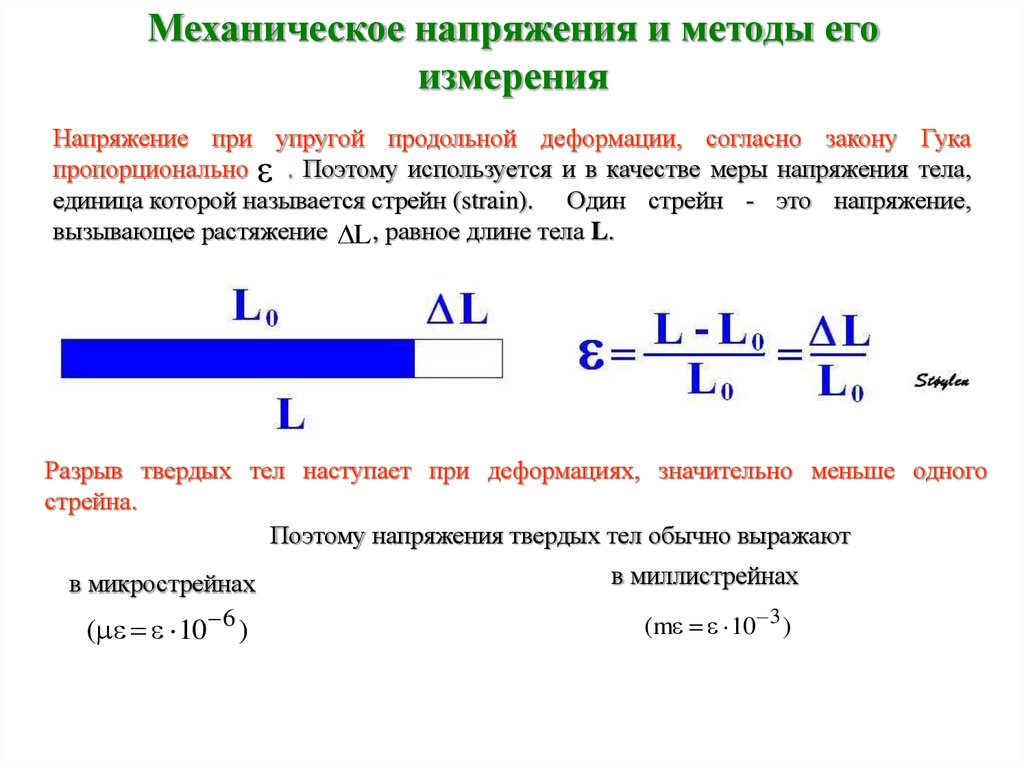 Ланцет Нейрол (2003) 2(8):506–11. 10.1016/S1474-4422(03)00487-3 [PubMed] [CrossRef] [Google Scholar]
Ланцет Нейрол (2003) 2(8):506–11. 10.1016/S1474-4422(03)00487-3 [PubMed] [CrossRef] [Google Scholar]
65. Рубенштейн Э. Связь старения ликвороциркуляторной системы с деменциями пожилых. Ланцет (1998) 351 (9098): 283–5. 10.1016/S0140-6736(97)09234-9 [PubMed][CrossRef][Google Scholar]
66. Чакраварти А. Объединяющая концепция болезни Альцгеймера, сосудистой деменции и нормотензивной гидроцефалии – гипотеза. Медицинские гипотезы (2004) 63 (5): 827–33. 10.1016/j.mehy.2004.03.029 [PubMed] [CrossRef] [Google Scholar]
67. De la Torre JC. Церебральная гемодинамика и сосудистые факторы риска: подготовка к болезни Альцгеймера. Дж. Альцгеймерс (2012) 32(3):553–67. 10.3233/JAD-2012-120793 [PubMed] [CrossRef] [Google Scholar]
68. Ли С.Дж. Возможный патогенез болезни Альцгеймера: черепно-челюстно-лицевая дисфункция, приводящая к локальному застою спинномозговой жидкости. Медицинские гипотезы (2009) 72 (2): 199–210. 10.1016/j.mehy.2008.09.044 [PubMed] [CrossRef] [Google Scholar]
69. O’Rourke MF, Hashimoto J. Механические факторы старения артерий: клиническая перспектива. J Am Coll Cardiol (2007) 50 (1): 1–13. 10.1016/j.jacc.2006.12.050 [PubMed] [CrossRef] [Google Scholar]
O’Rourke MF, Hashimoto J. Механические факторы старения артерий: клиническая перспектива. J Am Coll Cardiol (2007) 50 (1): 1–13. 10.1016/j.jacc.2006.12.050 [PubMed] [CrossRef] [Google Scholar]
70. Сафар М.Э., Нильссон П.М., Блахер Дж., Мимран А. Пульсовое давление, жесткость артерий и повреждение органов-мишеней. Представитель Curr Hypertens (2012) 14 (4): 339–44. 10.1007/s11906-012-0272-9 [PubMed] [CrossRef] [Google Scholar]
71. Hughes TM, Kuller LH, Barinas-Mitchell EJM, Mackey RH, McDade EM, Klunk WE, et al. Скорость пульсовой волны связана с отложением β-амилоида в мозгу очень пожилых людей. Неврология (2013) 81 (19): 1711–8. 10.1212/01.wnl.0000435301.64776.37 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
72. Zhong W, Cruickshanks KJ, Schubert CR, Carlsson CM, Chappell RJ, Klein BEK, et al. Скорость пульсовой волны и когнитивная функция у пожилых людей. Ассоциативная болезнь Альцгеймера (2013) 28:44–9. 10.1097/WAD.0b013e3182949f06 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
73. Hardy J, Allsop D. Отложение амилоида как центральное событие в этиологии болезни Альцгеймера. Trends Pharmacol Sci (1991) 12(10):383–8. 10.1016/0165-6147(91)-V [PubMed] [CrossRef] [Google Scholar]
Hardy J, Allsop D. Отложение амилоида как центральное событие в этиологии болезни Альцгеймера. Trends Pharmacol Sci (1991) 12(10):383–8. 10.1016/0165-6147(91)-V [PubMed] [CrossRef] [Google Scholar]
74. Breunig JJ, Guillot-Sestier M-V, Town T. Черепно-мозговая травма, нейровоспаление и болезнь Альцгеймера. Front Aging Neurosci (2013) 5:26. 10.3389/fnagi.2013.00026 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
75. Клинге П.М., Самии А., Нискен С., Бринкер Т., Сильверберг Г.Д. Амилоид головного мозга накапливается у старых крыс с каолино-индуцированной гидроцефалией. Нейроотчет (2006) 17(6):657–60. 10.1097/00001756-200604240-00020 [PubMed] [CrossRef] [Google Scholar]
76. Silverberg GD, Miller MC, Machan JT, Johanson CE, Caralopoulos IN, Pascale CL, et al. Амилоид и тау накапливаются в мозге старых гидроцефальных крыс. Brain Res (2010) 1317: 286–96. 10.1016/j.brainres.2009.12.065 [PubMed] [CrossRef] [Google Scholar]
77. Карневале Д., Лембо Г. «Альцгеймероподобная» патология в мышиной модели артериальной гипертензии. Biochem Soc Trans (2011) 39(4):939–44. 10.1042/BST03
«Альцгеймероподобная» патология в мышиной модели артериальной гипертензии. Biochem Soc Trans (2011) 39(4):939–44. 10.1042/BST03
78. Schreiber S, Drukarch B, Garz C, Niklass S, Stanaszek L, Kropf S, et al. Взаимодействие между возрастом, церебральным заболеванием мелких сосудов, паренхиматозным амилоидом-β и патологией тау: продольные исследования на крысах, склонных к гипертоническому инсульту. J Alzheimers Dis (2014) 42 (Приложение 3): S205–15. 10.3233/JAD-132618 [PubMed] [CrossRef] [Google Scholar]
79. Спирс Т.Л., Хайман Б.Т. Трансгенные модели болезни Альцгеймера: обучение на животных. NeuroRx (2005) 2(3):423–37. 10.1602/neurorx.2.3.423 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
80. LaFerla FM, Green KN. Животные модели болезни Альцгеймера. Перспектива Мед Колд Спринг Харб (2012) 2 (11) 423–37. 10.1101/cshperspect.a006320 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
81. Duyckaerts C, Potier M-C, Delatour B.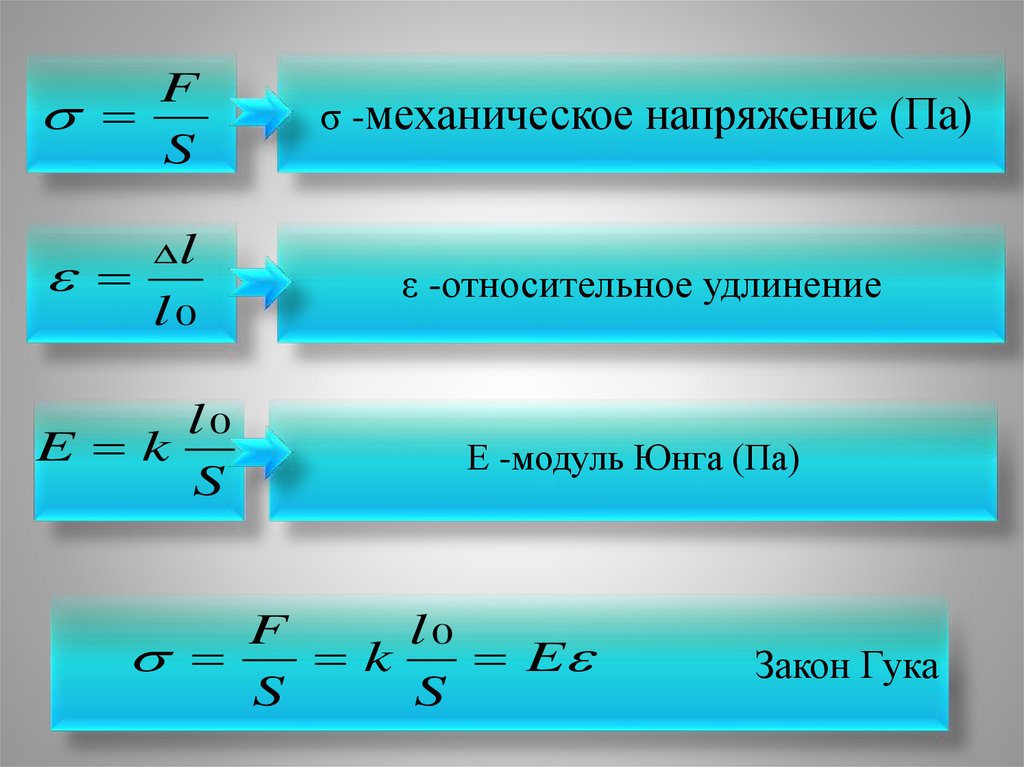 Модели болезни Альцгеймера и невропатология человека: сходства и различия. Acta Neuropathol (Берл) (2008) 115 (1): 5–38. 10.1007/s00401-007-0312-8 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Модели болезни Альцгеймера и невропатология человека: сходства и различия. Acta Neuropathol (Берл) (2008) 115 (1): 5–38. 10.1007/s00401-007-0312-8 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
82. Cohen RM, Rezai-Zadeh K, Weitz TM, Rentsendorj A, Gate D, Spivak I, et al. Трансгенная крыса с болезнью Альцгеймера с бляшками, патологией тау, нарушением поведения, олигомерным A? и откровенная потеря нейронов. J Neurosci (2013) 33 (15): 6245–56. 10.1523/JNEUROSCI.3672-12.2013 [PMC free article] [PubMed] [CrossRef] [Google Scholar]
патология тау и активация глии у старых мышей htau. J Neuropathol Exp Neurol (2013) 72(2):137–51. 10.1097/NEN.0b013e3182814cdf [PubMed] [CrossRef] [Google Scholar]
84. Abrahamson EE, Ikonomovic MD, Ciallella JR, Hope CE, Paljug WR, Isanski BA, et al.
Терапия ингибированием каспазы устраняет вызванное травмой головного мозга повышение уровня пептида Абета: значение для клинического исхода. Exp Neurol (2006) 197 (2): 437–50. 10.1016/j.expneurol.2005.10.011 [PubMed] [CrossRef] [Google Scholar]
10.1016/j.expneurol.2005.10.011 [PubMed] [CrossRef] [Google Scholar]
85. Yu F, Zhang Y, Chuang D-M. Литий уменьшает гиперэкспрессию BACE1, накопление β-амилоида и дефицит пространственного обучения у мышей с черепно-мозговой травмой. Дж Нейротравма (2012) 29(13): 2342–51. 10.1089/neu.2012.2449 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
86. Blasko I, Beer R, Bigl M, Apelt J, Franz G, Rudzki D, et al. Экспериментальная черепно-мозговая травма у крыс стимулирует экспрессию, продукцию и активность бета-секретазы болезни Альцгеймера (BACE-1). J Neural Transm (2004) 111 (4): 523–36. [PubMed] [Google Scholar]
87. Tran HT, LaFerla FM, Holtzman DM, Brody DL. Контролируемое травматическое повреждение коры головного мозга у мышей 3xTg-AD вызывает острое внутриаксональное накопление амилоида-β и независимо ускоряет развитие аномалий тау. Дж. Нейроски (2011) 31 (26): 9513–25. 10.1523/JNEUROSCI.0858-11.2011 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
88. Israelsson C, Bengtsson H, Kylberg A, Kullander K, Lewén A, Hillered L, et al.
Отчетливые клеточные паттерны повышенной экспрессии хемокинов подтверждают важную воспалительную роль при черепно-мозговой травме. Дж. Нейротравма (2008) 25(8):959–74. 10.1089/neu.2008.0562 [PubMed] [CrossRef] [Google Scholar]
Israelsson C, Bengtsson H, Kylberg A, Kullander K, Lewén A, Hillered L, et al.
Отчетливые клеточные паттерны повышенной экспрессии хемокинов подтверждают важную воспалительную роль при черепно-мозговой травме. Дж. Нейротравма (2008) 25(8):959–74. 10.1089/neu.2008.0562 [PubMed] [CrossRef] [Google Scholar]
89. Smith DH, Chen XH, Nonaka M, Trojanowski JQ, Lee VM, Saatman KE, et al. Накопление бета-амилоида и тау-белка и образование включений нейрофиламента после диффузного повреждения головного мозга у свиньи. J Neuropathol Exp Neurol (1999) 58(9):982–92. 10.1097/00005072-199
0-00008 [PubMed] [CrossRef] [Google Scholar]
90. Lewén A, Li GL, Nilsson P, Olsson Y, Hillered L. Черепно-мозговая травма у крыс вызывает изменения иммунореактивности белка-предшественника бета-амилоида. . Нейроотчет (1995) 6 (2): 357–60. 10.1097/00001756-199501000-00032 [PubMed] [CrossRef] [Google Scholar]
91. Яцив И., Григориадис Н., Симеониду С., Стахел П.Ф., Шмидт О.И., Александрович А.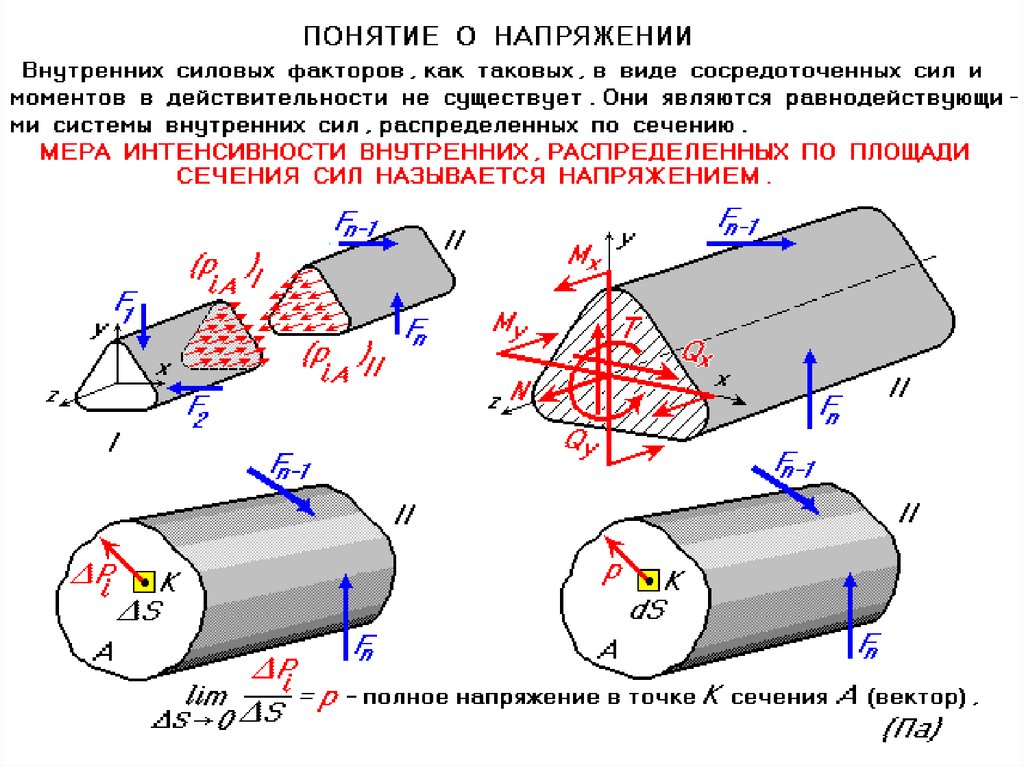 Г. и др.
Эритропоэтин оказывает нейропротекторное действие, улучшает функциональное восстановление и уменьшает апоптоз нейронов и воспаление в модели экспериментальной закрытой черепно-мозговой травмы у грызунов. ФАСЭБ Дж (2005) 19(12): 1701–1703. [PubMed] [Google Scholar]
Г. и др.
Эритропоэтин оказывает нейропротекторное действие, улучшает функциональное восстановление и уменьшает апоптоз нейронов и воспаление в модели экспериментальной закрытой черепно-мозговой травмы у грызунов. ФАСЭБ Дж (2005) 19(12): 1701–1703. [PubMed] [Google Scholar]
92. Raghupathi R, Conti AC, Graham DI, Krajewski S, Reed JC, Grady MS, et al. Легкая черепно-мозговая травма вызывает апоптозную гибель клеток коры головного мозга, которой предшествует снижение клеточной иммунореактивности Bcl-2. Неврология (2002) 110 (4): 605–16. 10.1016/S0306-4522(01)00461-4 [PubMed] [CrossRef] [Google Scholar]
93. Pierce JE, Trojanowski JQ, Graham DI, Smith DH, McIntosh TK. Иммуногистохимическая характеристика изменений в распределении белков-предшественников амилоида и бета-амилоидного пептида после экспериментального повреждения головного мозга у крыс. Джей Нейроски (1996) 16(3):1083–90. [Бесплатная статья PMC] [PubMed] [Google Scholar]
94. Bramlett HM, Kraydieh S, Green EJ, Dietrich WD.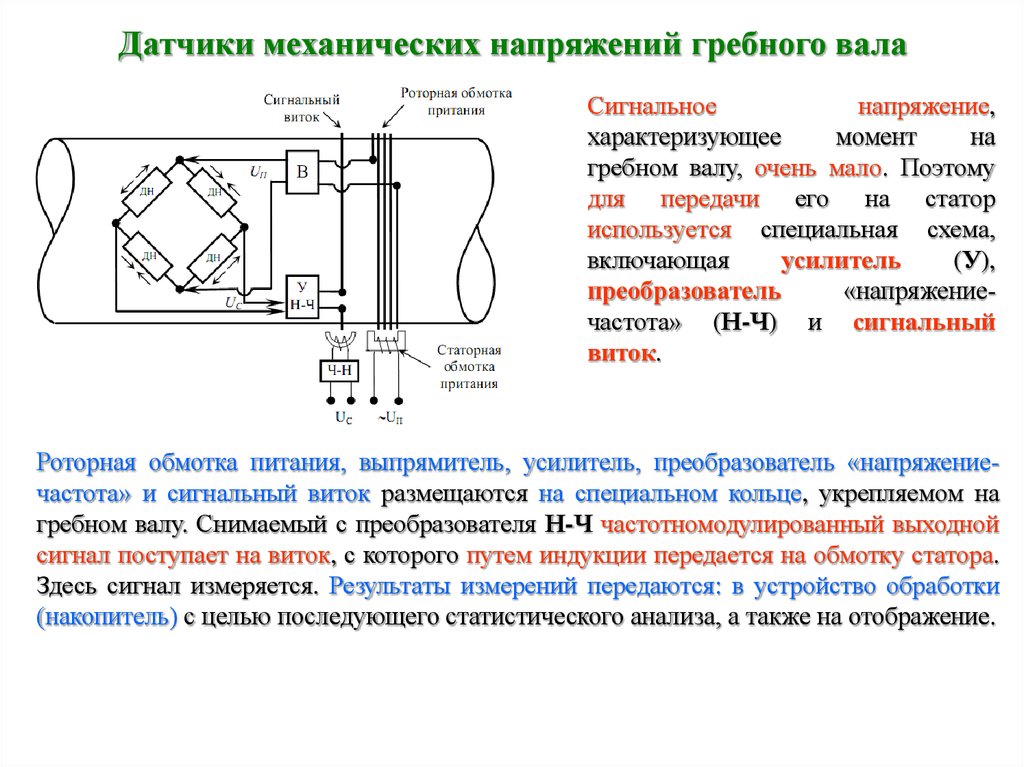 Временные и региональные паттерны повреждения аксонов после черепно-мозговой травмы: иммуноцитохимическое исследование белка-предшественника бета-амилоида у крыс. J Neuropathol Exp Neurol (1997) 56(10):1132–41. 10.1097/00005072-199710000-00007 [PubMed] [CrossRef] [Google Scholar]
Временные и региональные паттерны повреждения аксонов после черепно-мозговой травмы: иммуноцитохимическое исследование белка-предшественника бета-амилоида у крыс. J Neuropathol Exp Neurol (1997) 56(10):1132–41. 10.1097/00005072-199710000-00007 [PubMed] [CrossRef] [Google Scholar]
95. Hoshino S, Tamaoka A, Takahashi M, Kobayashi S, Furukawa T, Oaki Y, et al. Возникновение иммунореактивности фосфорилированного тау-белка и бета-амилоидного белка при хронической стадии перкуторного повреждения жидкостью головного мозга крыс. Нейроотчет (1998) 9(8):1879–83. 10.1097/00001756-199806010-00039 [PubMed] [CrossRef] [Google Scholar]
96. Ивата А., Чен X-H, Макинтош Т.К., Браун К.Д., Смит Д.Х. Длительное накопление бета-амилоида в аксонах после травмы головного мозга без стойкой активизации генов белков-предшественников амилоида. J Neuropathol Exp Neurol (2002) 61(12):1056–68. [PubMed] [Google Scholar]
97. Карбонелл В.С., Грейди М.С. Региональная и временная характеристика нейронального, глиального и аксонального ответа после черепно-мозговой травмы у мышей.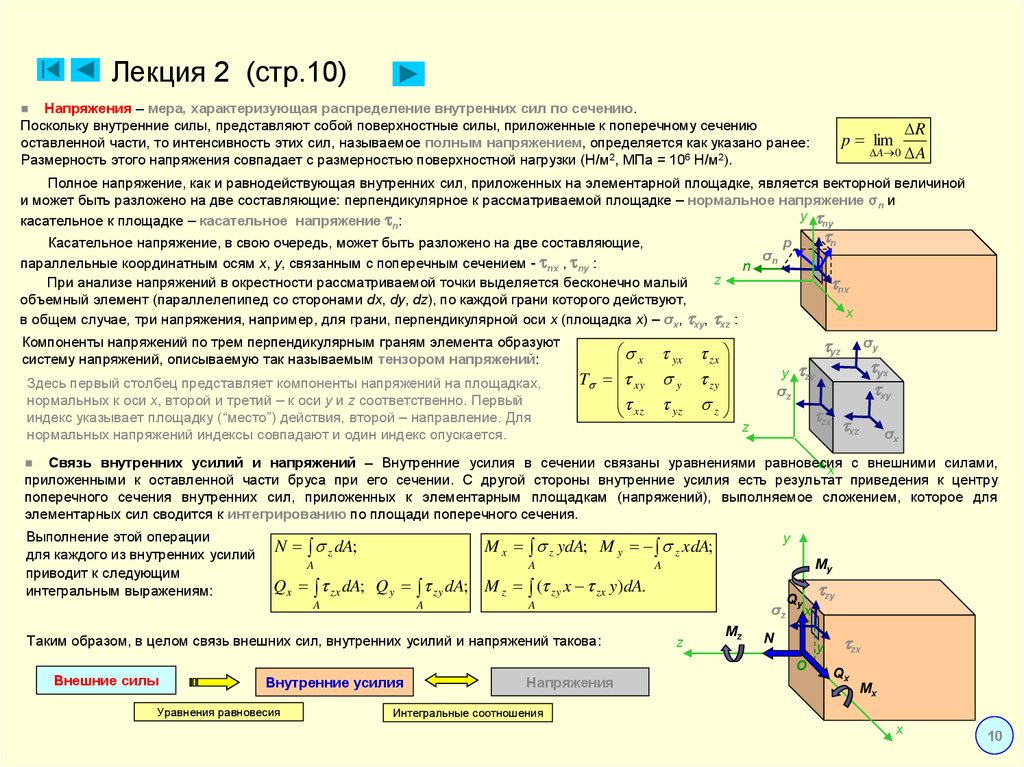 Акта Нейропатол (1999) 98(4):396–406. 10.1007/s004010051100 [PubMed] [CrossRef] [Google Scholar]
Акта Нейропатол (1999) 98(4):396–406. 10.1007/s004010051100 [PubMed] [CrossRef] [Google Scholar]
98. Hutchison JS, Derrane RE, Johnston DL, Gendron N, Barnes D, Fliss H, et al. Экспрессия белка, ингибирующего апоптоз нейронов, после черепно-мозговой травмы у мышей. Дж. Нейротравма (2001) 18(12):1333–47. 10.1089/08977150152725632 [PubMed] [CrossRef] [Google Scholar]
99. Yoshiyama Y, Uryu K, Higuchi M, Longhi L, Hoover R, Fujimoto S, et al. Усиленное образование нейрофибриллярных клубков, церебральная атрофия и когнитивный дефицит, вызванные повторяющимся легким повреждением головного мозга в модели трансгенных мышей с таупатией. Дж. Нейротравма (2005) 22(10):1134–41. 10.1089/neu.2005.22.1134 [PubMed] [CrossRef] [Google Scholar]
100. Kurata T, Lukic V, Kozuki M, Wada D, Miyazaki K, Morimoto N, et al.
Телмисартан уменьшает прогрессирующее накопление клеточного бета-амилоида и фосфорилированного тау-белка с воспалительными реакциями у старых крыс, устойчивых к спонтанно гипертоническому инсульту. J Инсульт Цереброваскулярная дисфункция (2014). 10.1016/j.jstrokecerebrovasdis.2014.05.023 [PubMed] [CrossRef] [Google Scholar]
J Инсульт Цереброваскулярная дисфункция (2014). 10.1016/j.jstrokecerebrovasdis.2014.05.023 [PubMed] [CrossRef] [Google Scholar]
Крысы Tx с компенсированной гидроцефалией. J Neurosurg Pediatr (2008) 1 (1): 68–74. 10.3171/PED-08/01/068 [PubMed] [CrossRef] [Google Scholar]
102. Mori F, Tanji K, Yoshida Y, Wakabayashi K. Ретроградная дегенерация таламуса у крыс с врожденной гидроцефалией связана с апоптотической гибелью клеток. Нейропатол (2002) 22(3):186–93. 10.1046/j.1440-1789.2002.00445.x [PubMed] [CrossRef] [Google Scholar]
103. Del Bigio MR, Zhang YW. Гибель клеток, повреждение аксонов и рождение клеток в мозге незрелых крыс после индукции гидроцефалии. Опыт Neurol (1998) 154 (1): 157–69. 10.1006/exnr.1998.6922 [PubMed] [CrossRef] [Google Scholar]
104. Aoyama Y, Kinoshita Y, Yokota A, Hamada T. Повреждение нейронов при гидроцефалии и его восстановление путем введения шунта при экспериментальной гидроцефалии: исследование с использованием метода иммуноокрашивания нейрофиламентов.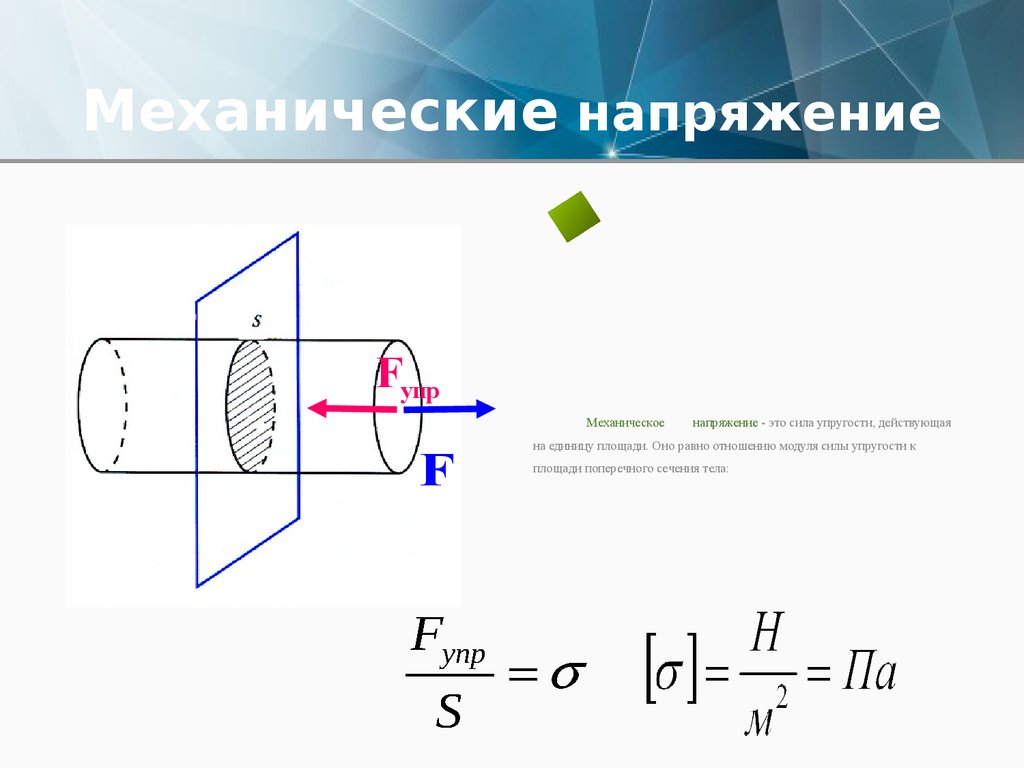 J Neurosurg (2006) 104 (5 Suppl): 332–9. [PubMed] [Google Scholar]
J Neurosurg (2006) 104 (5 Suppl): 332–9. [PubMed] [Google Scholar]
105. Хан О.Х., Энно Т.Л., Дель Бигио М.Р. Повреждение головного мозга у новорожденных крыс после индукции каолином гидроцефалии. Exp Neurol (2006) 200 (2): 311–20. 10.1016/j.expneurol.2006.02.113 [PubMed] [CrossRef] [Google Scholar]
106. Silverberg GD, Miller MC, Pascale CL, Caralopoulos IN, Agca Y, Agca C, et al. Индуцированная каолином хроническая гидроцефалия ускоряет отложение амилоида и сосудистые заболевания у трансгенных крыс, экспрессирующих высокие уровни АРР человека. Жидкостные барьеры CNS (2015) 12(1):2. 10.1186/2045-8118-12-2 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
107. Levy Nogueira M, Lafitte O, Steyaert J-M, Bakardjian H, Dubois B, Hampel H, et al. Механический стресс, связанный с атрофией головного мозга при болезни Альцгеймера. Демент Альцгеймера (2015). 10.1016/j.jalz.2015.03.005 [PubMed] [CrossRef] [Google Scholar]
108. Murphy MC, Curran GL, Glaser KJ, Rossman PJ, Huston J, III, Poduslo JF, et al. Магнитно-резонансная эластография головного мозга на мышиной модели болезни Альцгеймера: первые результаты. Magn Reson Imaging (2012) 30 (4): 535–9. 10.1016/j.mri.2011.12.019 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Магнитно-резонансная эластография головного мозга на мышиной модели болезни Альцгеймера: первые результаты. Magn Reson Imaging (2012) 30 (4): 535–9. 10.1016/j.mri.2011.12.019 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
109. Murphy MC, Huston J, III, Jack CR, Jr, Glaser KJ, Senjem ML, Chen J, и другие. Измерение характерной топографии жесткости мозга с помощью магнитно-резонансной эластографии. PLoS One (2013) 8(12):e81668. 10.1371/journal.pone.0081668 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
110. Тайлер В.Дж. Механобиология работы мозга. Nat Rev Neurosci (2012) 13 (12): 867–78. 10.1038/nrn3383 [PubMed] [CrossRef] [Google Scholar]
111. Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, et al. Магнитно-резонансная эластография: неинвазивное картирование эластичности тканей. Med Image Anal (2001) 5 (4): 237–54. 10.1016/S1361-8415(00)00039-6 [PubMed] [CrossRef] [Google Scholar]
112. Murphy MC, Huston J, Jack CR, Glaser KJ, Manduca A, Felmlee JP, et al.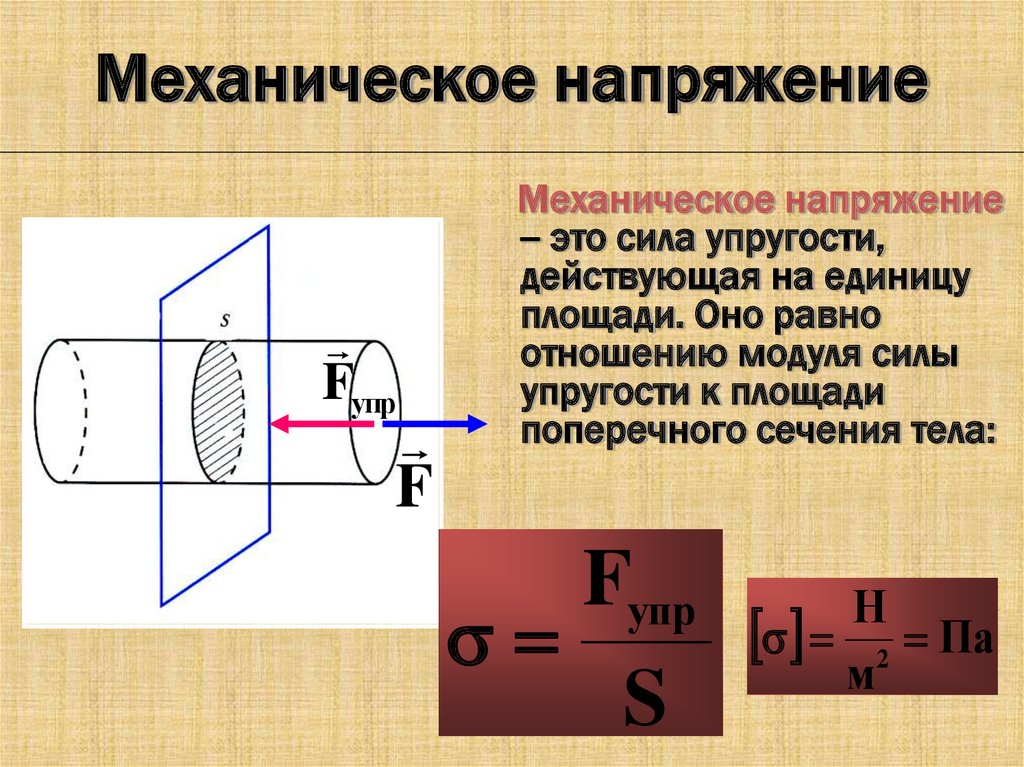


 Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение.
Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение. Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.
Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.
 {\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}
{\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}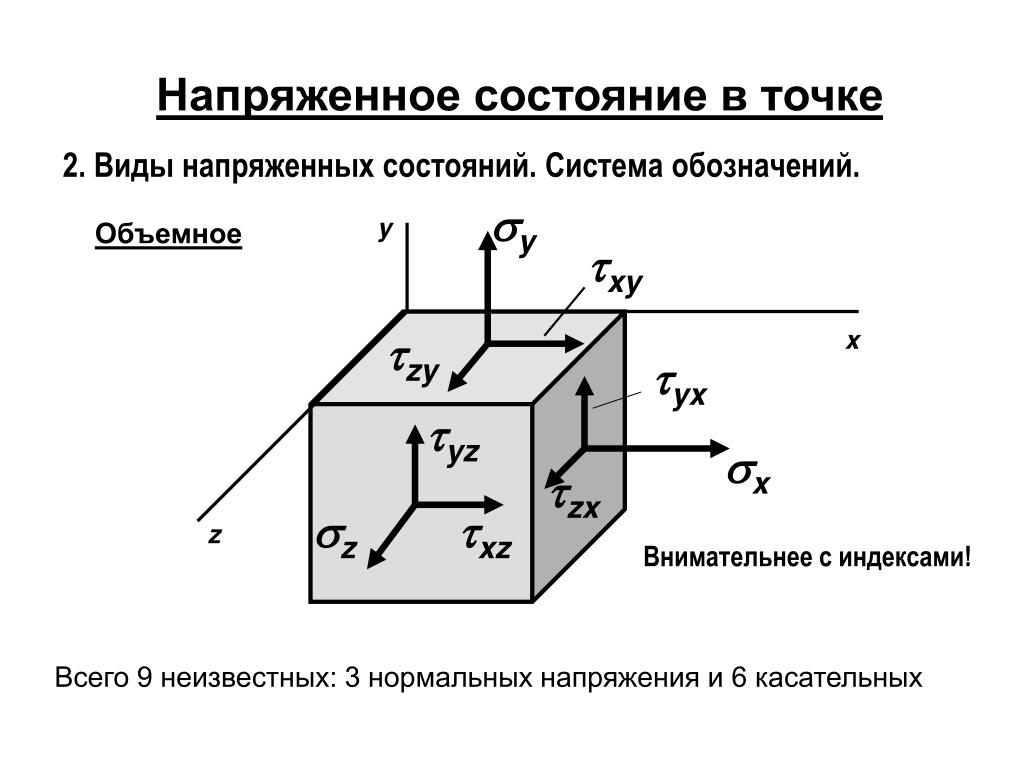
 Без силы или растяжения напряжение не может возникнуть.
Без силы или растяжения напряжение не может возникнуть. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.
Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения. Если на площадках действуют только нормальные напряжения (без касательных), то объемное (трехосное) напряженное состояние может быть охарактеризовано тремя величинами, напр. в цилиндрическом стержне — осевым, окружным и радиальным нормальным напряжением.
Если на площадках действуют только нормальные напряжения (без касательных), то объемное (трехосное) напряженное состояние может быть охарактеризовано тремя величинами, напр. в цилиндрическом стержне — осевым, окружным и радиальным нормальным напряжением.

 3.3. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела называется напряженным состоянием в данной точке.
3.3. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела называется напряженным состоянием в данной точке. Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;
Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;