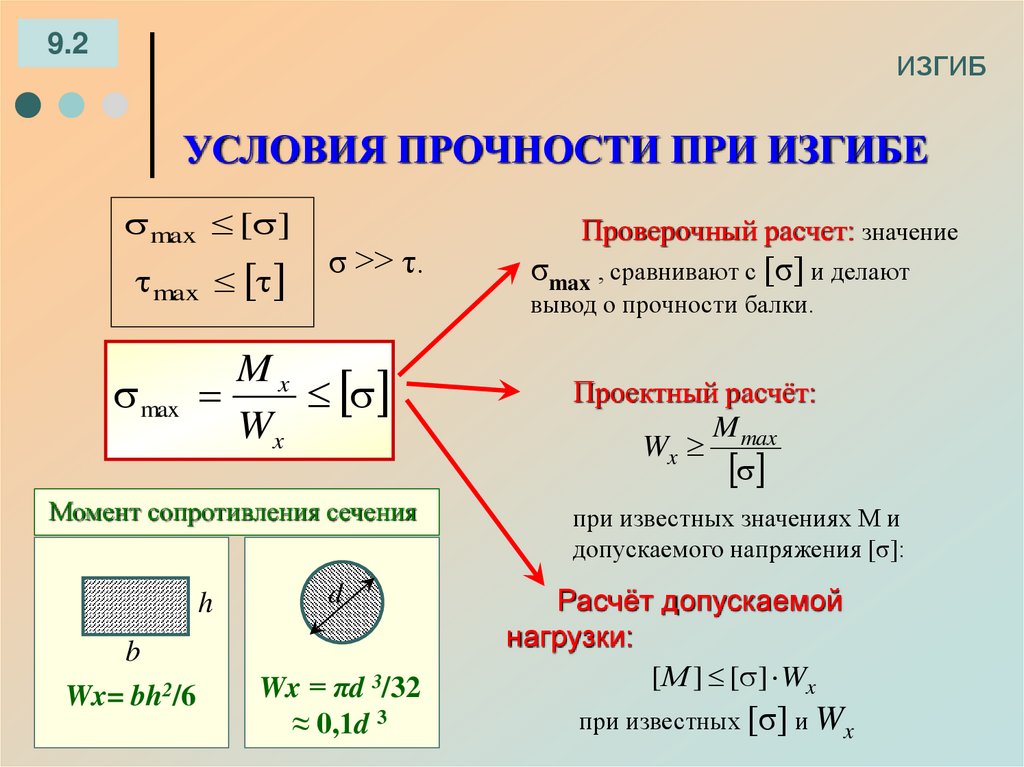
Механическое напряжение.
25. Модель строения твердых тел. Виды кристаллических структур.
Виды кристаллических структур.
В зависимости от характера сил взаимодействия и природы частиц, находящихся в узлах кристаллической решетки, различают 4 типа кристаллических решеток.
атомные кристаллы. В узлах кристаллической решетки находятся нейтральные атомы. Между ними существует связь, имеющая электрический характер. Эта связь осуществляется электронными парами, причем от каждого атома в ней участвует только только по одному электрону. Число связй, в которых может участвовать атом, определяется его валентностью. Примерами атомных кристаллов является графит, алмаз, кремний, германий.
Ионные кристаллы. В узлах кристаллической решетки этих кристаллов находятся ионы разных знаков. Связь между ними обусловлена электрическими силами взаимодействия между разноименными ионами.
Металлические кристаллы.
Молекулярные кристаллы. В узлах кристаллической решетки находятся молекулы, ориентированные определенным образом. Между молекулами действуют силы притяжения, характерные для взаимодействия молекул. К молекулярным кристаллам относятся нафталин, парафин, сухой лед, лед.
26. Механические свойства твердых тел. Виды деформаций. Механическое напряжение. Закон Гука.
Механические свойства твердых тел:
Деформация и напряжение Модуль упругости Диаграмма растяжения Дефекты в кристаллах
Деформацию сжатия и растяжения можно характеризовать абсолютным удлинением Δl , равным разности длин образца до растяжения l0 и после него l :
.
Абсолютное удлинение при растяжении положительно, при сжатии имеет отрицательное значение.
Отношение абсолютного удлинения к длине образца называется относительным удлинением :
. (30.1)
При деформации тела возникают силы упругости. Физическая величина, равная отношению модуля силы упругости к площади сечения тела, называется механическим напряжением :
. (30.2)
За единицу механического напряжения в СИ принят паскалъ (Па). .
Модуль упругости. При малых деформациях напряжение прямо пропорционально относительному удлинению:
. (30.3)
Коэффициент пропорциональности Е в уравнении (30.3) называется модулем упругости.Модуль упругости одинаков для образцов любой формы и размеров, изготовленных из одного материала:
. (30.4)
Из формулы (30.4) следует, что
. (30.5)
Сравнив
выражение (30.
5) с законом Гука, получим,
что жесткость k стержня
пропорциональна произведению модуля
Юнга на площадь поперечного сечения
стержня и обратно пропорциональна его
длине.
Диаграмма
растяжения. Зависимость
напряжения от
относительного удлинения является
одной из важнейших характеристик
механических свойств твердых тел.
Графическое изображение этой зависимости
называется
Закон
Гука выполняется при небольших
деформациях. Максимальное напряжение ,
при котором еще выполняется закон Гука,
называется пределом
пропорциональности. За
пределом пропорциональности напряжение
перестает быть пропорциональным
относительному удлинению; до некоторого
напряжения после снятия нагрузки размеры
тела восстанавливаются полностью. Такая
деформация называется упругой. Максимальное напряжение ,
при котором деформация еще остается
упругой, называется пределом
упругости.
Большинство
металлов испытывает упругую деформацию
до значений .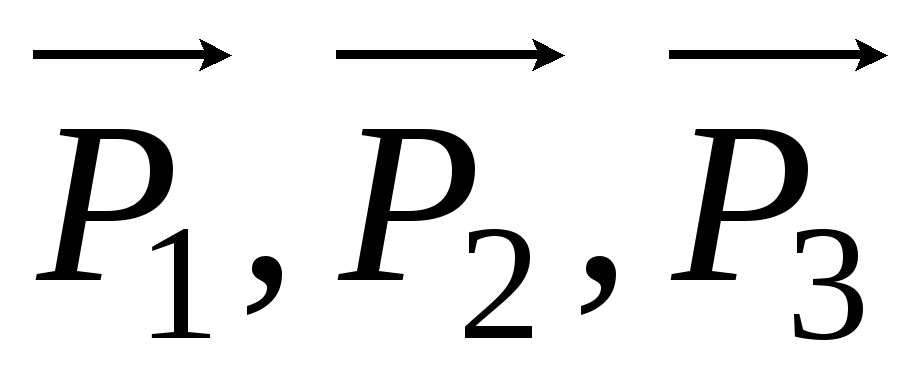
При напряжениях, превышающих предел упругости , образец после снятия нагрузки не восстанавливает свою форму или первоначальные размеры. Такие деформации называются остаточными или пластическими.
В области пластической деформации деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала.
Материалы, у котерых область текучести значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называются хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.
Дефекты в кристаллах. Способы повышения прочности твердых тел. Кристаллическими телами являются все металлические изделия — стальные каркасы зданий и мостов, рельсы железных дорог, линии электропередач, станки, машины, поезда, самолеты.
Одной
из важнейших задач науки и техники
является создание прочных и надежных
машин, станков и зданий с минимальной
затратой металлов и других материалов.
Сравнение реальной прочности кристаллов со значениями, полученными на основании теоретических расчетов, обнаруживает весьма существенные расхождения. Теоретический предел прочности в десятки и даже в сотни раз превосходит значения, получаемые при испытаниях реальных образцов.
Оказалось, что причина расхождения теории и эксперимента заключается в наличии внутренних и поверхностных дефектов в строении кристаллических решеток.
Самые простые дефекты в идеальной кристаллической решетке — точечные дефекты — возникают при замещении собственного атома чужеродным, внедрении атома в пространство между узлами решетки или при отсутствии атома в одном из узлов кристаллической решетки .
Другой вид дефектов — линейные дефекты — возникает при нарушениях в порядке расположения атомных плоскостей в кристаллах. Пример такого нарушения в структуре кристалла представлен на рисунке 104.
Деформация
и разрушение кристалла с линейным
дефектом облегчаются потому, что вместо
одновременного разрыва всех связей
между атомами двух плоскостей становится
возможным поочередный разрыв небольшого
числа связей между атомами с постепенным
перемещением дефекта в кристалле.
Для получения кристаллических материалов с высокой прочностью нужно выращивать монокристаллы без дефектов. Это очень сложная задача, и поэтому в практике этот путь пока широкого распространения не получил.
Большинство
современных методов упрочнения материалов
основано на другом способе. Для упрочнения
кристалла с дефектами в решетке можно
создать условия, при которых перемещение
дефектов в кристалле затрудняется.
Препятствием для перемещения дефектов
в кристалле могут служить другие дефекты,
специально созданные в кристаллической
решетке. Так, для увеличения прочности
стали применяется легирование стали —
введение в расплав небольших добавок
хрома, вольфрама и других элементов.
Внедрение атомов чужеродных элементов
в решетку кристаллов железа затрудняет
перемещение линейных дефектов при
деформации кристаллов, прочность стали
повышается при этом примерно в три раза.
Дополнительные дефекты в кристаллической
решетке создаются при протяжке,
дробеструйной обработке металлов.
Недеформируемых тел в природе не существует.
Деформация — изменение формы или объема тела под действием внешних сил. Деформация может быть упругая или неупругая.
Упругая деформация — деформация, при которой после прекращения действия силы размеры и форма тела восстанавливаются.
Виды деформаций:
1. Линейная:
а) Растяжение (тросы подъемных кранов, канатных дорог, буксирные тросы)
б) Сжатие (колонны, стены, фундаменты зданий).
2. Сд <SMILE>id=420 alt=’:Лопну от смеха:'</SMILE> <SMILE>id=420 alt=’:Лопну от смеха:'</SMILE>виг (заклепки, болты, соед. металлические конструкции, процесс разрезания ножницами бумаги).
3. Кручение (завинчивание
гаек, работа валов машин, сверление
металлов и т.
п.).
4.
Деформацию растяжения и сжатия можно охарактеризовать абсолютной деформацией ℓ, равной разности длин образца после растяжения ℓ и до него ℓ0: ℓ = ℓ – ℓ0
ℓ = ℓ – ℓ0
Отношение абсолютной деформации ℓ к первоначальной длине образцаℓo называют относительной деформацией:
Механическое
напряжение — мера внутренних сил,
возникающих в деформируемом теле под
влиянием внешних воздействий.
Механическое
напряжение в точке тела измеряется
отношением:
—
упругой силы, возникающей в теле при
деформации; к
—
площади малого элемента сечения,
перпендикулярного к этой силе.
В
системе СИ механическое напряжение
измеряется в паскалях.
Различают
две составляющие вектора механического
напряжения:
—
нормальное механическое напряжение,
направленное по нормали к сечению; и
—
касательное механическое напряжение
в плоскости сечения.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь F — сила натяжения стержня, Δl — абсолютное удлинение (сжатие) стержня, а kназывается коэффициентом упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как
Величина E называется Модулем
упругости первого рода или модулем
Юнга и
является механической характеристикой
материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов вещества.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности, связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
27. Плавление и кристаллизация. Теплота плавления.
Плавление и кристаллизация.
Плавлением
называют процесс перехода вещества из
твердого кристаллического состояния
в жидкое. Плавление происходит при
постоянной температуре с поглощением
тепла. Постоянство температуры объясняется
тем, что при плавлении вся подводимая
теплота идет на разупорядочение
регулярного пространственного
расположения атомов (молекул) в
кристаллической решетке.
При этом
среднее расстояние между атомами и,
следовательно, силы взаимодействия
изменяется незначительно. Для большинства
кристаллов (кроме воды, и некоторых
сплавов) температура плавления растет
с увеличением внешнего давления, так
как для отдаления атомов друг от друга
при большем давлении требуется большая
энергия тепловых движений, т. е. Более
высокая температура.
Кристаллизация — процесс фазового перехода вещества из жидкого состояния в твёрдое кристаллическое с образованием кристаллов.
Фазой называется однородная часть термодинамической системы отделённая от других частей системы(других фаз) поверхностью раздела, при переходе через которую химический состав, структура и свойства вещества изменяются скачками.
Или Кристаллизация — это процесс выделения твёрдой фазы в виде кристаллов из растворов или расплавов, в химической промышленности процесс кристаллизации используется для получения веществ в чистом виде.
Кристаллизация
начинается при достижении некоторого
предельного условия, например,
переохлаждения жидкости или пересыщения
пара, когда практически мгновенно
возникает множество мелких
кристалликов — центров
кристаллизации.
Кристаллики растут, присоединяя атомы или
молекулы из жидкости или пара. Рост
граней кристалла происходит послойно,
края незавершённых атомных слоев
(ступени) при росте движутся вдоль грани.
Зависимость скорости роста от условий
кристаллизации приводит к разнообразию
форм роста и структуры кристаллов
(многогранные, пластинчатые, игольчатые,
скелетные, дендритные и
другие формы, карандашные структуры
и т. д.). В процессе кристаллизации
неизбежно возникают различные дефекты.
Удельная теплота плавления.
Удельная теплота плавления— количество теплоты, которое необходимо сообщить одной единице массы кристаллического вещества в равновесном изобарно-изотермическом процессе, чтобы перевести его из твёрдого (кристаллического) состояния в жидкое (то же количество теплоты выделяется при кристаллизации вещества).
Теплота плавления — частный случай теплоты фазового перехода I рода.
Различают удельную теплоту плавления (Дж/кг) и молярную (Дж/моль)..
Удельная
теплота плавления обозначается
буквой (греческая
буква лямбда)
Формула расчёта удельной теплоты
плавления: ,
где —
удельная теплота плавления, — количество
теплоты, полученное веществом при
плавлении (или выделившееся при
кристаллизации), —
масса плавящегося (кристаллизующегося)
вещества.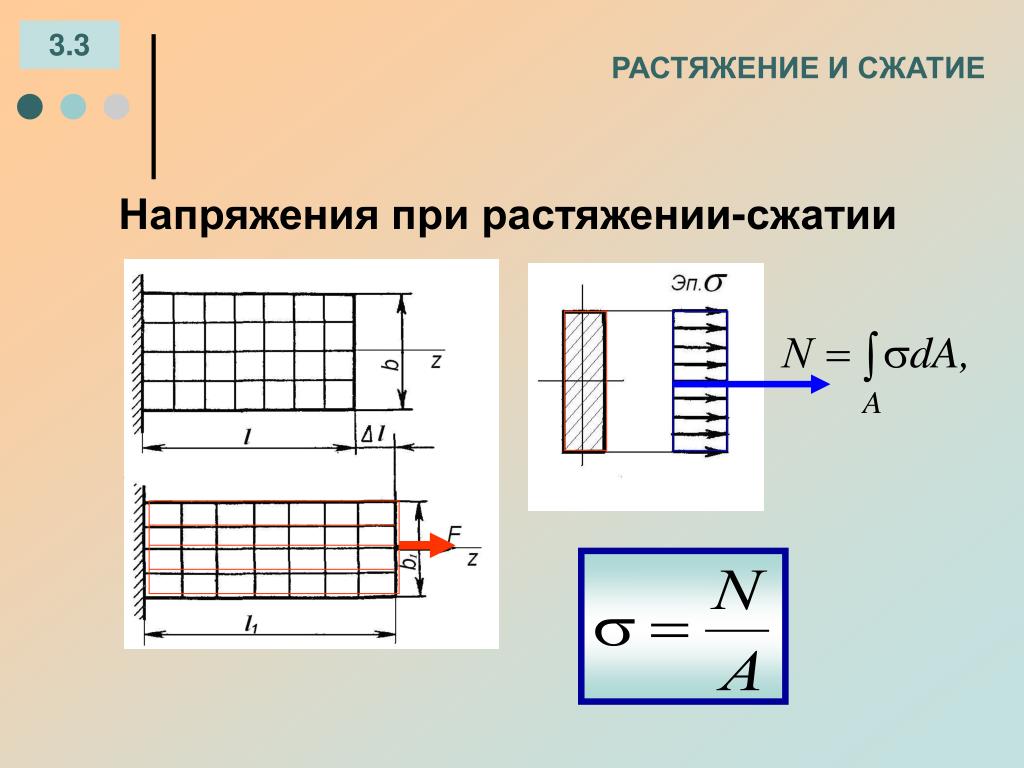
28. Основы термодинамики. Внутренняя энергия. Распределение энергии по степеням свободы.
Начала термодинамики — совокупность аксиом, лежащих в основе термодинамики. Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически.
Необходимость начал термодинамики связана с тем, что термодинамика описывает макроскопические параметры систем без конкретных предположений относительно их микроскопического устройства. Вопросами внутреннего устройства занимается статистическая физика.
Начала термодинамики независимы, то есть ни одно из них не может быть выведено из других начал.
определение, формула, единицы измерения :: SYL.ru
Только очень спелые груши без семян: в каком виде давать собакам овощи и фрукты
Только мать: стоит ли рожать ребенка «для себя», не имея мужа
Устраняет лишнюю влагу: кату раса (острый вкус) в аюрведе (польза и ограничения)
Прозрачное макси или неоновое мини: подборка платьев для весеннего отпуска
Близнецы смогут привлечь удачу: Таро-прогноз на первую неделю апреля
Подаем освежающее фруктовое блюдо с сочными ягодами: фиолетовый салат
Идеальна в начинку для пирожков.
Как использовать зелень редиса
Комплименты очень важны для нас: как научиться их принимать правильно
Может стать гимном всех свадеб: певица Глюкоза рассказала о новой песне
Салициловая кислота и гидроколлоидный пластырь: как убрать прыщ на один день
Автор Сенюкович Станислав
Степень изменения формы тела при деформации зависит не только от природы вещества, но и такой физической величиной, как механическое напряжение. Если рассматривать атомную кристаллическую решетку такого вещества, можно отметить постоянное взаимодействие молекул друг с другом.
Это состояние напрямую влияет на величину механического напряжения.
Что такое деформация? Виды деформации
Явление, при котором происходит изменение формы тела под действием какой-либо внешней силы, называется деформацией. Ее природа заключается в движении молекул вещества или целых слоев кристаллической решетки, что приводит к возникновению так называемых дефектов. Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение.
Выделяют несколько видов изменения формы тела:
- Деформация растяжения, когда внешняя сила воздействует вдоль всего тела. Имеет прикладное значение при изготовлении веревок, тросов и строительных материалов;
- Деформация сжатия. В этом случае вектор действия внешней силы совпадает с продольной осью тела, однако он направлен в сторону центра этого тела. Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;
- Деформация сдвига возникает под действием внешней силы, которая направлена перпендикулярно продольной оси и вызывает движение различных плоскостей тела относительно друг друга;
- Деформация изгиба характеризуется искривлением главной оси тела, например, когда имеется две точки опоры. Сила, которую может выдержать тот или иной предмет, а также механическое напряжение играют большую роль при создании строительных материалов;
- Деформация кручения возникает при повороте тела вокруг его продольной оси. Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.
Сила, которую может выдержать тот или иной предмет, а также механическое напряжение играют большую роль при создании строительных материалов;Упругая и пластическая деформация
Механическое напряжение, которое зависит от природы вещества, влияет на способность тела восстанавливать свою первоначальную форму после возникновения дефекта в кристаллической решетке. По этому признаку выделяют упругую и пластическую деформацию.
При пластической деформации тело после воздействия внешней силы не способно восстановить прежнюю форму. Например, пластилин при надавливании на него пальцем сохраняет образовавшуюся ямку.
Упругая деформация характерна для тех веществ, которые способны восстанавливать свою первоначальную форму после воздействия на них внешней силы.
Примером может служить та же пружина, которая при любом описанном выше виде деформации возвращается в первоначальное состояние.
Механическое напряжение: формула и определение
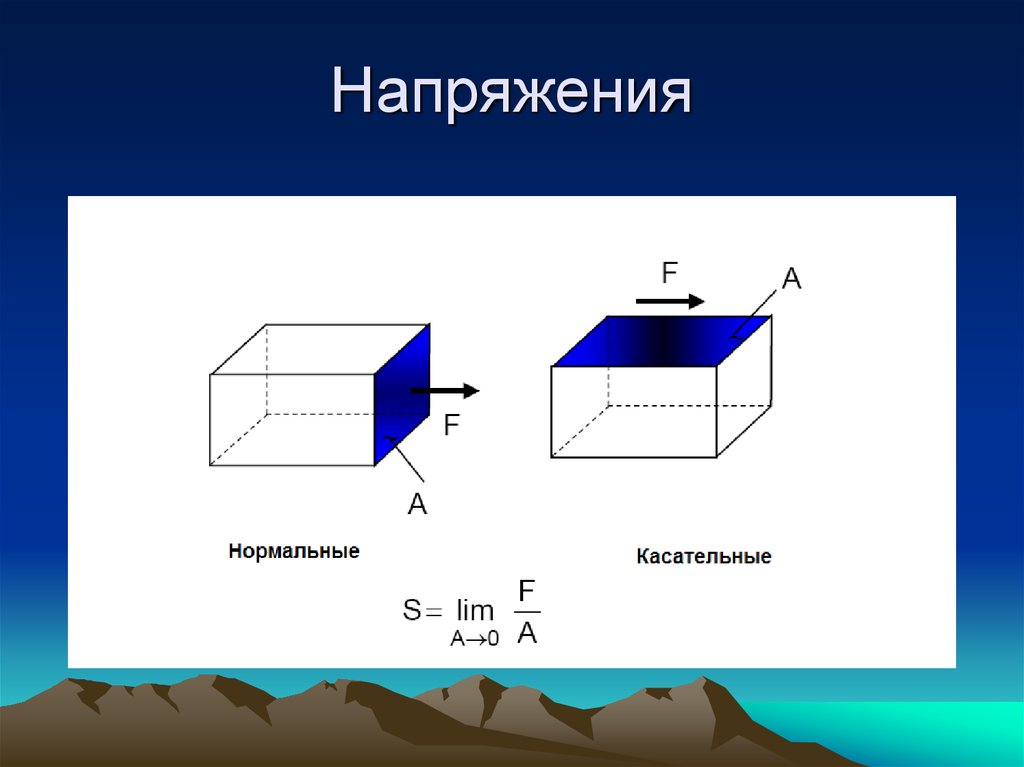
Величина механического напряжения характеризуется внутренними силами молекул, которые направлены против давления и деформации тела, на единицу площади.
Различают два вида напряжения:
- Нормальное напряжение приложено на единицу площади сечения, параллельного главной оси тела.
- Касательное механическое напряжение приложено на единицу площади сечения любой другой плоскости сечения.
Для математического вычисления механического напряжения используется формула: Q=F/S.
Единицы механического напряжения
Величина Q в СИ измеряется в паскалях (Па) и зависит от внутренней силы сопротивления деформации, а также площади тела. Сейчас можно встретить и другие единицы измерения механического напряжения. Среди них атмосфера, торр, бар, физическая и техническая атмосфера, метр водяного столба, миллиметр (дюйм) ртутного столба, фунт-сила на квадратный дюйм и т.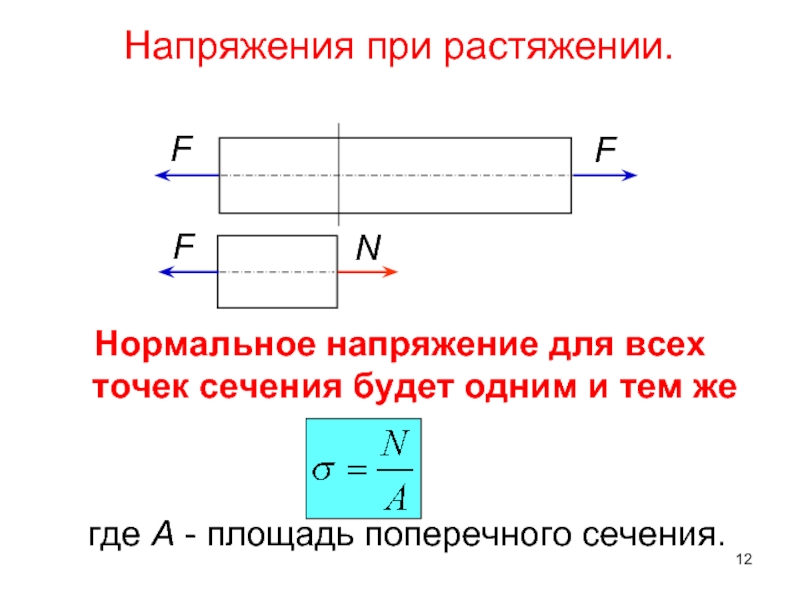
д.
Похожие статьи
- Регулятор напряжения генератора: схема, проверка
- Основные механические свойства твердых тел
- Сервопривод — что это такое? Устройство, подключение, принцип работы, назначение
- Устройство защиты многофункциональное УЗМ-51М: схема подключения, инструкция и особенности
- Динамо-машина своими руками для велосипеда, для зарядки телефона: устройство
- Основные механические свойства материалов и их применение
- Основные свойства жидкостей
Также читайте
Что такое механическое напряжение: Прочность материала
Внутренние силы сопротивления, действующие в направлении, противоположном приложенной внешней силе, препятствуют любому изменению размера и формы твердого тела.
Из-за механического напряжения или внешних сил тело изменяет свою форму. Мы можем выразить это изменение формы тела напряжением в механике. Это явление механического напряжения и деформации можно лучше всего понять, поняв кривую напряжения-деформации.
Что такое механическое напряжение?
Механическое напряжение мера внутреннего сопротивления, проявляемого телом или материалом при приложении к нему внешней силы. это обозначается сигмой (σ).
Предел упругости материала – это предел, при котором сила сопротивления становится равной приложенным силам. В пределе упругости внешние силы, действующие на тело, равны внутренним силам.
Формула механического напряжения
Математически механическое напряжение равно внутренней силе сопротивления, действующей на тело на единицу площади.
Напряжение – это свойство площади или поверхности.
Его значение в любой точке можно определить, рассматривая A→0
Единица напряжения
Единицей механического напряжения в системе СИ является Н/м². Но в паспорте материала это написано как МПа.
| Перевод единиц измерения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 МПа = 1 Н/мм² | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 кв. Дюйм (фунт на квадратный дюйм) = 6,895 Н / мм² | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1000 фунтов на кв.Пример напряжения, действующего на телоРассмотрим случай, когда вы кладете на стол резиновую ленту и мягко поднимаете ее. Какое механическое напряжение возникнет внутри резиновой ленты? Резиновая лента на столе Человек, тянущий резиновую лентуУдерживая резиновую ленту, Механический Напряжение внутри резиновой ленты не возникает , поскольку внешнее усилие не оказывает сопротивления резиновой ленте. Это явление известно как Движение твердого тела . При движении твердого тела объект перемещается из своего исходного положения без какой-либо физической деформации. Но если мы потянем резинку в противоположном направлении, чтобы произвести прогиб. Механическое напряжение будет производиться внутри резиновой ленты. Следовательно, мы можем сделать вывод, что механическое напряжение не будет возникать без прогиба или внутреннего сопротивления. Виды механического напряжения ?Механическое напряжение действует на площадь поперечного сечения тела. Мы можем классифицировать инженерное напряжение на следующие типы в зависимости от положения и направления приложенной внешней силы. Виды механического напряжения1) Одноосное нормальное напряжениеНапряжение, действующее на тело перпендикулярно площади его поперечного сечения, известно как одноосное нормальное напряжение. Это приводит либо к сжатию, либо к удлинению твердого тела. Мы можем классифицировать одноосное нормальное напряжение на два типа:
Напряжение растяжения Напряжение, действующее на тело из-за двух равных и противоположных внешних тяговых сил, известно как Напряжение растяжения Напряжение сжатияМеханическое напряжение, действующее на тело из-за двух равных и противоположных толкающих сил, известно как напряжение сжатия. Напряжение сжатия приводит к увеличению площади поперечного сечения и уменьшению длины тела. 2) Напряжение сдвигаНапряжение сдвигаНапряжение, действующее на тело из-за двух равных и противоположных сил, действующих по разным линиям действия, называется напряжением сдвига. Касательное напряжение действует по касательной к площади тела и приводит к угловой деформации. Мы измеряем касательное напряжение как угол. Формула напряжения сдвигаНапряжение сдвига (γ) = θ Таким образом, механическое напряжение — это внутреннее сопротивление, проявляемое телом при приложении к нему внешней силы. Мы будем продолжать добавлять информацию о различных типах напряжений, используемых в машиностроении. Поделитесь своими предложениями, комментариями или вопросами в поле для комментариев. Мы предлагаем вам также прочитать эту статью о факторе безопасности в машиностроении. Сопротивление материалов | Механика материаловПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript. Прочность материалов , также известная как механика материалов , ориентирована на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки. Стресс и напряжение Когда сила приложена к элементу конструкции, этот элемент будет испытывать как напряжение, так и деформацию в результате действия силы. где F — приложенная сила, а A — площадь поперечного сечения, на которое действует сила. Приложенная сила заставит элемент конструкции деформироваться на некоторую длину пропорционально его жесткости. Деформация – это отношение деформации к исходной длине детали: где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними). Существуют различные типы нагрузки, которые приводят к различным типам напряжения, как указано в таблице ниже:
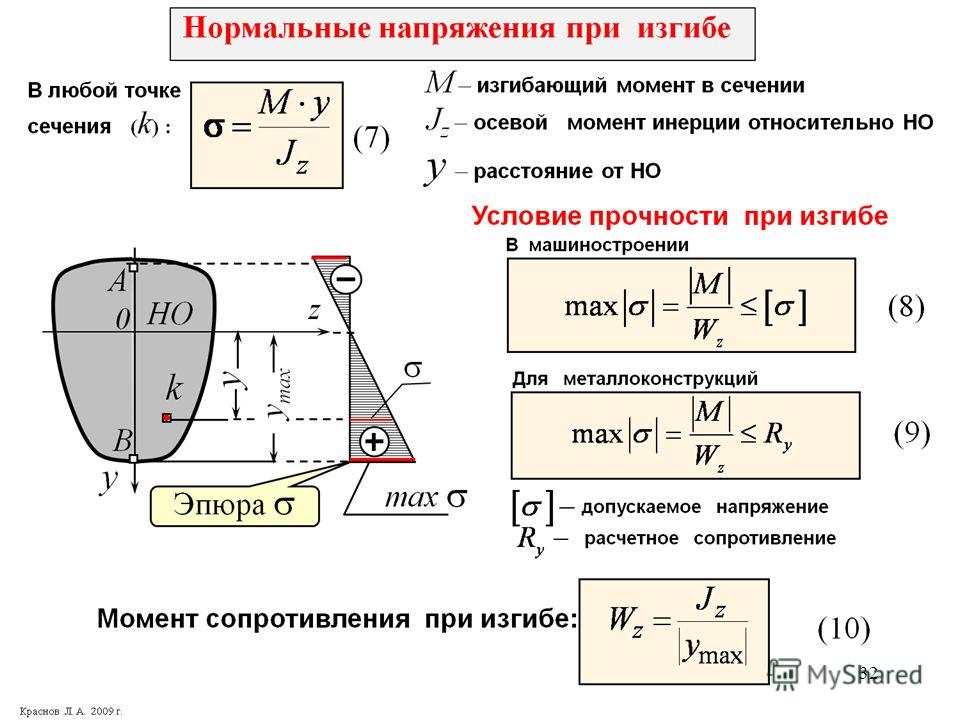
Осевое напряжение и напряжение изгиба являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно площади, противодействующей силе.
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — сила, а A — площадь поперечного сечения элемента. В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c – центральный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения кручения T — это кручение, r — радиус, а J — полярный момент инерции поперечного сечения. В случае осевого напряжения на прямолинейном участке напряжение распределяется равномерно по всей площади. В случае касательного напряжения распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F/A, и это среднее напряжение сдвига обычно используется при расчете напряжения. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и напряжения кручения максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках. Так же, как первичными типами напряжения являются нормальное напряжение и напряжение сдвига, первичными типами деформации являются нормальная деформация и деформация сдвига . В случае нормальной деформации деформация нормальна к области, воспринимающей силу: В случае деформации поперечного сдвига деформация параллельна площади, несущей силу: где γ – деформация сдвига (безразмерная), а ϕ — деформированный угол в радианах. В случае деформации кручения элемент скручивается на угол ϕ вокруг своей оси. Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется по формуле: где ϕ — угол закручивания, r — радиус стержня, а L — длина. Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом: где ρ — радиальное расстояние от оси стержня. Закон ГукаНапряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, где кривая является линейной). Нормальный стресс и деформация связаны: σ = E ϵ где E — модуль упругости материала, σ — нормальное напряжение, ϵ это нормальное напряжение. Касательное напряжение и деформация связаны соотношением: τ = G γ где G — модуль сдвига материала, τ — касательное напряжение, γ — сдвиговая деформация. где ν — коэффициент Пуассона. Закон Гука аналогичен уравнению силы пружины, F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно изменить, чтобы получить деформацию (удлинение) материала:
Энергия деформации Когда к элементу конструкции прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина. Энергия деформации (т. е. количество потенциальной энергии, накопленной в результате деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и выражается в дюйм-фунтах силы в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах предела упругости, то вся энергия деформации может быть восстановлена. Энергия деформации рассчитывается как:
Обратите внимание, что есть два уравнения для энергии деформации в пределе упругости. Первое уравнение основано на площади под кривой отклонения нагрузки. Второе уравнение основано на уравнении потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному. Более подробную информацию об энергии деформации можно найти здесь. ЖесткостьЖесткость, обычно называемая жесткостью пружины, представляет собой усилие, необходимое для деформации элемента конструкции на единицу длины. Все конструкции можно рассматривать как наборы пружин, а силы и деформации в конструкции связаны уравнением пружины: F = k δ макс. где k — жесткость, F — приложенная сила и δ max — максимальный прогиб элемента. Если прогиб известен, то жесткость элемента можно найти, решив k = F/δ max . Однако максимальное отклонение обычно неизвестно, поэтому жесткость необходимо рассчитывать другими способами. Таблицы прогиба балки можно использовать для общих случаев. Два наиболее полезных уравнения жесткости, которые нужно знать, — это уравнения жесткости для балки с осевой нагрузкой и для консольной балки с торцевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
Крутильный эквивалент уравнения пружины: T = k ϕ Особый интерес представляет жесткость вала при нагрузке на кручение:
Конструкция с несколькими путями нагрузкиЕсли в конструкции имеется несколько путей прохождения нагрузки (т. е. в конструкции есть несколько элементов, которые распределяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.
Если элементы на пути нагрузки нельзя рассматривать только как пружины, соединенные последовательно или как пружины, соединенные параллельно, а скорее они представляют собой комбинацию пружин, соединенных последовательно и параллельно, то проблему необходимо будет решать итеративно. Найдите подгруппу стержней, которые расположены последовательно или параллельно, и используйте предоставленные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одну пружину с рассчитанными жесткостью, силой и прогибом, и эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат. Концентрация стрессаМожно представить, что силы и напряжения протекают через материал, как показано на рисунке ниже. Когда геометрия материала изменяется, линии потока перемещаются ближе или дальше друг от друга, чтобы приспособиться. Если в материале есть разрыв, такой как отверстие или выемка, напряжение должно течь вокруг разрыва, и линии потока будут собираться вблизи этого разрыва. Эта внезапная упаковка линий потока вызывает резкий скачок напряжения — это пиковое напряжение называется концентрация напряжений . Элемент, вызывающий концентрацию напряжений, называется концентраторами напряжений . Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в непосредственной близости от несплошности, рассчитайте номинальное напряжение в этой области, а затем масштабируйте его с помощью соответствующего коэффициента концентрации напряжения: σ макс. где о max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, K — коэффициент концентрации напряжения. При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше следует использовать наименьшую площадь в основании скругления. Многие справочники содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрий. Двумя наиболее полными наборами факторов концентрации стресса являются факторы концентрации стресса Петерсона и формулы Рорка для стресса и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации напряжений. Концентрация напряжения будет рассеиваться по мере удаления от источника напряжения. Принцип Сен-Венана — это общее практическое правило, согласно которому расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку. Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах локальная текучесть позволит перераспределить напряжения и уменьшит напряжение вокруг райзера. По этой причине коэффициенты концентрации напряжений обычно не применяются к конструктивным элементам, изготовленным из пластичных материалов. Коэффициенты концентрации напряжения также обычно не применяются при наличии избыточного пути нагрузки, и в этом случае текучесть одного элемента позволит перераспределить силы на элементы на других путях нагрузки. Примером этого является шаблон болтов. Если один болт начнет прогибаться, то другие болты в схеме примут на себя большую нагрузку. Комбинированные напряженияВ любой точке нагруженного материала общее напряженное состояние можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью касательными напряжениями (по два в каждом направлении): Нижние индексы нормальных напряжений σ указывают направление нормальных напряжений. Обычно напряжения в одном направлении равны нулю, так что полное напряженное состояние возникает в одной плоскости, как показано на рисунке ниже. Это называется плоскостное напряжение . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Поверхностные напряжения обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и напряжение кручения максимальны на поверхности. На рисунке выше σ x и σ y — нормальные напряжения, τ — касательное напряжение. Напряжения уравновешиваются так, что точка находится в статическом равновесии. Поскольку все напряжения сдвига равны по величине, индексы для простоты опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y . Надлежащие соглашения о знаках показаны на рисунке. При нормальном напряжении растягивающее напряжение положительно, а сжимающее отрицательно. Для касательного напряжения направление по часовой стрелке является положительным, а против часовой стрелки — отрицательным. Если напряжения на рисунке выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ по отношению к горизонтали, как показано на рисунке ниже. Уравнения преобразования , приведенные ниже, дают значения нормального напряжения и напряжения сдвига в этой повернутой плоскости.
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки. В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимальны и минимальны.
Приведенные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и предельных касательных напряжений:
Углы, под которыми возникают главные напряжения, составляют 90 ° друг от друга. Главные напряжения всегда сопровождаются нулевым касательным напряжением. Пара полезных отношений:
Круг Мора Круг Мора — это способ визуализации напряженного состояния в точке нагруженного материала. Это дает интуитивное представление об уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы главные напряжения, экстремальные напряжения сдвига и углы, под которыми возникают эти напряжения. Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений: Поместите точки на круге, представляющие напряжения на гранях 90 146 x 90 147 и 90 146 y 90 147 элемента напряжения. Напряжения на грани x будут иметь координаты ( σ x , −τ ), а напряжения на грани y будут иметь координаты ( σ y , τ ). Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты ( σ 1 , 0 ), а минимальное главное напряжение будет иметь координаты ( σ 2 , 0 ). Поместите точки на окружность для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 2 ). Все точки будут лежать на периметре окружности. Напряженное состояние на x и y гранях напрягаемого элемента представлено черной линией в круге Мора, соединяющей точки ( σ x , −τ ) и ( σ y , τ ). Эта линия в круге Мора соответствует невращенному элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек в конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента. Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, очки за 9Грань 0146 x и грань y отстоят друг от друга на 180 градусов на круге Мора, но только на 90 градусов на элементе напряжения. Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в нагруженном элементе и как изменяется напряженное состояние в зависимости от угла поворота, см. прилагаемый калькулятор круга Мора. ПриложенияЕсть много структурных компонентов, которые обычно подвергаются анализу напряжения. Подробности анализа этих компонентов приведены в других разделах:
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции. Предел текучести материала обычно выбирают в качестве предела прочности, с которым сравнивают расчетные напряжения. Коэффициент безопасности , FS, рассчитывается как: где σ фактическое — расчетное напряжение в конструкции, а σ предел — максимальный предел напряжения, обычно прочность материала, такая как предел текучести (S ty). Коэффициент безопасности показывает, насколько фактическое напряжение ниже предельного напряжения. Запас прочности рассчитывается как: В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы безопасности обычно представляются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. При сообщении коэффициентов безопасности и пределов безопасности иногда требуемый коэффициент безопасности будет «запекаться» в сообщаемых факторах. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, чтобы FS req = 2. Для обеспечения необходимого коэффициента запаса прочности сообщаемые значения FS и MS рассчитываются как: Обратите внимание, что при включении требуемого коэффициента запаса прочности, FS req , сообщаемые FS и MS на самом деле являются запасами по отношению к FS req , а не по отношению к напряжению. PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице прочности материалов. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE. Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание! Просмотреть курс сейчас: Просмотреть курс Каталожные номера
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Напряжение растяжения приводит к общему увеличению длины и уменьшению площади поперечного сечения тела.
Внутри материала без деформации не возникает напряжения.
Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила/дюйм 2 (psi) для обычных единиц США и Н/м 2 (Па) для единиц СИ:
Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.
Модуль упругости и модуль сдвига связаны соотношением:
отклонение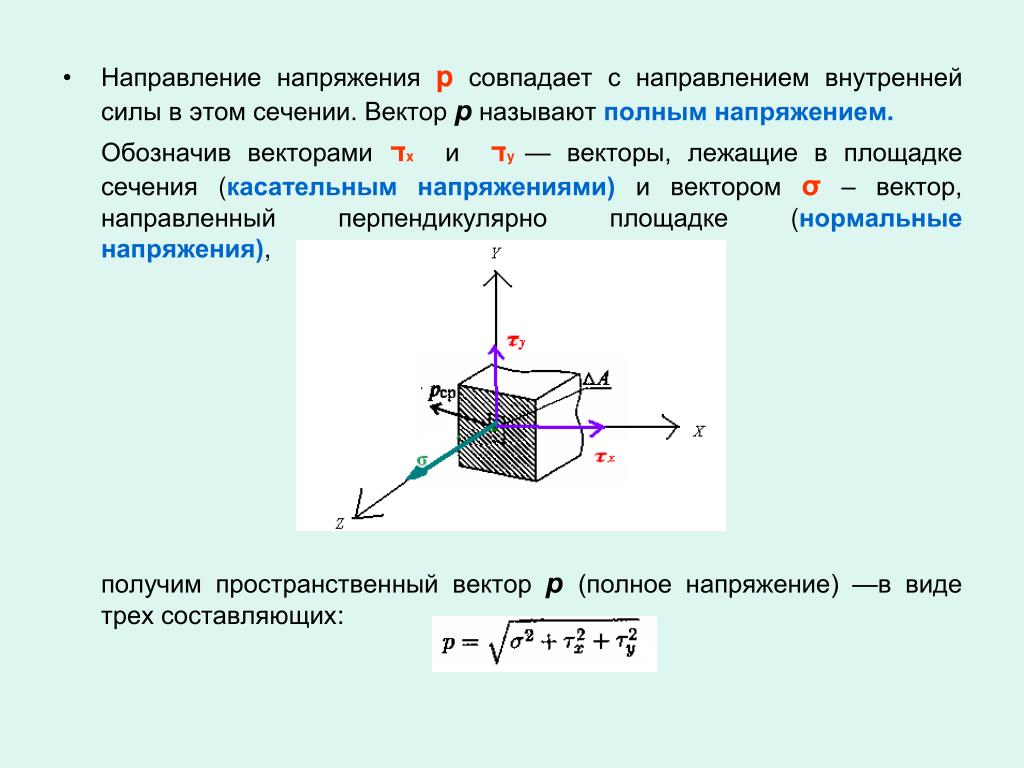 
..
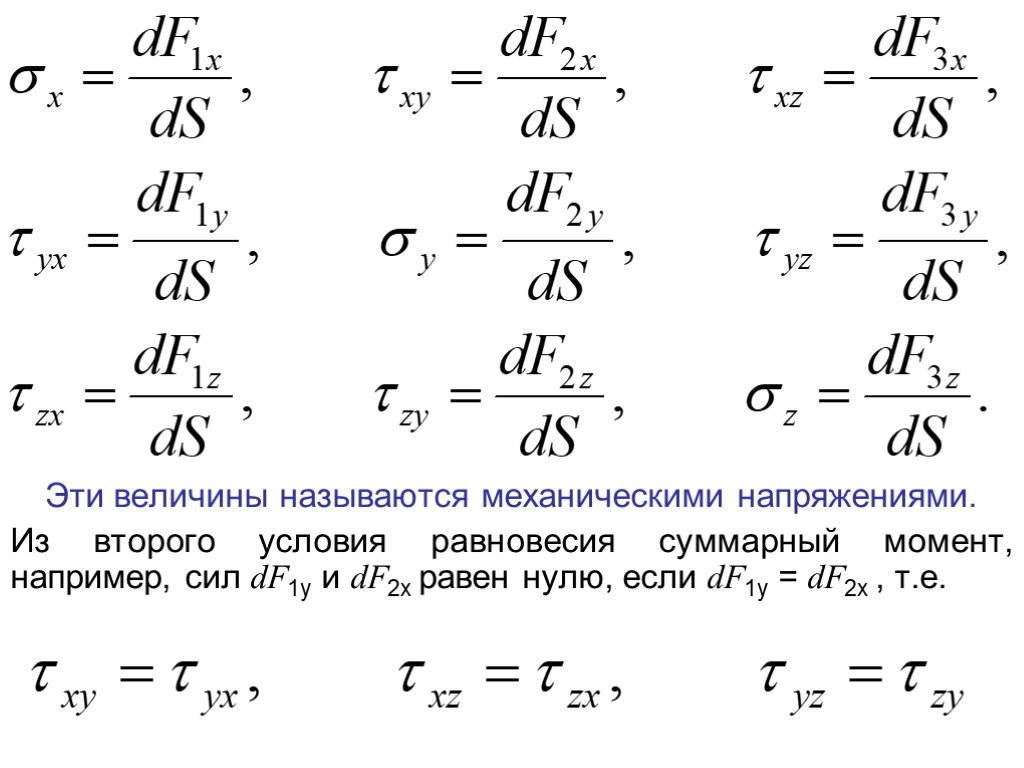= K σ ном. 
Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
)
Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
Углы, под которыми возникают предельные касательные напряжения, составляют 45 ° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ x + σ и ) / 2.
Пример круга Мора показан на рисунке ниже:
Окружность имеет радиус, равный величине предельных касательных напряжений:
Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию. Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10. 
Например, если предельное напряжение конструкции в 1,5 раза превышает фактическое напряжение, запас составляет 50 % (MS = 0,5).
