| Administrator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
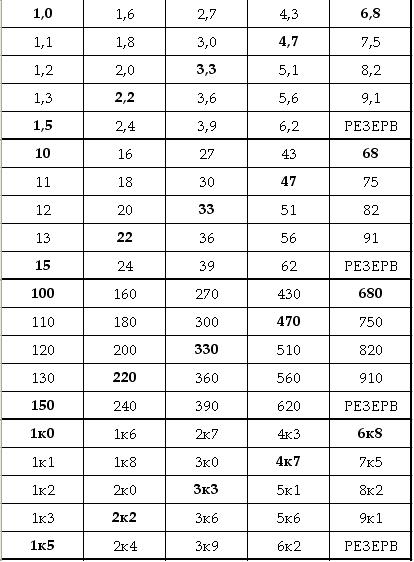
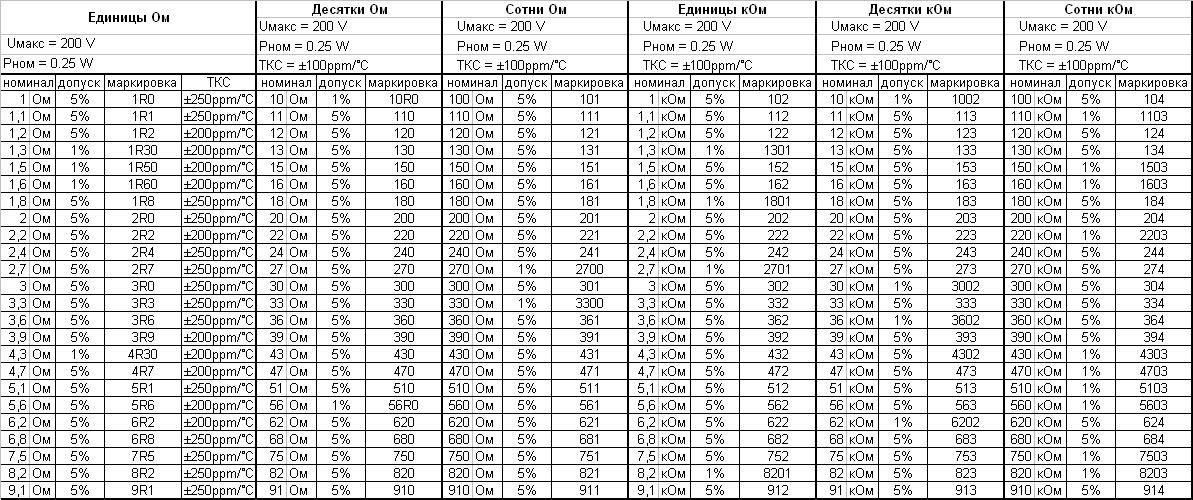
Номиналы промышленно выпускаемых радиодеталей (сопротивление резисторов, ёмкость конденсаторов, индуктивность небольших катушек индуктивности) имеют отнюдь не произвольные значения, а берутся из специальных номинальных рядов. Точнее, номиналы деталей могут быть произвольным числом из соответствующего ряда, умноженным на произвольный десятичный множитель (десять в произвольной (целой?) степени), например резистор из ряда E12 может иметь сопротивление 1,2 Ом, 12 Ом, 120 Ом, …, 1,2 МОм, 12 МОм, 1,5 Ом, 15 Ом и т. д. Название ряда указывает общее число элементов в нём, т. е. ряд E24 содержит 24 числа в интервале от 1 до 10, E12 — 12 чисел и т. д. Каждый ряд соответствует определённому допуску в номиналах деталей. Так, детали из ряда E6 имеют допустимое отклонение от номинала ±20 %, из ряда E12 — ±10 %, из ряда E24 — ±5 %. Компания «Новый свет» поставляет радиодетали любых номиналов. Посмотрите каталог электронных компонентов здесь. Мы продаем светодиоды DIP, светодиоды SMD; тонкопленочные, металлокерамические и SMD резисторы; светодиоды сверхяркие (Пиранья), цоколи для изготовления ламп, радиаторы для светодиодов, мощные светодиоды от 1Вт, алюминиевые платы для светодиодов, светодиодную оптику. Указание на схемах номиналов элементов, не принадлежащих никакому ряду без особого технического обоснования, считается неграмотностью. Поэтому хорошие радиоинженеры помнят ряд E24 наизусть. Значения номиналов для некоторых рядов приведены в таблице:
Видно, что ряд E12 получается вычёркиванием из ряда E24 каждого второго номинала, аналогично, E6 получается вычёркиванием из E12 каждого второго номинала. Простая формула для получения значений номиналов: V(n) = Round(100*exp((n-1)/N*ln(10))), где V(n) значение n-го номинала в классе E-N (N=192,96,48,24,12,6,3). Ряд E24 приблизительно представляет собой геометрическую прогрессию со знаменателем 101/24. Другими словами, в логарифмическом масштабе элементы этого ряда делят отрезок от 1 до 10 на 24 равные части. По некоторым, видимо историческим, соображениям некоторые элементы отличаются от идеальной прогрессии, хотя и никогда не больше, чем на 2,5 %. Номинальные ряды с меньшим количеством элементов получаются вычёркиванием элементов из ряда E24 через один. Номиналы из этих рядов образуют примерно геометрическую прогрессию со знаменателем 101/12 (E12), 101/6 (E6), 101/3 (E3). Ряд E3 практически не применяется. Номинальные ряды с большим числом элементов образуют уже абсолютно точную геометрическую прогрессию со знаменателем 101/n, где n — число элементов ряда. Число n всегда представляет собой степень двойки, умноженную на 3. Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %. Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 101/48 ≈ 1,04914, 101/96 ≈ 1,024275, 101/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.
|
Ряды номиналов электронных компонентов
Номиналы промышленно выпускаемых радиодеталей (сопротивление, ёмкость, индуктивность) имеют не произвольные значения, а берутся из специальных номинальных рядов.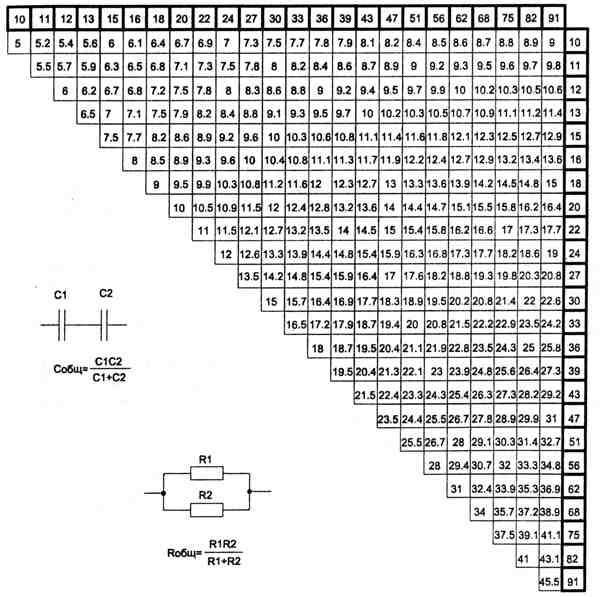
Точнее, номиналы деталей могут быть произвольным числом из соответствующего ряда, умноженным на произвольный десятичный множитель (десять в произвольной степени), например резистор из ряда E12 может иметь сопротивление 1,8 Ом, 18 Ом, 180 Ом, …, 1,8 МОм, 18 МОм, 1,5 Ом, 15 Ом и т. д.
Название ряда указывает общее число элементов в нём, т. е. ряд E24 содержит 24 числа в интервале от 1 до 10, E12 — 12 чисел и т. д. Каждый ряд соответствует определённому допуску в номиналах деталей. Так, детали из ряда E6 имеют допустимое отклонение от номинала ±20%, из ряда E12 — ±10%, из ряда E24 — ±5%.
Собственно, ряды устроены таким образом, что следующее значение отличается от предыдущего чуть меньше, чем на двойной допуск. Таблицу приведенную ниже можно считать неполной, поскольку выпускаются резисторы и с меньшими отклонениями — ±0,25%, ±0,1% и ±0,05%. Но принцип их построения остается неизменным, по сути своей представляет собой таблицу десятичных логарифмов.
Действительно, порядковый номер элемента в ряду минус 1 даёт мантиссу логарифма в виде простой дроби со знаменателем (m − 1)/n (m — номер элемента, n — порядок ряда, например, 24 для E24).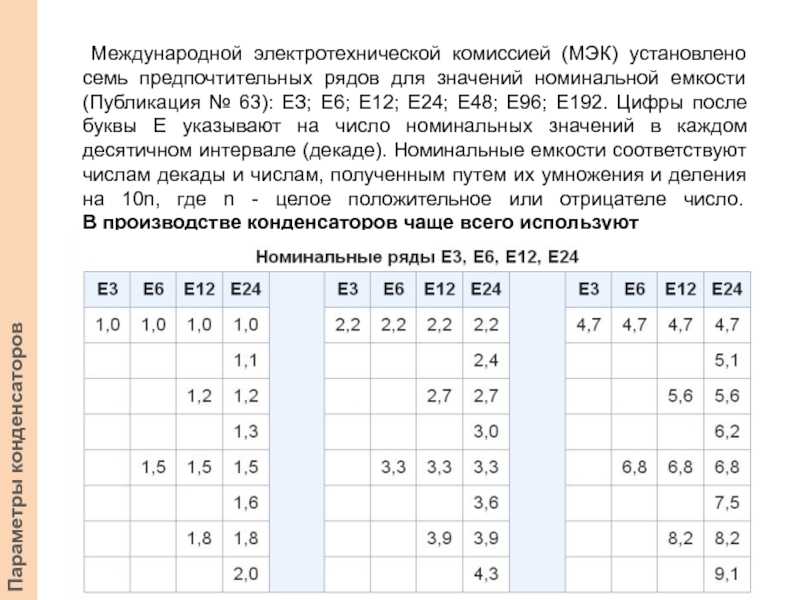
Зная наизусть ряд E24, можно, таким образом, в уме вычислять произведения чисел, квадратные корни небольших степеней из чисел, логарифмы чисел с точностью, примерно ±5%. Например вычислим квадратный корень из 1000. Десятичный логарифм этого числа равен 3, поделив его пополам, находим, что десятичный логарифм ответа 1,5 = 1 + 12/24, т. е. ответ есть 10 умноженное на элемент, стоящий в ряду E24 на 13-м месте, т. е. точно в середине ряда, т. е. получили примерно 33.
Номинальные ряды E3, E6, E12, E24
| E3 ±30% | E6 ±20% | E12 ±10% | E24 ±5% |
|---|---|---|---|
| 1,0 | 1,0 | 1,0 | 1,0 |
| 1,1 | |||
| 1,2 | 1,2 | ||
| 1,3 | |||
| 1,5 | 1,5 | 1,5 | |
| 1,6 | |||
| 1,8 | 1,8 | ||
| 2,0 | |||
| 2,2 | 2,2 | 2,2 | 2,2 |
| 2,4 | |||
| 2,7 | 2,7 | ||
| 3,0 | |||
| 3,3 | 3,3 | 3,3 | |
| 3,6 | |||
| 3,9 | 3,9 | ||
| 4,3 | |||
| 4,7 | 4,7 | 4,7 | 4,7 |
| 5,1 | |||
| 5,6 | 5,6 | ||
| 6,2 | |||
| 6,8 | 6,8 | 6,8 | |
| 7,5 | |||
| 8,2 | 8,2 | ||
| 9,1 |
Номинальные ряды E48, E96, E192
Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %, этот же ряд используется и для точности 0,25% и 0,1%.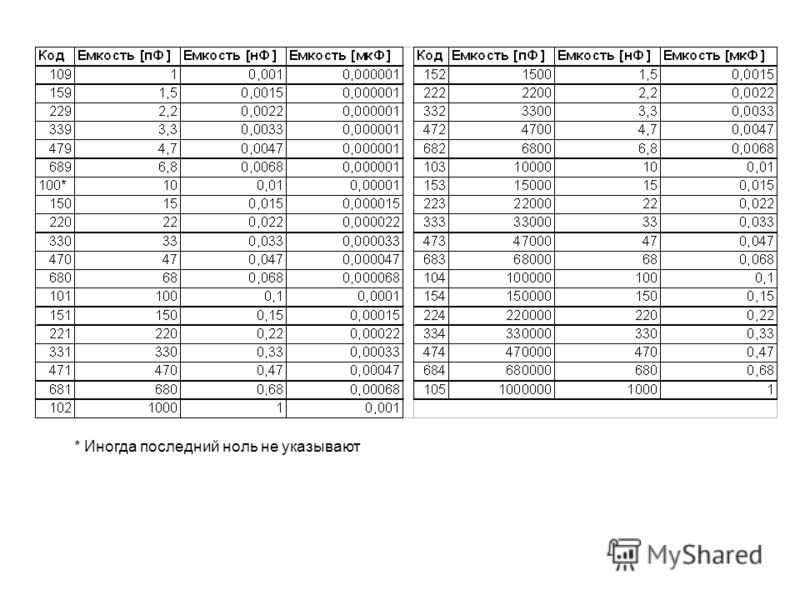
Элементы этих рядов образуют геометрическую прогрессию со знаменателями 101/48 ≈ 1,04914, 101/96 ≈ 1,024275, 101/192 ≈ 1,01206483 и могут быть вычислены на калькуляторе.
Разница между количественными, порядковыми и номинальными числами
Арифметика является элементарной частью теории чисел. Арифметика — это раздел математики, который состоит из изучения чисел и традиционных операций, таких как сложение, вычитание, умножение, деление, нахождение корней, экспонента и т. д. Он имеет дело со свойствами и манипуляциями с числами.
Числа и система счисления
Число является основной единицей математики. Это арифметическое значение, представленное в виде слова, символа, цифры и т. д. Числа используются для счета, вычислений, измерения и т. д. Примеры чисел: 1, 2, 3, 458, 102556 и т. д.
- 1, 3, 5, 89 и т. д. называются нечетными числами.
- 2, 4, 6, 8, 10, 1236 и т. д. называются четными числами.
Системы счисления представляют собой набор символов, представляющих числа.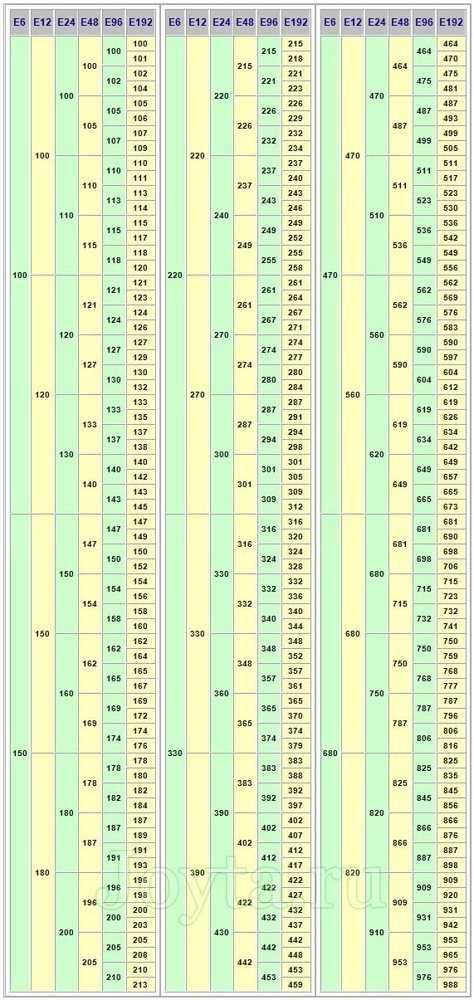
Он определяет набор значений для представления количества. В основном это представление чисел с помощью цифр или символов. Существует четыре основных типа систем счисления: двоичная система счисления, десятичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления.
В чем разница между количественными, порядковыми и номинальными числами?
Кардинальные числительные, порядковые числительные и номинальные числительные определены для десятичной системы счисления. Кардинальные числа, как следует из названия, используются для счета. Порядковые числа используются для организации различных номеров, а именные – для целей идентификации, например, номер паспорта человека является именном номером. Давайте посмотрим на разницу между всеми тремя типами чисел:
Числа | Порядковые числительные | Номинальные числительные |
Числа, используемые для счета. Это помогает нам узнать, сколько элементов существует. | Порядковые числа — это понятие натуральных чисел, которое используется для описания способа расположения различных элементов. | Номинальные номера могут быть определены как номера, которые используются для идентификации. |
| Наименьшее кардинальное число равно 1, а не 0, поскольку 0 не является счетным числом. | Обозначает позицию элемента по отношению к другим элементам. | Они используются для уникальной маркировки элементов. |
Примеры количественных чисел: 1,2,3,4 …. скоро. | Примеры порядковых номеров: 1-й- первый, 2-й- второй, 12-й- двенадцатый и т.д. |
Примеры задач
Вопрос 1: Какое кардинальное число наименьшее?
Ответ:
1 — наименьшее кардинальное число.
Вопрос 2: Что из следующего является примером порядковых числительных?
- 123
- Pincode: 851142
- Четвертый
- 2568
Ответ:
. Четвертый пример порядкового номера. Вопрос 3: Дни недели даны следующим образом: воскресенье понедельник вторник среда четверг пятница суббота Ответ: Вопрос 4: Каково кардинальное число множества X = {31, 50, 17, 1521, 400, 285819}? Ответ: Набор X содержит 6 элементов. Таким образом, кардинальное число множества X равно 6. Вопрос 5. Какие из следующих чисел являются четными? 25,12, 26 289, 20, 22, 86. Ответ: 12, 26, 20, 22, 86 — все четные числа, поскольку все они делятся на 2. Термины «кардинальный», «порядковый» и «номинальный» являются общепринятыми терминами, которые используются в статистике или общей математике. Термины используются для классификации чисел в категории, чтобы упростить их использование. Это часто сбивает с толку многих людей, но когда-то понятое, это довольно просто понять. Термин кардинал имеет два определения: одно в лингвистике, другое в математике. В лингвистике или традиционной грамматике термин «кардинал» — это часть речи, которая используется для подсчета или указания количества. Например, в мешке с 10 яблоками число 10, обозначающее количество яблок, будет количественным числом. Однако в математике количественные числа имеют немного другое значение. Кардинал относится к измерению кардинальности (количества присутствующих элементов) набора или между двумя наборами. Даже в этом смысле количественные числа должны иметь цифры или целые числа. Мощность конечного множества является натуральным числом, а трансфинитные количественные числа описывают размеры бесконечных множеств. Мощность определяется в терминах биективных функций, что требует однозначной функции. Для каждого элемента в одном наборе должен присутствовать элемент в парном наборе. Например, множество A {1, 2, 3} и множество B {5, 6, 7} не равны, но имеют мощность, поскольку множество A состоит из 3 элементов, как и множество B. Порядковые номера — это слова, обозначающие ранг и порядок в наборе. Порядок набора не имеет значения, а может по размеру, важности, хронологии и так далее. Его также можно использовать в английском языке с такими терминами, как первый, второй, третий и т. Номинальные числа, также известные как категориальные числа, в основном представляют собой числа, которые используются для идентификации чего-либо. Числовое значение почти совпадает с именем. Числовое значение не имеет значения, и они не указывают количество, ранг или любое другое измерение. Использование термина «номинальное» появилось совсем недавно и не получило широкого распространения. Термин происходит от статистического термина «номинальные данные», предполагающего, что номинальные числа являются «…просто утверждениями качественной категории членства». Они часто указывают числа как имя. Сравнение количественных, порядковых и номинальных числительных: Кардинальные числа Порядковые номера Номинальные номера Определение Cardinal используется для подсчета или указания количества. Порядковые числа — это слова, обозначающие ранг и порядок в наборе. Номинальные числа — это в основном числа, которые используются для идентификации чего-либо.
0090
Разница между количественными, порядковыми и номинальными числами
Ключевая разница: Кардинал используется для подсчета или указания количества. Порядковые числа — это слова, обозначающие ранг и порядок в наборе. Номинальные числа — это в основном числа, которые используются для идентификации чего-либо.
Числа являются определенными числами и не могут содержать дроби или десятичные дроби.
Д. Существует три варианта порядковых номеров: пространственный / хронологический, приоритет / эффект и греческий префикс. Пространственный/хронологический включает в себя такие термины, как первый, второй, третий. Приоритет / эффект включает в себя первичный, вторичный, третичный и т. Д. Наконец, греческий префикс является наиболее редко используемым и использует такие термины, как прото-, второ- и трито-.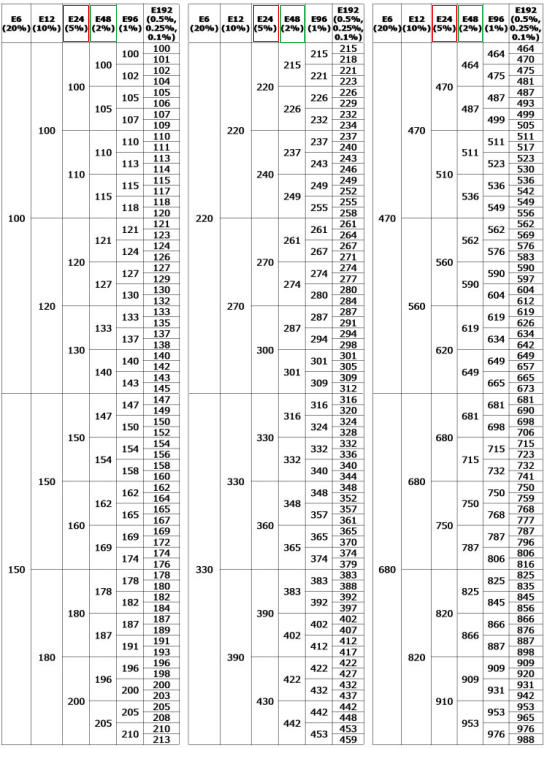
Номинальный номер можно разделить на два определения: «любое число, используемое для идентификации, как бы оно ни было присвоено», или «число, не имеющее никакой информации, кроме идентификации». Эти номера не ограничиваются использованием только цифр, но могут также включать алфавиты, что делает их буквенно-цифровыми, например, номерные знаки автомобилей и т. д.
