Номинальное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Зависимость допускаемой мощности электрической нагрузки ( в процентах от номинальной мощности рассеяния от температуры окружающего воздуха.| Зависимость допускаемой мощности электрической нагрузки ( в процентах от номинальной мощности рассеяния от атмосферного давления для резисторов типовМТ ОМЛТ, МЛТ, том ( ГОСТ 2825 — 67 в.  [1]

Номинальные сопротивления соответствуют приведенным в таблице числам и числам, полученным путем умножения на 10, где п — целое положительное или отрицательное число.  [2]

Номинальное сопротивление — значение, указанное на мере или приписанное ей. Номинальное значение меры должно выражаться числом 10, где п — целое положительное или отрицательное число.  [3]

Входная кассета основного звукового тракта ( кассета индивидуального регулятора КС-1.  [4]

Номинальное сопротивление, на которое нагружается выход основного звукового тракта, — 600 ом, минимальное — 150 ом.  [5]

Номинальное сопротивление для трансформатора тока в 2 представляет собой то результирующее кажущееся сопротивление, на которое может быть замкнута вторичная обмотка без вреда для данного класса прибора; предельное сопротивление трансформатора — то сопротивление, при котором ошибки в показаниях величины топ составляют 1 ( Хю ог номинального тока. Номинальная мощность в VA указывает, как велик может быть общий расход энергии во вс х присоединенных приборах соответственно требованиям, предъявляемым к измерительным приборам данного класса. Предельная мощность — мощность, которая получается при крайних допусках нагрева.  [6]

Номинальное сопротивление — это сопротивление, обозначенное на резисторе.  [7]

Номинальное сопротивление — электрическое сопротивление, значение которого обозначено на резисторе или указано в нормативной документации н которое является4 исходным для отсчета отклонений от этого значения. Диапазон номинальных сопротивлений установлен для резисторов: постоянных от долей ома до единиц тераом; переменных проволочных от 0 47 Ом до 1 МОм; переменных непроволочных от I Ом до 10 МОм.  [8]

Номинальное сопротивление и допускаемое отклонение фактического сопротивления резистора от его номинального значения ( допуск) обычно обозначены на самом резисторе.  [9]

Деформационные характеристики тензорезисторов из кремния.  [10]

Номинальное сопротивление тензорезисторов зависит от температуры, так как с ее изменением изменяются концентрация и подвижность носителей заряда. Температурная зависимость номинального сопротивления тензорезисторов имеет сложный характер. Однако для обычно используемых материалов со значительной концентрацией примесей можно считать в первом приближении, что температурный коэффициент сопротивления остается постоянным в рабочем диапазоне температур.

 [11]

Номинальные сопротивления ТС Rzo могут иметь значения ( у разных типов) от единиц ом до сотен килоом. У ТС одного и того же типа диапазон номинальных сопротивлений бывает несколько уже, так как Дао сильно зависит от конструкции ТС.  [12]

Номинальное сопротивление терморе-зистора задается при комнатной температуре. Для термисторов а — ( 0 8 — 6) 10 — 2к — 1 Этот же коэффициент для позисторов не является удобным, так как а сильно зависит от температуры.  [13]

Номинальное сопротивление Raoa — это сопротивление, обозначенное на резисторе. Фактическое сопротивление резистора может отличаться от обозначенного на величину, не превышающую допускаемого отклонения.  [14]

Номинальное сопротивление прибора типа Р4002 составляет 10 и 105 ом; при-бора типа Р4003 — 105 ом; прибора типа Р4004 — 106 ом; прибора типа Р4005 — 10 ом. Номинальное сопротивление одной ступени магазина типа Р4002 составляет 10е и 107 ом.

 [15]

Страницы:      1    2    3    4    5

Номинальное сопротивление по рядам

	Числовые коэффициенты
Е6 Е12 Е24	1; 1,5; 2,3; 3,3; 4,7; 6,8; 1; 1,2; 1,5; 1,8; 2,2; 2,7; 3,3; 3,9; 4,7; 5,6; 6,8; 8,2; 1; 1,1; 1,2; 1,3; 1,5; 1,6; 1,7; 2; 2,2; 2,4; 2,7; 3; 3,3; 3,6; 3,9; 4,3; 4,7; 5,1; 5,6; 6,2; 6,8; 7,5; 8,2; 9,1. Номинальное сопротивление будет сопротивление, которое соответствует указанным в таблице, или в результате умножения или деления на 10n

Действительное значение сопротивлений резисторов вследствие погрешностей изготовления могут отличаться от номинальных. Разница между номинальным и действительным сопротивлениями, называется допускаемым отклонением от номинального сопротивления или, кратко, допуском. Согласно ГОСТ 9664 – 14 установлен ряд допусков: ±0,001; ±0,002; ±0,005; ±0,01; ±0,02; ±0,05; ±0,1; ±0,25; ±0,5; ±1; ±2; ±5; ±10; ±20; ±30%.

Шумы резисторов.

Собственные шумы резисторов измеряют действующим значением ЭДС шумов и выражают в микровольтах на вольт приложенного напряжения. Значение ЭДС шумов большинства типов непроволочных резисторов от долей единиц до десятков микровольт на вольт. Исключения составляют лакопленочные и объемные композиционные резисторы, у которых ЭДС шумов может достигать сотен микровольт на вольт.

Шумы скольжения (вращения) присущи переменным резисторам. Они возникают в динамическом режиме при движении подвижного контакта по резистивному элементу в виде напряжения помех. В приемных устройствах эти помехи приводят к шорохам и трескам.

Уровень шумов перемещения значительно превышает уровень тепловых и токовых шумов. Даже ля сравнительно хороших непроволочных переменных резисторов напряжение шумов вращения может достигать десятки милливольт (15,…,50 мВ).

Полупроводниковые не линейные резисторы – это изделие электронной техники, основное свойство которых, в отличие от линейных резисторов, заключается в способности изменять свое электрическое сопротивление под действием управляющих факторов: температуры, напряжения, магнитного поля и др.

Терморезисторы, или термисторы – полупроводниковые резисторы с нелинейной ВАХ (вольтамперной характеристикой), отличительной способностью которых является резко выраженная зависимость электрического сопротивления от температуры. Существуют терморезисторы, как с отрицательным, так и с положительным температурным коэффициентом сопротивления – позисторы.

Термисторы характеризуются следующими параметрами:

1. номинальное сопротивление.

2. температурный коэффициент сопротивления.

3. максимально-допустимая мощность рассеивания.

4. коэффициент температурной чувствительности, который показывает, какова температурная зависимость для данного сопротивления.

5. постоянная времени T характеризует тепловую инерционность. T численно равна времени в течении которого t˚ термосопротивления при перенесении его из воздушной среды с t˚ C 0˚ в воздушную среду с t˚ C 100˚.

Варисторы – полупроводниковые резисторы с нелинейной ВАХ. Отличительная особенность, резко выраженная зависимость электрического сопротивления от приложенного к ним напряжения.

Их используют для стабилизации и защиты от перенапряжений. Преобразования частоты и напряжения, а также для регулирования усиления в системах автоматики, различных измерительных устройствах, источниках вторичного питания, в телевизионных приемниках, для подстройки частоты гетеродинов, в генераторах переменного и импульсного пилообразного напряжения, в системах размагничивания цветных кинескопов и др.

5. Презентация методов номинального сопротивления — оценка методов проектирования свай с использованием документации Advanced Data Analytics

Для сравнения рассчитанной и прогнозируемой нагрузок свай использовалось несколько методов расчета мощности сваи. Краткий обзор этих методов представлен в этой главе. Чтобы обеспечить пакетную обработку, методы емкости были запрограммированы на Python.

Рис. 5.1 Типичный вид профиля с заглубленной сваей и соответствующими символами

Предельная несущая способность, \(R_n\) (иначе номинальное сопротивление), забивных свай обычно определяется путем номинального сложения сопротивлений ствола и пальцев (уравнение 5.1). ).

(5.1)\[R_n = R_s + R_p = \sum f_s A_s + q_p A_p\]

где:

\(R_s\)

Сопротивление вала

\(ф_с\)

Сопротивление вала агрегата, сцепление

\(А_с\)

Площадь поверхности вала

\(Р_п\)

Сопротивление зацепу

\(q_p\)

Сопротивление схождения блока

\(А_р\)

Площадь поперечного сечения носка

Для открытых свай необходимо учитывать забивку грунта. В случае, когда свая забита, емкость рассчитывается по уравнению. 5.1 с использованием внешнего бокового сопротивления и сопротивления носка по всей ширине носка. Однако, когда свая с открытым концом врезается в слой грунта во время забивки, свая моделируется как не забитая или частично забитая, и уравнение 5.1 корректируется с учетом внутреннего и внешнего бокового сопротивления, а также сопротивления подошвы от площади поперечного сечения кольцевого сечения сваи. FHWA советует, вслед за Пайковски и Уитменом (1990) рекомендуется, чтобы статическое сопротивление сваи с открытым концом рассчитывалось по меньшей из формул 5.2 для закрытых условий и уравнения. 5.3 для условий без подключения к электросети (Ханниган и др., 2016a).

(5.2)\[R_n = \sum f_{so} A_{so} + q_{p} A_{pp}\]

(5.3)\[R_n = \sum f_{so} A_{so} + \sum f_{si} A_{si} + q_{p} A_{p} — W_p\]

где:

\(f_{so}\)

Сопротивление вала внешнего блока

\(А_{так}\)

площадь внешней поверхности

\(ф_{си}\)

сопротивление вала внутреннего блока

\(А_{си}\)

площадь внутренней поверхности

\(А_{пп}\)

площадь поперечного сечения сваи и грунтовой пробки у основания сваи

\(W_p\)

вес грунтовой пробки

5.

1. Метод Нордлунда для несвязных грунтов

Метод Нордлунд (Nordlund, 1963) рекомендован FHWA (Hannigan et al., 2016a) для точного определения несущей способности забивных свай в несвязных грунтах. Этот метод является полуэмпирическим и в значительной степени зависит от определения угла трения о грунт, \(\phi\). Нордлунд (Нордлунд, 1963; Nordlund, 1979) разработал свой метод расчета несущей способности свай в несвязных грунтах на основе всего лишь 41 испытания под нагрузкой на восьми различных полигонах. Хотя этот метод был разработан для свай диаметром менее 18 дюймов, он по-прежнему является наиболее широко используемым методом в Государственных DOT для проектирования всех забивных свай, включая LDOEP (NCHRP 2015).

Для однородных (неконических) свай боковое сопротивление по методу Нордлунда рассчитывается по формуле 5.4, ​​а сопротивление зацепа рассчитывается по уравнению. 5.5. Метод использует скорректированные значения SPT N (или, что предпочтительнее, полученные в лаборатории параметры прочности) для определения угла трения грунта для каждого слоя грунта и использует серию опубликованных таблиц и графиков для предположения корреляции для коэффициента бокового давления грунта и угол трения сваи о грунт. Эти значения используются вместе с эффективным давлением вскрышных пород для определения бокового сопротивления для каждого определенного слоя. Коэффициенты несущей способности наконечника сваи также коррелируют с углом трения грунта с помощью диаграмм. На поверхностное трение и сопротивление вершины сваи, \(R_p\), накладываются верхние пределы, чтобы ограничить величину расчетного удельного поверхностного сопротивления и сопротивления вершины и рассчитать более безопасную предельную грузоподъемность сваи.

(5.4)\[R_s = \sum K_d \, C_F \, \sigma’_d \, \sin(\delta) \, C_d \, \Delta d\]

(5.5)\[R_p = \alpha_t \, N’_q \, A_p \, \sigma’_p\]

где:

\(K_d\)

коэффициент бокового давления грунта на глубине \(d\)

\(C_F\)

Поправочный коэффициент для \(K_d\) при \(\delta \neq \phi\)

\(\сигма’_d\)

вертикальное эффективное напряжение в центре приращения глубины \(d\)

\(\дельта\)

угол трения между сваей и грунтом

\(C_d\)

Периметр сваи на глубине \(d\)

\(\Delta_d\)

длина сегмента сваи

\(\альфа_т\)

безразмерный коэффициент (зависит от отношения глубины сваи к ширине)

\(N’_q\)

Коэффициент несущей способности

\(\сигма’_p\)

вертикальное эффективное напряжение в носке сваи

5.

2. Метод Томлинсона для связных грунтов

В отчете FHWA о проектировании и строительстве фундаментов с забивными сваями (Hannigan et al., 2016a; Hannigan et al., 2016b) рекомендуется для свай диаметром менее 18 дюймов рассчитывать номинальное сопротивление с использованием \(\альфа\)-метод (Томлинсон, 1980) для связных грунтов. Подобно методу Нордлунда, это наиболее широко используемый метод в государственных DOT для проектирования всех забивных свай в связных грунтах, включая LDOEP (NCHRP 2015).

\(\alpha\)-метод — это эмпирический метод расчета полного напряжения, который использует прочность недренированного грунта на сдвиг для определения предельной несущей способности сваи. Единичное поверхностное сопротивление, как показывает Томлинсон, равно сцеплению грунта со сваей, которое определяется коэффициентом «альфа» (\(\альфа\)) и определяется свойствами грунта и сваи с использованием исходных таблиц и недренированного сдвига. сила, \(s_u\), с \(f_s = \alpha s_u\). Значения \(\alpha\) обратно пропорциональны прочности недренированного грунта на сдвиг и всегда меньше 1 из-за того, что сцепление между сваей и грунтом всегда меньше, чем сцепление внутри грунта.

В связных слоях боковое и носковое сопротивления, рассчитанные \(\альфа\)-методом, основаны на уравнении. 5.6 и уравнение 5.7. При работе со смешанными грунтовыми профилями Томлинсон предоставляет поправочные коэффициенты для учета стягивания более слабых грунтов более жесткими слоями — явления, которое происходит во время забивки свай и снижает боковое сопротивление. Эти факторы учитывались в наших расчетах.

(5.6)\[R_s = \sum f_s A_s = \sum C_\alpha A_s = \sum \alpha \, s_u \, A_s\]

(5.7)\[R_p = q_p A_p = N_c s_u A_p\]

где:

\(C_\alpha\)

адгезия

\(\альфа\)

Коэффициент сцепления

\(с_у\)

прочность на сдвиг в недренированном состоянии

\(А_с\)

площадь поверхности вала

\(N_c\)

Коэффициент несущей способности

Примечание

Для подключенных и отключенных анализов, уравнение. 5.4 через уравнение 5.7 должны быть скорректированы в соответствии с формулой. 5.2 и уравнение 5.3.

5.3. Метод

Инженерного корпуса армии США (USACE) Для бокового сопротивления в несвязных грунтах USACE указывает, что поверхностное трение увеличивается линейно до критической глубины \(D_c\) и остается постоянным ниже этой глубины. Критическая глубина, \(D_c\), является функцией диаметра сваи, \(b\), так что \(D_c = 10b\) для рыхлых песков, \(D_c = 15b\) для песков средней плотности и \ (D_c = 20b\) для плотных песков. Затем можно рассчитать боковое сопротивление по уравнению 8.

(5.8)\[R_s = \sum f_s A_s = \sum K \, \sigma’_v \, \tan \delta \, A_s\]

где:

\(K\)

Коэффициент бокового давления грунта

\(\сигма’_v\)

вертикальное эффективное давление вскрыши (\(\sigma’_v = \gamma’ D\), когда \(D

\(\дельта\)

угол трения между сваей и грунтом (из USACE, 1991)

\(\гамма’\)

эффективный удельный вес грунта

\(Д\)

глубина вдоль сваи

Для сопротивления схождения в несвязных грунтах можно использовать то же отношение критической глубины, что и для поверхностного трения. Затем можно рассчитать сопротивление зацепа по уравнению. 5.9.

(5.9)\[R_p = q_p A_p = \sigma’_v \, N_q \, A_p\]

где:

\(\sigma’_v\)

вертикальное эффективное давление вскрыши (\(\sigma’_v = \gamma’ D\), когда \(D

\(N’_q\)

Коэффициент несущей способности (от Terzaghi and Peck, 1967)

Для бокового сопротивления в связных грунтах метод USACE во многом аналогичен \(\альфа\)-методу в том смысле, что сопротивление обусловлено прилипанием связного материала к краю сваи и рассчитывается по уравнению. 5.10.

(5.10)\[R_s = \sum f_s A_s = \sum c_a \, A_s = \sum \alpha \, s_u \, A_s\]

где:

\(C_\alpha\)

сцепление между сваей и связным грунтом

\(\альфа\)

Коэффициент сцепления (по данным USACE, 1991)

Сопротивление схождения в связных грунтах рассчитывается USACE в соответствии с формулой. 5.11.

(5.11)\[R_p = q_p A_p = 9 \, s_u \, A_p\]

где:

\(s_u\)

Прочность на сдвиг в недренированном состоянии у носка сваи, обычно среднее значение на глубине, равной двум диаметрам сваи ниже носка

Примечание

Для подключенных и отключенных анализов, уравнение. 5.8 через уравнение 5.11 должны быть скорректированы в соответствии с формулой. 5.2 и уравнение 5.3.

5.4. Пересмотренный лямбда-метод

Лямбда-метод претерпел несколько изменений с момента его первого появления. Фохт и Виджайвергия (1972) предложили рассчитывать боковое сопротивление по уравнению. 5.12.

(5.12)\[R_s = \sum f_s A_s = \sum \lambda \, (\bar{\sigma’} + 2 \bar{s_u}) \, A_s\]

где:

\(\лямбда\)

коэффициент проникновения сваи

\(\бар{\сигма’}\)

среднее вертикальное эффективное напряжение между поверхностью грунта и носком сваи

\(\бар{s_u}\)

средняя прочность на сдвиг в недренированном состоянии

Крафт и др.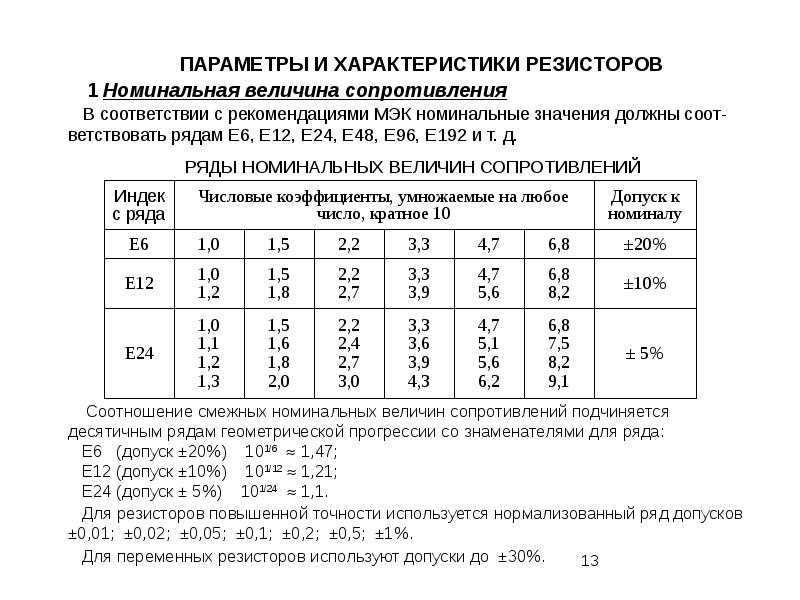 (1981) пересмотрели коэффициент проникновения сваи \(\лямбда\), предложив формулы для нормально консолидированных грунтов (уравнение 5.13) и переуплотненных грунтов (уравнение 5.14). Когда информация о консолидации отсутствовала или была ненадежной, связные грунты считались переуплотненными, если \(s_u/\sigma\) было равно или больше 0,1. 92 }{АЕУ}\)

\(б\)

диаметр сваи

\(f_{s.max}\)

пиковое единичное поверхностное трение

\(Д\)

длина встроенной сваи

\(А\)

площадь поперечного сечения

\(Е\)

модуль упругости

\(У\)

Смещение сваи, необходимое для развития бокового сдвига (обычно 0,1 дюйма)

5.5. Метод Американского нефтяного института (API)

Метод проектирования API широко считается лучшим методом проектирования LDOEP из-за долгой истории Института в области проектирования морских платформ. Он был представлен в отчете «Рекомендуемая практика» RP-2A в 1986 г. и был пересмотрен в 1987 и 1993 гг. Боковое сопротивление в несвязных грунтах можно рассчитать по уравнению. 5.15.

(5.15)\[R_s = \sum f_s A_s = \sum K \, \bar{\sigma’} \, \tan \delta \, A_s\]

где:

\(К\)

коэффициент бокового заземления

\(\бар{\сигма’}\)

среднее вертикальное эффективное напряжение

\(\дельта\)

угол трения сваи о грунт (АПИ РП-2А, 1993)

В таблице 5.1 приведены рекомендуемые значения коэффициента бокового заземления \(K\).

Таблица 5.1 Значения коэффициента бокового заземления, \(K\)

Состояние	К
незаглушенные, открытые трубчатые сваи (десятки и комп.)	0,8
сваи полного смещения	1,0

В таблице 5. 2 приведены рекомендации по \(\дельта\), углу трения между грунтом и стенкой сваи, а также по предельному единичному трению \(f_s\).

Таблица 5.2 Рекомендации API по боковому трению в кремнистых грунтах

Почва	\(\дельта\) , градусов	Ограничение, \(f_s\)
		тысяч фунтов/фут2 | кПа
От очень рыхлого до среднего, от песка до ила	15	1,0	47,8
От рыхлого до плотного, от песка до ила	20	1,4	67,0
От среднего до плотного, от песка до песчано-илистого	25	1,7	81,4
От плотного до очень плотного, от песка до песчано-илистого	30	2,0	95,8
От плотного до очень плотного, от гравия до песка	35	2,4	114,9

Сопротивление схождения в несвязных грунтах определяется уравнением. 5.16.

(5.16)\[R_p = q_p A_p = \sigma’ N_q \, A_p\]

где:

\(\sigma’\)

эффективное напряжение в носке сваи

\(N’_q\)

коэффициент несущей способности

Ни единичное сопротивление вала, \(f_s\), ни единичное сопротивление схождения, \(q_p\), не увеличиваются линейно без ограничений. API RP-2A ограничивает значения сопротивления вала и носка узла в зависимости от консистенции почвы, от очень рыхлого песка/ила до очень плотного песка/гравия.

В таблице 5.3 приведены рекомендации по \(N_q\), коэффициенту несущей способности а также ограничение, \(q_p\).

9{-0,25} & \textrm{if} \quad \psi > 1,0 \end{case} \quad \leq 1. 0\end{split}\]

где:

\(\alpha\)

коэффициент сцепления, определяемый формулой. 5.18 где \(\psi = s_u/\bar{\sigma’}\)

\(\бар{\сигма’}\)

среднее вертикальное эффективное напряжение

Наконец, сопротивление схождения в связных грунтах определяется уравнением. 5.19, так же, как и для метода USACE.

(5.19)\[R_p = q_p A_p = 9 \, s_u \, A_p\]

Важно

• Сопротивление схождения всегда должно сверяться с \(R_p = q_p A_{pp}\), где \(A_{pp}\) — площадь поперечного сечения грунтовой пробки в трубе с открытым концом или двутавровой свае в носке ворса.

• Прочность на сдвиг в недренированном состоянии у носка сваи, \(s_u\), обычно принимается как среднее значение на расстоянии двух диаметров ниже кончика сваи.

Примечание

Для подключенных и отключенных анализов, уравнение. 5.15 через уравнение 5.19должны быть скорректированы в соответствии с формулой. 5.2 и уравнение 5.3.

Для алгоритмической интерпретации Таблицы 5.2 и Таблицы 5.3 корреляция в Таблице 5.4 использовалась в пакетных вычислениях.

Таблица 5.3 Рекомендации API по сопротивлению схождения в кремнистых грунтах

Почва	\(N_q\)	Ограничение, \(q_p\)
		тысяч фунтов/фут 2 | МПа
От очень рыхлого до среднего, от песка до ила	8	40	1,9
От рыхлого до плотного, от песка до ила	12	60	2,9
От среднего до плотного, от песка до песчано-илистого	20	100	4,8
От плотного до очень плотного, от песка до песчано-илистого	40	200	9,6
От плотного до очень плотного, от гравия до песка	50

Таблица 5.4 Скорректированные корреляции SPT-N

Плотность	\(N_{кор}\) (бпф)	\(\фи\) (градус)
Очень свободный	0 — 4	< 28
Свободно	5 — 10	28 — 30
Среднеплотный	11 — 30	30 — 36
Плотный	31 — 50	36 — 41
Очень плотный	старше 50	> 41

В этом случае Таблицу 5.2, Таблицу 5.3 и Таблицу 5. 4 можно объединить, как в Таблицу 5.5.

Таблица 5.5 Рекомендации API по сопротивлению стержня и зацепа в кремнистом грунте со значениями SPT-N

Почва	\(N_{кор}\) (бпф)	\(\дельта\) (градус)	\(f_{s.lim}\) (ksf)	\(N_q\)	\(q_{p.lim}\) (ksf)
От очень рыхлого до среднего, от песка до ила	0 — 4	15	1,0	8	40
От рыхлого до плотного, от песка до ила	5 — 10	20	1,4	12	60
От среднего до плотного, от песка до песчано-илистого	11 — 30	25	1,7	20	100
От плотного до очень плотного, от песка до песчано-илистого	31 — 50	30	2,0	40	200
От плотного до очень плотного, от гравия до песка	старше 50 лет	35	2,4	50	250

5.

6. Olson 90 Method

Olson 90 method предназначен только для несвязных грунтов. Он был создан на основе базы данных 31 испытания на нагрузку стальных трубчатых свай. Olson 90 похож на метод Revised API с двумя основными отличиями. Во-первых, коэффициент бокового грунта \(K\) рассчитывается, а не берется из таблицы 5.1. В Олсон 90, \(K\) определяется уравнением 5.20.

(5.20)\[\begin{split}K = \begin{case} 0,16 + 0,015 \, N_{кор} и \textrm{неподвижные сваи}\\ 0,70 + 0,015 \, N_{cor} и \textrm{полноподвижные сваи} \end{cases}\end{split}\]

Olson 90 содержит пересмотренные рекомендации по сопротивлению вала и буксировки, которые сведены в Таблицу 5.6.

Таблица 5.6 Рекомендации Olson 90 по сопротивлению вала и пальца

Почва	\(N_{кор}\) (бпф)	\(\дельта\) (градус)	\(f_{s.lim}\) (ksf)	\(N_q\)	\(q_{p. lim}\) (ksf)
Гравий	0 — 4	[20]	[1,4]	[12]	[60]
	5 — 10	[25]	[1,7]	[20]	[100]
	11 — 30	[30]	[2.0]	[40]	[200]
	старше 30 лет	[35]	[2.4]	[60]	[250]
Песок/гравий	0 — 4	[20]	[1,4]	[12]	[60]
	5 — 10	[25]	[1,7]	[20]	[100]
	11 — 30	[30]	[2. 0]	[40]	[200]
	старше 30 лет	[35]	[2.4]	[60]	[250]
Песок	0 — 4	[20]	[1.0]	[50]	[40]
	5 — 10	30	1.1	120	120
	11 — 30	35	1,9	120	190
	31 — 50	40	2,6	120	190
	51 — 100	40	3,7	130	200
	свыше 100	40	3,8	220	530
Песок/Ил	0 — 4	10	[1. 0]	[10]	[10]
	5 — 10	10	[1.0]	[20]	[40]
	11 — 30	15	[1,4]	50	110
	31 — 50	20	2,0	100	160
	51 — 100	[30]	[2.0]	[100]	[200]
	101 — 200	[34]	[20]	[100]	[200]
	свыше 200	40	20	[100]	[200]
Ил	0 — 4	[10]	[1. 0]	[10]	[40]
	5 — 10	15	[1.0]	[10]	[40]
	11 — 30	20	[1,4]	[10]	[40]
	31 — 50	20	[1,4]	[12]	[60]
	старше 50 лет	[25]	[1,4]	[12]	[60]

Примечание

Для таблицы 5.6

• Не следует интерполировать. При использовании значений в таблице 5.6 используйте строку, соответствующую N = 4, для любого слоя с N, меньшим или равным 4, линию, соответствующую 10, для N = 5–10 и т. д.

• Число в скобках экстраполировано, нет подтверждающих данных.