Электрическое сопротивление никеля и железа. Удельное электрическое сопротивление. Определение

В качестве токопроводящих частей в электроустановках применяют проводники из меди, алюминия, их сплавов и железа (стали).

Медь является одним из лучших токопроводящих материалов. Плотность меди при 20°С 8,95 г/см 3 , температура плавления 1083° С. Медь химически мало активна, но легко растворяется в азотной кислоте, а в разбавленной соляной и серной кислотах растворяется только в присутствии окислителей (кислорода). На воздухе медь быстро покрывается тонким слоем окиси темного цвета, но это окисление не проникает в глубь металла и служит защитой от дальнейшей коррозии. Медь хорошо поддается ковке и прокатке без нагрева.

Для изготовления применяется электролитическая медь в слитках, содержащих 99,93% чистой меди.

Электропроводность меди сильно зависит от количества и рода примесей и в меньшей степени от механической и термической обработки. Удельное сопротивление меди при 20° С составляет 0,0172-0,018 ом х мм2/м.

Для изготовления проводников применяют мягкую, полутвердую или твердую медь с удельным весом соответственно 8,9, 8,95 и 8,96 г/см 3 .

Для изготовления деталей токоведущих частей широко используется медь в сплавах с другими металлами . Наибольшее применение получили следующие сплавы.

Латуни — сплав меди с цинком, с содержанием в сплаве не менее 50% меди, с присадкой других металлов. латуни 0,031 — 0,079 ом х мм2/м. Различают латунь — томпак с содержанием меди более 72% (обладает высокой пластичностью, антикоррозионным и антифрикционными свойствами) и специальные латуни с присадкой алюминия, олова, свинца или марганца.

Контакт из латуни

Бронзы — сплав меди с оловом с присадкой различных металлов. В зависимости от содержания в сплаве главного компонента бронзы называют оловянистыми, алюминиевыми, кремниевыми, фосфористыми, кадмиевыми. Удельное сопротивление бронзы 0,021 — 0,052 ом х мм 2 /м.

Латуни и бронзы отличаются хорошими механическими и физико-химическими свойствами. Они легко обрабатываются литьем и давлением, устойчивы против атмосферной коррозии.

Алюминий — по своим качествам второй после меди токопроводящий материал. Температура плавления 659,8° С. Плотность алюминия при температуре 20° — 2,7 г/см 3 . Алюминий легко отливается и хорошо обрабатывается. При температуре 100 — 150° С алюминий ковок и пластичен (может быть прокатан в листы толщиной до 0,01 мм).

Электропроводность алюминия сильно зависит от примесей и мало от механической и тепловой обработки. Чем чище состав алюминия, тем выше его электропроводность и лучше противодействие химическим воздействиям. Обработка, прокатка и отжиг значительно влияют на механическую прочность алюминия. При холодной обработке алюминия увеличивается его твердость, упругость и прочность на растяжение. Удельное сопротивление алюминия при 20° С 0,026 — 0,029 ом х мм 2 /м.

При замене меди алюминием сечение проводника должно быть увеличено в отношении проводимостей, т. е. в 1,63 раза.

При равной проводимости алюминиевый проводник будет в 2 раза легче медного.

Для изготовления проводников применяют алюминий, содержащий не менее 98% чистого алюминия, кремния не более 0,3%, железа не более 0,2%

Для изготовления деталей токоведущих частей используют алюминиевые сплавы с другими металлами , например: Дюралюмины — сплав алюминия с медью и марганцем.

Силумин — легкий литейный сплав из алюминия с примесью кремния, магния, марганца.

Алюминиевые сплавы обладают хорошими литейными свойствами и высокой механической прочностью.

Наибольшее применение в электротехнике получили следующие алюминиевые сплавы :

Алюминиевый деформируемый сплав марки АД , имеющий алюминия не менее 98,8 и прочих примесей до 1,2.

Алюминиевый деформируемый сплав марки АД1 , имеющий алюминия не менее 99,3 н прочих примесей до 0,7.

Алюминиевый деформируемый сплав марки АД31 , имеющий алюминия 97,35 — 98,15 и прочих примесей 1,85 -2,65.

Сплавы марок АД и АД1 применяются для изготовления корпусов и плашек аппаратных зажимов. Из сплава марки АД31 изготовляют профили и шины, применяемые для электрических токопроводов.

Изделия из алюминиевых сплавов в результате термической обработки приобретают высокие пределы прочности н текучести (ползучести).

Железо — температура плавления 1539°С. Плотность железа — 7,87. Железо растворяется в кислотах, окисляется галогенами и кислородом.

В электротехнике применяют стали различных марок, например:

Углеродистые стали — ковкие сплавы железа с углеродом и с другими металлургическими примесями.

Удельное сопротивление углеродистых сталей 0,103 — 0,204 ом х мм 2 /м.

Легированные стали — сплавы с дополнительно вводимыми в углеродистую сталь присадками хрома, никеля и других элементов.

Стали обладают хорошими .

В качестве добавок в сплавы, а также для изготовления припоев и осуществления токопроводящих металлов широко применяют:

Кадмий — ковкий металл. Температура плавления кадмия 321°С. Удельное сопротивление 0,1 ом х мм 2 /м. В электротехнике кадмий применяется для приготовления легкоплавких припоев и для защитных покрытий (кадмировання) поверхности металлов. По своим антикоррозийным свойствам кадмий близок к цинку, но кадмиевые покрытия менее пористы и наносятся более тонким слоем, чем цинковые.

Никель — температура плавления 1455°С. Удельное сопротивление никеля 0,068 — 0,072 ом х мм 2 /м. При обычной температуре не окисляется кислородом воздуха. Никель применяется в сплавах и для защитного покрытия (никелирования) поверхности металлов.

Олово — температура плавления 231,9°С. Удельное сопротивление олова 0,124 — 0,116 ом х мм 2 /м. Олово применяется для пайки защитного покрытия (лужения) металлов в чистом виде и в виде сплавов с другими металлами.

Свинец — температура плавления 327,4°С. Удельное сопротивление 0,217 — 0,227 ом х мм 2 /м. Свинец применяется в сплавах с другими металлами как кислотоупорный материал. Добавляется в паяльные сплавы (припои).

Серебро — очень ковкий, тягучий металл. Температура плавления серебра 960,5°С. Серебро — лучший проводник тепла и электрического тока. Удельное сопротивление серебра 0,015 — 0,016 ом х

Удельное сопротивление меди

Одной из физических величин, используемых в электротехнике, является удельное электрическое сопротивление. Рассматривая удельное сопротивление алюминия, следует помнить, что данная величина характеризует способность какого-либо вещества, препятствовать прохождению через него электрического тока. Блок: 1/3 | Кол-во символов: 298 Источник: https://electric-220.ru/news/udelnoe_soprotivlenie_aljuminija/2014-11-11-740 Медь – основной материал для проводников Квалифицированный выбор подходящего материала сопровождается комплексной оценкой нескольких факторов. Медный проводник не повреждается коррозией, потому что на поверхности образуется защитный слой из окислов. Структурная целостность сохраняется при малом радиусе поворота, после многократных изгибов. Отмеченные параметры пригодятся для оснащения помещений с повышенной влажностью и прокладки линий сложной конфигурации. Тем не менее, главным преимуществом является малое сопротивление проводов из меди. Кроме улучшения токопроводимости с одновременным снижением потерь при передаче энергии, следует отметить уменьшение веса и размеров кабельной продукции, по сравнению с альтернативными вариантами. Блок: 2/10 | Кол-во символов: 738 Источник: https://amperof.ru/bezopasnost/udelnoe-soprotivlenie-medi.html Таблица удельных сопротивлений проводников Материал проводника Удельное сопротивление ρ в Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль 0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5 Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки. Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо. Сопротивление проводника можно определить по формуле: где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2. Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2. Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2. Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника. Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки. Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом. Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки. Материал проводника характеризует его удельное сопротивление. По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец. Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается. У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается. Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи. температурный коэффициент сопротивления — это изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, обозначается буквой α. Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C). Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2). Таблица 2 Блок: 2/5 | Кол-во символов: 4384 Источник: http://bourabai.kz/toe/resistance.htm Понятия, связанные с удельным сопротивлением Величина, противоположная удельному сопротивлению, носит наименование удельной проводимости или электропроводности. Обычное электрическое сопротивление свойственно лишь проводнику, а удельное электрическое сопротивление характерно только для того или иного вещества. Как правило, эта величина рассчитывается для проводника, имеющего однородную структуру. Для определения электрического сопротивления однородных проводников используется формула: Физический смысл этой величины заключается в определенном сопротивлении однородного проводника с определенной единичной длиной и площадью поперечного сечения. Единицей измерения служит единица системы СИ Ом•м или внесистемная единица Ом•мм2/м. Последняя единица означает, что проводник из однородного вещества, длиной 1 м, имеющий площадь поперечного сечения 1 мм2, будет иметь сопротивление в 1 Ом. Таким образом, удельное сопротивление любого вещества можно вычислить, используя участок электрической цепи, длиной 1 м, поперечное сечение которого будет составлять 1 мм2. Блок: 2/3 | Кол-во символов: 1069 Источник: https://electric-220.ru/news/udelnoe_soprotivlenie_aljuminija/2014-11-11-740 Таблица удельных сопротивлений проводников. Таблица удельных сопротивлений металлов Проект Карла III Ребане и хорошей компании Раздел недели: Набор прочности бетоном. Время твердения бетона. Тепловыделение цемента (бетонной смеси) Мы в : DPVA.ru в Мы : Адрес этой страницы (вложенность) в справочнике dpva.ru:    / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Электрическое сопротивление и проводимость проводников, растворов, почв….  / / Таблица удельных сопротивлений проводников. Таблица удельных сопротивлений металлов. В разумных температурных пределах вокруг некоторой точки зависимость удельного сопротивления металлов от температуры описывается как: ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления. Ниже приведена таблица значений α для ряда металлов в диапазоне температур от 0 до 100 ° C. Зависимость сопротивления металлов от температуры. Температурный коэффициент электрического сопротивления металлов α . Проводник Удельное сопротивление ρ, Ом*мм2/м α, 10 -3*C-1(или K -1) Алюминий 0,028 4,2 Бронза 0,095 — 0,1 — Висмут 1,2 — Вольфрам 0,05 Железо 0,1 Золото 0,023 Иридий 0,0474 — Константан ( сплав Ni-Cu + Mn) 0,5 0,05! Латунь 0,025 — 0,108 0,1-0,4 Магний 0,045 3,9 Манганин (сплав меди марганца и никеля — приборный) 0,43 — 0,51 0,01!! Медь 0,0175 4,3 Молибден 0,059 — Нейзильбер (сплав меди цинка и никеля) 0,2 0,25 Натрий 0,047 — Никелин ( сплав меди и никеля) 0,42 0,1 Никель 0,087 6,5 Нихром ( сплав никеля хрома железы и марганц

Удельное сопротивление никелевой проволоки — Морской флот

Медно-никелевые термостойкие провода были созданы в результате научного исследования, ставящего цель получить проводник с очень высокой электропроводимостью из доступных металлов и с не сложной технологией производства.

Технология производства

Для получения сверхпроводника на медный провод в вакууме по всему периметру наносят токопроводящий слой, состоящий из сплава никеля и меди, с диффузией в поверхностный слой проволоки-основы. Снаружи наносится защитный слой металла. После чего полученный провод проходит отжиг в вакууме в течение 30 — 180 мин при 850-950 o С. Для создания медно-никелевого провода применяется чистые (99,99) медь и никель.

Эффект повышенной проводимости образуется в состоящем из двух металлов слое сплава, который представляет собой тонкостенную токопроводящую трубку-прослойку. Благодаря диффузионному взаимодействию слоев металла, примыкающих к трубке прослойке с обеих сторон, поверхность получается почти идеальной.

Нанесение слоев провода происходит в вакуумном оборудовании для исключения окисления проводящего слоя. Следовательно длина зависит от возможностей вакуумного оборудования.

Чертеж медно-никелевого проводника.

1 – медная или никелевая проволока основа

2 – токопроводящий слой из сплава меди и никеля. Толщина слоя делается достаточной для обеспечения неразрывности слоя

3 – защитный слой. Толщина выбирается достаточной для обеспечения защиты от механических воздействий

Расчет удельного сопротивления медно-никелевого провода

Высокая электропроводимость у меди и алюминия, а также у золота и серебра. В других металлах электропроводность существенно ниже.

Таблица удельного электрического сопротивления металлов

В связи с тем, что существует два типа электрических сопротивлений —

В связи с электромагнитными явлениями, возникающими в проводниках при прохождении через него переменного тока в них возникает два важных для их электротехнических свойств физических явления.

Два последних явления делают неэффективным применение проводников радиусом больше характерной глубины проникновения электрического тока в проводник. Эффективный диаметр проводников (2RБ_хар): 50Гц -7 Ом. Используя микроомметры, можно определить качество электрических контактов, сопротивление электрических шин, обмоток трансформаторов, электродвигателей и генераторов, наличие дефектов и инородного металла в слитках (например, сопротивление слитка чистого золота вдвое ниже позолоченного слитка вольфрама).

Для расчета длины провода, его диаметра и необходимого электрического сопротивления, необходимо знать удельное сопротивление проводников ρ.

В международной системе единиц удельное сопротивление ρ выражается формулой:

Оно означает: электрическое сопротивление 1 метра провода (в Омах), сечением 1 мм 2 , при температуре 20 градусов по Цельсию.

Таблица удельных сопротивлений проводников

Материал проводника	Удельное сопротивление ρ в
Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль	0,015 0,0175 0,023 0,025. 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095. 0,1 0,1 0,103. 0,137 0,12 0,22 0,42 0,43. 0,51 0,5 0,6 0,94 1,05. 1,4 1,15. 1,35 1,2 1,3. 1,5

Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм 2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм 2 . Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм 2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.

Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.

Сопротивление проводника можно определить по формуле:

где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм 2 .

Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм 2 .

Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм 2 .

Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.

Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм 2 . Определить необходимую длину проволоки.

Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.

Пример 5. Проволока сечением 0,5 мм 2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.

Материал проводника характеризует его удельное сопротивление.

По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.

Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.

У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.

Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.

Если при температуре t _{сопротивление проводника равно r, а при температуре t равно rt, то температурный коэффициент сопротивления}

Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).

Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).

Значения температурного коэффициента для некоторых металлов

Металл	α
Серебро Медь Железо Вольфрам Платина	0,0035 0,0040 0,0066 0,0045 0,0032	Ртуть Никелин Константан Нихром Манганин	0,0090 0,0003 0,000005 0,00016 0,00005

Из формулы температурного коэффициента сопротивления определим r_t:

Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.

Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.

Электрическая проводимость

До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.

Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.

Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.

Электрическая проводимость измеряется в (1/Ом) или в сименсах.

Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.

Если r = 20 Ом, то

Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,

Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)

Материалы высокой проводимости

К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10 -20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).

Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:

1. малое удельное сопротивление;
2. достаточно высокая механическая прочность;
3. удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
4. хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
5. относительная легкость пайки и сварки.

Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.

В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.

Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.

В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.

Алюминий

Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м 3 . Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.

Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.

Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.

Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.

Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg₂Si, которое сообщает высокие механические свойства сплаву.

Железо и сталь

Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.

В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.

Натрий

Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.

Литература по удельному сопротивлению проводников

1. Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
2. Бачелис Д. С., Белоруссов Н. И., Саакян А. Е. Электрические кабели, провода и шнуры. Справочник. — М.: Энергия, 1971.
3. Гершун А. Л. Кабель // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
4. Р. Лакерник, Д. Шарле. От меди к стеклу // Наука и жизнь. — 1986. — Вып. 08. — С. 50—54, 2-3 стр. цветной вкладки.

НОВОСТИ ФОРУМА Рыцари теории эфира

13.06.2019 — 05:11: ЭКОЛОГИЯ — Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center]

[center][b]Гибель пчел в Курчатовском районе [/center]

[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л

[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]

Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.

Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)

Горькая истина заключается в том, что людская толпа — это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.

Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.

Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.

Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция — есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.

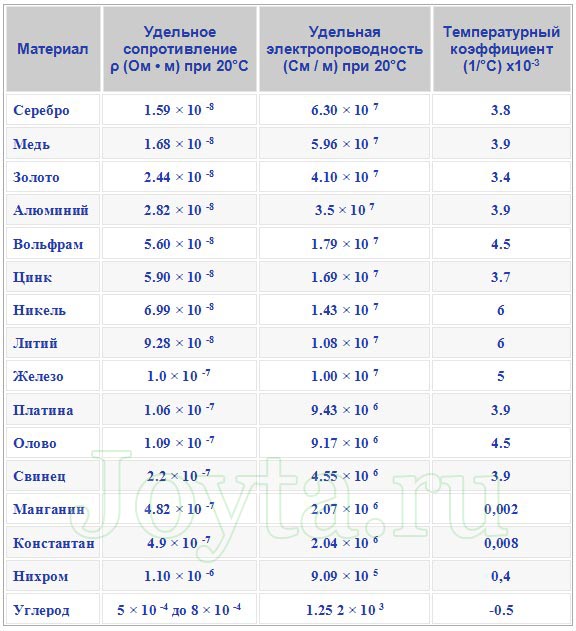
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.

Удельное сопротивление

Удельное электрическое сопротивление определяется как отношение между напряженностью электрического поля внутри металла к плотности тока в нем:

где:
ρ — удельное сопротивление металла (Ом⋅м),
Е — напряженность электрического поля (В/м),
J — величина плотности электрического тока в металле (А/м2)

Если напряженность электрического поля (Е) в металле очень большая, а плотность тока (J) очень маленькая, это означает, что металл имеет высокое удельное сопротивление.

Обратной величиной удельного сопротивления является удельная электропроводность, указывающая, насколько хорошо материал проводит электрический ток:

σ — проводимость материала, выраженная в сименс на метр (См/м).

Электрическое сопротивление

Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.

Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.

Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.

В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.

В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.

• Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
• Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка

Сопротивление провода

Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:

где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)

В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:

R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом

Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.

Поверхностное сопротивление

Величина поверхностного сопротивления рассчитывается таким же образом, как и сопротивление провода. В данном случае площадь сечения можно представить в виде произведения w и t:

Для некоторых материалов, таких как тонкие пленки, соотношение между удельным сопротивлением и толщиной пленки называется поверхностное сопротивление слоя RS:

где RS измеряется в омах. При данном расчете толщина пленки должна быть постоянной.

Часто производители резисторов для увеличения сопротивления вырезают в пленке дорожки, чтобы увеличить путь для электрического тока.

Свойства резистивных материалов

Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.

Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.

Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.

Удельное электрическое сопротивление — Википедия

Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.

Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.

Единицы измерения

Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м^[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом^[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10⁻⁶ от 1 Ом·м^[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом^[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².

Зависимость от температуры

В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов^[3].

В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.

Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.

Обобщение понятия удельного сопротивления

Кусок резистивного материала с электрическими контактами на обоих концах

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается законом Ома в дифференциальной форме:

E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}

Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением

Ei(r→)=∑j=13ρij(r→)Jj(r→).{\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}

В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.

Тензор ρij{\displaystyle \rho _{ij}} симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.

Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую

Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}

Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.

Связь с удельной проводимостью

В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством

ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:

Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}

Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:

ρ11=1det(σ)[σ22σ33−σ23σ32],{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}

ρ12=1det(σ)[σ33σ12−σ13σ32],{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}

где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3^[4].

Удельное электрическое сопротивление некоторых веществ

Металлические монокристаллы

В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C^[5].

Кристалл	ρ1=ρ2, 10−8 Ом·м	ρ3, 10−8 Ом·м
Олово	9,9	14,3
Висмут	109	138
Кадмий	6,8	8,3
Цинк	5,91	6,13
Теллур	2,90·109	5,9·109

Металлы и сплавы, применяемые в электротехнике

Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.

Металл ρ, Ом·мм²/м Серебро 0,015…0,0162 Медь 0,01724…0,018 Золото 0,023 Алюминий 0,0262…0,0295 Иридий 0,0474 Молибден 0,054 Вольфрам 0,053…0,055 Цинк 0,059 Никель 0,087 Железо 0,098 Платина 0,107 Олово 0,12 Свинец 0,217…0,227 Титан 0,5562…0,7837 Висмут 1,2

Сплав ρ, Ом·мм²/м Сталь 0,103…0,137 Никелин 0,42 Константан 0,5 Манганин 0,43…0,51 Нихром 1,05…1,4 Фехраль 1,15…1,35 Хромаль 1,3…1,5 Латунь 0,025…0,108 Бронза 0,095…0,1

Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.

Другие вещества

Тонкие плёнки

Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RW/L,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.

См. также

Примечания

1. ↑ ^{1 2} Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ ^{1 2} Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
3. ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
4. ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
5. ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.

Литература

• Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.

Удельное электрическое сопротивление Википедия

Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.

Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.

Единицы измерения[ | ]

Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м^[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в с

Удельное электрическое сопротивление — Википедия. Что такое Удельное электрическое сопротивление

Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.

Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.

Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.

Единицы измерения

Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м^[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом^[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10⁻⁶ от 1 Ом·м^[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом^[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².

Обобщение понятия удельного сопротивления

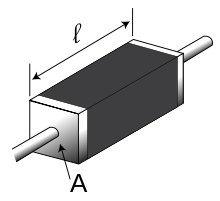Кусок резистивного материала с электрическими контактами на обоих концах

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается законом Ома в дифференциальной форме:

E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}

Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением

Ei(r→)=∑j=13ρij(r→)Jj(r→).{\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}

В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.

Тензор ρij{\displaystyle \rho _{ij}} симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.

Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую

Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}

Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.

Связь с удельной проводимостью

В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством

ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:

Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}

Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:

ρ11=1det(σ)[σ22σ33−σ23σ32],{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}

ρ12=1det(σ)[σ33σ12−σ13σ32],{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}

где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3^[3].

Удельное электрическое сопротивление некоторых веществ

Металлические монокристаллы

В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C^[4].

Кристалл	ρ1=ρ2, 10−8 Ом·м	ρ3, 10−8 Ом·м
Олово	9,9	14,3
Висмут	109	138
Кадмий	6,8	8,3
Цинк	5,91	6,13
Теллур	2,90·109	5,9·109

Металлы и сплавы, применяемые в электротехнике

Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.

Металл ρ, Ом·мм²/м Серебро 0,015…0,0162 Медь 0,01724…0,018 Золото 0,023 Алюминий 0,0262…0,0295 Иридий 0,0474 Молибден 0,054 Вольфрам 0,053…0,055 Цинк 0,059 Никель 0,087 Железо 0,098 Платина 0,107 Олово 0,12 Свинец 0,217…0,227 Титан 0,5562…0,7837 Висмут 1,2

Сплав ρ, Ом·мм²/м Сталь 0,103…0,137 Никелин 0,42 Константан 0,5 Манганин 0,43…0,51 Нихром 1,05…1,4 Фехраль 1,15…1,35 Хромаль 1,3…1,5 Латунь 0,025…0,108 Бронза 0,095…0,1

Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.

Другие вещества

Тонкие плёнки

Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RW/L,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.

Примечания

1. ↑ ^{1 2} Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ ^{1 2} Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
3. ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
4. ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.

См. также