Чем отличается непрерывный сигнал от дискретного • Мир электрики

На чтение: 3 минОбновлено: 23.06.2021Рубрика: Основы электротехникиАвтор: admin

Содержание

1. Особенности непрерывного сигнала
2. Что такое дискретный
3. Отличия двух видов сигналов

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции.

Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

• пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
• затруднения при передаче сигналов управления;
• трудности при сопряжении с компьютером и другими цифровыми устройствами;
• трудности шифрования.

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС.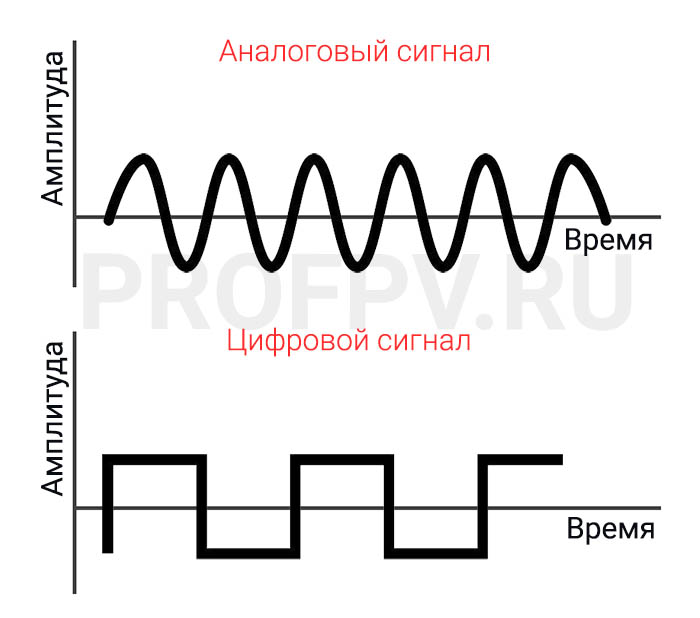 В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

• высокая помехозащищённость и возможность работы каналов связи при больших шумах;
• простота передачи команд управления каналами;
• возможность цифровой обработки сигналов;
• лёгкость засекречивания.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

• увеличение полосы частот, требуемой для передачи сообщений;
• для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
• требование синхронизации;
• плохая совместимость с уже имеющимися аналоговыми системами.

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

Рейтинг

( Пока оценок нет )

0

admin/ автор статьи

Понравилась статья? Поделиться с друзьями:

Что такое непрерывный сигнал в информатике?

Что такое непрерывный сигнал в информатике?

Сигнал называется непрерывным, если его параметр может принимать любое значение в пределах некоторого интервала (рис. 1). Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала (рис. 2).

Что значит непрерывный сигнал?

Непрерывная волна или непрерывный сигнал (англ. Continuous wave, CW) — электромагнитная волна с постоянными амплитудой, частотой и, в математическом анализе, с бесконечной продолжительностью.

Что такое дискретные сигналы?

discretus — «прерывистый», «разделённый») — сигнал, который является прерывистым (в отличие от аналогового) и который изменяется во времени и принимает любое значение из списка возможных значений. … Сэмплирования, который производит непрерывный сигнал дискретного времени

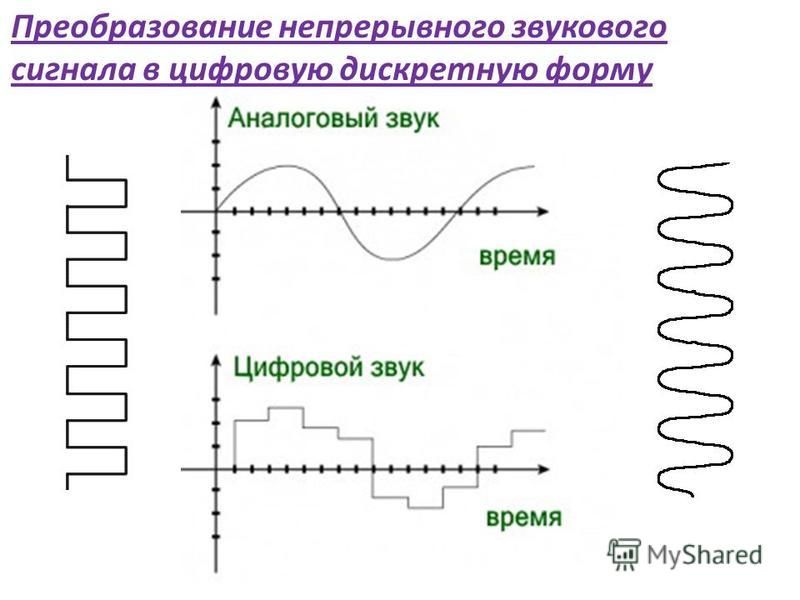
Как называется процесс преобразования аналогового непрерывного звука в цифровую форму?

Реальный аудио сигнал – это сложное по форме колебание, некая сложная зависимость амплитуды звуковой волны от времени. Преобразование аналогового звукового сигнала в цифровой вид называется аналогово-цифровым преобразованием или оцифровкой.

Как передать цифровой сигнал?

Чтобы передать цифровой сигнал по аналоговому каналу (радио или электрическому), его преобразуют, то есть модулируют. А при приеме — обратно демодулируют. Цифровой сигнал обладает важным свойством, которое заключается в возможности полностью его регенерировать в ретрансляторе.

Чем цифровой сигнал лучше аналогового?

Цифровая связь и вещания считаются более защищенными от помех и от внешних воздействий. Все дело в том, что при использовании «цифры» аналоговый сигнал с микрофона на передающей станции зашифровывается в цифровой код.

Что представляет собой цифровой сигнал?

Цифровой сигнал — сигнал, который можно представить в виде последовательности дискретных (цифровых) значений. В наше время наиболее распространены двоичные цифровые сигналы (битовый поток) в связи с простотой кодирования и используемостью в двоичной электронике.

Что такое цифровые и аналоговые приборы?

В аналоговых приборах — это схема считывания показаний датчика и передачи информации в аналоговом виде. В цифровых — каждый прибор является миниатюрным компьютером, содержит 8-разрядный микропроцессор с энергонезависимой флэш-памятью, в которой содержатся все настройки прибора и различные типы счетчиков.

Почему при использовании аналоговой техники передача информации всегда происходит с искажениями?

Дело в том, что при передаче сигнала всегда есть помехи, которые искажают его значения. В большинстве случаев эти искажения — случайные ошибки, не поддающиеся учёту. Фактически приёмник получает не исходный сигнал, посланный источником (сплошная линия на рис. 2.

Каковы преимущества цифровых устройств по сравнению с аналоговыми?

Аналоговые устройства могут работать с более быстро меняющимися сигналами, чем цифровые. Скорость обработки и передачи информации аналоговым устройством всегда может быть выше, чем скорость обработки и передачи цифровым устройством./span>

Что такое аналоговая связь?

Аналоговая связь — это передача непрерывного сигнала. Цифровая связь — это передача информации в дискретной форме (цифровом виде). Цифровой сигнал по своей физической природе является аналоговым, однако передаваемая с его помощью информация определяется конечным набором уровней сигнала.

Как происходит передача данных по сети?

Она используется для электронной связи и обмена информацией. Передача данных в сети Интернет происходит посредством коммуникационных протоколов TCP / IP UDP / IP, определяют правила, по которым происходит общение между компьютерами разных типов. … Практически все услуги сети построены на принципе клиент-сервер./span>

Что такое передача данных в мобильном телефоне?

Передача данных в телефоне или смартфоне означает мобильный интернет. Если нажать на указанную выше кнопку, включится мобильная передача данных, то есть мобильный интернет. Разумеется, интернет включится, если он поддерживается вашим тарифным планом. … То же самое можно увидеть и в меню смартфона.

Каким образом происходит передача информации?

Передача информации — физический процесс, посредством которого осуществляется перемещение информации в пространстве. … Информация представляется и передается в форме последовательности сигналов, символов. От источника к приёмнику сообщение передается через некоторую материальную среду.

Как происходит передача информации в компьютере?

История компьютера — Передача информации Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал. Этот сигнал посылается по каналу связи.

Выборка непрерывного сигнала — Wireless Pi

Большинство интересующих нас сигналов — волны беспроводной связи — являются непрерывными во времени, поскольку они должны проходить по реальному беспроводному каналу. Чтобы обработать такой сигнал с использованием методов цифровой обработки сигналов, сигнал необходимо преобразовать в последовательность чисел.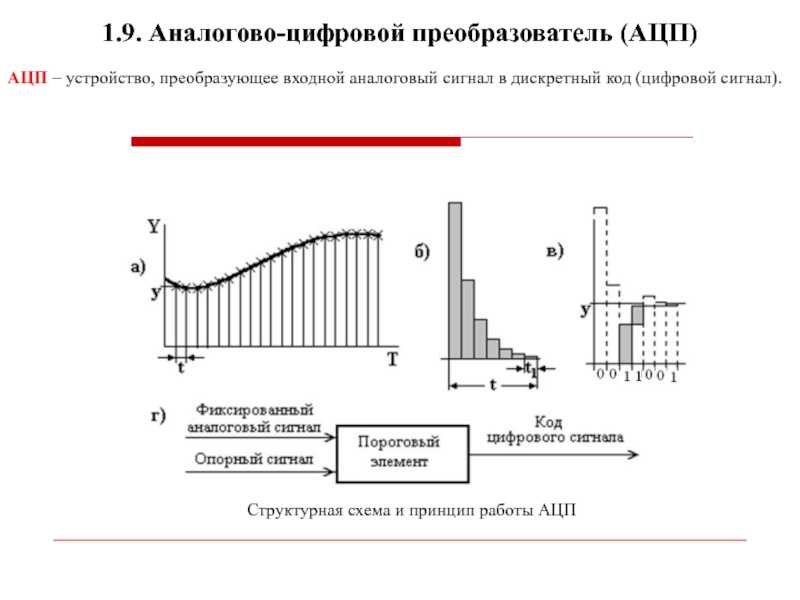 Это можно сделать с помощью процесса периодической выборки.

От непрерывного к дискретному времени

---

Рассмотрим ограниченный по полосе непрерывный сигнал $s(t)$ и его представление в частотной области $S(F)$ с полосой пропускания $B$, показанное на рисунке выше. Сигнал $s[n]$ с дискретным временем можно получить, взяв отсчеты $s(t)$ через равные интервалы в $T_S$ секунд. Этот процесс показан на рисунке ниже и математически представлен как
\begin{equation*}
s[n] = s(t)\bigg| _{t=nT_S} \quad -\infty

Интервал времени $T_S$ секунд между двумя последовательными выборками называется периодом выборки или интервалом выборки, а его обратная величина $1/T_S = F_S$ называется частотой выборки или частотой выборки. . Частота дискретизации $F_S$ является наиболее фундаментальным параметром, встречающимся в приложениях цифровой обработки сигналов.

Теорема дискретизации в частотной области

---

Давайте выясним, что происходит в частотной области в результате этого процесса. Рассмотрим непрерывный синусоидальный сигнал
\begin{equation*}
s(t) = A \cos (2\pi Ft + \theta)
\end{equation*}
и получить его выборочную версию со скоростью $F_S = 1/T_S$ отсчетов/ второй.
\begin{align}
s[n] &= s(t)| _{t=nT_S} \nonumber \\
&= A \cos \left(2\pi F nT_S + \theta\right) \nonumber \\
&= A \cos \left(2\pi F \frac{ n}{F_S} + \theta\right) \nonumber \\
&= A \cos \left(2 \pi \frac{F}{F_S} n + \theta\right) \label{eqIntroductionSampledSinusoid}

\end {align}

Обратите внимание, что $F/F_S$ выше — это частота дискретной синусоиды $s[n]$. Выберем с той же частотой $F_S$ другую синусоиду с непрерывной частотой $F + k F_S$, где $k = \pm 1, \pm 2,\cdots$.
\begin{align*}
s(t) &= A \cos \left\{2 \pi (F +kF_S) t + \theta)\right\}\nonumber \\
s[n] &= A \cos \{2 \pi (F + kF_S) nT_S + \theta\} \nonumber\\
&= A \cos \left(2 \pi \frac{F + kF_S}{F_S} n + \theta \right )\nonumber \\
&= A \cos \left(2 \pi \frac{F}{F_S} n + 2\pi kn + \theta\right) \nonumber\\
&= A \cos \left( 2 \pi \frac{F}{F_S} n + \theta\right)
\end{align*}
, что в точности совпадает с синусоидой дискретного времени в уравнении \eqref{eqIntroductionSampledSinusoid}.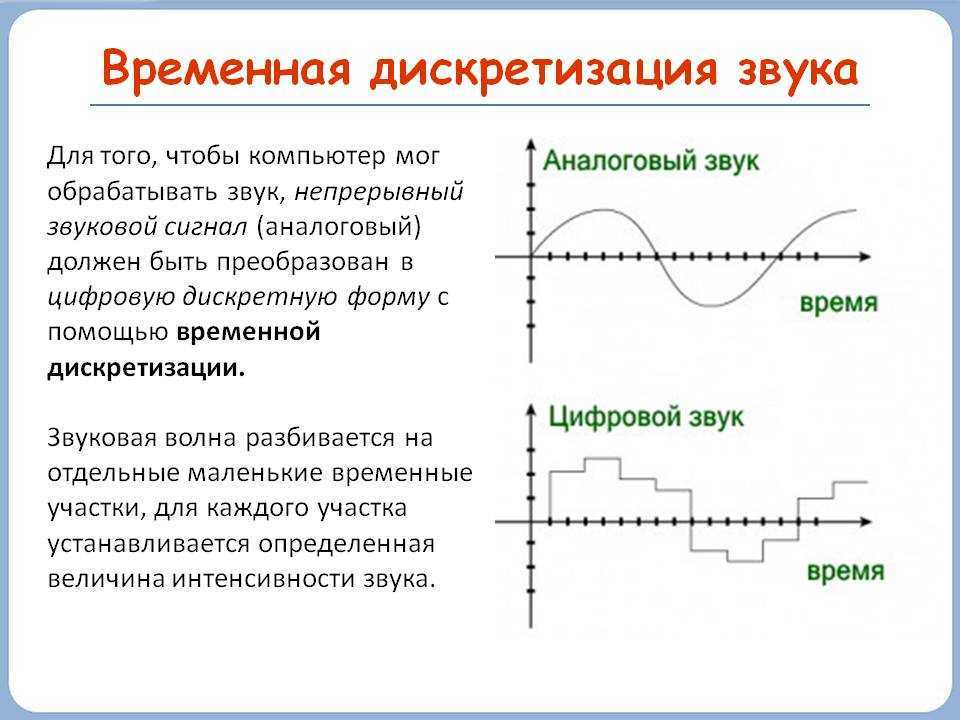

Можно сделать вывод, что на выходе процесса дискретизации невозможно различить два дискретных во времени сигнала, частоты которых разнесены на $F_S$ Гц. Итак, для произвольной частоты $F$ после дискретизации 9\circ
\end{align*}
Следовательно, все следующие диапазоны частот одинаковы:
\begin{equation}
\begin{aligned}
&\cdots\cdot \\
-2.5F_S \quad &\rightarrow \quad -1.5F_S \\
-1.5F_S \quad &\rightarrow \quad -0.5F_S
\end{aligned}
\end{equation}

\begin{equation*}
-0.5F_S \quad \rightarrow \ quad +0.5F_S
\end{equation*}

\begin{align*}
0.5F_S \quad &\стрелка вправо \quad 1.5F_S \\
1.5F_S \quad &\стрелка вправо \quad 2.5F_S \\
&\cdots\cdot
\end{align*}
Диапазон $-0.5F_S \rightarrow +0.5F_S$ называется основной зоной. Спектр непрерывного сигнала $s(t)$, показанный на предыдущем рисунке, теперь показан на рисунке ниже. Мы обозначили эту зону пунктирными красными линиями и обозначили ее спектральный состав сплошными линиями, а спектральные реплики — пунктирными линиями.

В свете вышеизложенного из приведенного выше рисунка, изображающего спектральные реплики, видно, что если непрерывный сигнал имеет ширину полосы $B$ больше, чем $0,5F_S$, он будет отображаться как псевдоним более низкой частоты. в диапазоне $-0.5F_S \le F

Следовательно, для сигнала с полосой пропускания B частота дискретизации должна быть такой, чтобы выполнялось следующее неравенство для предотвращения любых искажений в дискретизированном сигнале:
\begin{equation*}
0,5F_S > B \nonumber
\end{ уравнение*}
или записанное в другой форме

\begin{equation}
F_S > 2 B
\end{equation}

Теорема выборки

---

Как показано выше, выборка во временной области с интервалами $T_S$ создает периодичность в частотной области с периодом $F_S = 1/T_S$. Таким образом, ограниченный по полосе непрерывный сигнал с максимальной частотой (или шириной полосы) $B$ Гц может быть однозначно восстановлен из его отсчетов при условии, что частота дискретизации $F_S \ge 2B$ отсчетов в секунду.

Частота $2B$ называется скоростью Найквиста, а $0,5F_S$ называется частотой Найквиста или частотой сворачивания. Теорема дискретизации — одно из двух наиболее фундаментальных соотношений в цифровой обработке сигналов, второе — взаимосвязь между непрерывными и дискретными частотами.

Теорема выборки во временной области

---

Рассмотрим косинусоидальную волну, для которой берутся две выборки с интервалом $T_S$. Как показано на рисунке ниже, если частота равна нулю (сигнал обозначен цифрой 1), обе выборки одинаковы и путаницы нет. Для низкочастотного сигнала 2 снова можно взять две выборки, которые достаточно отличают его от сигнала 1. То же самое можно сказать о сигнале 3, период которого $T$ больше, чем $2T_S$ на рисунке ниже. Однако обратите внимание, что для сигнала 4 период времени здесь меньше $2T_S$, и, следовательно, он пересекает сигнал 3 в месте второй выборки. Это делает невозможным различение сигналов 3 и 4. Именно так можно понять теорему выборки во временной области.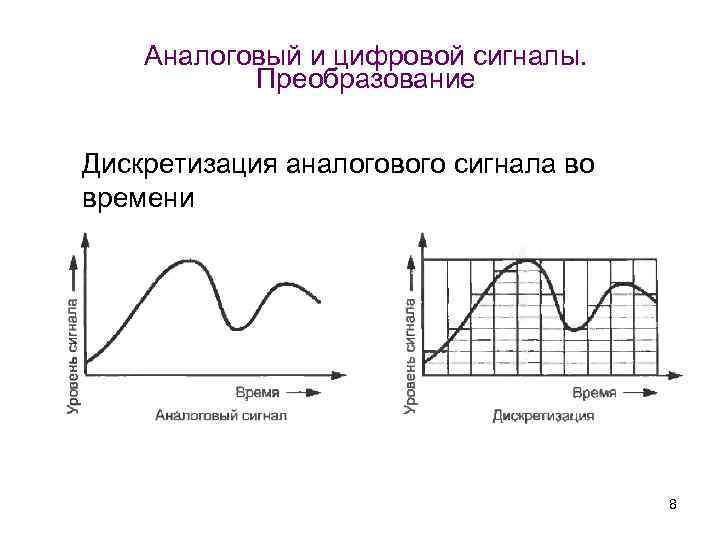

Из приведенного выше рисунка можно сказать, что для сигнала с частотой $F=1/T$ и частотой дискретизации $F_S=1/T_S$
\[
T > 2T_S, \qquad \text{или }\qquad \frac{1}{T}

Естественным расширением является понимание понятия времени в условиях дискретного времени. Зная интервал дискретизации или частоту дискретизации, можно легко определить период или частоту сигнала. Например, для синусоиды на рисунке ниже период $T$ явно равен $10$ выборкам, и чтобы найти его в фактических секундах, необходимо знать интервал выборки $T_S$ или частоту выборки $F_S$.

Для $T_S = 0,1$ секунды,
\begin{align*}
T &= 10 ~\frac{{образцы}}{{период}}~ \cdot ~ 0,1 ~\frac{{секунды}} {{sample}} = 1~ {second}
\end{align*}
и его частота $F = 1/T = 1$ Гц. Однако для $T_S = 0,002$ секунды та же самая синусоида с дискретным временем имеет
\begin{align*}
T &= 10 ~\frac{{samples}}{{period}}~ \cdot ~0,002 ~\ frac{{seconds}}{{sample}} = 0,02~ {seconds}
\end{align*}
с частотой $F = 1/T = 50$ Гц. Интересно, что выборки обеих синусоид будут храниться в памяти как последовательность чисел без разницы в дискретной области.

Всегда ли алиасинг вреден?

---

Алиасинг – повторное появление частот выше $0.5F_S$ в диапазоне $-0.5F_S \le F

1. Вредоносное искажение сигнала, которое искажает сигнал, и его следует избегать для правильного представления сигнала в дискретной области. Это когда $F_S
2. Полезный алиасинг, который бесплатно сдвигает спектральные полосы сигнала вверх и вниз до желаемой частоты благодаря тщательному проектированию системы. Это используется в системах, работающих на нескольких тактовых частотах.
3. Безобидный псевдоним, который ни хорош, ни плох для системы. Это происходит, например, при проектировании формы импульса с ограниченной полосой, чтобы избежать межсимвольной интерференции (ISI).

Ниже приведены некоторые замечания.

• Для фиксированного интервала времени сбора данных, чем больше выборок мы берем, тем выше энергия в результирующем сигнале с дискретным временем. Это связано с тем, что в дискретном сигнале будет больше выборок в течение одного и того же фиксированного интервала.
• Каждый дополнительный бит АЦП увеличивает отношение сигнала к шуму квантования на 6 дБ.

Что может служить примером непрерывного сигнала из «повседневной жизни»?

$\begingroup$

Пожалуйста, поделитесь ответом с простым примером из «повседневной» (разговорной) жизни людей для сигнала, который является «непрерывным», и объясните, что именно делает его «непрерывным».

Пожалуйста, используйте самый простой язык, как если бы вы хотели объяснить это ребенку.

Обновление

Перед созданием этого поста я уже провел некоторое исследование и нашел это определение:

Непрерывный временной сигнал — это непрерывная функция, т. е. в сигнале нет перерывов.

Но я подумал, что может быть объяснение, которое не является «математическим» (никаких «времени» и «функции» в применении к математике).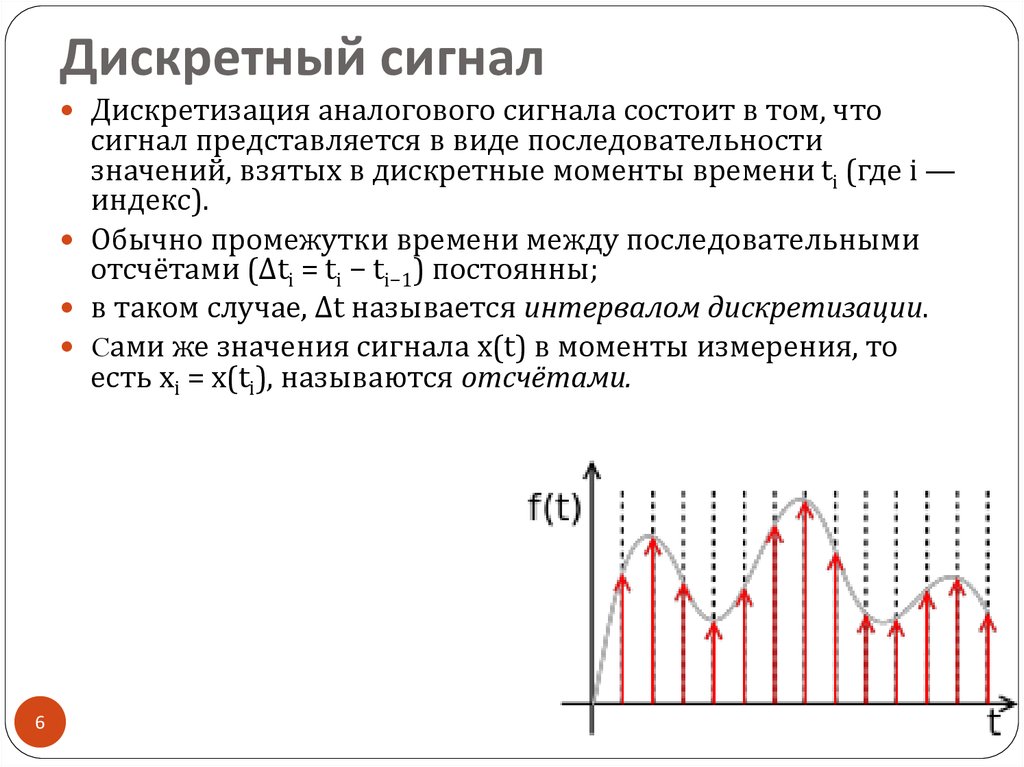

---

Документирование обсуждения в комментариях

гм, «объяснить без математики»: какой цели это служит? Что вам нужно, чтобы иметь возможность делать с этим знанием впоследствии? Потому что, если вы не знаете, что такое функция, ну, честно говоря, размышления о непрерывных и непостоянных сигналах практически не имеют смысла; вы не могли бы применить эти знания в любом месте.

Я знаю, что такое функция.

Три возможных назначения:

• Это даст представление о том, с чем работают специалисты по обработке сигналов (семя любопытства).

• Позволит человеку лучше классифицировать явления в реальности

• Позволит человеку понять более широкую тему, в которой термин напомнили в разговоре.

Я также добавлю, что в математическом образовании хорошо начинать изучение элементарных понятий на примерах из повседневной жизни («разговорных»), и если этот вопрос «обработки сигналов» все же является математическим, то пример из повседневной жизни может повысить шансы студент узнает об этом «абстрактные» данные.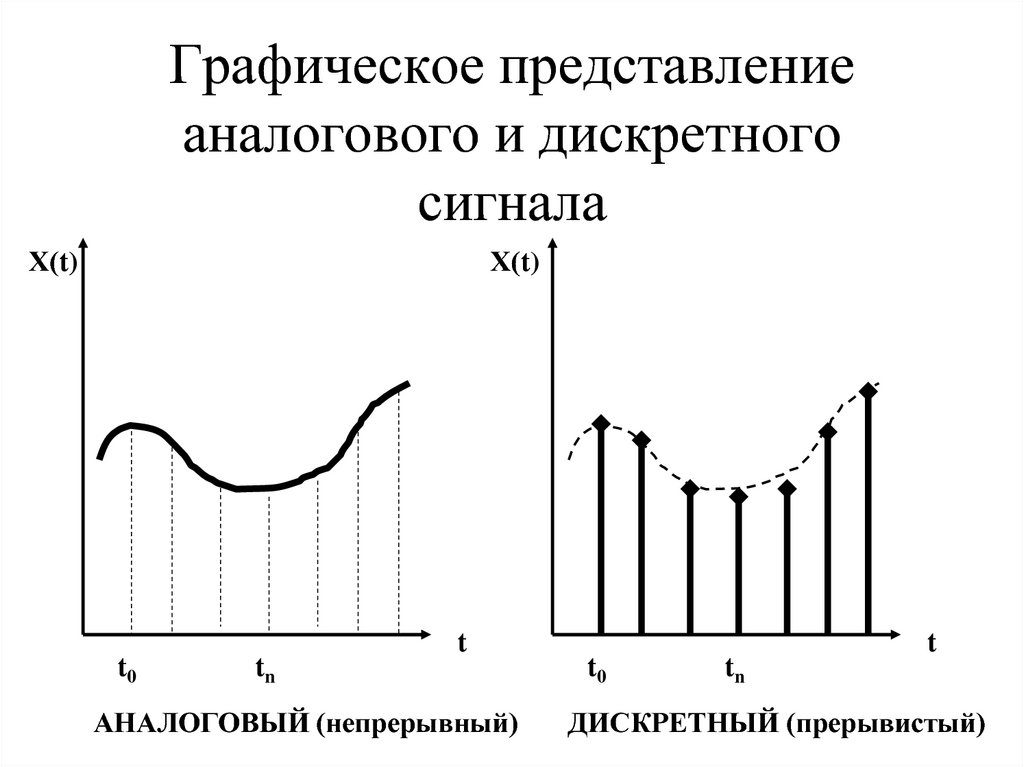

• непрерывные сигналы

$\endgroup$

17

$\begingroup$

Стандартный способ описания непрерывной кривой до строгих и доказуемых определений:

Что можно нарисовать на листе бумаги не отрывая ручки

Это довольно наглядно и относится и к сигналам. Конечно, это хорошо относится к кривым конечной длины. Фракталы и патологические функции, такие как $x\mapsto x \sin 1/x$ (ниже), являются примерами потребности в более формальных аксиомах непрерывности:

Если кто-то хочет уточнить, можно начать обсуждение того, что происходит, когда вы меняете ширину кончика пера, карандаша или кисти. Эта концепция близка разным размерам открытых множеств.

Есть настоящие примеры из каллиграфии, особенно скорописи, или (последовательности) букв, которые можно нарисовать одним мазком.