11. Однородное и неоднородные электрические поля

Электромагнитное поле – это итог взаимодействия электрического и магнитного полей, фундаментальное физическое поле, которое возникает вокруг заряженных тел. Таким образом, электрическое поле – это часть поля электромагнитного, которое в свою очередь порождает электромагнитные волны, распространяющиеся в пространстве со скоростью света. Это не что иное, как возмущения электромагнитного поля.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда.

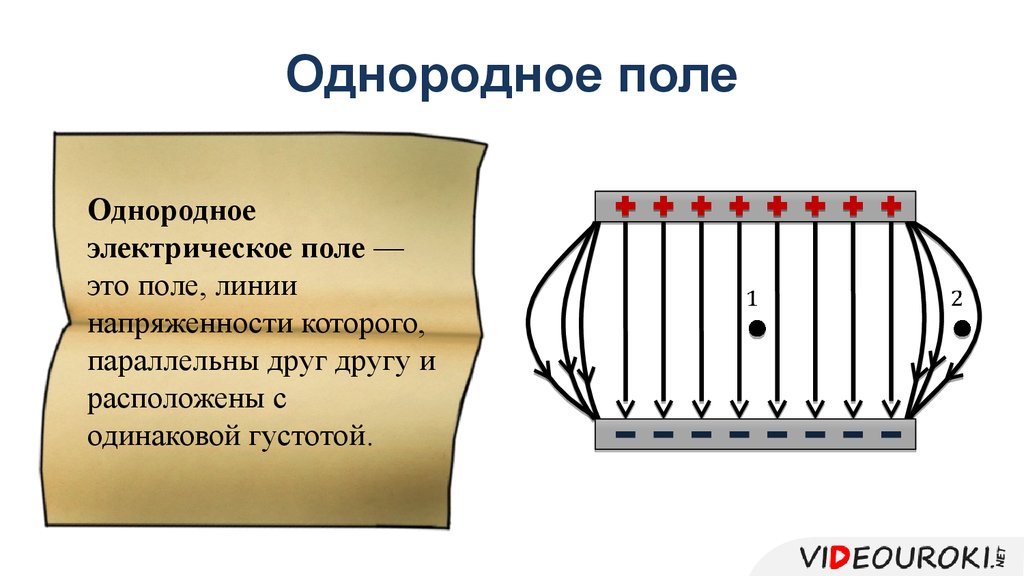
Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным электрическим полем.

Приблизительно однородным является электрическое поле между двумя разноименно заряженными плоскими металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу (рис. 109)

При равномерном распределении электрического заряда q по поверхности площади S поверхностная плотность заряда постоянна и равна

Можно доказать, что напряженность электрического поля бесконечной плоскости с поверхностной плотностью заряда одинакова в любой точке пространства и равна

Формула (17. 6) применяется для расчетов напряженности электрического поля около заряженных тел в том случае, когда форма равномерно заряженной поверхности близка к плоскости и расстояние от точки, в которой определяется напряженность поля, до поверхности тела значительно меньше размеров тела и расстояния до края заряженной поверхности.

Неоднородное поле — поле, значение (вектор) которого принимает различные значения и/или направления в разных точках.

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Конденсатор — электрический прибор, состоящий из двух проводящих пластин, разделенных слоем диэлектрика. Конденсаторы служат для накопления зарядов с целью их отдачи в нужный момент времени, а также в цепях переменного тока для деления зарядов (параллельное соединение) и для деления напряжения (последовательное соединение).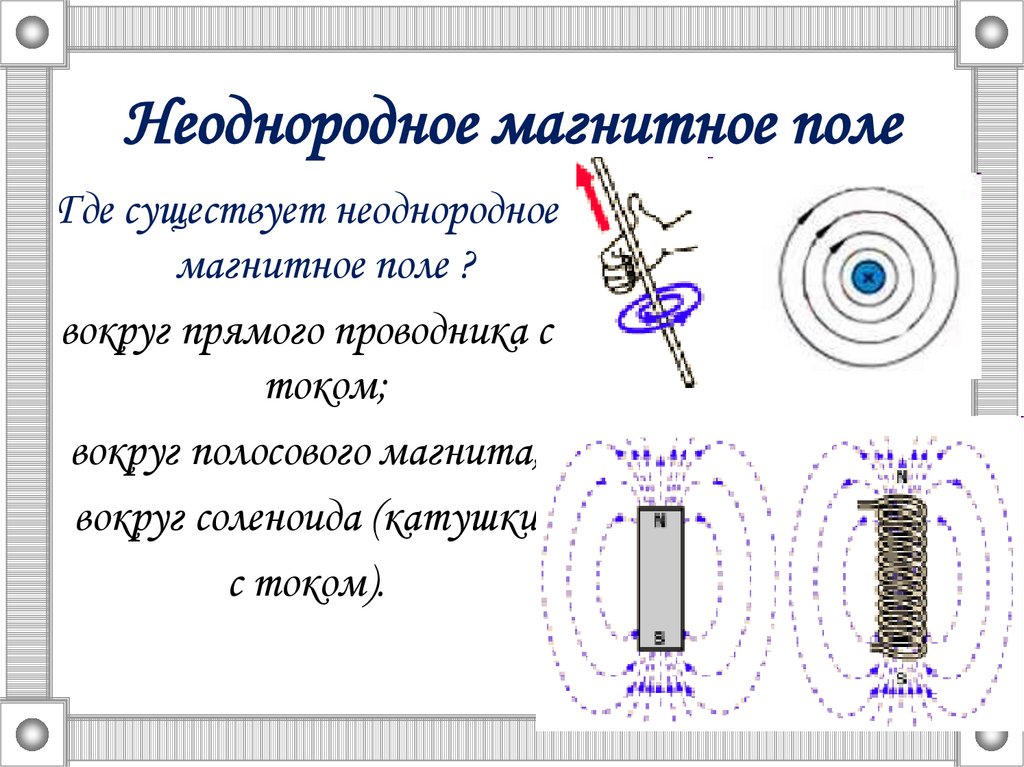

— емкость конденсатора (С).

— емкость плоского конденсатора.

Плоский конденсатор. Две плоские параллельные пластины одинаковой площади S, расположенные на расстоянии d друг от друга, образуют плоский конденсатор. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью , то при сообщении им заряда q напряженность электрического поля между пластинами равна , разность потенциалов равна . Таким образом, емкость плоского конденсатора.

| Неоднородное поле | Fiziku5

Неоднородное поле. В этом случае на положительный и отрицательный заряды диполя будут действовать неодинаковые силы (на рис. F2 > F1). Найдем выражение для силы, действующей на диполь для случая, когда напряженность зависит только от одной переменной х. Пусть поле характеризуется градиентом

dE/dx. Найдем результирующую силу F = F2 — F1.

	изменение напряженности на отрезке l×cosa, a — угол между векторами рэл и Е
	результирующая сила [12] и дипольный момент; подставляя, получим:
	сила, действующая на диполь в неоднородном электрическом поле

Таким образом, в неоднородном

электрическом поле диполь будет одновременно поворачиваться, растягиваться и втягиваться в область более сильного поля.

Работа по повороту диполя в однородном внешнем электрическом поле.

Если внести диполь в однородное электростатическое поле так, что его дипольный момент будет составлять угол a с вектором напряженности поля Е, силы поля F будут поворачивать диполь (на рис. – по часовой стрелке) до достижения им положения равновесия.

	работа при вращательном движении, М — вращающий момент, a — угол поворота
	работа по повороту диполя в однородном внешнем электростатическом поле

Если диполь из положения равновесия повернуть так, что между дипольным моментом и вектором напряженности внешнего поля образуется угол a, диполь получит запас потенциальной энергии Wпот. Так как работа равна убыли потенциальной энергии, то в общем случае получим:

	Изменение потенциальной энергии диполя во внешнем электростатическом поле
	Потенциальная энергия диполя во внешнем поле 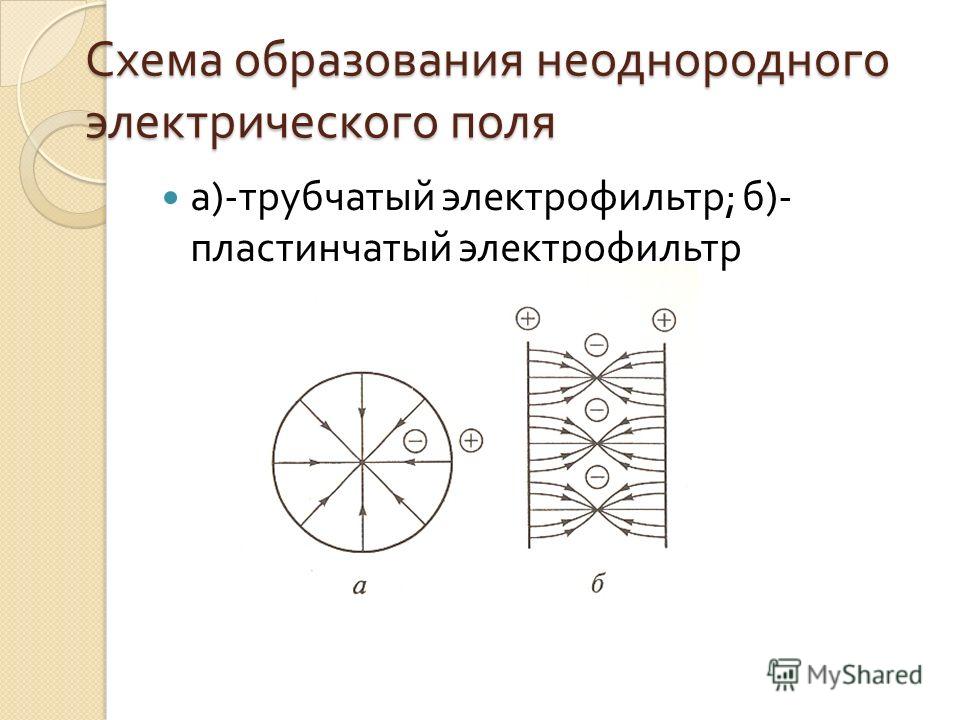. Для определения константы надо принять некоторое положение диполя за нулевое (какое хочешь). Скобки в формуле – скалярное произведение указанных векторов.

Поляризация диэлектриков.

Все вещества состоят из нейтральных атомов или молекул. И в атоме, и в молекуле поровну отрицательно заряженных частиц (электронов) и положительно заряженных ядер. В тех веществах, которые образуют металлические кристаллы,

от каждого атома (или молекулы) отрываются по 1-2 электрона, атомы становятся ионами, образуя кристаллическую решетку, а электроны свободно перемещаются по всему кристаллу. Эти электроны называют

свободными зарядами. Такие вещества называют металлическими проводниками, они хорошо проводят электрический ток.. [13] Другие твердые вещества образуются из нейтральных молекул, они практически не проводят электрический ток и их называют диэлектриками (а в электротехнике — изоляторами). Молекулы, особенно многоатомные, имеют сложное строение: ядра атомов в данной молекуле колеблются на определенных равновесных расстояниях друг от друга, вокруг них движется большая часть «своих» электронов, а часть электронов становятся «общими», и движутся вокруг всех ядер данной молекулы. Эти общие электроны как-бы цементируют атомы, и образуется молекула. Все виды молекул, из которых состоят диэлектрики, можно отнести к двум типам: полярные молекулы и неполярные молекулы. У неполярных молекул центры тяжести отрицательных и положительных зарядов совпадают. У полярных — эти центры смещены относительно друг друга, и полярная молекула представляет собой диполь. Примером полярной молекулы является молекула воды (см. рис.).

Если диэлектрик внести во внешнее электрическое поле, на его поверхностях появляются заряды. Это явление называется поляризацией диэлектриков, а сами заряды называются связанными, так как они могут смещаться только в пределах самой молекулы. При снятии внешнего поля поляризация практически мгновенно исчезает. В зависимости от того, из какого типа молекул состоит диэлектрик различают следующие типы поляризации.

1) Деформационная (электронная) поляризация наблюдается для веществ с неполярными молекулами. При внесении такого диэлектрика во внешнее электрическое поле, его молекулы растягиваются и образуют диполь с дипольным моментом рэл. При не очень сильных внешних полях рэл оказывается пропорциональным напряженности поля Е: рэл ~ Е и можно записать:

	индуцированный дипольный момент одной молекулы неполярного диэлектрика
a — коэффициент поляризуемости (поляризуемость) молекулы

Примерами веществ, для которых наблюдается деформационная поляризация, являются: водород Н2, парафин, ССl4 и др.

2) Ориентационная (дипольная) поляризация наблюдается для веществ с полярными молекулами. На рис. полярные молекулы символически показаны в виде диполей. При отсутствии внешнего поля молекулы ориентированы хаотически. Во внешнем поле молекулы-диполи стремятся ориентироваться по полю, но им «мешает» тепловое движение, поэтому строгой ориентации не происходит, но тем не менее на поверхностях диэлектрика появляются связанные заряды с поверхностной плотностью s¢связ. Средний дипольный момент молекул áрñ из-за влияния теплового движения оказывается не равным собственному дипольному моменту молекулы р0. Для не очень сильных внешних полей расчеты дают формулу:

средний дипольный момент одной полярной молекулы во внешнем электрическом поле р0 –собственный дипольный момент молекулы

К веществам с полярными молекулами относятся вода, HCl, NH3, CO и др.

3) Существует еще один тип поляризации диэлектриков – ионная поляризация. Например, кристалл NaCl представляет собой вдвинутые друг в друга решетки из положительных и отрицательных ионов. Под воздействием внешнего электрического поля происходит смещение одной кристаллической решетки относительно другой. Мы не будем подробно рассматривать этот тип поляризации.

Характеристики электрического поля в диэлектриках и их диэлектрических свойств.

Поляризация диэлектриков характеризуется физической величиной, называемой вектором поляризации (Р):

(Кл/м2) n

Здесь: pi – дипольный момент молекулы, V – объем диэлектрика. Вектор поляризации по смыслу представляет собой векторную сумму дипольных моментов всех молекул в единице объема диэлектрика.

Найдем связь величины вектора поляризации Р с поверхностной плотностью связанных зарядов s¢связ. Пусть кусок диэлектрика в форме параллелепипеда с боковой поверхностью S и длиной L помещен во внешнее поле с напряженностью Е. (см. рис.). На его поверхности образуются связанные заряды.

Измерение электрического поля, индуцированного магнитными катушками в неоднородных объемных проводниках: приложение к нейрогеометрии позвоночника человека

. 1991 г., июнь; 81 (3): 224–37.

doi: 10.1016/0168-5597(91)

-а.

П. Дж. Маккавей ¹ , В. Э. Амассиан, Л. П. Эберле, А. П. Руделл, Р. К. Кракко, К. С. Лай, М. Сомасундарум

принадлежность

• ¹ Отделение неврологии, Медицинский научный центр SUNY, Бруклин 11203.

• PMID: 1710972
• DOI: 10.1016/0168-5597(91)

  -а

PJ Maccabee et al. Электроэнцефалогр Клин Нейрофизиол. 1991 июня

. 1991 г., июнь; 81 (3): 224–37.

doi: 10.1016/0168-5597(91)

-а.

Авторы

П. Дж. Маккавей ¹ , В. Э. Амассиан, Л. П. Эберле, А. П. Руделл, Р. К. Кракко, К. С. Лай, М. Сомасундарум

принадлежность

• ¹ Отделение неврологии, Медицинский научный центр SUNY, Бруклин 11203.

• PMID: 1710972
• DOI: 10.1016/0168-5597(91)

  -а

Абстрактный

Измерялись электрические поля, наводимые круглыми и восьмерками магнитными катушками (МК) в однородных и неоднородных объемных проводниках. В однородных средах круглый МК, расположенный тангенциально (т.е. плоско) к объемному проводнику, индуцировал кольцевое электрическое поле. При удерживании круглого МК на ребро (т. е. ортогонально) объемному проводнику индуцированное электрическое поле состояло из двух петель, в основном параллельных поверхности объемного проводника и сближающихся непосредственно под контактирующей кромкой МК. Тангенциально ориентированная восьмерка МК аналогичным образом индуцировала две петли электрического поля, которые максимально сближали друг друга под областью перехода по его длинной оси. В сложном неоднородном по объему проводнике, таком как сегмент шейно-грудного отдела позвоночника человека, расположенный эксцентрично внутри большого цилиндрического резервуара и погруженный в изотонический раствор, направление электрических полей внутри позвоночного канала и через межпозвонковые нейрофорамины было аналогично наблюдаемому. в однородном объемном проводнике. Однако в одном нейроотверстии и вблизи него электрическое поле и особенно его первая пространственная производная были заметно повышены по сравнению с полем, зарегистрированным в пределах длинной центральной оси позвоночного канала. Потенциалы действия моторных единиц и сложных мышц, вызванные в мышцах конечностей стимуляцией MC шейного отдела позвоночника человека, подтвердили предсказания, полученные на основе физической модели. Прогнозы включали: (1) отсутствие стимуляции спинного мозга по сравнению с относительной легкостью стимуляции нервных корешков током, который, скорее всего, концентрируется в нейрофораминах. Когда стимулирующий ток направлен к периферии, предполагается, что наиболее вероятное место стимуляции с низким порогом находится дистальнее нейрофорамины. Подчеркивается, что при супрамаксимальной стимуляции могут возникать более дистальные участки возбуждения; 2) инвариантные латентные сдвиги пороговых интенсивностей при перемещении ТК вдоль рострокаудальной оси шейного отдела позвоночника; (3) существенное влияние (на пороги активации двигательных единиц) направления индуцированного тока, протекающего через нейрофорамины; (4) снижение стимуляции, когда целевые нервные корешки находятся близко к нулевой точке электрического поля, то есть между местами высокой напряженности электрического поля противоположной полярности; и (5) относительно очаговая стимуляция нервных корешков соединением поперечно ориентированной восьмерки MC, т. е. параллельно нервным корешкам.

Похожие статьи

• Механизмы стимуляции периферической нервной системы с помощью магнитной катушки.

  Maccabee PJ, Amassian VE, Cracco RQ, Eberle LP, Rudell AP. Маккаби П.Дж. и др. Электроэнцефалог Clin Neurophysiol Suppl. 1991;43:344-61. Электроэнцефалог Clin Neurophysiol Suppl. 1991. PMID: 1773773

• Пространственное распределение электрического поля, индуцируемого в объеме круглой и восьмеричной магнитными катушками: значение для активации сенсорных нервных волокон.

  Maccabee PJ, Eberle L, Amassian VE, Cracco RQ, Rudell A, Jayachandra M. Маккаби П.Дж. и др. Электроэнцефалогр Клин Нейрофизиол. 1990 г., август; 76 (2): 131–41. doi: 10.1016/0013-4694(90)-2. Электроэнцефалогр Клин Нейрофизиол. 1990. PMID: 1697241

• Анализ стимуляции периферических двигательных нервов у людей с помощью магнитной катушки.

  Maccabee PJ, Amassian VE, Cracco RQ, Cadwell JA. Маккаби П.Дж. и др. Электроэнцефалогр Клин Нейрофизиол. 1988 декабрь; 70 (6): 524-33. doi: 10.1016/0013-4694(88)

  -2. Электроэнцефалогр Клин Нейрофизиол. 1988 год. PMID: 2461286

• Стимуляция нервной системы человека с помощью магнитной катушки.

  Maccabee PJ, Amassian VE, Cracco RQ, Cracco JB, Eberle L, Rudell A. Маккаби П.Дж. и др. Дж. Клин Нейрофизиол. 1991 янв.; 8(1):38-55. doi: 10.1097/00004691-199101000-00006. Дж. Клин Нейрофизиол. 1991. PMID: 2019650 Обзор.

• Сопоставление фокальной и нефокальной стимуляции магнитной катушки со свойствами нервной системы человека: картирование полей двигательных единиц в моторной коре в отличие от изменения последовательных движений пальцев при стимуляции премоторной SMA.

  Amassian VE, Cracco RQ, Maccabee PJ, Bigland-Ritchie B, Cracco JB. Амассиан В.Е. и соавт. Электроэнцефалог Clin Neurophysiol Suppl. 1991;43:3-28. Электроэнцефалог Clin Neurophysiol Suppl. 1991. PMID: 1773769 Обзор.

Посмотреть все похожие статьи

Цитируется

• Электромагнитные силы и крутящие моменты: от диэлектрофореза до оптического пинцета.

  Риккарди М., Мартин О.Дж.Ф. Риккарди М. и соавт. Chem Rev. 2023 31 января; 123 (4): 1680-711. doi: 10.1021/acs.chemrev.2c00576. Онлайн перед печатью. Химическая версия 2023. PMID: 36719985 Бесплатная статья ЧВК. Обзор.

• Противоречия и клиническое применение неинвазивной трансспинальной магнитной стимуляции: критический обзор и исследовательское исследование наследственной спастической параплегии.

  Карра Р.Б., Силва Г.Д., Парагвай IBB, Диниз де Лима Ф., Менезес М.Р., Пинеда А.М., Нуньес Г.А., Симоэнс Д.С., Франса М.К. мл., Кьюри Р.Г. Карра РБ и соавт. Дж. Клин Мед. 2022 14 августа; 11 (16): 4748. дои: 10.3390/jcm11164748. Дж. Клин Мед. 2022. PMID: 36012986 Бесплатная статья ЧВК.

• Множественная регрессионная модель нормального времени центральной и периферической двигательной проводимости.

  Джейсер С.Р., Барнс Д.Д., Бейкер С.Н., Бейкер М.Р. Джайсер С.Р. и др. Мышечный нерв. 2015 май; 51(5):706-12. doi: 10.1002/mus.24427. Epub 2015 14 марта. Мышечный нерв. 2015. PMID: 25154476 Бесплатная статья ЧВК.

• Определение того, какие механизмы приводят к активации в моторной коре: исследование моделирования транскраниальной магнитной стимуляции с использованием реалистичных сигналов стимула и геометрии борозды.

  Сальвадор Р., Сильва С., Бассер П.Дж., Миранда П.С. Сальвадор Р. и др. Клин Нейрофизиол. 2011 г., апрель; 122(4):748-58. doi: 10.1016/j.clinph.2010.09.022. Epub 2010 28 октября. Клин Нейрофизиол. 2011. PMID: 21035390 Бесплатная статья ЧВК.

• Выяснение механизмов и локусов возбуждения нейронов транскраниальной магнитной стимуляцией с использованием конечно-элементной модели кортикальной борозды.

  Сильва С., Бассер П.Дж., Миранда П.С. Сильва С. и др. Клин Нейрофизиол. 2008 г., октябрь; 119 (10): 2405-13. doi: 10.1016/j.clinph.2008.07.248. Epub 2008 9 сентября. Клин Нейрофизиол. 2008. PMID: 18783986 Бесплатная статья ЧВК.

Просмотреть все статьи «Цитируется по»

термины MeSH

3.5: Сила на диполе в неоднородном электрическом поле

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5428

• Джереми Татум
• Университет Виктории

\(\text{РИСУНОК III. 4}\)

Рассмотрим простой диполь, состоящий из двух зарядов \(+Q\) и \(-Q\), разделенных расстоянием \(δx\), так что его диполь момент равен \(p = Q\, δx\). Представьте, что он находится в неоднородном электрическом поле, как показано на рисунке \(III\).4. Мы уже отмечали, что диполь в однородном 9Поле 0169 не испытывает результирующей силы, но мы можем видеть, что оно испытывает результирующую силу в неоднородном поле . Пусть поле в точке \(−Q \text{ равно }E\), а поле в точке \(+Q \text{ равно }E + δE\). Сила на \(−Q \text{ равна }QE\) слева, а сила на \(+Q \text{ равна }Q(E + δE)\) справа. Таким образом, справа от \(Q\, δE\) действует результирующая сила, или:

\[\label{3.5.1}\text{Force}=p\frac{dE}{dx}\]

Уравнение \ref{3.5.1} описывает ситуацию, когда диполь, электрическое поле и градиент параллельны 92V}{ ∂y ∂z}\) и т. д. Таким образом, в общем случае уравнение \ref{3.5.1} должно быть записано как

\[\begin{pmatrix}E_x \\ E_y \\ E_z \\ \end{ pmatrix} =-\begin{pmatrix}V_{xx} & V_{xy} & V_{xz} \\ V_{xy} & V_{yy} & V_{yz} \\ V_{xz} & V_{yz} & V_{zz} \\ \end{pmatrix}\begin{pmatrix}p_x \\ p_y \\ p_z \\ \end{pmatrix}\label{3.