Элементы Исключающее ИЛИ/Исключающее ИЛИ-НЕ/Нечётность/Чётность
| Библиотека: | Базовые |
| Введён в: | 2.0 Beta 1 для Исключающее ИЛИ/Нечётность/Чётность; 2.0 Beta 6 для Исключающее ИЛИ-НЕ |
| Внешний вид: |
Поведение
Элементы Исключающее ИЛИ, Исключающее ИЛИ-НЕ, Нечётность и Чётность вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. (Если все входы не подключены, то на выходе значение ошибки X.) Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню Проект > Параметры…, перейдя на вкладку Моделирование, и выбрав вариант
для Выход элемента при неопределённости
.
Двухвходовая таблица истинности для элементов следующая.
| x | y | Исключающее ИЛИ | Исключающее ИЛИ-НЕ | Нечётность | Чётность |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Как вы можете видеть, элементы Нечётность и Исключающее ИЛИ ведут себя одинаково в случае двух входов; аналогично, элементы Чётность и Исключающее ИЛИ-НЕ ведут себя одинаково. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго
Если на каких-либо входах значение ошибки (например, если противоречивые значения поступают на один и тот же провод) или плавающее значение, то на выходе будет значение ошибки.
Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия. Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ: официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут
.
Контакты (предполагается, что компонент направлен на восток)
- Западный край (входы, разрядность соответствует атрибуту Биты данных)
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Заметьте, что если вы используете фигурные элементы, то западный край элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет искривлён. Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании «Вида для печати», эти отрезки не будут отрисованы, если не подключены к проводам.
- Восточный край (выход, разрядность соответствует атрибуту Биты данных)
Выход элемента, значение на котором вычисляется на основании текущих значений на входах, как описано выше.
Атрибуты
Когда компонент выбран, или уже добавлен, клавиши от 0 до 9 меняют его атрибут Количество входов
, комбинации от Alt-0 до Alt-9 меняют его атрибут Биты данных
, а клавиши со стрелками меняют его атрибут Направление
.
- Направление
- Направление компонента (его выхода относительно его входов).
- Биты данных
- Разрядность входов и выходов компонента.
- Размер элемента
- Определяет, следует отрисовывать широкую или узкую версию компонента. Это не влияет на количество входов, которое определяется атрибутом Количество входов; правда, если количество входов превышает 3 (для узкого компонента) или 5 (для широкого), то элемент будет отрисовываться с «крыльями», чтобы вместить запрошенное количество входов.
- Количество входов
- Определяет, сколько контактов на западном крае будет иметь компонент.
- Метка
- Текст внутри метки, привязанной к элементу.
- Шрифт метки
- Шрифт, которым отрисовывается метка.
- Многовходовое поведение (только для Исключающее ИЛИ и Исключающее ИЛИ-НЕ)
- Когда входов три или более, то значение на выходе элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет основано или на том, что 1 строго на одном входе (по умолчанию), или на нечётном количестве входов.
Поведение Инструмента Нажатие
Нет.
Поведение Инструмента Текст
Позволяет редактировать привязанную к элементу метку.
Назад к Справке по библиотеке
Логический вентиль — Википедия
Материал из Википедии — свободной энциклопедии
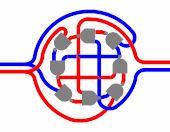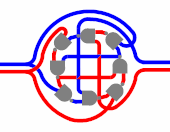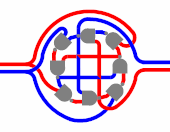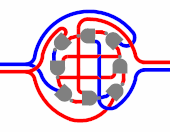
Логи́ческий ве́нтиль — базовый элемент цифровой схемы, выполняющий элементарную логическую операцию[1], преобразуя таким образом множество входных логических сигналов в выходной логический сигнал. Логика работы вентиля основана на битовых операциях[2] с входными цифровыми сигналами в качестве операндов. При создании цифровой схемы вентили соединяют между собой, при этом выход используемого вентиля должен быть подключён к одному или к нескольким входам других вентилей. В настоящее время в созданных человеком цифровых устройствах доминируют электронные логические вентили на базе полевых транзисторов, однако в прошлом для создания вентилей использовались и другие устройства, например, электромагнитные реле, гидравлические устройства, а также механические устройства. В поисках более совершенных логических вентилей исследуются квантовые устройства
В цифровой электронике логический уровень сигнала представлен в виде уровня напряжения (попадающего в один из двух диапазонов) или в виде значения тока. Это зависит от типа используемой технологии построения электронной логики
Впервые математически точно двоичная система счисления была подробно описана немецким математиком Готфридом Вильгельмом Лейбницем (публикация от 1705 года). Он также разъяснил, как с помощью этой системы можно объединить принципы арифметики и логики.
Первые логические вентили были реализованы механически. В 1837 году английский изобретатель Чарльз Бэббидж разработал вычислительную машину, названную им аналитической (англ. Analytical Engine), которая считается прообразом современного компьютера.
В 1847 году английский математик и логик Джордж Буль в своём трактате «Математический анализ логики» (англ. The Mathematical Analysis of Logic) заложил основы современной алгебры логики, связав её с логикой высказываний. При этом он ввёл свою алгебраическую систему, которая содержала следующие функции: конъюнкция (логическое умножение, оператор «AND»), дизъюнкция (логическое сложение, оператор «OR») и отрицание (оператор «NOT»). Впоследствии данная алгебра была названа булевой.
В том же 1847 году шотландский математик и логик Огастес де Морган опубликовал правила, связывающие пары логических операций при помощи логического отрицания (Законы де Моргана).
В 1881 г. американский математик и логик Чарльз Сандерс Пирс теоретически доказал, что функция «инверсия дизъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Пирса», знак операции — стрелка Пирса ↓. Позже, элемент, реализующий данную функцию, стали называть элементом Пирса или «ИЛИ-НЕ» (англ. NOR gate, см. таблицу). Данная работа была опубликована только в 1933 году.
В 1913 г. американский математик и логик Генри Морис Шеффер теоретически доказал, что функция «инверсия конъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Шеффера», знак операции — штрих Шеффера |. Позже элемент, реализующий данную функцию, стали называть элементом Шеффера или «И-НЕ» (англ. NAND gate, см. таблицу).
В 1927 г. российский советский математик и логик Иван Иванович Жегалкин представил алгебру логики как арифметику вычетов по модулю 2. Данная универсальная функция получила позднее название «полином Жегалкина», а знак операции — ⊕{\displaystyle \oplus }. Позже элемент, реализующий данную функцию, стали называть «исключающее ИЛИ» (англ. XOR gate).
В 1935 г. немецкий инженер Конрад Цузе разрабатывает для своей вычислительной машины Z1 первые действующие электромеханические вентили.
В 1906 г. американский изобретатель Ли де Форест вводит в вакуумную лампу Джона Флеминга третий электрод — управляющую сетку и получает триод, который может работать не только в качестве усилителя электрических сигналов, но и в качестве простейшего переключателя (вентиля).
В 1947 г. Уильям Шокли, Джон Бардин и Уолтер Браттейн в лабораториях Bell Labs впервые создают действующий биполярный транзистор. Позднее транзисторы заменили вакуумные лампы в большинстве электронных устройств, совершив революцию в создании интегральных схем.
 ТТЛ 2И-НЕ вентиль ТТЛ 2И-НЕ вентиль | 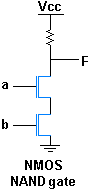 | 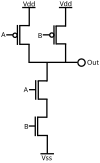 |  КМОП 2И-НЕ вентиль на кристалле в микросхеме КМОП 2И-НЕ вентиль на кристалле в микросхеме |
- ↑ gpntb.ru — Термины микроэлекроники
- ↑ Например: 2И-НЕ (NAND), XOR (исключающее ИЛИ) и другие.
- ↑ scientific.ru — Квантовый логический вентиль на сверхпроводниках
- ↑ pereplet.ru — Спиновые логические вентили на основе квантовых точек
- ↑ skms.impb.psn.ru — Электронный логический вентиль XOR на основе ДНК.
- ↑ Wang, Lei and Li, Baowen. Thermal Logic Gates: Computation with Phonons (англ.) // Physical Review Letters. — APS, 2007. — Vol. 99, no. 17.
- ↑ Наиболее известные это КМОП, ТТЛ, N-МОП, ЭСЛ, ДТЛ, РТЛ.
Элементы Исключающее ИЛИ/Исключающее ИЛИ-НЕ/Нечётность/Чётность
| Библиотека: | Базовые |
| Введён в: | 2.0 Beta 1 для Исключающее ИЛИ/Нечётность/Чётность; 2.0 Beta 6 для Исключающее ИЛИ-НЕ |
| Внешний вид: |
Поведение
Элементы Исключающее ИЛИ, Исключающее ИЛИ-НЕ, Нечётность и Чётность вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. (Если все входы не подключены, то на выходе значение ошибки X.) Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню Проект > Параметры…, перейдя на вкладку Моделирование, и выбрав вариант Ошибка для неопределённых входов
для Выход элемента при неопределённости
.
Двухвходовая таблица истинности для элементов следующая.
| x | y | Исключающее ИЛИ | Исключающее ИЛИ-НЕ | Нечётность | Чётность |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Как вы можете видеть, элементы Нечётность и Исключающее ИЛИ ведут себя одинаково в случае двух входов; аналогично, элементы Чётность и Исключающее ИЛИ-НЕ ведут себя одинаково. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество. Элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ имеют атрибут, названный Многовходовое поведение, который позволяет настроить их на использование поведения элементов Нечётность и Чётность.
Если на каких-либо входах значение ошибки (например, если противоречивые значения поступают на один и тот же провод) или плавающее значение, то на выходе будет значение ошибки.
Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия. Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ: официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут Многовходовое поведение
.
Контакты (предполагается, что компонент направлен на восток)
- Западный край (входы, разрядность соответствует атрибуту Биты данных)
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Заметьте, что если вы используете фигурные элементы, то западный край элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет искривлён. Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании «Вида для печати», эти отрезки не будут отрисованы, если не подключены к проводам.
- Восточный край (выход, разрядность соответствует атрибуту Биты данных)
Выход элемента, значение на котором вычисляется на основании текущих значений на входах, как описано выше.
Атрибуты
Когда компонент выбран, или уже добавлен, клавиши от 0 до 9 меняют его атрибут Количество входов
, комбинации от Alt-0 до Alt-9 меняют его атрибут Биты данных
, а клавиши со стрелками меняют его атрибут Направление
.
- Направление
- Направление компонента (его выхода относительно его входов).
- Биты данных
- Разрядность входов и выходов компонента.
- Размер элемента
- Определяет, следует отрисовывать широкую или узкую версию компонента. Это не влияет на количество входов, которое определяется атрибутом Количество входов; правда, если количество входов превышает 3 (для узкого компонента) или 5 (для широкого), то элемент будет отрисовываться с «крыльями», чтобы вместить запрошенное количество входов.
- Количество входов
- Определяет, сколько контактов на западном крае будет иметь компонент.
- Многовходовое поведение (только для Исключающее ИЛИ и Исключающее ИЛИ-НЕ)
- Когда входов три или более, то значение на выходе элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет основано или на том, что 1 строго на одном входе (по умолчанию), или на нечётном количестве входов.
Поведение Инструмента Нажатие
Нет.
Поведение Инструмента Текст
Нет.
Назад к Справке по библиотеке
НОУ ИНТУИТ | Лекция | Более сложные логические элементы
Аннотация: В лекции рассказывается о принципах работы, характеристиках и типовых схемах включения логических элементов, выполняющих сравнительно сложные функции – элементов Исключающее ИЛИ, И-ИЛИ-НЕ, триггеров Шмитта, а также приводятся схемотехнические решения, позволяющие реализовать на их основе часто встречающиеся функции.
Элементы Исключающее ИЛИ
Элементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
| Вход 1 | Вход 2 | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Рис. 4.1. Обозначения элементов Исключающее ИЛИ: зарубежные (слева) и отечественные (справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ «=1» как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж специфическая функция реализуется этими элементами.
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию так называемого суммирования по модулю 2. Поэтому эти элементы также называются сумматорами по модулю два. Как уже отмечалось в предыдущей лекции, обозначается суммирование по модулю 2 знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов, которые будут рассмотрены в следующей лекции.
В качестве сумматора по модулю 2 элемент Исключающее ИЛИ используется также в параллельных и последовательных делителях по модулю 2, служащих для вычисления циклических контрольных сумм. Но подробно эти схемы будут рассмотрены в лекциях 14,15.
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор
В случае, когда имеется два сигнала одинаковой полярности (положительные или отрицательные), и при этом их одновременный приход исключается, элемент Исключающее ИЛИ может быть использован для смешивания этих сигналов (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными. При положительных входных сигналах элемент Исключающее ИЛИ будет работать как элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда, при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще одно важнейшее применение элемента Исключающее ИЛИ — формирование коротких импульсов по любому фронту входного сигнала (рис. 4.4). В данном случае не важно, положительный фронт входного сигнала или отрицательный, на выходе все равно формируется положительный импульс. Входной сигнал задерживается с помощью конденсатора или цепочки элементов, а затем исходный сигнал и его задержанная копия поступают на входы элемента Исключающее ИЛИ. В обеих схемах в качестве элементов задержки используются также двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль). В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно, например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.
Операция «исключающее или»
О
 перация
исключающее ИЛИ (неравнозначность,
сложение по модулю два) обозначается
символом и отличается от логического
ИЛИ только приA=1
и B=1.
перация
исключающее ИЛИ (неравнозначность,
сложение по модулю два) обозначается
символом и отличается от логического
ИЛИ только приA=1
и B=1.
Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.
Определение данной операции может быть записано в виде таблицы истинности (таблица 6):
Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»
Х1
Х2
Y
1
1
0
1
0
1
0
1
1
0
0
0
Как видно из таблицы 6, логика работы элемента соответствует его названию.
Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.
Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).
Таблица 7 – Основные логические операции
Обозначение операции | Читается | Название операции | Альтернативные обозначения |
¬ | НЕ | Отрицание (инверсия) | Черта сверху |
^ | И | Конъюнкция (логическое умножение) | & |
v | ИЛИ | Дизъюнкция (логическое сложение) | + |
→ | Если … то | Импликация | |
↔ | Тогда и только тогда | Эквиваленция | ~ |
XOR | Либо … либо | ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2) | |
Порядок выполнения логических операций в сложном логическом выражении
Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.
При вычислении значения логического выражения принят определённый порядок выполнения логических операций.
1. Инверсия.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Логические выражения и таблицы истинности
Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «(2·2=5 или 2∙2=4) и (2∙2≠5 или 2∙2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0),
В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме:
« (А или В)
и (Ā или В)».
(А или В)
и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В)
& (Ā v В).
= (A v В)
& (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F =
(A
v
В)
&
(Ā v
В)
= (0
v
1)
&
(1
v
0)
= 1 & 1 = 1.
=
(A
v
В)
&
(Ā v
В)
= (0
v
1)
&
(1
v
0)
= 1 & 1 = 1.
Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В
нашем случае логическая функция 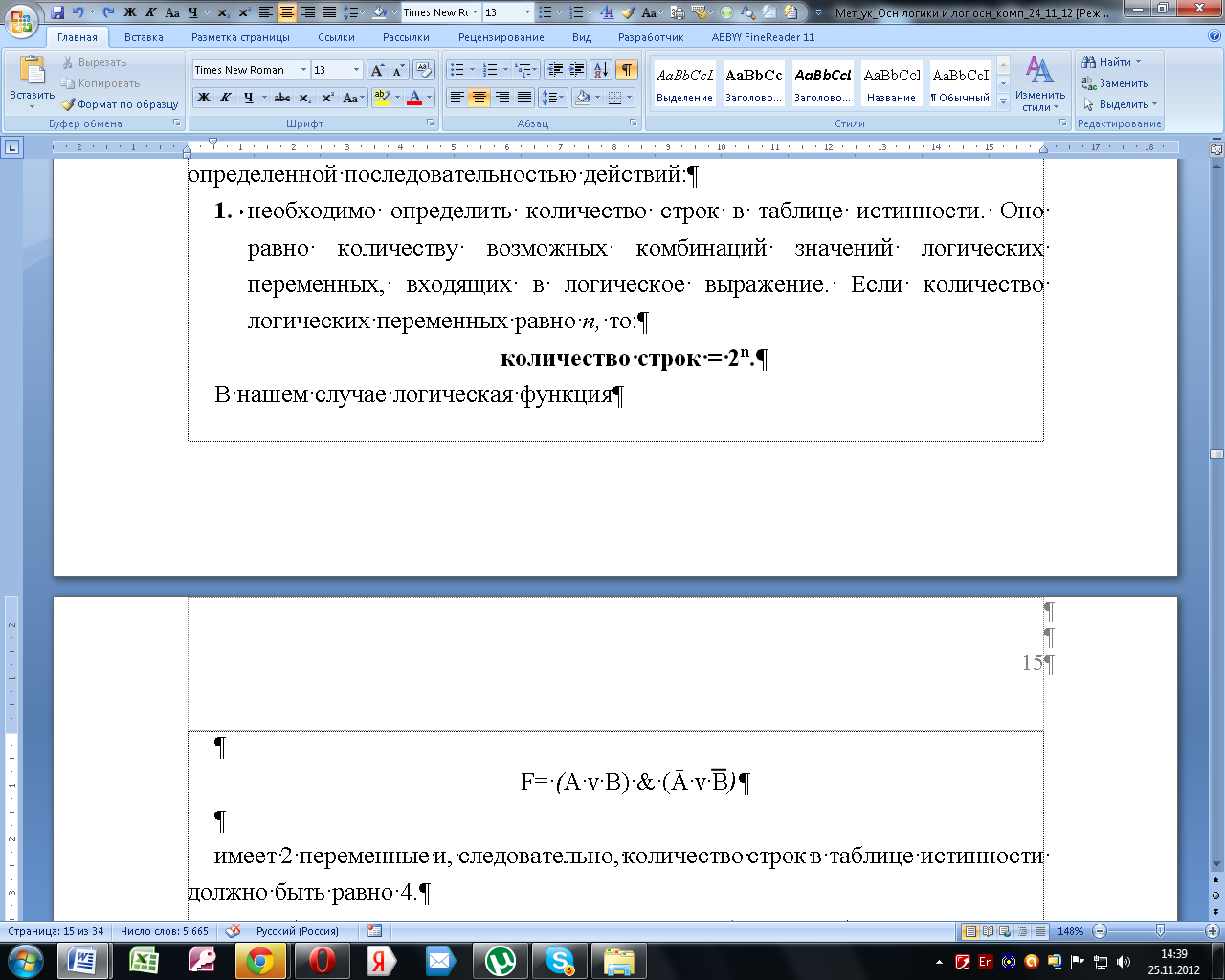
имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
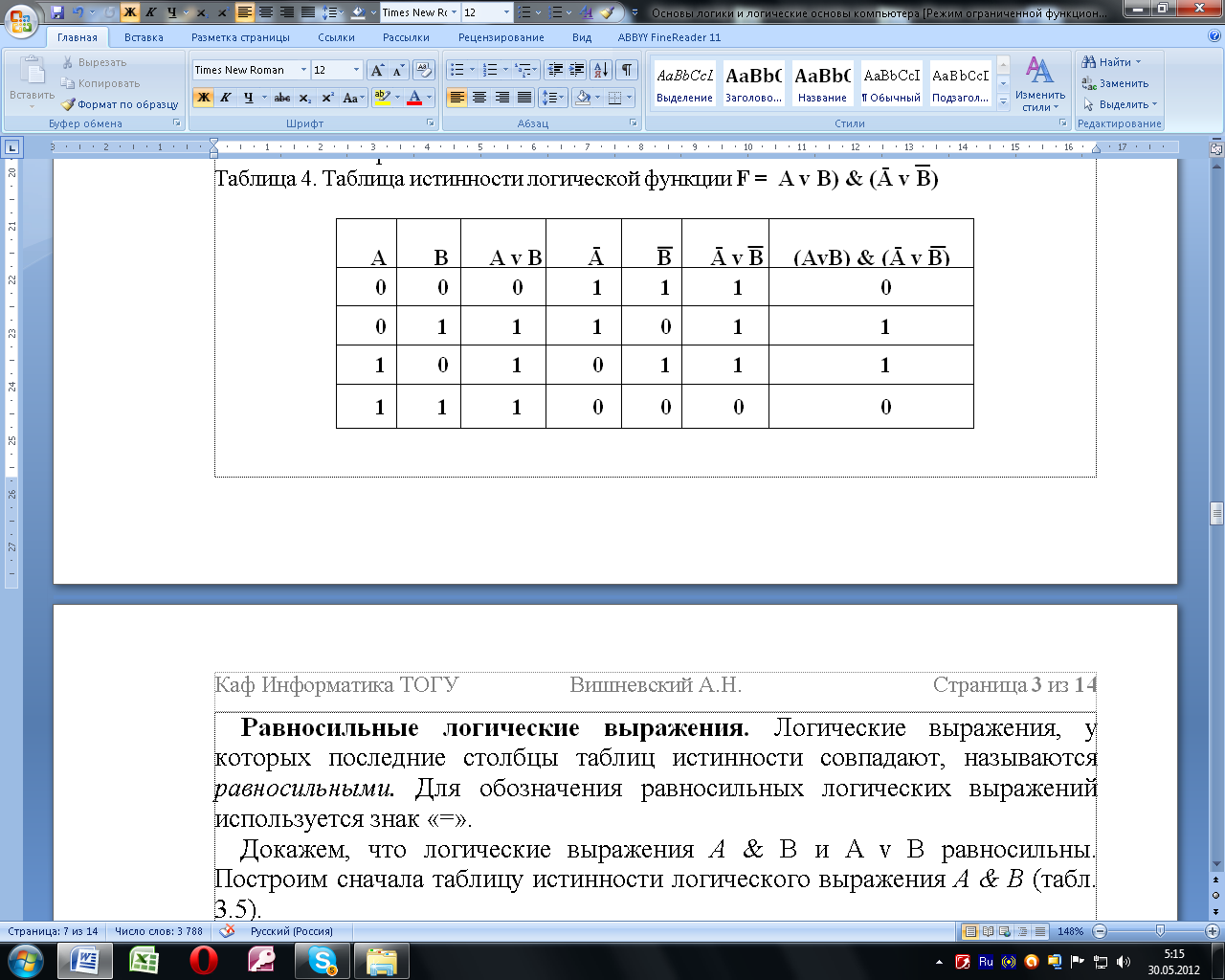
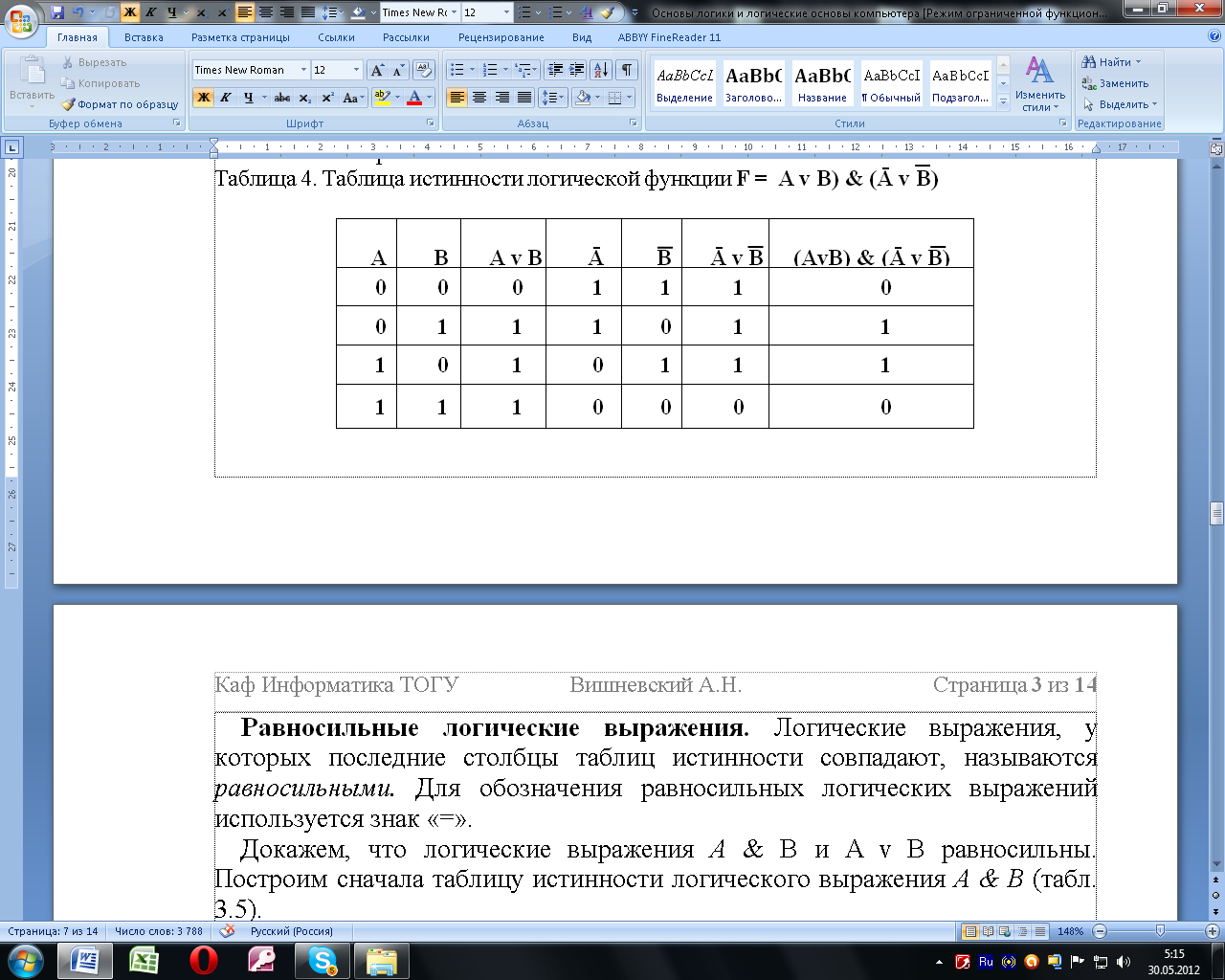
Таблица 8 – Таблица истинности логической функции
Побитовые операторы в C++: И, ИЛИ, НЕ и исключающее ИЛИ | Уроки С++
Обновл. 30 Дек 2019 |
Примечание: Для некоторых этот материал может показаться сложным. Если вы застряли или что-то не понятно — пропустите этот урок (и следующий), в будущем сможете вернуться и разобраться детальнее. Он не столь важен для прогресса в изучении C++, как другие уроки, и изложен здесь в большей мере для общего развития.
Побитовые операторы манипулируют отдельными битами в пределах переменной.
Зачем нужны побитовые операторы?
В далёком прошлом компьютерной памяти было очень мало и ею сильно дорожили. Это было стимулом максимально разумно использовать каждый доступный бит. Например, в логическом типе данных bool есть всего лишь два возможных значения (true и false), которые могут быть представлены одним битом, но по факту занимают целый байт памяти! А это, в свою очередь, из-за того, что переменные используют уникальные адреса памяти, а они выделяются только в байтах. Переменная bool занимает 1 бит, а другие 7 тратятся впустую.
Используя побитовые операторы, можно создавать функции, которые позволят уместить 8 значений типа bool в переменной размером 1 байт, что значительно сэкономит потребление памяти. В прошлом такой трюк был очень популярен. Но сегодня, по крайней мере, в прикладном программировании, это не так.
Теперь памяти существенно больше и программисты обнаружили, что лучше писать код так, чтобы было проще и понятнее его поддерживать, нежели усложнять его ради незначительной экономии памяти. Поэтому спрос на использование побитовых операторов несколько спал, за исключением случаев, когда необходима ну уже максимальная оптимизация (например: научные программы, которые используют огромное количество данных; игры, где манипуляции с битами могут быть использованы для дополнительной скорости; встроенные программы, где память по-прежнему ограничена).
Есть 6 побитовых операторов:
| Оператор | Символ | Пример | Операция |
| Побитовый сдвиг влево | << | x << y | Все биты в x смещаются влево на y бит |
| Побитовый сдвиг вправо | >> | x >> y | Все биты в x смещаются вправо на y бит |
| Побитовое НЕ | ~ | ~x | Все биты в x меняются на противоположные |
| Побитовое И | & | x & y | Каждый бит в x И каждый бит в y |
| Побитовое ИЛИ | | | x | y | Каждый бит в x ИЛИ каждый бит в y |
| Побитовое исключающее ИЛИ (XOR) | ^ | x ^ y | Каждый бит в x XOR каждый бит в y |
В побитовых операциях следует использовать только целочисленные типы данных unsigned, так как C++ не всегда гарантирует корректную работу побитовых операторов с целочисленными типами signed.
Правило: При работе с побитовыми операторами используйте целочисленные типы данных unsigned.
Побитовый сдвиг влево (<<) и побитовый сдвиг вправо (>>)
Примечание: В следующих примерах мы будем работать с 4-битными двоичными значениями.
В C++ количество используемых бит основывается на размере типа данных (в 1 байте находятся 8 бит). Оператор побитового сдвига влево (<<) сдвигает биты влево. Левый операнд является выражением, в котором они сдвигаются, а правый — на сколько мест нужно сдвинуть. Поэтому в выражении 3 << 1 мы имеем в виду «сдвинуть биты влево в литерале 3 на одно место».
Рассмотрим число 3, что в двоичной системе = 0011:
3 = 0011
3 << 1 = 0110 = 6
3 << 2 = 1100 = 12
3 << 3 = 1000 = 8
В последнем третьем случае, один бит перемещается за пределы самого литерала! Биты, сдвинутые за пределы двоичного числа, теряются навсегда.
Оператор побитового сдвига вправо (>>) сдвигает биты вправо. Например:
12 = 1100
12 >> 1 = 0110 = 6
12 >> 2 = 0011 = 3
12 >> 3 = 0001 = 1
В третьем случае мы снова переместили бит за пределы литерала. Он также потерялся навсегда.
Хотя в примерах выше мы смещаем биты в литералах, мы также можем смещать биты и в переменных:
unsigned int x = 4; x = x << 1; // x должен быть 8
unsigned int x = 4; x = x << 1; // x должен быть 8 |
Следует помнить, что результаты операций с побитовыми сдвигами в разных компиляторах могут отличаться.
Что!? Разве операторы << и >> используются не для вывода и ввода данных?
И для этого тоже.
Сейчас польза от использования побитовых операторов не так велика, как это было раньше. Сейчас в большинстве случаев оператор побитового сдвига влево используется для вывода данных. Например, рассмотрим следующую программу:
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; }
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; } |
Результат выполнения программы выше:
8
А как компилятор понимает, когда нужно применить оператор побитового сдвига влево, а когда выводить данные? Всё очень просто. std::cout переопределяет значение оператора << по умолчанию на новое (вывод данных в консоль). Когда компилятор видит, что левым операндом оператора << является std::cout, то он понимает, что должен произойти вывод данных. Если левым операндом является переменная целочисленного типа данных, то компилятор понимает, что должен произойти побитовый сдвиг влево (операция по умолчанию).
Побитовый оператор НЕ
Побитовый оператор НЕ (~), пожалуй, самый простой для объяснения и понимания. Он просто меняет каждый бит на противоположный, например: с 0 на 1 или с 1 на 0. Обратите внимание, результаты побитового НЕ зависят от размера типа данных!
Предположим, что размер типа данных составляет 4 бита:
4 = 0100
~ 4 = 1011 (двоичное) = 11 (десятичное)
Предположим, что размер типа данных составляет 8 бит:
4 = 0000 0100
~ 4 = 1111 1011 (двоичное) = 251 (десятичное)
Побитовые операторы И, ИЛИ и исключающее ИЛИ (XOR)
Побитовые операторы И (&) и ИЛИ (|) работают аналогично логическим операторам И и ИЛИ. Однако, побитовые операторы применяются к каждому биту отдельно! Например, рассмотрим выражение 5 | 6. В двоичной системе это 0101 | 0110. В любой побитовой операции операнды лучше всего размещать следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
А затем применять операцию к каждому столбцу с битами по отдельности. Как вы помните, логическое ИЛИ возвращает true (1), если один из двух или оба операнды истинны (1). Таким макаром работает и побитовое ИЛИ. Выражение 5 | 6 обрабатывается следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
-------
0 1 1 1 // 7
Результат:
0111 (двоичное) = 7 (десятичное)
Также можно обрабатывать и комплексные выражения ИЛИ, например, 1 | 4 | 6. Если хоть один бит в столбце равен 1, то результат целого столбца — 1. Например:
0 0 0 1 // 1
0 1 0 0 // 4
0 1 1 0 // 6
--------
0 1 1 1 // 7
Результатом 1 | 4 | 6 является десятичное 7.
Побитовое И работает аналогично логическому И: возвращается true, только если оба бита в столбце равны 1. Рассмотрим выражение 5 & 6:
0 1 0 1 // 5
0 1 1 0 // 6
--------
0 1 0 0 // 4
Также можно решать и комплексные выражения И, например, 1 & 3 & 7. Только при условии, что все биты в столбце равны 1, результатом столбца будет 1.
0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 0 0 1 // 1
Последний оператор — побитовое исключающее ИЛИ (^) (англ. «XOR» от «eXclusive OR«). При обработке двух операндов, исключающее ИЛИ возвращает true (1), только если один и только один из операндов является истинным (1). Если таких нет или все операнды равны 1, то результатом будет false (0). Рассмотрим выражение 6 ^ 3:
0 1 1 0 // 6
0 0 1 1 // 3
-------
0 1 0 1 // 5
Также можно решать и комплексные выражения XOR, например, 1 ^ 3 ^ 7. Если единиц в столбце чётное количество, то результат — 0. Если нечётное количество, то результат — 1. Например:
0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 1 0 1 // 5
Побитовые операторы присваивания
Как и в случае с арифметическими операторами присваивания, C++ предоставляет побитовые операторы присваивания для облегчения внесения изменений в переменные.
| Оператор | Символ | Пример | Операция |
| Присваивание с побитовым сдвигом влево | <<= | x <<= y | Сдвигаем биты в x влево на y бит |
| Присваивание с побитовым сдвигом вправо | >>= | x >>= y | Сдвигаем биты в x вправо на y бит |
| Присваивание с побитовой операцией ИЛИ | |= | x |= y | Присваивание результата выражения x | y переменной x |
| Присваивание с побитовой операцией И | &= | x &= y | Присваивание результата выражения x & y переменной x |
| Присваивание с побитовой операцией исключающего ИЛИ | ^= | x ^= y | Присваивание результата выражения x ^ y переменной x |
Например, вместо х = х << 1; мы можем написать х <<= 1;.
Заключение
При работе с побитовыми операторами (используя метод столбца) не забывайте о том, что:
При вычислении побитового ИЛИ, если хоть один из битов в столбце равен 1, то результат целого столбца — 1.
При вычислении побитового И, если все биты в столбце равны 1, то результат целого столбца — 1.
При вычислении побитового исключающего ИЛИ (XOR), если единиц в столбце нечётное число, то результат — 1.
Тест
1. Какой результат 0110 >> 2 в двоичной системе?
2. Какой результат 5 | 12 в десятичной системе?
3. Какой результат 5 & 12 в десятичной системе?
4. Какой результат 5 ^ 12 в десятичной системе?
Ответы
Ответ №1
Результатом 0110 >> 2 является двоичное 0001.
Ответ №2
Выражение 5 | 12:
0 1 0 1
1 1 0 0
--------
1 1 0 1 // 13 (десятичное)
Ответ №3
Выражение 5 & 12:
0 1 0 1
1 1 0 0
--------
0 1 0 0 // 4 (десятичное)
Ответ №4
Выражение 5 ^ 12:
0 1 0 1
1 1 0 0
--------
1 0 0 1 // 9 (десятичное)
Оценить статью:
 Загрузка…
Загрузка…Поделиться в социальных сетях:
Схема ИСКЛЮЧАЮЩЕЕ ИЛИ | Техника и Программы
Для вентилей И, И-НЕ и др. удобно использовать символы, поскольку они позволяют более наглядно представлять входные и выходные логические сигналы и рабочие характеристики таких вентилей. Поэтому, хотя и известны различные способы реализации схемы ИЛИ (на диодах, резисторах и диодах, на транзисторах), для их обозначения используется один символ.
Иногда используемую комбинацию логических схем можно представить одним символом, определяющим все свойства комбинированной сложной схемы, что делает ненужным изображение четырех, пяти или даже большего числа символических обозначений отдельных схем, применяемых для реализации некоторой операции. Примером может служить полусумматор, схема которого показана на рис. 8.8. По существу полусумматор состоит из схемы ИЛИ и двух схем И, одна из которых имеет инвертированный вход. Последняя схема является схемой ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (ЗАПРЕТ). Эти три логические схемы связаны между собой, как показано на рис. 8.8, а, хотя для индикации комбинации схем И и ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ, но без выхода для цифры переноса часто используют один символ, изображенный на рис. 8.8, б. Этот символ соответствует схеме ИСКЛЮЧАЮЩЕЕ ИЛИ [Эта логическая схема известна под названием схемы неравнозначности или двухвходовой суммы суммирования по модулю 2. — Прим. ред.]. Если после схемы, показанной на рис. 8.8,6, следует инвертор (рис. 8.8, в), то получаем схему ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (схема эквивалентности или равнозначности), символ которой изображен на рис.8.8,г.
Полные сумматоры (последовательного типа) могут быть получены путем использования двух полусумматоров, показанных на рис. 8.8, а. Полусумматоры применяются также для целей переключений и для преобразования кодов.
Рис. 8.8. Полусумматор (а) и условные обозначения схем ИСКЛЮЧАЮЩЕЕ ИЛИ (б), НЕ (в) и ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (г).
Если на .входы схемы ИЛИ поступают два импульса, то они одновременно появятся и на схеме И. Тогда на выходе этой схемы И возникает импульс, который поступает на вход схемы ЗАПРЕТ и закрывает эту схему, препятствуя вводу сигналов от схемы ИЛИ. Следовательно, логика работы данной схемы такова: когда на обоих входах схемы ИЛИ действуют 1, то на выходе «Сумма» появляется 0, а на выходе «Перенос» — 1.
Таблица 8.5
А | в | Сумма | Перенос |
0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 |
При подаче импульса только на один какой-нибудь вход схемы ИЛИ импульс запрета не формируется. В этом случае импульс, соответствующий 1, образуется только на выходе «Сумма». Выполняемая логическая операция соответствует правилу двоичного сложения 1 + 1 = 10 (двоичное число два). Поэтому, если на входах А и В действуют единичные сигналы, то выходной сигнал на выходе «Сумма» соответствует 0 (импульс отсутствует), но возникает импульс переноса на выходе «Перенос» представляемый 1 старшего разряда в двоичном числе 10.
Рис. 8.9. Преобразователь кода Грея в двоичный код.
На основе описания данной логической схемы может быть составлена таблица истинности (табл. 8.5), иллюстрирующая операции, выполняемые схемой (полусумматором).
Комбинацию схем ИСКЛЮЧАЮЩЕЕ ИЛИ можно использовать для преобразования кода Грея в двоичный код (рис. 8.9). Код Грея называют также циклическим кодом или кодом с минимальными ошибками. Код Грея широко применяется в вычислительных и управляющих системах, поскольку при этом уменьшаются случайные ошибки в дроцессе работы. Это объясняется тем, что по мере возрастания чисел в коде Грея в некоторый момент времени изменяется только одна цифра. В двоичном коде это не так (табл. 8.6).
В преобразователе, показанном на рис. 8.9, количество логических схем ИСКЛЮЧАЮЩЕЕ ИЛИ равно количеству разрядов преобразуемых чисел. Предположим, что слева в схему вводится число в коде Грея 1010 (01010). [Заметим, что на выходах схем сигнала переноса не образуется (1 + 1=0).] Нуль, цо-ступающий на верхний вход схемы А, передается и на выход, поскольку вход непосредственно соединен с выходом. При подаче 1 на нижний вход схемы А на выходе этой схемы также формируется 1. Но выход этой схемы связан с входом схемы В. Поскольку на нижний вход схемы В сигнал не поступает (подается сигнал, соответствующий нулю), на выходе формируется 1. Эта 1 подается на верхний вход схемы С и так как на нижний вход этой схемы также поступает 1, то на ее выходе получаем 0. Аналогично этому, поскольку на входы схемы D сигналы не поступают (подаются нули) , то на выходе также получается 0. Таким образом, число 1010 в коде Грея преобразуется в двоичное число 1100 (табл. 8.6).
Таблица 8.6
Десятичное число | Двоичный код | Код Грея |
0 | 0000 | 0000 |
1 | 0001 | 0001 |
2 | 0010 | 0011 |
3 | 0011 | 0010 |
4 | 0100 | 0110 |
5 | 0101 | 0111 |
6 | 0110 | 0101 |
7 | 0111 | 0100 |
8 | 1000 | 1100 |
9 | 1001 | 1101 |
10 | 1010 | 1111 |
11 | 1011 | 1110 |
12 | 1100 | 1010 |
Рис. 8.10. Схема считывания двоичного числа в прямом и обратном кодах.