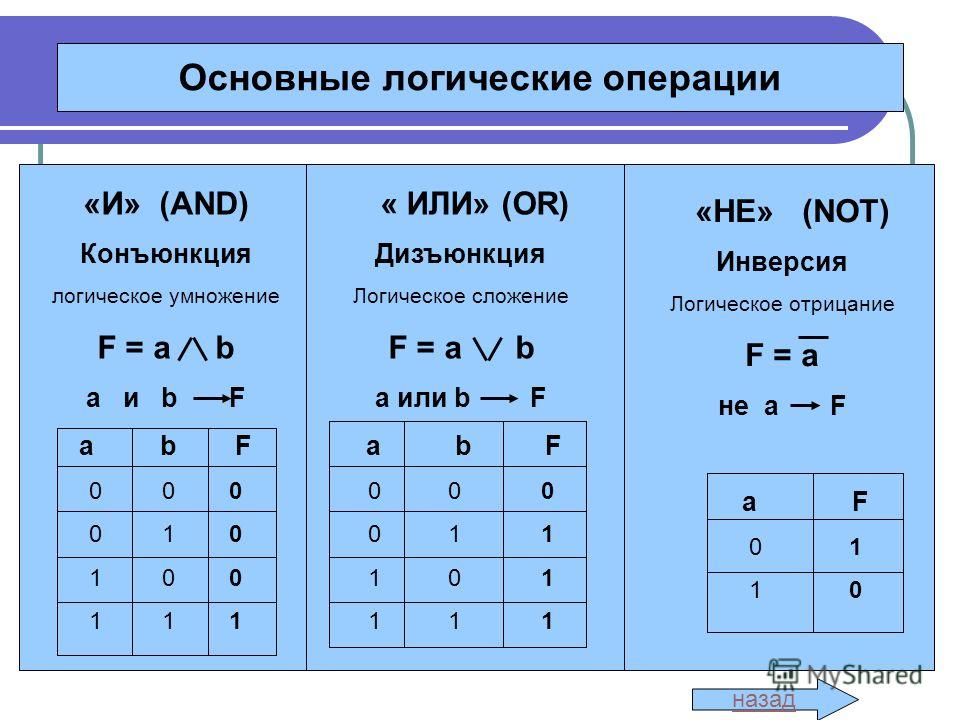
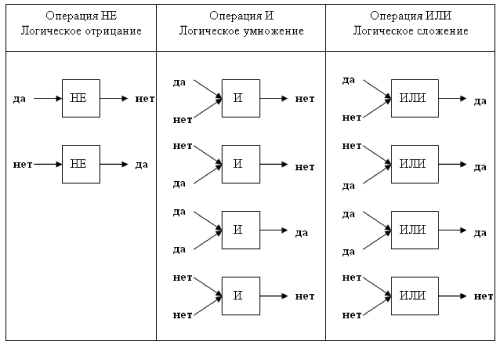
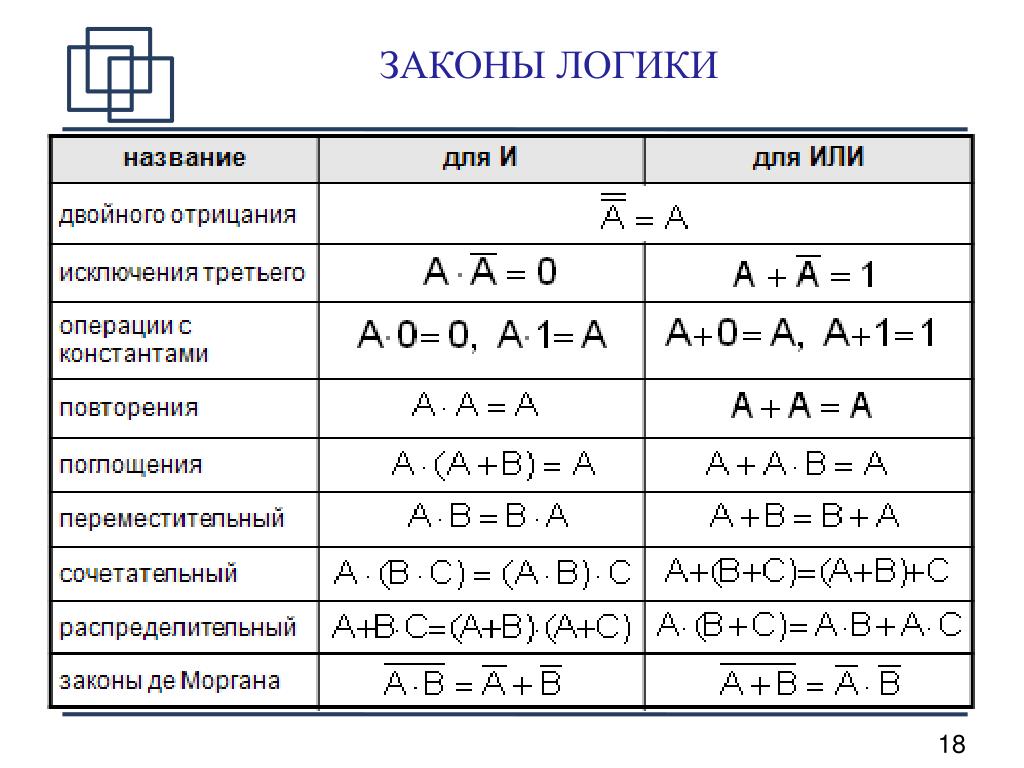
Логические выражения и логические операции
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель). Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить,истинно оно или ложно. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Примеры высказываний:
Высказывания 1 и 3 являются истинными. Следующие предложения высказываниями не являются:
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают. С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примеры высказываний:
Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в пермом предложении — погоды, во втором — окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь». В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно — 0. Простые высказывания назвали логическими переменными, а сложные — логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С. Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита. Существуют разные варианты обозначения истинности и ложности логических переменных:
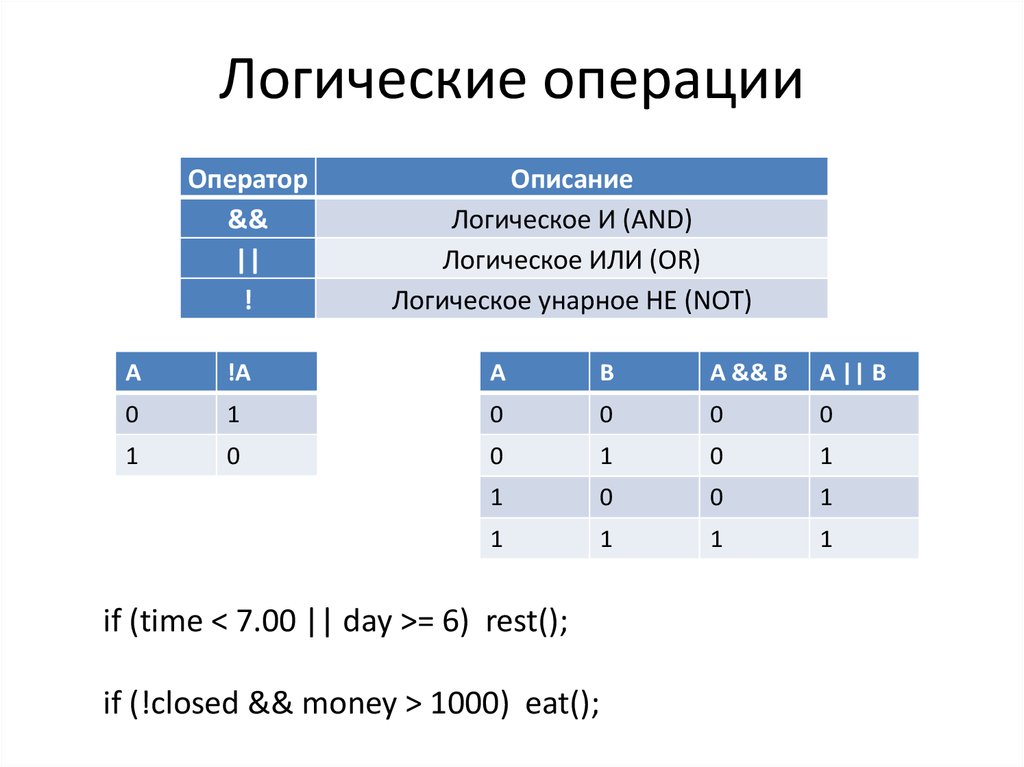
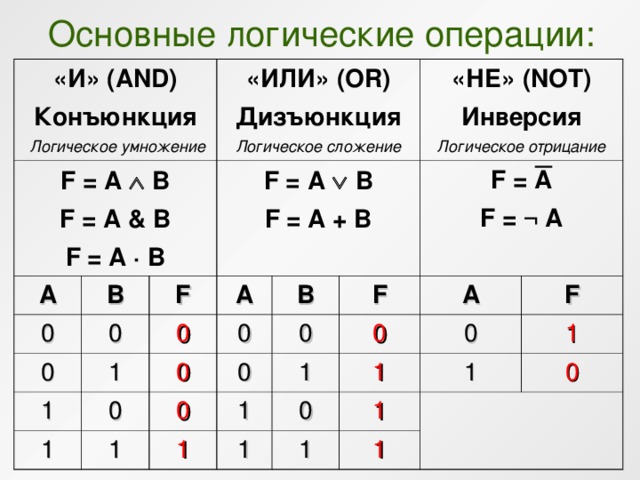
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанныхлогическими операциями. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением). Логическое выражение — это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение. Введем перечисленные логические операции. Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь):
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Итак, если два высказывания соединены союзом «И», то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
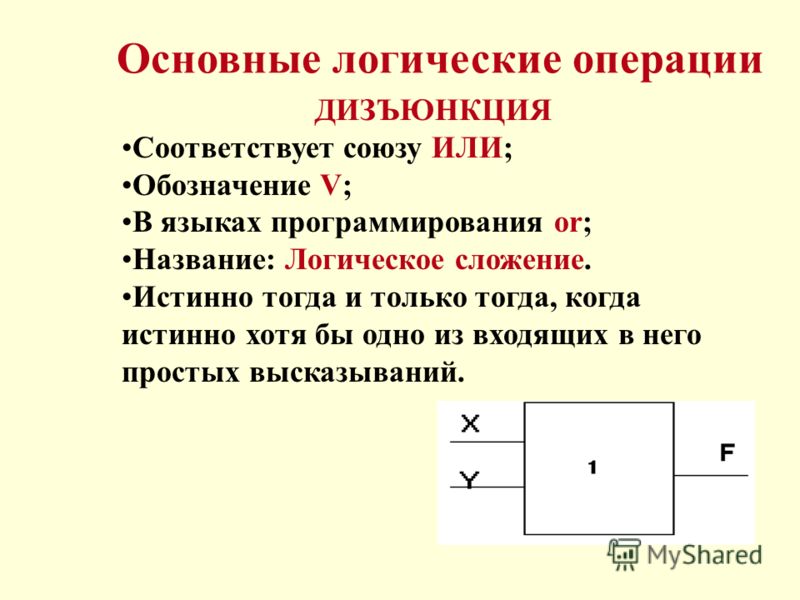
Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение, различие):
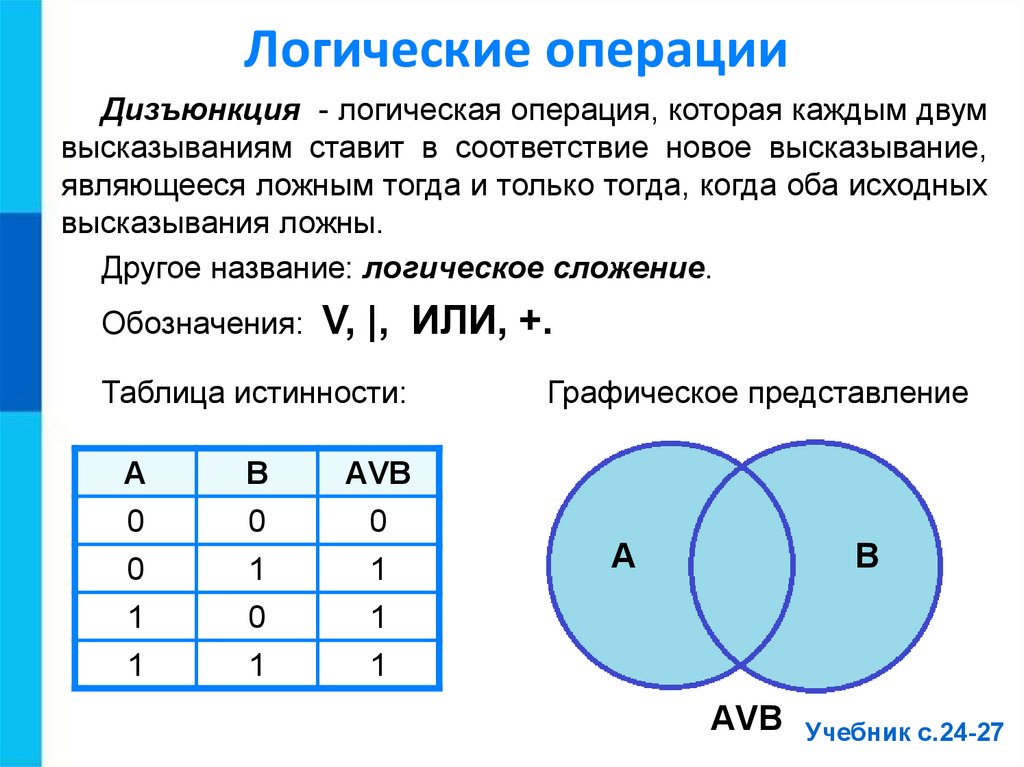
Дизъюнкция — это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Итак, если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний. Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание. Инверсия — отрицание (от латинского disjunctio — разобщение, различие):
Отрицание — логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.
Итак, если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация): Высказывание, составленное из двух высказываний при помощи связки «если .
A => B «Из А следует В» Итак, новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) — истинно, а следствие (заключение В) — ложно и истинно во всех остальных случаях. Пример. Дано сложное высказывание: «Если выглянет солнце, то станет тепло». Требуется записать его в виде логической формулы. Обозначим через А простое высказывание «выглянет солнце», а через В — «станет тепло». Тогда логической формулой этого сложного высказывания будет импликация: A -> B.
Эквивалентность (логическое тождество): Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называетсяэквивалентностью (эквивалентность — логическое тождество, равнозначность, взаимная обусловленность. )
A <=> B «А равносильно В» Итак, новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Примеры записи сложных высказываний с помощью обозначения логических связок:
|
Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества. 
.., то …», называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю). 
» (В. Шекспир) А V ¬ A <=> ВPage not found — Сайт skobelevserg!
- Главная
- Информатика
- Практикумы
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- Главная
- Информатика
- 5 класс (ФГОС)
- Информация вокруг нас
- Компьютер — универсальная машина для работы с информацией
- Ввод информации в память компьютера
- Управление компьютером
- Хранение информации
- Передача информации
- Кодирование информации
- Текстовая информация
- Представление информации в виде таблиц
- Наглядные формы представления информации
- Компьютерная графика
- Обработка информации
- 6 класс (ФГОС)
- Объекты окружающего мира
- Компьютерные объекты
- Отношения объектов и их множеств
- Разновидности объектов и их классификация
- Системы объектов
- Персональный компьютер как система
- Как мы познаем окружающий мир
- Понятие как форма мышления
- Информационное моделирование
- Знаковые информационные модели
- Табличные информационные объекты
- Графики и диаграммы
- Схемы
- Что такое алгоритм
- Исполнители вокруг нас
- Формы записи алгоритмов
- Типы алгоритмов
- Управление исполнителем Чертежник
- Компьютерный практикум
- 7 класс (ФГОС)
- Информация и информационные процессы
- Компьютер универсальное устройство для работы с информацией
- Обработка графической информации
- Обработка текстовой информации
- Технология мультимедиа
- 8 класс (ФГОС)
- Математические основы информатики
- Основы алгоритмизации
- Начала программирования
- 9 класс (ФГОС)
- Моделирование и формализация
- Алгоритмизация и программирование
- Обработка числовой информации в электронных таблицах
- Коммуникационные технологии
- 10 класс (ФГОС)
- Информация и информационные процессы
- Компьютер и его программное обеспечение
- Представление информации в компьютере
- Элементы теории множеств и алгебры логики
- Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- Обработка информации в электронных таблицах
- Алгоритмы и элементы программирования
- Информационное моделирование
- Сетевые информационные технологии
- Основы социальной информатики
- Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
- Блоги
- Сайты
Quick-R: Операторы
Двоичные и логические операторы R покажутся программистам очень знакомыми.
Обратите внимание, что бинарные операторы работают с векторами и матрицами так же, как со скалярами.
Арифметические операторы
| Оператор | Описание | |
| + | дополнение | |
| — | вычитание 9или ** | возведение в степень |
| х %% г | Модуль(x mod y) 5%%2 равен 1 | |
| х %/% г | целочисленное деление 5%/%2 равно 2 |
Логические операторы
| Оператор | Описание |
| < | меньше |
| <= | меньше или равно |
| > | больше |
| больше или равно | |
| == | точно равно |
| != | не равно |
| !x | Не х |
| х | у | х ИЛИ у |
| х и у | х И у |
| ИСТИНА(х) | проверка, если X истинно |
# Пример
x <- c(1:10)
x[(x>8) | (x<5)]
# дает 1 2 3 4 9 10
# Как это работает
x <- c(1:10)
x
1 2 3 4 5 6 7 8 9 10
x > 8
F F F F F F F F T T
x < 5
T T T T F F F F F F
x > 8 | x < 5
T T T T F F F F T T
x[c(T,T,T,T,F,F,F,F,T,T)]
1 2 3 4 9 10
Идти дальше
Чтобы попрактиковаться в работе с логическими операторами в R, попробуйте бесплатную первую главу об условиях этого интерактивного курса.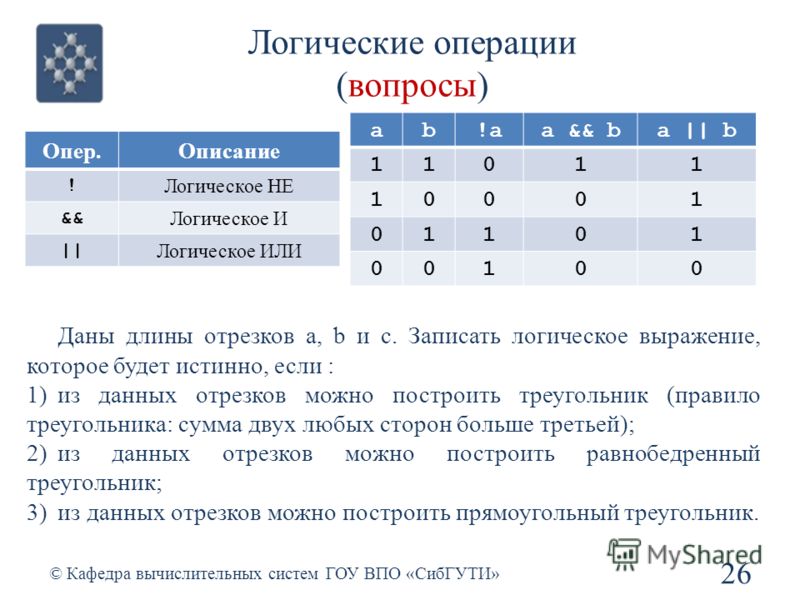
Реляционные и логические операторы C++ (с примерами)
В этом руководстве мы изучим реляционные и логические операторы с помощью примеров.
В C++ реляционные и логические операторы сравнивают два или более операнда и возвращают значения true или false .
Мы используем эти операторы при принятии решений.
Операторы отношения C++
Оператор отношения используется для проверки отношения между двумя операндами. Например,
// проверяет, больше ли a, чем b а > б;
Здесь > — оператор отношения. Он проверяет, больше ли
Если отношение верно , оно возвращает 1 , а если отношение ложно , оно возвращает 0 .
В следующей таблице приведены реляционные операторы, используемые в C++.
| Оператор | Значение | Пример |
|---|---|---|
== | равно | 3 == 5 дает нам ложь |
!= | Не равно | 3 != 5 дает нам истинное |
> | Больше | 3 > 5 дает нам ложь |
< | Менее | 3 < 5 дает нам истинное |
>= | Больше или равно | 3 >= 5 дайте нам ложь |
<= | Меньше или равно | 3 <= 5 дает нам истинное |
== Оператор
Равно == оператор возвращает
-
true- если оба операнда равны или одинаковы -
ложь- если операнды не равны
Например,
int x = 10; интервал у = 15; интервал г = 10; х == у // ложь x == z // true
Примечание: Оператор отношения == не совпадает с оператором присваивания = .
Оператор присваивания = присваивает значение переменной, константе, массиву или вектору. Он не сравнивает два операнда.
!= Оператор
Оператор не равно != возвращает
-
true- если оба операнда не равны -
false- если оба операнда равны.
Например,
int x = 10; интервал у = 15; интервал г = 10; х != у // правда x != z // false
> Оператор
Оператор больше > возвращает
-
true- если левый операнд больше правого -
false- если левый операнд меньше правого
Например,
int x = 10; интервал у = 15; х > у // ложь y > x // true
< Operator
Оператор меньше чем < возвращает
-
true- если левый операнд меньше правого -
false- если левый операнд больше правого
Например,
int x = 10; интервал у = 15; х < у // правда у < х // ложь
>= Оператор
Оператор больше или равен >= возвращает
-
-
false- если левый операнд меньше правого
Например,
int x = 10; интервал у = 15; интервал г = 10; х >= у // ложь у >= х // правда z >= x // true
<= Оператор
Меньше или равно оператору <= возвращает
-
true- если левый операнд меньше или равен правому -
false- если левый операнд больше правого
Например,
int x = 10; интервал у = 15; х > у // ложь y > x // true
Чтобы узнать, как можно использовать реляционные операторы со строками, обратитесь к нашему руководству здесь.
Логические операторы C++
Мы используем логические операторы, чтобы проверить, является ли выражение истина или ложь . Если выражение true , оно возвращает 1 , тогда как если выражение false , оно возвращает 0 .
| Оператор | Пример | Значение |
|---|---|---|
&& | выражение1 && выражение 2 | Логическое И. истинно, только если все операнды истинны. |
|| | выражение1 || выражение 2 | Логическое ИЛИ. истина, если хотя бы один из операндов истинен. |
! | ! выражение | Логическое НЕ. истина, только если операнд ложен. |
Логический оператор И C++
Логический оператор И && возвращает
-
true- тогда и только тогда, когда все операндыtrue.
-
ложь- если один или несколько операндов являютсяложью.
Таблица истинности оператора &&
Пусть a и b будут двумя операндами. 0 представляет false , а 1 представляет true . Затем
| и | б | а && б |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Как видно из приведенной выше таблицы истинности, оператор && возвращает значение true только в том случае, если a и b верны.
Примечание. Логический оператор И && не следует путать с побитовым оператором И и .
Пример 1: оператор C++ OR
// Программа C++, демонстрирующая таблицу истинности оператора &&
#include <иопоток>
использование пространства имен std;
интервал основной () {
инт а = 5;
интервал б = 9;
// ложь && ложь = ложь
cout << ((a == 0) && (a > b)) << endl;
// ложь && правда = ложь
cout << ((a == 0) && (a < b)) << endl;
// правда && ложь = ложь
cout << ((a == 5) && (a > b)) << endl;
// истина && истина = истина
cout << ((a == 5) && (a < b)) << endl;
вернуть 0;
} Выход
0 0 0 1
В этой программе мы объявляем и инициализируем две переменные int a и b со значениями 5 и 9 соответственно.
Затем мы печатаем логическое выражение
((a == 0) && (a > b))
Здесь a == 0 оценивается как false , поскольку значение a равно 5 . а>б тоже false , так как значение a меньше, чем значение b . Затем мы используем оператор AND && , чтобы объединить эти два выражения.
Из таблицы истинности оператора && мы знаем, что false && false (т.е. 0 && 0 ) приводит к оценке false ( 0 ). Это результат, который мы получаем на выходе.
Аналогичным образом мы оцениваем три других выражения, которые полностью демонстрируют таблицу истинности && оператор.
C++ Логический оператор ИЛИ
Логический оператор ИЛИ || возвращает
-
true- если один или несколько операндовtrue. -
ложь- тогда и только тогда, когда все операндыложь.
Таблица истинности || Оператор
Пусть a и b будут двумя операндами. Затем
| и | б | а || б |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Как видно из приведенной выше таблицы истинности, || оператор возвращает false, только если оба a и b являются ложными.
Пример 2: оператор C++ OR
// Программа C++, демонстрирующая || таблица истинности оператора
#include <иопоток>
использование пространства имен std;
интервал основной () {
инт а = 5;
интервал б = 9;
// ложь && ложь = ложь
cout << ((a == 0) || (a > b)) << endl;
// ложь && истина = истина
cout << ((a == 0) || (a < b)) << endl;
// истина && ложь = истина
cout << ((a == 5) || (a > b)) << endl;
// истина && истина = истина
cout << ((a == 5) || (a < b)) << endl;
вернуть 0;
} Выход
0 1 1 1
В этой программе мы объявляем и инициализируем две переменные int a и b со значениями 5 и 9 соответственно.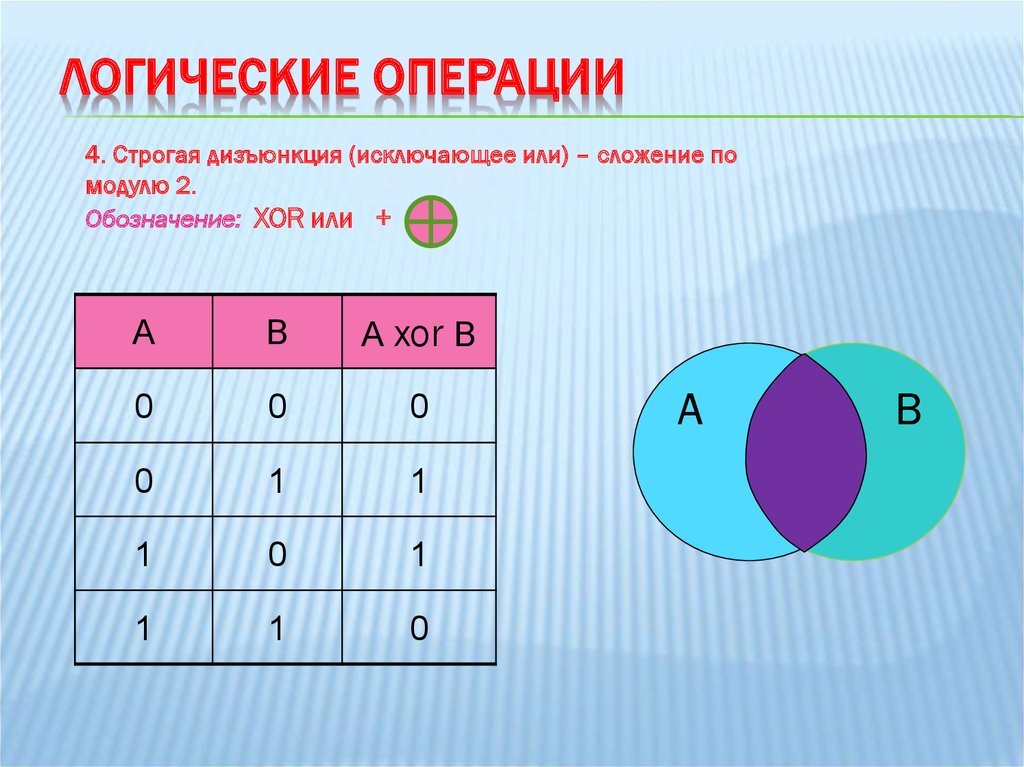
Затем мы печатаем логическое выражение
((a == 0) || (a > b))
Здесь a == 0 оценивается как false , поскольку значение a равно 5 . a > b также ложь , так как значение a меньше, чем значение b . Затем мы используем оператор ИЛИ || , чтобы объединить эти два выражения.
Из таблицы истинности || , мы знаем, что false || false (т.е. 0 || 0 ) приводит к оценке false ( 0 ). Это результат, который мы получаем на выходе.
Аналогичным образом мы оцениваем три других выражения, которые полностью демонстрируют таблицу истинности || оператор.
C++ Логический оператор NOT !
Логический оператор НЕ ! — унарный оператор, т. е. он принимает только один операнд.
Возвращает true , если операнд false , и false , если операнд true .
