§7.2. Электрическое поле. Напряженность.
1. Взаимодействие частиц на расстоянии
в физике описывают с помощью особого
вида материи – силового поля. Примером
является гравитационное поле: оно
создается частицей, имеющей массу, и
действует на другую частицу, помещенную
в гравитационное поле и обладающую
массой. Аналогичным образом можно
рассматривать взаимодействие частиц,
обладающих зарядами. Заряд изменяет
свойства окружающего его пространства,
создавая в нем электрическое поле.
Обнаруживает себя это поле силой,
действующей на другой заряд. Рассмотрим
закон Кулона (формула 7.1.1). Будем считать,
что первый заряд создает поле, и это
поле действует на второй заряд, причем,
зависит только от источника поля, и от
положения точки поля относительно
источника, т.е. является силовой
характеристикой поля. Можно сказать,
что поле первого заряда бдительно
следит за появлением «чужака», и, как
только он где-либо в поле появится, тут
же действует на него соответствующей
силой.
(7.2.1)
Поле, созданное неподвижными зарядами, называется электростатическим. Напряженность поля точечного заряда q в точке, заданной вектором , проведенным из заряда
(7.2.2)
Вектор
напряженности электростатического
поля точечного заряда направлен вдоль
прямой, соединяющей точку, где находится
заряд, с данной точкой поля. Он выходит
из точки поля и направлен от заряда,
если он положительный, и к заряду, если
он отрицательный. Величина напряженности
Он выходит
из точки поля и направлен от заряда,
если он положительный, и к заряду, если
он отрицательный. Величина напряженности
E=(7.2.3)
Пусть имеется система точечных зарядов qi (i
(7.2.4)
Полученный результат называется принципом суперпозиции (независимого сложения) электрического поля: если имеется несколько источников, то каждый из них создает свое поле независимо от всех прочих, и эти поля, складываясь, дают результирующее поле1. Формула принципа суперпозиции такова:
(7. 2.5)
2.5)
2. Поле известно, если известен вектор напряженности в каждой точке. Электрическое поле можно изображать графически векторами напряженности. Этот способ удобен для изображения поля в отдельных точках. Если поле надо нарисовать в некоторой области пространства, то используют линии напряженности (их называют еще силовыми линиями). Касательная к силовой линии указывает направление в данной точке поля, густота (плотность) силовых линий вблизи этой точки равна величине напряженности.
На рис. 34 показаны силовые линии поля положительного и отрицательного точечных зарядов, поля диполя, а также области некоторого электростатического поля — образующие его заряды находятся вне рассматриваемой области.
Рис. 34
34
Диполь – два точечных разноименных зарядов одинаковой величины. На рис. 34 в одной из точек поля диполя показано построение вектора напряженности с помощью принципа суперпозиции. Силовые линии – воображаемые, но их можно сделать видимыми (вспомните лекционные демонстрации).
10. Вопросы к зачету по теме «Электростатика»
Вопросы для подготовки к зачету по теме «Электростатика.»
21. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона.
22. Напряжённость электрического поля. Принцип суперпозиции электрических полей. Графическое изображение электрических полей. Свойства линий напряженности электрического поля.
23. Работа сил электрического поля по переносу заряда. Потенциал, разность потенциалов. Напряжение.
24. Конденсаторы. Электроемкость плоского конденсатора. Энергия заряженного конденсатора.
Ответы.
Часть 1. Основные физические величины, единицы их измерения, формулы для нахождения.
|
Наименование |
Обозначения |
Единицы измерения в СИ |
Формулы |
|
Электрический заряд |
q |
Кл (кулон) |
— |
|
Закон сохранения электрического заряда |
— |
— |
q1 + q2 + q3 + … +qn = const |
|
Закон Кулона |
— |
— |
|
|
Напряженность |
E |
Н/Кл (ньютон на кулон) В/м (вольт на метр |
|
|
Принцип суперпозиции электрических полей |
— | — | |
|
Работа сил электрического поля по переносу заряда. |
A | Дж (джоуль) | A |
|
Потенциал |
φ |
В (вольт) | |
|
Разность потенциалов |
φ1-φ2 | В (вольт) | φ1-φ2 = U |
|
Напряжение |
U | В |
U = А/q |
| Электроемкость | С | Ф (фарад) |
|
|
Электроемкость плоского конденсатора |
С | Ф (фарад) | |
|
Энергия заряженного конденсатора |
W | Дж (джоуль) |
Часть 2.
1. Электрический заряд (определение, обозначение, ед. измерения).
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Он определяет интенсивность электромагнитных взаимодействий.
Электрический заряд обычно обозначается буквами q или Q.
Единица измерения электрического заряда — Кл (кулон)
2. Закон сохранения электрического заряда (определение, формула).
Закон сохранения электрического заряда:
q1 + q2 + q3 + … +qn = const
3. Закон Кулона (определение, формула).
Закон Кулона (определение, формула).
Закон Кулона: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
, где k — коэффициент пропорциональности, равный
Тогда получаем:
4. Электрическое поле (определение).
Электрическое поле – это особая форма материи, которая существует независимо от нас и от наших знаний о нем, порождается электрическими зарядами и определяется по действию на электрические заряды.
Главное свойство электрического поля — действие на электрические заряды с некоторой силой.
5. Напряженность электрического поля (определение, обозначение, формула, ед. измерения).
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда.
или
Напряженность электрического поля – это векторная величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы.
Напряженность обозначается буквой Е.
Единица напряженности электростатического поля в СИ — Н/Кл (ньютон на кулон)
1 Н/Кл = 1 В/м
6. Принцип суперпозиции электрических полей.
Если электрическое поле создается несколькими заряженными телами, то выполняетсяпринцип суперпозиции (наложения) полей точечных зарядов: напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами по отдельности:
7. Графическое изображение электрических полей.
Для наглядного представления электрического поля используют силовые линии.
Силовой линией или линией напряженности называется такая линия, в каждой точке которой вектор напряженности поля направлен по касательной к ней.
При изображении электрического поля с помощью силовых линий, их густота пропорциональна модулю вектора напряженности поля.
8. Свойства линий напряженности электрического поля.
Линии напряженности электрического поля:
1) никогда не пересекаются;
2) не могут быть замкнуты сами на себя;
3) имеют начало на положительном заряде (или в бесконечности) и заканчиваются на отрицательном заряде (или в бесконечности).
9. Работа сил электрического поля по переносу заряда.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2)
10. Потенциал.
Потенциал.
Потенциалом φ электрического поля — называют физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.
Потенциал обозначается буквой φ.
Единица измерения потенциала — В (вольт)
11. Разность потенциалов (напряжение) (определение, обозначение, формула, ед. измерения).
Разность потенциалов φ1 – φ2 или напряжение между двумя точками поля численно равно работе сил поля по перемещению единичного заряда q между этими точками.
φ1 – φ2 = U = А / q
Разность потенциалов обозначается φ1 – φ2 , а напряжение обозначается U.
Единица измерения разности потенциалов (напряжения) — В (вольт)
12. Конденсатор (определение). Энергия заряженного конденсатора (формула)..
Конденсатор (определение). Энергия заряженного конденсатора (формула)..
Система проводников, электроемкость которой не зависит от внешних условий и от расположения окружающих тел, получила название конденсатора, а проводники, составляющие конденсатор, называются обкладками.
Простейший конденсатор – плоский конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
13. Электрическая емкость (определение, обозначение, формула, ед. измерения).
Электрическая емкость (электроемкость) — это физическая величина, характеризующая способность проводника или системы проводников накапливать электрический заряд.
Электроемкость обозначается C
Единица измерения электроемкости — Ф (фарад)
14. Энергия заряженного конденсатора.
Энергия заряженного конденсатора.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением q = CU.
Электрическую энергию We следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе.
Расширения для Joomla
- Подробности
- Просмотров: 15196
4.5: Нормальные, растягивающие и другие примеры сил
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1501
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять нормальную силу и силу растяжения.

- Применять законы движения Ньютона для решения задач, связанных с различными силами.
- Используйте тригонометрические тождества для разложения веса на компоненты.
Нормальная сила
Вес (также называемая силой тяжести) представляет собой всепроникающую силу, действующую постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы определенно заметили, что должны поддерживать вес тяжелого предмета, отталкиваясь от него, когда держите его неподвижно, как показано на рисунке (а). Но как неодушевленные предметы, такие как стол, выдерживают вес помещенного на них груза, как показано на рисунке (b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже твердые предметы деформируются при приложении к ним силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину).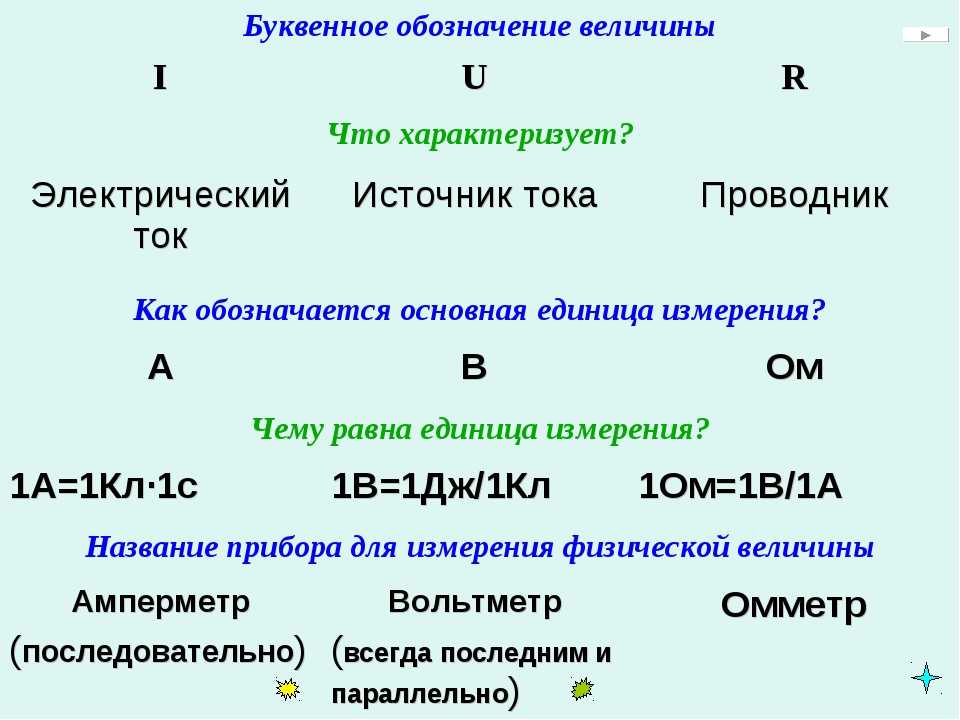 Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока возвращающая сила не станет такой же, как вес груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро, причем провис небольшой, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока возвращающая сила не станет такой же, как вес груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро, причем провис небольшой, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая груз, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь обозначен символ \(N\). (Это не единица силы Н.) Слово нормальное означает перпендикулярно поверхности. Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.
Если сила, поддерживающая груз, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь обозначен символ \(N\). (Это не единица силы Н.) Слово нормальное означает перпендикулярно поверхности. Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.
РАСПРОСТРАНЕННОЕ ЗАБЛУЖДЕНИЕ: НОРМАЛЬНАЯ СИЛА (Н) ПРОТИВ. НЬЮТОН (Н)
В этом разделе мы ввели величину нормальной силы, которая представлена переменной \(Н\). Не следует путать ее с символом ньютона, который также обозначается буквой Н. Эти символы особенно важно различать, потому что единицами нормальной силы \(N\) являются ньютоны (N). Например, нормальная сила \(N\), с которой пол действует на стул, может быть \(N = 100 \, N\). Одно важное отличие состоит в том, что нормальная сила является вектором, а ньютон — просто единицей. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях! По мере изучения физики вы обнаружите больше сходства между переменными и единицами. Другим примером этого является количество работы \(Вт\) и единица измерения ватт (Вт).
Другим примером этого является количество работы \(Вт\) и единица измерения ватт (Вт).
Пример \(\PageIndex{1}\): вес на склоне, двумерная задача
Рассмотрим лыжника на склоне, показанном на рисунке. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если известно, что трение равно 45,0 Н?
Рисунок \(\PageIndex{2}\): Поскольку движение и трение параллельны склону, удобнее всего спроецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). \(N\) перпендикулярен наклону, а \(f\) параллелен наклону, но \(w\) имеет компоненты вдоль обеих осей, а именно \(w_{\perp} \) и \(w_{\ параллельно} \) \(N\) равно по модулю \(w_{\perp} \), так что движение перпендикулярно склону отсутствует, но \(f\) меньше, чем \(w_{\parallel }\), так что есть нисходящее ускорение (вдоль параллельной оси).Стратегия
Это двумерная задача, поскольку силы, действующие на лыжника (исследуемая система), не параллельны.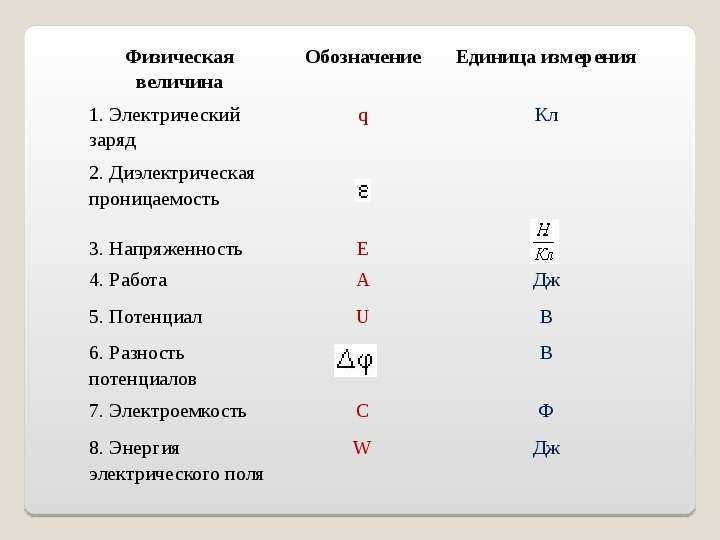 Подход, который мы использовали в двумерной кинематике, также очень хорошо работает здесь. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав две связанные одномерные задачи для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы \(\perp\) и \(\parallel\) для обозначения перпендикулярности и параллельности соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные \(w,\) \(f\) и \(N\) на рисунке. \(N\) всегда перпендикулярен склону, а \(f\) параллелен ему. Но \(w\) не направлена ни к одной из осей, и поэтому первый шаг, который мы делаем, состоит в том, чтобы спроецировать его на компоненты вдоль выбранных осей, определяя \(w_{\parallel}\) как компонент веса, параллельный наклону и \( w_{\perp} \) составляющая веса, перпендикулярная наклону.
Подход, который мы использовали в двумерной кинематике, также очень хорошо работает здесь. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав две связанные одномерные задачи для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы \(\perp\) и \(\parallel\) для обозначения перпендикулярности и параллельности соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные \(w,\) \(f\) и \(N\) на рисунке. \(N\) всегда перпендикулярен склону, а \(f\) параллелен ему. Но \(w\) не направлена ни к одной из осей, и поэтому первый шаг, который мы делаем, состоит в том, чтобы спроецировать его на компоненты вдоль выбранных осей, определяя \(w_{\parallel}\) как компонент веса, параллельный наклону и \( w_{\perp} \) составляющая веса, перпендикулярная наклону. o) -f}{м}. \] 92, \]
o) -f}{м}. \] 92, \]
, которое представляет собой ускорение, параллельное наклону, когда существует встречное трение 45,0 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. На самом деле общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно \(a = g\space sin\space \theta, \) независимо от массы. Это связано с ранее обсуждавшимся фактом, что все тела падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
РАЗЛОЖЕНИЕ ВЕСА НА КОМПОНЕНТЫ
Рисунок \(\PageIndex{3}\): Объект покоится на наклонной поверхности, составляющей угол θ с горизонтом. Когда объект покоится на наклонной плоскости, составляющей угол \(\theta \) с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, \(w_{\perp } \) и сила, действующая параллельно плоскости, \(w_{\parallel}.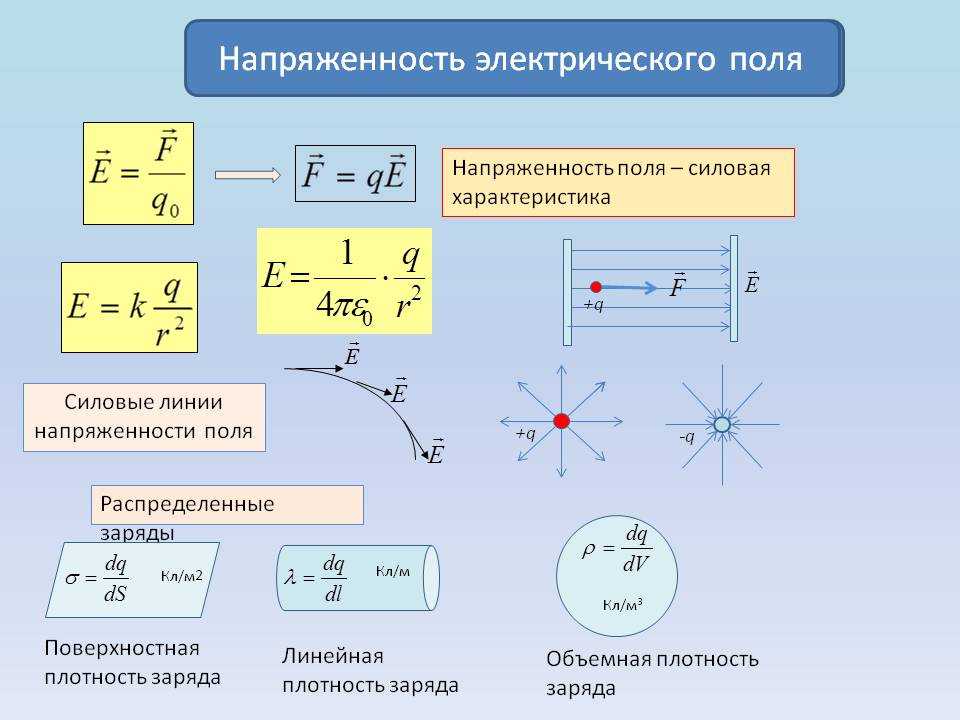 \) Перпендикулярная сила веса, \(w_{\perp}\) обычно равна по величине и противоположна по направлению нормальной силе , \(N\). Сила, действующая параллельно плоскости, \(w_{\parallel}\) заставляет объект ускоряться вниз по склону. Сила трения \(f\) противодействует движению тела, поэтому она действует вверх по плоскости.
\) Перпендикулярная сила веса, \(w_{\perp}\) обычно равна по величине и противоположна по направлению нормальной силе , \(N\). Сила, действующая параллельно плоскости, \(w_{\parallel}\) заставляет объект ускоряться вниз по склону. Сила трения \(f\) противодействует движению тела, поэтому она действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона находится под углом \(\theta\) к горизонтали, то величины компонентов веса равны
\[w_{\parallel} = w\space sin\space (\theta) = mg \, sin \, (\theta) \] и
\[ w_{\perp} = w\space sin\space (\theta) = mg \, sin \, (\theta) \]
Вместо запоминания эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона \(\theta\) равен углу, образованному между \(w\) и \(w_{\perp} \). Зная это свойство, можно с помощью тригонометрии определить величину составляющих веса:
\[ cos\space (\theta) = \dfrac{w_{\perp}}{w}\]
\[ w_{\perp} = w\space cos \, (\theta) = mg \, cos \, (\theta) \]
\[sin \, (\theta) = \dfrac{w_{\parallel}}{w} \]
\[w_{\parallel} = w\space sin \ , (\theta) = mg \, sin \, (\theta) \]
ЗАБИРАЙТЕ НА ДОМУ ЭКСПЕРИМЕНТ: ПАРАЛЛЕЛЬНАЯ СИЛА
Чтобы исследовать, как изменяется сила, параллельная наклонной плоскости, найдите резиновую ленту, несколько предметов, чтобы повесить с конца резинки, а доску можно расположить под разными углами. На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?
На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?
Натяжение
Натяжение — это сила по длине среды, особенно сила, переносимая гибкой средой, такой как веревка или кабель. Слово «натяжение » происходит от латинского слова, означающего «растягивать». Не случайно гибкие шнуры, передающие мышечные силы к другим частям тела, называются сухожилиями . Любой гибкий соединитель, такой как струна, веревка, цепь, проволока или кабель, может натягивать только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю. Важно понимать, что натяжение — это натяжение соединителя. В отличие от этого, рассмотрим фразу: «Вы не можете толкнуть веревку».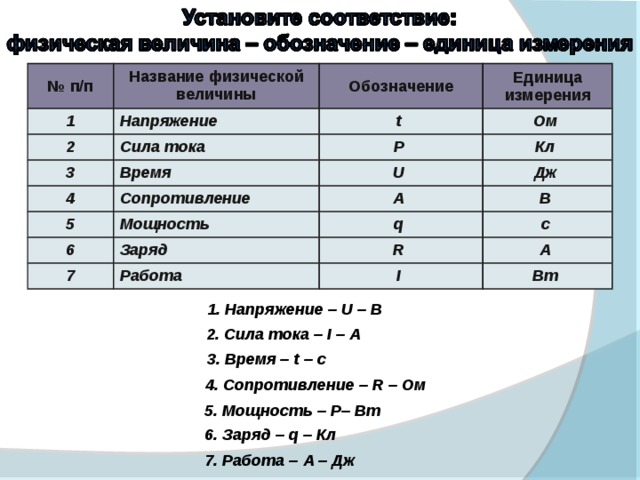 Сила натяжения тянет наружу вдоль двух концов веревки.
Сила натяжения тянет наружу вдоль двух концов веревки.
Рассмотрим человека, держащего груз на веревке, как показано на рисунке.
Рисунок \(\PageIndex{4}\): Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу \(T\), которая должна быть параллельна длине веревки, как показано. Натяжение такого гибкого соединителя представляет собой натяжение. Обратите внимание, что веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Это пример третьего закона Ньютона. Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково. Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки. Натяжение веревки должно равняться весу поддерживаемой массы, что можно доказать с помощью второго закона Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю и, следовательно, \(F_{net} = 0. \) Единственными внешними силами, действующими на массу, являются ее вес \(w\) и натяжение \(T\), поставляемый веревкой. Таким образом, \[ F_{net} = T — w = 0, \] где \(T\) и \(w\) — величины натяжения и веса, а их знаки указывают направление, причем up здесь положителен. Таким образом, как и следовало ожидать, натяжение равно весу поддерживаемой массы: 92) = 49,0 \, Н \]
\) Единственными внешними силами, действующими на массу, являются ее вес \(w\) и натяжение \(T\), поставляемый веревкой. Таким образом, \[ F_{net} = T — w = 0, \] где \(T\) и \(w\) — величины натяжения и веса, а их знаки указывают направление, причем up здесь положителен. Таким образом, как и следовало ожидать, натяжение равно весу поддерживаемой массы: 92) = 49,0 \, Н \]
Если мы разрежем веревку и вставим пружину, пружина растянется на длину, соответствующую силе 49,0 Н, обеспечивая прямое наблюдение и измерение силы натяжения веревки.
Гибкие соединители часто используются для передачи усилий на поворотах, например, в больничной вытяжной системе, пальцевом шарнире или тормозном тросе велосипеда. Если трения нет, то напряжение передается без уменьшения. Меняется только его направление, и он всегда параллелен гибкому соединителю. Это показано на рисунках (а) и (б).
Рисунок \(\PageIndex{5}\): (a) Сухожилия в пальце переносят силу \(T\) от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно без трения). (b) Тормозной трос велосипеда передает натяжение \(T\) от руля к тормозному механизму. Опять же, меняется направление, но не величина \(T\).
(b) Тормозной трос велосипеда передает натяжение \(T\) от руля к тормозному механизму. Опять же, меняется направление, но не величина \(T\).Пример \(\PageIndex{1}\): Каково натяжение каната?
Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рисунке.
Рисунок \(\PageIndex{5}\): Вес канатоходца вызывает провисание троса на 5,0 градусов. Система, представляющая интерес, представляет собой точку на проволоке, в которой стоит канатоходец.Стратегия
Как видно на рисунке, провод не идеально горизонтален (не может быть!), а прогибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, имеющими те же направления, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес \(w\) и два натяжения \(T_L\) (левое натяжение) и \(T_R\) (правое натяжение), как показано. Весом самого провода разумно пренебречь. Суммарная внешняя сила равна нулю, так как система неподвижна. Теперь можно использовать небольшую тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из части (б) рисунка видно, что величины напряжений \(T_L\) и \(T_R\) должны быть равны. Это связано с тем, что в веревке нет горизонтального ускорения, а влево и вправо действуют только силы \(T_L\) и \(T_R\). Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.
Весом самого провода разумно пренебречь. Суммарная внешняя сила равна нулю, так как система неподвижна. Теперь можно использовать небольшую тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из части (б) рисунка видно, что величины напряжений \(T_L\) и \(T_R\) должны быть равны. Это связано с тем, что в веревке нет горизонтального ускорения, а влево и вправо действуют только силы \(T_L\) и \(T_R\). Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.
Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну ось горизонтальную, а другую вертикальную. Мы называем горизонтальную ось \(х\), а вертикальную ось \(у\).
Решение
Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает нарисовать новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему.
Это помогает нарисовать новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему.
Рассмотрим горизонтальные составляющие сил (обозначаются нижним индексом \(x\)):
\[F_{net \, x} = T_{Lx} — T_{Rx}. \]
Чистая внешняя горизонтальная сила \(F_{net \, x} = 0 \), поскольку человек неподвижен. Таким образом, 9о) \]
\[ T_L = T_R = T \]
как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначаемые нижним индексом \(y\)), мы можем найти \(T\). Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что net \(F_y = 0 \). Таким образом, как показано на диаграмме свободного тела на рисунке,
\[ F_{net \, y}= T_{Ly} + T_{Ry} — w = 0 \]
Наблюдая рисунок, мы можем использовать тригонометрию для определяют отношение между \(T_{Ly},\space T_{Ry}\) и \(T\). Как мы определили из анализа в горизонтальном направлении, \(T_L = T_R = T\). 92)}{2 (0,0872)}, \]
Как мы определили из анализа в горизонтальном направлении, \(T_L = T_R = T\). 92)}{2 (0,0872)}, \]
\[ T = 3900 \, Н. \]
Обсуждение
Обратите внимание, что вертикальное натяжение в проволоке действует как нормальная сила, поддерживающая вес канатоходец. Натяжение почти в шесть раз превышает вес 686 Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь малую часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.
Если мы хотим создать очень большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное гибкому соединителю, как показано на рисунке. Как мы видели в последнем примере, вес канатоходца действовал как сила, перпендикулярная веревке. Мы видели, что натяжение каната связано с весом канатоходца следующим образом:
\[ T = \dfrac{w}{2 \, sin \, (\theta)} \]
Мы можем расширьте это выражение, чтобы описать натяжение \(T\), создаваемое перпендикулярной силой \((F_{\perp}) \) в середине гибкого соединителя:
\[ T = \dfrac{F_{\perp}}{2 \, sin \, (\theta)}. \]
\]
Обратите внимание, что \(\theta\) — это угол между горизонталью и изогнутым соединителем. В этом случае \(T\) становится очень большим, когда \(\theta\) приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, так как если бы он был горизонтальным (т. е. \(\theta = 0 \) и \(sin \, \theta = 0 \)), возникло бы бесконечное напряжение). (См. рис.)
Рисунок, за исключением того, что показанные здесь напряжения передаются на автомобиль и дерево, а не действуют в точке приложения \(F_{\perp}\).Рисунок \(\PageIndex{9}\): Если не будет приложено бесконечное натяжение, любой гибкий соединитель, такой как цепь в нижней части рисунка, будет провисать под собственным весом, образуя характерную кривую, когда вес равномерно распределяется по длине. Висячие мосты, такие как мост Золотые Ворота, показанный на этом изображении, по существу представляют собой очень тяжелые гибкие соединители. Вес моста равномерно распределяется по длине гибких соединителей, обычно тросов, которые принимают характерную форму. (кредит: Листовка, Викисклад)
(кредит: Листовка, Викисклад)Расширенная тема: Реальные силы и инерциальные системы отсчета
Существует еще одно различие между силами в дополнение к уже упомянутым типам. Одни силы реальны, другие нет. Реальные силы — это те, которые имеют какое-то физическое происхождение, например гравитационное притяжение. Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Конечно, здесь происходит то, что Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). 9Инерциальная система отсчета 0046 — это система, в которой все силы реальны, и, что эквивалентно, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
9Инерциальная система отсчета 0046 — это система, в которой все силы реальны, и, что эквивалентно, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета. Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать.
Решающим фактором при определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, рассматриваются в инерциальных системах отсчета.
Все силы, обсуждаемые в этом разделе, являются реальными силами, но есть ряд других реальных сил, таких как подъемная сила и тяга, которые в этом разделе не рассматриваются. Они более специализированы, и нет необходимости обсуждать каждый тип силы. Однако естественно задаться вопросом, где в длинном списке сил находится основная простота, которую мы стремимся найти в физике. Являются ли некоторые более простыми, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как будет показано в следующем (расширенном) разделе и в трактовке современной физики далее в тексте.
Они более специализированы, и нет необходимости обсуждать каждый тип силы. Однако естественно задаться вопросом, где в длинном списке сил находится основная простота, которую мы стремимся найти в физике. Являются ли некоторые более простыми, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как будет показано в следующем (расширенном) разделе и в трактовке современной физики далее в тексте.
ИССЛЕДОВАНИЯ PHET: СИЛА В ОДНОМ ИЗМЕРЕНИИ
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Просмотрите диаграмму всех сил свободного тела (включая гравитационные и нормальные силы).
Рисунок \(\PageIndex{10}\): Силы в 1 измеренииСводка
- Когда объекты лежат на поверхности, поверхность прикладывает к объекту силу, поддерживающую вес объекта.
 Эта поддерживающая сила действует перпендикулярно поверхности и от нее. Это называется нормальной силой, \(T\)
Эта поддерживающая сила действует перпендикулярно поверхности и от нее. Это называется нормальной силой, \(T\) - Когда объекты покоятся на горизонтальной поверхности без ускорения, величина нормальной силы равна весу объекта:
\[ N = mg \]
- Когда объекты покоятся на наклонной плоскости, образующей угол \(\theta \) с горизонтальной поверхностью, вес объекта можно разложить на составляющие, действующие перпендикулярно \(( w_{\perp})\) и параллельно \(w_{\parallel}) \) поверхности плоскости. Эти компоненты можно рассчитать, используя:
\[w_{\parallel} = w \, sin \, (\theta) = mg \, sin \, (\theta) \]
\[ w_{\perp} = w \, cos \, ( \theta) = mg \, cos \, (\theta) \]
- Сила тяги, действующая вдоль натянутого гибкого соединителя, такого как веревка или трос, называется натяжением, \(T\). Когда веревка поддерживает вес покоящегося объекта, натяжение веревки равно весу объекта:
\[ T = мг. \]
- В любой инерциальной системе отсчета (в которой нет ускорения или вращения) законы Ньютона имеют простую форму, приведенную в этой главе, и все силы являются реальными силами, имеющими физическое происхождение.

Глоссарий
- инерциальная система отсчета
- система координат не ускоряется; все силы, действующие в инерциальной системе отсчета, являются реальными силами, в отличие от фиктивных сил, наблюдаемых благодаря ускоряющей системе отсчета
- нормальное усилие
- сила, с которой поверхность воздействует на объект, чтобы выдержать вес объекта; действует перпендикулярно поверхности, на которой лежит предмет
- натяжение
- тяговое усилие, действующее вдоль среды, особенно на растянутый гибкий соединитель, такой как веревка или кабель; когда веревка поддерживает вес объекта, сила, действующая на объект из-за веревки, называется силой натяжения
Эта страница под названием 4.5: Normal, Tension, and Other Examples of Forces используется в соответствии с лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- инерциальная система отсчета
- нормальное усилие
- источник@https://openstax.
 org/details/books/college-physics
org/details/books/college-physics - Напряжение
8.5: Натяжение веревки
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24470
- Питер Доурмашкин
- Массачусетский технологический институт через MIT OpenCourseWare
Определение натяжения веревки
Вернемся к нашему примеру с очень легкой веревкой (объект 2 с \(m_{2} \simeq 0\)), прикрепленной к блоку (объект 1) в точке B , и тянется приложенной силой в точке A \(\overrightarrow{\mathbf{F}}_{\mathrm{A}, 2}\) (рис. 8.18а).
Рис. 8.18a Безмассовая веревка, тянущая блок Выберите систему координат с единичным вектором \(\hat{\mathbf{j}}\), направленным вверх в нормальном направлении к поверхности, и \(\hat{\ mathbf{i}}\) — единичный вектор, указывающий в положительном направлении x (рис. 8.18b). Диаграммы сил для системы, состоящей из каната и блока, показаны на рис. 8.19., а для веревки и блока отдельно на рис. 8.20, где \(\overrightarrow{\mathbf{F}}_{2,1}\) сила, действующая на блок (объект 1) от веревки (объект 2), и \(\overrightarrow{\mathbf{F}}_{1,2}\) — сила, действующая на веревку из-за блока.
8.18b). Диаграммы сил для системы, состоящей из каната и блока, показаны на рис. 8.19., а для веревки и блока отдельно на рис. 8.20, где \(\overrightarrow{\mathbf{F}}_{2,1}\) сила, действующая на блок (объект 1) от веревки (объект 2), и \(\overrightarrow{\mathbf{F}}_{1,2}\) — сила, действующая на веревку из-за блока.
Сумма сил, действующих на канат и блок, должна равняться нулю. Поскольку веревка не ускоряется, второй закон Ньютона, примененный к веревке, требует, чтобы \(F_{\mathrm{A}, 2}-F_{1,2}=m_{2} a\) (где мы используем величины для все силы).
Рисунок 8.19 Отдельные диаграммы сил для веревки и блокаПоскольку мы предполагаем, что масса веревки пренебрежимо мала, поэтому
\[F_{\mathrm{A}, 2}-F_{1,2}=0 ; \quad \text { (безмассовая веревка) } \nonumber \]
Если рассматривать случай, когда веревка очень легкая, то силы, действующие на концах веревки, почти горизонтальны. Тогда, если система канат-блок движется с постоянной скоростью или в состоянии покоя, второй закон Ньютона теперь равен
\[F_{\mathrm{A}, 2}-F_{1,2}=0 \nonumber \]
Второй закон Ньютона, примененный к блоку в \(+\hat{\mathbf{i}}\)-направлении, требует, чтобы \(F_{2,1}-f=0\) Третий закон Ньютона, примененный к пара взаимодействия блок-веревка требует, чтобы \(F_{1,2}=F_{2,1}\). Следовательно,
Следовательно,
\[F_{\mathrm{A}, 2}=F_{1,2}=F_{2,1}=f \nonumber \]
Таким образом, приложенная тяговая сила передается через веревку на блок так как она имеет ту же величину, что и сила веревки на блоке. Кроме того, приложенная тянущая сила также равна силе трения о блок.
Как определить «натяжение» в какой-либо точке веревки? Предположим, сделайте воображаемый срез веревки в точке P, на расстоянии \(x_{P}\) от точки B, где веревка прикреплена к блоку. Воображаемый срез делит веревку на две секции, обозначенные буквами L (левая) и R (правая), как показано на рис. 8.20.
Рис. 8.20 Воображаемый разрез веревки Теперь между левой и правой частями веревки действует пара сил третьего закона. Обозначим силу, действующую на левую секцию, через \(\overrightarrow{\mathbf{F}}_{\mathrm{R}, \mathrm{L}}\left(x_{P}\right)\), а силу, действующую на правом участке \(\overrightarrow{\mathbf{F}}_{\mathrm{L}, \mathrm{R}}\left(x_{P}\right)\) Третий закон Ньютона требует, чтобы силы в эти пары взаимодействия равны по величине и противоположны по направлению.
\[\overrightarrow{\mathbf{F}}_{\mathrm{R}, \mathrm{L}}\left(x_{p}\right)=-\overrightarrow{\mathbf{F}}_{ \mathrm{L}, \mathrm{R}}\left(x_{P}\right) \nonumber \]
Диаграммы сил для левой и правой секций показаны на рис. 8.21, где \(\overrightarrow{\mathbf {F}}_{1, \mathrm{L}}\) — сила, действующая на левый отрезок каната за счет взаимодействия блока с канатом. (Ранее мы обозначали эту силу через \(\overrightarrow{\mathbf{F}}_{1,2}\)) Теперь обозначим силу на правом отрезке стороны веревки, вызванную тянущей силой в точке A, через \(\overrightarrow{\mathbf{F}}_{\mathrm{A}, \mathrm{R}}\) (которые мы ранее обозначали как \(\overrightarrow{\mathbf{F}}_{\mathrm{ А}, 2}\)).
Рисунок 8.21 Диаграмма сил для левой и правой секций канатаНатяжение \(T\left(x_{P}\right)\) в точке P каната, лежащей на расстоянии x от левого конца каната, есть величина пары сил действие-противодействие, действующих в точке P ,
\[T\left(x_{p}\right)=\left|\overrightarrow{\mathbf{F}}_{\mathrm{ R}, \mathrm{L}}\left(x_{P}\right)\right|=\left|\overrightarrow{\mathbf{F}}_{\mathrm{L}, \mathrm{R}}\ влево(x_{P}\вправо)\вправо| \номер \]
Для веревки незначительной массы, натянутой, как в предыдущем случае (даже если веревка ускоряется), сумма горизонтальных сил, приложенных к левому и правому участкам веревки, равна нулю , и поэтому натяжение равномерно и равно приложенной силе тяги,
\[T=F_{\mathrm{A}, \mathrm{R}} \nonumber \]
Пример 8. 3 Натяжение массивной веревки
3 Натяжение массивной веревки
Рассмотрим блок массы \(m_{1}\), лежащий на горизонтальной поверхности. Коэффициент кинетического трения между блоком и поверхностью равен \(\mu_{k}\). К блоку привязана однородная веревка массы \(m_{2}\) и длины d. Веревку тянут со стороны, противоположной блоку, с приложенной силой величины \(\left|\overrightarrow{\mathbf{F}}_{\mathrm{A}, 2}\right|=F_{\mathrm{A }, 2}\). Поскольку веревка стала массивной, сила тяги образует угол \(\phi\) по отношению к горизонтали, чтобы уравновесить силу тяжести на веревке (рис. 8.22а). Определить натяжение веревки в зависимости от расстояния x от блока.
Решение: В следующем анализе мы будем предполагать, что угол \(\phi\) очень мал, и изображать тянущие и растягивающие силы как в основном действующие в горизонтальном направлении, хотя должна быть некоторая небольшая вертикальная составляющая, чтобы уравновесить гравитационные силы.
Ключевым моментом, который необходимо понять, является то, что веревка теперь массивна, и мы должны учитывать инерцию веревки при применении второго закона Ньютона. Рассмотрим воображаемый разрез веревки на расстоянии х от блока (рис. 8.22б), разделяющий веревку на две части. Правый участок имеет длину \(d-x\) и массу \(m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\). \begin{уравнение}m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\end{уравнение}. Левая часть имеет длину x и массу \(m_{\mathrm{L}}=\left(m_{2} / d\right)(x)\).
Рассмотрим воображаемый разрез веревки на расстоянии х от блока (рис. 8.22б), разделяющий веревку на две части. Правый участок имеет длину \(d-x\) и массу \(m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\). \begin{уравнение}m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\end{уравнение}. Левая часть имеет длину x и массу \(m_{\mathrm{L}}=\left(m_{2} / d\right)(x)\).
Диаграммы силы свободного тела для двух секций веревки показаны на рисунке 8.22c, где T (x) — натяжение веревки на расстоянии x от блока, а \ (F_{1, \mathrm{L}}=\left|\overrightarrow{\mathbf{F}}_{1, \mathrm{L}}\right| \equiv\left|\overrightarrow{\mathbf{F} }_{1,2}\right|\) — величина силы, действующей на левый отрезок каната из-за взаимодействия каната с блоком.
Рисунок 8.22c Диаграмма усилия для левой и правой частей канатаПрименить второй закон Ньютона к правому отрезку веревки, получив
\[F_{\mathrm{A}, \mathrm{R}}-T(x)=m_{\mathrm{R}} a_{\mathrm{ R}}=\frac{m_{2}}{d}(dx) a_{\mathrm{R}} \nonumber \]
, где \(a_{\mathrm{R}}\) — x -компонента ускорения правого участка каната. Примените второй закон Ньютона к левому отрезку веревки, получив
Примените второй закон Ньютона к левому отрезку веревки, получив
\[T(x)-F_{1, \mathrm{L}}=m_{\mathrm{L}} a_{\mathrm{L}}=\ слева (m_ {2} / d \ справа) x a _ {\ mathrm {L}} \ nonumber \]
где \(a_{\mathrm{L}}\) — x -компонента ускорения левого отрезка веревки.
Рисунок 8.23 Диаграмма усилия на скользящем блокеДиаграмма усилия на блоке показана на рисунке 8.23. Второй закон Ньютона для блока в направлении \(+\hat{\mathbf{i}}\)- равен \(F_{\mathrm{L}, 1}-f_{k}=m_{1} a_{1 }\) и в направлении \(+\hat{\mathbf{j}}\)- \(N-m_{1} g=0\) Кинетическая сила трения, действующая на блок, равна \(f_{k }=\mu_{k} N=\mu_{k} m_{1} g\) Второй закон Ньютона для блока в направлении \(+\hat{\mathbf{i}}\) становится равным
\[F_{\mathrm{L}, 1}-\mu_{k} m_{1} g=m_{1} a_{1} \nonumber \]
Третий закон Ньютона для взаимодействия блока с канатом: определяется выражением \(F_{\mathrm{L}, 1}=F_{1, \mathrm{L}}\). Уравнение (8.5.8) тогда принимает вид
\[T(x)-\left(\mu_{k} m_{1} g+m_{1} a_{1}\right)=\left(m_{2} / d\right) x a_{\mathrm{L}} \nonumber \]
Поскольку веревка и блок движутся вместе, ускорения равны, что мы обозначаем символом \(a \equiv a_{1}=a_{ \mathrm{L}}\). Тогда уравнение (8.5.10) становится
Тогда уравнение (8.5.10) становится
\[T(x)=\mu_{k} m_{1} g+\left(m_{1}+\left(m_{2} / d\right) x\right) a \nonumber \]
Этот результат не является неожиданным, поскольку натяжение ускоряет как блок, так и левую секцию и противодействует силе трения.
В качестве альтернативы диаграмма сил на систему, состоящую из каната и блока, показана на рис. 8.24.
Рисунок 8.24 Диаграмма сил в системе блок-веревкаВторой закон Ньютона принимает вид
\[F_{\mathrm{A}, \mathrm{R}}-\mu_{k} m_{1} g=\left(m_{ 2}+m_{1}\right) a \nonumber \]
Решите уравнение (8.5.12) для \(F_{\mathrm{A}, \mathrm{R}}\) и подставьте его в уравнение (8.5.7), а затем решите уравнение текучести на растяжение (8.5.11) .
Пример 8.4 Натяжение подвешенного каната
Однородный канат массой M и длиной L подвешен к потолку (рис. 8.25). Величина ускорения свободного падения равна g. а) Найдите натяжение веревки на верхнем конце, где веревка прикреплена к потолку. б) Найдите натяжение веревки в зависимости от расстояния до потолка. (c) Найдите уравнение для скорости изменения натяжения по отношению к расстоянию от потолка через M , L и g .
б) Найдите натяжение веревки в зависимости от расстояния до потолка. (c) Найдите уравнение для скорости изменения натяжения по отношению к расстоянию от потолка через M , L и g .
Решение: (a) Начните с выбора системы координат с началом на потолке и положительным направлением y, указывающим вниз (рис. 8.26). Для того чтобы найти натяжение на верхнем конце веревки, выберем в качестве системы всю веревку. Силы, действующие на веревку, — это сила при y = 0, удерживающая веревку, T (y = 0), и сила тяжести, действующая на всю веревку. Диаграмма силы свободного тела показана на рис. 8.27.
Рисунок 8.27 Диаграмма силы на канатеПоскольку ускорение равно нулю, второй закон Ньютона для веревки равен \(Mg-T(y=0)=0\). Следовательно, натяжение на верхнем конце равно \(T(y=0)=Mg\).
(б) Напомним, что напряжение в точке есть величина пары сил действие-противодействие, действующих в этой точке. Сделайте воображаемый разрез веревки на расстоянии y от потолка, разделив веревку на верхний отрезок 1 и нижний отрезок 2 (рис. 8.28а). Выберем верхний отрезок как систему с массой \(m_{1}=(M / L) y\). Силы, действующие на верхний отрезок, — это сила тяжести, сила T ( y = 0), удерживающая веревку вверх, и натяжение T(y) в точке y, которое тянет верхний отрезок вниз. Диаграмма силы свободного тела показана на рис. 8.28б.
8.28а). Выберем верхний отрезок как систему с массой \(m_{1}=(M / L) y\). Силы, действующие на верхний отрезок, — это сила тяжести, сила T ( y = 0), удерживающая веревку вверх, и натяжение T(y) в точке y, которое тянет верхний отрезок вниз. Диаграмма силы свободного тела показана на рис. 8.28б.
. Применим второй закон Ньютона к верхнему отрезку: \(m_{1} g+T(y)-T(y=0)=0\). Следовательно, натяжение на расстоянии y от потолка равно \(T(y)=T(y=0)-m_{1}g\). Поскольку \(m_{1}=(M / L) y\) — это масса сегмента, а Mg — натяжение на верхнем конце, второй закон Ньютона принимает вид
\[T(y)=M g(1 -y / L) \nonumber \]
В качестве проверки отметим, что при \(y=L\) натяжение \(T(y=L)=0\), что мы и ожидаем, поскольку силы нет действует на нижний конец веревки.
(c) Дифференцируйте уравнение (8.5.13) по y, получая
\[\frac{d T}{d y}=-(M / L) g \nonumber \]
Скорость изменяется с постоянной скоростью по отношению к расстоянию от вершины каната.
Непрерывные системы и второй закон Ньютона как дифференциальные уравнения
Мы можем определить натяжение на расстоянии y от потолка в примере 8.4 альтернативным методом, который можно обобщить на многие типы «непрерывных систем». Выберите систему координат с началом на потолке и положительным направлением y, указывающим вниз, как показано на рис. 8.25. Рассмотрим в качестве системы небольшой элемент веревки между точками y и \(y+\Delta y\). Этот маленький элемент имеет длину \(\Delta y\) Малый элемент имеет массу \(\Delta m=(M / L) \Delta y\) и показан на рис. 8.29..
\[\Delta m=(M / L) \Delta y \nonumber \]
Силы, действующие на малый элемент, это натяжение T(y) при y, направленное вверх, натяжение \(T( y+\Delta y)\) при \(y+\Delta y\) направлена вниз, а сила тяжести \(\Delta m g\) направлена вниз. Натяжение \(T(y+\Delta y)\) равно натяжению T ( y) плюс небольшая разница \(\Delta T\)
\[T(y+\Delta y)=T(y)+ \Delta T \nonumber \]
Небольшая разница в общем случае может быть положительной, нулевой или отрицательной. Диаграмма силы свободного тела показана на рис. 8.30.
Диаграмма силы свободного тела показана на рис. 8.30.
Теперь применим второй закон Ньютона к элементу малой массы
\[\Delta m g+T(y)-(T(y)+\Delta T)=0 \nonumber \ ]
Тогда разница в натяжении равна \(\Delta T=-\Delta m g\). Подставим теперь наш результат на массу элемента \(\Delta m=(M / L) \Delta y\) и найдем, что
\[\Delta T=-(M / L) \Delta y g \ nonumber \]
Разделить на \(\Delta y\), получив \(\Delta T / \Delta y=-(M / L) g\). Теперь возьмем предел, при котором длина маленького элемента стремится к нулю, \(\Delta y \rightarrow 0\)
\[\lim _{\Delta y \rightarrow 0} \frac{\Delta T}{\Delta y}=-(M / L) g \nonumber \]
Напомним, что левая часть уравнения ( 8.5.18) является определением производной натяжения по y , поэтому мы приходим к уравнению (8.5.14),
\[\frac{d T}{d y}=-(M / L) g \nonumber \]
Мы можем решить дифференциальное уравнение (8.5.14) с помощью метода, называемого разделением переменных.




 Эта поддерживающая сила действует перпендикулярно поверхности и от нее. Это называется нормальной силой, \(T\)
Эта поддерживающая сила действует перпендикулярно поверхности и от нее. Это называется нормальной силой, \(T\)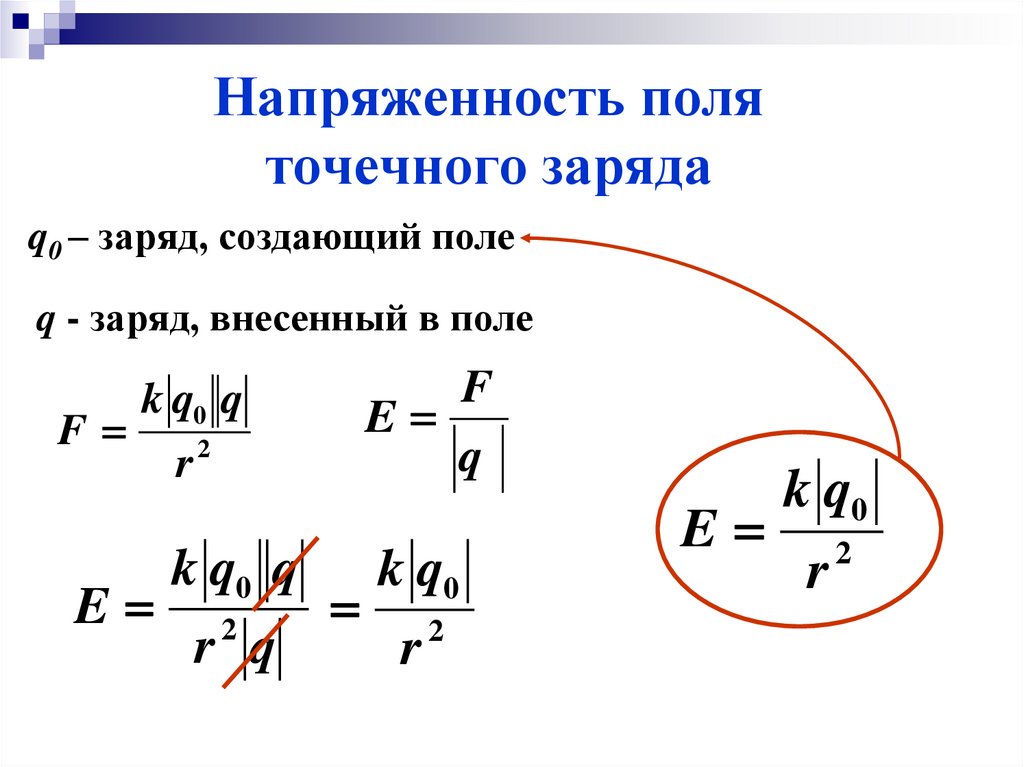
 org/details/books/college-physics
org/details/books/college-physics