2.3. Связанные заряды. Электрическое поле в диэлектриках
Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью .
Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью , а на другой положительные заряды с плотностью .
С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами и , которые отстоят друг от друга на расстояние

С другой стороны, электрический момент единицы объема равен , где — угол, между направлением нормали к основанию призмы и вектором P. Произведение есть объем призмы.
Приравняв друг к другу оба выражения для электрического момента, получаем,
что поверхностная плотность связанных зарядов равна нормальной составляющей
вектора поляризации:
,
где n — единичный вектор нормали к поверхности диэлектрика.Если вектор поляризации P различен в разных точках объема диэлектрика,
то в диэлектрике возникают объемные поляризационные заряды, объемная
плотность которых .
Электрическое поле в диэлектрике. Рассмотрим плоский однородный
диэлектрический слой, расположенный между двумя разноименно заряженными
плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое
создается этими плоскостями в вакууме, равна ,

,
где — поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика.
Поверхностная плотность связанных зарядов меньше плотности свободных зарядов, и не все поле E0 компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее . Таким образом,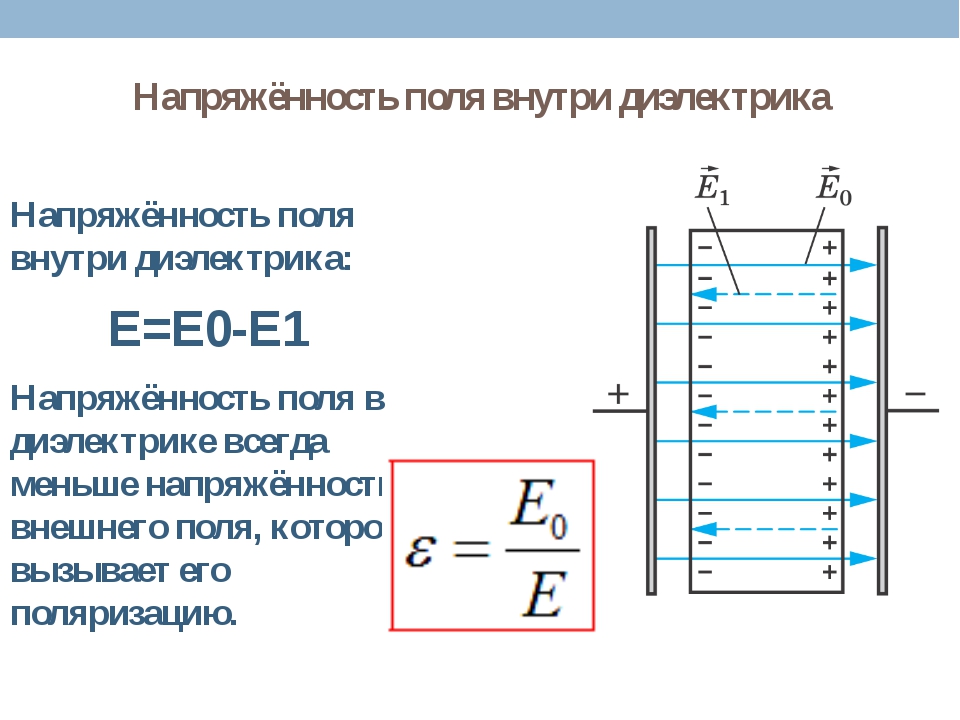 Для вакуума ,
для диэлектриков .
Для вакуума ,
для диэлектриков .Вопросы
1) Почему заряды имеют различные названия: связанные, свободные заряды, сторонние, поляризационные2) Какой физический смысл имеет диэлектрическая проницаемость среды. Может ли величина диэлектрической проницаемости быть меньше 1
3) Чему равна: поверхностная и объемная плотность поляризационных зарядов
Диэлектрики, поляризация и пробивная напряженность диэлектриков
31.08.2010 10:29Вещества (тела) с очень малой электропроводностью (практически несущественной), называются диэлектриками (изоляторами). К диэлектрикам принадлежат газы, некоторая часть жидкостей (как правило это минеральные масла, лаки) и почти все твёрдые материалы, за исключением металлов (которые все обладают разной электропроводностью) и угля (графита).
Однако же, в некоторых случаях в диэлектриках начинается расщепление молекул на ионы (например, под воздействием высокой температуры или в сильном электрическом поле), и тогда диэлектрики теряют свои изолирующие свойства и превращаются в проводники.
Диэлектрики имеют свойство поляризоваться и в них возможно длительное существование электростатического поля.
Поляризация диэлектриков
Если электрическое поле создаётся в вакууме, то величина и направление вектора напряженности поля в данной точке зависят только от величины и места расположения зарядов, создающих поле. Если же поле создается в каком-либо диэлектрике, то в молекулах данного диэлектрика идут физические процессы, которые оказывают влияние на воздействующее электрическое поле.
Под воздействием сил электрического поля электроны на орбитах смещаются в направлении, противоположном направлению воздействующего поля. В результате этого те молекулы, которые ранее были нейтральными, становятся диполями с равными зарядами ядра и электронов на орбитах. Это явление называется поляризацией диэлектрика. При исчезновении поля пропадает и смещение. Молекулы вновь становятся электрически нейтральными.
Поляризованные молекулы — диполи, создают своё электрическое поле, направление которого противоположно направлению основного (внешнего) воздействующего поля, поэтому добавочное поле, складываясь с основным, ослабляет его.
Соответственно, чем сильнее поляризуется диэлектрик, тем слабее будет результирующее поле, и тем меньше становится его напряжённость в каждой точке при тех же зарядах, которые создают основное поле, а следовательно, диэлектрическая проницаемость такого диэлектрика выше.
Когда диэлектрик находится в переменном электрическом поле, тогда и смещение электронов становится тоже переменным. Такой процесс приводит к усилению движения частиц и, соответственно, к нагреву диэлектрика.
И чем чаще изменяется электрическое поле, тем сильнее будет нагреваться диэлектрик. На практике это явление используется для нагрева мокрых (влажных, сырых) материалов с целью их просушки или получения химических реакций, которые происходят при повышенной температуре.
Пробивная напряженность диэлектриков
В нормальных условиях диэлектрик обладает совсем незначительной электропроводностью. Это полезное свойство сохраняется, пока напряженность электрического поля не увеличится до некоторого критического значения.
В сильном электрическом поле происходит расщепление молекул диэлектрика на ионы и тело, которое в слабом поле было диэлектриком, становится проводником.
Напряженность электрического поля, при достижении которой начинается ионизация молекул диэлектрика, называется пробивной напряженностью (электрической прочностью) диэлектрика.
Величина напряженности электрического поля, которая допускается в диэлектрике при его использовании в электрических установках, называется допустимой напряженностью. Допустимая напряженность, как правило, в несколько раз меньше пробивной. Отношение пробивной напряженности к допустимой определяет запас прочности диэлектрика.
Лучшими изоляторами (диэлектриками) являются вакуум и газы, особенно при высоком давлении.
Надо сказать, что у газов и жидких диэлектриков изолирующие свойства восстанавливаются при уменьшении напряженности поля до величины, меньшей пробивной напряженности данного диэлектрика.
В таблице ниже указаны значения пробивной напряженности (при нормальных условиях и в однородном постоянном ноле) наиболее распространенных диэлектриков (некоторых).
Значения пробивной напряженности диэлектриков
| Материал | |
| Бумага, пропитанная парафином | 10,0-25,0 |
| Воздух | 3,0 |
| Масло минеральное | 6,0 -15,0 |
| Мрамор | 3,0 — 4,0 |
| Миканит | 15,0 — 20,0 |
| Электрокартон | 9,0 — 14,0 |
| Слюда | 80,0 — 200,0 |
| Стекло | 10,0 — 40,0 |
| Фарфор | 6,0 — 7,5 |
| Шифер | 1,5 — 3,0 |
Презентация по физике «Электрическое поле в диэлектрике»
Презентация на тему: Электрическое поле в диэлектрикеСкачать эту презентацию
Скачать эту презентацию
№ слайда 1 Описание слайда:ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХТипы диэлектриков и их поляризацияДиэлектрики — вещества, в которых практически отсутствуют свободные носители заряда. Диэлектрики при обычных условиях не проводят электрический ток. Термин «диэлектрики» введен Фарадеем. Идеальных диэлектриков в природе не существует, так как все вещества в какой-то степени проводят электрический ток. Диэлектрики проводят электрический ток примерно на 15 — 20 порядков хуже, чем вещества, называемые проводниками.Диэлектрик, как и всякое вещество, состоит из атомов и молекул. Молекулы диэлектрика электрически нейтральны. Положительный заряд всех ядер молекулы равен суммарному заряду электронов.Молекулу можно рассматривать как электрический диполь с электрическим моментом , где Q — суммарный положительный заряд атомных ядер в молекуле, l — вектор, проведенный из «центра тяжести» отрицательных зарядов электронов в молекуле в «центр тяжести» положительных зарядов — атомных ядер.
Диэлектрики при обычных условиях не проводят электрический ток. Термин «диэлектрики» введен Фарадеем. Идеальных диэлектриков в природе не существует, так как все вещества в какой-то степени проводят электрический ток. Диэлектрики проводят электрический ток примерно на 15 — 20 порядков хуже, чем вещества, называемые проводниками.Диэлектрик, как и всякое вещество, состоит из атомов и молекул. Молекулы диэлектрика электрически нейтральны. Положительный заряд всех ядер молекулы равен суммарному заряду электронов.Молекулу можно рассматривать как электрический диполь с электрическим моментом , где Q — суммарный положительный заряд атомных ядер в молекуле, l — вектор, проведенный из «центра тяжести» отрицательных зарядов электронов в молекуле в «центр тяжести» положительных зарядов — атомных ядер.
Диэлектрик называют неполярным (с ковалентной неполярной химической связью между атомами в молекулах), если в отсутствие внешнего электрического поля «центры тяжести» положительных и отрицательных зарядов в молекулах совпадают, и, следовательно, электрический момент р молекул таких диэлектриков равен нулю (примером является: N2, Н2, О2, СО2, СН4). Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные — по полю, отрицательные — против поля) и молекулы приобретают дипольный момент.
Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные — по полю, отрицательные — против поля) и молекулы приобретают дипольный момент.
Диэлектрик называют полярным (с ковалентной полярной химической связью между атомами в молекулах), если даже при отсутствии внешнего электрического поля «центры тяжести» положительных и отрицательных зарядов не совпадают. Молекулы таких диэлектриков всегда обладают дипольным моментом. Примером таких молекул являются: Н2О, Nh4, SO2, CO. При отсутствии внешнего поля дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий дипольный момент.
№ слайда 4 Описание слайда:Диэлектрик называют ионным, молекулы которого имеют ионное (кристаллическое) строение (примеры: NaCl, КС1, КВг). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать кристаллы можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать кристаллы можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
При внесении всех трех групп диэлектриков во внешнее магнитное поле происходит поляризация диэлектрика — процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. В результате чего возникает отличный от нуля суммарный дипольный момент молекул диэлектрика.
№ слайда 6 Описание слайда:Соответственно трем группам диэлектриков различают три вида поляризации: электронная, или деформационная, поляризация диэлектрика с неполярными молекулами.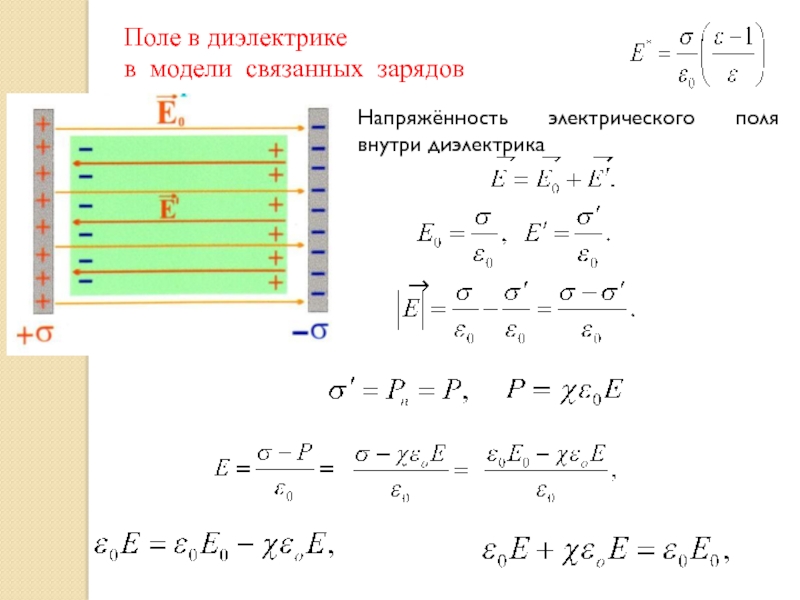 заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит; ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами,заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура; ионная поляризация диэлектриков с ионными кристаллическими решетками. заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.
заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит; ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами,заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура; ионная поляризация диэлектриков с ионными кристаллическими решетками. заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.
Поляризованность. Напряженность поля в диэлектрике Поляризацию диэлектрика характеризуют векторной величиной — поляризованностью, определяемой дипольным моментом единицы объема диэлектрика:где дипольный момент диэлектрика — дипольный момент i-й молекулы. В случае изотропных диэлектриков и не сильных полях поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то æ — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; æ — величина безразмерная, причем всегда æ > 0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц.
В случае изотропных диэлектриков и не сильных полях поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то æ — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; æ — величина безразмерная, причем всегда æ > 0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц.
Пластина из однородного диэлектрика, заполняющая пространство между двумя бесконечными параллельными разноименно заряженными плоскостями и находящуюся, следовательно, в однородном внешнем электрическом поле Е0. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов. Положительные смещаются вправо по полю, а отрицательные влево — против поля. На правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +σ, на левой грани, стороне положительной пластины, избыток отрицательного заряда с поверхностной плотностью –σ.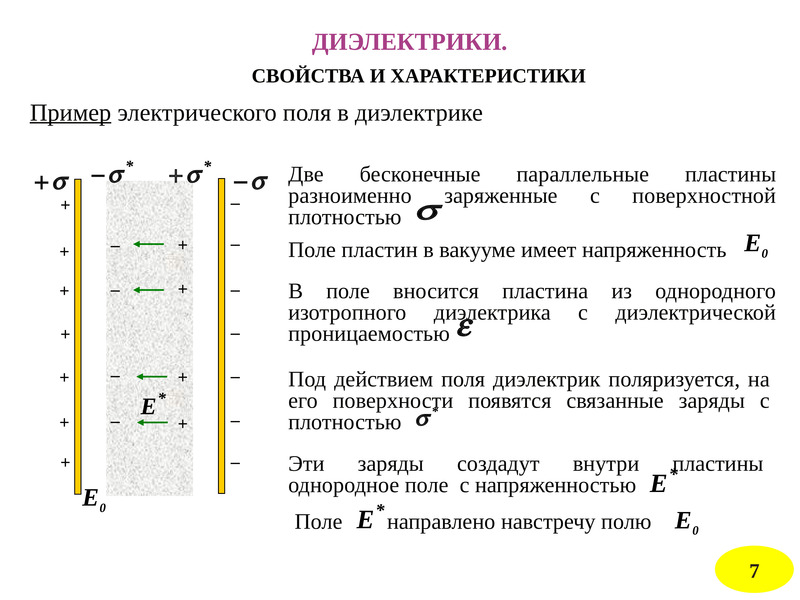 Эти некомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называют связанными.
Эти некомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называют связанными.
Из-за появления на диэлектрике связанных зарядов часть линий напряженности не пройдет сквозь диэлектрик. Они будут заканчиваться (или начинаться) на связанных зарядах. Соответственно напряженность электрического поля внутри диэлектрика будет меньше, чем Е0. Появление связанных зарядов приводит к возникновению дополнительного электрического поля Е’ (поля, создаваемого связанными зарядами). Это поле направлено против внешнего поля E0 (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика , созданное двумя бесконечными заряженными плоскостями;
№ слайда 10 Описание слайда:Определим поверхностную плотность связанных зарядов σ’. Из определения поляризованости получим, что полный дипольный момент пластинки диэлектрика pV = PV = PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, по определению равен произведению связанного заряда каждой грани. (Q’ = σ’S) на расстояние d между ними, d = lТаким образом. pV =PSd= σ’Sd а значит σ’= Р,т. е. поверхностная плотность σ’ связанных зарядов равна поляризованности Р.
С другой стороны, полный дипольный момент, по определению равен произведению связанного заряда каждой грани. (Q’ = σ’S) на расстояние d между ними, d = lТаким образом. pV =PSd= σ’Sd а значит σ’= Р,т. е. поверхностная плотность σ’ связанных зарядов равна поляризованности Р.
Подставив в выражения σ’= Р и получимоткуда напряженность результирующего поля внутри диэлектрика равнаБезразмерную величинуназывают диэлектрической проницаемостью среды.
№ слайда 12 Описание слайда:Сравнивая формулы Можно сделать два вывода. Диэлектрическая проницаемость среды — ε — показывает, во сколько раз поле ослабляется диэлектриком, — характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.
№ слайда 13 Описание слайда:Электрическое смещениеВектор напряженности электростатического поля зависит от свойств среды, и при переходе через границу диэлектрика претерпевает скачкообразное изменение, создавая затруднения при расчете полей. Поэтому помимо вектора Е для характеристики электростатического поля используют вектор электрического смещения, не претерпевающий разрыва на границе двух сред.Для изотропной среды вектор электрического смещениягде ε0 — электрическая постоянная; ε — диэлектрическая проницаемость среды.
Поэтому помимо вектора Е для характеристики электростатического поля используют вектор электрического смещения, не претерпевающий разрыва на границе двух сред.Для изотропной среды вектор электрического смещениягде ε0 — электрическая постоянная; ε — диэлектрическая проницаемость среды.
Покажем, что вектор D не терпит разрыва на границе двух диэлектриков с ε1 и ε2.
№ слайда 15 Описание слайда:Используя, вектор электрического смещения можно выразить какЕдиница электрического смещения в СИ — кулон на метр в квадрате (Кл/м2:).
№ слайда 16 Описание слайда:Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля. Внешнее поле создается системой свободных электрических зарядов. В диэлектрике существует электростатическое поле свободных зарядов и, дополнительно, электростатическое поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому оно зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле. Вектор D характеризует электростатическое поле, создаваемое свободными зарядами, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Поле D, как и поле Е, изображается с помощью силовых линий вектора электрического смещения, направление и густота которых определяются точно так же, как и для линий вектора напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому оно зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле. Вектор D характеризует электростатическое поле, создаваемое свободными зарядами, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Поле D, как и поле Е, изображается с помощью силовых линий вектора электрического смещения, направление и густота которых определяются точно так же, как и для линий вектора напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Поток вектора D. Теорема Гаусса для поля в диэлектрикеЧисло линий вектора D, пронизывающих элементарную площадку dS, нормаль п которой образует угол α с вектором D, DdScosα = DndS,Поток вектора электрического смещения сквозь площадку dS аналогично потоку вектора Е
Теорема Гаусса для поля в диэлектрикеЧисло линий вектора D, пронизывающих элементарную площадку dS, нормаль п которой образует угол α с вектором D, DdScosα = DndS,Поток вектора электрического смещения сквозь площадку dS аналогично потоку вектора Е
Поток вектора D — зависит не только от конфигурации поля D, но и от выбора направления п. Единица ФD потока вектора D в СИ — кулон (Кл). 1 Кл равен потоку электрического смещения, связанному с суммарным свободным зарядом 1 Кл.Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность
№ слайда 19 Описание слайда:Теорема Гаусса для электростатического поля в диэлектрикеПоток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В случае непрерывного распределения заряда в пространстве с объемной плотностью теорему Гаусса для электростатического поля в диэлектрике можно записать в видеПоток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен свободному заряду, заключенному в объеме, ограниченном этой поверхностью.
Условия для электростатического поля на границе раздела двух диэлектриков Найдем связь между векторами поля (Е и D) на границе раздела двух однородных изотропных диэлектриков с диэлектрическими проницаемостями ε1, и ε2. Границу раздела будем считать плоской и на ней свободные заряды отсутствуют.Вблизи границы раздела диэлектриков 1 и 2 построим небольшой замкнутый контур в виде прямоугольника ABCDA длиной l, две стороны которого параллельны границе раздела, а две другие — перпендикулярны ей.
№ слайда 22 Описание слайда:Согласно теореме о циркуляции вектора Е,откуда (знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы).
№ слайда 23 Описание слайда:Разделив слева и справа на Проекция вектора напряженности, параллельная границе раздела называется тангенциальной составляющей вектора Тангенциальная вектора Еτ одинакова по обе стороны границы раздела (не претерпевает скачка), т. е. является непрерывной
е. является непрерывной
Согласно формуле заменив проекции тангенциальные вектора Еτ проекциями вектора Dτ, деленными на εε0, получими окончательно:Тангенциальная составляющая вектора D на границе раздела двух диэлектриков претерпевает скачок (преломляется).
№ слайда 25 Описание слайда:Для получения условий для нормальных составляющих векторов Е и D построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса, для поля в диэлектрике, где нет свободных зарядов (нормали n и n’ к основаниям цилиндра направлены противоположно). Нормальная составляющая вектора D является непрерывной, не претерпевая скачка.
№ слайда 26 Описание слайда:Заменив, всогласно проекции вектора D проекциями вектора Е, умноженными на εоε, получимНормальная составляющая вектора Е на границе раздела двух диэлектриков претерпевает скачок.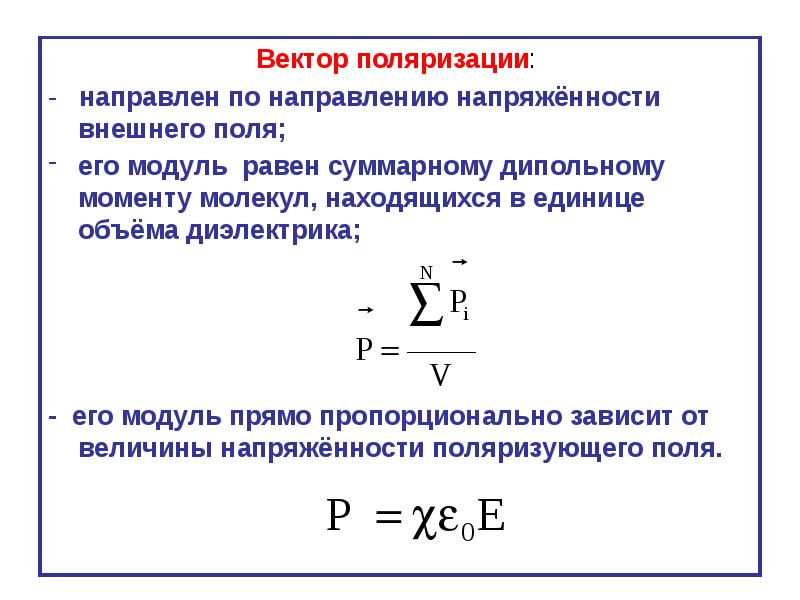 Таким образом, если на границе раздела двух однородных изотропных диэлектриков свободных зарядов нет, то при переходе этой границы составляющие Еτ и Dn изменяются непрерывно (не претерпевают скачка), а составляющие Еп и Dτ претерпевают скачок.Из условий для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются).
Таким образом, если на границе раздела двух однородных изотропных диэлектриков свободных зарядов нет, то при переходе этой границы составляющие Еτ и Dn изменяются непрерывно (не претерпевают скачка), а составляющие Еп и Dτ претерпевают скачок.Из условий для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются).
Сегнетоэлектрики — кристаллические диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью. Поляризованность, в отсутствие внешнего электрического поля, существенно изменяется под влиянием внешних воздействий таких как изменения температуры, электрического поля, деформации. Впервые эти свойства обнаружены И.В. Курчатовым и П.П. Кобеко (1930) при исследовании кристаллов сегнетовой соли NаКС4Н4О64Н,О. Она и дала название сегнетоэлектрики этому типу кристаллов. В дальнейшем оказалось, что подобными свойствами обладают титанат бария, дигидрофосфат калия и т. д.
д.
При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой как бы мозаику из доменов. Доменами называются области с различными направлениями поляризованности. На рисунке стрелками указаны направления вектора поляризованности. В смежных доменах эти направления различны, и в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов доменов по полю. Возникшее при этом суммарное электрическое поле доменов будет поддерживать их некоторую ориентацию даже после прекращения действия внешнего поля. Поэтому сегнетоэлектрики имеют аномально большие значения диэлектрической проницаемости (для сегнетовой соли, например, сегн ~ 104).
№ слайда 29 Описание слайда:Свойства сегнетоэлектриков сильно зависят от температуры. Каждый сегнетоэлектрик характеризуется так называемой точкой Кюри. Точка Кюри это характерная для каждого типа сегнетоэлектриков температура, выше которой их необычные электрические свойства исчезают. При этом сегнетоэлектрик превращается в обычный полярный диэлектрик. При охлаждении материала сегнетоэлектрические свойства восстанавливаются.Как правило, сегнетоэлектрики имеют только одну точку Кюри; исключение составляют лишь сегнетова соль (—18 и +24 °С) и изоморфные с нею соединения. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, происходящее в точке Кюри, сопровождается фазовым переходом II рода.
Точка Кюри это характерная для каждого типа сегнетоэлектриков температура, выше которой их необычные электрические свойства исчезают. При этом сегнетоэлектрик превращается в обычный полярный диэлектрик. При охлаждении материала сегнетоэлектрические свойства восстанавливаются.Как правило, сегнетоэлектрики имеют только одну точку Кюри; исключение составляют лишь сегнетова соль (—18 и +24 °С) и изоморфные с нею соединения. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, происходящее в точке Кюри, сопровождается фазовым переходом II рода.
В сегнетоэлектриках наблюдается явление диэлектрического гистерезиса (запаздывания), заключающегося в том, что сегнетоэлектрик имеет разные значения поляризованное при одной и той же напряженности электрического поля (в зависимости от значения предварительной поляризованности образца). При увеличении напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая l). Уменьшение Р с уменьшением Е происходит по кривой 2, и при E = 0 сегнетоэлектрик сохраняет остаточную поляризованность Рос, т. е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля.
При увеличении напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая l). Уменьшение Р с уменьшением Е происходит по кривой 2, и при E = 0 сегнетоэлектрик сохраняет остаточную поляризованность Рос, т. е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля.
Чтобы уничтожить остаточную поляризованность, надо приложить электрическое поле обратного направления (-E.). Величину Eс называют коэрцитивной силой (от лат. coercitio — удерживание). Если далее изменять Е, то Р изменяется по кривой 3 петли гистерезиса.Следует упомянуть еще о пьезоэлектриках — кристаллических веществах, в которых при сжатии или растяжении в определенных направлениях возникает поляризованность даже в отсутствие внешнего электрического поля (прямой пьезоэффект).Наблюдается и обратный пьезоэффект — появление механической деформации под действием электрического поля. У некоторых пьезоэлектриков решетка положительных ионов при нагреве смещается относительно решетки отрицательных ионов, в результате чего они оказываются поляризованными даже без внешнего электрического поля. Такие кристаллы называются пироэлектриками.Еще существуют электреты — диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов). Эти группы веществ находят широкое применение в технике и бытовых устройствах.
У некоторых пьезоэлектриков решетка положительных ионов при нагреве смещается относительно решетки отрицательных ионов, в результате чего они оказываются поляризованными даже без внешнего электрического поля. Такие кристаллы называются пироэлектриками.Еще существуют электреты — диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов). Эти группы веществ находят широкое применение в технике и бытовых устройствах.
Поляризованность. Напряженность поля в диэлектрике
При помещении диэлектрика во внешнее электростатическое поле он поляризуется, т. е. приобретает отличный от нуля дипольный момент, где рi — дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью,определяемой как дипольный момент единицы объёма диэлектрика:
Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков, см. §91) поляризованность Р линейно зависит от напряженности поля Е. В случае если диэлектрик изотропный и Е не чересчур велико, то
§91) поляризованность Р линейно зависит от напряженности поля Е. В случае если диэлектрик изотропный и Е не чересчур велико, то
где c— диэлектрическая восприимчивость
вещества,характеризующая свойства диэлектрика; c — величина безразмерная; притом всегда c>0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц (хотя, к примеру, для спирта cʼʼ25, для воды c=80).
Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электростатическое поле Е0 (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика, расположив ее так, как показано на рис. 135. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +s’, на левой — отрицательного заряда с поверхностной плотностью -s’. Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными.Так как их поверхностная плотность s’ меньше плотности а свободных зарядов плоскостей, то не
Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными.Так как их поверхностная плотность s’ меньше плотности а свободных зарядов плоскостей, то не
все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е=Е0. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, появление связанных зарядов приводит к возникновению дополнительного электрического поля Е’ (поля, создаваемого связанными зарядами), которое направлено против внешнего поля Е0 (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика
E=E0—E‘.
Поле E‘=s’/e0 (поле, созданное двумя бесконечными заряженными плоскостями; см. формулу (82.2)), в связи с этим
E=E0-s/e0. (88.3)
Определим поверхностную плотность связанных зарядов s‘. По (88.1), полный дипольный момент пластинки диэлектрика pV=PV=PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, согласно (80.3), равен произведению связанного заряда каждой грани Q’ = s’S на расстояние d между ними, т. е. pV=s’Sd. Таким образом,
PSd=s’Sd,
или
s’=Р, (88.4)
т. е. поверхностная плотность связанных зарядов s’ равна поляризованности Р.
Подставив в (88.3) выражения (88.4) и (88.2), получим
Е=Е0-cЕ,
откуда напряженность результирующего поля внутри диэлектрика равна
E=E0/(1+c)=E0/e. (88.5) Безразмерная величина
(88.5) Безразмерная величина
e=1+c (88.6)
принято называть диэлектрической проницаемостью среды.Сравнивая (88.5) и (88.6), видим, что e показывает, во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойство диэлектрика поляризоваться в электрическом поле.
Заключительная частьОтветы на вопросы. Подведение итогов
Электричество и магнетизм
Применим теорему Остроградского — Гаусса к электрическому полю в диэлектрике. Поток вектора напряженности через замкнутую поверхность пропорционален алгебраической сумме зарядов (свободных и поляризационных), находящихся внутри ограниченного этой поверхностью объема
|
(3.27) |
где qi — свободные, а q ‘i — поляризационные заряды.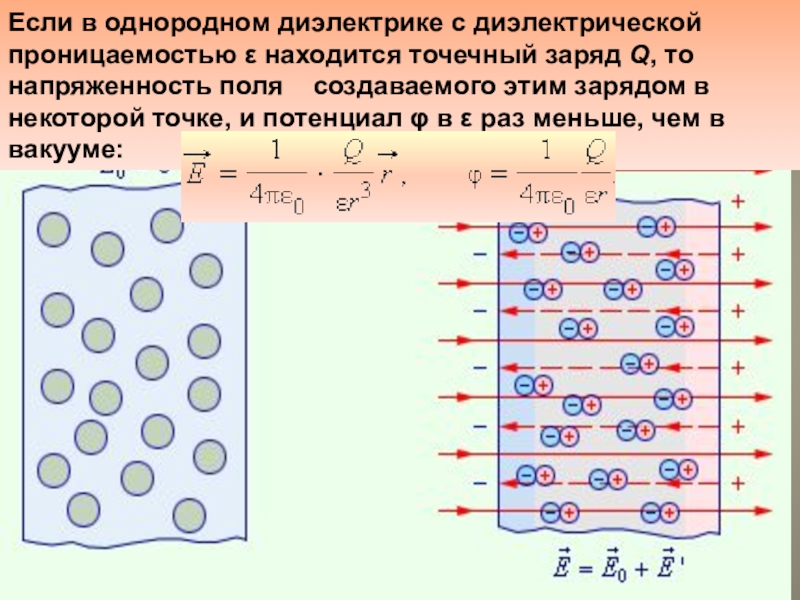 Это выражение неудобно, так как в него входят поляризационные заряды, которые, в свою очередь, зависят от напряженности электрического поля в данной точке диэлектрика.
Это выражение неудобно, так как в него входят поляризационные заряды, которые, в свою очередь, зависят от напряженности электрического поля в данной точке диэлектрика.
Рассмотрим теперь поток вектора электрического смещения
|
(3.28) |
Так как напряженность поля поляризационных зарядов можно записать в виде
то
|
(3.29) |
Следовательно,
откуда
|
(3.30) |
где qi — свободные заряды. Следует подчеркнуть, что линии вектора D могут начинаться и заканчиваться на свободных зарядах, но не на поляризационных.
Следует подчеркнуть, что линии вектора D могут начинаться и заканчиваться на свободных зарядах, но не на поляризационных.
Следует обратить внимание на отсутствие в правой части множителя , который имеется в аналогичном выражении для потока вектора напряженности в вакууме.
Из теоремы Остроградского — Гаусса для точечного заряда q внутри диэлектрика следует
|
(3.31) |
Вектор D не определяет силу, действующую на заряд со стороны внешнего электрического поля. Силовой характеристикой, по-прежнему, является , то есть . При линейной зависимости от для вычисления силы следует воспользоваться соотношением
откуда
Получим теперь закон Кулона для таких диэлектриков. Свободный заряд q2 создает в диэлектрике электрическое смещение
Свободный заряд q2 создает в диэлектрике электрическое смещение
откуда следует выражение для силы взаимодействия с другим свободным зарядом q1
|
(3.32) |
Соответственно, изменится выражение для потенциала, создаваемого свободным зарядом q
|
(3.33) |
и, как следствие, формулы для работы по перемещению свободного заряда в поле и энергии взаимодействия свободных зарядов. Мы замечаем, что по сравнению с аналогичными формулами для систем зарядов в вакууме, для диэлектриков надо произвести замену Поскольку приведенные выражения являлись основным источником всех прочих соотношений, выведенных нами для вакуума, мы немедленно получаем, например, выражения для емкостей плоского (2. 12), цилиндрического (2.14) и сферического (2.17) конденсаторов, заполненных однородным диэлектриком (рис 3.25, 3.26, 3.27, 3.28)
12), цилиндрического (2.14) и сферического (2.17) конденсаторов, заполненных однородным диэлектриком (рис 3.25, 3.26, 3.27, 3.28)
Рис. 3.25. Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик
|
|
(3.34) |
Рис. 3.26. Плоский конденсатор с диэлектриком
Рис. 3.27. Цилиндрический конденсатор с диэлектриком
Рис. 3.28. Сферический конденсатор с диэлектриком
Для плотности энергии электрического поля (2.57) теперь можно написать выражение
|
|
(3. |
которое может быть представлено в векторной форме:
|
|
(3.36) |
Макроскопическое поле в диэлектрике — Мегаобучалка
Макроскопическое поле характеризуется средней напряженностью электрического поля в объеме, превышающем размеры молекулы, но достаточно малом, так что напряженность в пределах этого объема изменяется мало. В противоположность этому локальное поле — это поле, действующее на молекулу или другую способную поляризоваться частицу. В вакууме обе напряженности, макроскопическая и локальная, равны друг другу. В диэлектрической среде, кроме среднего макроскопического поля, на молекулу действуют поля соседних молекул. Таким образом, в диэлектрике (веществе) макроскопическое и локальное поля различны.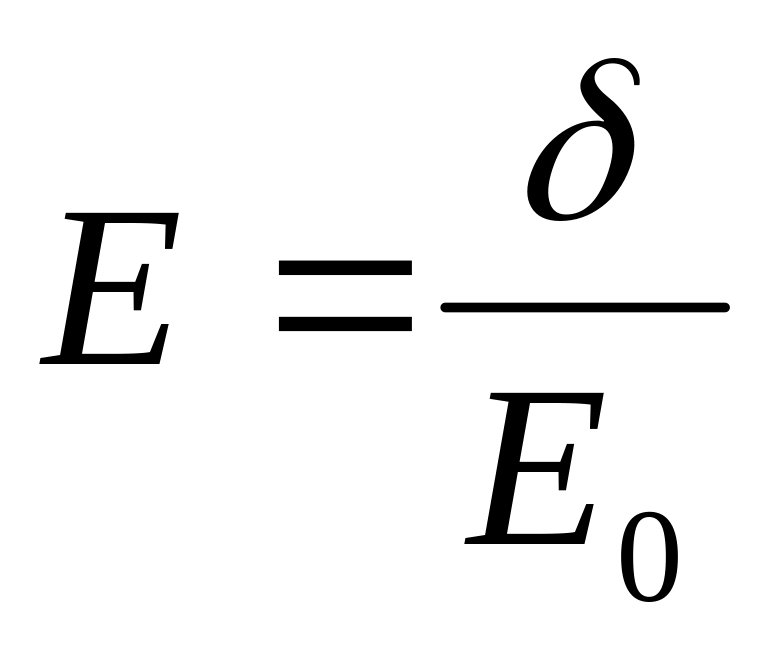
Поле в вакууме определяется распределением зарядов в про- странстве. Зная распределение зарядов, можно вычислить напряженность электрического поля, например, решая уравнение Пуассона
,
где D — оператор Лапласа,
j— потенциал электростатического поля, ρ — плотность объемного заряда,
напряженность поля находят из выражения
.
Уравнение можно представить в виде
.
Отсюда видно, что в областях, где нет объемных зарядов дивергенция напряженности электрического поля равна нулю .
Потенциал j можно вычислить, пользуясь формулой
,
где первый интеграл берется по всему пространству,
r — расстояние до элемента объема dV, в котором объемная плотность равна ρ, или до элемента поверхности dS, на котором поверхностная плотность равна σ;
второй интеграл берется по всем поверхностям, на которых имеются заряды с поверхностной плотностью σ.
Энергия W электростатического поля Е, создаваемого объемными зарядами с плотностью ρ и поверхностными зарядами с плотностью σ, определяется выражением
.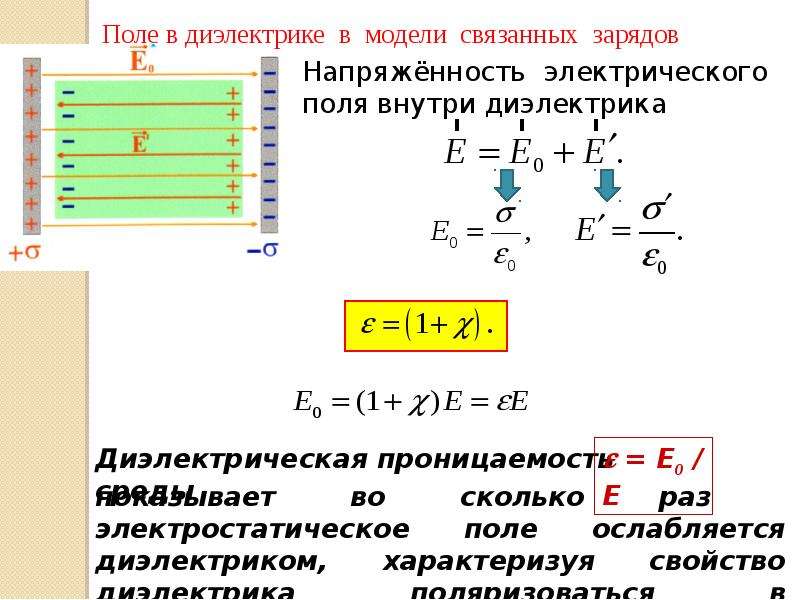
Если имеется поверхность,на которой плотность заряда равна σ, то между нормальными составляющими электрического поля в областях 1 и 2 (Рис. 6‑1) и плотностью заряда σ соблюдается соотношение
,
где Е2n — проекция напряженности поля в области 2 на направление нормали к поверхности ;
Е1n — проекция напряженности поля в области 1 на направление нормали .
| Рис. 6‑1. Изменение напряженности электрического поля при переходе из области 1 в область 2 через заряженную плоскость с плотностью поверхностного заряда σ |
Заряд, внесенный в диэлектрик (или избыточный заряд в диэлектрике), принято называть свободным зарядом q.
Электрическое поле Е заряда q в диэлектрике с диэлектрической проницаемостью ε в ε раз меньше, чем в вакууме:
.
Уменьшение поля от свободного заряда в диэлектрике по сравнению с полем от такого же свободного заряда в вакууме связано с поляризацией диэлектрика.
Если диэлектрик неполярный, его молекулы в электрическом поле приобретают индуцированные моменты, т. е. поляризуются, как показано на Рис. 6‑2; свободный заряд + q помещен в центре шарового диэлектрика, и молекулы изображены сильно увеличенными.
| Рис. 6‑2. Поляризация молекул неполярного диэлектрика в поле положительного заряда +q. |
У свободных зарядов в сферической области, сечение которой на рисунке представлено внутренней тонкой, линией, имеется избыток связанных отрицательных зарядов — qс. На внешней поверхности диэлектрика, за пределами сферы, изображенной на рисунке внешней (тонкой) окружностью, выделяется положительный связанный заряд +qс, равный по абсолютной величине отрицательному заряду —qс.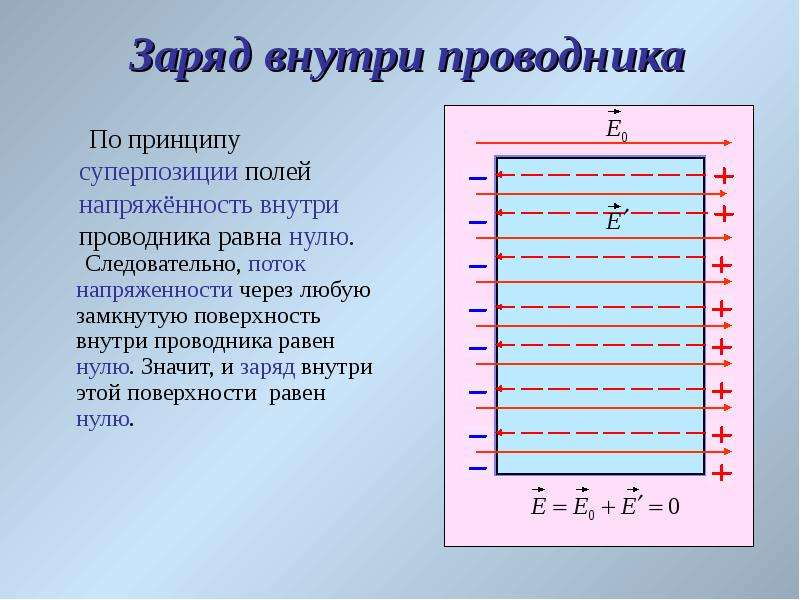 В шаровом слое между двумя этими сферами положительные и отрицательные заряды компенсируются, т.е. суммарный заряд равен нулю.
В шаровом слое между двумя этими сферами положительные и отрицательные заряды компенсируются, т.е. суммарный заряд равен нулю.
Если заряженная частица q находится в дипольном диэлектрике, дипольные молекулы поворачиваются, так что вокруг этой частицы появляется отрицательный связанный заряд. Поэтому напряженность поля в диэлектрике
.
С другой стороны, E можно выразить через величину свободного заряда q и диэлектрическую проницаемость ε. Из сравнения выражений и следует, что связанный заряд qc. определяется значениями диэлектрической проницаемости ε и свободного заряда q:
.
Потенциал электрического поля в диэлектрике может быть определен из уравнений или . Однако под ρ и σ следует понимать суммарные плотности свободного и связанного зарядов. Эти уравнения для диэлектрической среды принимают вид:
,
где ρ и σ — объемная и поверхностная плотности свободного заряда;
ρс и σс — объемная и поверхностная плотности связанного заряда.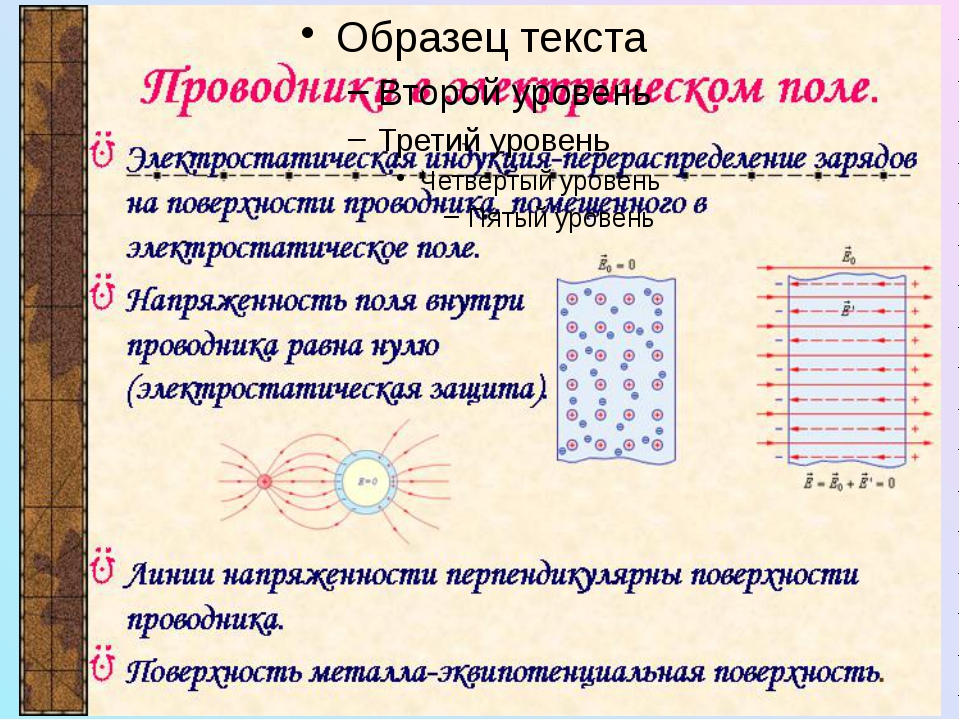
Электрическое поле в диэлектрике может быть определено через поляризацию диэлектрика . Пусть в плоском конденсаторе, левый электрод которого является анодом, а правый — катодом, находится нейтральный диэлектрик. Молекулы диэлектрика поляризуются, так что у анода появляется отрицательный, а у катода положительный связанный заряд (Рис. 6‑3, а).
Поскольку электрическое поле Е в плоском конденсаторе однородно, каждая молекула приобретает индуцированный момент , где — поле, действующее на молекулу (локальное), которое может быть больше Е.
Если в единице объема находится п молекул, то момент единицы объема
.
Величина , равная nα, называется диэлектрической восприимчивостью диэлектрика. В случае неоднородного поля под поляризацией вещества понимают отношение электрического момента некоторого малого объема диэлектрика к величине этого объема :
| Рис. 6‑3. Поляризация диэлектрика в плоском конденсаторе: а — возникновение индуцированных моментов молекул под действием электрического поля; б — образование связанных зарядов на поверхности у электродов |
.
Выражения и справедливы в случае всех механизмов поляризации, кроме спонтанной поляризации в сегнетоэлектриках.
Выделим в плоском конденсаторе столбик единичного сечения; на Рис. 6‑3, б он отмечен более густой штриховкой. Заряд на электродах такого элемента равен поверхностной плотности σ.
Плотность зарядов на электродах вакуумного конденсатора σв в ε раз меньше плотности зарядов σ на электродах конденсатора с диэлектриком
,
а напряженности при одинаковых напряжениях одинаковы для обоих конденсаторов.
Напряженность поля связана с плотностью зарядов на обкладках вакуумного конденсатора соотношением
Поле в конденсаторе с диэлектриком создается свободным зарядом на электродах с плотностью σ и связанным зарядом на поверхности диэлектрика с плотностью σс. Свободный и связанный заряды в плоском конденсаторе создают поля, направленные навстречу друг другу. Результирующее поле
Так как напряженность поля в том и другом конденсаторе одинакова, приравняв правые части формул и , получим согласно
отсюда
Сравнивая формулы и , видим, что оба соотношения между величинами свободного и связанного зарядов подобны друг другу.
Принимая во внимание, что в плоском конденсаторе , из находим
,
откуда
.
Как видно из , при заданном свободном заряде на электродах σ поле в конденсаторе зависит от ε. В плоском конденсаторе электрическая индукция (электрическое смещение) определяется величиной свободного заряда:
.
В случае изотропных диэлектриков справедливо векторное равенство
Подставляя в это равенство величину получаем
.
Отсюда находим соотношение между диэлектрической проницаемостью ε и диэлектрической восприимчивостью х
Из следует, что
.
Если в диэлектрике или на границе раздела диэлектриков имеется заряженная поверхность с поверхностной плотностью свободных зарядов σ, то вместо соотношения получаем
,
где ε1 и ε2 — значения диэлектрической проницаемости в областях 1 и 2 и D2nи D1n — проекции вектора электрической индукции в областях 1 и 2 на направление внешней нормали к поверхности, ограничивающей область 1 (см. Рис. 6‑1).
Рис. 6‑1).
В частности, если на поверхностях раздела диэлектриков 1 и 2 нет свободных зарядов, то
.
Следовательно, при отсутствии свободных зарядов на поверхности раздела двух различных диэлектриков ( ) нормальная составляющая электрической индукции на этой поверхности остается непрерывной, а нормальная составляющая напряженности испытывает скачок.
На грани двух различных диэлектриков 1 и 2 тангенциальные составляющие напряженности электрического поля остаются непрерывными, а тангенциальные составляющие электрической индукции испытывают скачок
,
где E1tи Dlt — тангенциальные составляющие напряженности электрического поля и электрической индукции на поверхности раздела в первом диэлектрике;
E2tи D2t — тангенциальные составляющие напряженности электрического поля и электрической индукции на поверхности раздела во втором диэлектрике.
Из выражений и вытекает, что на поверхности раздела двух сред с диэлектрической проницаемостью ε1 и ε2 силовые линии электрического поля Е и параллельные им линии электрической индукции испытывают преломление:
| Рис. 6‑4. Преломление силовых линий электрического поля при переходе через поверхность раздела двух диэлектриков с различными диэлектрическими проницаемостями |
,
где β1 и β2 — углы, образующиеся между нормалью к поверхностям раздела и направлением силовых линий в средах 1 и 2 (Рис. 6‑4).
Линии электрического поля Е могут оканчиваться на поверхностях раздела диэлектриков. Линии электрической индукции D непрерывны на поверхностях раздела диэлектриков, если на этих поверхностях нет свободных зарядов. Линии электрической индукции начинаются на положительном и оканчиваются на отрицательном свободном заряде. В частности, если имеется проводник, на поверхности которого находится заряд с плотностью σ, то
,
где — внешняя нормаль к поверхности проводника;
ε — диэлектрическая проницаемость диэлектрика, окружающего проводник.
Энергия электрического поля диэлектрика определяется выражением
где ρ и σ — объемная и поверхностная плотности свободного заряда;
j — потенциал электрического поля в диэлектрике.
Это выражение подобно формуле , определяющей энергию электрона в вакууме через плотность свободного заряда. Влияние диэлектрика сказывается в том, что при одинаковом распределении свободных зарядов потенциал в диэлектрике j отличается от потенциала в вакууме.
Зависимость поляризованности диэлектрика от напряженности поля
При помещении диэлектрика во внешнее электростатическое поле он поляризуется, т.е. приобретает отличный от нуля дипольный момент
где – дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной – поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:
Из опыта следует, что для большого класса диэлектриков поляризованность P линейно зависит от напряженности поля E. Если диэлектрик изотропный и E не слишком велико, то
Если диэлектрик изотропный и E не слишком велико, то
где – диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; – величина безразмерная; притом всегда >0 и для большинства диэлектриков составляет несколько единиц.
Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электростатическое поле E (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика.
Под действием поля диэлектрик поляризуется, т.е. происходит смещение зарядов: положительные смещаются по полю, отрицательные – против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +, на левой – отрицательного заряда с поверхностной плотностью -. Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их поверхностная плотность / меньше плотности свободных зарядов плоскостей, то не все поле E компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть – обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика E=E.
Так как их поверхностная плотность / меньше плотности свободных зарядов плоскостей, то не все поле E компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть – обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика E=E.
Таким образом, появление связанных зарядов приводит к возникновению дополнительного электрического поля E / (поля связанных зарядов), которое направлено против внешнего поля (поля свободных зарядов) и ослабляет его. Результирующее поле внутри диэлектрика
Поле (поле, созданное двумя бесконечными параллельными разноименно заряженными плоскостями), поэтому
Определим поверхностную плотность связанных зарядов / . По (1), полный дипольный момент пластинки диэлектрика ,
где S – площадь грани пластинки, d – ее толщина. С другой стороны, полный дипольный момент равен произведению связанного заряда каждой грани на расстоянии d между ними, т. е.
е.
т.е. поверхностная плотность связанных зарядов / равна поляризованности P.
Подставив в (4) выражения (5) и (2), получим
откуда напряженность результирующего поля внутри диэлектрика равна
называется диэлектрической проницаемостью среды. Сравнивая (6) и (7), видим, что показывает, во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойство диэлектрика поляризоваться в электрическом поле.
Поляризация всех рассмотренных диэлектриков во внешнем электрическом поле приводит к изменению электрического поля внутри них. На рис.3 представлен образец диэлектрика, помещенный в однородное внешнее электрическое поле с напряженностьюE . Электрическое поле создается двумя параллельными разноименно заряженными плоскостями с поверхностными плотностями зарядов + s и -.s. В диэлектрике происходит смещение зарядов: положительные – по полю, отрицательные против поля. На правой грани образуется избыток положительных зарядов с поверхностной плотностью + s / , на левой – избыток отрицательных ( — s / ). Эти связанные заряды образуют свое внутреннее поле с напряженностью E / , направленное против внешнего поля. В результате внешнее поле внутри диэлектрика ослабляется. Однако не все поле E компенсируется зарядами диэлектрика: часть силовых линий внешнего поля пройдет сквозь диэлектрик, а часть оборвется на связанных зарядах (рис.3). Отсюда напряженность результирующего поля внутри диэлектрика будет
Эти связанные заряды образуют свое внутреннее поле с напряженностью E / , направленное против внешнего поля. В результате внешнее поле внутри диэлектрика ослабляется. Однако не все поле E компенсируется зарядами диэлектрика: часть силовых линий внешнего поля пройдет сквозь диэлектрик, а часть оборвется на связанных зарядах (рис.3). Отсюда напряженность результирующего поля внутри диэлектрика будет
Рис.3 Линии напряженности электрического поля E
и электрического поля E / в диэлектрике
Поле, созданное двумя бесконечными заряженными плоскостями рассчитывается по формуле:
.
По аналогии напряженность поля связанных зарядов внутри диэлектрика
. (4)
В электростатике установлено, что поверхностная плотность связанных зарядов равна поляризованности диэлектрика
. (5)
С учетом формул (3),(4) и (5) получаем
Отсюда напряженность результирующего поля внутри диэлектрика:
(7)
где e — диэлектрическая проницаемость вещества.
Диэлектрическая проницаемость e =1+c является одной из основных характеристик диэлектрика. Диэлектрическая проницаемость показывает во сколько раз напряженность электрического поля в диэлектрике меньше напряженности электрического поля в вакууме. Она количественно характеризует свойство диэлектрика поляризоваться во внешнем электрическом поле.
Диэлектрическая проницаемость неполярных диэлектриков e невелика (1-2,4) и сравнительно слабо уменьшается с ростом температуры. Диэлектрическая проницаемость полярных диэлектриков значительно выше: e жидкостей достигает 80, в кристаллах до 300 и даже несколько тысяч. С ростом температуры диэлектрическая проницаемость полярных диэлектриков значительно уменьшается. Диэлектрическая проницаемость ионных диэлектриков имеет широкий диапазон значений (от 4 до 3000) в зависимости от состава и строения диэлектрика и также убывает с ростом температуры.
Сегнетоэлектрики
Особую группу среди полярных диэлектриков составляют сегнетоэлектрики, которые обладают рядом разнообразных электрических свойств. Название этой группе дано по первому исследованному веществу – сегнетовой соли NaKCl4H4O6 × 4H2O , поляризационные характеристики которой изучались советскими физиками И.В. Курчатовым, П.П. Кобеко и др.
Название этой группе дано по первому исследованному веществу – сегнетовой соли NaKCl4H4O6 × 4H2O , поляризационные характеристики которой изучались советскими физиками И.В. Курчатовым, П.П. Кобеко и др.
Свойства сегнетоэлектриков обусловлены особенностями их строения. Благодаря сильному взаимодействию частиц весь объем сегнетоэлектрика делится (в определенном температурном интервале) на отдельные макроскопические области – «домены», которые возникают самопроизвольно (спонтанно). Каждый домен поляризован, так как дипольные моменты его молекул ориентированы одинаково. Однако в отсутствие внешнего электрического поля поляризованность доменов различна и кристалл сегнетоэлектрика в целом дипольным моментом не обладает (рис.4). При внесении сегнетоэлектрика во внешнее электрическое поле сразу целые поляризованные области начинают ориентироваться вдоль поля. Происходит изменение самих доменов: растут наиболее выгодно ориентированные домены (случай острых углов между векторами поляризации P и напряженности внешнего электрического поляE) за счет невыгодных (угол > 90 0 ). Кроме того, электрические моменты доменов поворачиваются в направлении поля, а также одновременно происходит образование и рост зародышей новых доменов с электрическими моментами, ориентированными вдоль поля.
Кроме того, электрические моменты доменов поворачиваются в направлении поля, а также одновременно происходит образование и рост зародышей новых доменов с электрическими моментами, ориентированными вдоль поля.
Рис.4. Области самопроизвольной поляризации (домены) в сегнетоэлектриках и направ-ление в них вектора поляризации (поляризованности):а) — сегнетоэлектрик в целом неполяризован; б) — сегнетоэлектрик поляризован во внешнем электрическом поле.
Зависимость поляризованности P сегнетоэлектрика от напряженности внешнего поля носит необратимый характер в отличие от обратимости функцииP= f (E) для всех других типов диэлектриков.
Диэлектрическая проницаемость сегнетоэлектриков аномально высока (e » 10 4 ), зависит от напряженности внешнего электрического поля (рис.5) и температуры.
Рис. 5. Зависимость диэлектрической проницаемости сегнетоэлектрика от
напряженности внешнего электрического поля при 20 0 С.
Явление гистерезиса
Для сегнетоэлектриков характерно явление диэлектрического гистерезиса («гистерезис» по-гречески означает «запаздывание»), чем и обусловлена необратимость поляризации. График зависимости поляризованности от напряженности внешнего электрического поля представлен на рис.6. С ростом напряженности поля поляризованность кристалла увеличивается от 0 до Pn, что соответствует участку кривой ОА В точке А сегнетоэлектрик «насыщен». В этом случае (рис.6) поляризованность всех доменов сориентирована по направлению внешнего электрического поля.
Рис.6. Петля диэлектрического гистерезиса в сегнетоэлектрике
Последующее увеличение E (отрезок АВ) соответствует линейному росту P (угол a мал), обусловленному чисто электронной поляризацией. При снижении Eвнеш до точки Eа значение P убывает по прямой BA, а затем изменение P отстает от измененияE. При E = 0 сегнетоэлектрик остается поляризованным (P — остаточная поляризация). Для снятия последней к сегнетоэлектрику надо приложить противоположное по знаку поле. Напряженность этого поля ( -Eк ). называется коэрцитивной силой. Дальнейшее увеличение напряженности поля с обратной полярностью приведет кривую в точку A / , симметричную A. При увеличении напряженности электрического поля от –Ea до +Ea функция P = f (E) пройдет по кривой A / MA. Полученная замкнутая кривая называется петлей гистерезиса. Это петля предельного цикла (сплошная линия, рис.6). Если же при максимальной напряженности внешнего поля насыщения не достигнуто, то получится меньшая петля гистерезиса, называемая частным циклом (пунктирная линия, рис.6).
При E = 0 сегнетоэлектрик остается поляризованным (P — остаточная поляризация). Для снятия последней к сегнетоэлектрику надо приложить противоположное по знаку поле. Напряженность этого поля ( -Eк ). называется коэрцитивной силой. Дальнейшее увеличение напряженности поля с обратной полярностью приведет кривую в точку A / , симметричную A. При увеличении напряженности электрического поля от –Ea до +Ea функция P = f (E) пройдет по кривой A / MA. Полученная замкнутая кривая называется петлей гистерезиса. Это петля предельного цикла (сплошная линия, рис.6). Если же при максимальной напряженности внешнего поля насыщения не достигнуто, то получится меньшая петля гистерезиса, называемая частным циклом (пунктирная линия, рис.6).
Петлю гистерезиса можно наблюдать, если подвести к образцу из сегнетоэлектрика с посеребренными поверхностями (сегнетоконденсатор) переменное напряжение. Часть электрической энергии в диэлектрике переходит в тепло и называется диэлектрическими потерями, которые принято характеризовать тангенсом угла диэлектрических потерь tgd. Если W — максимальная плотность энергии, запасенная в конденсаторе, Wт — энергия, перешедшая в тепло в единице объема диэлектрика за время одного периода, тогда
Если W — максимальная плотность энергии, запасенная в конденсаторе, Wт — энергия, перешедшая в тепло в единице объема диэлектрика за время одного периода, тогда
(8)
Математический анализ параметров петли гистерезиса позволяет преобразовать формулу (8) в выражение:
,
где SГ — площадь петли гистерезиса в координатах x, y;
x и y — координаты вершины петли гистерезиса.
Дата добавления: 2016-09-03 ; просмотров: 993 | Нарушение авторских прав
Вопрос. Что такое поляризация диэлектрика?
Ответ. Поляризацией называется состояние вещества, при котором элементарный объем диэлектрика приобретает электрический момент.
Вопрос. За счет чего возникает электрический момент в объеме диэлектрика?
Ответ. Возникновение электрического момента в объеме образца диэлектрического материала или участка электрической изоляции может происходить под действием электрического поля, механических напряжений или спонтанно (самопроизвольно)./19585.gif)
Вопрос. Что называется относительной диэлектрической проницаемостью?
Ответ. Относительная диэлектрическая проницаемость представляет собой отношение суммарного заряда конденсатора с диэлектриком к заряду того же конденсатора, если поместить его в вакууме без диэлектрика.
Вопрос. Какие диэлектрики называются линейными и нелинейными?
Ответ. Для линейных диэлектриков зависимость поляризованности от напряженности поля носит линейный характер, для нелинейных
| Corning 0010 (калий, сода, свинец) | 24 | ε ′ / ε ν | 6,68 | 6,63 | 6,57 | 6,503 | 6,503 | 6,33 | — | 6,1 | 5,96 | 5,87 | & gt; 17 | 8,9 | 7,0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan δ | 77,5 | 00050005515 | 23 | — | 60 | 90 | 110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Corning 0014 (свинец, барий) | 25 | ε ′ / ε | 6,77 | 6,76 | 6,75 | 6,73 | 6,72 | 6,70 | 6,69 | — | 6,64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 14,4 | 12,2 | 12,4 | 13,8 | 17,0 | 19,5 | — | 70 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Corning 0080 (натронная известь) | 9000 ′8,30 | 7,70 | 7,35 | 7,08 | 6,90 | 6,82 | 6,75 | — | 6,71 | 6,71 | 00049,62 | 6,71 | 9,62 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan δ | 780 | 400 | 220 | 140 | 100 | 85 | 90 | — | 126 | 170 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 35)
35) 18
18