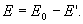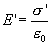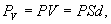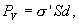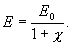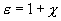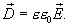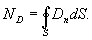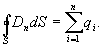2. Напряженность поля в диэлектрике. Поляризованность.
При помещении диэлектрика во внешнее поле он поляризуется, то есть приобретает отличный от нуля дипольный момента
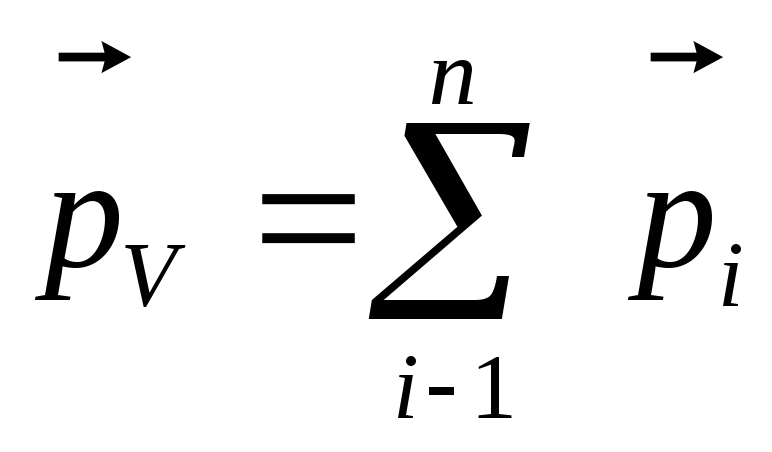 ,
,
где 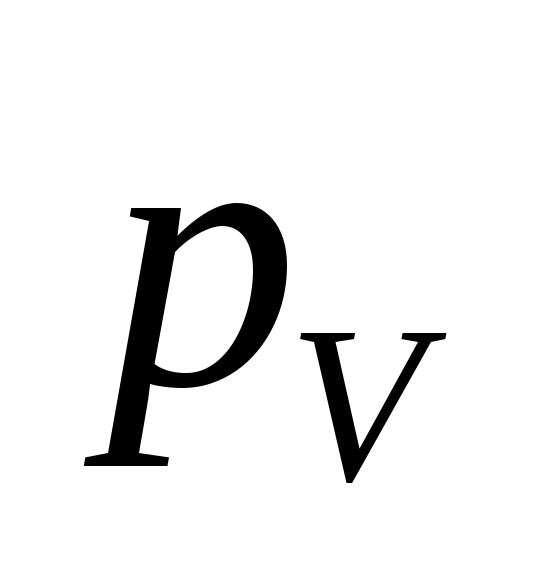 — дипольный момент всего диэлектрика,
— дипольный момент всего диэлектрика,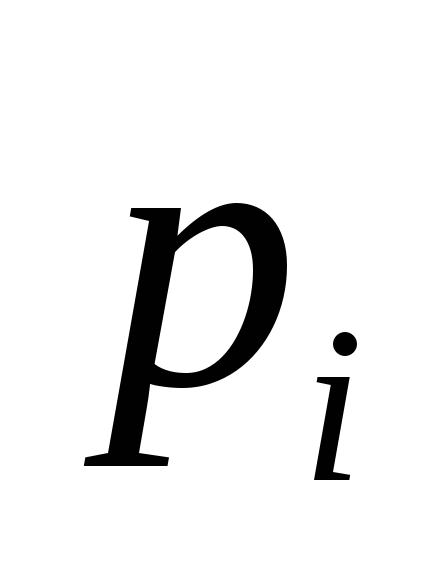 — дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной – поляризованностью,
определяемой как дипольный момент
единицы объема диэлектрика
— дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной – поляризованностью,
определяемой как дипольный момент
единицы объема диэлектрика
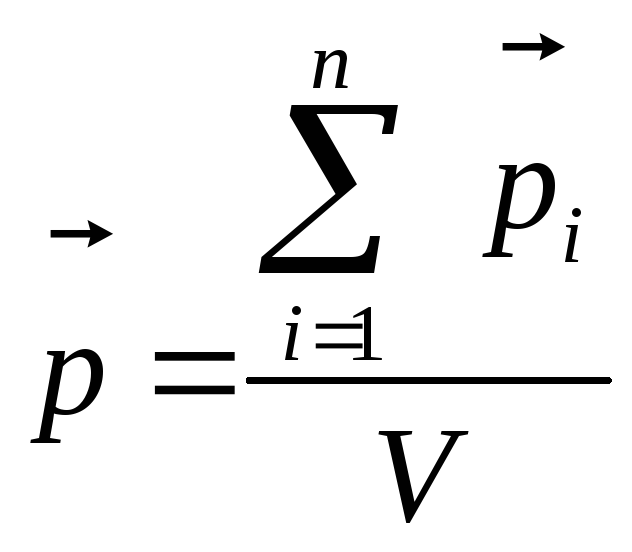 ,
(1)
,
(1)
где 
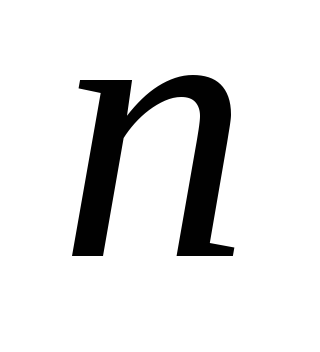 — число молекул в объеме
— число молекул в объеме .
. Для всех диэлектриков (за исключением
сегнетоэлектриков) поляризованность 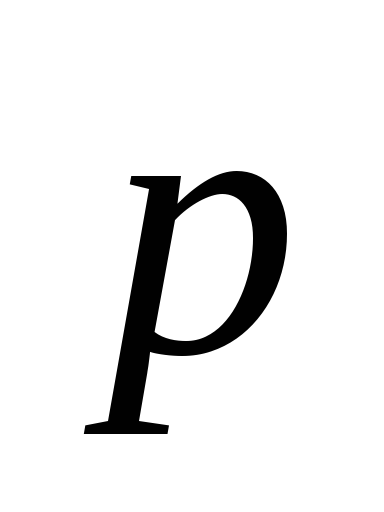 линейно зависит от напряженности поля
линейно зависит от напряженности поля ,
если
,
если не слишком велико,
не слишком велико,
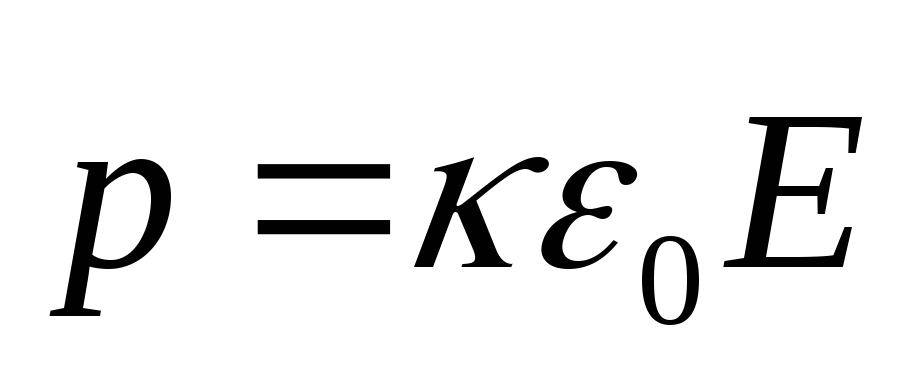
где  — диэлектрическая восприимчивость
вещества.
— диэлектрическая восприимчивость
вещества.
Для установления количественных закономерностей поля в диэлектрике внесем в однородное поле пластинку из диэлектрика. Под действием поля весь диэлектрик поляризуется. Положительные заряды смещаются по полю, отрицательные – против поля. В результате на правой грани будет избыток положительных зарядов, на левой – отрицательных зарядов. Заряды, появляющиеся в результате поляризации называются связанными.
| Концентрация
связанных зарядов Поле, которое будет устанавливаться в диэлектрике равно: |
Рис.3. |
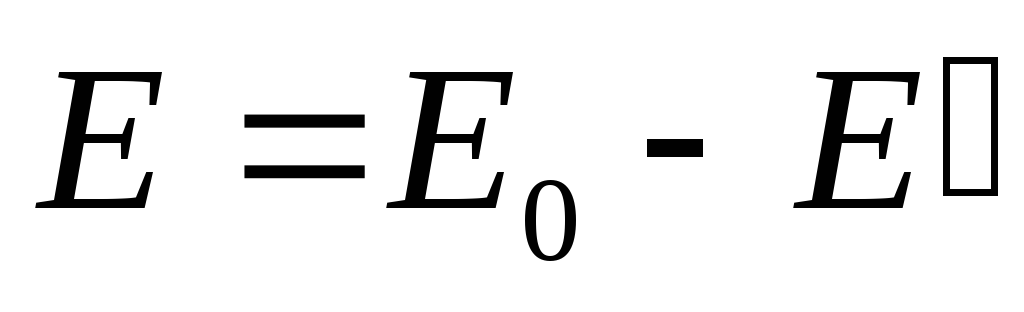 ,
,
где 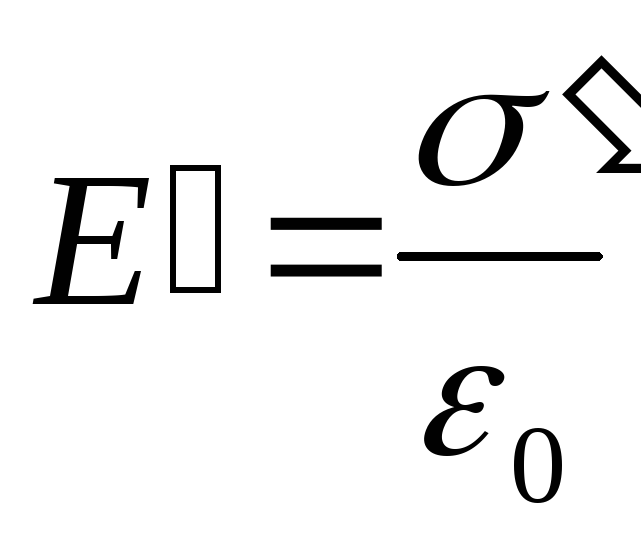 (поле, создаваемое двумя бесконечными
плоскостями). Тогда
(поле, создаваемое двумя бесконечными
плоскостями). Тогда
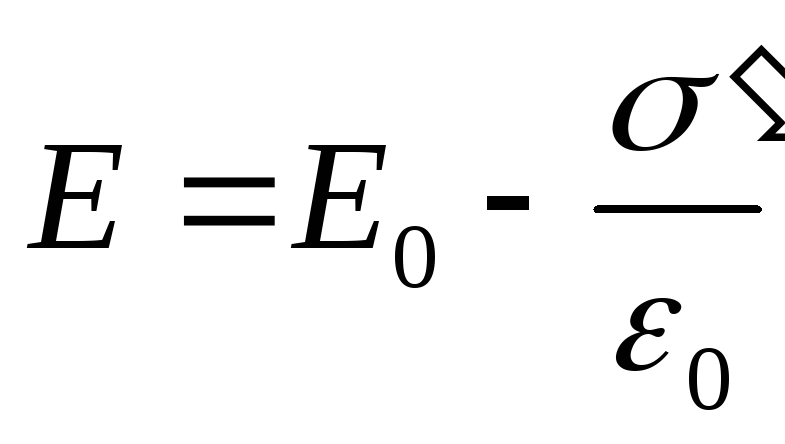 .
(3)
.
(3)
Определим поверхностную плотность
связанных зарядов 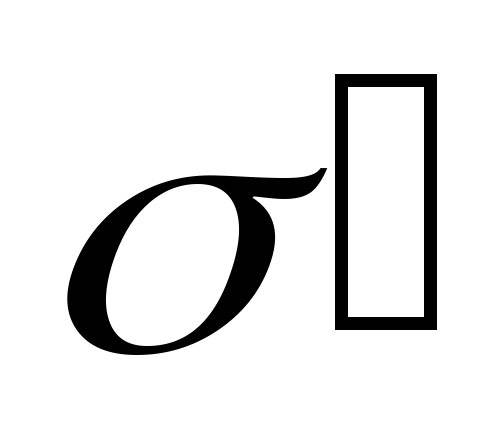
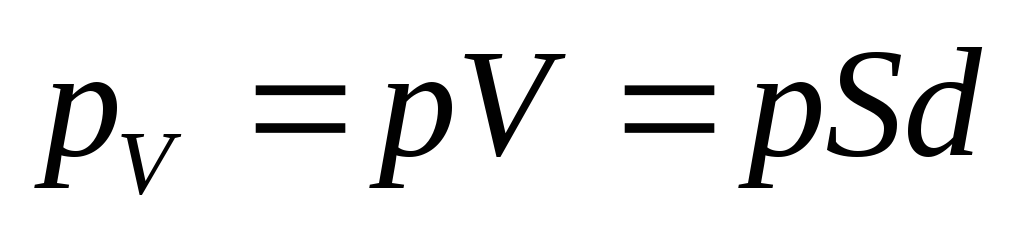 ,
(4)
,
(4)
где 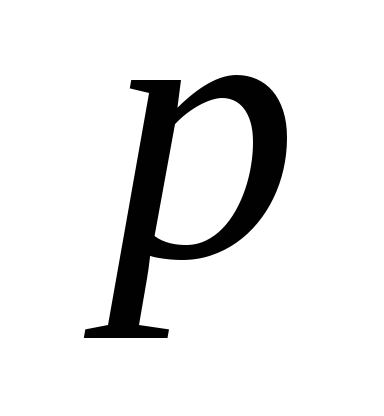 — поляризованность диэлектрика,- объем диэлектрика,
— поляризованность диэлектрика,- объем диэлектрика, — площадь грани пластины,
— площадь грани пластины, — ее толщина.
— ее толщина.
Дипольный момент пластины можно еще
определить как произведение связанного
заряда каждой грани 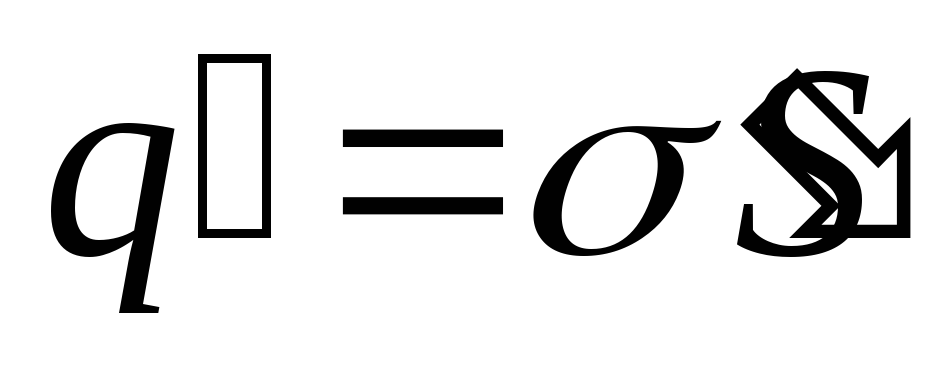
 .
. 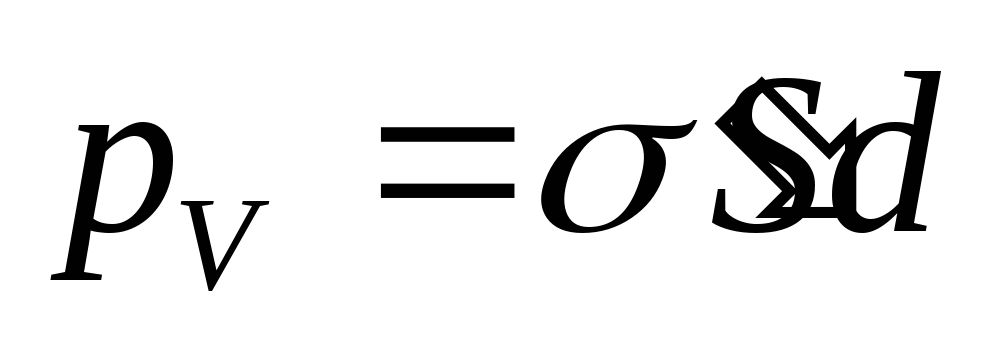 .
(5)
.
(5)
Из сравнения (4) и (5) получаем, что
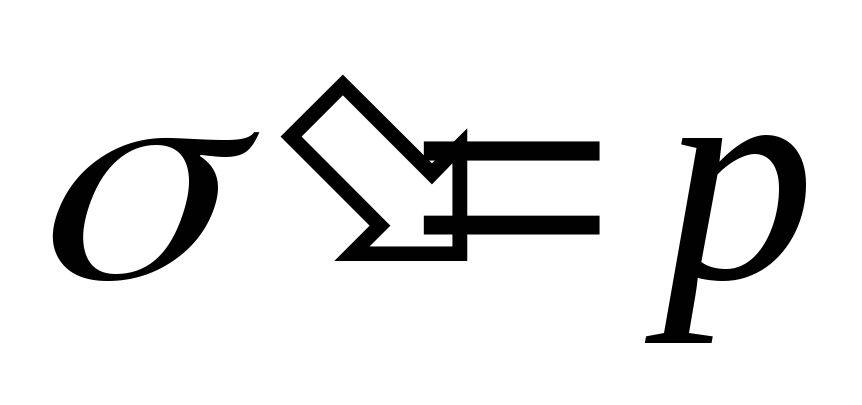 .
(6)
.
(6)
Поверхностная плотность связанных
зарядов равна поляризованности 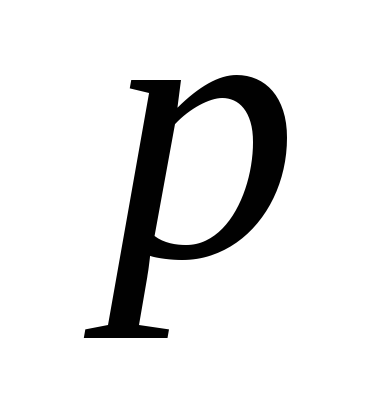 .
Подставив (6) в (3) и учитывая (2) получим
.
Подставив (6) в (3) и учитывая (2) получим
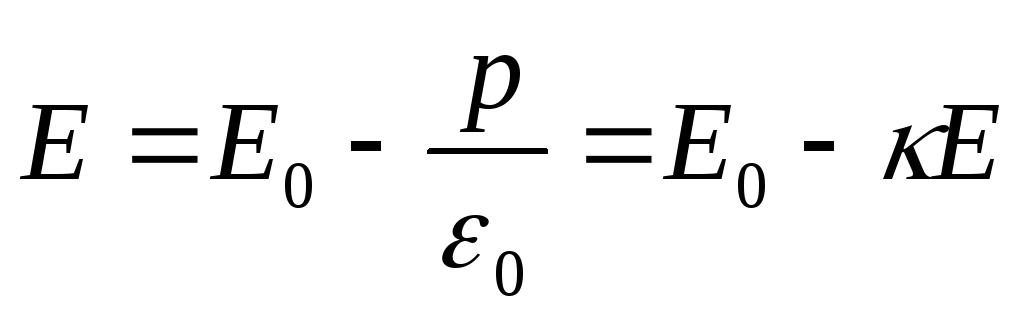 .
.
Отсюда следует
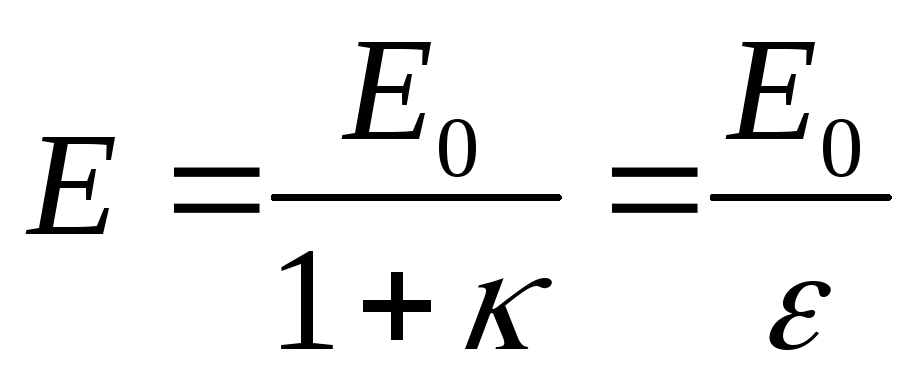 ,
(7)
,
(7)
где 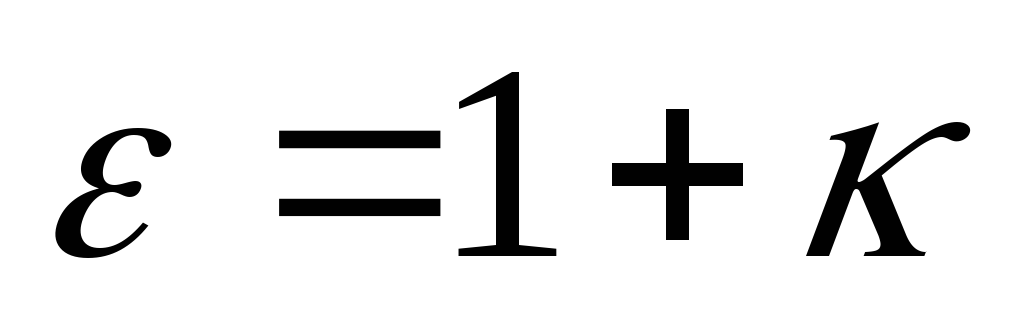 — диэлектрическая проницаемость среды,
показывающая во сколько раз поле
ослабляется за счет диэлектрика.
— диэлектрическая проницаемость среды,
показывающая во сколько раз поле
ослабляется за счет диэлектрика.
3. Электрическое смещение. Теорема Остроградского-Гаусса для электростатического поля в диэлектрике.
Согласно принципу суперпозиции полей, напряженность поля в диэлектрике равна геометрической сумме напряженностей полей свободных и связанных зарядов
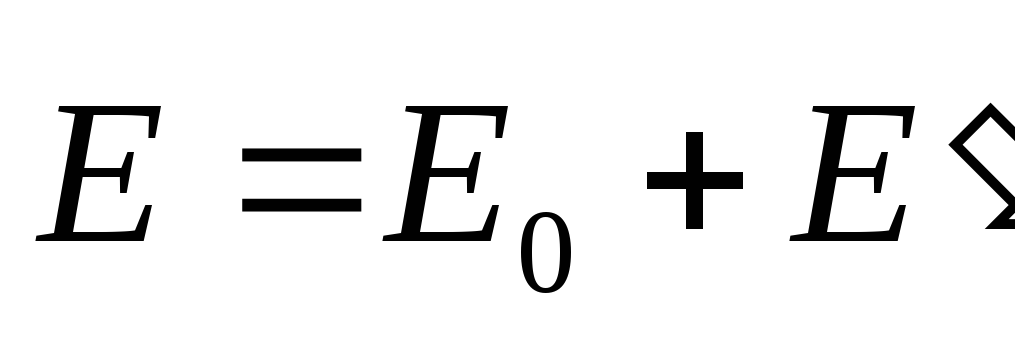
Теорема Остроградского-Гаусса для
электростатического поля в вакууме
может быть распространена на
электростатическое поле в среде, если
под  понимать алгебраическую сумму всех
свободных и связанных зарядов, охватываемых
замкнутой поверхностью.
понимать алгебраическую сумму всех
свободных и связанных зарядов, охватываемых
замкнутой поверхностью.
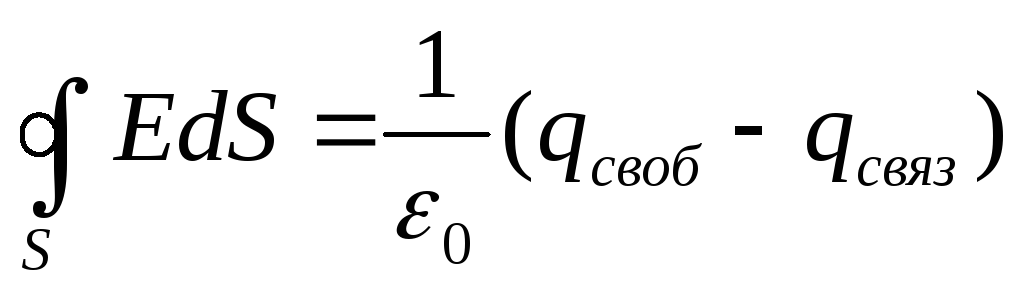 (8)
(8)
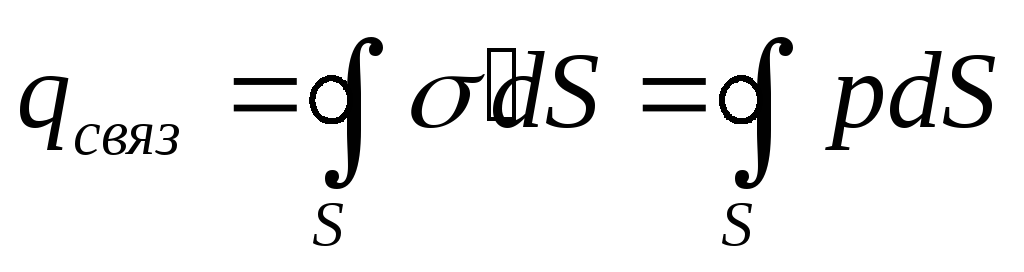 (9)
(9)
Подставим (9) в (8)
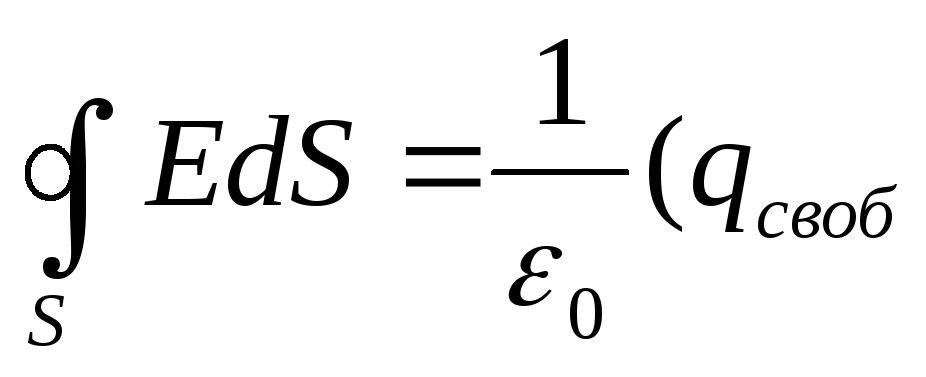
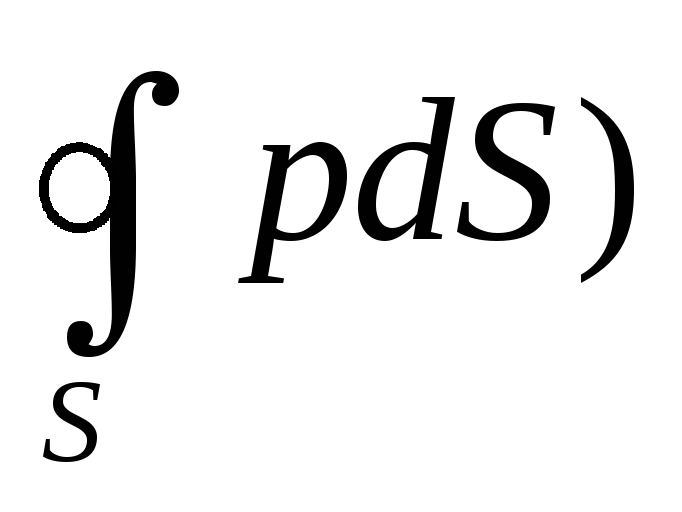
или
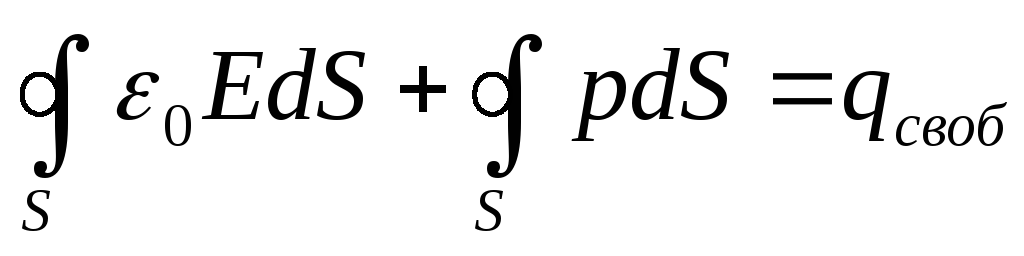 .
.
В обоих интегралах интегрирование
проводится по одной и той же замкнутой
поверхности  .
Поэтому
.
Поэтому
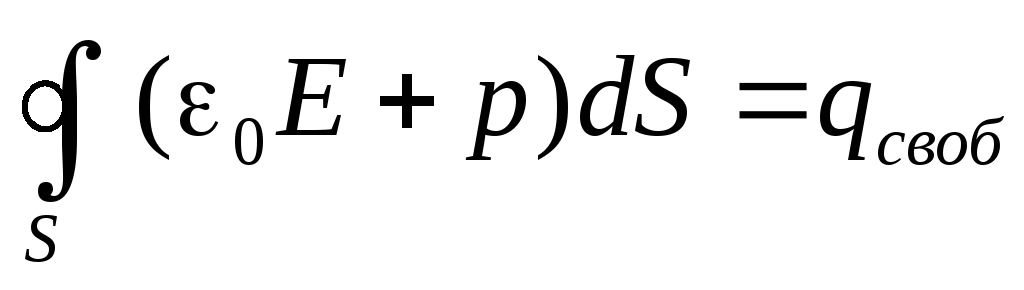
Вектор
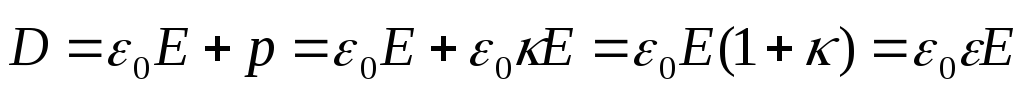 (10)
(10)
называется электрическим смещением. Размерность [D]=Кл/м 2. Тогда теорема Остроградского-Гаусса для электростатического поля в диэлектрике запишется в форме
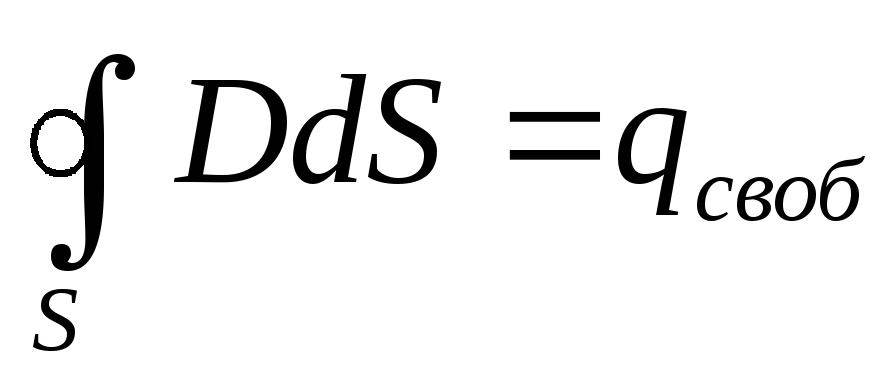 .
(11)
.
(11)
Поток электрического смещения электростатического поля сквозь произвольную замкнутую поверхность, проведенную в поле, равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.
При расчете полей в среде удобней
пользоваться электрическим смещением 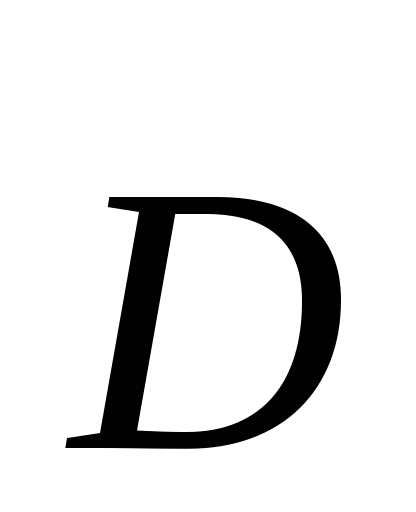 ,
так как оно в отличие от напряженности
поля
,
так как оно в отличие от напряженности
поля не испытывает скачкообразные изменения
при переходе через границу диэлектриков.
не испытывает скачкообразные изменения
при переходе через границу диэлектриков.
Напряженность поля в диэлектрике. Электрическое смещение
Напряженность поля в диэлектрике. Электрическое смещение.
Рассмотрим
диэлектрическую пластинку, заполняющую
плоский конденсатор (рис.14.5) и находящуюся,
следовательно, в практически однородном
внешнем поле 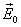 .
.
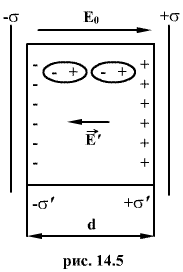
В результате
поляризации на гранях диэлектрика,
обращенных к пластинам конденсатора,
концы молекулярных диполей окажутся
нескомпенсированными соседними диполями.
Поэтому на правой грани, обращенной к
отрицательной пластине конденсатора,
окажется избыток положительного заряда
с некоторой поверхностной плотностью 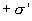
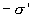 .
Эти так называемые поляризационные,
или связанные заряды не могут быть
переданы соприкосновением другому телу
без разрушения молекул диэлектрика,
т.к. они обусловлены самими поляризованными
молекулами. Возникновение поляризованных
зарядов приводит к возникновению
дополнительного электрического поля
.
Эти так называемые поляризационные,
или связанные заряды не могут быть
переданы соприкосновением другому телу
без разрушения молекул диэлектрика,
т.к. они обусловлены самими поляризованными
молекулами. Возникновение поляризованных
зарядов приводит к возникновению
дополнительного электрического поля 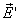
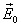 .
Результирующее электрическое поле Е
внутри диэлектрика равно
.
Результирующее электрическое поле Е
внутри диэлектрика равно
| (14.2) |
Для
определения 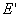 применим
формулу вычисления напряженности
применим
формулу вычисления напряженности 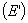 конденсатора
конденсатора
| (14.3) |
Свяжем 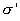 с
вектором поляризации Р. Для этого
определим полный дипольный момент (во
всем объеме) диэлектрика. Осуществим
это двумя способами:
с
вектором поляризации Р. Для этого
определим полный дипольный момент (во
всем объеме) диэлектрика. Осуществим
это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
| (14.4) |
где S — площадь пластины конденсатора.
С другой
стороны рассмотрим диэлектрик как
большой диполь, у которого с одной
стороны заряд 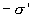 ,
а с другой
,
а с другой 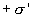 и
расстояние d. Отсюда
и
расстояние d. Отсюда
| (14.5) |
Приравнивая (14.4) и (14.5), получим
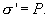
Подставляя 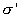 в
(14.3), и затем результат в (14.2), получим
в
(14.3), и затем результат в (14.2), получим
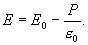
Подставим значение Р из выражения (14.1), тогда
| (14.6) |
Величина
| (14.7) |
называется
диэлектрической проницаемостью или
относительной диэлектрической
проницаемостью. Диэлектрическая
проницаемость 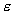 показывает
во сколько раз уменьшается напряженность
в диэлектрике по сравнению с напряженностью
в вакууме.
показывает
во сколько раз уменьшается напряженность
в диэлектрике по сравнению с напряженностью
в вакууме. 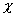 и
и 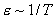 ,
т.е. с ростом температуры диэлектрические
свойства ухудшаются.
,
т.е. с ростом температуры диэлектрические
свойства ухудшаются.
В
неоднородной диэлектрической среде 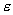 имеет
различные значения, изменяясь на границах
диэлектриков скачкообразно (претерпевая
разрыв). Это затрудняет применение
формул, описывающих взаимодействие
зарядов в вакууме. Что касается теоремы
Гаусса, то в этих условиях она вообще
теряет смысл. В самом деле, благодаря
различной поляризуемости разнородных
диэлектриков напряженности поля в них
будут различными. Поэтому различно и
число силовых линий в каждом диэлектрике
(рис.14.6).
имеет
различные значения, изменяясь на границах
диэлектриков скачкообразно (претерпевая
разрыв). Это затрудняет применение
формул, описывающих взаимодействие
зарядов в вакууме. Что касается теоремы
Гаусса, то в этих условиях она вообще
теряет смысл. В самом деле, благодаря
различной поляризуемости разнородных
диэлектриков напряженности поля в них
будут различными. Поэтому различно и
число силовых линий в каждом диэлектрике
(рис.14.6).
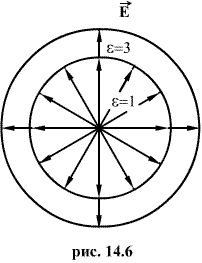
Часть
линий, исходящих из зарядов, окруженных
замкнутой поверхностью, будет заканчиваться
на границе раздела диэлектриков и не
пронижет данную поверхность. Это
затруднение можно устранить, введя в
рассмотрение новую физическую
характеристику поля – вектор электрического
смещения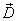
| (14.8) |
Вектор 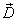 направлен
в ту же сторону, что и
направлен
в ту же сторону, что и 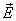 .
В отличие от напряженности
поля
.
В отличие от напряженности
поля 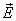 вектор
вектор 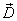 имеет
постоянное значение во всех диэлектриках.
Поэтому электрическое поле в неоднородной
диэлектрической среде удобнее
характеризовать не напряженностью
имеет
постоянное значение во всех диэлектриках.
Поэтому электрическое поле в неоднородной
диэлектрической среде удобнее
характеризовать не напряженностью 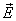 ,
а смещением
,
а смещением 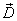 .
С этой целью вводится понятие линий
вектора
.
С этой целью вводится понятие линий
вектора 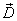 и
потока смещения, аналогично понятию
силовых линий и потока напряженности
и
потока смещения, аналогично понятию
силовых линий и потока напряженности
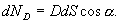
или
| (14.9) |
Используя теорему Гаусса
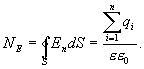
домножим
обе части на 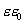
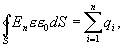
С учетом (14.8) получаем
| (14.10) |
Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.
Напряженность электрического поля в диэлектрике
Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределениемзарядоввнутри проводящих тел, а также поляризацией внутренних микроструктур[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.
58 Электри́ческий
ди́польный моме́нт — векторнаяфизическая
величина, характеризующая, наряду с
суммарным зарядом (и реже используемыми
высшими мультипольными моментами),
электрические свойства системызаряженных
частиц(распределениязарядов)
в смысле создаваемого ею поля и действия
на нее внешних полей. Главная после
суммарного заряда и положения системы
в целом (ее радиус-вектора) характеристика
конфигурации зарядов системы при
наблюдении ее издали. Дипольный
момент — первыймультипольный
момент.
Простейшая система зарядов, имеющая
определенный (не зависящий от выбора
начала координат) ненулевой дипольный
момент — этодиполь(две точечные частицы с одинаковыми по
величине разноимёнными зарядами).
Электрический дипольный момент такой
системы по модулю равен произведению
величины положительного заряда на
расстояние между зарядами и направлен
от отрицательного заряда к положительному,
или: 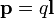 — где q — величина положительного
заряда,
— где q — величина положительного
заряда,  —
вектор с началом в отрицательном заряде
и концом в положительном.
Для системы изN частиц электрический дипольный момент
равен
—
вектор с началом в отрицательном заряде
и концом в положительном.
Для системы изN частиц электрический дипольный момент
равен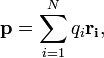 где
где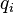 —
заряд частицы с номером
—
заряд частицы с номером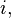 а
а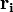 —
её радиус-вектор; или, если суммировать
отдельно по положительным и отрицательным
зарядам:
—
её радиус-вектор; или, если суммировать
отдельно по положительным и отрицательным
зарядам: 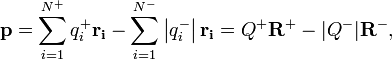 где
где 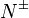 —
число положительно/отрицательно
заряженных частиц,
—
число положительно/отрицательно
заряженных частиц,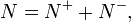
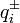 —
их заряды;
—
их заряды;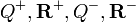 —
суммарные заряды положительной и
отрицательной подсистем и радиус-векторы
их «центров тяжести».
—
суммарные заряды положительной и
отрицательной подсистем и радиус-векторы
их «центров тяжести».
59 Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядоввдиэлектрикеили поворотом электрическихдиполей, обычно под воздействием внешнегоэлектрического поля, иногда под действием других внешних сил или спонтанно. Поляризацию диэлектриков характеризуетвектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков). Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема. Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектрикахв отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры. Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.
Для количественного описания поля в диэлектриках внесем диэлектрик в однородное электростатическое поле. Поле создается двумя бесконечными равномерно заряженными плоскостями. Пластинка из однородного диэлектрика расположена как на рис. 2.4. Заряды, входящие в состав диполей диэлектриков, называются связанными. Под действием электрического поля они не могут покинуть пределов молекулы, в состав которой входят, а лишь смещаются из своих положений равновесия. Поляризация диэлектриков сопровождается появлением поверхностных зарядов на его границах.
В
тех местах, где линии напряженности
выходят из диэлектрика, на поверхности
возникают положительные связанные
заряды, то есть положительные заряды
смещаются по полю, отрицательные –против
поля (рис. 2.4) Таким образом, на правой
грани диэлектрика, обращенного к
отрицательной плоскости, будет избыток
положительного заряда с поверхностной
плотностью (+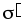 ),а
на левой
– избыток отрицательного заряда с
поверхностной плотностью (–
),а
на левой
– избыток отрицательного заряда с
поверхностной плотностью (–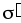 ).
Плотность связанных зарядов определяет
поляризованность диэлектрика:
).
Плотность связанных зарядов определяет
поляризованность диэлектрика: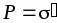 .
Таким
образом, появление нескомпенсированных
поверхностных связанных зарядов
приводит к возникновению внутри
диэлектрика дополнительного электрического
поля с напряженностью
.
Таким
образом, появление нескомпенсированных
поверхностных связанных зарядов
приводит к возникновению внутри
диэлектрика дополнительного электрического
поля с напряженностью 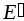 (поле,
созданное двумя бесконечными заряженными
плоскостями, т.е. гранями), которое
направлено против внешнего поля и
ослабляет его
(поле,
созданное двумя бесконечными заряженными
плоскостями, т.е. гранями), которое
направлено против внешнего поля и
ослабляет его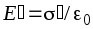 (2.4)Внешнее
поле – это поле, созданное свободными
зарядами, в данном случае бесконечными
заряженными пластинами.
Напряженность
внешнего поля определяется по
формуле
(2.4)Внешнее
поле – это поле, созданное свободными
зарядами, в данном случае бесконечными
заряженными пластинами.
Напряженность
внешнего поля определяется по
формуле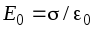 (2.5)
Результирующая напряженность поля
внутри диэлектрика равна:
(2.5)
Результирующая напряженность поля
внутри диэлектрика равна: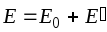 или в скалярном
виде с учетом направления
или в скалярном
виде с учетом направления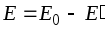 .(2.6)
Напряженность
электрического поля определяется всеми
зарядами: и сторонними
.(2.6)
Напряженность
электрического поля определяется всеми
зарядами: и сторонними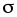 ,
и связанными
,
и связанными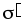 .
С учетом (2.4) и (2.5) можно записать
.
С учетом (2.4) и (2.5) можно записать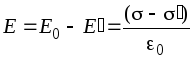 электри́ческое
смеще́ние)
— векторная
величина, равная сумме векторанапряжённости
электрического поляивектора
поляризации. В СИ:
электри́ческое
смеще́ние)
— векторная
величина, равная сумме векторанапряжённости
электрического поляивектора
поляризации. В СИ: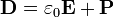 .
В СГС:
.
В СГС: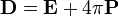 .
Величина
электрической индукции в системеСГСизмеряется в СГСЭ или СГСМ единицах, а
вСИ—
вкулонахна м² (L−2TI).
В рамках СТОвекторы
.
Величина
электрической индукции в системеСГСизмеряется в СГСЭ или СГСМ единицах, а
вСИ—
вкулонахна м² (L−2TI).
В рамках СТОвекторы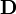 и
и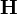 объединяются в единый тензор, аналогичныйтензору
электромагнитного поля.
объединяются в единый тензор, аналогичныйтензору
электромагнитного поля.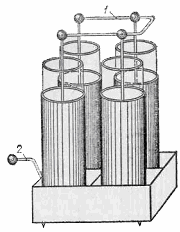
60 Электроемкость— Это отношение количества электричества, имеющегося на каком-либо проводящем теле, к величине потенциала этого тела при условии, что все проводящие тела, находящиеся вблизи этого тела, соединены с землей. Обозначая Э. тела через С, заряд на теле через Q и потенциал через V, имеем C = Q/V. Практической единицей Э. принимается ныне фарада или, еще чаще, миллионная доля фарады, называемая микрофарадой. Фарада обозначается обыкновенно через F, микрофарада — через μ F. Фарада — это электроемкость такого тела, в котором при потенциале равном 1 вольту, содержится один кулон электричества. Для сравнения электроемкостей тел существует несколько способов. Упомянем только о трех, наиболее часто употребляемых. В настоящее время имеются ящики электроемкостей, т. е. ящики, содержащие в себе конденсаторы различных электроемкостей, долей микрофарады, а также целых микрофарад, которые можно комбинировать в желаемые группы. Сами конденсаторы изготовляются из тонких листов олова (станиоль), отделенных друг от друга листами парафинированной бумаги, и заливаются парафином.
Различные
типы конденсаторов.
заряжая любой изолированный проводник,
мы одновременно создаем противоположный
заряд на окружающих проводниках,
соединенных с Землей и образующих
вместе с этим телом конденсатор. Однако
емкость такого конденсатора мала. Чтобы
получить большую емкость, необходимо
взять проводники в виде металлических
пластин, возможно близко расположенных
друг к другу (так называемые обкладки
конденсатора). Мы видели, что емкость
плоского конденсатора прямо пропорциональна
площади обкладок и обратно пропорциональна
расстоянию между ними. Поэтому при
большой поверхности обкладок и при
тонком слое диэлектрика между ними
емкость конденсатора очень велика, и
на нем можно накопить («сгустить»)
значительные заряды даже при небольшом
напряжении. Отсюда происходит и название
«конденсатор» (от латинского слова
condensare — сгущать).
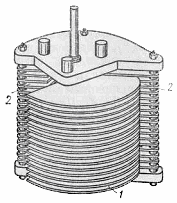
Для увеличения
емкости конденсаторы соединяют в
батареи. На рис. 60 изображена батарея
из четырех лейденских банок. Все внешние
и все внутренние обкладки Рис.
60. Батарея из четырех лейденских банок:
1 — стержень для зарядки внутренних
обкладок, 2 — стержень для заземления
внешних обкладок Рис.
61. Конденсатор переменной емкости
состоит из двух изолированных систем
металлических пластин 1 и 2, которые
входят друг в друга при вращении
рукоятки соединены
между собой, и поэтому батарею можно
рассматривать как один большой
конденсатор, у которого площадь обкладок
равна сумме площадей обкладок отдельных
банок. Емкость батареи при таком
соединении (оно называется параллельным
соединением) равна сумме емкостей
отдельных конденсаторов.
На рис. 61
показан конденсатор переменной емкости,
широко употребляющийся в радиотехнике.
Он состоит из двух изолированных систем
металлических пластин, которые входят
друг в друга при вращении рукоятки.
Вдвигание и выдвигание одной системы
пластин в другую изменяют емкость
конденсатора (§ 33). 61
Энергия
системы зарядов Энергия
взаимодействия системы точечных
зарядов, вычисляемая по формуле (3),
может быть как положительной, так и
отрицательной. Например она отрицательная
для двух точечных зарядов противоположного
знака. Формула (3) определяет не полную
электростатическую энергию системы
точечных зарядов, а только их взаимную
потенциальную энергию. Каждый заряд
qi,
взятый в отдельности обладает
электрической энергией. Она называется
собственной энергией заряда и представляет
собой энергию взаимного отталкивания
бесконечно малых частей, на которые
его можно мысленно разбить. Эта энергия
не учитывается в формуле (3). Учитывается
только работа затрачиваемая на сближение
зарядов qi,
но не на их образование.
Полная
электростатическая энергия системы
точечных зарядов учитывает также
работу, на образование зарядов qiиз
бесконечно малых порций электричества,
переносимых из бесконечности. Полная
электростатическая энергия системы
зарядов всегда положительная. Это легко
показать на примере заряженного
проводника. Рассматривая заряженный
проводник как систему точечных зарядов
и учитывая одинаковое значение потенциала
в любой точке проводника, из формулы
(3) получим: 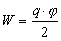 .
(4)
.
(4)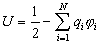 ,
(3)
,
(3)
Энергия
заряженного проводника Как
известно,
заряд сосредоточивается на поверхности
проводника, причем поверхность проводника
эквипотенциальна. Разбивая эту
поверхность на маленькие участки,
каждый из которых имеет заряд Δq,
и учитывая, что потенциал в месте
расположения каждого из зарядов
одинаков, имеем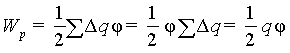 (6.7)
Так
как емкостьпроводникаC=q/φ
, то выражение (6.7) может быть также
представлено, как
(6.7)
Так
как емкостьпроводникаC=q/φ
, то выражение (6.7) может быть также
представлено, как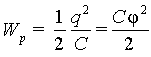 (6.8)
(6.8)
Энергия
заряженного конденсатора
Пусть
заряд +q находится на обкладке с потенциалом
φ1 а заряд —q на
обкладке с потенциалом φ2.
Тогда на основании тех же рассуждений,
которые привели к выражению (6.7),
получим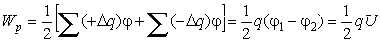 гдеU — разность потенциалов на обкладках
конденсатора. Аналогично переходу от
(6.7) к (6.8) выражение для энергии конденсатора
может быть представлено также в виде
гдеU — разность потенциалов на обкладках
конденсатора. Аналогично переходу от
(6.7) к (6.8) выражение для энергии конденсатора
может быть представлено также в виде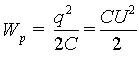
Электрическое
поле — одна из составляющих электромагнитного
поля; особый видматерии,
существующий вокругтелиличастиц,
обладающихэлектрическим
зарядом, а также возникающий при
изменениимагнитного
поля(например, вэлектромагнитных
волнах). Электрическое поле
непосредственно невидимо, но может
быть обнаружено благодаря его силовому
воздействию назаряженные
тела.
Для количественного определения
электрического поля вводится силовая
характеристика —напряжённость
электрического поля—векторнаяфизическая величина, равная отношению
силы, с которой поле действует на
положительный пробный заряд, помещённый
в данную точку пространства, к величине
этого заряда. Направление вектора
напряженности совпадает в каждой точке
пространства с направлением силы,
действующей на положительный пробный
заряд.
Вклассической
физике, применимой при рассмотрении
крупномасштабных (больше размера атома)
взаимодействий, электрическое поле
рассматривается как одна из составляющих
единого электромагнитного поля и
проявление электромагнитного
взаимодействия. Вквантовой
электродинамике— это компонент
электрослабого взаимодействия.
В
классической физике системауравнений
Максвеллаописывает взаимодействие
электрического поля, магнитного поля
и воздействие зарядов на эту систему
полей.Сила
Лоренцаописывает воздействие
электромагнитного поля на частицу.Эффект
поля заключается в том, что при воздействии
электрического поля на поверхность
электропроводящей среды в её
приповерхностном слое изменяется
концентрация свободных носителей
заряда. Этот эффект лежит в основе
работы полевых транзисторов.
Основным
действием электрического поля является силовое
воздействие на неподвижные (относительно наблюдателя) электрически
заряженные тела или частицы. Если
заряженное тело фиксировано в
пространстве, то оно под действием силы
не ускоряется. На движущиеся заряды
силовое воздействие оказывает и магнитное
поле (вторая составляющая силы
Лоренца).Электрическое поле обладает
энергией. Плотность этой энергии
определяется величиной поля и может
быть найдена по формуле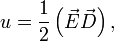 гдеE — напряжённость
электрического поля,D — индукция
электрического поля.
гдеE — напряжённость
электрического поля,D — индукция
электрического поля.
62 Электродвижущая
сила (ЭДС) — скалярная физическая
величина, характеризующая работу
сторонних (непотенциальных) сил висточникахпостоянного или переменного тока. В
замкнутом проводящем контуре ЭДС равнаработеэтих сил по перемещению единичного
положительногозарядавдоль контура.
ЭДС можно выразить
черезнапряжённость
электрического полясторонних сил
(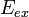 ).
В замкнутом контуре (
).
В замкнутом контуре (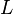 )
тогда ЭДС будет равна:
)
тогда ЭДС будет равна: 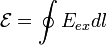 ,
где
,
где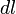 —
элемент длины контура.ЭДС
так же, как и напряжение,
измеряется ввольтах.
Можно говорить об электродвижущей силе
на любом участке цепи. Это удельная
работа сторонних сил не во всем контуре,
а только на данном участке. ЭДС
гальванического элемента есть работа
сторонних сил при перемещении единичного
положительного заряда внутри элемента
от одного полюса к другому. Работа
сторонних сил не может быть выражена
через разность потенциалов, так как
сторонние силы непотенциальны и их
работа зависит от формы траектории.
Так, например, работа сторонних сил при
перемещении заряда между клеммами тока
вне самого источника равна нулю.
—
элемент длины контура.ЭДС
так же, как и напряжение,
измеряется ввольтах.
Можно говорить об электродвижущей силе
на любом участке цепи. Это удельная
работа сторонних сил не во всем контуре,
а только на данном участке. ЭДС
гальванического элемента есть работа
сторонних сил при перемещении единичного
положительного заряда внутри элемента
от одного полюса к другому. Работа
сторонних сил не может быть выражена
через разность потенциалов, так как
сторонние силы непотенциальны и их
работа зависит от формы траектории.
Так, например, работа сторонних сил при
перемещении заряда между клеммами тока
вне самого источника равна нулю.
2.3. Напряженность электрического поля в диэлектрике
Для количественного описания поля в диэлектриках внесем диэлектрик в однородное электростатическое поле. Поле создается двумя бесконечными равномерно заряженными плоскостями. Пластинка из однородного диэлектрика расположена как на рис. 2.4.
Заряды, входящие в состав диполей диэлектриков, называются связанными. Под действием электрического поля они не могут покинуть пределов молекулы, в состав которой входят, а лишь смещаются из своих положений равновесия. Поляризация диэлектриков сопровождается появлением поверхностных зарядов на его границах.
В
тех местах, где линии напряженности
выходят из диэлектрика, на поверхности
возникают положительные связанные
заряды, то есть положительные заряды
смещаются по полю, отрицательные –против
поля (рис. 2.4) Таким образом, на правой
грани диэлектрика, обращенного к
отрицательной плоскости, будет избыток
положительного заряда с поверхностной
плотностью (+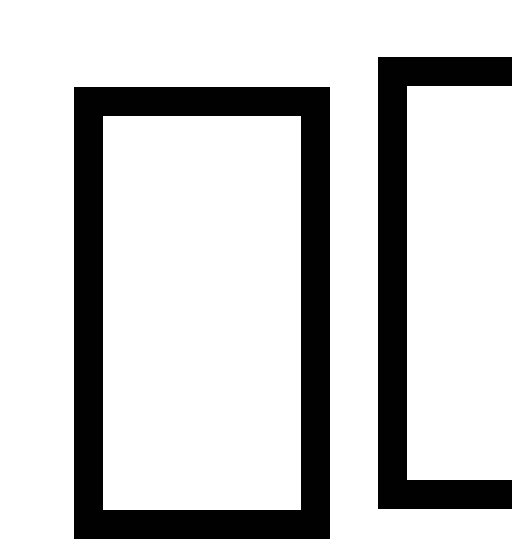 ),а
на левой – избыток
отрицательного заряда с поверхностной
плотностью (–
),а
на левой – избыток
отрицательного заряда с поверхностной
плотностью (–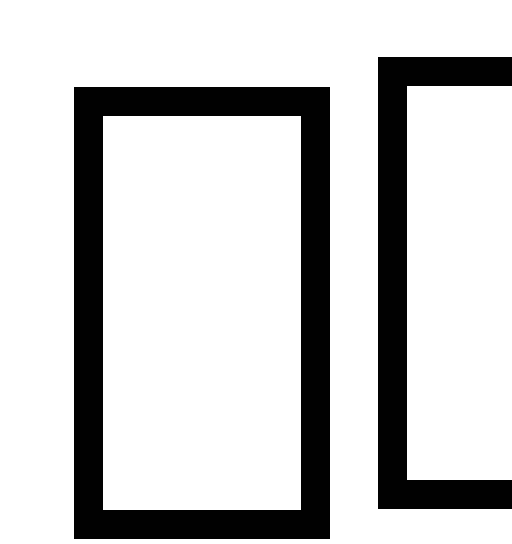 ).
Плотность связанных зарядов определяет
поляризованность диэлектрика:
).
Плотность связанных зарядов определяет
поляризованность диэлектрика: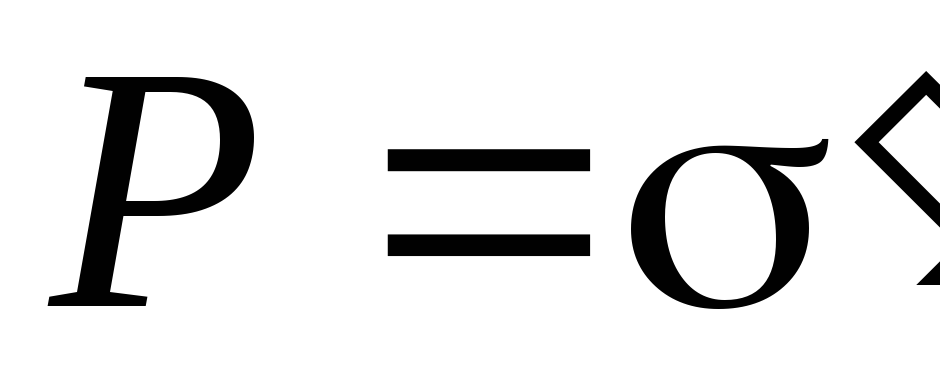 .
.
Таким
образом, появление нескомпенсированных
поверхностных связанных зарядов приводит
к возникновению внутри диэлектрика
дополнительного электрического поля
с напряженностью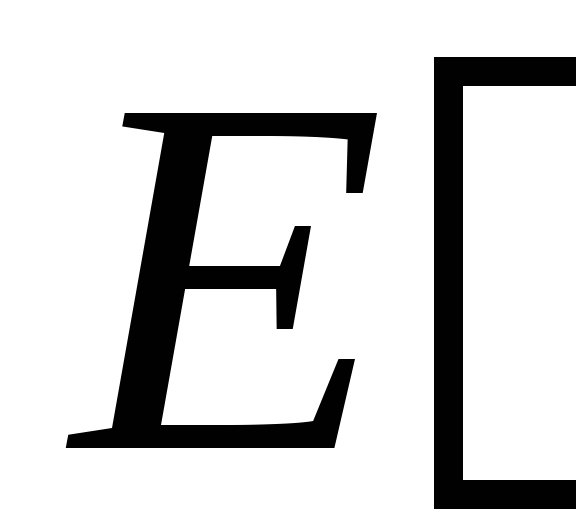 (поле, созданное двумя бесконечными
заряженными плоскостями, т.е. гранями),
которое направлено против внешнего
поля и ослабляет его
(поле, созданное двумя бесконечными
заряженными плоскостями, т.е. гранями),
которое направлено против внешнего
поля и ослабляет его
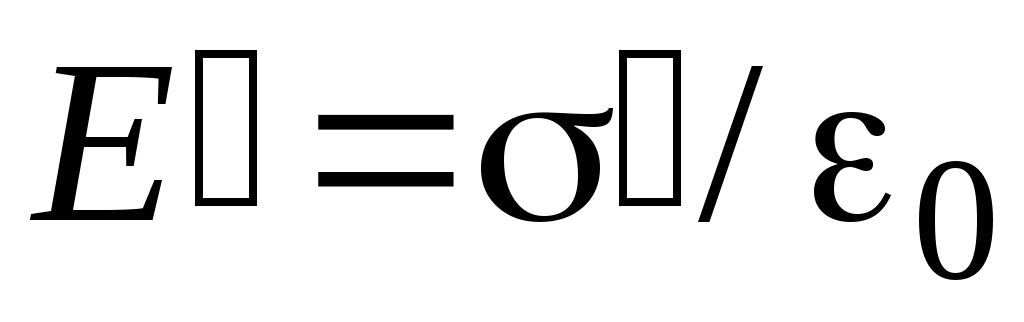 . (2.4)
. (2.4)
Внешнее поле – это поле, созданное свободными зарядами, в данном случае бесконечными заряженными пластинами.
Напряженность внешнего поля определяется по формуле
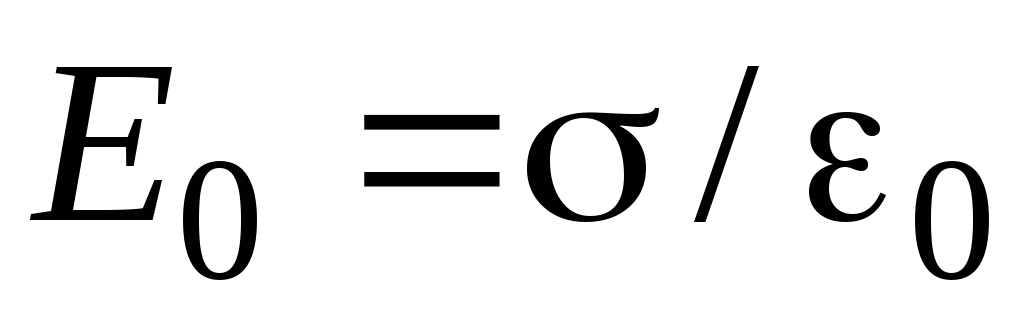 . (2.5)
. (2.5)
Результирующая напряженность поля внутри диэлектрика равна:
или в скалярном виде с учетом направления
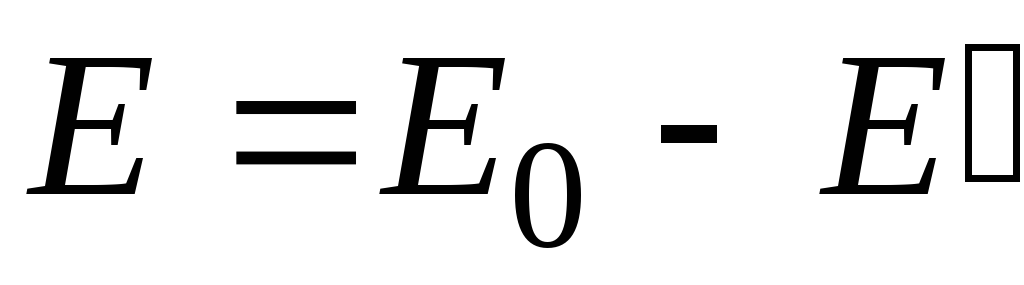 . (2.6)
. (2.6)
Напряженность
электрического поля определяется всеми
зарядами: и сторонними  ,
и связанными
,
и связанными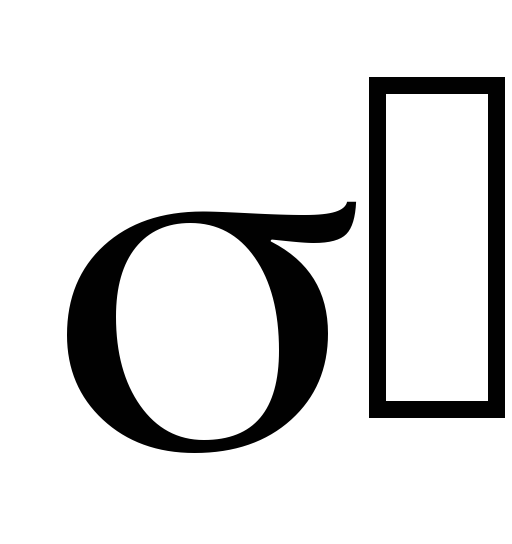 .
С учетом (2.4) и (2.5) можно записать
.
С учетом (2.4) и (2.5) можно записать
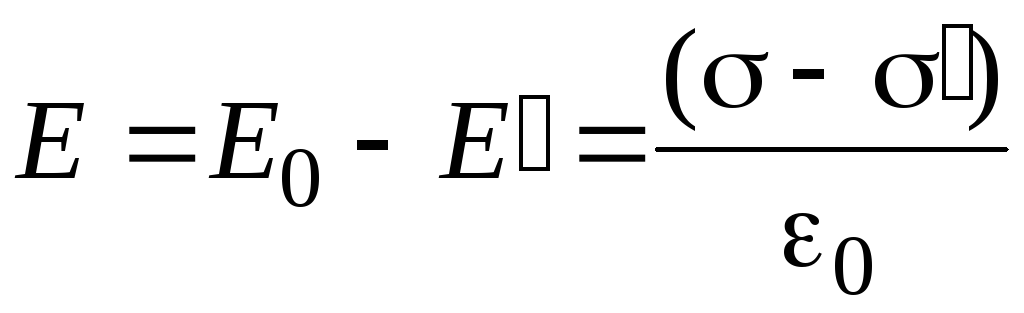 . (2.7)
. (2.7)
Так
как поверхностная плотность связанных
зарядов 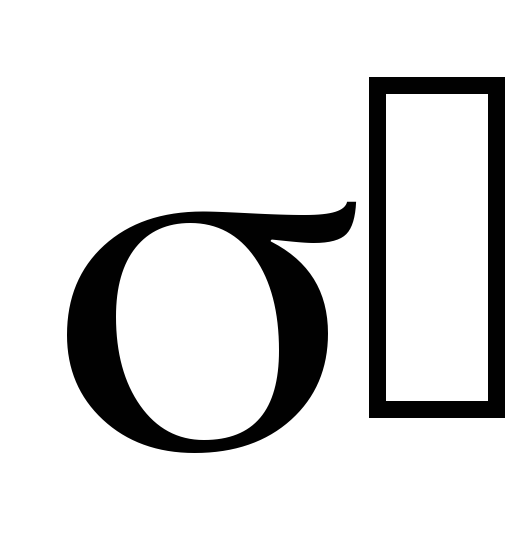 меньше поверхностной плотности свободных
зарядов, то не все поле компенсируется
зарядами диэлектрика, часть линий
напряженности поля пройдет сквозь
диэлектрик, другая же обрывается на
связанных зарядах (рис. 2.4).
меньше поверхностной плотности свободных
зарядов, то не все поле компенсируется
зарядами диэлектрика, часть линий
напряженности поля пройдет сквозь
диэлектрик, другая же обрывается на
связанных зарядах (рис. 2.4).
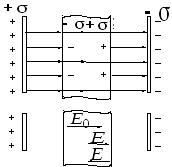
Рис. 2.4. Диэлектрик в однородном электростатическом поле
Следовательно,
результирующее поле внутри диэлектрика
меньше, чем внешнее поле. Величина,
показывающая во сколько раз поле в
вакууме больше, чем поле в диэлектрике,
называется относительной диэлектрической
проницаемостью вещества 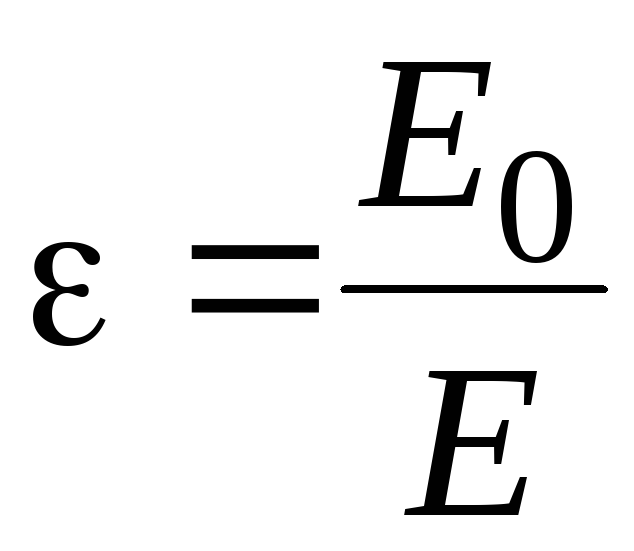 .
.
Относительная диэлектрическая проницаемость связана с диэлектрической восприимчивостью вещества
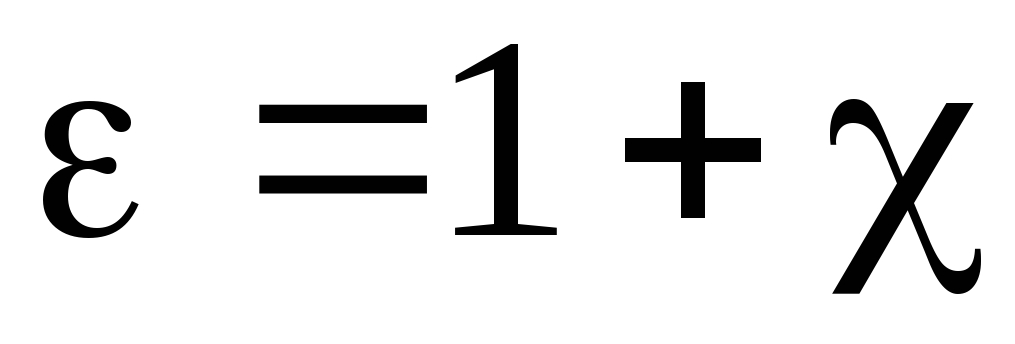 . (2.8)
. (2.8)
Отсюда
следует, что диэлектрическая проницаемость  больше
диэлектрической восприимчивости для
всех веществ.
больше
диэлектрической восприимчивости для
всех веществ.
Таким образом, результирующее поле внутри диэлектрика будет определяться по формуле
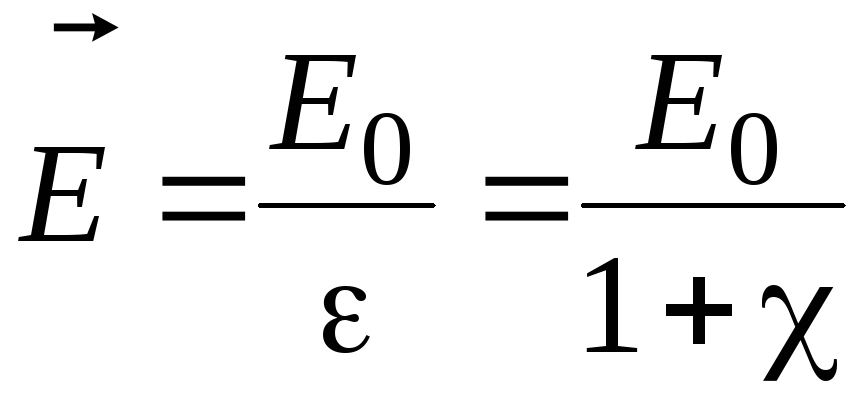 . (2.9)
. (2.9)
Следовательно, относительная диэлектрическая проницаемость ε характеризует электрические свойства диэлектрика, т.е. способность диэлектрика к поляризации.
2.4. Теория метода
Эквивалентная схема электрической цепи для измерения относительной диэлектрической проницаемости представлена на рис. 2.5.
 C R
C R
~ u0
Рис. 2.5. Схема электрической цепи
для измерения относительной диэлектрической проницаемости
Реактивное сопротивление конденсатора цепи переменного синусоидального тока определяется выражением
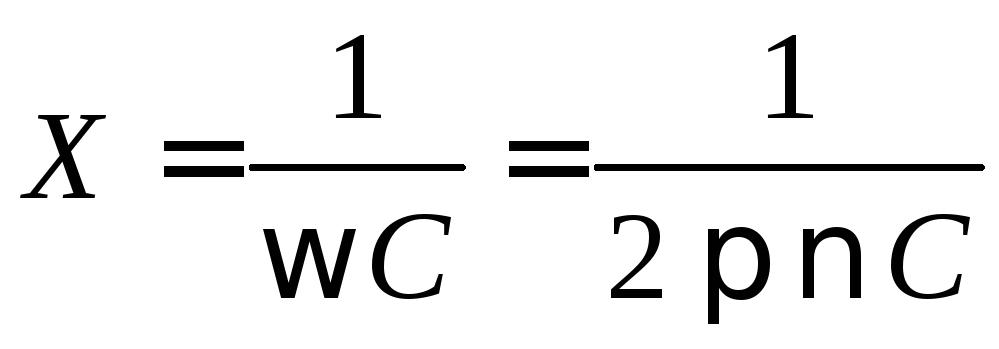 , (2.10)
, (2.10)
где C – емкость конденсатора, – частота переменного напряжения (тока).
Величину переменного тока можно определить по закону Ома, обобщенного для цепей переменного тока:
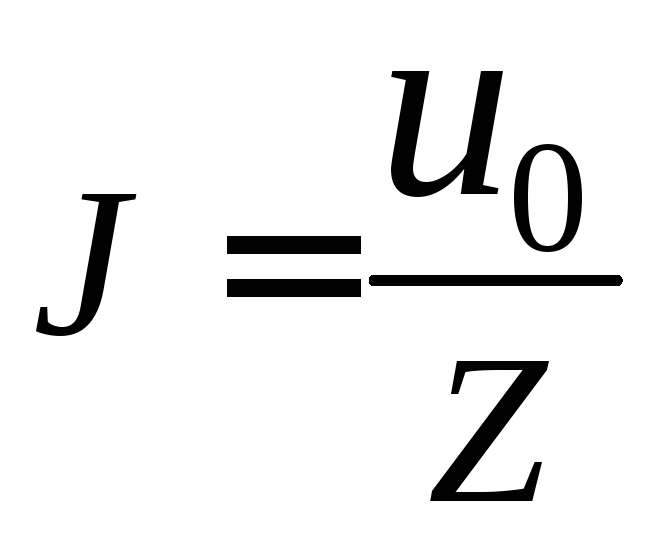 (2.11)
(2.11)
или
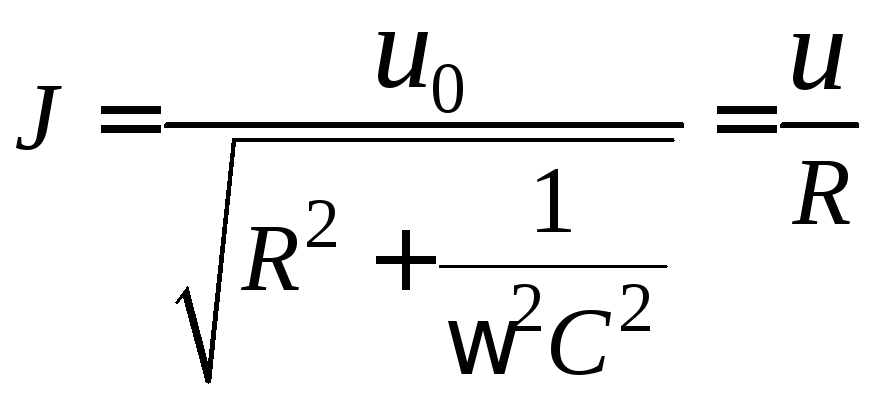 , (2.12)
, (2.12)
где u0 – напряжение на выходе генератора, Z – полное сопротивление цепи, R – активное сопротивление, u – падение напряжения на активном сопротивлении, регистрируемое цифровым вольтметром.
Возведя выражение (2.11) в квадрат получим:
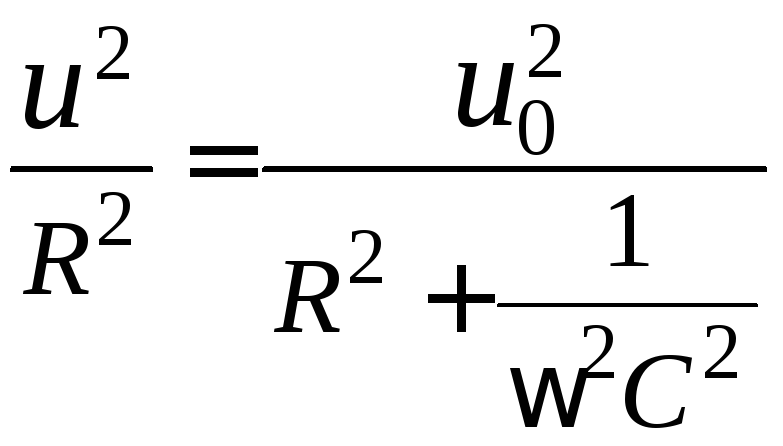 , (2.13)
, (2.13)
откуда
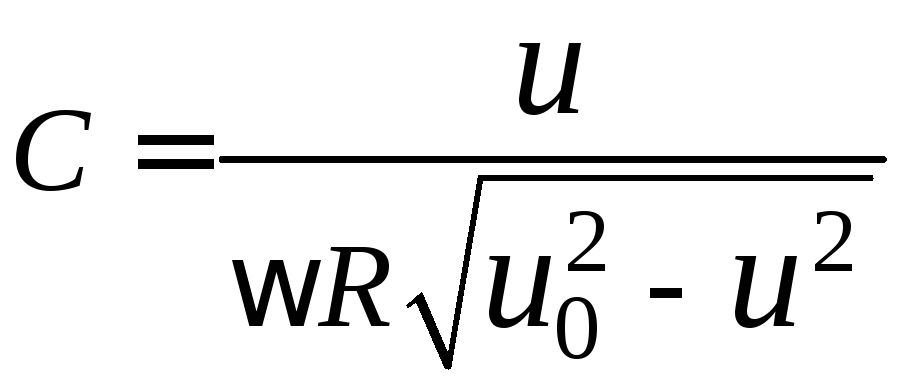 .
.
Используя формулу для расчета емкости плоского конденсатора
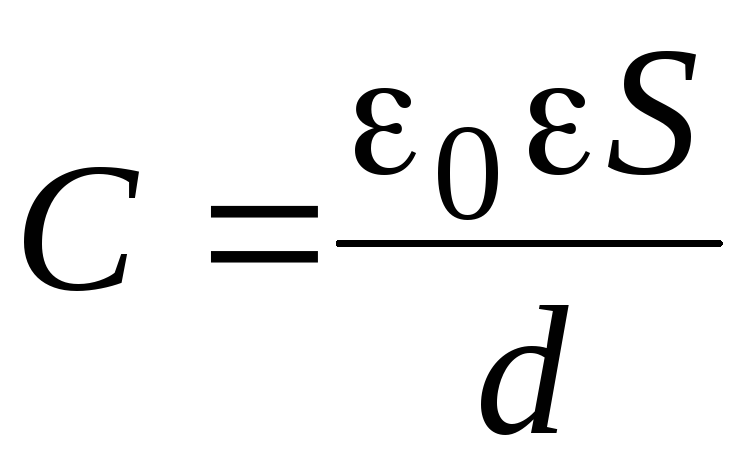 , (2.14)
, (2.14)
можно получить выражение для вычисления относительной диэлектрической проницаемости
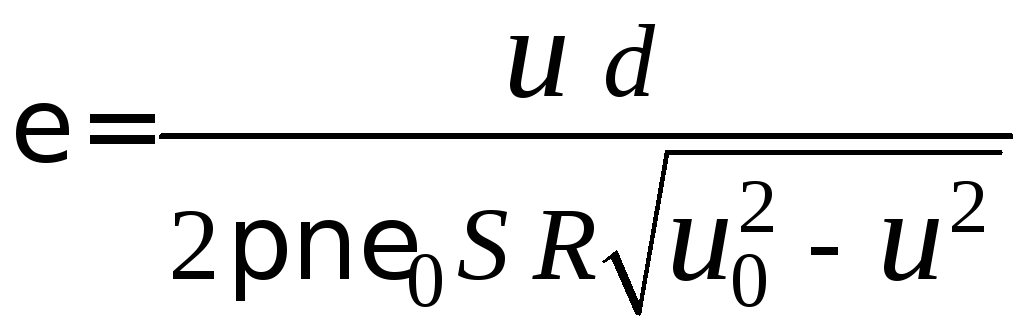 . (2.15)
. (2.15)
Если
величины R и С подобрать таким образом, чтобы в
используемом диапазоне частот выполнялось
условие: 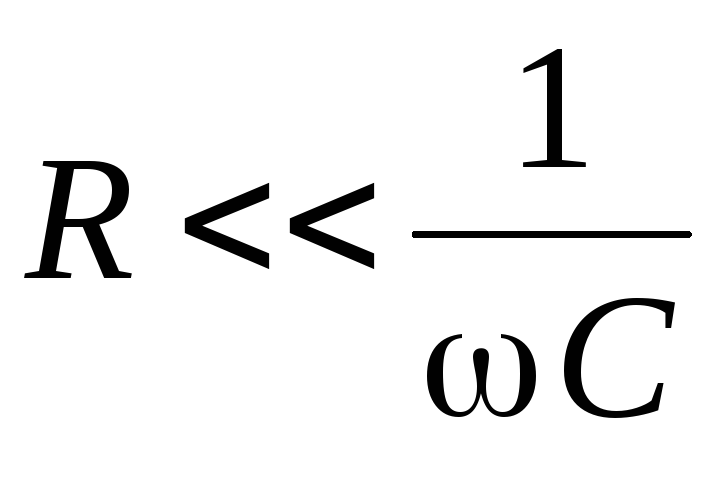 ,
то значениемu в подкоренном выражении соотношения
(2.16) можно пренебречь, так как u << u0.
,
то значениемu в подкоренном выражении соотношения
(2.16) можно пренебречь, так как u << u0.
Тогда выражение (2.16) можно упростить и представить в виде
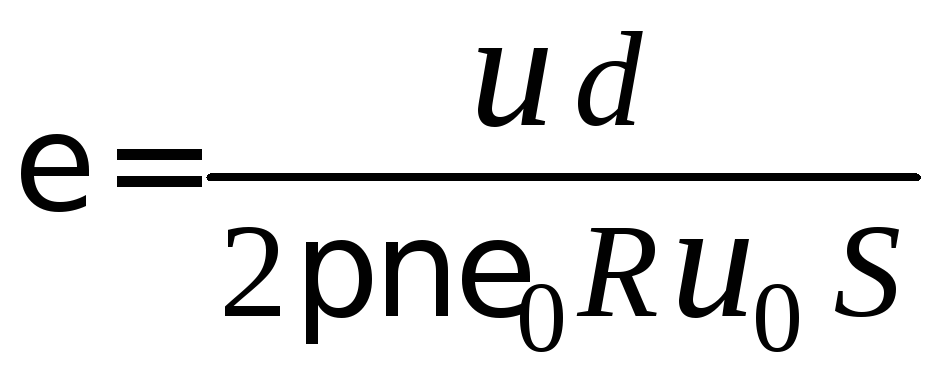 . (2.17)
. (2.17)
2.3. Напряженность электрического поля в диэлектрике
Для количественного описания поля в диэлектриках внесем диэлектрик в однородное электростатическое поле. Поле создается двумя бесконечными равномерно заряженными плоскостями. Пластинка из однородного диэлектрика расположена как на рис. 2.4.
Заряды, входящие в состав диполей диэлектриков, называются связанными. Под действием электрического поля они не могут покинуть пределов молекулы, в состав которой входят, а лишь смещаются из своих положений равновесия. Поляризация диэлектриков сопровождается появлением поверхностных зарядов на его границах.
В
тех местах, где линии напряженности
выходят из диэлектрика, на поверхности
возникают положительные связанные
заряды, то есть положительные заряды
смещаются по полю, отрицательные –против
поля (рис. 2.4) Таким образом, на правой
грани диэлектрика, обращенного к
отрицательной плоскости, будет избыток
положительного заряда с поверхностной
плотностью (+ ),а
на левой – избыток
отрицательного заряда с поверхностной
плотностью (–
),а
на левой – избыток
отрицательного заряда с поверхностной
плотностью (–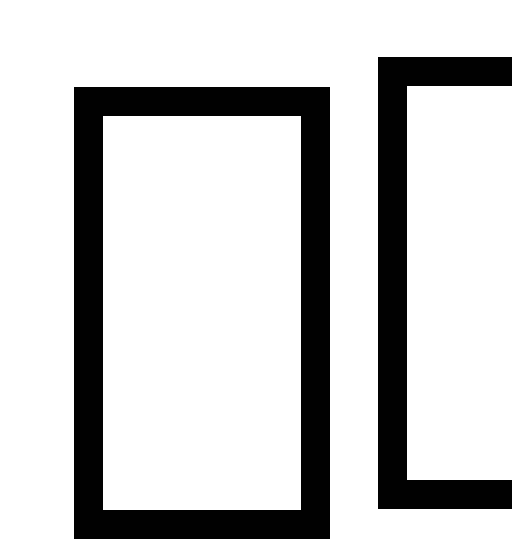 ).
Плотность связанных зарядов определяет
поляризованность диэлектрика:
).
Плотность связанных зарядов определяет
поляризованность диэлектрика: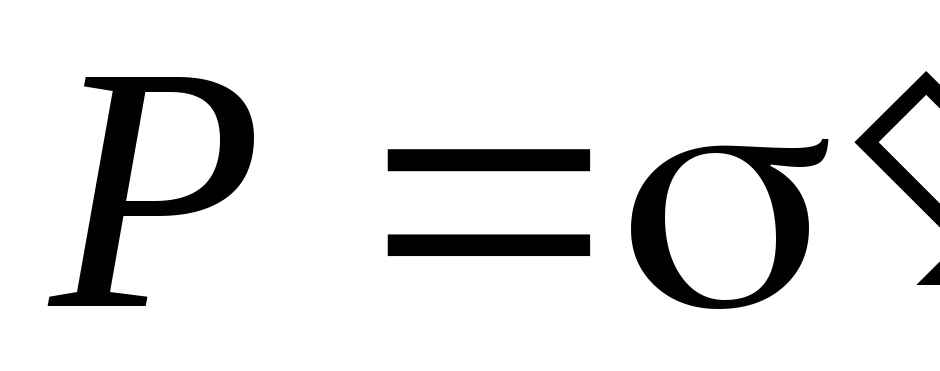 .
.
Таким
образом, появление нескомпенсированных
поверхностных связанных зарядов приводит
к возникновению внутри диэлектрика
дополнительного электрического поля
с напряженностью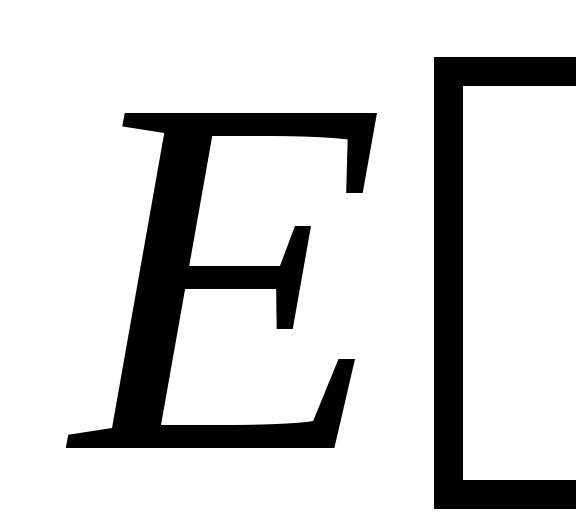 (поле, созданное двумя бесконечными
заряженными плоскостями, т.е. гранями),
которое направлено против внешнего
поля и ослабляет его
(поле, созданное двумя бесконечными
заряженными плоскостями, т.е. гранями),
которое направлено против внешнего
поля и ослабляет его
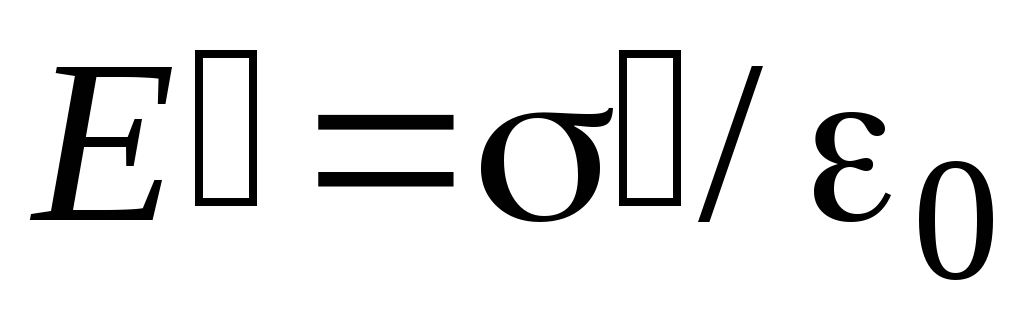 . (2.4)
. (2.4)
Внешнее поле – это поле, созданное свободными зарядами, в данном случае бесконечными заряженными пластинами.
Напряженность внешнего поля определяется по формуле
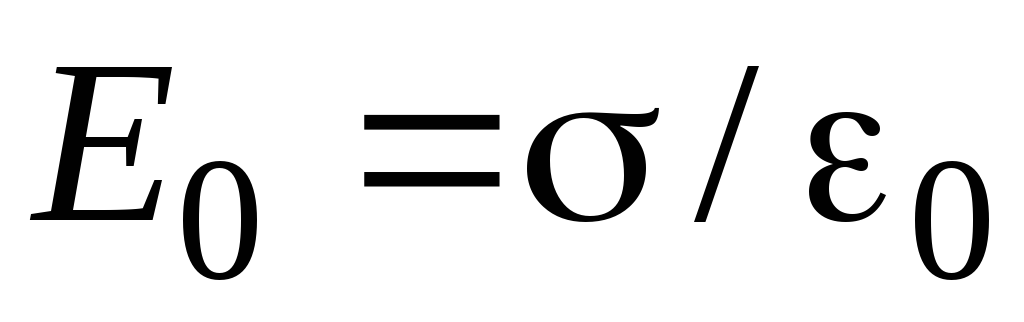 . (2.5)
. (2.5)
Результирующая напряженность поля внутри диэлектрика равна:
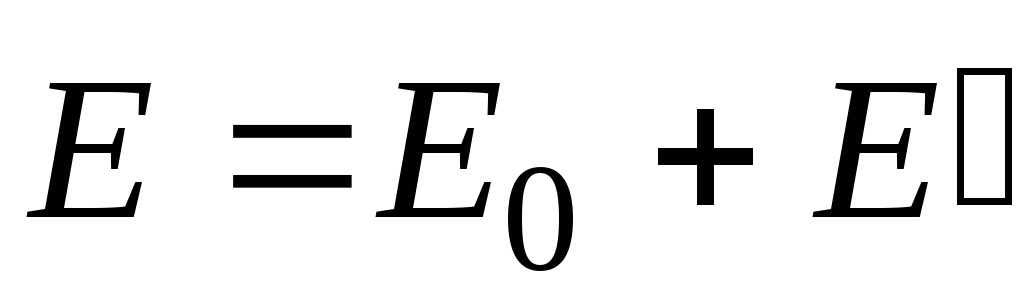
или в скалярном виде с учетом направления
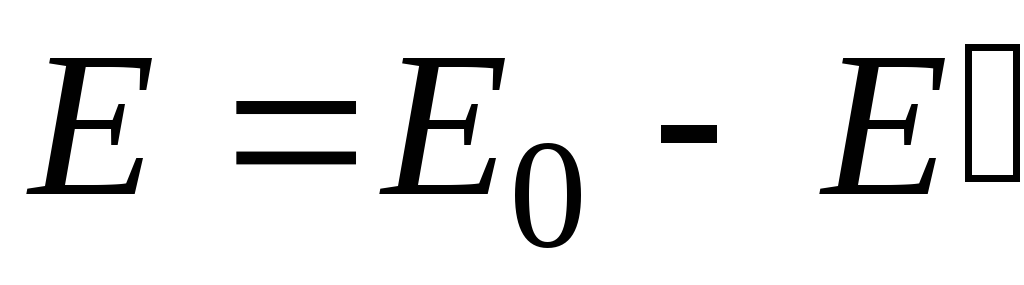 . (2.6)
. (2.6)
Напряженность
электрического поля определяется всеми
зарядами: и сторонними  ,
и связанными
,
и связанными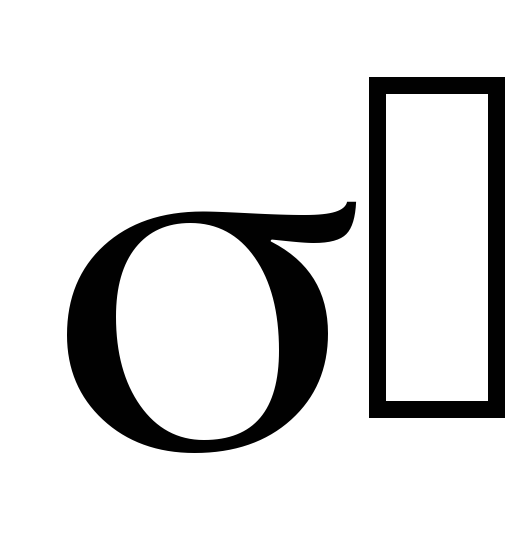 .
С учетом (2.4) и (2.5) можно записать
.
С учетом (2.4) и (2.5) можно записать
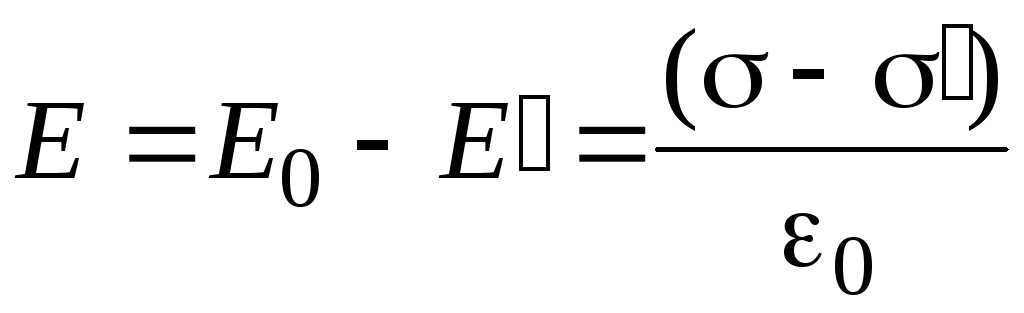 . (2.7)
. (2.7)
Так
как поверхностная плотность связанных
зарядов 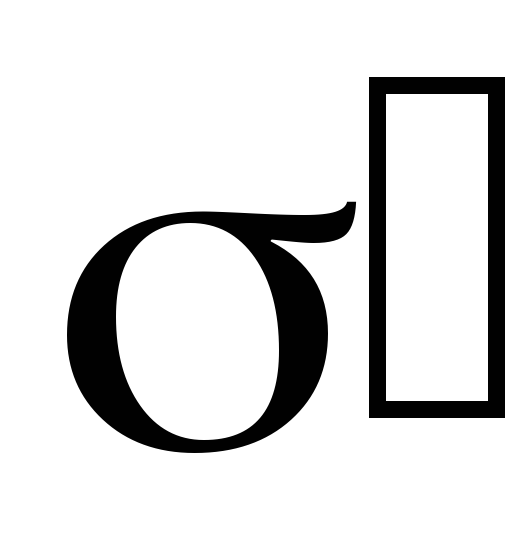 меньше поверхностной плотности свободных
зарядов, то не все поле компенсируется
зарядами диэлектрика, часть линий
напряженности поля пройдет сквозь
диэлектрик, другая же обрывается на
связанных зарядах (рис. 2.4).
меньше поверхностной плотности свободных
зарядов, то не все поле компенсируется
зарядами диэлектрика, часть линий
напряженности поля пройдет сквозь
диэлектрик, другая же обрывается на
связанных зарядах (рис. 2.4).
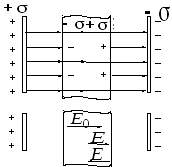
Рис. 2.4. Диэлектрик в однородном электростатическом поле
Следовательно,
результирующее поле внутри диэлектрика
меньше, чем внешнее поле. Величина,
показывающая во сколько раз поле в
вакууме больше, чем поле в диэлектрике,
называется относительной диэлектрической
проницаемостью вещества 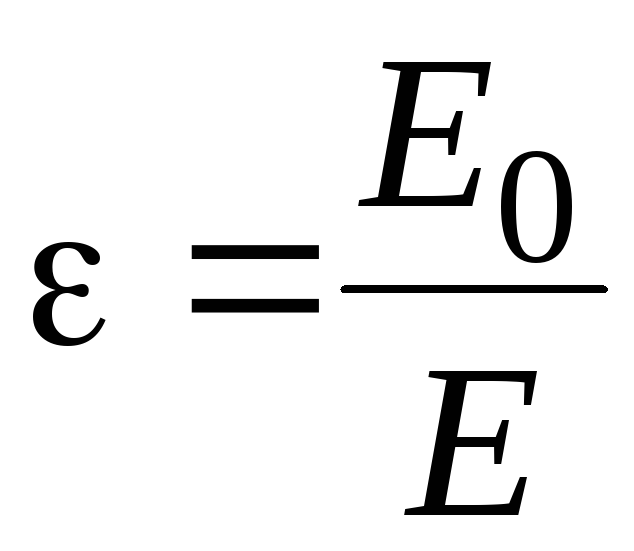 .
.
Относительная диэлектрическая проницаемость связана с диэлектрической восприимчивостью вещества
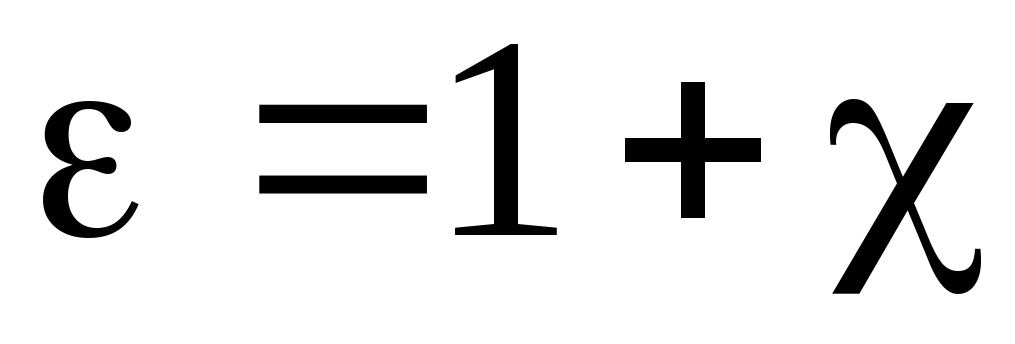 . (2.8)
. (2.8)
Отсюда
следует, что диэлектрическая проницаемость  больше
диэлектрической восприимчивости для
всех веществ.
больше
диэлектрической восприимчивости для
всех веществ.
Таким образом, результирующее поле внутри диэлектрика будет определяться по формуле
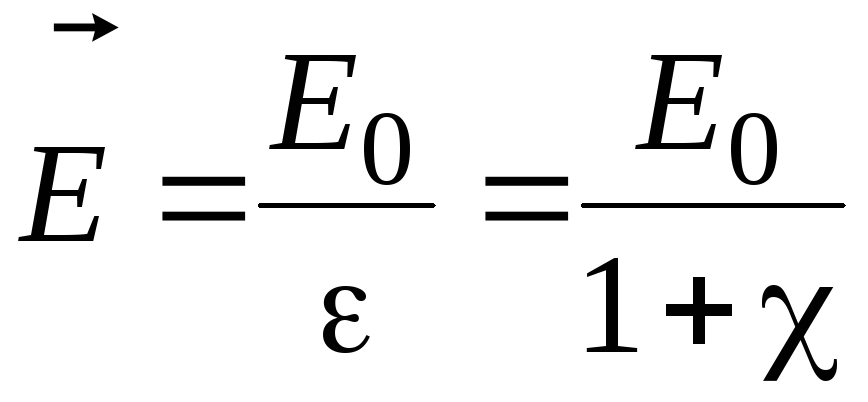 . (2.9)
. (2.9)
Следовательно, относительная диэлектрическая проницаемость ε характеризует электрические свойства диэлектрика, т.е. способность диэлектрика к поляризации.
2.4. Теория метода
Эквивалентная схема электрической цепи для измерения относительной диэлектрической проницаемости представлена на рис. 2.5.
 C R
C R
~ u0
Рис. 2.5. Схема электрической цепи
для измерения относительной диэлектрической проницаемости
Реактивное сопротивление конденсатора цепи переменного синусоидального тока определяется выражением
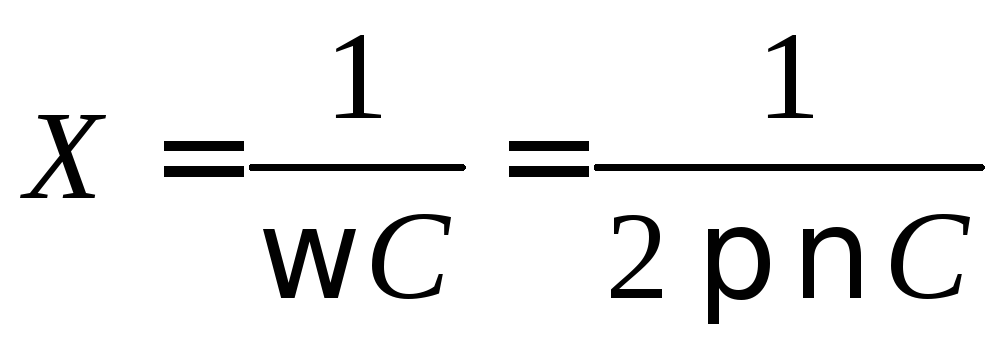 , (2.10)
, (2.10)
где C – емкость конденсатора, – частота переменного напряжения (тока).
Величину переменного тока можно определить по закону Ома, обобщенного для цепей переменного тока:
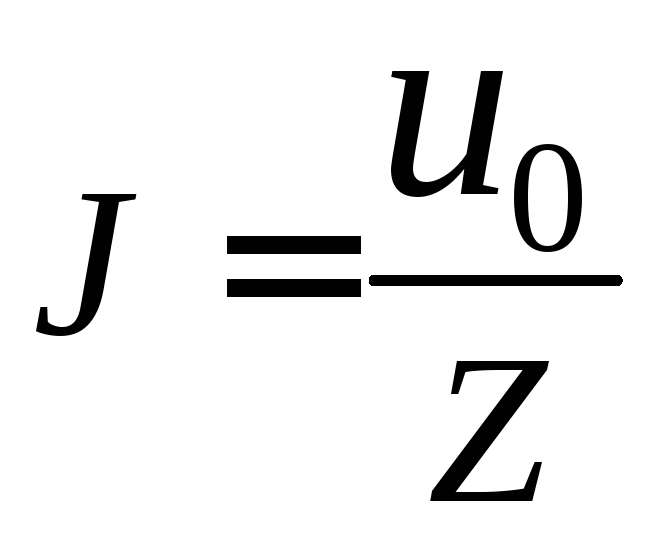 (2.11)
(2.11)
или
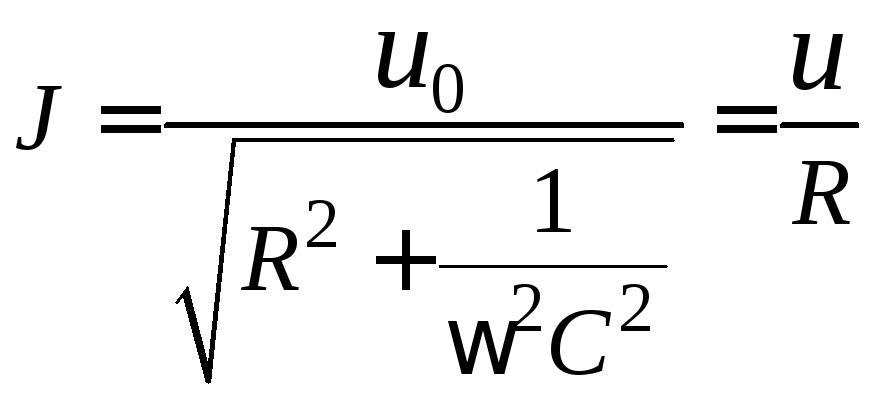 , (2.12)
, (2.12)
где u0 – напряжение на выходе генератора, Z – полное сопротивление цепи, R – активное сопротивление, u – падение напряжения на активном сопротивлении, регистрируемое цифровым вольтметром.
Возведя выражение (2.11) в квадрат получим:
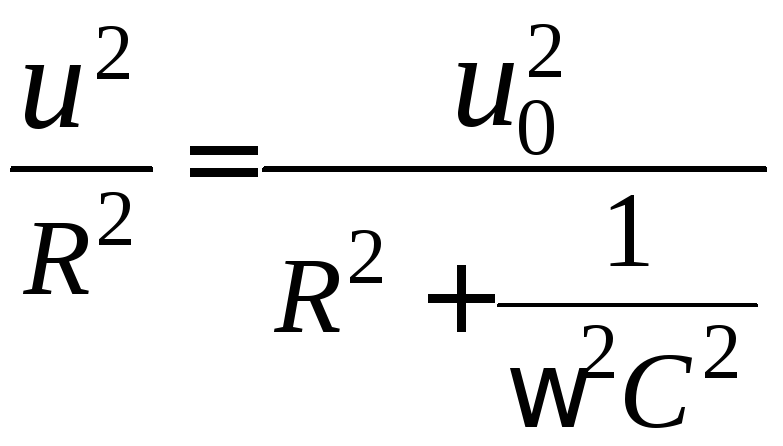 , (2.13)
, (2.13)
откуда
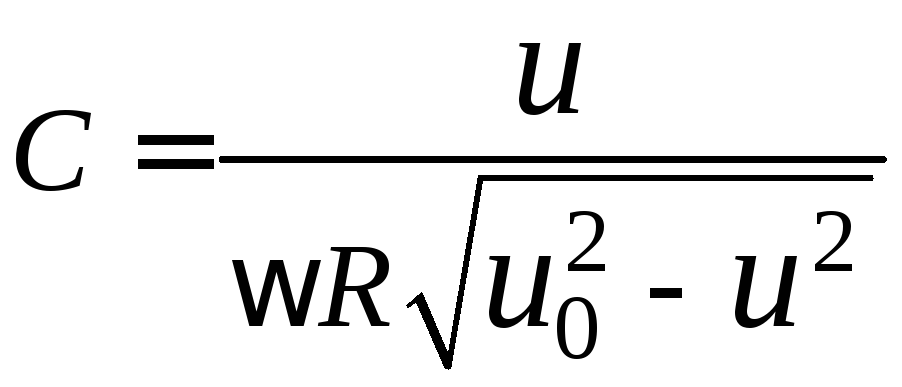 .
.
Используя формулу для расчета емкости плоского конденсатора
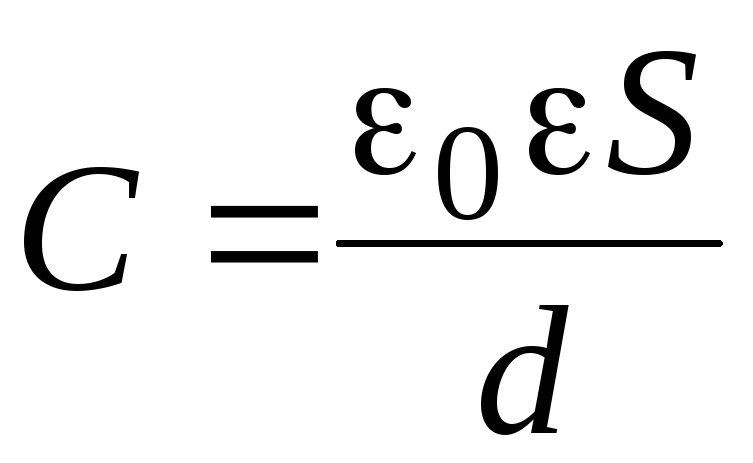 , (2.14)
, (2.14)
можно получить выражение для вычисления относительной диэлектрической проницаемости
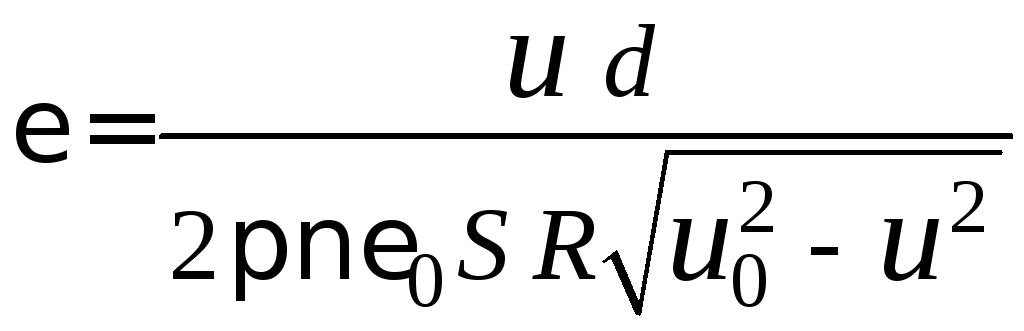 . (2.15)
. (2.15)
Если
величины R и С подобрать таким образом, чтобы в
используемом диапазоне частот выполнялось
условие: 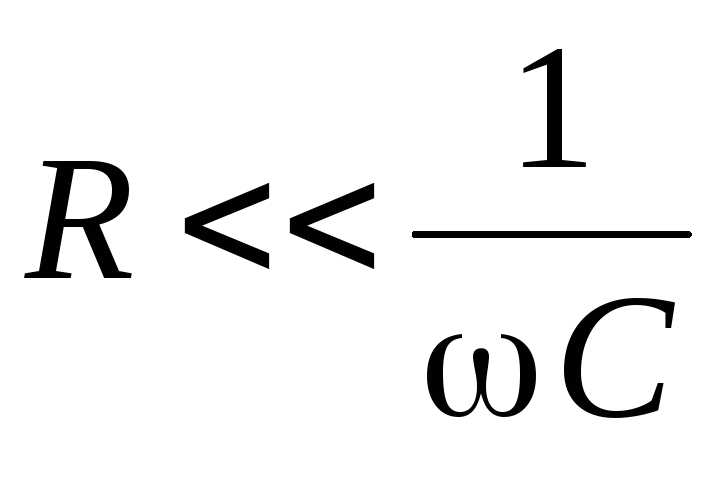 ,
то значениемu в подкоренном выражении соотношения
(2.16) можно пренебречь, так как u << u0.
,
то значениемu в подкоренном выражении соотношения
(2.16) можно пренебречь, так как u << u0.
Тогда выражение (2.16) можно упростить и представить в виде
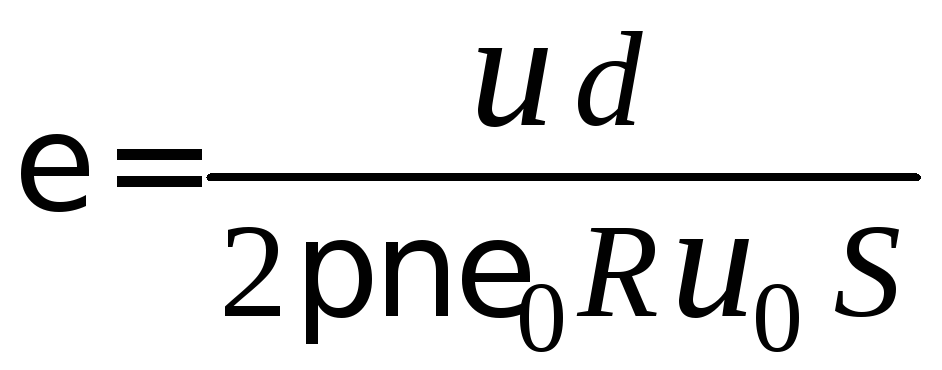 . (2.17)
. (2.17)
Напряженность электрического поля в диэлектрике
Для количественного описания поля в диэлектриках внесем диэлектрик в однородное электростатическое поле. Поле создается двумя бесконечными равномерно заряженными плоскостями. Пластинка из однородного диэлектрика расположена как на рис. 2.4.
Заряды, входящие в состав диполей диэлектриков, называются связанными. Под действием электрического поля они не могут покинуть пределов молекулы, в состав которой входят, а лишь смещаются из своих положений равновесия. Поляризация диэлектриков сопровождается появлением поверхностных зарядов на его границах.
В тех местах, где линии напряженности
выходят из диэлектрика, на поверхности
возникают положительные связанные
заряды, то есть положительные заряды
смещаются по полю, отрицательные –против
поля (рис. 2.4) Таким образом, на правой
грани диэлектрика, обращенного к
отрицательной плоскости, будет избыток
положительного заряда с поверхностной
плотностью (+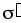 ),а на левой–
избыток отрицательного заряда с
поверхностной плотностью (–
),а на левой–
избыток отрицательного заряда с
поверхностной плотностью (–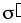 ).
Плотность связанных зарядов определяет
поляризованность диэлектрика:
).
Плотность связанных зарядов определяет
поляризованность диэлектрика: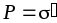 .
.
Таким образом, появление нескомпенсированных
поверхностных связанных зарядов приводит
к возникновению внутри диэлектрика
дополнительного электрического поля
с напряженностью 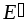 (поле,
созданное двумя бесконечными заряженными
плоскостями, т.е. гранями), которое
направлено против внешнего поля и
ослабляет его
(поле,
созданное двумя бесконечными заряженными
плоскостями, т.е. гранями), которое
направлено против внешнего поля и
ослабляет его
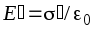 . (2.4)
. (2.4)
Внешнее поле – это поле, созданное свободными зарядами, в данном случае бесконечными заряженными пластинами.
Напряженность внешнего поля определяется по формуле
. (2.5)
Результирующая напряженность поля внутри диэлектрика равна:
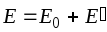
или в скалярном виде с учетом направления
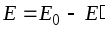 . (2.6)
. (2.6)
Напряженность электрического поля
определяется всеми зарядами: и сторонними 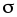 ,
и связанными
,
и связанными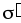 .
С учетом (2.4) и (2.5) можно записать
.
С учетом (2.4) и (2.5) можно записать
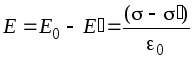 .
.
электри́ческое смеще́ние) — векторная величина, равная сумме векторанапряжённости электрического поляивектора поляризации.
В
СИ: 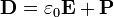 .
.
В
СГС: 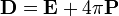 .
.
Величина
электрической индукции в системе СГСизмеряется в СГСЭ или СГСМ единицах, а
вСИ— вкулонахна м² (L−2TI).
В рамках СТОвекторы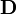 и
и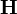 объединяются
в единый тензор, аналогичныйтензору
электромагнитного поля.
объединяются
в единый тензор, аналогичныйтензору
электромагнитного поля.
60Электроемкость*
— Это отношение количества электричества, имеющегося на каком-либо проводящем теле, к величине потенциала этого тела при условии, что все проводящие тела, находящиеся вблизи этого тела, соединены с землей. Обозначая Э. тела через С, заряд на теле через Q и потенциал через V, имеем C = Q/V.
Практической единицей Э. принимается ныне фарада или, еще чаще, миллионная доля фарады, называемая микрофарадой. Фарада обозначается обыкновенно через F, микрофарада — через μ F. Фарада — это электроемкость такого тела, в котором при потенциале равном 1 вольту, содержится один кулон электричества.
Для сравнения электроемкостей тел существует несколько способов. Упомянем только о трех, наиболее часто употребляемых.
В настоящее время имеются ящики электроемкостей, т. е. ящики, содержащие в себе конденсаторы различных электроемкостей, долей микрофарады, а также целых микрофарад, которые можно комбинировать в желаемые группы. Сами конденсаторы изготовляются из тонких листов олова (станиоль), отделенных друг от друга листами парафинированной бумаги, и заливаются парафином.
Различные типы конденсаторов.
заряжая любой изолированный
проводник, мы одновременно создаем
противоположный заряд на окружающих
проводниках, соединенных с Землей и
образующих вместе с этим телом конденсатор.
Однако емкость такого конденсатора
мала. Чтобы получить большую емкость,
необходимо взять проводники в виде
металлических пластин, возможно близко
расположенных друг к другу (так называемые
обкладки конденсатора). Мы видели, что
емкость плоского конденсатора прямо
пропорциональна площади обкладок и
обратно пропорциональна расстоянию
между ними. Поэтому при большой поверхности
обкладок и при тонком слое диэлектрика
между ними емкость конденсатора очень
велика, и на нем можно накопить («сгустить»)
значительные заряды даже при небольшом
напряжении. Отсюда происходит и название
«конденсатор» (от латинского слова
condensare — сгущать).
Для увеличения
емкости конденсаторы соединяют в
батареи. На рис. 60 изображена батарея
из четырех лейденских банок. Все внешние
и все внутренние обкладки 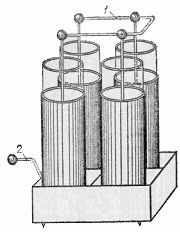 Рис.
60. Батарея из четырех лейденских банок:
1 — стержень для зарядки внутренних
обкладок, 2 — стержень для заземления
внешних обкладок
Рис.
60. Батарея из четырех лейденских банок:
1 — стержень для зарядки внутренних
обкладок, 2 — стержень для заземления
внешних обкладок 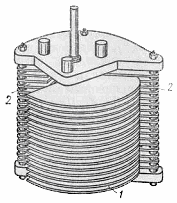 Рис.
61. Конденсатор переменной емкости
состоит из двух изолированных систем
металлических пластин 1 и 2, которые
входят друг в друга при вращении
рукоятки соединены
между собой, и поэтому батарею можно
рассматривать как один большой
конденсатор, у которого площадь обкладок
равна сумме площадей обкладок отдельных
банок. Емкость батареи при таком
соединении (оно называется параллельным
соединением) равна сумме емкостей
отдельных конденсаторов. На рис. 61
показан конденсатор переменной емкости,
широко употребляющийся в радиотехнике.
Он состоит из двух изолированных систем
металлических пластин, которые входят
друг в друга при вращении рукоятки.
Вдвигание и выдвигание одной системы
пластин в другую изменяют емкость
конденсатора (§ 33). 61Энергия
системы зарядов
Рис.
61. Конденсатор переменной емкости
состоит из двух изолированных систем
металлических пластин 1 и 2, которые
входят друг в друга при вращении
рукоятки соединены
между собой, и поэтому батарею можно
рассматривать как один большой
конденсатор, у которого площадь обкладок
равна сумме площадей обкладок отдельных
банок. Емкость батареи при таком
соединении (оно называется параллельным
соединением) равна сумме емкостей
отдельных конденсаторов. На рис. 61
показан конденсатор переменной емкости,
широко употребляющийся в радиотехнике.
Он состоит из двух изолированных систем
металлических пластин, которые входят
друг в друга при вращении рукоятки.
Вдвигание и выдвигание одной системы
пластин в другую изменяют емкость
конденсатора (§ 33). 61Энергия
системы зарядов
Энергия взаимодействия системы точечных зарядов, вычисляемая по формуле (3), может быть как положительной, так и отрицательной. Например она отрицательная для двух точечных зарядов противоположного знака.
Формула (3) определяет не полную электростатическую энергию системы точечных зарядов, а только их взаимную потенциальную энергию. Каждый заряд qi, взятый в отдельности обладает электрической энергией. Она называется собственной энергией заряда и представляет собой энергию взаимного отталкивания бесконечно малых частей, на которые его можно мысленно разбить. Эта энергия не учитывается в формуле (3). Учитывается только работа затрачиваемая на сближение зарядов qi, но не на их образование.
Полная электростатическая энергия системы точечных зарядов учитывает также работу, на образование зарядов qiиз бесконечно малых порций электричества, переносимых из бесконечности. Полная электростатическая энергия системы зарядов всегда положительная. Это легко показать на примере заряженного проводника. Рассматривая заряженный проводник как систему точечных зарядов и учитывая одинаковое значение потенциала в любой точке проводника, из формулы (3) получим:
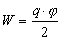 .
(4)
.
(4) 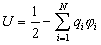 ,
(3)
,
(3)
Поляризованность. Напряженность поля в диэлектрике
При помещении
диэлектрика во внешнее электрическое
поле он поляризуется, т. е. приобретает
отличный от нуля дипольный момент 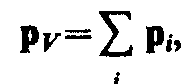 где рi — дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной — поляризованностью, определяемой как дипольный момент
единицы объема диэлектрика:
где рi — дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной — поляризованностью, определяемой как дипольный момент
единицы объема диэлектрика:
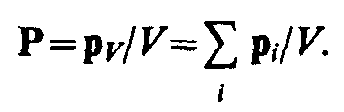 (88.1)
(88.1)
Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков, см. § 91) поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то
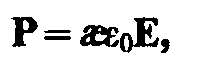 (88.2)
(88.2)
где — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; – величина безразмерная; притом всегда > 0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта 25, для воды =80).
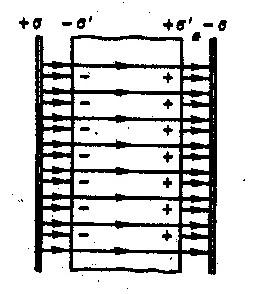
Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле Е0 (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика, расположив ее так, как показано на рис. 135. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +‘, на левой — отрицательного заряда с поверхностной плотностью –‘. Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их поверхностная плотность ‘ меньше плотности свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е=Е0.
Таким образом, появление связанных зарядов приводит к возникновению дополнительного электрического поля Е‘ (поля, создаваемого связанными зарядами), которое направлено против внешнего поля Е0 (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика
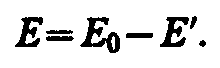
Поле Е’=‘/0 (поле, созданное двумя бесконечными заряженными плоскостями; см. формулу (82.2)), поэтому
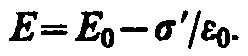 (88.3)
(88.3)
Определим поверхностную плотность связанных зарядов ‘. По (88.1), полный дипольный момент пластинки диэлектрика pV =PV = PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, согласно (80.3), равен произведению связанного заряда каждой грани Q‘ =‘ S на расстояние d между ними, т. е. рV = ‘ Sd. Таким образом, PSd= ‘ Sd, или
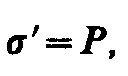 88.4)
88.4)
т. е. поверхностная плотность связанных зарядов ‘ равна поляризованности Р. Подставив в (88.3) выражения (88.4) и (88.2), получим
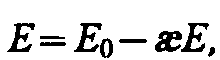
откуда напряженность результирующего поля внутри диэлектрика равна
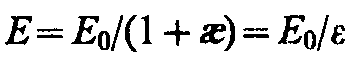 (88.5)
(88.5)
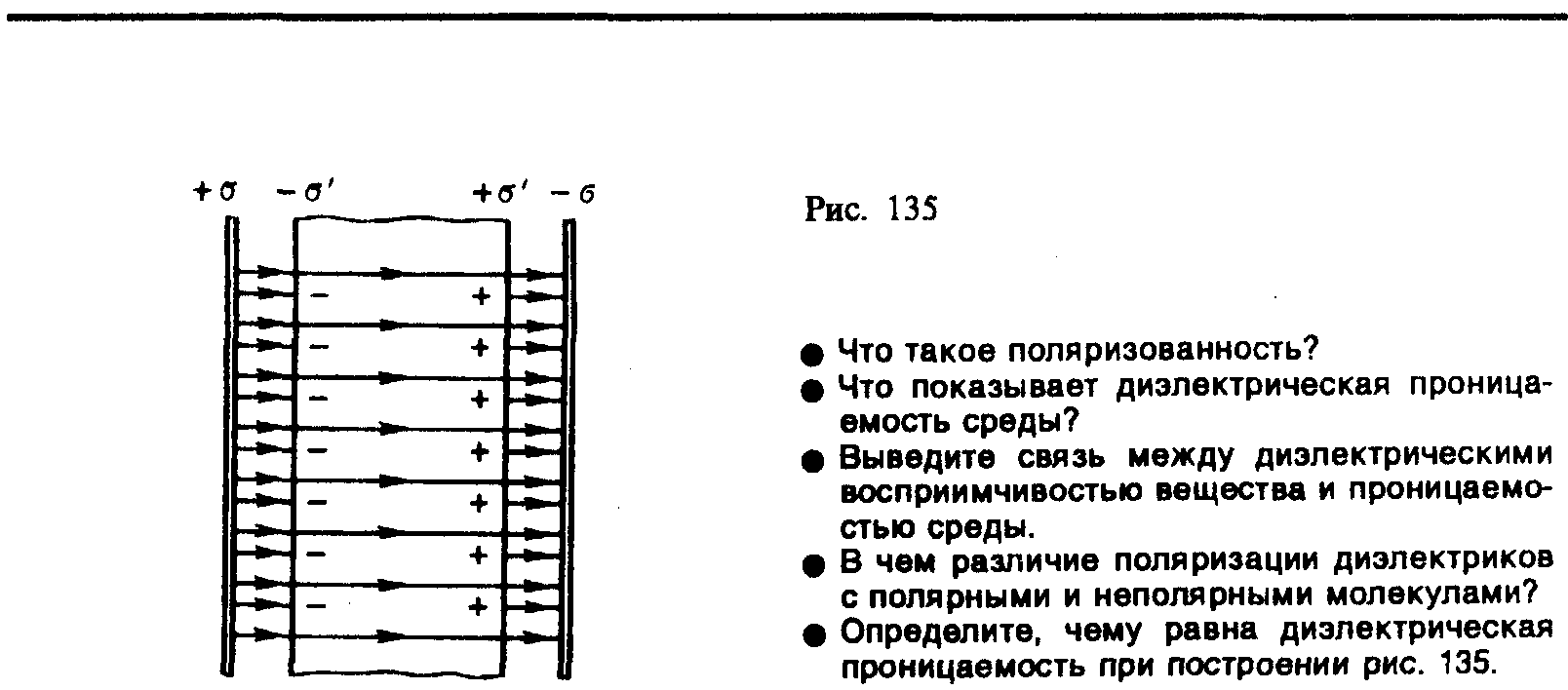
Безразмерная величина
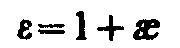 (88.6)
(88.6)
называется диэлектрической проницаемостью среды. Сравнивая (88.5) и (88.6), видим, что показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.


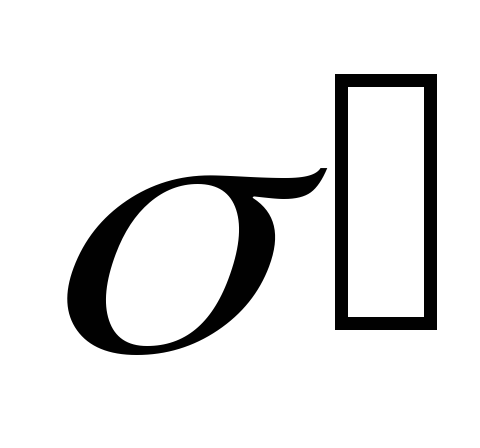 меньше,
чем свободных
меньше,
чем свободных ,
поэтому поле создаваемое связанными
зарядами
,
поэтому поле создаваемое связанными
зарядами не полностью компенсирует поле,
создаваемое свободными зарядами
не полностью компенсирует поле,
создаваемое свободными зарядами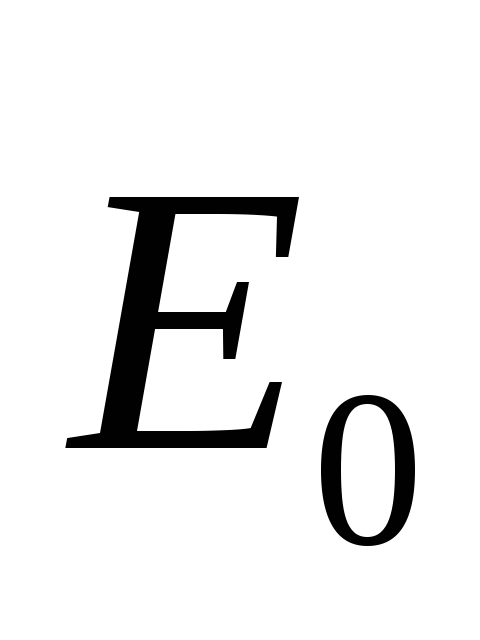 .
Часть линий напряженности пройдет
сквозь диэлектрик, другая часть
оборвется на связанных зарядах.
.
Часть линий напряженности пройдет
сквозь диэлектрик, другая часть
оборвется на связанных зарядах.