§1. Напряженность электростатического поля. Потенциал.

I. Краткие теоретические сведения

Точечным зарядомназывается заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.

Закон Кулона:Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей эти заряды прямой.

,

где k– коэффициент пропорциональности,q₁иq₂– величины взаимодействующих зарядов,r– расстояние между ними,e₁₂– единичный вектор направленный от заряда1к заряду2,F₁₂– сила, действующая на заряд2со стороны заряда1.

Коэффициент kопределяется следующим образом:

,

где ₀

= 8,85 10^-12Ф/м – электрическая постоянная.

Напряженность поля, создаваемого точечным зарядомqпрямо пропорциональна заряду и обратно пропорциональна квадрату расстояния от заряда до данной точки поля:

,

вектор направлен вдоль прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателе.

Принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

.

Потенциал поля точечного заряда:

.

По принципу суперпозиции потенциал системы точечных зарядов равен:

.

II. Примеры решения задач

Пример 1.1.Тонкая проволока, представляющая по форме четверть кольца радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кривизны.

Решение.

Выбираем на кольце элементарный заряд , гдеиd— угол под которым из центра кривизны виден элементdl. Напряженность поля, создаваемого этим элементарным зарядом, равна:

Рис.1.1

.

Введем оси координат и находим проекции напряженности поля на выбранные оси:

.

Тогда:

.

Тогда суммарная напряженность будет равна:

.

Вектор напряженности направлен под углом 45к осих.

Пример 1.2Находящейся в вакууме тонкий прямой стержень длины 2азаряжен равномерно с зарядомq. Найти модуль напряженности электрического поля как функцию расстояния

rот центра стержня до точки прямой, совпадающей с осью стержняr >a.

Решение.

Вводим обозначения: . Выделим на стержне элементdl, заряд этого элемента равен:. Напряженность поля, создаваемого в точке наблюдения таким зарядом равна:

,

где l– расстояние от центра стержня до элементаdl. Поле, создаваемое всем стерж7нем будет равно:

Рис. 1.2

III. Задачи для самостоятельного решения

1.1.Кольцо радиусаRимеет зарядq. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLдо его центра.

Ответ:.

1.2.Тонкая проволока, представляющая по форме кольцо радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кольца.

Ответ:.

1.3.Тонкое полукольцо радиусаRимеет положительный зарядq. Найти напряженность в центре кривизны этого полукольца.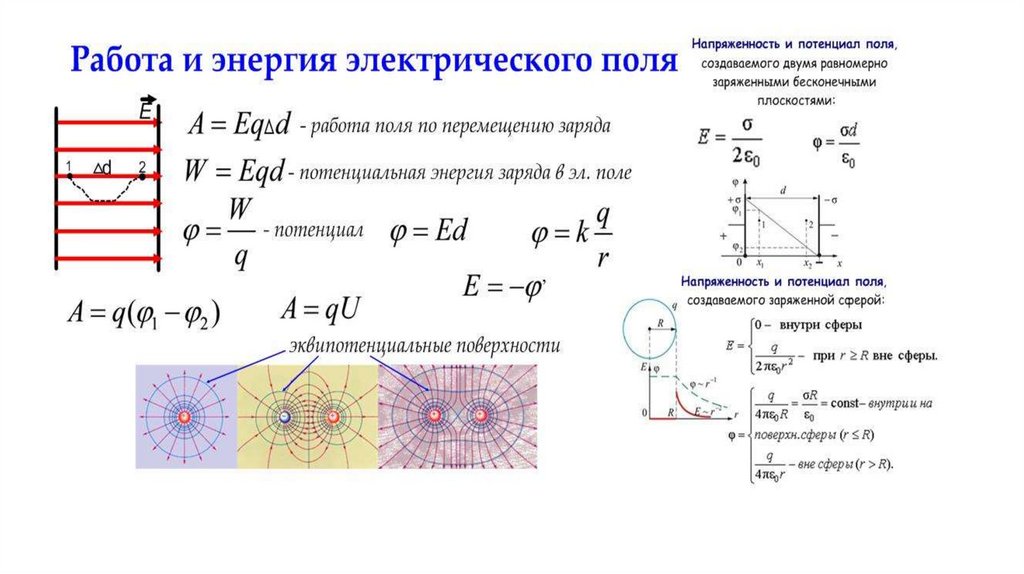

Ответ:.

1.4. Тонкая проволока, представляющая по форме три четверти кольца радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кривизны.

Ответ:.

1.5. Тонкое непроводящее кольцо радиусаRзаряжено с линейной плотностью, где- азимутальный угол. Найти напряженность: а) в центре кольца, б) на оси кольца в зависимости от расстоянияL.

Ответ:.

1.6. Тонкое непроводящее кольцо радиусаRзаряжено с линейной плотностью, где- азимутальный угол. Найти напряженность в центре кольца.

Ответ:.

1.7.Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити.

Ответ:.

1.8. Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити, проходящем через один из ее концов.

Ответ:.

1.9. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой, перпендикулярной стержню и проходящей через его центр.

Ответ:.

1.10.Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой совпадающей с осью стержня, если.

Ответ:.

1.11.Равномерно заряженная нить, на единицу длины которой приходится заряд, имеет конфигурацию, показанную на рис.1.3. Радиус закругленияRгораздо меньше длинны нити. Найти модуль напряженности электрического поля в точке О.

Ответ:.

1. 12.Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти модуль напряженности электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ:.

1.13. Плоское кольцо, внутренний радиус которого а, внешний в, заряжено с поверхностной плотностью. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLот его центра.

Ответ:.

1.14.Зарядqраспределен равномерно по объему шара радиусаR. Найти потенциал:

а) в центре шара ₀, б) внутри шара(r), в) вне шара(r), гдеr- расстояние от центра шара.

Ответ:.

1.15. Потенциал поля внутри заряженного шара, гдеаиb– постоянные. Найти зависимость объемной плотности заряда(r) от расстояния от центра шара.

Ответ:.

1.16.По сфере радиусаRравномерно распределены заряды с поверхностной плотностьюНайти потенциал в зависимости от расстояния до центра сферы.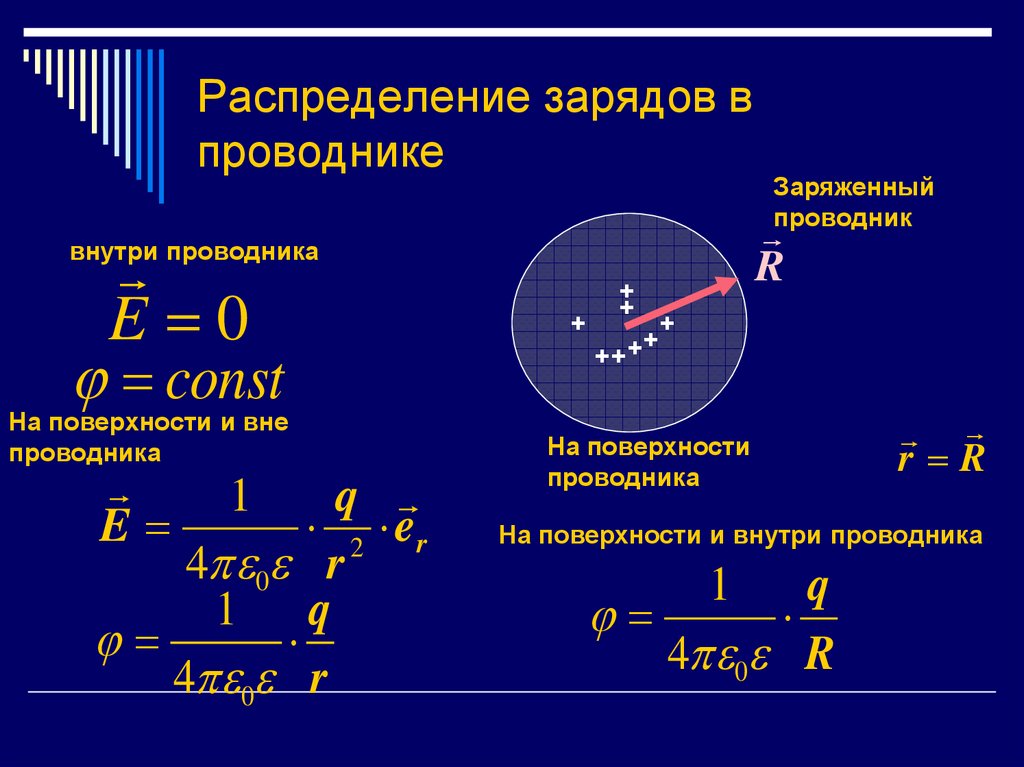

Ответ:.

1.17. Плоское кольцо, внутренний радиус которогоа, внешнийb, заряжено с поверхностной плотностью. Найти потенциал в центре кольца.

Ответ:.

1.18.Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти потенциал электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ:.

1.19. Две длинные одноименно заряженные нити расположены на расстояниидруг от друга. Линейная плотность заряда на нитях. Найти величину и направление напряженности результирующего электрического поля в точке, находящейся на расстоянииот каждой нити.

Ответ:.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2. 1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4. 1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5. 5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

ньютонов гравитации — связь между напряженностью поля и потенциалом?

спросил 10 лет, 2 месяца назад

Изменено 10 лет, 2 месяца назад

Просмотрено 4к раз

$\begingroup$

С точки зрения гравитации и электрических полей, я не уверен, в чем разница между силой поля и потенциалом и как они связаны? Как с использованием математики, так и без.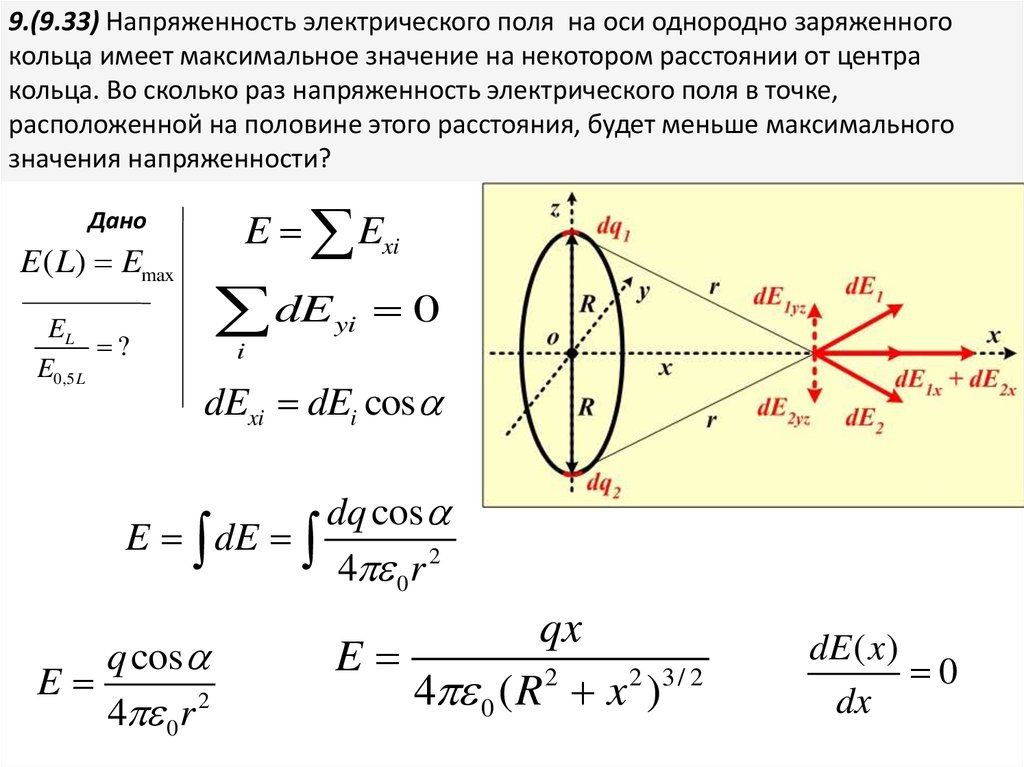

• ньютоновская гравитация
• электрические поля

$\endgroup$

$\begingroup$

Напряженность поля является отрицательной первой производной потенциала.

Например, в декартовых координатах при электрическом потенциале $V = V(x,y,z)$ электрическое поле равно:

$$ \boldsymbol E =-\nabla V= -\frac{\partial V}{\partial x}\boldsymbol i — \frac{\partial V}{\partial y}\boldsymbol j — \frac{\partial V}{ \partial z}\boldsymbol k $$

Обратите внимание, что вы можете добавить или вычесть произвольный постоянный потенциал к $V$, и это не повлияет на напряженность поля, так как ее производная будет равна 0.

Для поля/потенциала вы можете рассчитать силу/энергию, просто умножение на заряд. В терминах гравитационного поля используйте $\boldsymbol g$ вместо $\boldsymbol E$ и умножайте на массу, а не на заряд, чтобы получить $\boldsymbol F$.

«Физический» способ думать о производных состоит в том, что они показывают, как быстро изменяется потенциал в пространстве; большие изменения потенциала на коротком расстоянии создают большие поля в направлении максимального изменения.

Обратите внимание, что приведенная выше связь между электрическим полем и потенциалом верна только для статических полей. Более общая формула:

$$ \boldsymbol E=-\nabla V-\frac{\partial\boldsymbol A}{\partial t} $$

где $\boldsymbol A$ — магнитный векторный потенциал.

$\endgroup$

2

$\begingroup$

Единицы электрического поля здесь должны быть большой подсказкой: Вольт/метр. Это буквально электрический потенциал на единицу длины вдоль вектора поля.

$\endgroup$

7

$\begingroup$

С точки зрения электромагнетизма потенциал определяется калибровочным полем $A_\mu$, тогда как напряженность поля определяется как $F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_ \mu. $ Основное отличие состоит в том, что само поле может быть изменено на другое значение с помощью так называемого калибровочного преобразования (которое задается элементом группы $U(1)$), а сама напряженность поля инвариантно (не изменяется) ею. 9{cb},\end{equation}

, где $a$ и $b$ — индексы, которые преобразуются при выполнении SU(3).

$\endgroup$

2

$\begingroup$

Сила поля определяет силу в уравнении Ньютона. Он отвечает за изменение скорости.

Потенциал не имеет такого значения — его абсолютное значение не имеет значения, если оно остается постоянным на протяжении всего рассмотрения. Таким образом, его абсолютное значение является вопросом удобства. Он участвует в таком понятии, как полная энергия. А абсолютное значение скорости изменится только при изменении потенциала. Частица ощущает не сам потенциал, а силу (локальную разность потенциалов в направлении максимального изменения потенциала).

Локальная разность потенциалов $\phi(x+\delta x)-\phi(x)\;$, деленная на $\delta x\;$ с малым $\delta x\;$, определяет напряженность поля в $x$ .

$\endgroup$

$\begingroup$

Вы должны рассматривать поле как векторное поле, т. е. для каждой точки у вас будет вектор, то есть $E$, который представляет силу, с которой единичный заряд будет ощущаться в этой точке, и направление сила. Если вас не устраивают единицы измерения Вольт/метр, используйте N/C (Ньютоны/Кулоны). Это если: сила на единицу заряда, которая оказывается такой же, как вольт/метр.

Потенциал говорит об энергии. Потенциал теперь представляет собой скалярное поле, то есть: для каждой точки пространства у нас есть число, это число представляет энергию, которую имел бы единичный заряд, если бы он находился там (потенциальная электрическая энергия). По определению потенциалы определяются так, что их градиент представляет собой силу: $E=-\nabla V$, как кто-то сказал ранее, в единицах, мы имеем $N/C=[V]/m$, будучи $N$= ньютоны, $C$=кулоны, $m$=метр и $[V]$ единицы нашей новой потенциальной единицы, и мы решили назвать это вольтами, как видите, мера электрического поля такая же, как вольт/метр: $В/м$

Смотрите как наклон потенциала, вот как он определяется: $-\nabla V$, поле опускается/повышается на $x$ вольт на метр в точке $P$.

$\endgroup$

$\begingroup$

В области с электрическим потенциалом $V$, изменяющимся в зависимости от положения, электрическое поле $E$ направлено в направлении наибольшего уменьшения потенциала. Положительный заряд, естественно, направляется к точкам с более низким электрическим потенциалом, поэтому в любом заданном положении на него будет действовать сила, пропорциональная напряженности электрического поля в этой точке, ибо поле $E$ направлено вниз, так сказать, именно туда, где частица вынуждена уйти.

Можно представить, что поле $V$ определяет ландшафт с холмами и долинами — значение $V$ определяет высоту этих холмов и долин. Поле $E$ указывает единственное направление, которое быстрее всего идет вниз.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

электростатика — зависимость напряженности электрического поля от электрического потенциала

спросил 5 лет, 6 месяцев назад

Изменено 5 лет, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Это простая вещь, в которой я запутался.

Насколько я понимаю, электростатическая сила от заряда наружу на определенное расстояние обратно пропорциональна квадрату расстояния (а напряженность электрического поля измеряется в ньютонах на кулон или вольтах на метр). Но электрический потенциал или напряжение обратно пропорциональны расстоянию (r).

Теперь я понял, что электромагнитные сигналы/силы уменьшают силу или энергию, которую они могут передать, на квадрат расстояния. Однако разве напряжение не создает силу и мощность на расстоянии? Другими словами, может ли электростатическая/электромагнитная энергия передаваться обратно пропорционально расстоянию, а не квадрату расстояния?

• электростатика
• электрические поля
• потенциал
• потенциал-энергия
• напряжение

$\endgroup$

$\begingroup$

Разница между электрическими потенциалами в двух точках пропорциональна работе, совершаемой перемещением заряженной частицы в текущем поле.