Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| jast321 |
| ||
10/02/17 |
| ||
| |||
| Alex-Yu |
| |||
21/08/10 |
| |||
| ||||
| profrotter |
| |||
16/02/11 |
| |||
| ||||
| StaticZero |
| |||
22/06/12 |
| |||
| ||||
| jast321 |
| ||
10/02/17 |
| ||
| |||
| wrest |
| ||
05/09/16 |
| ||
| |||
| realeugene |
| ||
27/08/16 |
| ||
| |||
| jast321 |
| ||
10/02/17 |
| ||
| |||
| realeugene |
| ||
27/08/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
36.
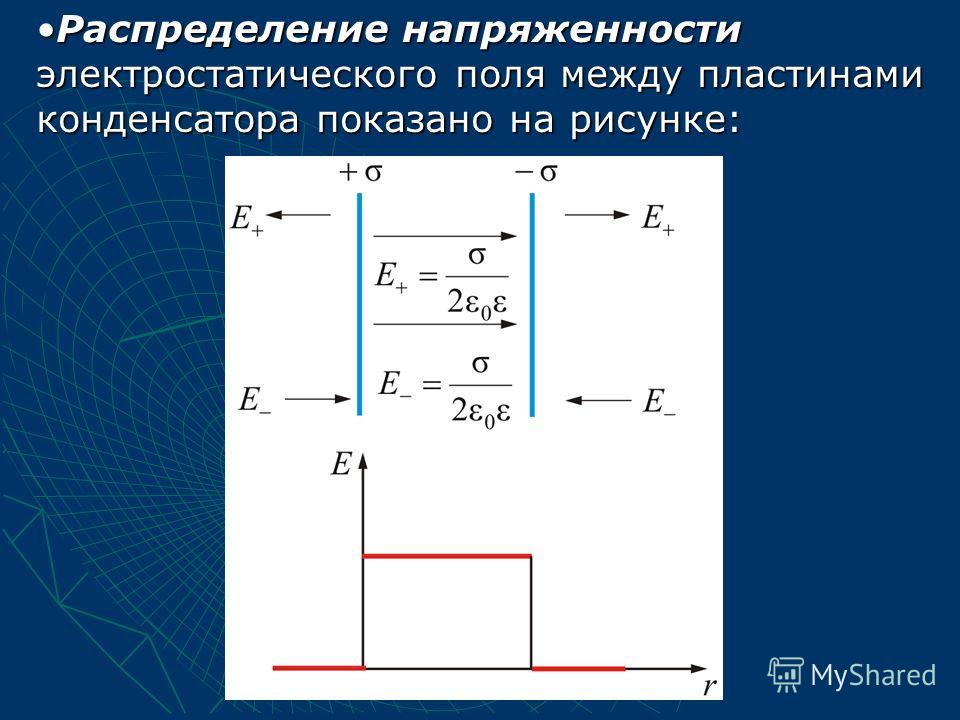 Расчет поля плоского конденсатора
Расчет поля плоского конденсатораРассмотри плоский конденсатор (рис. 15.17а). Расстояние между пластинами конденсатора – d. К обкладкам приложено напряжение – U. Свободные заряды между пластинами отсутствуют. Требуется рассчитать поле между пластинами.
а) б)
Рис. 15.17. Поле плоского конденсатора при отсутствии зарядов
Поле при отсутствии в расчетной области свободных зарядов подчиняется уравнению Лапласа: .
В общем случае это уравнение записывается
Если предположить, что в направлении осей y и z поле не меняется, то уравнение упрощается:
После интегрирования получаем
Постоянные интегрирования находятся из граничных условий.
Без
нарушения картины распределения поля
можно принять потенциал одной из пластин,
равным нулю.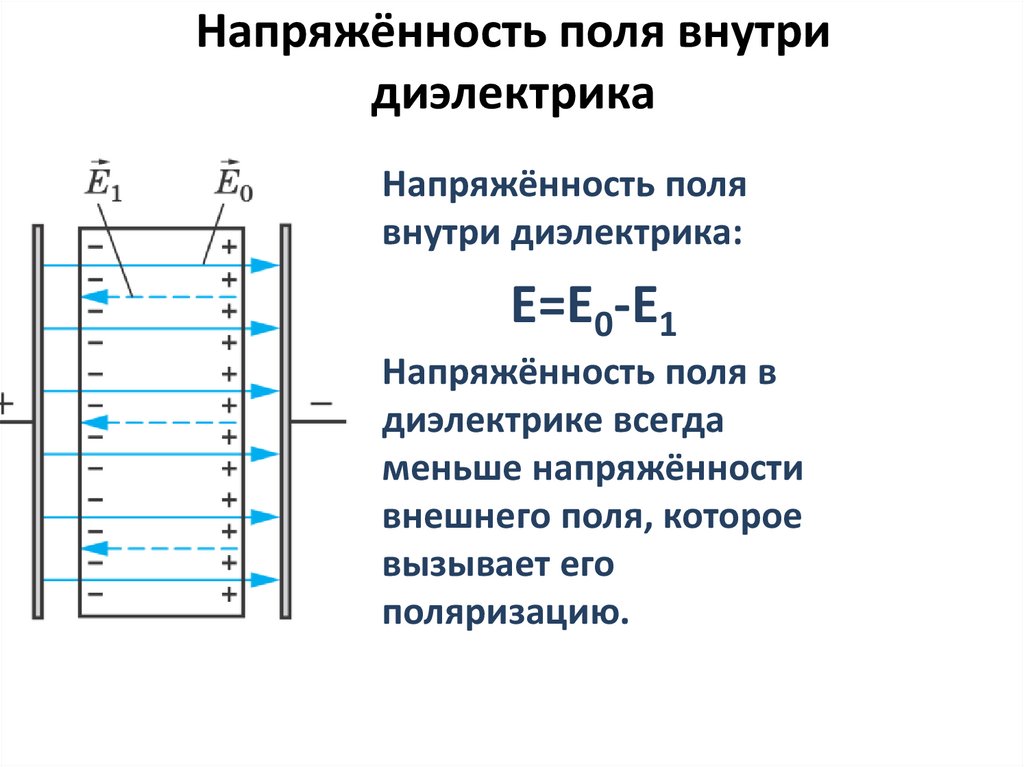 Тогда потенциал другой
будет равен приложенному напряжению.
При x = 0 потенциал
= U;
а при x = d –
= 0:
Тогда потенциал другой
будет равен приложенному напряжению.
При x = 0 потенциал
= U;
а при x = d –
= 0:
;
;
. (15.44)
Следовательно, между пластинами потенциал линейно уменьшается от величины U до нуля (рис. 15.17б).
Напряженность поля
(15.45)
Напряженность поля не зависит от координаты x и численно равна U/d.
Выделим в проводящей среде небольшой параллелепипед объемом V (рис. 16.1).
Рис. 16.1. Параллелепипед в проводящей среде
Длина ребер параллелепипеда l, площадь поперечного сечения s.
Расположим его так, чтобы напряженность поля была в нем направлена параллельно ребру. В силу малости объема можно считать, что напряженность поля одна и та же во всем элементарном объеме:
где – единичный вектор по направлению .
Ток:
(16.2)
Напряжение на элементе объема:
(16.3)
Сопротивление элемента объема:
, (16.4)
где – удельная проводимость среды.
Поставив в (16.3) выражения (16.2) и (16.4) получим:
,
. (16.5)
Выражение (16.5) называют законом Ома в дифференциальной форме. Это уравнение справедливо для областей вне источников ЭДС. В областях, занятых источниками ЭДС, существует также так называемое стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи. Это поле обусловлено химическими, электрохимическими, тепловыми и термоэлектрическими процессами. Закон Ома в дифференциальной форме для областей, занятых источниками ЭДС
(16.6)
Уравнение
(16.6) называется обобщенным законом Ома. Если от обеих частей взять интеграл по
замкнутому контуру, то получим второй
закон Кирхгофа в дифференциальной
форме.
Если от обеих частей взять интеграл по
замкнутому контуру, то получим второй
закон Кирхгофа в дифференциальной
форме.
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, входящий в объем, равняется току, выходящему из объема, иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Математически это записывают так:
(16.7)
Разделим правую и левую часть уравнения (16.7) на объем и возьмем предел в случае, когда объем стремится к нулю
(16.8)
Соотношение (16.8) называется первым законом Кирхгофа в дифференциальной форме. Он гласит, что в установившемся режиме (при постоянном токе) в любой точке тока нет ни истока, ни стока линий тока проводимости .
емкость — Последовательно соединенные диэлектрики, напряженность электрического поля
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 302 раза
$\begingroup$
Я пытаюсь приложить сильное электрическое поле к пористому материалу, прикладывая сильное напряжение к двум проводящим параллельным пластинам, расположенным между материалом.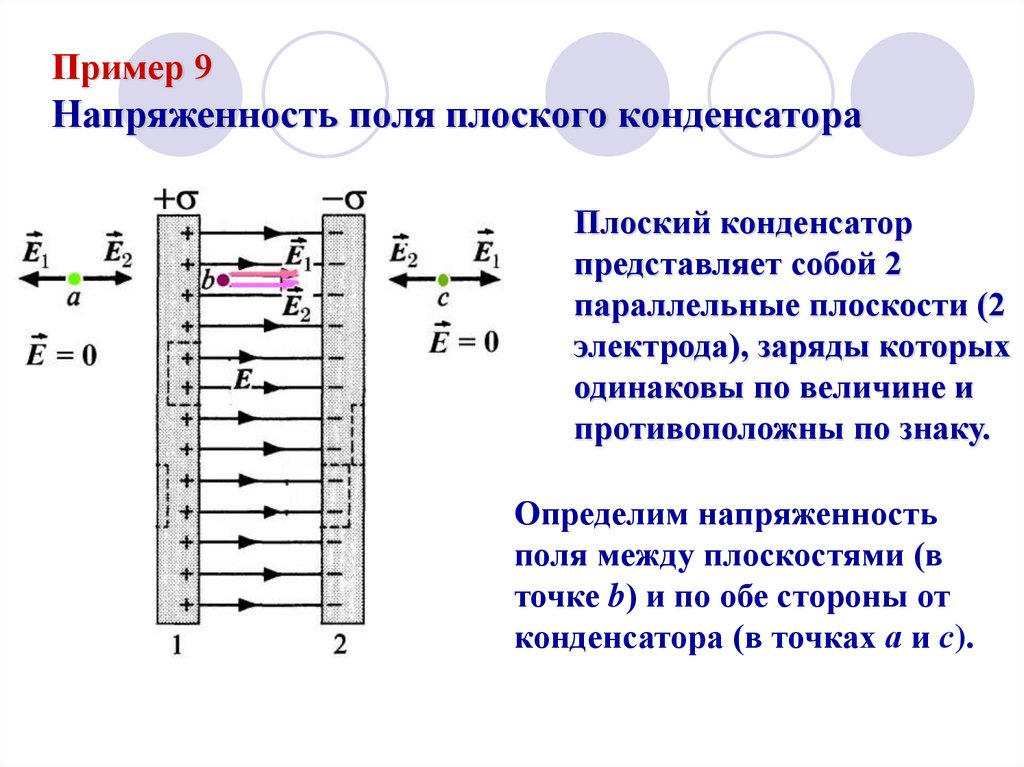 Цель состоит в том, чтобы выровнять диполи в материале. Я не могу добиться достаточно высокой напряженности поля из-за диэлектрического пробоя воздуха в порах материала, поэтому я экспериментирую с покрытием материала маслом. Это позволяет применять более сильное электрическое поле, но будет ли мой материал все еще видеть это сильное электрическое поле или присутствие диэлектрической жидкости будет работать против напряженности электрического поля?
Цель состоит в том, чтобы выровнять диполи в материале. Я не могу добиться достаточно высокой напряженности поля из-за диэлектрического пробоя воздуха в порах материала, поэтому я экспериментирую с покрытием материала маслом. Это позволяет применять более сильное электрическое поле, но будет ли мой материал все еще видеть это сильное электрическое поле или присутствие диэлектрической жидкости будет работать против напряженности электрического поля?
Другой способ задать этот вопрос может быть таким: можно ли рассматривать конденсатор с параллельными пластинами с последовательно соединенными диэлектриками как отдельные последовательно соединенные конденсаторы с плоскими пластинами, где мой материал по-прежнему видит приложенное электрическое поле, а не эффективное электрическое поле после поля поляризации диэлектрик вычитается?
Я работал с уравнениями и рад поделиться количественными рассуждениями, если только у кого-то нет быстрого ответа на этот вопрос.
Спасибо!
- электрические поля
- емкость
- диэлектрик
$\endgroup$
1
$\begingroup$
мой материал все еще увидит это сильное электрическое поле или наличие работы диэлектрической жидкости против электрического поля сила?
Если напряжение, приложенное к конденсатору, останется прежним, добавление масла вызовет разделение этого напряжения между исходным материалом и двумя слоями масла, предположительно образовавшимися между материалом и пластинами, что ослабит поле в материал.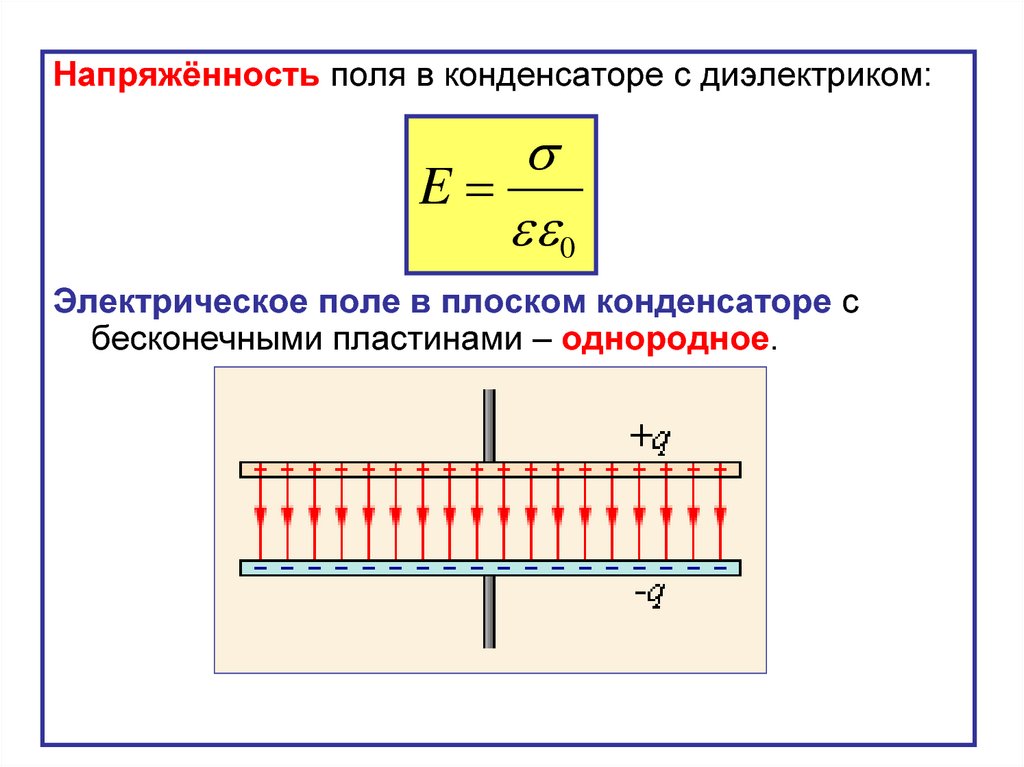
Другой способ задать этот вопрос может быть — может ли параллельная пластина конденсатор с последовательно соединенными диэлектриками следует рассматривать как отдельные параллельные пластинчатые конденсаторы серии
Да. Вы по-прежнему будете иметь пониженную долю напряжения в вашем материале и, следовательно, уменьшите электрическое поле.
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Конденсаторы
Параллельные пластины
Если вы знаете разность потенциалов между двумя параллельными пластинами, вы можете легко рассчитать напряженность электрического поля между пластинами. Пока вы не находитесь рядом с краем пластин, электрическое поле между пластинами постоянно, а его напряженность определяется уравнением:
Обратите внимание, что при разности потенциалов V в вольтах и расстоянии между пластинами в метрах единицами измерения напряженности электрического поля являются вольты на метр [В/м]. Ранее единицы измерения напряженности электрического поля приводились в виде ньютонов на кулон [Н/Кл]. Легко показать, что они эквивалентны:
Вопрос: Величина напряженности электрического поля между двумя противоположно заряженными параллельными металлическими пластинами составляет 2,0×10 3 ньютонов на кулон.
Точка P расположена посередине между пластинами.
(A) Нарисуйте не менее пяти линий электрического поля, представляющих поле между двумя противоположно заряженными пластинами.
(Б) Электрон находится в точке Р между пластинами. Вычислите величину силы, действующей на электрон со стороны электрического поля.Ответ:
(А)
(Б)
Конденсаторы
Параллельные проводящие пластины, разделенные изолятором, могут использоваться для накопления электрического заряда. Эти устройства бывают разных размеров и известны как конденсаторы с параллельными пластинами. Количество заряда, которое конденсатор может хранить на одной пластине при заданной разности потенциалов между пластинами, называется емкостью устройства, выраженной в кулонах на вольт, также известной как фарад (Ф). Фарад — это очень большая величина емкости, поэтому большинство конденсаторов имеют номиналы в микрофарадах, нанофарадах и даже в пикофарадах.


 Считайте, что расстояние между пластинами хоть и изменяется, но все равно остается много меньше, чем длина и ширина пластины (иначе это уже не плоский конденсатор). И подумайте, что происходит с зарядом в никуда не подключенном конденсаторе.
Считайте, что расстояние между пластинами хоть и изменяется, но все равно остается много меньше, чем длина и ширина пластины (иначе это уже не плоский конденсатор). И подумайте, что происходит с зарядом в никуда не подключенном конденсаторе.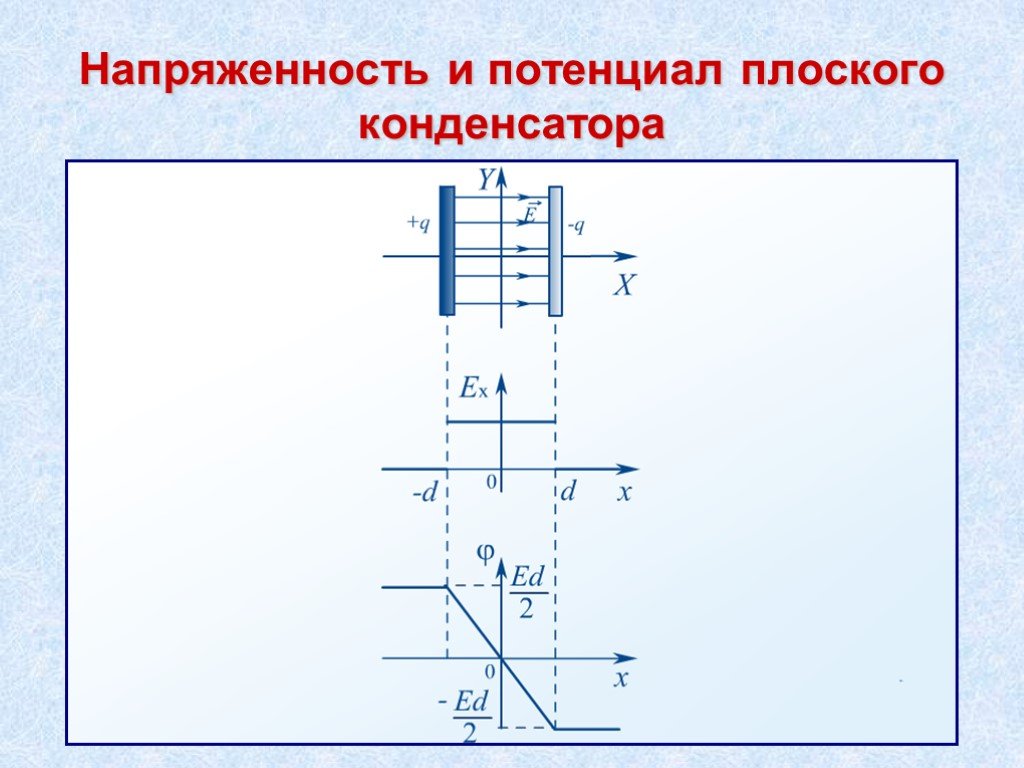
 Если с бесконечными плоскими равномерно заряженными пластинами, то все ок, напряжение растёт. Если поискать потенциал одной пластины на бесконечности, то будет бесконечность.
Если с бесконечными плоскими равномерно заряженными пластинами, то все ок, напряжение растёт. Если поискать потенциал одной пластины на бесконечности, то будет бесконечность. 12.2017, 12:04
12.2017, 12:04 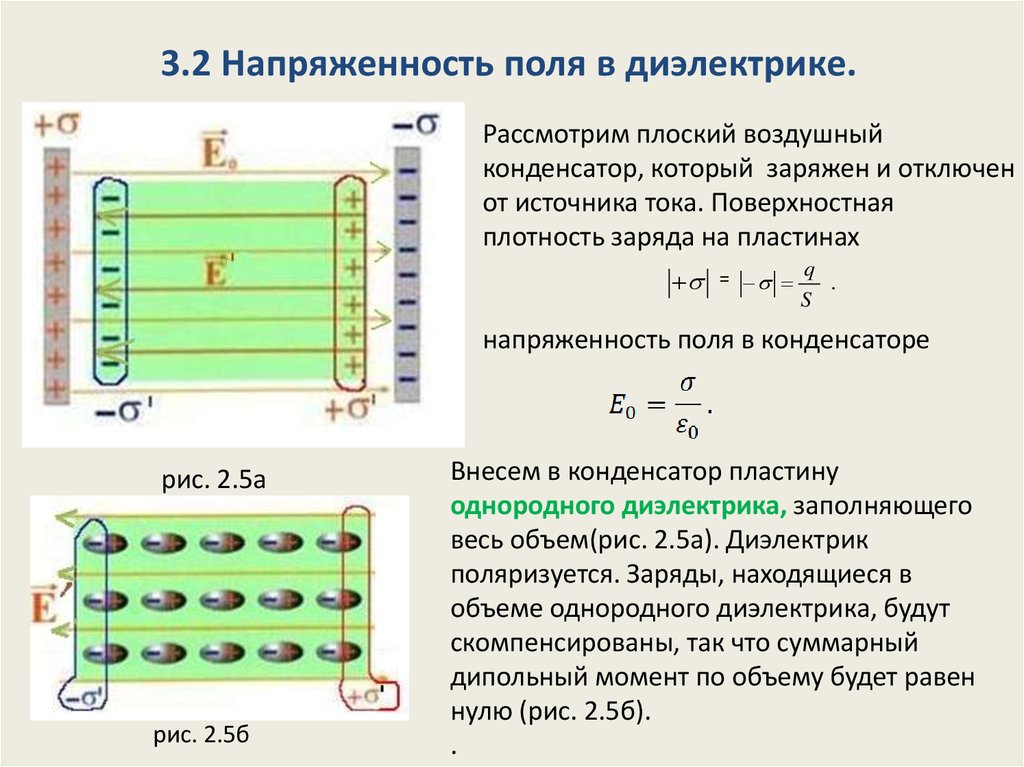 напряжённость поля прямоугольной плотности заряда на поверхности, и убывает пропорционально расстоянию в квадрате.
напряжённость поля прямоугольной плотности заряда на поверхности, и убывает пропорционально расстоянию в квадрате. Куда девается затраченная энергия?
Куда девается затраченная энергия?