Напряженность электрического поля между обкладками конденсатора
Содержание
- 1 В чем измеряется емкость конденсатора
- 2 Формула энергии конденсатора
- 3 Формула заряда конденсатора
- 4 Формула тока утечки конденсатора
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.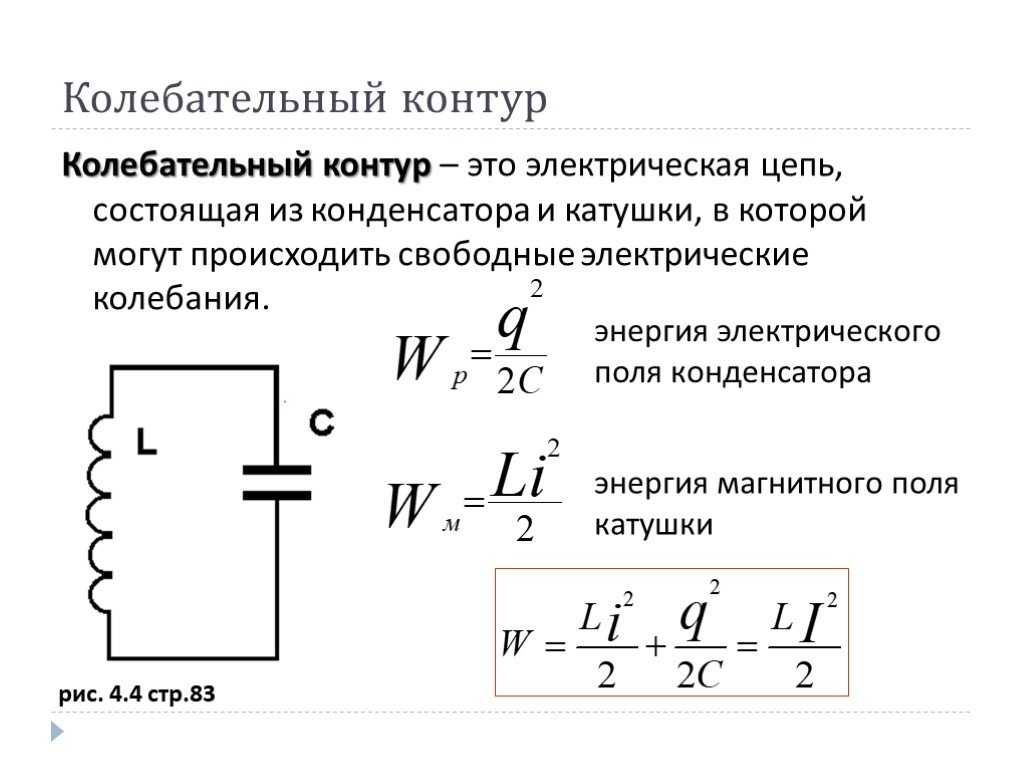
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.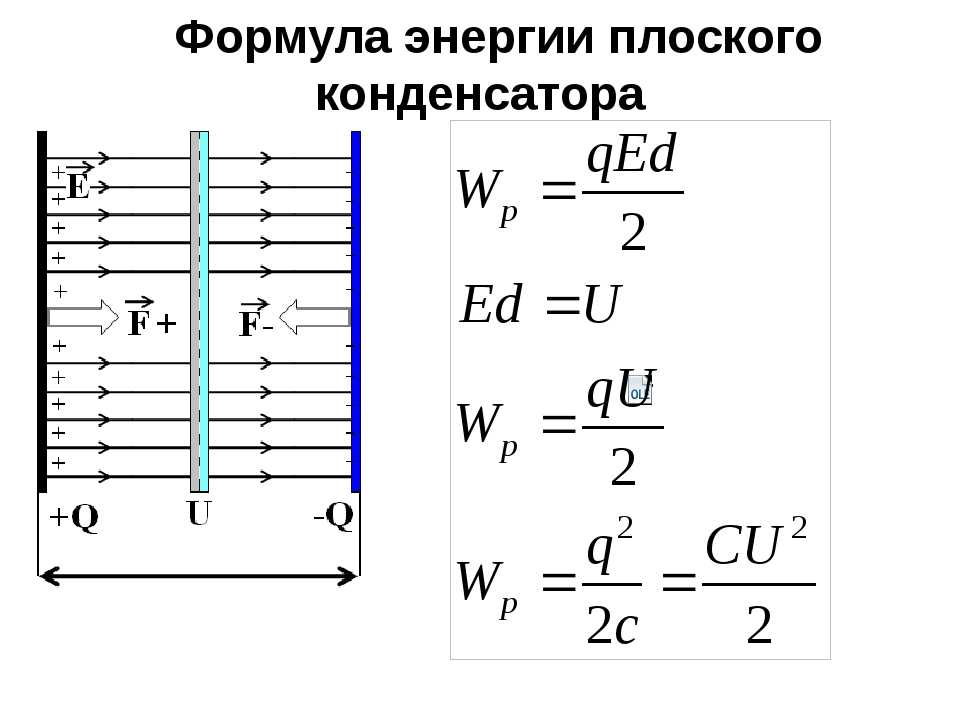
Напряженность поля между обкладками плоского конденсатора 6000 В/м. Определить массу пылинки, помещенной в это поле, если она несет заряд 10 -7 Кл и находится в равновесии.
Дано:
Решение:
Т.к. пылинка находится в равновесии, то сила Кулона равна силе тяжести
Ответ:
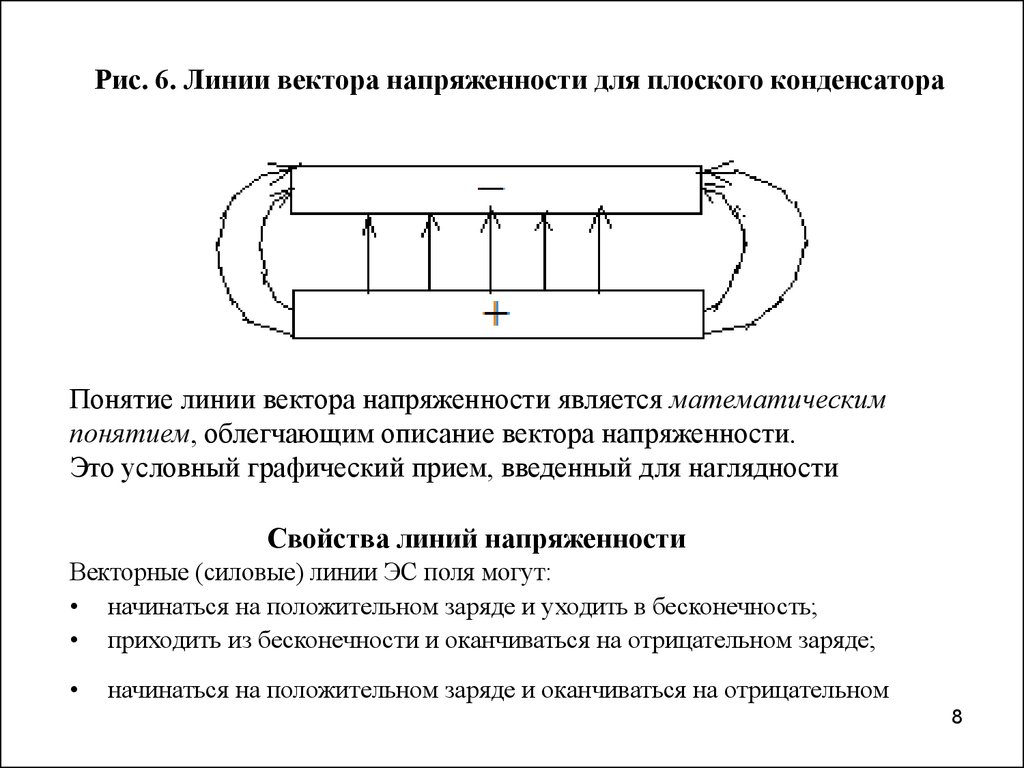
Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:
где E1=E2=σ2ε0⋅ε=q2ε0⋅ε⋅S — напряженности электрических полей каждой из обкладок конденсатора, σ — поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х: справа и слева от пластин — Eх=0; между пластин — E=2E1=qε0⋅ε⋅S.
Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна
Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю E=0. Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называется однородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.
Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).
В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ .
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей
Вне плоскостей напряженность поля .
Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке .
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): , т.е. .
Механические силы, действующие между заряженными телами, называют пондермоторными.Тогда сила притяжения между пластинами конденсатора: где S – площадь о,кладок конденсатора. Т.к. , то . Это формула для расчета пондермоторной силы.
Не нашли то, что искали? Воспользуйтесь поиском:
Напряженность электрического поля в конденсаторе.
 Калькулятор онлайн.
Калькулятор онлайн.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор вычисления напряженности электрического поля в конденсаторе, позволит найти напряженность E плоского, цилиндрического и сферического конденсаторов и даст подробное решение.

Калькулятор вычислит:
Напряженность электрического поля в плоском конденсаторе.
Напряженность электрического поля в цилиндрическом конденсаторе.
Напряженность электрического поля в сферическом конденсаторе.
Напряженность электрического поля в плоском конденсаторе
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Напряженность электрического поля в плоском конденсаторе определяется формулой, где
Q — заряд на пластине
ε0 – электрическая постоянная, ε0 = 8. -24]
-24]
Напряженность электрического поля в цилиндрическом конденсаторе
Цилиндрический конденсатор представляет собой конденсатор, обкладками, которого являются два цилиндра, внутренний с радиусом R Напряженность электрического поля в цилиндрическом конденсаторе определяется формулой, где Единицей измерения напряженности электрического поля является — Вольт (В, V).
Q — заряд
π – число Пи (3.14)
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
l – длина цилиндра
r — расстояние от оси симметрии цилиндров до точки, в которой необходимо найти напряженность электрического поля. Важно R1
Диэлектрическая проницаемость ε =
Радиус r = Метр (м)Декаметр дам (dam) × [10^1]Гектометр гм (hm) × [10^2]Километр км (km) × [10^3]Мегаметр Мм (Mm) × [10^6]Гигаметр Гм (Gm) × [10^9]Тераметр Тм (Tm) × [10^12]Петаметр Пм (Pm) × [10^15]Эксаметр Эм (Em) × [10^18]Зеттаметр Зм (Zm) × [10^21]Иоттаметр Им (Ym) × [10^24]Дециметр дм (dm) × [10^-1]Сантиметр см (cm) × [10^-2]Миллиметр мм (mm) × [10^-3]Микрометр мкм (µm) × [10^-6]Нанометр нм (nm) × [10^-9]Пикометр пм (pm) × [10^-12]Фемтометр фм (fm) × [10^-15]Аттометр ам (am) × [10^-18]Зептометр зм (zm) × [10^-21]Иоктометр им (ym) × [10^-24]
Длина l = Метр (м)Декаметр дам (dam) × [10^1]Гектометр гм (hm) × [10^2]Километр км (km) × [10^3]Мегаметр Мм (Mm) × [10^6]Гигаметр Гм (Gm) × [10^9]Тераметр Тм (Tm) × [10^12]Петаметр Пм (Pm) × [10^15]Эксаметр Эм (Em) × [10^18]Зеттаметр Зм (Zm) × [10^21]Иоттаметр Им (Ym) × [10^24]Дециметр дм (dm) × [10^-1]Сантиметр см (cm) × [10^-2]Миллиметр мм (mm) × [10^-3]Микрометр мкм (µm) × [10^-6]Нанометр нм (nm) × [10^-9]Пикометр пм (pm) × [10^-12]Фемтометр фм (fm) × [10^-15]Аттометр ам (am) × [10^-18]Зептометр зм (zm) × [10^-21]Иоктометр им (ym) × [10^-24]
Единица измерения напряженности поля E Вольт (В)Декавольт даВ (daV) × [10^1]Гектовольт гВ (hV) × [10^2]Киловольт кВ (kV) × [10^3]Мегавольт МВ (MV) × [10^6]Гигавольт ГВ (GV) × [10^9]Теравольт ТВ (TV) × [10^12]Петавольт ПВ (PV) × [10^15]Эксавольт ЭВ (EV) × [10^18]Зеттавольт ЗВ (ZV) × [10^21]Иоттавольт ИВ (YV) × [10^24]Децивольт дВ (dV) × [10^-1]Сантивольт сВ (cV) × [10^-2]Милливольт мВ (mV) × [10^-3]Микровольт мкВ (µV) × [10^-6]Нановольт нВ (nV) × [10^-9]Пиковольт пВ (pV) × [10^-12]Фемтовольт фВ (fV) × [10^-15]Аттовольт аВ (aV) × [10^-18]Зептовольт зВ (zV) × [10^-21]Иоктовольт иВ (yV) × [10^-24]
Напряженность электрического поля в сферическом конденсаторе
Сферический конденсатор представляет собой конденсатор, обкладками которого являются две концентрические сферы, радиусами R1 и R2, между которыми расположен диэлектрик, с диэлектрической проницаемостью ε. -24]
-24]
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Энергия электрического поля конденсатора
Проводники и диэлектрики, по-отдельности помещенные в электрическое поле, проявляют собственные индивидуальные качества. Именно проявление этих качеств сделало возможным применить их совместно. В результате, к электротехническим элементам добавились конденсаторы. При проведении дальнейших исследований были установлены основные физические свойства этих устройств, в том числе и энергия электрического поля конденсатора, выделяемая в процессе разрядки. Эта величина представляет собой потенциальную энергию, возникающую при взаимодействии обкладок конденсатора, поскольку, заряженные разноименно, они создают взаимное притяжение.
При проведении дальнейших исследований были установлены основные физические свойства этих устройств, в том числе и энергия электрического поля конденсатора, выделяемая в процессе разрядки. Эта величина представляет собой потенциальную энергию, возникающую при взаимодействии обкладок конденсатора, поскольку, заряженные разноименно, они создают взаимное притяжение.
Емкость – основное свойство конденсатора
Прежде чем рассматривать энергию конденсатора, следует остановиться на его основном свойстве – емкости. Когда двум проводникам, изолированным один от другого, сообщаются заряды q1 и q2, между ними наблюдается появление определенной разности потенциалов Δφ. Данная разность полностью зависит от величины зарядов и геометрической конфигурации проводников. Эта величина, возникающая в электрическом поле между двумя точками, известна также, как напряжение, обозначаемое символом U.
Наибольшее практическое значение имеют заряды проводников с одинаковым модулем и противоположными знаками: q1 = – q2 = q.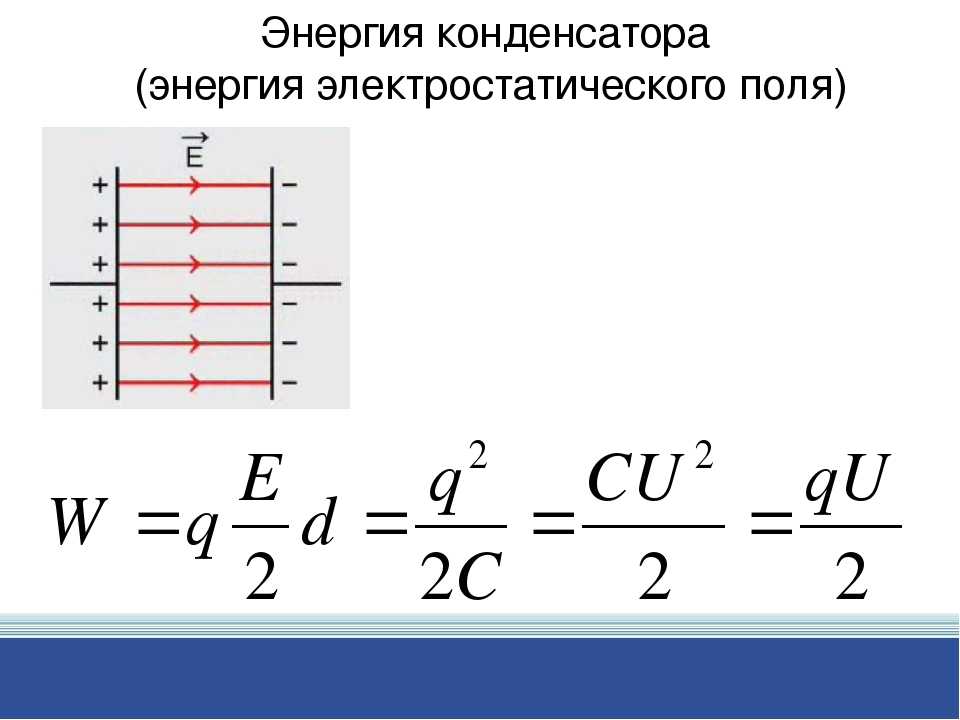 С их помощью выводится такое понятие, как электрическая емкость системы, состоящей из двух проводников. Данная категория представляет собой физическую величину, в которой заряд q какого-либо проводника, соотносится с разностью потенциалов Δφ. В виде формулы это будет выглядеть следующим образом: Системой СИ в качестве единицы электроемкости установлен фарад, который равен: 1Ф = 1Кл/1В
С их помощью выводится такое понятие, как электрическая емкость системы, состоящей из двух проводников. Данная категория представляет собой физическую величину, в которой заряд q какого-либо проводника, соотносится с разностью потенциалов Δφ. В виде формулы это будет выглядеть следующим образом: Системой СИ в качестве единицы электроемкости установлен фарад, который равен: 1Ф = 1Кл/1В
Электроемкость может иметь разную величину, в зависимости от форм и размеров проводников, а также от свойств диэлектрика, разделяющего эти проводники. Изменение значения емкости позволяет определить, как изменится энергия электрического поля конденсатора при использовании некоторых конфигураций проводников возникает электрическое поле, сосредоточенное лишь на определенном участке. Подобные системы получили название конденсаторов, в которых функцию обкладок выполняют проводники.
Конструкция простейшего конденсатора включает в себя две плоские проводящие пластины, расположенные параллельно между собой на расстоянии, меньшем, чем толщина самих пластин. Обе пластины разделяет слой диэлектрика. Такая система получила название плоского конденсатора. Его электрическое поле локализуется преимущественно между пластинами. Кроме того, слабое поле возникает около краев пластин, а также в окружающем их пространстве. Оно называется полем рассеяния, которое не оказывает существенного влияния на многие решаемые задачи. Поэтому в большинстве случаев учитывается только электрическое поле, сосредоточенное только между обкладками конденсатора.
Обе пластины разделяет слой диэлектрика. Такая система получила название плоского конденсатора. Его электрическое поле локализуется преимущественно между пластинами. Кроме того, слабое поле возникает около краев пластин, а также в окружающем их пространстве. Оно называется полем рассеяния, которое не оказывает существенного влияния на многие решаемые задачи. Поэтому в большинстве случаев учитывается только электрическое поле, сосредоточенное только между обкладками конденсатора.
Модуль напряженности электрического поля, создаваемого заряженными пластинами плоского конденсатора, представляет собой соотношение: Е1 = Ϭ/2ε0. Соответственно, сумма напряженности каждой пластины, равна общей напряженности поля. Положительные и отрицательные векторы напряженности, расположены параллельно внутри конденсатора, поэтому напряженность суммарного поля будет равна: Е = 2Е1 = Ϭ/ε0. Вне пластин положительный и отрицательный векторы оказываются направленными в разные стороны, в связи с чем Е = 0.
Заряд пластин обладает поверхностной плотностью Ϭ, равной q/S. В данной формуле q является величиной заряда, а S – площадью пластин. Разность потенциалов (Δφ) однородного электрического поля будет равна Ed, где величина d является расстоянием между пластинами. После соединения всех этих соотношений, получается формула, определяющая электрическую емкость плоского конденсатора:
В данной формуле q является величиной заряда, а S – площадью пластин. Разность потенциалов (Δφ) однородного электрического поля будет равна Ed, где величина d является расстоянием между пластинами. После соединения всех этих соотношений, получается формула, определяющая электрическую емкость плоского конденсатора:
Из этой формулы видно, что между электроемкостью плоского конденсатора и площадью обкладок существует прямая пропорция, и обратная пропорция с расстоянием между этими обкладками.
Энергия электрического поля
Как показывает практика, все заряженные конденсаторы обладают определенным запасом энергии. Данная величина является равной работе внешних сил, затрачиваемой для зарядки конденсатора. Непосредственная зарядка конденсатора происходит в виде последовательного переноса зарядов небольшими порциями с одной пластины на другую. В это время осуществляется постепенная зарядка одной обкладки положительным зарядом, а другой – отрицательным.
Перенос каждой порции выполняется при наличии на обкладках некоторого заряда q. Между обкладками имеется определенная разность потенциалов. В связи с этим, в процессе переноса каждой порции заряда, внешними силами совершается работа: ΔА = UΔq = qΔq/C.
Между обкладками имеется определенная разность потенциалов. В связи с этим, в процессе переноса каждой порции заряда, внешними силами совершается работа: ΔА = UΔq = qΔq/C.
Существует максимальная энергия электрического поля конденсатора, формула которой отображается таким образом: We = A = Q2/2C, где We – энергия конденсатора, А – работа, C и Q – соответственно емкость и заряд конденсатора. Если использовать соотношение Q = CU, то формула энергии заряженного конденсатора может быть выражена в другой форме: We = Q2/2C = CU2 = QU/2
Электрическая энергия We по своим физическим качествам аналогична потенциальной энергии, накопленной в заряженном конденсаторе. Как уже отмечалось, локализация электрической энергии конденсатора осуществляется между его обкладками, то есть в электрическом поле. Поэтому она получила название энергия электрического поля конденсатора, формула которой выводится из нескольких понятий и определений.
Если в качестве примера взять плоский заряженный конденсатор, то напряженность его однородного поля составит E = U/d, а его емкость будет равна С = ε0 εS/d. В результате, энергия электрического поля будет выражена в следующем виде: We = CU2/2 = ε0 εSЕ2d2/2d = (ε0 εЕ2/2) x V. В этой формуле V является пространственным объемом между обкладками, заполненным электрическим полем. Таким образом, We в качестве физической величины представляет собой электрическую или потенциальную энергию единицы пространственного объема, в котором существует электрическое поле. Эта величина также известна, как объемная плотность электроэнергии.
В результате, энергия электрического поля будет выражена в следующем виде: We = CU2/2 = ε0 εSЕ2d2/2d = (ε0 εЕ2/2) x V. В этой формуле V является пространственным объемом между обкладками, заполненным электрическим полем. Таким образом, We в качестве физической величины представляет собой электрическую или потенциальную энергию единицы пространственного объема, в котором существует электрическое поле. Эта величина также известна, как объемная плотность электроэнергии.
Напряженность электрического поля. Закон Кулона.
Электрическое поле – это одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженною частицу с силой, пропорциональной заряду частицы и не зависящей от ее скорости.
Векторную величину, характеризующую электрическое поле и определяющую силу, действующую на заряженную частицу со стороной электрического поля, называют напряженностью электрического поля в данной точке:
Е=F/Q (1)
Напряженность электрического поля точечного заряда (В/м)
(2)
где r – расстояние между зарядом и точкой, в которой определяется напряженность поля, м; εа – абсолютная диэлектрическая проницаемость среды, характеризующая диэлектрические свойства диэлектрика, Ф/м.
Напряженность в любой точке поля, создаваемая нескольким точечными зарядами, определяется геометрической суммой напряженностей полей:
Е = Е1 + Е2 +…+ Еп,
где Е1, Е2, …, Еп – напряженности электрического поля, создаваемые каждым зарядом и определяемые по формуле (2).
Силу взаимодействия двух точечных пробных зарядов Q1 и Q2, выражаемую в ньютонах (Н), определяют по закону Кулона:
(3)
где Q1 и Q2 – электрические заряды, Кл; r – расстояние между зарядами, м.
Абсолютная диэлектрическая проницаемость вакуума равна электрической постоянной: εо = 8,85·10-12 Ф/м.
Диэлектрическую проницаемость других сред обычно выражают в относительных единицах:
где ε – относительная диэлектрическая проницаемость вещества.
Электрическое напряжение и потенциал.При перемещении заряда Q в равномерном поле на расстояние l по направлению сил поля совершается работа
При этом между крайними точками перемещения заряда существует напряжение U – скалярная величина, характеризуемая работой, которая производится при перемещении единицы положительного заряда между двумя точками поля:
или (4)
Напряжение между данной точкой электрического поля и другой произвольно выбранной точкой поля, потенциал которой условно принят равным нулю, называют потенциалом φ данной точки поля. В электротехнике нулевым потенциалом считать принято потенциал земли.
В электротехнике нулевым потенциалом считать принято потенциал земли.
Напряжение между двумя точками электрического поля (В), имеющими потенциалы φ1 и φ2,
U = φ1 – φ2. (5)
В веществе, помещаемом в электрическом поле, под действием сил электрического поля возникает направленное движение носителей зарядов (электронов, ионов) – электрический ток. Это свойство называют электропроводностью вещества. Степень электропроводности вещества оценивают удельной электрической проводимостью материала.
Все вещества подразделяют на проводники, полупроводники и диэлектрики.
При внесении диэлектрика в электрическое поле происходит его поляризация, в результате чего ослабляется основное поле.
Диэлектрическая проницаемость ε показывает, во сколько раз ослабляется основное поле вследствие поляризации.
Напряженность поля, при которой происходит пробой диэлектрика, называют электрической прочностью диэлектрика Епр, а напряжение при пробое – пробивным напряжением Uпр, причем
(6)
где d – толщина пластины.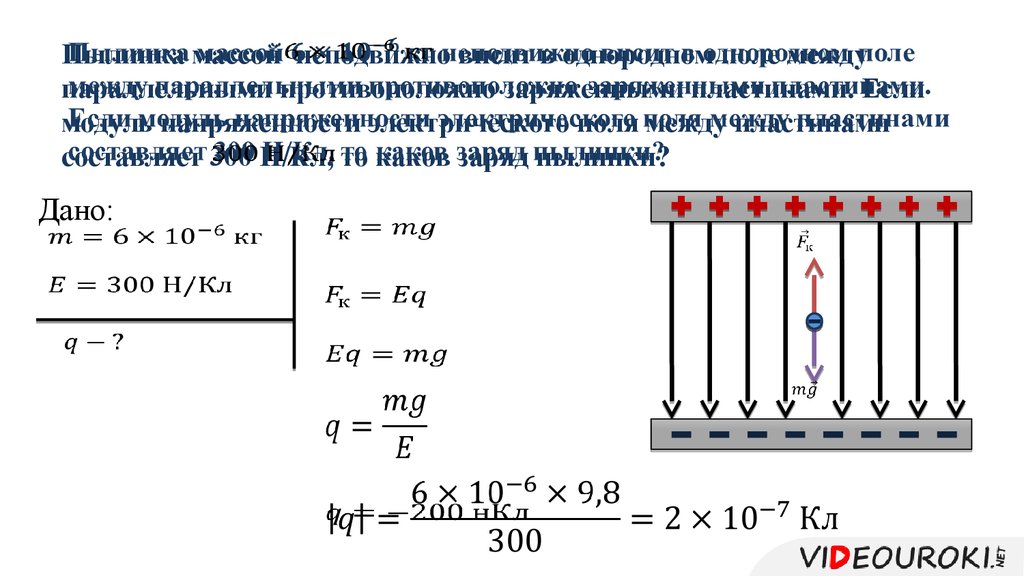
Электрическая емкость конденсатора.Электрический конденсатор – это система из двух проводников (обкладок, пластин), разделенных диэлектриком.
Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку.
Электрический заряд Q каждой из обкладок пропорционален напряжению U между ними:
(7)
Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конденсатора и выражают в фарадах (Ф).
Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и расстояния между обкладками, а также от свойств диэлектрика. Наиболее распространенным в технике являются плоский конденсатор.
Емкость плоского конденсатора
(8)
где S – площадь каждой обкладки, пластины, м2; d – расстояние между обкладками, м.
Напряженность электрического поля плоского конденсатора
(9)
где U – напряжение, приложенное к зажимам конденсатора, В.
Конденсаторы могут быть соединены последовательно, параллельно и смешано (последовательно-параллельно).
Последовательное соединение. При таком соединении на обкладках всех конденсаторов будут одинаковые по величине заряды, т.е.
Напряжения на конденсаторах будут различны, так как они зависят от их емкостей:
Общее напряжение
Общая, или эквивалентная, емкость
откуда
Для двух последовательно включенных конденсаторов
(10)
Параллельное соединение. При параллельном соединении напряжение на всех конденсаторах одинаково.
Заряды на обкладках отдельных конденсаторов при различной их емкости
Заряд, полученный всеми параллельно соединенными конденсаторами,
Общая, или эквивалентная, емкость
(11)
Энергия электрического поля (Дж)
(12)
Типовые задачи с решениями
1. На заряд Q = 16·10-8 Кл действует сила F = 2,4·10-3 H. Найти напряженность электрического поля в данной точке. Определить заряд Q0, создающий это поле, если он удален от этой точки на расстояние r = 0,3 м в вакууме.
На заряд Q = 16·10-8 Кл действует сила F = 2,4·10-3 H. Найти напряженность электрического поля в данной точке. Определить заряд Q0, создающий это поле, если он удален от этой точки на расстояние r = 0,3 м в вакууме.
Решение. Напряженность поля в данной точке
Значение заряда при данной напряженности
2. Два разнополярных заряда в стекле Q1 = +3,5·10-9 Кл и Q2 = -3,5·10-9 Кл находятся на расстоянии r = 18 см друг от друга. Заряд Q3 = +2·10-8 Кл расположен на расстоянии r = 24 см от этих зарядов. Определить значение и направление напряженности поля Е в точке, находящейся посередине между зарядами Q1 и Q2.
Решение. Определим напряженность электрического поля от действия заряда Q1 в искомой точке
Напряженность Е2 = 550 В/м, так как Q1 = Q2 и r1 = r2.
Для определения напряженности в этой же точке от действия заряда Q3 необходимо найти расстояние r3 этой точки от заряда Q3: из прямоугольного треугольника имеем
Найдем напряженность Е3:
Определим вектор напряженности поля в указанной точке:
Е = Е1 + Е2 + Е3.
Векторы Е1 и Е2 направлены в одну сторону (так как заряды Q1 и Q2 разноименные) и Е1 2 = Е1 + Е2 = 550 + 550 = 1100 В/м.
Вектор Е3 направлен перпендикулярно вектору Е1 2 и суммарный вектор напряженности:
При определении направления вектора Е необходимо помнить, что оно совпадает с направлением силы, действующей на положительны заряд.
3. К выводам плоского воздушного конденсатора приложено напряжение U = 800 В.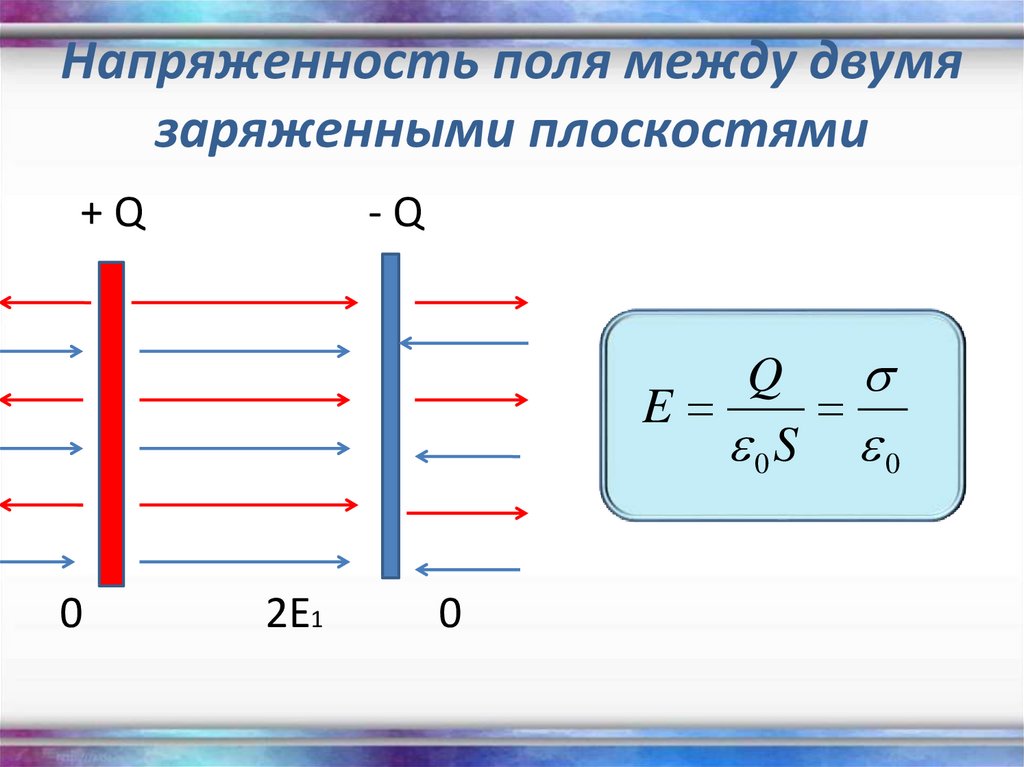 Определить напряженность электрического поля конденсатора при расстоянии между пластинами d = 5 мм и силу, действующую в этом поле на единичный заряд Q = 1,5·10-7 Кл. определить емкость конденсатора, если площадь каждой пластины S = 24 cм2. Как изменится его емкость, если конденсатор поместить в спирт?
Определить напряженность электрического поля конденсатора при расстоянии между пластинами d = 5 мм и силу, действующую в этом поле на единичный заряд Q = 1,5·10-7 Кл. определить емкость конденсатора, если площадь каждой пластины S = 24 cм2. Как изменится его емкость, если конденсатор поместить в спирт?
Решение. Напряженность электрического поля плоского конденсатора
Если заряд помещен в электрическое поле конденсатора, то
Емкость плоского воздушного конденсатора
Если конденсатор помещен в спирт, диэлектрическая проницаемость которого ε = 33, емкость увеличивается в 33 раза при неизменных расстоянии между пластинами и площади пластин:
4. Два плоских конденсатора емкостями С1 = 0,5 мкФ и С2 = 1,5 мкФ соединены последовательно и подключены к источнику питания. При этом на обкладках конденсаторов появился заряд Q = 4,5·10-4 Кл. оба конденсатора имеют одинаковые площади пластин и одинаковый диэлектрик. Определить общую (эквивалентную) емкость соединения, подведенное напряжение, падение напряжения на обоих конденсаторах и расстояние между пластинами первого конденсатора, если напряженность электрического поля второго конденсатора Е = 2000 В/см. Определить энергию электрического поля эквивалентного конденсатора.
оба конденсатора имеют одинаковые площади пластин и одинаковый диэлектрик. Определить общую (эквивалентную) емкость соединения, подведенное напряжение, падение напряжения на обоих конденсаторах и расстояние между пластинами первого конденсатора, если напряженность электрического поля второго конденсатора Е = 2000 В/см. Определить энергию электрического поля эквивалентного конденсатора.
Решение. Определим напряжения U1 и U2 на конденсаторах:
Напряжение, подведенное к зажимам цепи, U = U1 + U2 = 900 + 300 = 1200В.
Общая, или эквивалентная, емкость последовательно соединенных конденсаторов
или
Определим расстояние между пластинами второго конденсатора по (9):
Если конденсаторы имеют одинаковые площади пластин и один и тот же диэлектрик, то откуда
Энергию электрического поля найдем по (12)
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот. ..
..
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Поле сферического конденсатора
Обкладками сферического конденсатора являются две концентрические сферы (R1иR2). Сообщим этим поверхностям одинаковые по величине, но разноимённые заряды+qи–qи вычислим электрическое поле, создаваемое этими зарядами в пространстве (рис. 2.10.).
Сферы делят пространство на 3 области:
I— внутри первой сферы (r1<R1),
II— между обкладками (R1r2<R2),
III— за пределами
конденсатора (r3>R2).
Рис. 2.10.
Область I.
Выберем замкнутую гауссову поверхность внутри первой области. Разумно, руководствуясь соображениями симметрии, эту поверхность выбрать сферической (r1).
Поток вектора напряжённости через эту поверхность (по определению потока) равен:
Этот поток, согласно теореме Гаусса, пропорционален заряду, заключённому внутри поверхности. Но внутри сферы радиуса r1заряд отсутствует. Поэтому и поток равен нулю
(!)
Отсюда заключаем, что в области Iполе равно нулю
0 < r<R1,E= 0 (2.18)
Область II.
Вновь в качестве замкнутой поверхности
выберем сферу, но теперь её радиус r2лежит в пределах отR1доR2.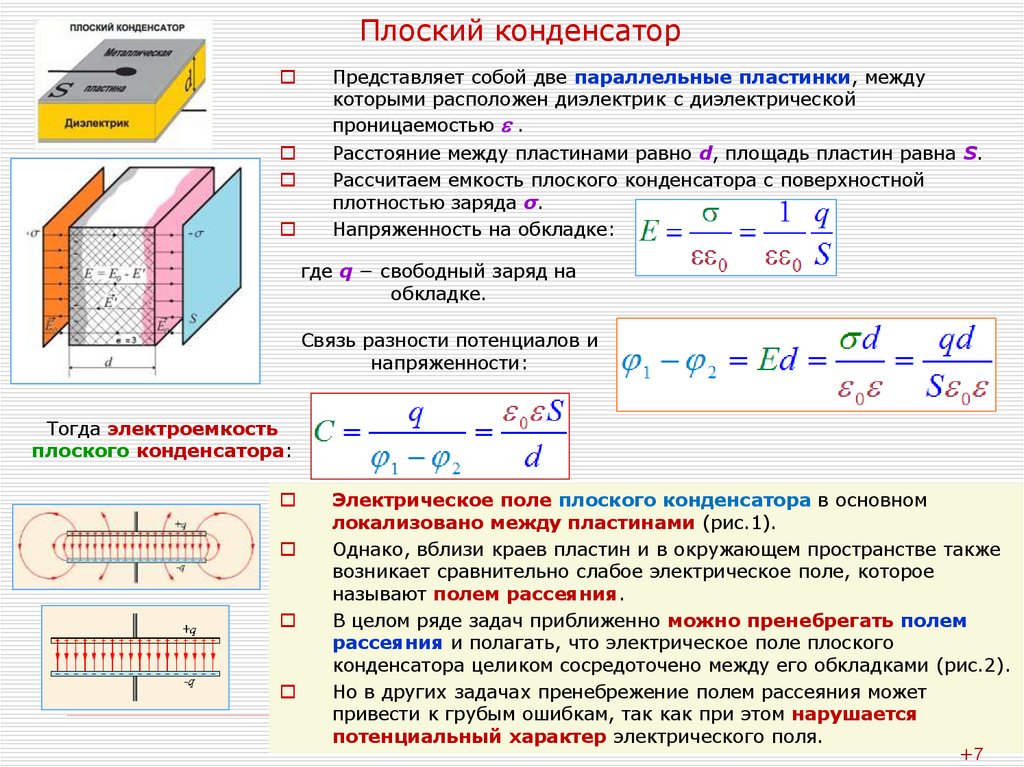
Вычислим поток вектора напряжённости поля через эту гауссову поверхность.
Воспользуемся теорией Гаусса: :
Оказывается, что электрическое поле между обкладками сферического конденсатора неотличимо от поля точечного заряда
. (2.19)
Посмотрим теперь, как выглядит поле в области III.
Вновь выберем замкнутую гауссову сферическую поверхность (радиус r3>R2). Вычисляем поток вектора напряжённости
Этот поток равен нулю, так как он пропорционален алгебраической сумме зарядов, заключённых внутри этой поверхности. Но алгебраическая сумма одинаковых разноимённых зарядов равна нулю
Отсюда следует, что Е = 0 (r3R2)/
График Е=Е(r)
приведён на рисунке 2. 11.
11.
Рис. 2.11.
Лекция 3 «Потенциал электростатического поля»
План лекции
3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
3.2. Теорема о циркуляции вектора напряжённости электростатического поля.
3.3. Связь напряжённости и потенциала электростатического поля.
3.4. Примеры расчёта потенциала электростатического поля.
3.4.1. Потенциал поля точечного заряда.
3.4.2. Разность потенциалов на обкладках сферического конденсатора.
Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.
Потенциал — энергетическая характеристика
поля, связанная и с энергией заряда в
электростатическом поле и с работой,
совершаемой электрической силой при
перемещении заряда.
Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
Рассмотрим произвольное перемещение (1–а–2) зарядаqв электростатическом поле. Пусть поле создаётся неподвижным точечным зарядомQ(рис. 3.1.). В процессе перемещения на зарядq действует кулоновская сила:
. (3.1)
Рис. 3.1.
Её работа на перемещении равна:
. (3.2)
Здесь dr=dlсos— толщина сферической оболочки, окружающей зарядQ. Полная работа электрической силы равна сумме работ на всех участках траектории:
. (3.3)
Теперь несложно показать, что эта работа
не зависит от формы траектории и остаётся
неизменной, если начальная и конечная
точки траектории не меняют своего
положения. Рассмотрим, например,
перемещение того же заряда q из начальной точки 1 в конечную 2 по
новой траектории 1–b–2.
При преодолении прежнего сферического
слоя на перемещенииэлектрическая сила совершит работу:
Рассмотрим, например,
перемещение того же заряда q из начальной точки 1 в конечную 2 по
новой траектории 1–b–2.
При преодолении прежнего сферического
слоя на перемещенииэлектрическая сила совершит работу:
. (3.4)
Но ведь эта работа в точности совпадает с работой на перемещении dl(3.2) по первоначальной траектории 1–а–2.
Полная работа, равная сумме элементарных работ на всех участках новой траектории, будет равна работе электрической силы на траектории 1–а–2:
. (3.5)
Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.
Мы пришли к выводу, что кулоновская
сила консервативна. Впрочем, ничего
неожиданного в этом выводе нет: ведь
сила взаимодействия двух точечных
зарядов может быть отнесена к классу
центральных сил, а все центральные силы,
как было установлено в механике,
консервативны.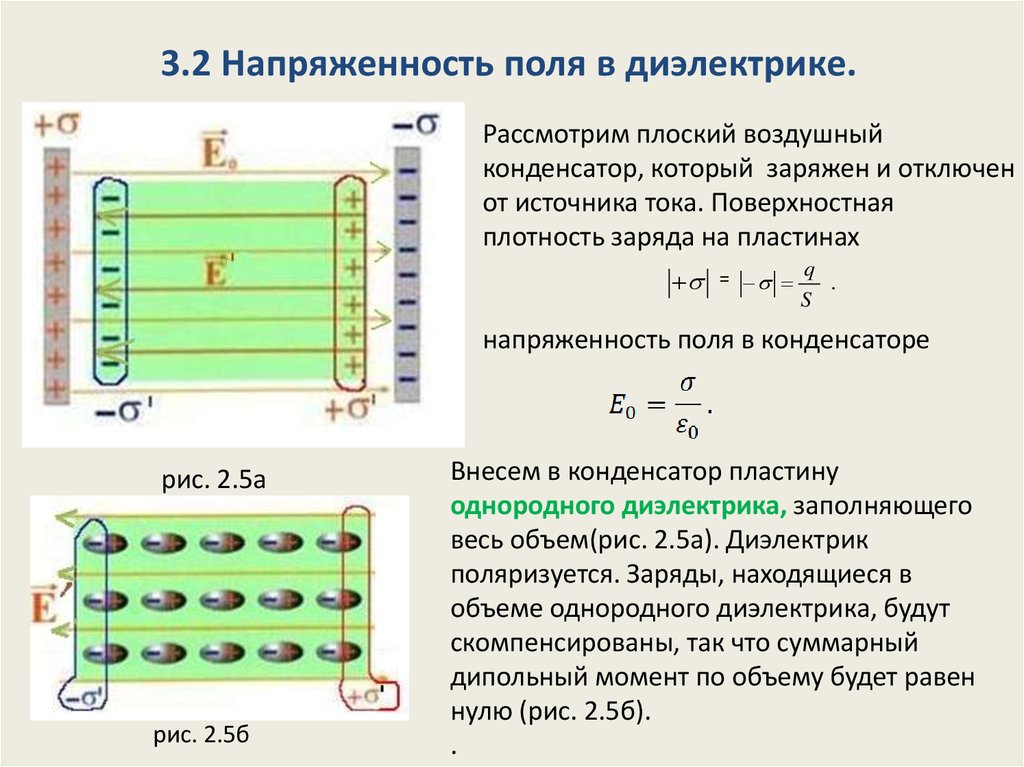
Итак, вычислим работу кулоновской силы при перемещении заряда qиз точки 1 в положение 2 (по любой траектории):
(3.6)
Как и следовало ожидать, величина работы никак не связана с видом траектории. Она зависит только от положения её начальной (r1) и конечной (r2) точек.
В механике было показано, что работа консервативной силы равна убыли потенциальной энергии системы:
. (3.7)
Присмотримся внимательнее к результату (3.6):
.
Сопоставив этот результат с теоремой о работе консервативной силы (3.7), запишем уравнение:
,
из которого следует, что потенциальная энергия системы:
+const. (3.9)
Это потенциальная энергия системы двух
точечных зарядов, или, что то же самое,
энергия заряда qв
электрическом поле точечного зарядаQ.
Константа в выражении (3.9) принимается обычно равной нулю. Это означает, что принимается равной нулю энергия взаимодействия зарядов qиQна бесконечном удалении их друг от друга (приr= ∞).Тогда на расстоянииrэнергия взаимодействия равна. (3.10)
Потенциальная энергия заряженной частицы в электрическом поле зависит, таким образом, от величины заряда qи от его положения в поле относительно зарядаQ, создающего поле.
Энергия единичного (q= 1) точечного заряда уже не будет связана с величиной этого пробного зарядаqи может быть принята в качестве энергетической характеристики данной точки электростатического поля:
.
Эта энергетическая характеристика поля получила название потенциал — .
Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.
Можно придать потенциалу и иной физический
смысл.
Поместим заряд qв поле точечного зарядаQ. Первоначально расстояние между зарядами —r. Отпустим зарядq. Под действием электрической силы отталкивания зарядqудалится в бесконечность (рис. 3.2.). На этом перемещении кулоновская сила совершит работу:
. (3.11)
Эта работа не зависит от формы траектории, поэтому мы её вычислили, считая, что заряд qудаляется по радиусу.
Рис. 3.2.
Сравнивая (3.10) и (3.11), заключаем, что:
. (3.12)
Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность.
Теперь вычислим потенциал поля, созданного
системой точечных зарядов Q1,Q2, …,QN.
При перемещении заряда qиз точки 1 в бесконечность электрическая сила совершит работу, равную алгебраической сумме работ сил, действующих на движущийся заряд со стороны зарядовQ1,Q2, …,QN(рис. 3.3.):
Рис. 3.3.
Согласно (3.12) работа каждой силы равна:
. (3.13)
Здесь — потенциал поля, создаваемого в точке 1 зарядомQi.
Таким образом, суммарная работа равна:
,
где .
Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности:
. (3.14)
Результат (3.14) известен как «принцип
суперпозиции для потенциала». Это
очень важный вывод, позволяющий
использовать понятие потенциала не
только для характеристики полей точечных
зарядов, но и для любых произвольных
электростатических полей.
Ещё раз обратимся к вычислению работы электрической силы при перемещении заряда qиз точки 1 теперь уже произвольного электростатического поля в бесконечность. Поскольку эта работа не зависит от формы траектории, унося заряд в бесконечность, пройдём предварительно точку 2 электростатического поля (рис. 3.4.).
Рис. 3.4.
Ясно, что вся работа на этом перемещении складывается из двух частей:
.
Разделив это равенство на величину переносимого заряда q, получим:
,
или:
. (3.15)
Здесь —разность потенциаловдвух точек поля. Она равна работе, совершаемой электрической силой при перемещении единичного заряда из первой точки во вторую:
. (3.16)
Таким образом, зная разность потенциалов двух точек поля, легко вычислить работу электрического поля, совершаемую при перемещении заряда qмежду этими точками:
. (3.17)
(3.17)
В международной системе единиц СИ потенциал (и разность потенциалов) измеряется в вольтах:
.
Разность потенциалов двух точек электростатического поля равна одному вольту, если при переносе заряда q= 1Кл между этими точками, электрическая сила совершает работуА(Fэл.) = 1 Дж.
Напряженность электрического поля в диэлектрике.
В соответствии с принципом суперпозиции электрическое поле в диэлектрике векторно складывается из внешнего поля и поля поляризационных зарядов (рис.3.11).
или по абсолютной величине
Мы видим, что величина напряженности поля в диэлектрике меньше, чем вакууме. Другими словами, любой диэлектрик ослабляет внешнее электрическое поле.
Рис.3.11. Электрическое поле в диэлектрике.
Индукция электрического поля , где , , то есть . С другой стороны, , откуда находим, что ε0Е0= ε0εЕ и, следовательно, напряженность электрического поля в изотропном диэлектрике есть:
Эта формула раскрывает физический смысл диэлектрической проницаемости и показывает, что напряженность электрического поля в диэлектрике в раз меньше, чем в вакууме. Отсюда следует простое правило: чтобы написать формулы электростатики в диэлектрике, надо в соответствующих формулах электростатики вакуума рядом с приписать .
Отсюда следует простое правило: чтобы написать формулы электростатики в диэлектрике, надо в соответствующих формулах электростатики вакуума рядом с приписать .
В частности, закон Кулона в скалярной форме запишется в виде:
14. Электрическая емкость. Конденсаторы (плоский, сферический, цилиндрический), их емкости.
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создавается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостьюконденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками:
Под емкостьюконденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками:
(1)
Найдем емкость плоского конденсатора, который состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если считать, что расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами на пластинах можно пренебречь и поле между обкладками считать однородным. Его можно найти используя формулу потенциала поля двух бесконечных параллельных разноименно заряженных плоскостей φ1-φ2=σd/ε0. Учитывая наличие диэлектрика между обкладками:
(2)
где ε — диэлектрическая проницаемость. Тогда из формулы (1), заменяя Q=σS, с учетом (2) найдем выражение для емкости плоского конденсатора:
(3)
Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2(r2 > r1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов
Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов
(4)
Подставив (4) в (1), найдем выражение для емкости цилиндрического конденсатора:
(5)
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов
(6)
Подставив (6) в (1), получим
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
где — заряд, — потенциал проводника.
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса Rравна (в системе СИ):
где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость.
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком иливакуумом, — к конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
15. Соединение конденсаторов (параллельное и последовательное)
Помимо показанного на рис. 60 и 61, а также на рис. 62, а параллельного соединения конденсаторов, при котором соединены между собой все положительные и все отрицательные обкладки, иногда соединяют конденсаторы последовательно, т. е. так, чтобы отрицательная обкладка
Рис. 62. Соединение конденсаторов: а) параллельное; б) последовательное
первого конденсатора была соединена с положительной обкладкой второго, отрицательная обкладка второго — с положительной обкладкой третьего и т. д. (рис. 62, б). В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов U, но заряды на них могут быть различными. Если емкости их равны С1, С2,…, Сn, то соответствующие заряды будут
Общий заряд на всех конденсаторах
и, следовательно, емкость всей системы конденсаторов
(35. 1)
1)
Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.
В случае последовательно соединенных конденсаторов (рис. 62, б) одинаковы заряды на всех конденсаторах. Действительно, если мы поместим, например, заряд +q на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд —q, а на левой обкладке второго конденсатора — заряд +q. Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд —q, а на левой обкладке третьего конденсатора — заряд +q и т. д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен q. Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:
где Сi — емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторов
Следовательно, емкость всей системы конденсаторов
определяется выражением
(35. 2)
2)
Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
16. Энергия электрического поля и её объёмная плотность.
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
Тогда объемная плотность энергии электрического поля равна
C учетом соотношения можно записать
В изотропном диэлектрике направления векторов D и E совпадают и
Подставим выражение , получим
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет
Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно, .
Следовательно, .
Вектор P связан с вектором E соотношением . Подставив это выражение в формулу для работы, получим
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика
.
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:
17. Постоянный электрический ток, его характеристики и условия существования. Закон Ома для однородного участка цепи (интегральная и дифференциальная формы)
Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Источник тока — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.
В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.
Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.
Основные понятия.
Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.
где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.
Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.
где j —плотность тока, S — площадь сечения проводника.
Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.
Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.
где A — полная работа сторонних и кулоновских сил, q — электрический заряд.
Электрическое сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
где ρ — удельное сопротивление проводника,l — длина участка проводника, S — площадь поперечного сечения проводника.
Проводимостью называется величина, обратная сопротивлению
где G — проводимость.
Законы Ома.
Дата добавления: 2016-07-22; просмотров: 5586; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
электростатика — Поле между пластинами плоского конденсатора с использованием закона Гаусса
Задавать вопрос
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 91к раз
$\begingroup$
Рассмотрим следующий плоский конденсатор, состоящий из двух пластин с одинаковой площадью $A$ и одинаковой поверхностной плотностью заряда $\sigma$:
Электрическое поле, создаваемое положительной пластиной, равно
$$\frac{\sigma }{\epsilon_0}$$
И величина электрического поля из-за отрицательной пластины такая же. Эти поля будут добавлены между конденсатором, что даст чистое поле:
Эти поля будут добавлены между конденсатором, что даст чистое поле:
$$2\frac{\sigma}{\epsilon_0}$$
Если мы попытаемся получить результирующее поле, используя закон Гаусса, заключив пластину в гауссову поверхность, как показано, поток будет только через грань, параллельную положительной пластине, и вне ее (поскольку другая грань находится в проводнике, а электрическая поле скользит по всем остальным граням).
$$\Phi = \oint \vec{E}\cdot\vec{dA} = EA$$
где $E$ — электрическое поле между пластинами конденсатора. По закону Гаусса это равно заряду $Q$ на пластинах, деленному на $\epsilon_0$
$$\frac{Q}{\epsilon_0}\ подразумевает E = \frac{Q}{A\epsilon_0} = \frac{\sigma}{\epsilon_0}$$
Я знаю, что в мои предположения или понимание, потому что я часто получаю противоречивые результаты при расчете электрических полей с использованием закона Гаусса. Однако мне не удается идентифицировать это.
Редактировать: Кроме того, я заметил еще одну проблему, заключающуюся в том, что даже если мы удалим отрицательную пластину из конденсатора, а затем применим закон Гаусса таким же образом, поле все равно будет равно $\sigma/\epsilon_0$, что равно явно неправильно, так как отрицательная пластина вносит свой вклад в поле. Так что, возможно, проблема в применении закона Гаусса.
Так что, возможно, проблема в применении закона Гаусса.
- электростатика
- электрические поля
- емкость
- закон Гаусса
$\endgroup$
1
$\begingroup$
Это чрезвычайно распространенная ошибка в вводной ЭМ — от студентов, которые действительно тратят время на обдумывание задачи, так или иначе 😉 Используйте закон Гаусса в обоих случаях:
В случае бесконечных пластин у вас не будет результата, который вы дай сначала. Гауссовский цилиндр имеет два диска по обе стороны пластины, поэтому $$E_1(2A)=\frac{\sigma A}{\epsilon_0}\rightarrow E_1=\frac{\sigma}{2\epsilon_0}$$ И из суперпозиции вы получите полное электрическое поле $$E=\frac{\sigma}{\epsilon_0}$$
Ваш второй случай верен, но заряд, заключенный в вашей поверхности, равен $Q/2$ по сравнению с первым случаем (сохранение заряда, если хотите тот же ответ лучше иметь одинаковый общий заряд на тарелках), поэтому
$$E_1A=\frac{(\sigma/2) A}{\epsilon_0}\rightarrow E_1=\frac{\sigma}{2\epsilon_0}$$
Что снова дает вам тот же ответ, когда вы применяете суперпозицию.
$\endgroup$
$\begingroup$
Сначала рассмотрим одну бесконечную проводящую пластину. Чтобы применить закон Гаусса с одним концом цилиндра внутри проводника, необходимо предположить, что проводник имеет некоторую конечную толщину. При этом плотность поверхностного заряда $\sigma$ должна быть распределена по обеим сторонам (представьте себе это как конечную пластину небольшой толщины, а затем растяните ее до бесконечности. Используя закон Гаусса с этой пластиной (либо положить один конец цилиндр в проводнике или один конец с обеих сторон) дает результат $E = \frac{\sigma}{\epsilon_{0}}=\frac{Q}{2A\epsilon_0}$.
Теперь представьте, что вторую пластину с противоположной плотностью заряда $-\sigma$ вносят из бесконечности. Поскольку эти пластины являются проводниками, заряды в каждой пластине будут перемещаться, чтобы нейтрализовать поле от противоположной пластины внутри проводника (помните, что $E = 0$ внутри проводника). Поскольку электрическое поле, создаваемое каждой пластиной, постоянно, это может быть достигнуто в проводнике с суммарным положительным зарядом путем перемещения плотности заряда $+\sigma$ в сторону пластины, обращенной к отрицательно заряженной пластине, и $-\ сигма$ на другую сторону. Противоположное будет сделано в отрицательно заряженной пластине. Теперь можно применить закон Гаусса с цилиндром вокруг положительной пластины, чтобы найти $E = \frac{2\sigma}{\epsilon_{0}}=\frac{Q}{A\epsilon_{0}}$. Это согласуется с добавлением электрического поля, создаваемого каждой из пластин в отдельности.
Поскольку электрическое поле, создаваемое каждой пластиной, постоянно, это может быть достигнуто в проводнике с суммарным положительным зарядом путем перемещения плотности заряда $+\sigma$ в сторону пластины, обращенной к отрицательно заряженной пластине, и $-\ сигма$ на другую сторону. Противоположное будет сделано в отрицательно заряженной пластине. Теперь можно применить закон Гаусса с цилиндром вокруг положительной пластины, чтобы найти $E = \frac{2\sigma}{\epsilon_{0}}=\frac{Q}{A\epsilon_{0}}$. Это согласуется с добавлением электрического поля, создаваемого каждой из пластин в отдельности.
Если вы внимательно посмотрите на электрические поля на рисунке, который вы нарисовали выше, то увидите, что электрическое поле внутри проводника действительно отлично от нуля. Чтобы удерживать электрическое поле внутри проводящих пластин равным нулю, необходимо учитывать эти индуцированные заряды.
Теперь также очевидно, что электрическое поле зависит от отрицательно заряженной пластины. Если бы заряд на этой пластине был изменен или полностью удален, то явно изменился бы индуцированный заряд на положительной пластине, что привело бы к изменению электрического поля.
Если бы заряд на этой пластине был изменен или полностью удален, то явно изменился бы индуцированный заряд на положительной пластине, что привело бы к изменению электрического поля.
$\endgroup$
4
$\begingroup$
В конденсаторе пластины заряжаются только на границе раздела, обращенной к другой пластине. Это потому, что «правильный» способ увидеть эту проблему — это рассматривать ее как поляризованный кусок металла, две поляризованные части которого обращены друг к другу.
В принципе, каждая плотность заряда создает поле величиной $\sigma/2 \epsilon$. Просто фактическая геометрия пластинчатого конденсатора такова, что эти поля складываются в области пластины и исчезают снаружи, что объясняет результат, который вы получаете с помощью закона Гаусса. Помните, что закон Гаусса говорит вам об общем электрическом поле, а не только о том, что связано с зарядом, который вы окружаете. {(2)}= E_{ext}$, а их вычитание дает $E_{int} = \frac{\sigma} {\эпсилон} + E_{ext}$. Здесь я не использовал тот факт, что это был настоящий конденсатор с металлическими пластинами, я просто представил бесконечные пластины противоположного заряда, обращенные друг к другу. Таким образом, нормально обнаружить, что общее решение может быть суммой любого внешнего поля + поле, созданное этими листами.
{(2)}= E_{ext}$, а их вычитание дает $E_{int} = \frac{\sigma} {\эпсилон} + E_{ext}$. Здесь я не использовал тот факт, что это был настоящий конденсатор с металлическими пластинами, я просто представил бесконечные пластины противоположного заряда, обращенные друг к другу. Таким образом, нормально обнаружить, что общее решение может быть суммой любого внешнего поля + поле, созданное этими листами.
Если вообразить случай, когда внешнее поле равно нулю, или тот факт, что в системе действительно есть металлические пластины, то мы получим обычный результат: поле равно $\frac{\sigma}{\epsilon}$ внутри и равно нулю снаружи.
$\endgroup$
4
Формула, Величина, Направление, Имп Часто задаваемые вопросы – Lambda Geeks
В этой статье мы будем использовать закон Гаусса для расчета электрического поля между двумя пластинами и электрического поля конденсатора.
Электрическое поле между двумя пластинами: Электрическое поле — электрическое свойство, связанное с любым зарядом в пространстве. Таким образом, электрическое поле — это любая физическая величина, принимающая различные значения электрической силы в разных точках данного пространства.
Таким образом, электрическое поле — это любая физическая величина, принимающая различные значения электрической силы в разных точках данного пространства.
Электрическое поле — это область или область, в каждой точке которой действует электрическая сила.
Электрические поля можно описать в общем виде как электрическую силу на единицу заряда.
Если мы рассмотрим бесконечную плоскость с однородным зарядом на единицу площади, т. е. ර, то для бесконечной плоскости электрическое поле можно определить как:
Давайте посмотрим на электрическое поле, когда задействованы две заряженные пластины. .
Между двумя заряженными пластинами существует однородное электрическое поле: Согласно закону Кулона электрическое поле вокруг точечного заряда уменьшается по мере удаления от него. Однако однородное электрическое поле можно создать, расположив две бесконечно большие проводящие пластины параллельно друг другу.
«Если в каждой точке данного пространства напряженность электрического поля остается неизменной, то говорят, что электрическое поле является однородным электрическим полем».
Силовые линии однородного электрического поля стремятся быть параллельными друг другу, и расстояние между ними также равно.
Параллельные силовые линии и однородное электрическое поле между двумя параллельными пластинами обеспечивают одинаковую силу притяжения и отталкивания пробного заряда, где бы он ни находился в поле.
Линии поля всегда проводятся от областей с высоким потенциалом к областям с низким потенциалом.
Направление электрического поля между двумя пластинами:Электрическое поле распространяется от положительно заряженной пластины к отрицательно заряженной пластине.
Например, предположим, что верхняя пластина положительная, а нижняя отрицательная, тогда направление электрического поля задается, как показано на рисунке ниже.
Положительные и отрицательные заряды чувствуют силу под действием электрического поля, но ее направление зависит от тип заряда, положительный или отрицательный. Положительные заряды ощущают силы в направлении электрического поля, тогда как отрицательные заряды чувствуют силы в противоположном направлении .
Электрическое поле между двумя параллельными пластинами с одинаковым зарядом:Предположим, у нас есть две бесконечные пластины, параллельные друг другу, имеющие положительную плотность заряда ර. Теперь здесь мы вычисляем суммарное электрическое поле, создаваемое этими двумя заряженными параллельными пластинами.
Оба электрических поля противостоят друг другу в центре двух пластин. В результате они компенсируют друг друга, что приводит к нулевому чистому электрическому полю внутри.
∴Ein = 0
Оба электрических поля направлены в одном направлении вне пластин, т. е. слева и справа. Таким образом, его векторная сумма будет равна ?/?0.
е. слева и справа. Таким образом, его векторная сумма будет равна ?/?0.
Eout = E1 + E2
Электрическое поле между двумя параллельными пластинами противоположного заряда:Предположим, у нас есть две пластины с плотностью заряда +ර и -ර. Расстояние d разделяет эти две пластины.
Пластина с положительной плотностью заряда создает электрическое поле E=µ/2ε0. И направление его направлено наружу или от пластины, в то время как пластина с отрицательной плотностью заряда имеет противоположное направление, т.е. направление внутрь.
Итак, когда мы используем принцип суперпозиции на обеих сторонах пластин снаружи и внутри пластин, мы можем видеть, что вне пластины оба вектора электрического поля имеют одинаковую величину и противоположное направление, и, таким образом, оба электрических поля компенсируют друг друга. другой аут. Итак, вне пластин электрического поля не будет.
∴Eout =0
Поскольку они поддерживают друг друга в одном направлении, результирующее электрическое поле между двумя пластинами равно E=µ/ε0.
E in = E 1 + E 2
Это факт, который мы используем для формирования плоского конденсатора.
Электрическое поле между двумя пластинами при заданном напряжении:В физике либо разность потенциалов ΔV, либо электрическое поле E используется для описания любого распределения заряда. Разность потенциалов ΔV тесно связана с энергией, а электрическое поле E имеет отношение к силе.
E — векторная величина, подразумевающая, что она имеет как величину, так и направление, тогда как ΔV — скалярная переменная без направления.
Когда между двумя проводящими пластинами, расположенными параллельно друг другу, подается напряжение, создается однородное электрическое поле.
Сила электрического поля прямо пропорциональна приложенному напряжению и обратно пропорциональна расстоянию между двумя пластинами.
Электрическое поле между двумя плоскопараллельными конденсаторами: Плоскопластинчатый конденсатор:Плоскопластинчатый конденсатор состоит из двух проводящих металлических пластин, соединенных параллельно и разделенных определенным расстоянием. Диэлектрическая среда заполняет зазор между двумя пластинами.
Диэлектрическая среда представляет собой изолирующий материал, и это может быть воздух, вакуум или некоторые непроводящие материалы, такие как слюда, стекло, электролитический гель, бумажная вата и т. д. Диэлектрический материал препятствует прохождению через него тока из-за его непроводимости. ведение имущества.
Однако при подаче напряжения на параллельные пластины атомы диэлектрической среды будут поляризоваться под действием электрического поля. В процессе поляризации будут формироваться диполи, и эти положительные и отрицательные заряды будут накапливаться на пластинах плоского конденсатора. Ток течет через конденсатор по мере накопления зарядов до тех пор, пока разность потенциалов между двумя параллельными пластинами не сравняется с потенциалом источника.
В процессе поляризации будут формироваться диполи, и эти положительные и отрицательные заряды будут накапливаться на пластинах плоского конденсатора. Ток течет через конденсатор по мере накопления зарядов до тех пор, пока разность потенциалов между двумя параллельными пластинами не сравняется с потенциалом источника.
Напряженность электрического поля конденсатора не должна превышать напряженность поля пробоя диэлектрического материала в конденсаторах с параллельными пластинами. Если рабочее напряжение конденсатора превышает его предел, пробой диэлектрика вызывает короткое замыкание между пластинами, немедленно разрушая конденсатор.
Таким образом, для защиты конденсатора от такой ситуации не следует превышать предел применяемого напряжения и выбирать диапазон напряжения конденсаторов.
Электрическое поле между пластинчатыми конденсаторами:
На следующем рисунке показан плоскопараллельный конденсатор.
В этом случае возьмем две большие проводящие пластины, расположенные параллельно друг другу, и разделим их на d. Здесь плотность заряда 1-й пластины +ර, а плотность заряда 2-й пластины -ර. Пластина 1 имеет общий заряд Q, а пластина 2 имеет общий заряд -Q. Как мы видели ранее, если взять две параллельные пластины с противоположным распределением заряда, электрическое поле во внешней области будет равно нулю. В результате результирующее электрическое поле в центре плоского конденсатора можно рассчитать следующим образом: E = E1 + E2 = ර/2ε + ර/2ε = ර/ε Где ර — поверхностная плотность заряда пластины Из приведенного выше уравнения мы можем сказать, что диэлектрическая среда вызывает уменьшение напряженности электрического поля, но она используется для увеличения емкости и удержания проводящих пластин в контакте. Если принять во внимание две неопределенно большие пластины, напряжение не подается, то величина электрического поля по закону Гаусса должна быть постоянной. Но электрическое поле между двумя пластинами, как мы говорили ранее, зависит от плотности заряда пластин. Следовательно, если две пластины имеют одинаковую плотность заряда, то электрическое поле между ними равно нулю, а в случае противоположной плотности заряда электрическое поле между двумя пластинами имеет постоянную величину. Когда на заряженные пластины подается напряжение, величина электрического поля определяется разностью потенциалов между ними. Более высокая разность потенциалов создает сильное электрическое поле, а большее расстояние между пластинами приводит к слабому электрическому полю. Таким образом, расстояние между пластинами и разность потенциалов являются существенными факторами для напряженности электрического поля. Часто задаваемые вопросы: Ответ. Электрические поля между параллельными пластинами и вокруг заряженной сферы неодинаковы. Посмотрим, как они различаются. Электрическое поле между параллельными пластинами зависит от плотности заряда пластин. Если они заряжены противоположно, то поле между обкладками равно µ/ε0, а если они имеют несколько зарядов, то поле между ними будет равно нулю. Вне заряженной сферы электрическое поле определяется выражением, тогда как поле внутри сферы равно нулю. В этом случае r представляет собой расстояние между точкой и центром. Ответ. E=µ/ε0 определяет электрическое поле между плоскопараллельными конденсаторами по закону Гаусса. Согласно закону Гаусса электрическое поле остается постоянным, поскольку оно не зависит от расстояния между двумя пластинами конденсатора. Если говорить о разности потенциалов, то она прямо пропорциональна расстоянию между двумя пластинами конденсатора и равна Таким образом, если расстояние увеличить в два раза, то увеличивается и разность потенциалов. Ответ. В конденсаторах с параллельными пластинами обе пластины заряжены противоположно. Таким образом, электрическое поле вне пластин будет уравновешено. Обе пластины заряжены противоположно, поэтому поля между пластинами будут поддерживать друг друга. Кроме того, между двумя пластинами присутствует диэлектрическая среда, поэтому диэлектрическая проницаемость диэлектрика также будет существенным фактором. Закон Гаусса и концепция суперпозиции используются для расчета электрического поля между двумя пластинами. E = E1 + E2 = = , где ර — плотность поверхностного заряда ε — проницаемость Dielectric Material. Ответ. Когда диэлектрический материал помещается между параллельными пластинами конденсатора во внешнем электрическом поле, атомы диэлектрического материала поляризуются. Накопление заряда на обкладках конденсатора вызвано индуцированным зарядом в диэлектрическом материале. Как показано на рисунке ниже, это накопление заряда создает электрическое поле между двумя пластинами, которые сопротивляются внешнему электрическому полю. На приведенном выше рисунке показана диэлектрическая пластина между двумя пластинами конденсатора, поскольку диэлектрическая пластина индуцирует противоположное электрическое поле; следовательно, результирующее электрическое поле между пластинами конденсатора уменьшается. Ans. Емкость плоского конденсатора, состоящего из двух одинаковых металлических пластин, рассчитывается следующим образом: Где C — емкость плоского конденсатора A — площадь каждой пластины D — это расстояние между параллельными пластинами , скажем, плотность поверхностного заряда составляет Теперь чистое электрическое поле можно определить, Потенциальные различия представлены, Таким подставив вышеприведенные значения в это уравнение, получим разность потенциалов Ответ. Электрическое поле падает, когда диэлектрический материал вводится между параллельными пластинами конденсатора из-за накопления заряда на параллельных пластинах, что создает электрическое поле в направлении, противоположном внешнему полю. Электрическое поле определяется выражением Электрическое поле и напряжение пропорциональны друг другу; таким образом, напряжение также уменьшается. Емкость конденсатора, с другой стороны, увеличивается, поскольку она пропорциональна диэлектрической проницаемости диэлектрического материала. Ответ. Магнитные поля существуют между двумя пластинами только тогда, когда электрическое поле между двумя пластинами изменяется. Таким образом, когда конденсатор заряжается или разряжается, электрическое поле между двумя пластинами изменяется, и только в это время существует магнитное поле. Ответ. Конденсаторы — это электрические устройства, которые используют постоянное электрическое поле для накопления электрических зарядов в виде электрической энергии. Между пластинами конденсатора находится диэлектрический материал. Если приложенное внешнее электрическое поле превышает напряженность поля пробоя диэлектрического материала, то изолирующий диэлектрический материал становится проводящим. Электрический пробой приводит к возникновению искры между двумя пластинами, которая разрушает конденсатор. Каждый конденсатор имеет различную емкость в зависимости от используемого диэлектрического материала, площади пластин и расстояния между ними. Допуск конденсатора находится где-то в пределах от заявленного значения. Ответ. Закон Гаусса имеет различные применения. В некоторых случаях расчет электрических полей требует жесткой интеграции и становится довольно сложным. Мы используем закон Гаусса, чтобы упростить оценку электрических полей без сложного интегрирования. Где ? — линейная плотность заряда проволоки. Анс. Поддерживая электрическое поле, конденсаторы используются для хранения электрических зарядов в электрической энергии. Когда пластины разделены воздухом или пространством, формула для конденсатора с параллельными пластинами: , где C — емкость конденсатора. A Плоский конденсатор имеет две проводящие пластины с одинаковой площадью поверхности, которые действуют как электроды. Одна пластина действует как положительный электрод, а другая — как отрицательный, когда к конденсатору приложена разность потенциалов. Две пластины разделены зазором, заполненным диэлектрическим материалом. Диэлектрические материалы являются электроизоляционными и непроводящими, что означает, что они не проводят ток и могут удерживать электростатические заряды, выделяя при этом минимальную энергию в виде тепла или токов утечки. Диэлектрические материалы обладают способностью к электрической поляризации. Электрическая поляризация — это тенденция молекул материала приобретать электрический дипольный момент, когда материал помещается во внешнее электрическое поле. Электрические заряды материала разделяются пропорционально электрическому полю, создавая два полюса, отрицательный и положительный. Процесс электрической поляризации подобен намагничиванию, когда магнитный диполь индуцируется в магнитном материале, когда он находится рядом с магнитом. Поэтому, когда диэлектрические материалы помещаются во внешнее электрическое поле, дипольный момент, возникающий в единице объема диэлектрического материала, также известен как электрическая поляризация. Это описывается приведенным ниже уравнением, где k — безразмерная диэлектрическая проницаемость , E — диэлектрическая проницаемость материала, а Eo — диэлектрическая проницаемость вакуума, которая составляет около 8,85 × 10 — 12 фарад на метр (Ф/м) . Две пластины плоскопараллельного конденсатора подключены к источнику питания. Пластина, соединенная с положительным полюсом батареи, приобретает положительный заряд, а пластина, соединенная с отрицательным полюсом, приобретает отрицательный заряд. Это происходит потому, что положительный полюс отталкивает электроны к противоположной пластине. Из-за притяжения между положительными и отрицательными зарядами, полученными в положительных и отрицательных пластинах, заряды накапливаются внутри пластин конденсатора. Линии электрического поля формируются между двумя пластинами от положительных зарядов к отрицательным, как показано на рисунке 1. Поляризация диэлектрического материала пластин приложенным электрическим полем увеличивает поверхностный заряд конденсатора пропорционально напряженности электрического поля. в котором он размещен. Рис. 1. Конфигурация конденсатора с параллельными пластинами. Источник: toppr.com. Поскольку обе пластины заряжены, отрицательный заряд одной из них уменьшает отрицательный заряд другой. С другой стороны, положительный заряд на одной из пластин увеличивает разность потенциалов между пластинами. Однако отрицательный заряд отрицательно заряженной пластины оказывает большее влияние, поэтому положительный заряд может быть передан положительно заряженной пластине. При напряжении 9На конденсатор подается 0059 В , сохраняется заряд Ом . Это принцип конденсатора с параллельными пластинами. Две пластины конденсатора с параллельными пластинами разделены расстоянием d , измеренным в м , которое заполнено атмосферным воздухом. Площадь поперечного сечения каждой пластины A измеряется в м 2 . Электрическое поле E каждой пластины равно следующему, где σ — поверхностная плотность. Если разность потенциалов между двумя пластинами равна V, подставив найденное уравнение для электрического потенциала, мы получим: Теперь, подставив емкость в полученное напряжение, мы получим: Видно, что емкость зависит от расстояния между пластинами. Накопленный заряд пропорционален площади поверхности и обратно пропорционален расстоянию. Это также можно подтвердить, рассмотрев характеристики кулоновской силы, когда одноименные заряды отталкиваются, а разноименные притягиваются. Сила между зарядами уменьшается с расстоянием. Чем больше пластины, тем больше емкость хранения заряда, поскольку заряды распределяются больше. Таким образом, запасаемый заряд увеличивается при увеличении площади. Точно так же, чем ближе пластины, тем больше сила притяжения между противоположными зарядами, поэтому емкость должна увеличиваться при уменьшении расстояния. На каждую пластину подается заданный заряд. Время, в течение которого конденсатор может удерживать заряд, зависит от качества диэлектрического материала, используемого в конденсаторе. В конденсаторе с параллельными пластинами при приложении напряжения между двумя проводящими пластинами создается однородное электрическое поле между пластинами. Однако на краях двух параллельных пластин силовые линии электрического поля не параллельны и не однородны, а слегка изогнуты вверх из-за геометрии пластин. Это известно как окантовка или краевой эффект (см. рис. 2). Напряженность электрического поля конденсатора прямо пропорциональна приложенному напряжению и обратно пропорциональна расстоянию между пластинами. Рисунок 2. Диаграмма, показывающая окантовку электрического поля на краях двух пластин. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в дефибрилляторах сердца и включает следующее: схема. Причина, по которой конденсаторы нельзя использовать в качестве батарей, заключается в том, что они не могут удерживать энергию в течение длительного времени из-за токов утечки. Вы можете сделать конденсатор с параллельными пластинами в домашних условиях, используя два листа бумаги, которые склеены вместе, с листом алюминиевой фольги, приклеенным к каждой стороне бумаги. Затем вам нужно прикрепить медные провода к верхнему правому и нижнему левому углам и соединить каждый провод с электродами батареи. Плоский конденсатор имеет емкость 5 мФ. Определить емкость после того, как расстояние между ними уменьшилось на треть от первоначального расстояния, а расстояние между двумя пластинами имело диэлектрическую проницаемость 7. Решение: Получим выражение, связывающее данную емкость и новая емкость с уменьшенным расстоянием. Конденсатор квадратной длины — это конденсатор с одинаковой шириной и длиной. Следовательно, его площадь можно вычислить по квадрату длины. Определите площадь конденсатора, если разность потенциалов между обкладками 0,5 В, расстояние между обкладками 3 мм и в конденсаторе накоплен заряд 1,2 ⋅ 10 -9 Кл. Решение : Мы используем уравнение, связывающее разность потенциалов с площадью. Затем мы заменяем, используя данные значения в единицах СИ. Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. Конденсатор — это устройство, используемое для накопления электрического заряда. Количество заряда [латекс]{Q}[/латекс], которое может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер. Количество заряда [латекс]{Q}[/latex], которое может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора. , например, его размер. Система, состоящая из двух одинаковых параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами. Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]{Q}[/латекс] Поле пропорционально заряду: [латекс]{E \propto Q},[/латекс] , где символ [латекс]{\пропто}[/латекс] означает «пропорционально». Из обсуждения в главе 19.2 Электрический потенциал в однородном электрическом поле, мы знаем, что напряжение на параллельных пластинах равно [латекс]{V = Ed}[/латекс]. Таким образом, [латекс]{V \propto E}.[/латекс] Отсюда следует, что [latex]{V \propto Q}[/latex], и наоборот, [латекс]{Q \propto V}.[/латекс] В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больший заряд в нем хранится. Различные конденсаторы сохраняют различное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. [латекс]{Q = CV}.[/латекс] Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора, [латекс]{C}[/латекс], и напряжение, ВВ . Преобразовывая уравнение, мы видим, что емкость [латекс]{C}[/латекс] – это количество заряда, накопленного на вольт, или [латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс] Емкость [латекс]{C}[/латекс] — это количество заряда, накопленного на вольт, или [латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс] Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками. Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности [латекс]{A}[/латекс], разделенную расстоянием [латекс]{d}[/латекс] (без материала между тарелки). Когда к конденсатору прикладывается напряжение [латекс]{V}[/латекс], он накапливает заряд [латекс]{Q}[/латекс], как показано на рисунке. Мы можем увидеть, как его емкость зависит от [латекс]{А}[/латекс] и [латекс]{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ([латекс]{А}[/латекс] и [латекс]{d}[/латекс]), которые влияют на его емкость [латекс]{С}[ /латекс]. Емкость конденсатора с плоскими пластинами в виде уравнения равна [латекс] {C = {\ varepsilon}_0} [/латекс] [латекс] {\ гидроразрыва {A} {d}}. [/латекс] Зазор заполнен диэлектрической средой, как показано на рисунке. Расстояние d между двумя пластинами значительно меньше площади каждой пластины. Следовательно, мы можем написать d<
Зазор заполнен диэлектрической средой, как показано на рисунке. Расстояние d между двумя пластинами значительно меньше площади каждой пластины. Следовательно, мы можем написать d<



В.
Почему электрическое поле между пластинами конденсаторов уменьшается при введении диэлектрической пластины? Объясните с помощью схемы. 
Q.
Две одинаковые металлические пластины получили положительный заряд Q1 и Q2 соответственно. Если их собрать вместе, чтобы образовать плоский конденсатор емкостью C, то разность потенциалов между ними составит ……..  Электрическое поле, напряжение и емкость изменяются, когда мы вводим диэлектрический материал между параллельными пластинами конденсатора.
Электрическое поле, напряжение и емкость изменяются, когда мы вводим диэлектрический материал между параллельными пластинами конденсатора.

Q. Формула для емкости с параллельными пластинами:
Формула для емкости с параллельными пластинами: Плоский конденсатор: происхождение, электрическое поле, применение

Как работает конденсатор с плоскими пластинами?


Конденсатор с параллельными пластинами: производное

Конденсатор с параллельными пластинами: токи утечки
 Поскольку не существует идеального диэлектрического материала, который мог бы идеально удерживать заряд, увеличение потенциала приводит к току утечки, что приводит к нежелательному разряду конденсатора после его отключения от цепи.
Поскольку не существует идеального диэлектрического материала, который мог бы идеально удерживать заряд, увеличение потенциала приводит к току утечки, что приводит к нежелательному разряду конденсатора после его отключения от цепи. Конденсатор с параллельными пластинами: электрическое поле

Использование конденсаторов с плоскими пластинами

Конденсатор с параллельными пластинами — основные выводы

Резюме
 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]{+Q}[/латекс] и [латекс]{-Q}[/латекс], разделены на две его пластины. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]{Q}[/латекс].
1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]{+Q}[/латекс] и [латекс]{-Q}[/латекс], разделены на две его пластины. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]{Q}[/латекс]. Конденсатор

Количество заряда
Q Конденсатор может хранить Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.
Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе. Мы определяем их емкость [латекс]{C}[/латекс] так, чтобы заряд [латекс]{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латексу]{С}[/латексу]. Заряд, хранящийся в конденсаторе, равен 9.0003
Мы определяем их емкость [латекс]{C}[/латекс] так, чтобы заряд [латекс]{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латексу]{С}[/латексу]. Заряд, хранящийся в конденсаторе, равен 9.0003 Емкость
 {-3} \;\text{F})}[/latex].
{-3} \;\text{F})}[/latex]. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]{C}[/латекс] должен быть больше для большего [латекса]{А}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, [латекс]{C}[/латекс] должен быть больше для меньшего [латекса]{d}[/латекс].
Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]{C}[/латекс] должен быть больше для большего [латекса]{А}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, [латекс]{C}[/латекс] должен быть больше для меньшего [латекса]{d}[/латекс]. Емкость плоскопараллельного конденсатора 92}[/латекс].
 Небольшое числовое значение [латекс] {{\ varepsilon}_0} [/латекс] связано с большим размером фарада. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.)
Небольшое числовое значение [латекс] {{\ varepsilon}_0} [/латекс] связано с большим размером фарада. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.)
Пример 1. Емкость и заряд в конденсаторе с параллельными пластинами
93 \;\text{V}}[/latex] применяется к нему?Стратегия
Нахождение емкости [латекс]{С}[/латекс] является прямым применением уравнения [латекс]{С = {\varepsilon}_0 А/д}[/латекс]. Как только [латекс]{C}[/латекс] найден, накопленный заряд можно найти с помощью уравнения [латекс]{Q = CV}[/латекс].
Решение для (a)
Ввод данных значений в уравнение для емкости плоского конденсатора дает
[латекс]\begin{array}{r @{{}={}} l} { C}\;= & {{\varepsilon}_0 \frac{A}{d} = (8,85 \times 10^{-12} \;\frac{F}{m}) \frac{1,00 \;\text {m}^2}{1. {-9} \;\text{F} = 8,85 \;\text{nF}}. \end{array}[/latex]
{-9} \;\text{F} = 8,85 \;\text{nF}}. \end{array}[/latex]
Обсуждение для (a)
Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.
Решение для (b)
Заряд, хранящийся в любом конденсаторе, определяется уравнением [латекс]{Q = CV}[/латекс]. Ввод известных значений в это уравнение дает 96 \;\text{V} / \text{m}}[/latex], на этом конденсаторе нельзя накопить больше заряда за счет увеличения напряжения.
Еще один интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. На мембране существует разность потенциалов около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 96 \;\text{V} / \text{m}}. [/latex]
[/latex]
Этого электрического поля достаточно, чтобы вызвать пробой воздуха.
Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если [латекс]{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]{E = V/d}[/латекс]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и сделать [латекс]{d}[/латекс] как можно меньше. Мало того, что меньший [латекс]{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.
Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс] {C = {\ varepsilon} _0 \ frac {A} {d}} [/ латекс], на коэффициент [латекс] {\ каппа} [/latex], называемая диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами равна
Емкость плоского конденсатора с диэлектриком между пластинами равна
[латекс] {C = \ каппа {\ varepsilon} _0} [/ латекс] [латекс] {\ гидроразрыва {A} {d}} [/ латекс] [латекс] {{\ текст {параллельный конденсатор с диэлектриком} )}.[/латекс]
Значения диэлектрической проницаемости [латекс]{\каппа}[/латекс] для различных материалов приведены в таблице 1. Обратите внимание, что [латекс]{\каппа}[/латекс] для вакуума точно равен 1, поэтому приведенное выше уравнение действует и в этом случае. Если используется диэлектрик, возможно, путем помещения тефлона между пластинами конденсатора в примере 1, то емкость увеличивается в [латекс] {\ каппа} [/латекс], что для тефлона составляет 2,1.
Самостоятельный эксперимент: изготовление конденсатора
Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой. 96}[/латекс]
 Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC
Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, ведут себя так же, как конденсаторы с вакуумом между пластинами , за исключением того, что воздух может стать проводящим, если напряженность электрического поля станет слишком большой. . (Напомним, что [латекс]{E = V/d}[/латекс] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью, для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин. Например, в примере 1 расстояние составляет 1,00 мм, поэтому предел напряжения для воздуха равен 94 \;\text{V})} \\[1em]= & {1. 1 \;\text{mC}.} \end{массив}[/latex]
1 \;\text{mC}.} \end{массив}[/latex]
Это в 42 раза больше заряда того же воздушного конденсатора.
Диэлектрическая прочность
Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость [латекс] {\ каппа} [/латекс]. Вода, например, является полярной молекулой, потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рис. 5 схематично показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]{d}[/латекс].
Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]{d}[/латекс].
Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]{V}[/латекс] для того же заряда [латекс]{Q}[/латекс]; поскольку [латекс]{С = Q/V}[/латекс], емкость [латекс]{С}[/латекс] больше.
Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]{V}[/латекс] для того же заряда [латекс]{Q}[/латекс]; поскольку [латекс]{С = Q/V}[/латекс], емкость [латекс]{С}[/латекс] больше.
Диэлектрическая проницаемость обычно определяется как [латекс]{\каппа = E_0/E}[/латекс] или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и она тесно связана с поляризуемостью материал.
Вещи большие и малые
Субмикроскопическое происхождение поляризации
Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0003 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0003 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
В главе 30 «Атомная физика» мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и путей планет в их орбиты вокруг Солнца). Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. Рисунок 7 иллюстрирует разделение заряда в молекуле воды, которая имеет два атома водорода и один атом кислорода [латекс]{\текст{Н}_2 \текст{О}}[/латекс]. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
PhET Explorations: Capacitor Lab
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Рис. 8. Конденсаторная лаборатория
8. Конденсаторная лаборатория- Конденсатор — это устройство, используемое для накопления заряда.
- Количество заряда [латекса]{Q}[/латекса], которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость [латекс]{C}[/латекс] представляет собой количество накопленного заряда на вольт , или
[латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс]
- Емкость конденсатора с параллельными пластинами равна [латекс]{C ={\varepsilon}_0}{\frac{A}{d}}[/латекс], когда пластины разделены воздухом или свободным пространством. [latex][{\varepsilon}_0}[/latex] называется диэлектрической проницаемостью свободного пространства.
- Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением
[латекс] {C = \ каппа {\ varepsilon} _0} [/ латекс] [латекс] {\ гидроразрыва {A} {d}}, [/латекс]
, где [латекс]{\каппа}[/латекс] — диэлектрическая проницаемость материала.

- Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
- конденсатор
- устройство, накапливающее электрический заряд
- емкость
- количество накопленного заряда на единицу вольта
- диэлектрик
- изоляционный материал
- диэлектрическая прочность
- максимальное электрическое поле, при превышении которого изоляционный материал начинает разрушаться и становится проводящим
- Плоский конденсатор
- две одинаковые проводящие пластины, разделенные расстоянием
- полярная молекула
- молекула с присущим разделением зарядов
Свойства конденсаторов и диэлектриков
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept
AP Physics 2 Help » Электричество и магнетизм » Схемы » Компоненты схемы » Свойства конденсаторов и диэлектриков
Заполните пропуски.
Диэлектрики __________ емкость, поскольку емкость __________ связана с напряженностью электрического поля, а диэлектрики __________ эффективной напряженностью электрического поля.
Возможные ответы:
уменьшение . . . обратно . . . увеличить
увеличить . . . напрямую . . . увеличить
увеличить . . . обратно . . . увеличить
увеличить . . . обратно . . . уменьшить
уменьшить . . . напрямую . . . уменьшить
Правильный ответ:
увеличить . . . обратно . . . уменьшить
Объяснение:
Причина, по которой диэлектрики уменьшают эффективную напряженность электрического поля, заключается в том, что при добавлении диэлектрика среда поляризуется, что создает электрическое поле, противоположное существующему электрическому полю.
Когда электрическое поле уменьшается, емкость увеличивается, потому что пластины способны накапливать больше заряда при одинаковом приложенном напряжении, потому что меньше силы отталкивает электроны от скопления на пластине.
Сообщить об ошибке
Две параллельные проводящие пластины, разделенные расстоянием , подключены к батарее под напряжением . Если расстояние между ними удвоилось, а батарея остается подключенной, какие из следующих утверждений верны?
Возможные ответы:
Электрический заряд на пластинах удвоился
Емкость не изменилась
Разность потенциалов между пластинами удвоилась
Разность потенциалов между пластинами уменьшилась вдвое
Электрический заряд на пластинах уменьшается вдвое
Правильный ответ:
Электрический заряд на пластинах уменьшается вдвое
Объяснение:
Уравнение для емкости параллельных проводящих пластин:
При удвоении расстояния емкость изменяется на:
Батарея по-прежнему подключена к пластинам, разность потенциалов не изменилась. Поскольку емкость уменьшается вдвое, а напряжение остается прежним, она обязательно должна упасть вдвое, чтобы учесть изменение.
Поскольку емкость уменьшается вдвое, а напряжение остается прежним, она обязательно должна упасть вдвое, чтобы учесть изменение.
Сообщить об ошибке
Емкости следующие:
Какова общая емкость системы на диаграмме выше?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните уравнения, используемые для сложения конденсаторов:
На схеме конденсаторы A и B соединены параллельно, а конденсаторы C и D соединены параллельно, и эти две системы соединены последовательно.
Используйте приведенное выше уравнение, чтобы найти эквивалентную емкость конденсаторов A и B.
Используйте приведенное выше уравнение, чтобы найти эквивалентную емкость конденсаторов C и D.
Используйте приведенное выше уравнение, чтобы найти общую емкость путем сложения двух последовательно соединенных систем конденсаторов.
Следовательно, общая емкость равна
Сообщить об ошибке
Емкости следующие:
3 90 Рассмотрим диаграмму выше. Если батарея имеет разность потенциалов , какова полная энергия системы после ее полной зарядки?
Возможные ответы:
Не хватает информации, чтобы найти энергию системы
Правильный ответ:
Объяснение:
Уравнения для сложения конденсаторов:
Чтобы найти полную энергию, нам нужно знать общую емкость. Для этого мы соединяем конденсаторы в соответствии с приведенными выше правилами.
Конденсаторы A и B включены параллельно.
Конденсаторы C и D включены параллельно.
Сложите вместе системы конденсаторов. Они в серии.
Они в серии.
Общая емкость равна
Уравнение для нахождения энергии конденсатора:
Подставьте известные значения и решите.
Таким образом, в полностью заряженной системе сохраняется энергия.
Сообщить об ошибке
Между пластинами изолированного заряженного плоскопараллельного конденсатора помещен диэлектрик. Какие из следующих утверждений является верным?
Возможные ответы:
Разность потенциалов увеличивается
Заряд на пластинах уменьшается
Разность потенциалов уменьшается
Уменьшается емкость
Заряд на пластинах увеличивается
Правильный ответ:
Разность потенциалов уменьшается
Пояснение:
Если в конденсатор добавить диэлектрик, его емкость увеличится. В нашей задаче говорится, что система заряжена и изолирована, что означает, что никакой заряд не выйдет из системы. Поэтому заряд на пластинах останется прежним.
Поэтому заряд на пластинах останется прежним.
Уравнение для емкости:
Поскольку заряд остается прежним, а емкость увеличивается, разность потенциалов должна уменьшаться, чтобы может увеличиваться.
Сообщить об ошибке
Предположим, у меня есть однородное электрическое поле внутри плоского конденсатора.
Предположим, что пластины конденсатора имеют длину и ширину, а расстояние между пластинами равно .
Учитывая, что емкость равна , при какой разности напряжений требуется конденсатор для накопления заряда?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить это, мы можем использовать формулу:
Где – накопленный заряд, – разность напряжений на конденсаторе и – емкость.
Решение для ,
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Изучите концепцию
Напряженность электрического поля в конденсаторе.
 Онлайн калькулятор.
Онлайн калькулятор.| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн-калькулятор расчета напряженности электрического поля в конденсаторе поможет вам рассчитать напряженность Е в плоских (плоских конденсаторах), цилиндрических и сферических конденсаторах и дает подробное решение. Единицы измерения могут включать любые префиксы СИ.
 Калькулятор автоматически преобразует один префикс системы СИ в другой.
Калькулятор автоматически преобразует один префикс системы СИ в другой. Калькулятор вычисляет:
Напряженность электрического поля в плоском конденсаторе.
Напряженность электрического поля в цилиндрическом конденсаторе.
Напряженность электрического поля в сферическом конденсаторе.
Калькулятор напряженности электрического поля в пластинчатом конденсаторе
Плоский конденсатор состоит из двух параллельных проводящих пластин, разделенных диэлектриком, расположенных на небольшом расстоянии друг от друга. В конденсаторе с плоскими пластинами электрическое поле Е однородно и не зависит от расстояния d между пластинами, так как расстояние d мало по сравнению с размерами пластин. Напряженность электрического поля в плоском конденсаторе определяется по формуле, где Единицей напряженности электрического поля в СИ является вольт (В). Калькулятор напряженности электрического поля в цилиндрическом конденсаторе Цилиндрический конденсатор – это конденсатор, обкладки которого представляют собой два цилиндра, внутренний с радиусом R 1 и внешний с радиусом Р 2 . Между пластинами находится диэлектрик, диэлектрическая проницаемость которого равна ε. Напряженность электрического поля в цилиндрическом конденсаторе определяется по формуле, где Единицей напряженности электрического поля в системе СИ является вольт (В). Калькулятор напряженности электрического поля в сферическом конденсаторе Сферический конденсатор представляет собой конденсатор, обкладки которого представляют собой две концентрические сферы с радиусами R 1 и R 2 , между которыми находится диэлектрик, диэлектрическая проницаемость которого это ε. Напряженность электрического поля в сферическом конденсаторе определяется по формуле, где Mechanics Optics Electricity and Magnetism Конденсаторы
Ом — заряд на пластине
ε 0 — диэлектрическая проницаемость вакуума, ε диэлектрика
S — Площадь одной пластины (предполагается, что пластины одинаковые) 9-24]
9-24]
Ом — электрический заряд
π — число Пи (3,1415926535897932384626433832795…)
ε 0 – vacuum permittivity, ε 0 = 8.85418781762039 × 10 -12
ε – permittivity of dielectric
l – length of the cylinder
r is the distance from the axis of symmeters of the cylinders до точки, в которой необходимо найти напряженность электрического поля. Важно R1 9-24]
9-24]
Ом — электрический заряд
π — число Пи (3,1415926535897932384626433832795…)
ε 0 9-24]
You may also find the following calculators helpful Physics Calculators Speed Time Distance Calculator Acceleration Speed Distance Calculator Калькулятор времени перемещения Калькулятор времени Калькулятор второго закона Ньютона Gravitational Force Calculator Momentum Calculator Impulse Calculator Object Weight Calculator Light Reflection and Refraction Calculator Калькулятор закона Ома Калькулятор закона Кулона Калькулятор прочности электрического поля точечный калькулятор электрического заряда Q Проявление. 
DISMALE OF GRACK CALCUTUTUTOR DISSICE DISSATUTURE DISMAN Калькулятор емкости проводника и сферы Емкость параллельной пластины, цилиндрического и сферического конденсатора калькулятор Прочность на электрическом поле в параллельной пластине, цилиндрическое и сферическое калькулятор Краткое (потенциальное разность). Калькулятор пластинчатых конденсаторов Калькулятор площади пластин параллельных конденсаторов Калькулятор энергии, накопленной в заряженном конденсаторе Энергия, накопленная в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах Калькулятор Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов Астрономические калькуляторы Вес объекта на других планетах Гравитационное ускорение на планетах Солнечной системы и их спутниках Converters Length Converter Speed Converter Acceleration Converter Calculators (Number theory) Mathematical Expressions Calculator Calculator Parentheses Prime Калькулятор факторизации Калькулятор Gcd и Lcm с шагами Калькулятор Gcd и Lcm с использованием алгоритма Евклида Калькулятор Gcd и Lcm для любого количества чисел Разбить число на его значение Разделить число на отношение.  Онлайн -калькулятор с шагами
Онлайн -калькулятор с шагами Процентный калькулятор с шагами Научная нотация к калькулятору для десятичного преобразования .0830 Logarithm Calculator Quadratic Equations Calculator With Steps Remainder Calculator Root Calculator Decimal Period Calculator Big Number Calculator Rounding Numbers Calculator Калькулятор свойств корней и показателей Калькулятор комплексных чисел Fraction Calculators Simplifying Fractions Calculator Improper to Mixed Fraction Calculator Mixed Fraction to Improper Calculator Fractions Calculator With Step by Step Solution Raising a Fraction to a Сила.  Онлайн калькулятор.
Онлайн калькулятор. Преобразование десятичной дроби в дробь Преобразование дроби в десятичную дробь Compare Fractions Calculator Common Denominator Calculator Trigonometers Calculators Sine Calculator Cosine Calculator Tangent Calculator Cotangent Calculator Калькулятор секанса Калькулятор косеканса Калькулятор арксинуса Arccosine Calculator Arctangent Calculator Arccotangent Calculator Arcsecant Calculator Arccosecant Calculator Numeral Systems Calculators Roman Numeral Calculator Римские цифры от 1 до 3999 Калькулятор систем счисления Двоичный калькулятор.  Сложение, вычитание, умножение и деление двоичных чисел.
Сложение, вычитание, умножение и деление двоичных чисел. Area Calculators Area of a Square Calculator Area of a Rectangle Calculator Combinatorics Calculators Permutations of N Elements Calculator Combinations of N Elements by M Calculator Перестановки N элементов с помощью M Calculator Linear Algebra and Analytical Geometers Calculators Matrix Addition and Subtraction Calculator Matrix Multiplication Calculator Matrix Transpose Calculator Matrix Determinant Calculator Inverse Matrix Calculator Длина сегмента линии. Онлайн-калькулятор расстояния между точками. Калькулятор векторных координат по двум точкам Калькулятор векторного модуля (длины) Калькулятор векторного сложения и вычитания Калькулятор векторного скалярного произведения.  Используя длину векторов и косинус угла между векторами.
Используя длину векторов и косинус угла между векторами. Калькулятор векторного скалярного произведения. Используя векторные координаты. Калькулятор векторного произведения. Используя векторные координаты. Векторный калькулятор тройного произведения Vector Multiplication by Number Calculator Angle Between Vectors Calculator Vector Collinearity Check Calculator Vector Coplanarity Calculator Math Trainers Addition Math Trainer Subtraction Math Тренажер Математический тренажер умножения Дивизионный математический тренажер Математический тренажер таблицы умножения Онлайн-тренажер счета для дошкольников Онлайн-тренажер внимательности для дошкольников Онлайн-тренажер сложения, вычитания и умножения. 

