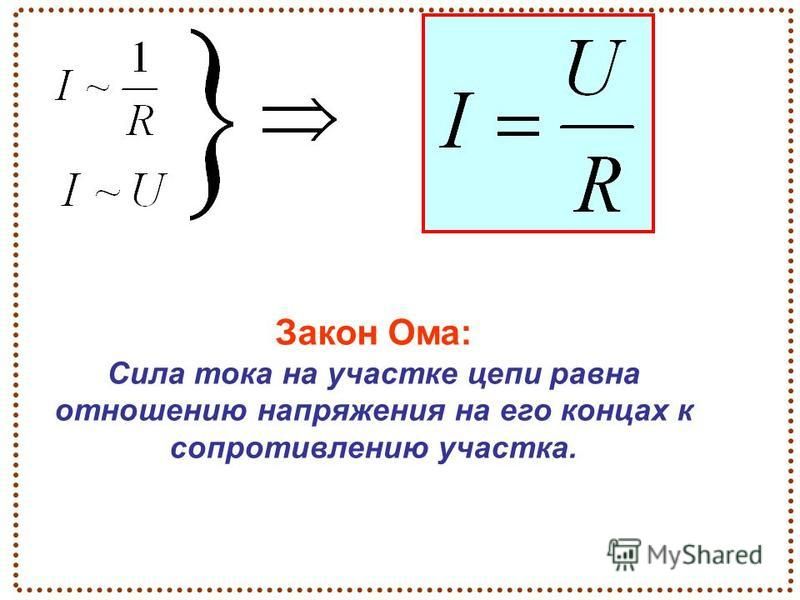
Какой буквой обозначается потенциал
Напряженность электрического поля. Физическая природа электрического поля и его графическое изображение. В пространстве вокруг электрически заряженного тела существует электрическое поле, представляющее собой один из видов материи. Электрическое поле обладает запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные тела. Простейшие электрические поля: а — одиночных положительного и отрицательного зарядов; б — двух разноименных зарядов; в — двух одноименных зарядов; г — двух параллельных и разноименно заряженныx пластин однородное поле.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Потенциал электрического поля.
Разность потенциалов - Справочник химика 21
- ИНФОФИЗ — мой мир…
- 3.1.5 Потенциальность электростатического поля
- Работа в электрическом поле. Потенциал
- Электрокинетический потенциал и его определение
- § 2.4. Напряжение на участке цепи
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Физика 10 класс (Урок№27 — Напряжённость и потенциал электростатического all-audio.proть потенциалов.)
Потенциал электрического поля. Разность потенциалов
Регистрация Вход. Ответы Mail. Вопросы — лидеры Правильна ли Специальная теория относительности? Магнитный воин -какие силы стоят за эффектом Джанибекова? Решите задачу по физике 1 ставка. Какая польза народному хозяйству от астрономии и теории эволюции? Независимые ученые узнали, что Человечество не вызвало Глобального Потепления. А Кто вызвал? Бес или Бог?
Вопросы — лидеры Правильна ли Специальная теория относительности? Магнитный воин -какие силы стоят за эффектом Джанибекова? Решите задачу по физике 1 ставка. Какая польза народному хозяйству от астрономии и теории эволюции? Независимые ученые узнали, что Человечество не вызвало Глобального Потепления. А Кто вызвал? Бес или Бог?
Лидеры категории Антон Владимирович Искусственный Интеллект. Кислый Высший разум. Какой буквой обозначется потенциал в Физике Александр Мастер , закрыт 7 лет назад. Лучший ответ. Остальные ответы. Vladimir Профи 9 лет назад Фи. Иван Федоров Просветленный 9 лет назад Смотря какой потенциал.
Греческой буквой «фи» традиционно обозначается электрический потенциал. А вот потенциал магнитного поля векторный потенциал обозначается буквой «A». Есть и другие потенциалы например, гравитационный. Вообще в физике нет строго фиксированных букв для обозначения определенных величин.
Есть традиции, которых можно придерживаться, а можно и не придерживаться — физика от этого не пострадает.
Похожие вопросы. Также спрашивают.
Справочник химика 21
У вас уже есть абонемент? Электрическое поле действует на помещенный в него заряд с силой, которая определяется величиной заряда и напряженностью поля в данной точке. Если эта сила перемещает заряд — то она совершает работу. Даже если заряда в поле нет, то потенциал ьно эта работа все равно может быть совершена, как только он там окажется. Из опыта других разделов физики мы знаем, что работа связана с энергией. Для решения некоторых задач удобно использовать энергетическую модель описания электрического поля.
Соотношение между электро-кинетическим потенциалом и общей разностью электро-кинетическим потенциалом и обозначают греческой буквой 2.
ИНФОФИЗ — мой мир…
Напряжение на участке цепи. Под, напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. На рис. Пусть ток I течет от точки а к точке b от более высокого потенциала к более низкому. В электротехнике разность потенциалов на концах сопротивления называют либо напряжением на сопротивлении, либо падением напряжения. В дальнейшем разность потенциалов на концах сопротивления, т. Положительное направление падения напряжения на каком-либо участке направление отсчета этого напряжения , указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
На рис. Пусть ток I течет от точки а к точке b от более высокого потенциала к более низкому. В электротехнике разность потенциалов на концах сопротивления называют либо напряжением на сопротивлении, либо падением напряжения. В дальнейшем разность потенциалов на концах сопротивления, т. Положительное направление падения напряжения на каком-либо участке направление отсчета этого напряжения , указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
3.1.5 Потенциальность электростатического поля
Согласно современной теории строения двойного электрического слоя получили объяснение электрические явления, а также проблемы строения и устойчивости коллоидных частиц лиофобных золей. Установлено, что при относительном движении жидкой и твердой фаз в электрическом поле плоскость скольжения их лежит на некотором расстоянии от твердой фазы. При этом слой жидкой фазы толщиной в молекулы при движении фаз остается неподвижным вместе с твердой фазой. Иными словами, непосредственно у поверхности коллоидной частицы образуется адсорбционный слой, включающий не только ПОИ, но и часть противоионов, которые в обычных условиях считаются неподвижными и при движении твердой фазы перемещаются вместе с ней. Остальная часть противоионов составляет диффузный слой, в котором концентрация ионов по мере удаления от поверхности коллоидной частицы постепенно убывает.
Иными словами, непосредственно у поверхности коллоидной частицы образуется адсорбционный слой, включающий не только ПОИ, но и часть противоионов, которые в обычных условиях считаются неподвижными и при движении твердой фазы перемещаются вместе с ней. Остальная часть противоионов составляет диффузный слой, в котором концентрация ионов по мере удаления от поверхности коллоидной частицы постепенно убывает.
Разность потенциалов. Известно, что одно тело можно нагреть больше, а другое меньше.
Работа в электрическом поле. Потенциал
Тема: Потенциал и разность потенциалов. Связь между напряжённостью и разностью потенциалов. Цели урока: обучить навыкам нахождения работы по перемещению заряда в электрическом поле, показать взаимосвязь между напряжённостью и разностью потенциалов, добиться овладения и закрепления качества знаний, дать практику в решении задач. Цели для обучающихся:. План урока:.
Электрокинетический потенциал и его определение
Студенческий блог для электромеханика. Обучение и практика, новости науки и техники. В помощь студентам и специалистам. Вы можете следить за обновлениями блога по RSS. После подписки по RSS ваш браузер или приложение, которым вы пользуетесь, будет оповещать вас о новых статьях на блоге. Также можно подписаться по email , используя форму ниже. Достаточно ввести свой email и нажать на кнопку «Подписаться».
Обучение и практика, новости науки и техники. В помощь студентам и специалистам. Вы можете следить за обновлениями блога по RSS. После подписки по RSS ваш браузер или приложение, которым вы пользуетесь, будет оповещать вас о новых статьях на блоге. Также можно подписаться по email , используя форму ниже. Достаточно ввести свой email и нажать на кнопку «Подписаться».
Потенциалом данной точки поля называется работа, которую поля φ1 — φ2 называется напряжением, измеряется в вольтах и обозначается буквой U.
§ 2.4. Напряжение на участке цепи
Регистрация Вход. Ответы Mail. Вопросы — лидеры Правильна ли Специальная теория относительности? Магнитный воин -какие силы стоят за эффектом Джанибекова?
Электрическое поле одного тела оказывает силовое действие на другое заряженное тело, и наоборот. Напряженность электрического поля — это векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы.
Для того, чтобы электронный компонент совершал полезную работу: лампа — горела, двигатель — вращался, через него должен протекать электрический ток. Ток создаётся электрическим потенциалом.
Пусть мы имеем бесконечное равномерное электрическое поле. На это перемещение заряда будет затрачена энергия электрического поля. Потенциалом данной точки поля называется работа, которую затрачивает электрическое поле, когда оно перемещает положительную единицу заряда из данной точки поля в бесконечно удаленную точку. Если заряд, равный 1 кулону, из бесконечно удаленной точки перемещается в точку поля, потенциал которой равен 1 вольту, то при этом совершается работа в 1 джоуль. Чтобы переместить 10 кулонов электричества из точки А с потенциалом 20 в в точку В с потенциалом 15 в, поле должно совершить работу.
В зависимости от количества зарядов и их величины изменяется энергия электрического поля, создаваемого этими зарядами. В практике очень часто приходится сравнивать различные по величине поля. Это сравнение производится по действиям полей на единичный положительный заряд так называемый пробный заряд. Поясним это.
Как обозначается потенциал электрического поля. Смотреть что такое «потенциал (в физике)» в других словарях
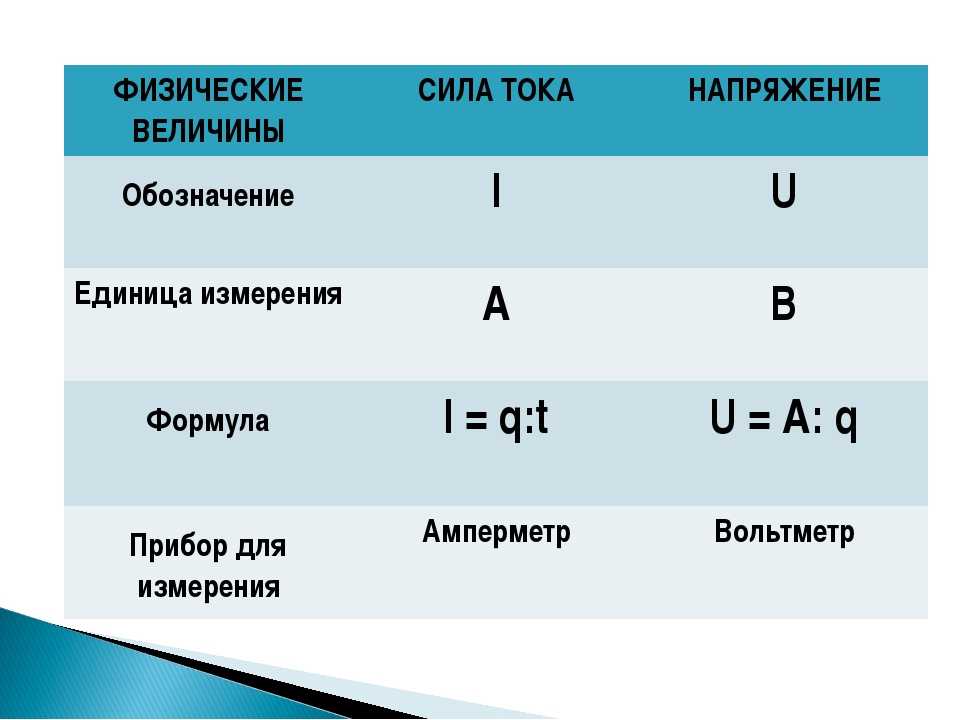
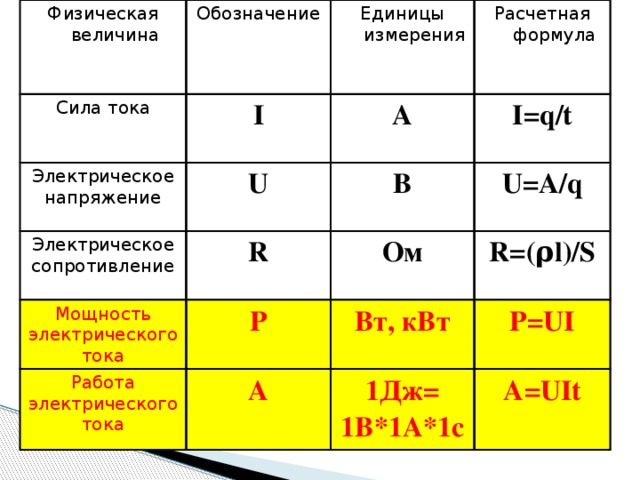
1. Электрический заряд (определение, обозначение, ед. измерения)
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Он определяет интенсивность электромагнитных взаимодействий.
Электрический заряд обычно обозначается буквами q или Q .
Единица измерения электрического заряда — Кл (кулон)
2. Закон сохранения электрического заряда (определение, формула)
Закон сохранения электрического заряда: в изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
q 1 + q 2 + q 3 + … + q n = const
3. Закон Кулона (определение, формула)
Закон Кулона: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Где k — коэффициент пропорциональности, равный
Тогда получаем:
4. Электрическое поле (определение)
Электрическое поле – это особая форма материи, которая существует независимо от нас и от наших знаний о нем, порождается электрическими зарядами и определяется по действию на электрические заряды.
Главное свойство электрического поля — действие на электрические заряды с некоторой силой.
5. Напряженность электрического поля (определение, обозначение, формула, ед. измерения)
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда.
Напряженность электрического поля – это векторная величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы.
Напряженность обозначается буквой Е .
Единица напряженности электростатического поля в СИ — Н/Кл (ньютон на кулон)
1 Н/Кл = 1 В/м
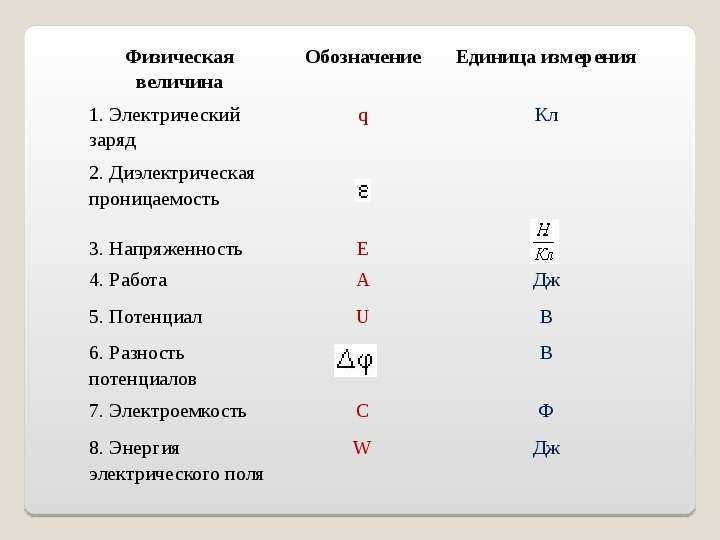
6. Потенциал точки поля (определение, обозначение, формула, ед. измерения)
Потенциалом φ электрического поля — называют ф изическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда .
Потенциал обозначается буквой
Единица измерения потенциала — В (вольт)
7. Разность потенциалов (напряжение) (определение, обозначение, формула, ед. измерения)
Разность потенциалов φ 1 – φ 2 или напряжение между двумя точками поля численно равно работе сил поля по перемещению единичного заряда q между этими точками.
φ 1 – φ 2 = U = А / q
Разность потенциалов обозначается φ 1 – φ 2 , а напряжение обозначаетсяU .
Единица измерения разности потенциалов (напряжения) — В (вольт)
8. Конденсатор (определение). Энергия заряженного конденсатора (формула).
Система проводников, электроемкость которой не зависит от внешних условий и от расположения окружающих тел, получила название
Простейший конденсатор – плоский конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика .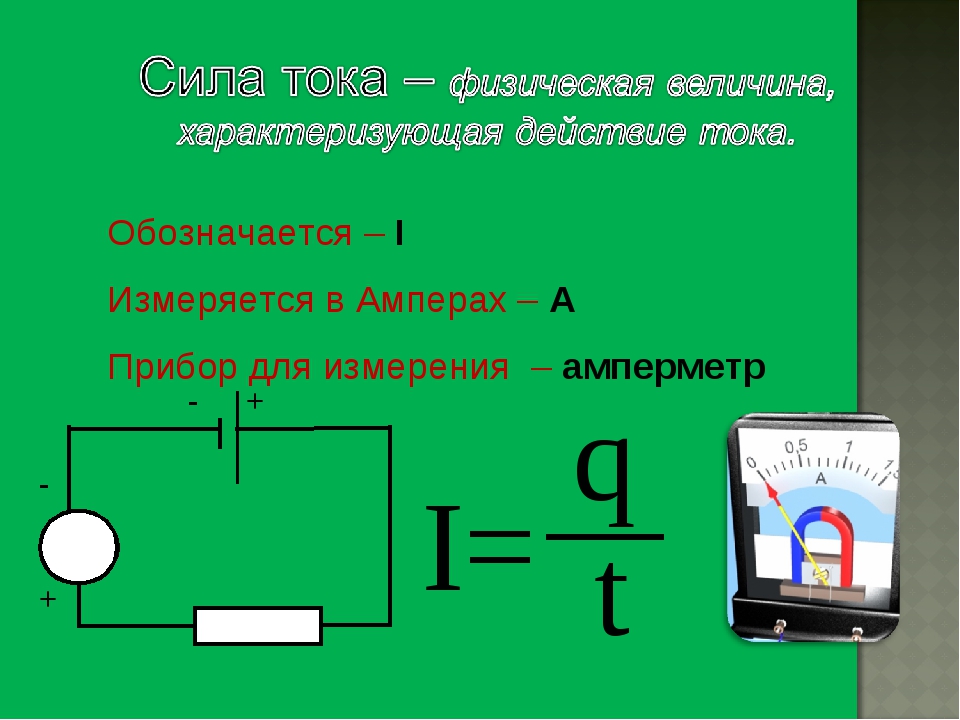
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
9. Электрическая емкость (определение, обозначение, формула, ед. измерения)
8, Основные топологические понятия теории электрических цепей: граф электрической цепи, дерево графа, связи графа: определения. Топологическая формула. Способы получения независимых контуров.
Граф электрической цепи – условное изображение цепи, на котором ветви показаны линиями, узлы – точками.
Ветви графа не стоит путать с закоротками.
Идеальные источники тока на графе не учитываются.
Ветви и узлы на графе обычно нумеруются. Один из узлов выбирается в качестве базисного (базового). Он нумеруется арабской цифрой 0, остальные узлы – произвольно, начиная с 1 (хотя желательно, чтобы какое-то правило обхода узлов всё-таки было).
За базисный узел
желательно брать самый “загруженный”
узел, т. е. узел, в котором соединяется
наибольшее количество ветвей. При
одинаковом количестве ветвей в узлах
за базовый лучше взять узел, в котором
меньше всего идеальных источников
тока. Эти рекомендации могут немного
упростить расчёт цепи.
е. узел, в котором соединяется
наибольшее количество ветвей. При
одинаковом количестве ветвей в узлах
за базовый лучше взять узел, в котором
меньше всего идеальных источников
тока. Эти рекомендации могут немного
упростить расчёт цепи.
Иногда бывает полезным в качестве базисного выбирать узел, к которому подсоединён отрицательный вывод идеального источника ЭДС. В этом случае, если потенциал базисного узла принять равным нулю, то потенциал положительного полюса источника напряжения будет равен величине ЭДС источника.
Номера узлов обводят кружочком, чтобы не было путаницы в нумерации ветвей и узлов.
Ветви нумеруются произвольно, начиная с 1 (в этом случае также желательно иметь какой-нибудь порядок нумерации).
Дерево графа – часть графа, не имеющая ни одного контура и включающая в себя все узлы схемы. Как правило, оно изображается утолщёнными линиями для выделения ветвей дерева графа от остальных.
Для конкретной
цепи с помощью различных комбинаций
ветвей можно составить большое число
деревьев графа.
Связи графа – ветви, не входящие в выбранное дерево графа. Если к дереву графа поочерёдно добавлять связи, то будут получаться независимые контуры, поэтому количество независимых контуров равно количеству связей .
Исходя из вышесказанного, можно составить правило для выбора независимых контуров (если он не очевиден):
изобразить дерево графа;
поочерёдно к дереву добавлять связи графа, получая при этом независимые контуры.
Количество ветвей у дерева графа равно n у – 1 , а связей (а значит, и независимых контуров)
n н.к = n в – (n у – 1) = n в – n у + 1 .
Эту формулу называют топологической формулой .
Задача анализа электрических цепей
Дана цепь со всеми
своими элементами, параметры которых
известны, т. е. заданы ЭДС идеальных
источников напряжения, токи идеальных
источников тока, сопротивления
резисторов, также могут задаваться
внутренние сопротивления источников.
е. заданы ЭДС идеальных
источников напряжения, токи идеальных
источников тока, сопротивления
резисторов, также могут задаваться
внутренние сопротивления источников.
Расчёт электрической цепи (задача анализа электрической цепи) заключается в определении токов во всех её ветвях.
Для анализа электрических цепей применяются различные законы и правила, а также разработаны разные способы и методы расчёта электрических цепей, позволяющие упростить решаемую задачу.
11,Правила выбора базового узла и независимых контуров. Расчёт цепи при наличии в ней ветви с нулевым сопротивлением, ветви с идеальным источником ЭДС. Методы решения получаемой системы линейных алгебраических уравнений (СЛАУ).
Если
в цепи, состоящей из У узлов
и Р рёбер,
известны все характеристики звеньев
(полные сопротивления R ,
величины источников ЭДС E и
тока J ),
то возможно вычислить токи I i во
всех рёбрах и потенциалы φ i во
всех узлах.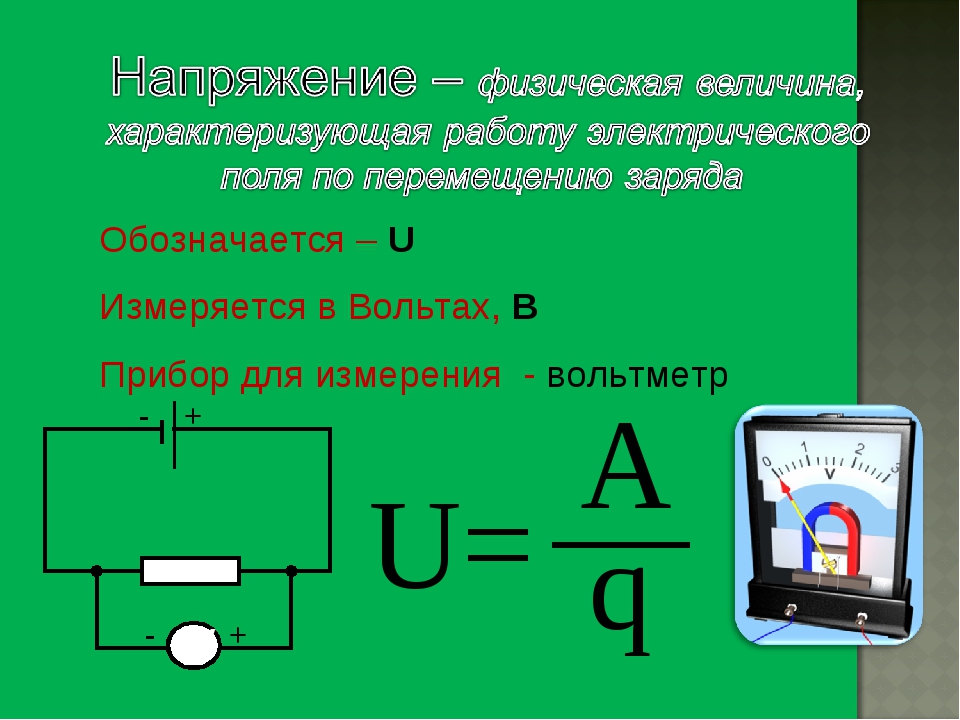 Поскольку электрический
потенциал определён с точностью до
произвольного постоянного слагаемого,
то потенциал в одном из узлов (назовём
его базовым узлом) можно принять равным
нулю, а потенциалы в остальных узлах
определять относительно базового
узла. Таким образом, при расчёте цепи
имеем У +Р –1
неизвестных переменных: У –1
узловых потенциалов и Р токов
в рёбрах.
Поскольку электрический
потенциал определён с точностью до
произвольного постоянного слагаемого,
то потенциал в одном из узлов (назовём
его базовым узлом) можно принять равным
нулю, а потенциалы в остальных узлах
определять относительно базового
узла. Таким образом, при расчёте цепи
имеем У +Р –1
неизвестных переменных: У –1
узловых потенциалов и Р токов
в рёбрах.
Не все из указанных переменных независимы. Например, исходя из закона Ома для участка цепи, токи в звеньях полностью определяются потенциалами в узлах:
С другой стороны, токи в рёбрах однозначно определяют распределение потенциала в узлах относительно базового узла:
Таким образом, минимальное число независимых переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус 1, в зависимости от того, какое из этих чисел меньше.
При
расчёте цепей чаще всего используются
уравнения, записываемые, исходя из
законов Кирхгофа. Система состоит
из У –1
уравнений по 1-му закону Кирхгофа (для
всех узлов, кроме базового) и К уравнений
по 2-му закону Кирхгофа для каждого
независимого контура. Независимыми
переменными в уравнениях Кирхгофа
являются токи звеньев. Поскольку
согласно формуле
Эйлера для плоского графа число
узлов, рёбер и независимых контуров
связаны соотношением
Независимыми
переменными в уравнениях Кирхгофа
являются токи звеньев. Поскольку
согласно формуле
Эйлера для плоского графа число
узлов, рёбер и независимых контуров
связаны соотношением
то число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа уравнений является метод узловых потенциалов. Переменными в системе уравнений являются У –1 узловых потенциалов. Уравнения записываются для всех узлов, кроме базового. Уравнения для контуров в системе отсутствуют.
Уравнение для потенциала в узлах
Рис. 1. Фрагмент цепи: узел с примыкающими звеньями
Рассмотрим фрагмент цепи, состоящий из узла и примыкающих к нему звеньев (рис. 1). Согласно 1-му закону Кирхгофа сумма токов в узле равна нулю.
Модельный потенциал для описания сильного взаимодействия между адронами. Энергия взаимодействия между адронами, выраженная через потенциал Юкавы, выглядит где g константа, задающая интенсивность ядерного взаимодействия, k постоянная с… … Википедия
Потенциал (от лат. potentia сила), в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой либо задачи; …
potentia сила), в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой либо задачи; …
— (потенциальная функция) (от лат. potentia сила), хар ка векторных полей, к к рым относятся мн. силовые поля (эл. магн., гравитационное), а также поле скоростей в жидкости и т. п. Если П. векторного поля а(r) скалярная ф ция j(r), такая, что… … Физическая энциклопедия
потенциал — 1. В физике величина, характеризующая в данной точке силовое поле электрическое, магнитное, гравитационное и пр. Соответственно различаются потенциал электрический, магнитный и пр. 2. Совокупность наличных средств, возможностей в некоей области,… … Большая психологическая энциклопедия
Содержание 1 Биология 2 Математика 3 Физика и химия 4 Лингвистика … Википедия
У этого термина существуют и другие значения, см. Потенциал … Википедия
I Потенциал (от лат. potentia сила) в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой… … Большая советская энциклопедия
potentia сила) в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой… … Большая советская энциклопедия
Потенциальная функция, одна из характеристик векторного поля. Скалярный потенциал скалярная функция v(M).такая, что a=gradv(M).во всех точках области задания поля а (М).(иногда, напр, в физике, П. наз. величину, противоположную по знаку). Если… … Математическая энциклопедия
Потенциал — в широком смысле средства, запасы, источники, имеющиеся в наличии, а также средства, которые могут быть мобилизованы, приведены в действие, использованы для достижения определенной цели, решения какой либо задачи; возможности отдельного лица,… … Краткий словарь оперативно-тактических и общевоенных терминов
— (от лат. potentia сила) в физике понятие, характеризующее физ. силовые поля (электрич., магн., гравитац.) и вообще поля векторных физ величин (напр. , поле скоростей в жидкости). П. представляет собой вспомогат. скалярную или векторную функцию, т … Большой энциклопедический политехнический словарь
, поле скоростей в жидкости). П. представляет собой вспомогат. скалярную или векторную функцию, т … Большой энциклопедический политехнический словарь
Книги
- Статистическая физика сложных систем. От фракталов до скейлинг-поведения , С. Г. Абаимов. Многообразие происходящих в природе явлений, на первый взгляд, не подчиняется каким-то унифицированным принципам, и каждое явление требует введения своих законовописания поведения. Однако…
- Статистическая физика сложных систем. От фракталов до скейлинг-поведения. Выпуск № 57 , Абаимов С.Г.. Многообразие происходящих в природе явлений, на первый взгляд, не подчиняется каким-то унифицированным принципам, и каждое явление требует введения своих законовописания поведения. Однако…
Помогите решить / разобраться (Ф)
| Michaele |
| ||
19/05/17 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| drug39 |
| ||
08/12/08 |
| ||
| |||
| FeelUs |
| ||
10/11/11 |
| ||
| |||
| drug39 |
| ||
08/12/08 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| drug39 |
| ||
08/12/08 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Pphantom, Jnrty, Aer, Парджеттер, Eule_A, photon, whiterussian, profrotter, Супермодераторы
Статическое равновесие
Статическое равновесиеМожно сказать, что объект по адресу остаток находится в равновесии или в статическое равновесие.
Объект в состоянии покоя описывается законом Ньютона. Первый закон движения. Объект в статическом равновесии имеет нулевую чистую сила, действующая на него.
Первое состояние Равновесие состоит в том, что вектор сумма всех действующих сил на теле пропадает. Это можно записать как
Ф = Ф 1 + Ф 2 + Ф 3 + Ф 4 +. . . = 0
где , греческая буква сигма снова означает суммирование всего, что следует за суммирование сил в данном случае.
Вот и все!
Однако помните после
Убедитесь, что вы включили все силы. Это означает тщательно нарисовать свободную диаграмму тела. Включите гравитацию (т. вес) и все контактные силы.Помните, что силы являются векторами.

Это означает, что первое условие равновесия,
Ф = 0 на самом деле означает
F х = 0 и
F y = 0
Пример. Рассмотрим вес в 98 ньютонов (или массу 10 кг). поддерживается веревкой.Натяжение каната, прикрепленного к вес в 98 ньютонов всего 98 ньютонов.
Но эта веревка теперь связана вместе с двумя другими веревками, как показано здесь.

Какие силы действуют на другой две веревки?
Чтобы ответить на этот вопрос, посмотрите на силы воздействует на узел, в котором соединены три веревки. Узел в покоится, поэтому сумма сил, действующих на него, должна быть равна нулю.
Нарисуйте диаграмму свободного тела, показывающую только те силы.
T — величина силы на узел из веревки, прикрепленный непосредственно к грузу. Т Л — величина силы на узле со стороны веревки на влево, образующий с горизонтом угол 45°. А также T R — величина усилия на узле от веревка справа, образующая угол 30° с горизонтальный. Эти три силы должны добавиться к нулю. Графически они можно добавить, как показано здесь; векторы сил образуют замкнутую треугольник.
Теперь применим первое условие равновесие,
Ф = 0 , что на самом деле означает
Сначала разложите все силы на их x- и y-компоненты.
F х = 0 F y = 0 
F х = 0 F x = — T L cos 45 или + T R cos 30 или = 0
— 0,707 Т Д + 0,866 Т Р = 0
0,866 Т Р = 0,707 Т Л
Ф у = 0 F y = T L син 45 или + Т Р sin 30 или — 98 N = 0
0,707 Т Д + 0,5 Т Р — 98 Н = 0
0,707 Т Д + 0,5 Т Р = 98 Н
Теперь мы можем заменитель, 0,707 Т Д + 0,5 Т Р = 98 Н 0,866 Т Р + 0,5 Т Р = 98 Н
( 0,866 + 0,5 ) Т Р = 98 Н
1,366 Т Р = 98 №
Т Р = 98 Н/ 1,366
Т Р = 71,7 №
0,866 Т Р = 0,707 Т Л Т Д = (0,866 / 0,707) Т Р
Т Д = 1,22 Т Р
Т Д = 1,22 (71,7 Н )
Т Д = 87,8 №
Вращательное равновесие Второе условие равновесия Возврат ToC, Вращательная динамика (c) 2005, Дуг Дэвис; все права защищены
4.
 5 Нормальные, растягивающие и другие примеры сил — College Physics 2e
5 Нормальные, растягивающие и другие примеры сил — College Physics 2eЦели обучения
К концу этого раздела вы сможете:
- Определение нормальной силы и силы растяжения.
- Применяйте законы движения Ньютона для решения задач, связанных с различными силами.
- Используйте тригонометрические тождества для разложения веса на компоненты.
Силы имеют множество названий, например, толкание, тяга, тяга, подъемная сила, вес, трение и напряжение. Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. В этом разделе обсуждаются наиболее важные из этих категорий вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.
Нормальная сила
Вес (также называемый силой тяжести) — это всепроникающая сила, действующая постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы определенно заметили, что должны поддерживать вес тяжелого объекта, отталкиваясь от него, когда держите его неподвижно, как показано на рис. 4.11 (а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис. 4.11(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже твердые предметы деформируются при приложении к ним силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока возвращающая сила не станет такой же, как вес груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро, причем провис небольшой, поэтому мы его не замечаем.
Вы определенно заметили, что должны поддерживать вес тяжелого объекта, отталкиваясь от него, когда держите его неподвижно, как показано на рис. 4.11 (а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис. 4.11(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже твердые предметы деформируются при приложении к ним силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока возвращающая сила не станет такой же, как вес груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро, причем провис небольшой, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
Но это похоже на провисание батута, когда на него забираешься.
Рисунок 4.11 (a) Человек, держащий пакет с кормом для собак, должен приложить направленную вверх силу FhandFhand, равную по величине и противоположную по направлению весу корма ww. (b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу NN, равную по модулю и противоположную по направлению весу груза.
Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая груз, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь дается символ NN. (Это не единица силы Н.) Слово нормальное означает перпендикулярно поверхности.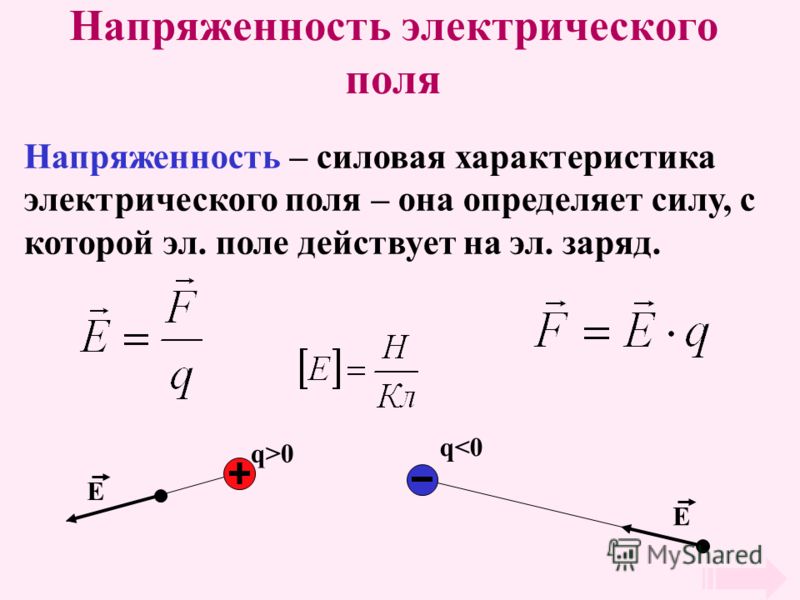 Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.
Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.
Распространенное заблуждение: нормальная сила (Н) против силы Ньютона (Н)
В этом разделе мы ввели величину нормальной силы, которая представлена переменной NN. Его не следует путать с символом ньютона, который также обозначается буквой N. Эти символы особенно важно различать, поскольку единицами измерения нормальной силы (NN) являются ньютоны (Н). Например, нормальная сила NN, с которой пол действует на стул, может быть N=100 NN=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица измерения. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях! По мере изучения физики вы обнаружите больше сходства между переменными и единицами. Другим примером этого является количество работы (WW) и единица мощности (Вт).
Пример 4,5
Вес на склоне, двумерная задача
Рассмотрим лыжника на склоне, показанном на рис.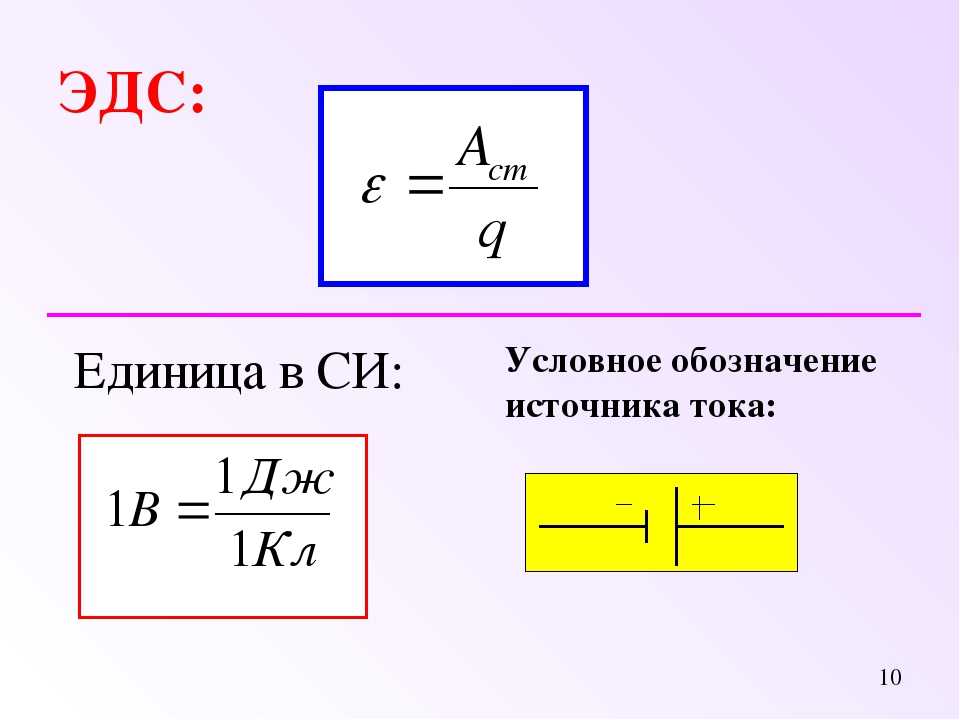 4.12. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если известно, что трение равно 45,0 Н?
4.12. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если известно, что трение равно 45,0 Н?
Рисунок 4.12 Поскольку движение и трение параллельны склону, удобнее всего спроецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). NN перпендикулярен склону и f параллелен склону, но ww имеет компоненты вдоль обеих осей, а именно w⊥w⊥ и w∥ w∥ . NN равно по величине w⊥w⊥, так что нет движения перпендикулярно склону, но ff меньше, чем w∥ w∥ , так что есть ускорение вниз по склону (вдоль параллельной оси).
Стратегия
Это двумерная задача, поскольку силы, действующие на лыжника (исследуемая система), не параллельны. Подход, который мы использовали в двумерной кинематике, также очень хорошо работает здесь. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав два подключенных один -мерные проблемы для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы ⊥⊥ и ∥ ∥ для обозначения перпендикулярности и параллельности соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные ww, ff и NN на рис. 4.12. NN всегда перпендикулярно склону, а ff параллельно ему. Но ww не направлена ни к одной из осей, поэтому первый шаг, который мы предпримем, — это спроецировать его на компоненты вдоль выбранных осей, определив w∥ w∥ как компонент веса, параллельный наклону, и w⊥w⊥ составляющая веса перпендикулярна склону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы ⊥⊥ и ∥ ∥ для обозначения перпендикулярности и параллельности соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные ww, ff и NN на рис. 4.12. NN всегда перпендикулярно склону, а ff параллельно ему. Но ww не направлена ни к одной из осей, поэтому первый шаг, который мы предпримем, — это спроецировать его на компоненты вдоль выбранных осей, определив w∥ w∥ как компонент веса, параллельный наклону, и w⊥w⊥ составляющая веса перпендикулярна склону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна w∥ =wsin(25º)=mgsin(25º)w∥ =wsin(25º)=mgsin(25º), а величина составляющей веса, перпендикулярной к наклону w⊥=wcos(25°)=mgcos(25°)w⊥=wcos(25°)=mgcos(25°).
(a) Пренебрегая трением. Поскольку ускорение параллельно наклону, нам нужно рассматривать только силы, параллельные наклону. (Силы, перпендикулярные склону, складываются в ноль, так как ускорение в этом направлении отсутствует.) Силы, параллельные склону, представляют собой массу веса лыжника, параллельного склону, w∥ w∥ и силы трения ff. Используя второй закон Ньютона с нижними индексами для обозначения величин, параллельных наклону,
a∥ =Fnet ∥ ma∥ =Fnet ∥ m
4,30
где Fnet ∥ =w∥ =mgsin(25°)Fnet ∥ =w∥ =mgsin(25°), в предположении отсутствия трения в этой части, так что
a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)
4,31
(9,80 м/с2)(0,4226)= 4,14 м/с2(9,80 м/с2)(0,4226)=4,14 м/с2
4,32
— ускорение.
(b) Включая трение. Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно противодействует движению между соприкасающимися поверхностями. Таким образом, чистая внешняя сила теперь равна 9.0010
Fnet ∥ =w∥ −f,Fnet ∥ =w∥ −f,
4,33
и подставив это во второй закон Ньютона, a∥ =Fnet ∥ ma∥ =Fnet ∥ m, получим
a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.
4,34
Подставляем известные значения, чтобы получить
0,4226)−45,0 N60,0 кг,
4,35
что дает
a∥ =3,39 м/с2, a∥ =3,39 м/с2,
4.36
, которое представляет собой ускорение, параллельное наклону, когда встречное трение составляет 45,0 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. На самом деле общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно a=gsinθa=gsinθ, независимо от массы . Это связано с ранее обсуждавшимся фактом, что все тела падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
На самом деле общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно a=gsinθa=gsinθ, независимо от массы . Это связано с ранее обсуждавшимся фактом, что все тела падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
Разложение веса на компоненты
Рисунок 4.13 Объект лежит на склоне, который составляет угол θ с горизонтом.
Когда объект покоится на наклонной плоскости, составляющей угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости,
w⊥w⊥ , и сила, действующая параллельно плоскости,
ш∥ ш∥ . Перпендикулярная сила веса,
ж⊥ш⊥ , обычно равна по величине и противоположна по направлению нормальной силе,
НН. Сила, действующая параллельно плоскости,
w∥ w∥ , заставляет объект ускоряться вниз по склону. Сила трения,
ff, противодействует движению объекта, поэтому действует вверх по плоскости.
Сила, действующая параллельно плоскости,
w∥ w∥ , заставляет объект ускоряться вниз по склону. Сила трения,
ff, противодействует движению объекта, поэтому действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона составляет угол θθ к горизонту, то величины компонентов веса равны
w∥ =wsin(θ)=mgsin(θ)w∥ =wsin(θ)=mgsin(θ)
4,37
и
w⊥=wcos(θ)=mgcos(θ).w⊥= wcos(θ)=mgcos(θ).
4.38
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона θθ равен углу, образованному между ww и w⊥w⊥ . Зная это свойство, можно с помощью тригонометрии определить величину составляющих веса:
cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)
4,39
sin(θ)= w∥ ww∥ =wsin(θ)=mgsin(θ)sin(θ)=w∥ ww∥ =wsin(θ)=mgsin(θ)
4,40
Захватывающий эксперимент: Force Parallel
Чтобы исследовать, как изменяется сила, параллельная наклонной плоскости, возьмите резиновую ленту, несколько предметов, которые можно повесить на конец резинки, и доску, которую можно расположить под разными углами. На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?
На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?
Напряжение
Натяжение — это сила по длине среды, особенно сила, передаваемая гибкой средой, такой как веревка или кабель. Слово «натяжение » происходит от латинского слова, означающего «растягивать». Не случайно гибкие шнуры, передающие мышечные силы к другим частям тела, называются сухожилиями . Любой гибкий соединитель, такой как струна, веревка, цепь, проволока или кабель, может натягивать только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю. Важно понимать, что натяжение — это натяжение соединителя. В отличие от этого, рассмотрим фразу: «Вы не можете толкнуть веревку». Сила натяжения тянет наружу вдоль двух концов веревки.
Важно понимать, что натяжение — это натяжение соединителя. В отличие от этого, рассмотрим фразу: «Вы не можете толкнуть веревку». Сила натяжения тянет наружу вдоль двух концов веревки.
Рассмотрим человека, держащего груз на веревке, как показано на рис. 4.14.
Рисунок
4.14
Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу TT, эта сила должна быть параллельна длине веревки, как показано на рисунке. Натяжение такого гибкого соединителя представляет собой натяжение. Обратите внимание, что веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Это пример третьего закона Ньютона. Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково. Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.
Натяжение веревки должно равняться весу поддерживаемой массы, что можно доказать с помощью второго закона Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю, и, следовательно, Fnet=0Fnet=0. Единственными внешними силами, действующими на массу, являются ее вес ww и натяжение TT, создаваемое веревкой. Таким образом,
Fnet=T−w=0,Fnet=T−w=0,
4,41
, где TT и ww — величины натяжения и веса, а их знаки указывают направление, причем up здесь положителен. Таким образом, как и следовало ожидать, натяжение равно весу поддерживаемой массы:
T=w=мг.T=w=мг.
4,42
Тогда для массы 5,00 кг (без учета массы веревки) получаем, что
T=mg=(5,00 кг)(9,80 м/с2)=49,0 N.T=mg=(5,00 кг)(9,80 м/с2)=49,0 Н.
4,43
Если разрезать веревку и вставить пружину, пружина растягивается на длину, соответствующую силе 49,0 Н, обеспечивая прямое наблюдение и измерение силы натяжения веревки.
Гибкие соединители часто используются для передачи усилий на поворотах, например, в больничной системе вытяжения, пальцевом шарнире или тормозном тросе велосипеда. Если трения нет, то напряжение передается без уменьшения. Меняется только его направление, и он всегда параллелен гибкому соединителю. Это показано на рис. 4.15 (а) и (б).
Рисунок 4.15 (а) Сухожилия в пальце передают силу TT от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно свободны от трения). (b) Тормозной трос велосипеда передает натяжение TT от руля к тормозному механизму. Опять же, меняется направление, но не величина TT.
Пример 4.6
Что такое натяжение каната?
Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рис. 4.16.
Рисунок
4.16
Вес канатоходца заставляет проволоку прогибаться на 5,0 градусов. Система, представляющая интерес, представляет собой точку на проволоке, в которой стоит канатоходец.
Стратегия
Как видно на рисунке, провод не идеально горизонтален (не может быть!), а прогибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, имеющими те же направления, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес ww и два напряжения TLTL (слева натяжение) и TRTR (правильное натяжение), как показано на рисунке. Весом самого провода разумно пренебречь. Суммарная внешняя сила равна нулю, так как система неподвижна. Теперь можно использовать небольшую тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из части (б) рисунка видно, что величины натяжений TLTL и TRTR должны быть равны. Это связано с тем, что веревка не имеет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR.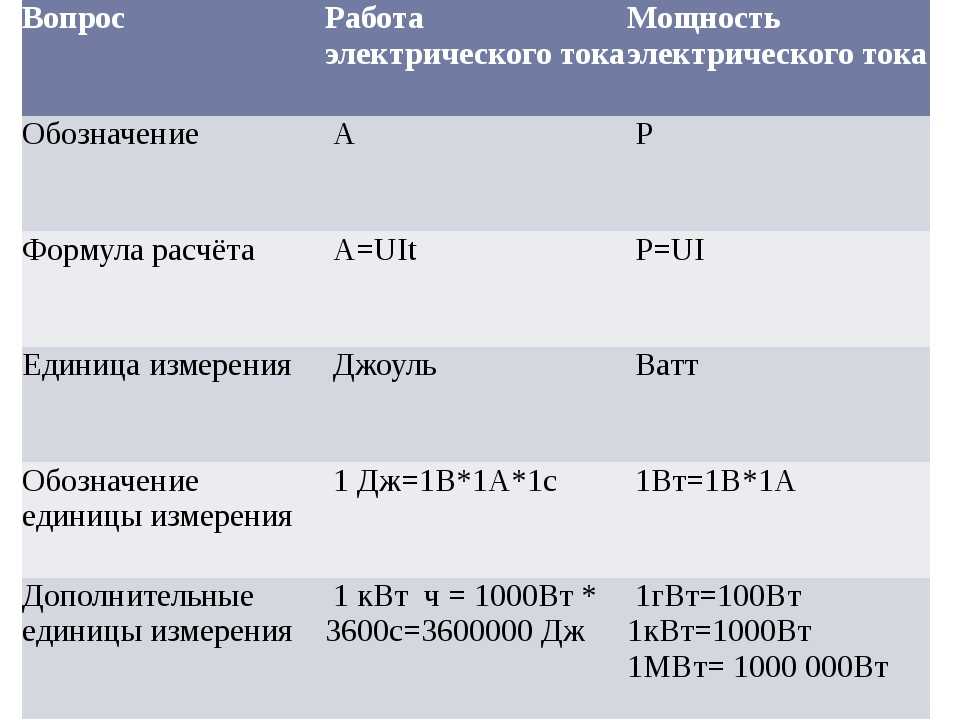 Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.
Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.
Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну ось горизонтальную, а другую вертикальную. Мы называем горизонтальную ось xx, а вертикальную ось yy.
Решение
Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает нарисовать новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему.
Рисунок
4.17
Когда векторы проецируются на вертикальную и горизонтальную оси, их компоненты вдоль этих осей должны в сумме равняться нулю, поскольку канатоходец неподвижен. Малый угол приводит к тому, что TT намного больше, чем ww.
Рассмотрим горизонтальные составляющие сил (обозначенные нижним индексом xx):
Fnet x=TLx-TRx.Fnet x=TLx-TRx.
4.44
Суммарная внешняя горизонтальная сила Fnet x=0Fnet x=0, поскольку человек неподвижен. Таким образом,
Fnet x=0=TLx-TRxTLx=TRx.Fnet x=0=TLx-TRxTLx=TRx.
4,45
Теперь обратите внимание на рисунок 4.17. Вы можете использовать тригонометрию, чтобы определить величину TLTL и TRTR. Обратите внимание, что:
cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°)=TRxTRTRx=TRcos(5,0°).cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°) =TRxTRTRx=TRcos(5,0º).
4,46
Приравнивание TLxTLx и TRxTRx:
TLcos(5,0°)=TRcos(5,0°).TLcos(5,0°)=TRcos(5,0°).
4,47
Таким образом,
TL=TR=T,TL=TR=T,
4,48
, как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначаемые индексом yy), мы можем найти TT.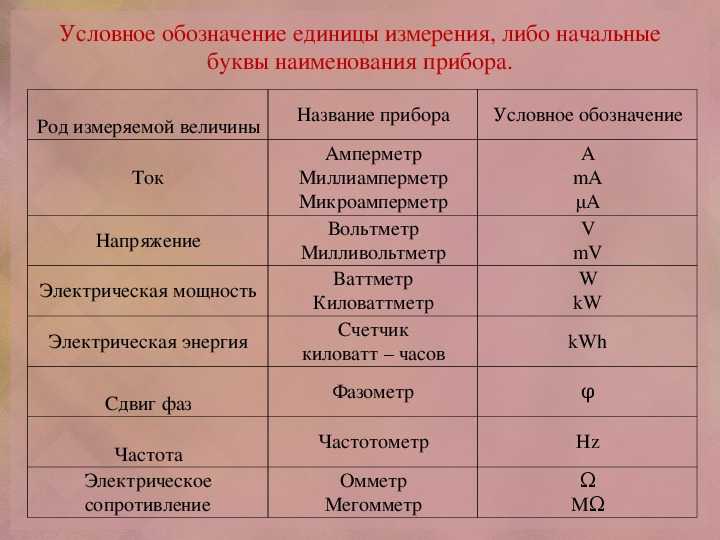 Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что net Fy=0Fy=0. Таким образом, как показано на диаграмме свободного тела на рис. 4.17,
Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что net Fy=0Fy=0. Таким образом, как показано на диаграмме свободного тела на рис. 4.17,
Fnet y=TLy+TRy-w=0.Fnet y=TLy+TRy-w=0.
4,49
Наблюдая за рисунком 4.17, мы можем использовать тригонометрию для определения соотношения между ТЛиТЛы, ПОПРОБУЙ, и ТТ. Как мы определили из анализа в горизонтальном направлении, TL=TR=TTL=TR=T:
sin(5.0º)=TLyTLTLy=TLsin(5.0º)=Tsin(5.0º)sin(5.0º)=TRyTRTRy=TRsin(5.0º)=Tsin(5.0º).sin(5.0º)=TLyTLTLy=TLsin (5,0°)=Tsin(5,0°)sin(5,0°)=TRyTRTRy=TRsin(5,0°)=Tsin(5,0°).
4,50
Теперь мы можем подставить значения TlyTLy и TRyTRy в уравнение результирующей силы в вертикальном направлении: º)−w=02Tsin(5,0°)−w=02Tsin(5,0°)=wFnet y=TLy+TRy−w=0Fnet y=Tsin(5,0°)+Tsin(5,0°)−w=02Tsin(5,0°) −w=02Tsin(5,0º)=w
4,51
и
T=w2sin(5,0°)=mg2sin(5,0°),T=w2sin(5,0°)=mg2sin(5,0°),
4,52
, так что
T=(70,0 кг м/с2)2(0,0872),T=(70,0 кг)(9,80 м/с2)2(0,0872),
4,53
и натяжение
T=3900 N.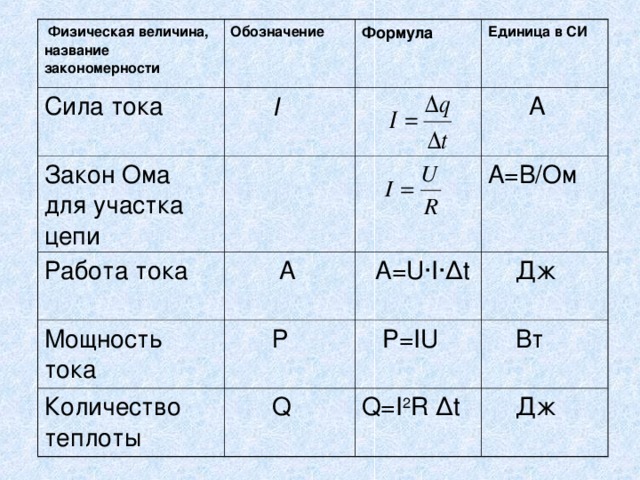 T=3900 Н.
T=3900 Н.
4,54
0 Обсуждение
Обратите внимание, что вертикальное натяжение троса действует как нормальная сила, поддерживающая вес канатоходца. Натяжение почти в шесть раз превышает вес 686-Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь малую часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.
Если мы хотим создать очень большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное гибкому соединителю, как показано на рис. 4.18. Как мы видели в последнем примере, вес канатоходца действовал как сила, перпендикулярная веревке. Мы видели, что натяжение каната связано с весом канатоходца следующим образом:
T=w2sin(θ). T=w2sin(θ).
T=w2sin(θ).
4,55
Мы можем расширить это выражение для описания натяжения TT, создаваемого перпендикулярной силой (F⊥F⊥) к середине гибкого соединителя:
T=F⊥2sin(θ).T=F⊥2sin(θ).
4,56
Обратите внимание, что θθ — это угол между горизонталью и изогнутым соединителем. В этом случае TT становится очень большим, когда θθ приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, поскольку в горизонтальном положении возникло бы бесконечное натяжение (т. θ=0θ=0 и sinθ=0sinθ=0). (См. рис. 4.18.)
Рисунок
4.18
Мы можем создать очень большое натяжение цепи, надавив на нее перпендикулярно ее длине, как показано на рисунке. Предположим, мы хотим вытащить машину из грязи, когда эвакуатора нет. Каждый раз, когда автомобиль движется вперед, цепь натягивается, чтобы он оставался как можно более прямым. Натяжение цепи определяется как T=F⊥2sin(θ)T=F⊥2sin(θ) ; поскольку θθ мало, TT очень велико.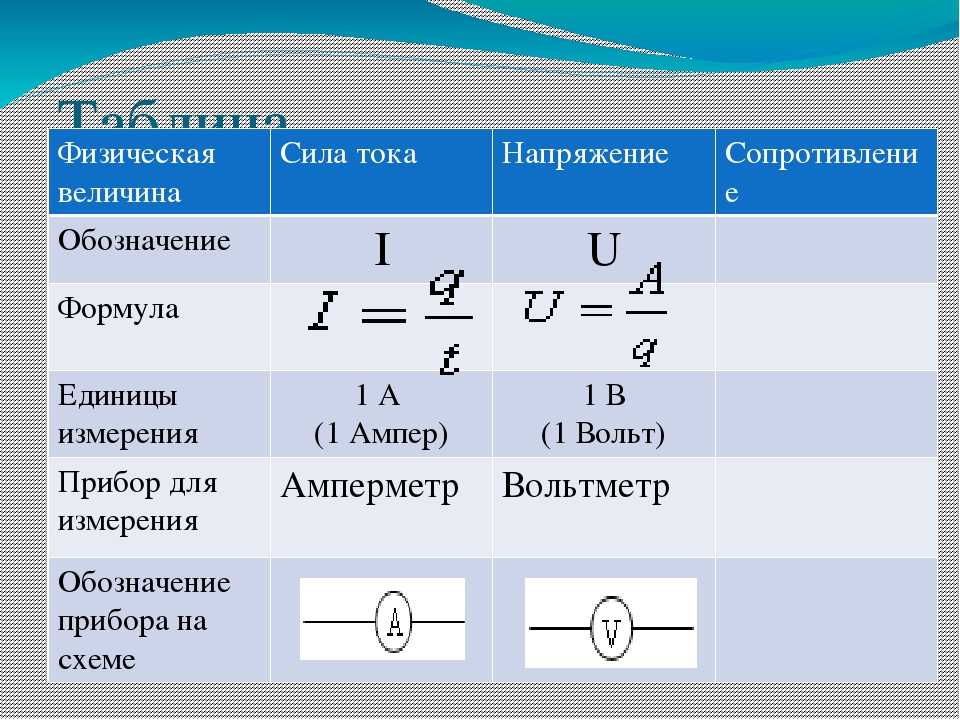 Эта ситуация аналогична канатоходцу, показанному на рис. 4.16, за исключением того, что показанные здесь напряжения передаются на автомобиль и дерево, а не действуют в точке приложения F⊥F⊥.
Эта ситуация аналогична канатоходцу, показанному на рис. 4.16, за исключением того, что показанные здесь напряжения передаются на автомобиль и дерево, а не действуют в точке приложения F⊥F⊥.
Рисунок 4.19 Если не будет приложено бесконечное натяжение, любой гибкий соединитель, такой как цепь внизу рисунка, будет прогибаться под собственным весом, образуя характерную кривую, когда вес равномерно распределен по длине. Висячие мосты, такие как мост Золотые Ворота, показанный на этом изображении, по существу представляют собой очень тяжелые гибкие соединители. Вес моста равномерно распределяется по длине гибких соединителей, обычно тросов, которые принимают характерную форму. (кредит: Листовка, Викисклад)
Расширенная тема: Реальные силы и инерциальные системы отсчета
Существует еще одно различие между силами в дополнение к уже упомянутым типам. Одни силы реальны, другие нет. Реальные силы — это те, которые имеют какое-то физическое происхождение, например гравитационное притяжение. Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Конечно, здесь происходит то, что Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Инерциальная система отсчета — это система, в которой все силы реальны, и, что то же самое, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Конечно, здесь происходит то, что Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Инерциальная система отсчета — это система, в которой все силы реальны, и, что то же самое, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета. Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать.
Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать.
Решающим фактором при определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, рассматриваются в инерциальных системах отсчета.
Все силы, обсуждаемые в этом разделе, являются реальными силами, но есть ряд других реальных сил, таких как подъемная сила и тяга, которые в этом разделе не рассматриваются. Они более специализированы, и нет необходимости обсуждать каждый тип силы. Однако естественно задаться вопросом, где в длинном списке сил находится основная простота, которую мы стремимся найти в физике.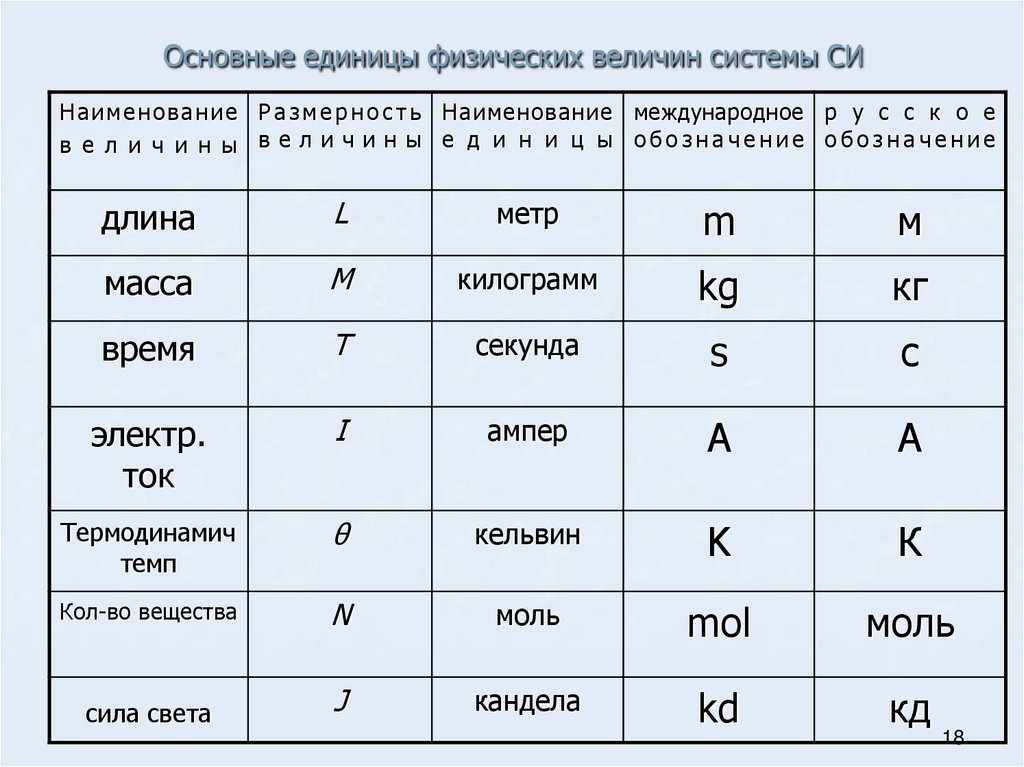 Являются ли некоторые более простыми, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как будет показано в следующем (расширенном) разделе и в трактовке современной физики далее в тексте.
Являются ли некоторые более простыми, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как будет показано в следующем (расширенном) разделе и в трактовке современной физики далее в тексте.
Исследования ФЕТ
Силы в 1 измерении
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Просмотрите диаграмму всех сил свободного тела (включая гравитационные и нормальные силы).
Нажмите, чтобы просмотреть содержимое.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 02.2019, 09:14
02.2019, 09:14  02.2019 10:04:51 —
02.2019 10:04:51 —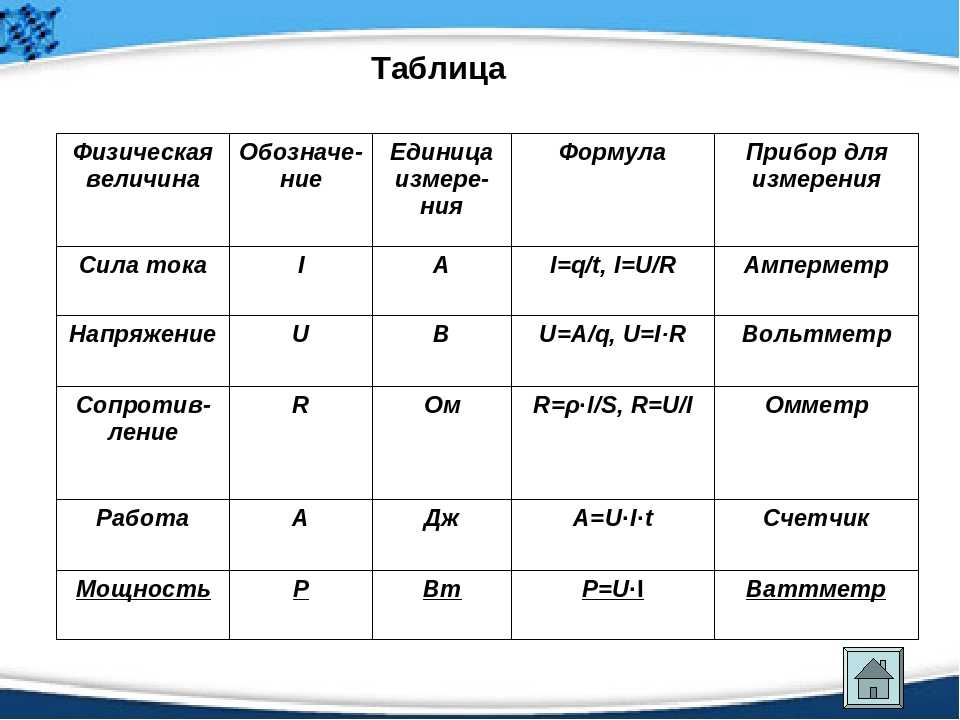 Спросили бы лучше, почему её назвали индукцией, а не напряженностью. Сивухин по этому поводу был очень недоволен.
Спросили бы лучше, почему её назвали индукцией, а не напряженностью. Сивухин по этому поводу был очень недоволен.
 254, а также // ufn.- 1979. — № 10. — С. 335-338. Если кратко, то он считал, что терминология нерациональна, но так сложилось по историческим причинам. Индукция — это некое умозаключение, то, что следует. Поэтому как раз с электрической индукцией всё сразу понятно. А вот с магнитной индукцией якобы вышла историческая несправедливость из-за аналогии с магнитными зарядами, которые, как выяснилось, не существуют… Но более важно другое. Аналогия между электростатическим и магнитостатическим полями именно такова, что следует правильность принятой терминологии.
254, а также // ufn.- 1979. — № 10. — С. 335-338. Если кратко, то он считал, что терминология нерациональна, но так сложилось по историческим причинам. Индукция — это некое умозаключение, то, что следует. Поэтому как раз с электрической индукцией всё сразу понятно. А вот с магнитной индукцией якобы вышла историческая несправедливость из-за аналогии с магнитными зарядами, которые, как выяснилось, не существуют… Но более важно другое. Аналогия между электростатическим и магнитостатическим полями именно такова, что следует правильность принятой терминологии.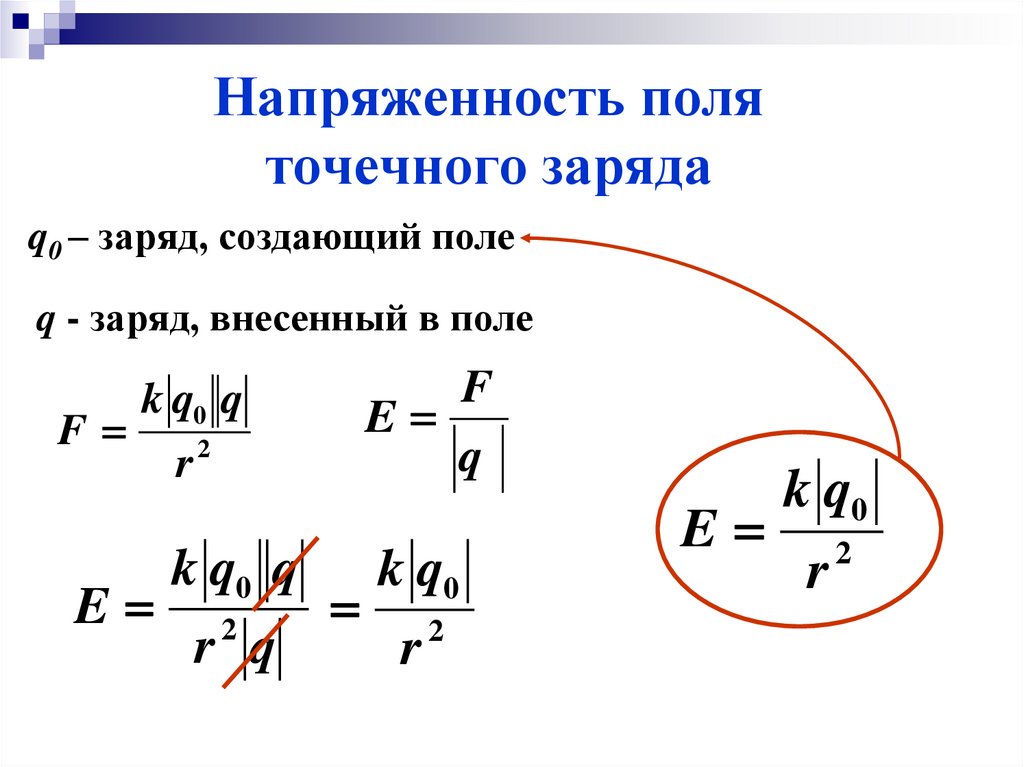 02.2019, 19:48
02.2019, 19:48  02.2019, 06:46
02.2019, 06:46  Допустим, что мы пока не знаем, как назвать , индукцией или напряжённостью. Но если назвать индукцией, то следует очень полезное мнемоническое правило, которое работает в произвольном случае и во всём пространстве. А именно. Напряженность магнитного поля тела с намагниченностью равна напряженности электрического поля такого же тела с поляризованностью , равной . Всё это в системе СГС. Есть ещё 2-я часть этого мнемонического правила. Индукция электрического поля тела с поляризованностью равна индукции магнитного поля такого же тела с намагниченностью , равной . Если отталкиваться от этого, то терминология выбрана верно. Знал ли об этом Максвелл, сказать точно не могу, возможно.
Допустим, что мы пока не знаем, как назвать , индукцией или напряжённостью. Но если назвать индукцией, то следует очень полезное мнемоническое правило, которое работает в произвольном случае и во всём пространстве. А именно. Напряженность магнитного поля тела с намагниченностью равна напряженности электрического поля такого же тела с поляризованностью , равной . Всё это в системе СГС. Есть ещё 2-я часть этого мнемонического правила. Индукция электрического поля тела с поляризованностью равна индукции магнитного поля такого же тела с намагниченностью , равной . Если отталкиваться от этого, то терминология выбрана верно. Знал ли об этом Максвелл, сказать точно не могу, возможно. Объект в состоянии покоя описывается законом Ньютона.
Первый закон движения. Объект в статическом равновесии имеет нулевую чистую
сила, действующая на него.
Объект в состоянии покоя описывается законом Ньютона.
Первый закон движения. Объект в статическом равновесии имеет нулевую чистую
сила, действующая на него. 

 Это еще не все, что нужно знать о силах. Это подготовка к уроку. Более подробные примечания и примеры приведены в конспектах занятий, презентациях и демонстрациях (нажмите здесь). (Ваш преподаватель может вместо этого дать вам ссылку на Google Apps.
Это еще не все, что нужно знать о силах. Это подготовка к уроку. Более подробные примечания и примеры приведены в конспектах занятий, презентациях и демонстрациях (нажмите здесь). (Ваш преподаватель может вместо этого дать вам ссылку на Google Apps. Обычно для этого используются системы уравнений.
Обычно для этого используются системы уравнений.


 Величина этой силы трения представляет собой процент от нормальной силы, прижимающей две поверхности друг к другу.
Величина этой силы трения представляет собой процент от нормальной силы, прижимающей две поверхности друг к другу. phy-astr.gsu.edu/Hbase/Mechanics/frictire.html
phy-astr.gsu.edu/Hbase/Mechanics/frictire.html Это потому, что штаны двигаются относительно поверхности слайда.
Это потому, что штаны двигаются относительно поверхности слайда.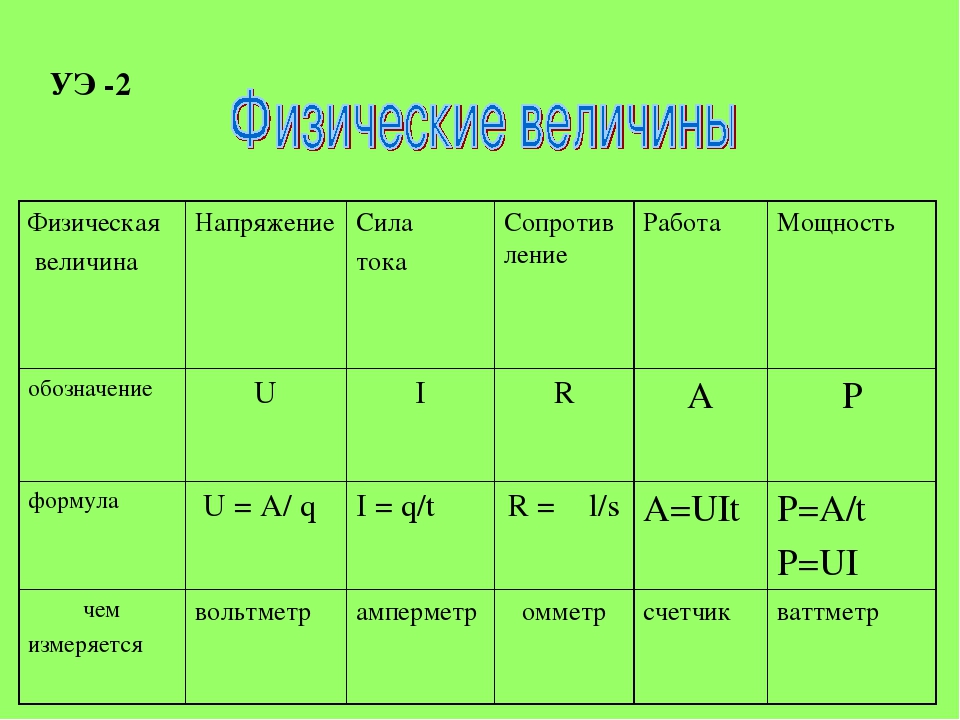 Трение скольжения и начальное трение называются соответственно кинетическим и статическим трением.
Трение скольжения и начальное трение называются соответственно кинетическим и статическим трением.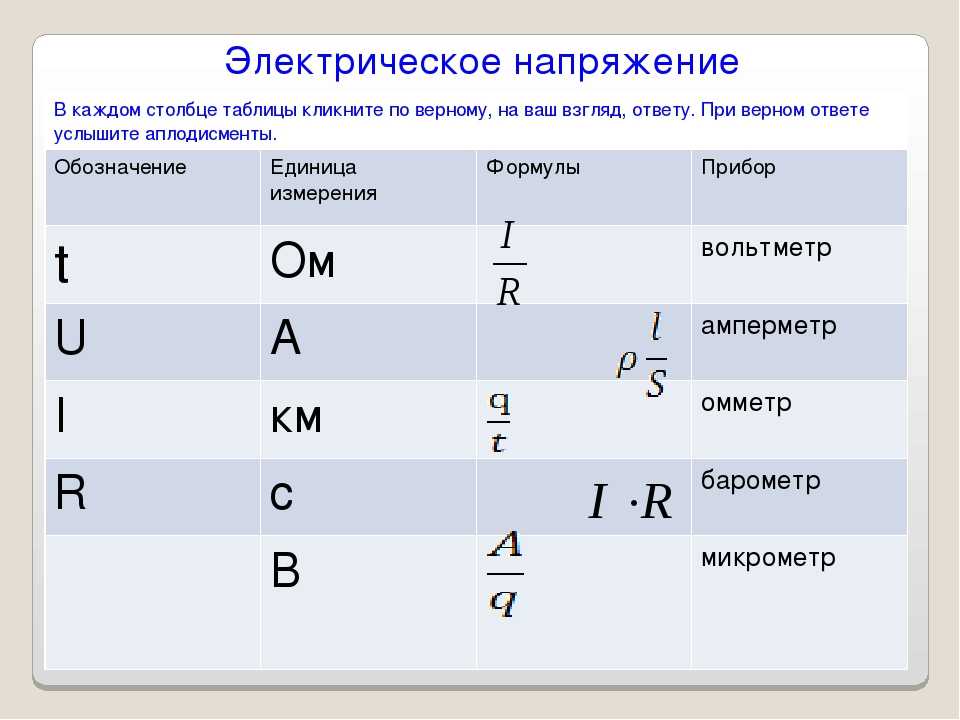
 Обычно мы говорим о веревках и цепях как о натянутых, но любое тело может быть растянуто. Напряжение – это пара равных и противоположных сил.
Обычно мы говорим о веревках и цепях как о натянутых, но любое тело может быть растянуто. Напряжение – это пара равных и противоположных сил.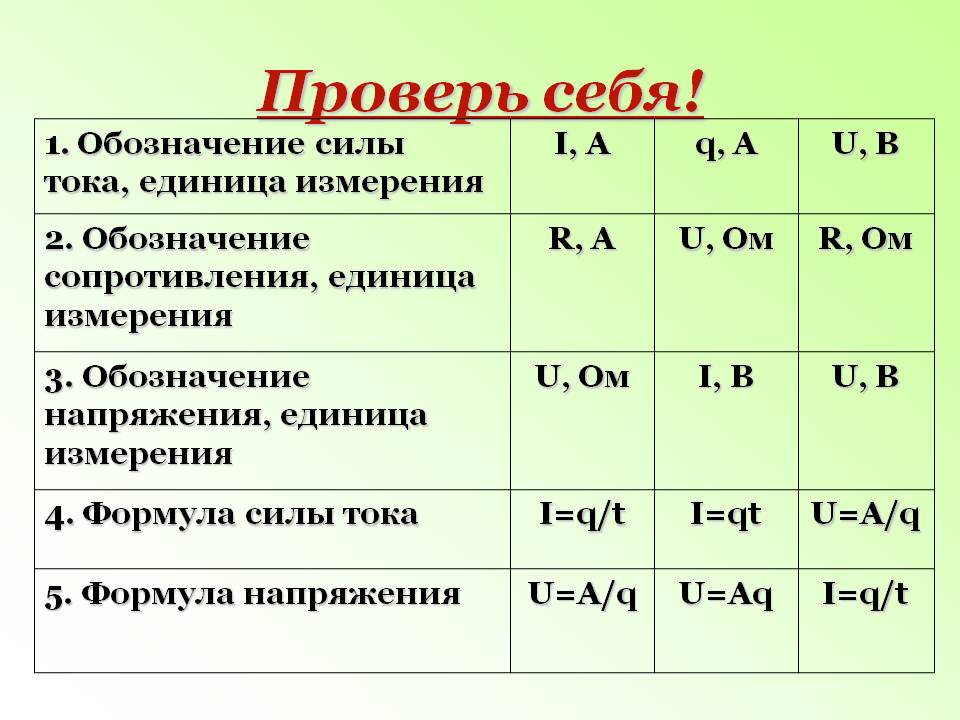
 Пример: когда вас нанимают на работу, работодатель обещает 10 долларов в час. Но когда вы получаете зарплату, ваша зарплата NET составляет 7 долларов в час. Это потому, что федеральное правительство, правительство штата и кто-то по имени «FICA» взяли 3 доллара. Работодатель мог бы сказать, что ваша оплата составляет 10 долларов в час, но ваша чистая оплата будет 7 долларов в час.
Пример: когда вас нанимают на работу, работодатель обещает 10 долларов в час. Но когда вы получаете зарплату, ваша зарплата NET составляет 7 долларов в час. Это потому, что федеральное правительство, правительство штата и кто-то по имени «FICA» взяли 3 доллара. Работодатель мог бы сказать, что ваша оплата составляет 10 долларов в час, но ваша чистая оплата будет 7 долларов в час.