Электричество и магнетизм — Служебный Дом
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений. При уменьшении сопротивления, мощность тока в цепи увеличивается, так как с уменьшением сопротивления возрастает сила тока: I=U/R. Мощность тока в цепи равна: p=U2/R=UI При изменении расстояния между пластинами плоского заряженного конденсатора, отключённого от сети, изменяется его ёмкость, но заряд на обкладках остаётся прежним. При уменьшении расстояния между пластинами ёмкость увеличивается. при увеличении электроёмкости напряжение на конденсаторе падает при постоянном заряде. При изменении расстояния между пластинами конденсатора, подключённого к источнику тока, его ёмкость изменяется, напряжение остаётся прежним, заряд на обкладках изменяется. С увеличением электроёмкости увеличивается заряд конденсатора при неизменном напряжении: q=UС. Сопротивление длинного однородного проводника пропорционально его длине: R=ρl/S. Сопротивление проводника прямо пропорционально его длине и удельному сопротивлению и обратно пропорционально площади сечения. Если внутренним сопротивлением источника тока можно пренебречь, то напряжение на клеммах источника тока при подключении к цепи равно ЭДС источника. Иначе, напряжение на выводах всегда меньше ЭДС. Если ε=U, то при подключении к цепи параллельно ещё одного сопротивления напряжение на первой нагрузке никак не изменится, а значит не изменится и сила тока в ней. Суммарный ток в цепи увеличится. Мощность тепла, выделяющегося в начальной нагрузке не изменится, так как согласно закону Джоуля-Ленца, она пропорциональна произведению квадрата силы тока и величины напряжения. Период электрических колебаний в колебательном контуре связан с ёмкостью конденсатора соотношением T=2π√(LC). Ёмкость конденсатора пропорциональна площади пластины: C=εS/d. Если источник тока обладает внутренним сопротивлением, то при увеличении внешнего сопротивления, напряжение на нём увеличится, а на внутреннем уменьшится, так как падение напряжения прямо пропорционально величине сопротивления. ЭДС источника и напряжение, которое он выдаёт в сеть — не одно и то же. ЭДС по закону Ома равна сумме падений напряжения в сети. Если у источника внутреннее сопротивление отличается от нуля, то часть напряжения будет падать уже внутри него. При этом вольтметр, присоединённый к выводам источника тока при подключённой нагрузке будет показывать напряжение, которое ниже ЭДС источника тока. При уменьшении сопротивления проводника, мощность тока в нём увеличивается. Закон Ома для полной цепи: I=ε/(R+r). ЭДС источника тока при подключённой нагрузке равна ε=I(R+r). При этом напряжение на выводах U=IR, а падение напряжения внутри источника Ir. При уменьшении площади поперечного сечения проводника, сила и мощность тока в нём уменьшаются, а сопротивление увеличивается. При уменьшении расстояния между пластинами конденсатора в колебательном контуре, ёмкость контура увеличивается, а значит увеличивается период колебаний T=2π√(LC), частота уменьшается: v=1/T, длина волны увеличивается: λ=с/v=сT. Разность потенциалов между пластинами конденсатора равна U=q/C. Энергия плоского конденсатора равна W=q2/2C. Сила тока равна отношению заряда ко времени, за которое он прошёл: I=q/t. Циклическая частота собственных колебаний в контуре равна ω=1/√(LC). Зависимость величины заряда на обкладке конденсатора от времени равна q(t)=-qmcos(ωt) — если в начальный момент времени заряд на конденсаторе был максимальным. I(t)=q'(t)=ωqmsin(ωt)=Imsin(ωt). qm=CUm Амплитуда заряда равна qm=Im/ω Амплитуда напряжения равна Um=Im/ωC. Зависимость напряжения на конденсаторе от времени: U=Umcos(ωt). ЭДС индукции εi=-LΔI/Δt. Модуль напряжённости электрического поля точечного заряд обратно пропорционален квадрату расстояния от него. Заряд на проводящем шаре скапливается на его поверхности. Электрическое поле внутри шара равно нулю (экранировка). Снаружи от заряженного шара электрическое поле такое же, как от точечного заряда, помещённого в центр шара: E=kq/r2. Сила Лоренца равна FЛ=qvBsinα. Сила Лоренца выражает собой силу, действующую на заряд q, движущийся в магнитном поле с индукцией B со скоростью v под углом скорости к вектору магнитной индукции α. Сила Лоренца, действующая на электроны в движущемся проводнике равна FЛ=|e|vBsinα. Модуль разности потенциалов, возникающий между концами проводника равен φ=Blvsinα, так как под действием силы Лоренца электроны движутся вдоль проводника, при этом концы проводника оказываются заряженными зарядами противоположных знаков. Напряжённость электрического поля равна отношению разности потенциалов двух точек к расстоянию между ними: E=φ/l. Напряжённость электрического поля в проводнике, движущемся в магнитном поле, равна: E=φ/l=Blvsinα/l=vBsinα. Магнитный поток через площадь, «замещаемую» проводником за интервал времени равна vBlΔtsinα. Заряд конденсатора, присоединённого к сопротивлению, уменьшается пор закону q=q0*2-t/T, где T — период полуразрядки, q0 — начальный заряд. Энергия конденсатора |
Урок 0: Раздел 2: Напряжение, ток, сопротивление, мощность
Tutorials > Урок 0: Основные термины > w3.org/1999/xhtml» align=»left»> Урок 0: Раздел 2: Напряжение, ток, сопротивление, мощностьРаздел 2: Напряжение, ток, сопротивление и мощностьВ этом разделе будут описаны некоторые основные понятия электроники с использованием механических аналогий. Рисунок 1.3.1: Повсеместная аналогия с водонапорной башней Пока
аналогия с водой не идеальна, первая аналогия, которую я приведу,
помочь многим понять эти понятия — рассмотрим резервуар для воды и
водяная башня. Вода представляет собой электроны. Вода в баке на
грунт может обеспечить определенное давление воды на уровне земли.
Поднимите такое же количество воды на вершину башни, и мы получим
повышенное давление, которое может быть обеспечено на уровне земли.
повышение давления воды вызвано увеличением потенциала
энергия. Мы поработали над этой водой, так что мы можем получить больше работы от
воды. Если мы пропускаем воду через трубу, количество воды, проходящей через труба в любом заданном сечении является током. У вашего крана, если вы приоткрой немного кран, получишь слабый ток. Если вы откроете кран много, вы получаете сильное течение. Это одно из тех счастливых времен, когда слова и понятия совпадают. Рисунок 1.3.2: Ток от небольшого резервуара по сравнению с большой водонапорной башней Если вы думаете
о том, какое давление в ваших трубах, могло бы течь намного больше воды
чем ваш кран позволяет. Ваш кран оказывает сопротивление
текущий поток. В электронике резисторы сопротивляются протеканию тока.
большие резисторы пропускают меньший ток. Смеситель сопротивляется протеканию воды больше, чем садовый шланг, что снижает ток. Резервуар на рис. 1.3.3 действует как конденсатор, он накапливает воду, если ток слишком велик для стока. Когда бассейн наполняется, вода в бассейне оказывает большее давление на слив. Если ток перестанет течь из крана, раковина некоторое время будет удерживать ток через слив. Индуктивность Индуктивность немного сложнее описать по аналогии с водой. Представьте, что между вашим краном и запорным клапаном установлена турбина (рис. 1.3.4). При открытом кране на кране потребуется некоторое время, чтобы раскрутить турбину. Сначала вода не будет течь быстро. Турбина реагирует на начало потока воды, забирая часть энергии у движущейся воды и превращаясь во вращательное вращение. Рисунок 1.3.4: Турбина ведет себя как индуктор (щелкните, чтобы увеличить) Давайте скажем, у вас есть труба, выходящая из вашей водонапорной башни, и она собирается привести в действие турбину. Вы хотели бы знать, сколько энергии вы могли бы разумно получить. Интуитивно это должно быть функцией давления. (наша способность выполнять работу), и это должно иметь какое-то отношение к тому, как как быстро может течь вода… струйка не даст большой силы. Получается, что: Механическая: Мощность = (Сила от давления) * Скорость В приведенной выше аналогии с водным бассейном (рис. Рисунок 1.3.5: Эквивалентность модели схемы
|
Лаборатория напряжения, тока, сопротивления и мощности
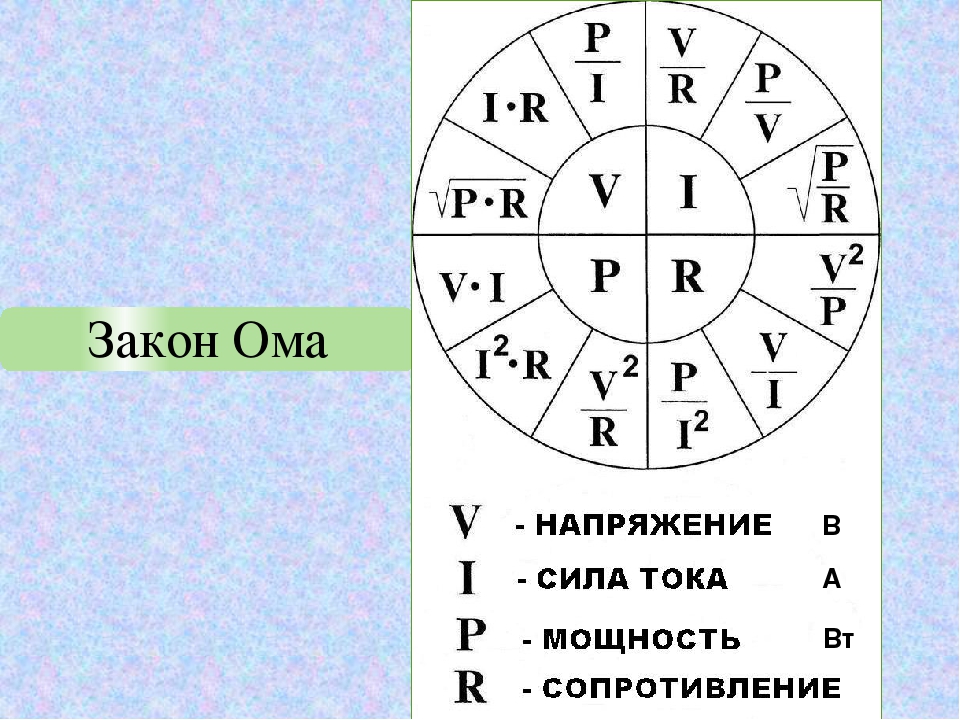
Нравится эта страница? Следуйте за нами в Google+ yaaaaaayy 🙂 Быстрые ссылки: Введение Метод и данные Видео Заключение Введение Как мощность батареи повлияет на температуру лампочки, к которой она подключена? Если для зажигания лампочки используется батарея большей мощности, то лампочка будет горячее по сравнению с лампочкой, зажженной от батареи меньшей мощности. **В гипотезе я использовал термин «мощность» вместо напряжения и тока, но напряжение x ток — это мощность, как показано на P=iV, так что независимой переменной также может быть мощность** Зависимая переменная (1 pt): Температура (градусы Цельсия) лампочки в результате мощности, которую батарея обеспечивает лампочке при включении в цепь Прогнозируемая зависимость (1 балл): Прямое, поскольку P=iV, поэтому чем больше ток или напряжение (больше мощность), тем больше рассеивается энергия. Справочная информация Эта лабораторная работа основана на Законе Ома, P=iV. P означает мощность, измеренную в ваттах (Вт) i означает силу тока, измеренную в амперах (А) V означает напряжение, измеренное в вольтах (В) Поскольку мощность — это скорость рассеяния энергии , чем больше мощность проходит через цепь, тем больше энергии рассеивается. С точки зрения этой лаборатории, чем больше мощность проходит через цепь (с лампочкой в качестве резистора), тем больше света и тепла (энергии) выбрасывается. Нашей независимой переменной является мощность батареи, поэтому мы варьировали размеры и типы батарей, которые предлагали разные токи и напряжения. Мы считаем, что лампочка, подключенная к батарее с наибольшей мощностью, будет светиться ярче и иметь самую высокую температуру (при условии отсутствия короткого замыкания). Изображение аппарата Быстрая ссылка: заключение
Быстрые ссылки: Введение Метод и данные Видео Заключение Метод и данные Метод 3. Подсоедините лампочку с двумя полосатыми концами провода к каждому концу всех шести батарей. D 4. Дав ей немного нагреться, с помощью поверхностного термометра измерьте температуру лампочки в градусах Цельсия. I 5. Используйте уравнение мощности (P=i(ток)*V(напряжение)) для определения мощности каждой батареи. 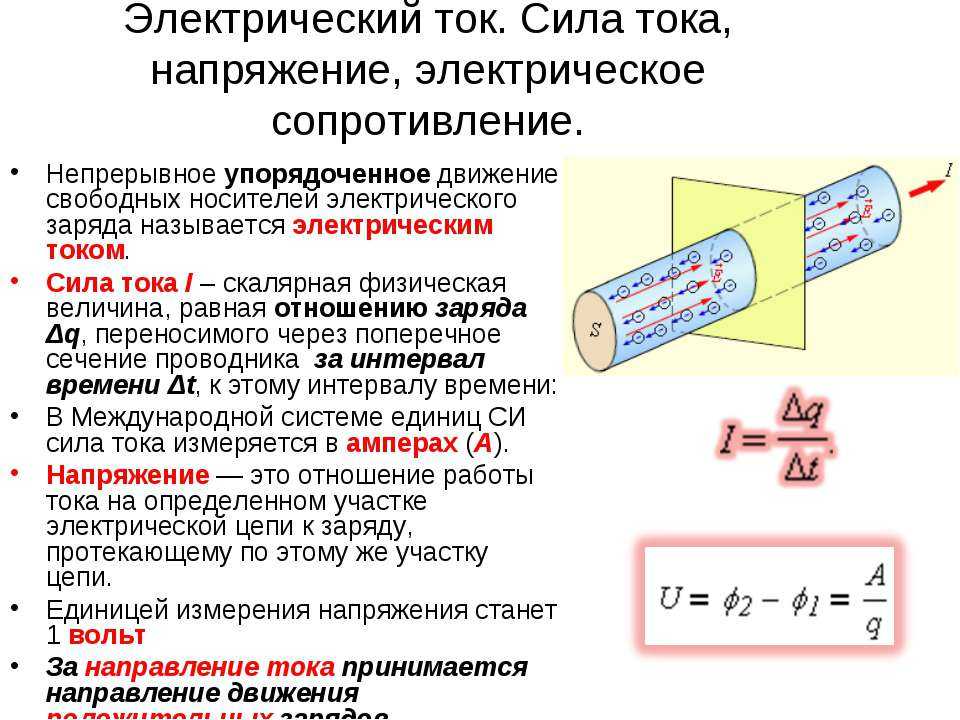 |




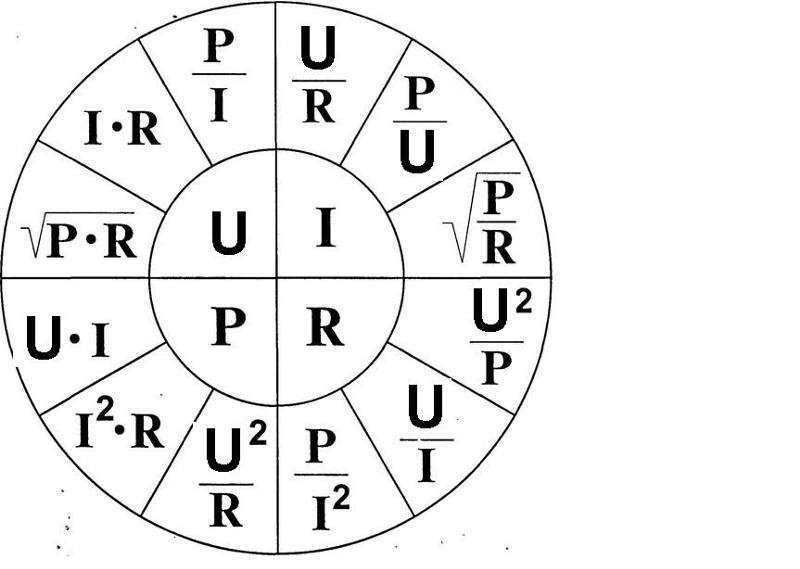

 При этом между концами возникает разность потенциалов, величину которой можно найти из того, что действие электрического поля в точности уравновешивается силой Лоренца.
При этом между концами возникает разность потенциалов, величину которой можно найти из того, что действие электрического поля в точности уравновешивается силой Лоренца.

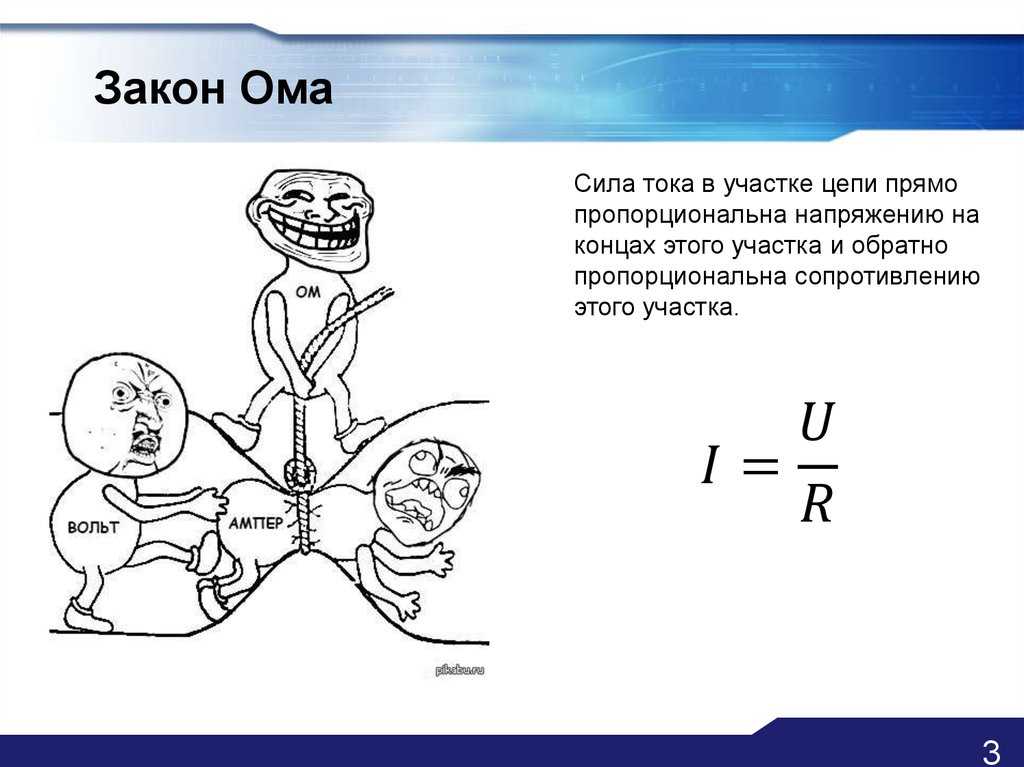 Если запорный клапан закрыт, энергия, накопленная в турбине, будет вытягивать воду из резервуара и некоторое время поддерживать движение воды из трубы. Опять же, турбина реагирует на остановку потока воды, забирая энергию от вращения и превращая ее в движущуюся воду.
Если запорный клапан закрыт, энергия, накопленная в турбине, будет вытягивать воду из резервуара и некоторое время поддерживать движение воды из трубы. Опять же, турбина реагирует на остановку потока воды, забирая энергию от вращения и превращая ее в движущуюся воду. 1.3.4) мы нарисовали серию рисунков и линии для представления системы. В электронике схемы рисуются с использованием набора стандартных чертежей, представляющих компоненты. Представление цепи называется схемой, а схематическая версия рисунка 1.3.4 показана на рисунке 1.3.5.
1.3.4) мы нарисовали серию рисунков и линии для представления системы. В электронике схемы рисуются с использованием набора стандартных чертежей, представляющих компоненты. Представление цепи называется схемой, а схематическая версия рисунка 1.3.4 показана на рисунке 1.3.5. Это связано с тем, что мощность — это скорость рассеивания, поэтому чем больше мощности имеет что-то (в данном случае лампочка), тем больше энергии оно будет рассеивать. Свет и тепло — это формы энергии, которые выбрасываются из лампочки. Таким образом, чем больше мощность у лампочки, тем больше света и тепла будет излучаться из нее.
Это связано с тем, что мощность — это скорость рассеивания, поэтому чем больше мощности имеет что-то (в данном случае лампочка), тем больше энергии оно будет рассеивать. Свет и тепло — это формы энергии, которые выбрасываются из лампочки. Таким образом, чем больше мощность у лампочки, тем больше света и тепла будет излучаться из нее.
 Мы измерили ток и напряжение каждой батареи с помощью мультиметра. Таким образом, мы не использовали аппаратуру для изменения независимой переменной, но использовали ее для обнаружения вариации. Мы использовали инфракрасный термометр для измерения температуры лампочки через несколько секунд после того, как она загорелась.
Мы измерили ток и напряжение каждой батареи с помощью мультиметра. Таким образом, мы не использовали аппаратуру для изменения независимой переменной, но использовали ее для обнаружения вариации. Мы использовали инфракрасный термометр для измерения температуры лампочки через несколько секунд после того, как она загорелась.