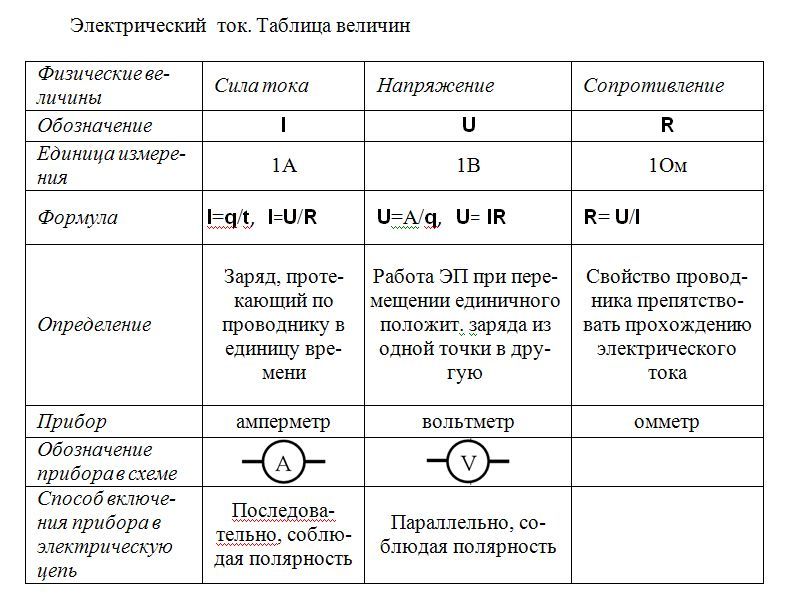
Напряжение Сил 6 Букв — ответ на кроссворд и сканворд
Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы Н
Ниже вы найдете правильный ответ на Напряжение сил 6 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Пятница, 26 Апреля 2019 Г.
НАТУГА
предыдущий следующий
другие решения
УСИЛИЕ
НАТУГА
ответ:
связанные кроссворды
- Натуга
- Усилие
- Натуга
- Напряжение сил (разг.
) 6 букв - Надрыв 6 букв
- От неё развязывается пупок 6 букв
) 6 буквпохожие кроссворды
- Ослабить напряжение мышц, а также ослабить вообще внутреннее напряжение 12 букв
- Чрезмерное напряжение, усилие 7 букв
- Трудное, напряжение положение в какой-нибудь области деятельности 10 букв
- Напряжение мышц для какого-нибудь действия 6 букв
- Ослабить напряжение мышц 12 букв
- Потерять силу, напряжение; ослабеть 5 букв
- Лекарственное средство, подавляющее нервное напряжение, расстройство 14 букв
- Напряжение сил (физических, умственных) 6 букв
- Крайнее напряжение (переносн) 5 букв
- Напряжение сил- физических 6 букв
- Напряжение сил (разг.
- Нервное напряжение 6 букв
- Напряжение сил, усилие 6 букв
Напряжение Сил (Разг.) 6 Букв
Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы Н
Ниже вы найдете правильный ответ на Напряжение сил (разг.
ответ на кроссворд и сканворд
Вторник, 24 Сентября 2019 Г.
НАТУГА
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Натуга
- Усилие
- Перенапряг
- Натуга
- Напряжение сил 6 букв
- Надрыв, напряг, надсадность 6 букв
- Надрыв 6 букв
- От неё развязывается пупок 6 букв
похожие кроссворды
- Ослабить напряжение мышц, а также ослабить вообще внутреннее напряжение 12 букв
- Чрезмерное напряжение, усилие 7 букв
- Трудное, напряжение положение в какой-нибудь области деятельности 10 букв
- Напряжение сил 6 букв
- Крайнее напряжение, упорство 11 букв
- Напряжение мышц для какого-нибудь действия 6 букв
- Ослабить напряжение мышц 12 букв
- Нечеловеческое напряжение 6 букв
- Потерять силу, напряжение; ослабеть 5 букв
- Лекарственное средство, подавляющее нервное напряжение, расстройство 14 букв
- Напряжение сил (физических, умственных) 6 букв
- Крайнее напряжение (переносн) 5 букв
- Напряжение мышц 6 букв
- Напряжение сил- физических 6 букв
- Нервное напряжение 6 букв
- Напряжение сил, усилие 6 букв
- Напряжение 6 букв
Что такое сила натяжения?
Рассмотрено
Фейсал Файез Элиян, доктор философии |
Последнее обновление: 16 мая 2021 г.
Что означает сила натяжения?
Сила растяжения – это сила, возникающая при приложении нагрузки к одному или нескольким концам материала в направлении, перпендикулярном поперечному сечению материала. Силу натяжения часто называют «тянущей» силой. Нагрузка, приложенная к материалу, должна быть приложена в осевом направлении, чтобы быть силой растяжения.
Силы растяжения, которым подвергается компонент или конструкция, имеют большое значение при выборе материалов, способных выдерживать нагрузки.
Сила натяжения в физике — это сила, возникающая в веревке, струне или кабеле при растяжении под действием приложенной силы. Натяжение действует по длине каната/троса в направлении, противоположном приложенной к нему силе. Напряжение также иногда можно назвать стрессом, напряженностью или натянутостью.
Сила натяжения относится к категории контактных сил, поскольку она может проявляться только при наличии контакта между кабелем и рассматриваемым объектом.
Этот тип силы всегда тянет, но никогда не толкает. Уменьшение вытягивания снижает напряжение, а увеличение вытягивания увеличивает напряжение.
Напряжение позволяет передавать силу на относительно большие расстояния.
Реклама
Коррозионпедия объясняет Сила натяжения
Сила натяжения — одна из самых распространенных сил. Для этого многие материалы характеризуются так называемой прочностью на растяжение. Прочность на растяжение помогает разработчикам понять, какое усилие натяжения может выдержать материал. Из того, что известно как предел текучести при растяжении, можно рассчитать величину силы растяжения, которая может вызвать пластическую деформацию материала. По пределу прочности на растяжение можно рассчитать силу растяжения, при которой произойдет разрушение материала.
Силы натяжения встречаются во многих различных приложениях. Одним из примеров силы натяжения является зажим ремня безопасности в автомобиле при ударе.
Зажим ремня безопасности должен выдерживать силу тела, толкаемого вперед во время дорожно-транспортного происшествия. Другим примером является менее острый пример силы натяжения, возникающей в подвесном мосту, который постоянно подвергается посадке и разгрузке автомобилей. Если материал кабеля не обладает достаточной прочностью на растяжение, может произойти разрушение моста.
Не существует единой формулы для расчета силы натяжения при любых обстоятельствах. Часто для расчета нормальной силы используется второй закон Ньютона:
Каждый физический объект, находящийся в контакте с другим объектом, оказывает на него некоторую силу, и наоборот. Контактные силы обозначаются разными терминами в зависимости от природы объектов. Если одна из рассматриваемых сил, которая является действующим объектом, представляет собой веревку, трос или цепь, это называется натяжением.
Реклама
Поделись этим термином
Связанные термины
- Кривая растяжения
- Удлинение при растяжении
- Модуль упругости при растяжении
- Испытание на растяжение
- Напряжение растяжения
- Прочность на растяжение
- Коэффициент нагрузки
- Предел текучести
- Процентное удлинение
- Прочность на сдвиг
Связанное Чтение
- Выбор системы футеровки, пригодной для эксплуатации, для технологических сосудов
- Разработка и тестирование нового решения для ремонта композитных материалов, соответствующего требованиям ISO/ASTM
- Взгляд на новую бестраншейную технологию для водной инфраструктуры
- Взаимосвязь между коррозионной усталостью и коррозионным растрескиванием под напряжением
- Влияние коррозии на сдвиговое поведение материалов
- Гальваническая коррозия металлов, связанных с полимерами, армированными углеродным волокном
Теги
Подбор материаловНаучные свойстваИзмерение физических свойствАвтомагистрали и мостыИнжиниринг и составление спецификацийАктуальные статьи
Покрытия
5 наиболее распространенных типов металлических покрытий, о которых должен знать каждый
Защита от коррозии
Основы катодной защиты
Защита от коррозии
Введение в серию Galvanic: гальваническая совместимость и коррозия
Покрытия
4 типа покрытий для бетонных полов (и что нужно знать о каждом)
Напряжение: значение, примеры, силы и физика
Напряжение — это не только чувство, которое вы испытываете перед экзаменом.
Что касается физики, напряжение является типом силы. Сила натяжения действует аналогично другим приложенным силам, например, если вы должны тянуть коробку по полу. Однако вместо того, чтобы тянуть коробку руками, вы будете тянуть коробку веревкой, шнуром, цепью или подобным предметом, чтобы это считалось натяжением. Поскольку напряжение похоже на приложенную силу, для него нет конкретного уравнения или формулы. Примером натяжения является ситуация, когда собака тянет поводок, пока вы берете ее на прогулку, — поводок тянет вас вперед с силой натяжения.
Определение напряжения
Напряжение убивает меня! Что такое напряжение?
В физике мы определяем натяжение как силу, возникающую, когда веревка, шнур или подобный предмет натягивает объект.
Натяжение представляет собой тянущую силу (поскольку вы не можете толкать веревкой) и действует в направлении веревки. Мы рассматриваем натяжение как контактную силу , поскольку веревка должна коснуться объекта, чтобы воздействовать на него силой.
Напряжение в физике
Следует отметить, что натянутая веревка прикладывает одинаковую силу к каждому прикрепленному объекту. Например, когда мы упомянули прогулку с собакой, мы описали, как собака, дергающая за поводок, приложит к вам силу натяжения. Если бы нас интересовали только силы, действующие на вас, это все, что нас интересовало бы. Но что, если бы мы также захотели узнать силы, действующие на собаку? Мы заметим, что, когда собака тянет поводок, есть сила, которая удерживает или тянет ее обратно. Сила натяжения, тянущая вас вперед, такая же (имеет ту же величину), что и сила натяжения, удерживающая его назад. Как показано ниже, мы можем нанести на поводок две стрелки, чтобы показать эти две силы.
Силы натяжения
Натяжение в результате межатомных электрических сил. Межатомные электрические силы являются причиной всех контактных сил. Для натяжения веревка состоит из множества атомов и молекул, связанных вместе. По мере того как веревка становится натянутой под действием силы, одна из связей между атомами растягивается все дальше друг от друга на микроскопическом уровне.
Атомы хотят оставаться рядом в своем естественном состоянии, поэтому электрические силы, удерживающие их вместе, возрастают. Все эти крошечные силы складываются вместе, чтобы создать одну силу натяжения. Этот принцип делает стрелки на рис. 1 более понятными: если собака и человек тянут поводок наружу, силы, удерживающие поводок вместе, направлены на поводок.
Уравнение натяжения
Не существует специального уравнения для силы натяжения, в отличие от сил трения и упругости. Вместо этого нам нужно использовать диаграмму свободного тела и Второй закон движения Ньютона для решения напряженности.
Нахождение натяжения с помощью диаграммы свободного тела и второго закона Ньютона
Диаграммы свободного тела помогают визуализировать силы, действующие на объект. Для ящика, тянущегося по полу веревкой, как показано на рисунке ниже,
Рис. 2 – Веревка, тянущая коробку
мы бы добавили стрелки для всех сил, действующих на коробку.
Рис. 3 — Здесь представлены все силы, действующие на коробку.
Эта цифра включает все силы, которые могут действовать в данной ситуации, включая трение \(F_\text{f} \), гравитацию \(F_g\), нормальное \(F_\text{N} \) и напряжение \(Т\).
Помните: всегда отводите стрелки силы натяжения от объекта. Напряжение — это сила притяжения, поэтому сила всегда будет направлена наружу.
Второй закон движения Ньютона утверждает, что ускорение объекта зависит от силы, действующей на объект, и массы объекта
Следующее уравнение:
$$\sum \vec F =m\vec a \mathrm{,}$$
является результатом второго закона Ньютона.
Это уравнение применимо к каждому направлению, поэтому обычно мы хотим включить одно для направления \(y\) и одно для направления \(x\). В нашем примере на рисунках выше нет никакого напряжения, действующего в направлении \(y\), поэтому для определения напряжения мы можем сосредоточиться на направлении \(x\), где у нас есть сила трения, действующая влево и напряжение, действующее вправо.
Выбирая право быть положительным, наше результирующее уравнение выглядит так:
$$-F_\text{f} + T =ma\mathrm{.}$$
Затем мы можем переставить для решения натяжения:
$$T=ma+F_\text{f} \mathrm{ .}$$
Если коробка находится на поверхности без трения, сила трения равна нулю, поэтому натяжение будет равно произведению массы коробки на ускорение коробки.
Примеры напряженности
В задачах по физике вы можете увидеть много сценариев, связанных с напряженностью, но вы будете использовать один и тот же метод для решения каждой из них. Ниже приведены некоторые проблемы, с которыми вы можете столкнуться, и способы их решения.
Веревка между двумя объектами
Теперь давайте все перемешаем и сделаем пример с двумя объектами, соединенными веревкой.
Рис. 4 — Веревка между двумя объектами.
На приведенном выше рисунке показана веревка между двумя ящиками и одним тянущим ящиком 2 вправо. Как мы упоминали в случае с собачьим поводком, натяжение, действующее на коробку 1, такое же, как и на коробку 2, поскольку это та же самая веревка.
Поэтому на рисунке мы обозначили их одинаково \(T_1 \).
В любой задаче мы можем выбрать, какой объект или группу объектов анализировать на диаграмме свободного тела. Допустим, мы хотели найти \(T_1\) и \(T_2\). Мы могли бы начать с просмотра поля 1, потому что это более простая сторона, и мы ищем только одно неизвестное. На следующем рисунке показана диаграмма свободного тела для коробки 1:
Рис. 5 — Диаграмма свободного тела ящика 1.
Поскольку натяжение действует только в направлении \(x\), мы можем пренебречь силами, действующими в направлении \(y\). Выбрав положительное значение, уравнение второго закона Ньютона будет выглядеть так: \(T_1 \)
$$T_1 = m_1 a + F_{\text{f}1}\mathrm{;}$$
чтобы найти \(T_2 \), мы могли посмотреть силы только на поле 2 , показано здесь:
Рис. 6. Диаграмма свободного тела коробки 2.
Снова игнорируя направление \(y\), уравнение для направления \(x\) будет следующим:
$$-T_1 — F_ {\text{f}2} + T_2 = m_2 a\mathrm{.
}$$
Поскольку мы знаем, что \(T_1 \) одинаково для каждого ящика, мы можем взять \(T_1 \), который мы узнали из блок 1 и применить его к блоку 2 путем замены
$$-(m_1 a + F_{\text{f}1}) — F_{\text{f}2} +T_2 = m_2 a$$
, а затем мы можем решить для \(T_2 \),
$$T_2 = (m_2 + m_1 )a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$
Однако, если нам не нужно знать \(T_1 \), мы всегда можем посмотреть на оба ящика вместе, как если бы они были одним целым. Ниже мы можем увидеть, как выглядит диаграмма свободного тела, когда вы группируете два ящика:
Рис. 7. Диаграмма свободного тела обоих ящиков вместе.
Если мы запишем уравнение второго закона Ньютона для направления \(x\), мы получим
$$-(F_{\text{f}1} + F_{\text{f}2})+T_2 = (m_1 +m_2 )a$$
и может переставить его, чтобы найти \(T_2 \),
$$T_2 = (m_1 + m_2 )a + F_{\text{f}1} + F_{\text {f}2}\mathrm{.}$$
Мы видим, что это дает тот же результат, что и при рассмотрении блоков по отдельности, а затем составлении уравнений вместе.
Любой метод работает для поиска \(T_2 \) (вы можете решить, какой из них проще, и использовать любой из них), но иногда переменную, которую вам нужно найти, можно найти, только сосредоточившись на одном конкретном объекте.
Тяга под углом
Теперь давайте сделаем пример со всеми любимыми: углы.
Рис. 8 — Тяга каната под углом.
На рисунке выше веревка тянется за ящик под углом, а не вдоль горизонтальной поверхности. В результате коробка скользит по поверхности горизонтально. Чтобы найти напряжение, мы использовали бы суперпозиция сил для разделения угловой силы на часть силы, действующую в направлении \(x\), и часть силы, действующую в направлении \(y\).
Рис. 9 — Диаграмма свободного тела с разделением натяжения на компоненты \(x\) и \(y\).
Это показано красным на рисунке выше на диаграмме свободного тела. Тогда мы можем написать отдельное уравнение для направления \(x\) и направления \(y\) в соответствии с диаграммой свободного тела.
\(T_x = T\cos{\theta}\) и \(T_y = T\sin{\theta}\).
В этом примере теперь у нас есть некоторое напряжение, действующее в направлении \(y\), поэтому мы не хотим игнорировать гравитационную и нормальную силы, как мы делали в примерах выше. Поскольку ящик не ускоряется в направлении \(y\), сумма сил в направлении \(y\) равна нулю
$$F_\text{N} + T\sin{\theta } -F_g =0\mathrm{,}$$
и преобразование для нахождения \(T\) дает
$$T=\frac{F_g — F_\text{N} }{\sin{\theta}} \\\mathrm{.}$$
Направление \(x\) похоже на то, что мы сделали выше, но только с компонентом \(x\) угловой силы натяжения:
$$-F_\text{f} + T\cos{\theta} = ma\mathrm{.}$$
Затем перегруппируем, чтобы найти \(T\):
$$T=\frac {ma+F_\text{f}}{\cos{\theta}}\\\mathrm{.}$$
Оба этих результата дадут вам одно и то же значение для \(T\), поэтому в зависимости от того, что информации, которую вы получили, вы можете либо сосредоточиться только на \(x\)-направлении, либо только на \(y\)-направлении, либо на обоих.
Свободно висящий объект
Когда объект висит на веревке, как показано ниже,
Рис. 10. Объект, подвешенный на веревке
Единственными силами, действующими на него, являются гравитационная сила, тянущая его вниз, и натяжение, удерживающее его вверх.
Это показано на диаграмме свободного тела ниже.
Рис. 11. Диаграмма свободного тела объекта, подвешенного на веревке
Результирующее уравнение будет выглядеть следующим образом: переставить, чтобы найти \(T\) и подставить \(mg\) для гравитационной силы, мы получим
$$T=ma +mg\mathrm{.}$$
Если бы объект не ускорялся, натяжение и гравитационная сила были бы равны и противоположны, поэтому \(T=mg\).
Тяг за наклонную поверхность
Когда к ящику на наклонной поверхности прикладывается натяжение, мы используем ту же стратегию, что и при натяжении веревки под углом.
Рис. 12 – Натяжение объекта на наклонной поверхности
Сначала начните с диаграммы свободного тела.
Рис. 13 – Схема растяжения свободного тела на наклонной поверхности
Имея дело с наклонной поверхностью, помните, что нормальная сила всегда действует перпендикулярно поверхности, а гравитационная сила (вес) всегда действует прямо вниз.
Вместо того, чтобы разбивать силу натяжения на компоненты \(x\) и \(y\), мы хотим разбить гравитационную силу на компоненты. Если мы наклоним нашу систему координат, чтобы она соответствовала углу поверхности, как показано ниже, мы увидим, что натяжение действует в новом направлении \(x\), а нормальная сила действует в новом направлении \(y\)- направление. Гравитационная сила — единственная сила под углом, так что мы разделили бы ее на компоненты, следующие новым направлениям \(x\) и \(y\), показанным ниже красным.
Рис. 14 — Диаграмма свободного тела с новой системой координат и гравитационной силой, разделенной на компоненты \(x\) и \(y\)
Тогда мы применим второй закон Ньютона в каждом направлении, как и в любой другой задаче.
Подвешивание на двух веревках
Когда объект подвешен на нескольких веревках, натяжение неравномерно распределяется по веревкам, если только они не находятся под одинаковыми углами.
Рис. 15. Объект, подвешенный на двух веревках
В этом примере мы подставим действительные числа, чтобы найти \(T_1 \) и \(T_2 \). 92}=0\mathrm{.}$$
Мы можем решить эти два уравнения и два неизвестных алгебраически любым удобным для нас способом. В этом примере мы решим первое уравнение для \(T_1 \) и заменим его вторым. Решение для \(T_1 \) дает
$$\begin{align*} \frac{1}{\sqrt{2}} T_1 &= \frac{1}{2} T_2 \\ T_1 &= \frac{ \sqrt{2}}{2} T_2 \mathrm{,} \\ \end{align*}$$
и подстановка этого во второе уравнение для нахождения \(T_2 \) дает
$$\begin{align *} \frac{\sqrt{2}}{2} T_2 \times \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} T_2 — 147,15\,\mathrm{ N} &= 0 \\ \frac{1+\sqrt{3}}{2} T_2 &= 147,15\,\mathrm{N} \\ T_2 &= 107,72\,\mathrm{N.} \\ \end {выравнивание*}$$
Затем подстановка \(T_2 \) обратно в первое уравнение для решения для \(T_1 \) дает нам окончательный ответ
$$\begin{align*} T_1 &= 107,72\,\mathrm{N} \ раз \frac{\sqrt{2}}{2} \\ T_1 &= 76,17\,\mathrm{N.
} \\ \end{align*}$$
Шкив, наклон и подвешенный объект
Пример На изображении ниже сочетается многое из того, что мы обсуждали в каждом из приведенных выше примеров.
Рис. 17. Наклон, шкив и подвешенный объект
На следующем рисунке показано, как будут выглядеть силы, воздействующие на каждый объект, с учетом того, что сила трения может действовать в противоположном направлении в зависимости от того, как движется система.
Рис. 18. Силы, показанные для сценария выше
Ниже приведены советы, которые мы узнали в каждой из приведенных выше задач, которые также применимы к этой задаче:
- Мы можем смотреть на один объект отдельно и выполнять отдельные диаграмма тела и уравнения второго закона Ньютона.
- Веревка оказывает одинаковое натяжение на каждый объект.
- Мы можем наклонить нашу систему координат. У нас даже может быть своя система координат для каждого объекта, если мы будем анализировать силы, воздействующие на каждый объект в отдельности.
