Элеком37, Потенциал. Разность потенциалов. Напряжение. физика.

Потенциал. Разность потенциалов. Напряжение.

---

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что

потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности

. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

          φ – потенциал электрического поля.

          ∆φ – разность потенциалов.

          W – потенциальная энергия заряда во внешнем электрическом поле.

          A – работа электрического поля по перемещению заряда (зарядов).

          q – заряд, который перемещают во внешнем электрическом поле.

          U – напряжение.

          E – напряженность электрического поля.

          d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности.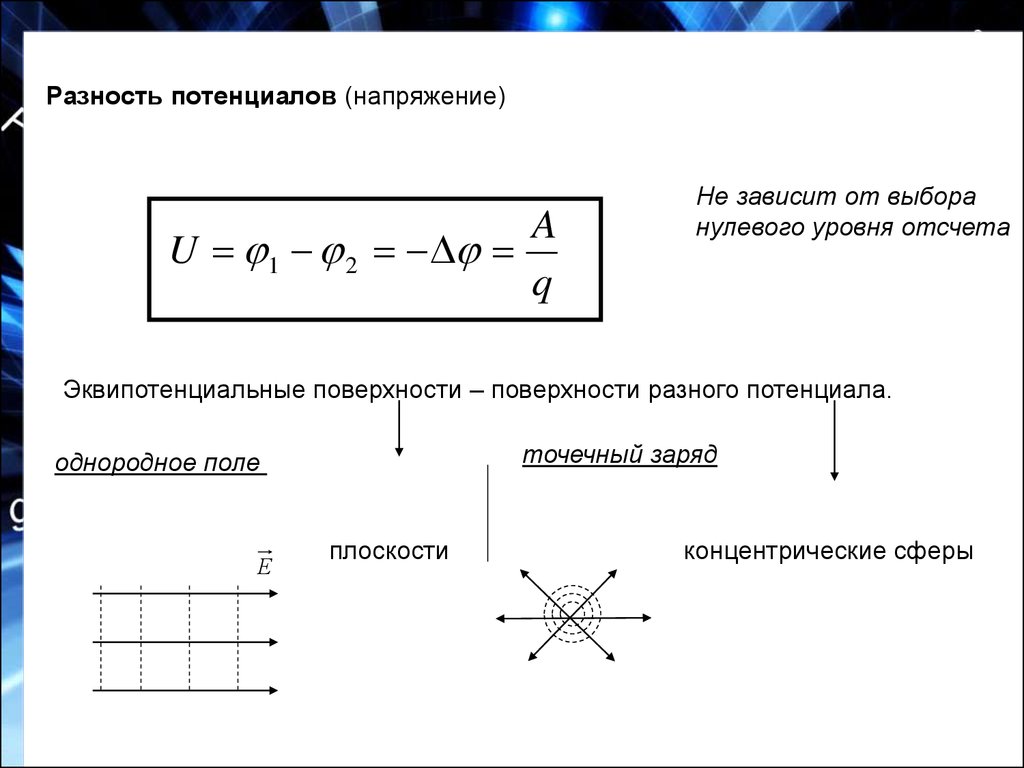 Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

---

---

Разность потенциалов

Разность потенциалов между двумя точками в схеме представляет со­бой разность их напряжений (относительно общей точки, обычно зе­мли). Например, разность потенциалов между точками А и В на рис. 1.8 VAВ = (VA — VВ), где VA — напряжение в точке А и VВ — напряжение в точке В. Напряжения Уд и Уд измеряются относительно провода Е, име­ющего нулевой потенциал. Напряжение в любой точке электрической схемы измеряется относительно нулевого провода, корпуса или земли.

Например, если VA = 5 В и VВ = 3 В, то VAВ = VA — VВ = 5 — 3 = 2 В (рис. 1.9(а)).

Напряжения могут отличаться по знаку — быть отрицательными и по­ложительными. Разность потенциалов между двумя точками, имеющими напряжения с противоположными знаками, равна сумме этих напряже­ний.

Например, если VС = 3 В, а VD = -2 В, то V = VС + VD = 3 + 2 = 5 В (рис. 1.9(б)).

Итак, если два напряжения имеют одинаковую полярность, или оди­наковые знаки, то разность потенциалов между ними равна их разности. Если же напряжения имеют разные знаки, то разность потенциалов ме­жду ними равна их сумме.

 

 

Рис. 1.9. Наглядное представление напряжений с разными знаками относи­тельно линии нулевого потенциала

 

Параллельное соединение резисторов

 

На рис. 1.10 изображены два резистора, R1 и R2 соединенные парал­лельно. Ток I от батареи разветвляется в точке А на ток I1, протека­ющий через сопротивление R1, и ток I2, протекающий через сопротив­ление R2. В точке В эти токи складываются и образуют полный ток I = I1 + I2.

Рис. 1.10. Два резистора, соединенные параллельно

 

С другой стороны, к каждому резистору приложено полное напряже­ние V, т. е.

Полное напряжение V = напряжению на R1

= напряжению на R2.

 

Общее сопротивление

Общее сопротивление (R) двух резисторов, соединенных параллельно, определяется формулой:

Заметим, что общее сопротивление двух параллельных резисторов всегда меньше, чем сопротивление меньшего из них. Общее сопротивление двух параллельно соединенных резисторов, имеющих одинаковое сопротивле­ние, равно половине сопротивления одного из них.

 

Параллельное соединение трех и более резисторов

В общем случае общее сопротивление произвольного числа резисторов, соединенных параллельно, можно определить по формуле выше.

Пример 4

Определить общее сопротивление схемы, изображенной на рис. 1.11(а).

Решение

R1 и R2 соединены последовательно и их общее сопротивление RТ1 = R1 + R2 = 6 + 8 = 14 Ом.

Теперь, после замены резисторов R1 и R2 их общим сопротивлением RТ1, (схема на рис. 1.11(б)), резистор R3 оказался включенным параллельно с RТ1, равным ему по величине. Следовательно, их общее сопротивление RТ2 вполовину меньше каждого из них. Теперь схема примет вид, как показано на рис. 1.11(в), где RТ2 = 7 Ом и соединено последовательно с R4. Отсюда общее сопротивление схемы между точками А и В равно RТ2 + R4 = 7 + 3 = 10 Ом

Рис. 1.11

 

Добавить комментарий

В чем разница между электрическим потенциалом, разностью потенциалов и напряжением?

спросил 5 лет, 10 месяцев назад

Изменено 3 года, 7 месяцев назад

Просмотрено 32к раз

$\begingroup$

Я вижу, что время от времени используются оба термина. Они взаимозаменяемы?

• потенциал
• напряжение
• определение

$\endgroup$

2

$\begingroup$

Электрический потенциал – это энергия на единицу заряда, полученная или потерянная при перемещении заряда из некоторой контрольной точки, в которой потенциал равен нулю.

Напряжение — это разность потенциалов между двумя произвольными точками, в которых потенциал не обязательно равен нулю.

Например, потенциал в точке А относительно определенной контрольной точки (иногда находящейся на бесконечном расстоянии) может составлять 10000 вольт, а потенциал в точке В может составлять 10100 вольт. Тогда напряжение между B и A равно 100 вольт.

Хотя они представляют один и тот же тип количества, они имеют несколько разные коннотации.

$\endgroup$

$\begingroup$

Будучи немного педантичным, электрический потенциал является абсолютным числом, после выбора манометра, конечно.

С другой стороны, «напряжение» на самом деле представляет собой РАЗНИЦУ двух потенциалов. Разность потенциалов в одной точке и в другой. Но мы обычно устанавливаем ссылку «0 вольт», поэтому они взаимозаменяемы.

$\endgroup$

1

$\begingroup$

По моему опыту, «напряжение» не является формальным термином и поэтому никогда не получает формального определения.

Однако на практике оно в основном используется для обозначения «того, что мы измеряем вольтметром». это рабочее определение.

Если использовать вольтметр в статическом поле или в цепи постоянного тока, то имеется четко определенный потенциал, и вольтметр измеряет разность потенциалов.

Осциллограф также является разновидностью вольтметра. Допустим, вы используете осциллограф для измерения ЭДС, наведенной в катушке изменяющимся магнитным полем. Тогда то, что мы измеряем, измеряется в вольтах и, вероятно, может быть названо напряжением, но это не разность потенциалов. В этом случае нет четко определенного электрического потенциала.

$\endgroup$

электрические цепи — Что именно описывает термин «разность потенциалов напряжения»?

спросил 3 года, 6 месяцев назад

Изменено 1 месяц назад

Просмотрено 425 раз

$\begingroup$

Является ли напряжение (разность потенциалов) похожей на гравитационную потенциальную энергию? Есть ли у них сходство? Если нет, то к чему относится «разность потенциалов »?

• электрические цепи
• электричество
• потенциальная энергия
• напряжение

$\endgroup$

1

$\begingroup$

Напряжение похоже на гравитационный потенциал а не гравитационная потенциальная энергия .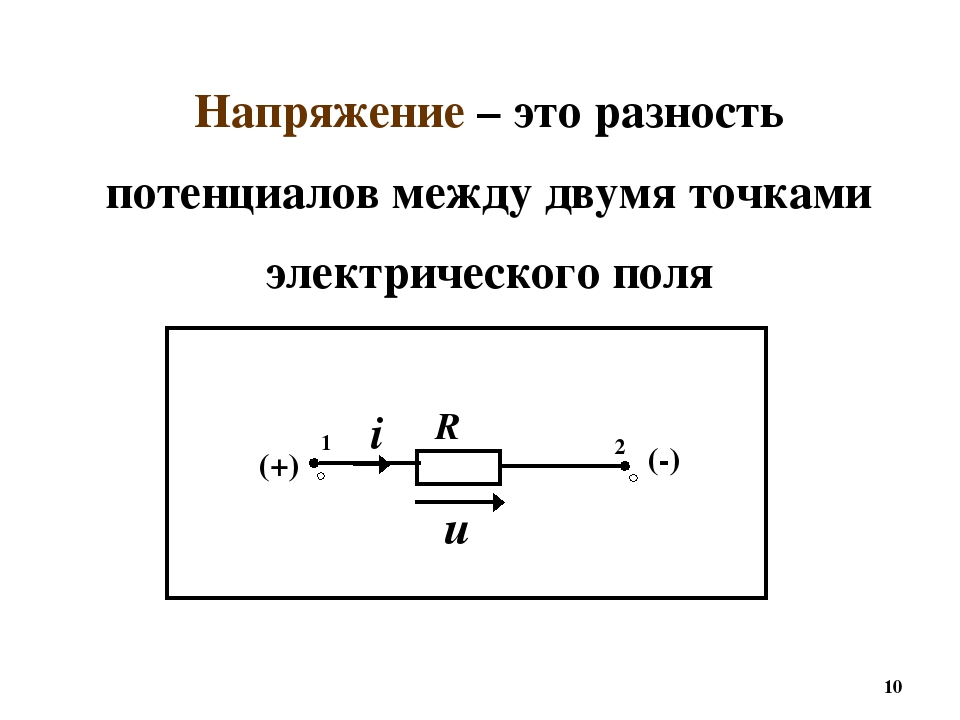 Позвольте мне прояснить разницу.

Гравитационная Потенциальная Энергия: это энергия частицы в силу ее положения. Возьмем, к примеру, этот пример. Если вы поместите частицу на некотором расстоянии от планеты, скажем, от Земли, частица начнет ускоряться по направлению к планете. Как только он начинает двигаться, мы говорим, что он обладает кинетической энергией. Откуда взялась эта кинетическая энергия? Это потенциальная энергия, которая превратилась в кинетическую энергию.

Гравитационный потенциал: Это потенциальная энергия единицы массы в точке. это просто указывает на потенциальную энергию единицы массы (скажем, 1$ кг). Теперь, если вас попросили найти потенциальную энергию частицы массой 10 кг, вы просто умножаете гравитационный потенциал на 10 и получаете гравитационную потенциальную энергию.

Чем полезен гравитационный потенциал? Гравитационный потенциал можно рассматривать как функцию точек в пространстве. $G(x,y,z)$.