PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Урок 30. Лабораторная работа № 07. Изучение закона Ома для участка цепи.
Тема: «Изучение закона Ома для участка цепи»
Цель работы: установить на опыте зависимость силы тока от напряжения и сопротивления.
Оборудование: амперметр лабораторный, вольтметр лабораторный, источник питания, набор из трёх резисторов сопротивлениями 1 Ом, 2 Ом, 4 Ом, реостат, ключ замыкания тока, соединительные провода.
Ход работы.
Краткие теоритические сведения
Электрический ток — упорядоченное движение заряженных частиц
Количественной мерой электрического тока служит
Сила тока — – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:
В Международной системе единиц СИ сила тока измеряется в амперах [А].
[1A=1Кл/1с]
Прибор для измерения силы тока Амперметр. Включается в цепь последовательно
На схемах электрических цепей амперметр обозначается .
Напряжение – это физическая величина, характеризующая действие электрического поля на заряженные частицы, численно равно работе электрического поля по перемещению заряда из точки с потенциалом
U12 = φ1 – φ2
U – напряжение
A – работа тока
q – электрический заряд
Единица напряжения – Вольт [В]
[1B=1Дж/1Кл]
Прибор для измерения напряжения – Вольтметр. Подключается в цепь параллельно тому участку цепи, на котором измеряется разность потенциалов.
На схемах электрических цепей амперметр обозначается .
Величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника и хаотическим движением его частиц, называется электрическим сопротивлением проводника.
Электрическое сопротивление проводника зависит от размеров и формы проводника и от материала, из которого изготовлен проводник.
S – площадь поперечного сечения проводника
l – длина проводника
ρ – удельное сопротивление проводника
В СИ единицей электрического сопротивления проводников служит ом [Ом].
Графическая зависимость силы тока I от напряжения U — вольт-амперная характеристика
Закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Назван в честь его первооткрывателя Георга Ома.
Практическая часть
1. Для выполнения работы соберите электрическую цепь из источника тока, амперметра, реостата, проволочного резистора сопротивлением 2 Ом и ключа.
2. Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи. Включите ток. При помощи реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.
Таблица 1. Сопротивление участка 2 Ом
|
Напряжение, В |
|||
|
Сила тока, А |
3. По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.
4. Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах. Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.
Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.
Таблица 2. Постоянное напряжение на участке 2 В
|
Сопротивление участка, Ом |
|||
|
Сила тока, А |
5. По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.
6. Ответьте на контрольные вопросы.
Контрольные вопросы
1. Что такое электрический ток?
2. Дайте определение силы тока. Как обозначается? По какой формуле находится?
Дайте определение силы тока. Как обозначается? По какой формуле находится?
3. Какова единица измерения силы тока?
4. Каким прибором измеряется сила тока? Как он включается в электрическую цепь?
5. Дайте определение напряжения. Как обозначается? По какой формуле находится?
6. Какова единица измерения напряжения?
7. Каким прибором измеряется напряжение? Как он включается в электрическую цепь?
8. Дайте определение сопротивления. Как обозначается? По какой формуле находится?
9. Какова единица измерения сопротивления?
10. Сформулируйте закон Ома для участка цепи.
Вариант выполнения измерений.
Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи. Включите ток. При помощи реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.
Таблица 1. Сопротивление участка 2 Ом
|
Напряжение, В |
1 |
2 |
3 |
|
Сила тока, А |
0,5 |
1,0 |
1,5 |
По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.
Сделайте вывод.
Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах. Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.
Таблица 2. Постоянное напряжение на участке 2 В
|
Сопротивление участка, Ом |
1 |
2 |
4 |
|
Сила тока, А |
2,0 |
1,0 |
0,5 |
По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.
Сделайте вывод.
Презентация: «Лабораторная работа: «Изучение закона Ома для участка цепи» .
{edocs}fizpr/lr7f.pptx,800,600{/edocs}
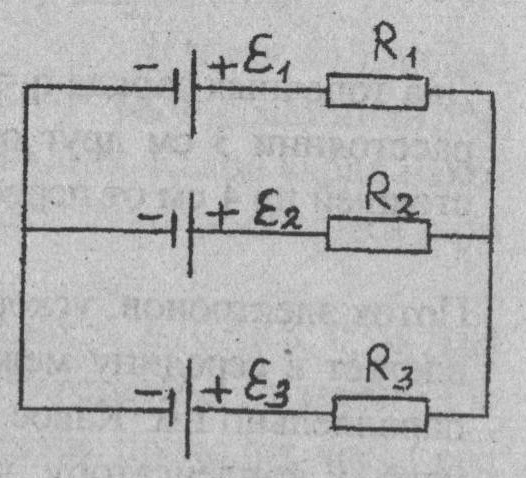
Ом — Нахождение напряжения в цепи, состоящей из последовательной и параллельной?
Как вы правильно сделали, вы начинаете с узла , на котором есть \$60\:\textrm{V}\$, а затем замечаете, что они указывают точный ток, выходящий из этого узла (\$6\:\textrm{A }\$) и по какому маршруту (резистор \$5\:\Omega\$.) Поскольку весь этот ток должен «проходить» через этот резистор, отсюда следует, что должно быть \$6\:\textrm{A}\ cdot 5\:\Omega = 30\:\textrm{V} \$ через резистор. Единственная проблема на данный момент — спросить себя, означает ли это, что пункт A равно \$V_A=60\:\textrm{V}+30\:\textrm{V}=90\:\textrm{V}\$ или, если это \$V_A=60\: \textrm{V}-30\:\textrm{V}=30\:\textrm{V}\$. По соглашению ток считается «положительным», поэтому ток течет от более положительного конца к более отрицательному концу. Стрелка показывает это и означает, что \$V_A=60\:\textrm{V}-30\:\textrm{V}=30\:\textrm{V}\$.
Стрелка показывает это и означает, что \$V_A=60\:\textrm{V}-30\:\textrm{V}=30\:\textrm{V}\$.
Хорошая работа!
Хорошо. Итак, теперь вы столкнулись с параллельно расположенной парой резисторов. Что здесь происходит? Ну, ток делит. Кто-то идет в одном направлении, а кто-то в другом. Сумма, конечно, по-прежнему \$6\:\textrm{A}\$. Вы начинаете решать эту проблему, признавая, что напряжение на этих двух резисторах должно быть одинаковым, поскольку они подключены с обоих концов. Узел A может иметь некоторое напряжение \$V_A\$, а узел B может иметь некоторое напряжение \$V_B\$. Но узел B не может иметь два разных напряжения. Так же как и узел A . У узла может быть только одно напряжение. Таким образом, напряжение на резисторе \$3\:\Omega\$ должно быть точно таким же, как и на резисторе \$6\:\Omega\$. Однако дело в том, что ток делится (и пока единственное, что вы знаете, это то, что сумма должна быть \$6\:\textrm{A}\$), должно быть так, что напряжение, развивающееся на верхнем резисторе должно быть таким же, как напряжение, развиваемое на нижнем резисторе. Это напряжение будет \$V_B — V_A\$. Это простой факт.
Это напряжение будет \$V_B — V_A\$. Это простой факт.
Итак, давайте запишем это:
$$\begin{align*} V_B — V_A &= I_{3\:\Omega}\cdot 3\:\Omega\\\\ V_B — V_A &= I_{6\:\Omega}\cdot 6\:\Omega\\\\ &\поэтому ~~~~~I_{3\:\Omega}\cdot 3\:\Omega = I_{6\:\Omega}\cdot 6\:\Omega \end{align*}$$
Но, конечно, вы также знаете:
$$I_{3\:\Omega}+I_{6\:\Omega} = 6\:\textrm{A}$$
Вы можете решить эти два уравнения, чтобы найти это:
$$\begin{align*} I_{3\:\Omega} &= 4\:\textrm{A}\\\\ I_{6\:\Omega} &= 2\:\textrm{A} \end{выравнивание*}$$
Отсюда вы знаете, что падение напряжения должно быть \$12\:\textrm{V}\$, чтобы \$V_B=V_A-12\:\textrm{V}=18\:\textrm{V}\ $.
Теперь, как и все, есть ярлыки, разработанные, когда одно и то же делается снова и снова. Никому не нравится решать два одновременных уравнения каждый раз, когда они встречаются с такой парой параллельных резисторов. Поэтому они придумали полезные правила, которым нужно следовать . (Это то же самое, что изучение таблицы умножения и умножение от руки — это избавит вас от сложения, когда вы столкнетесь с проблемой умножения.)
(Это то же самое, что изучение таблицы умножения и умножение от руки — это избавит вас от сложения, когда вы столкнетесь с проблемой умножения.)
Одно правило, которое следует усвоить, состоит в том, что вы можете заменить параллельную пару резисторов одним эквивалентным резистором, преобразовав их в проводимости (насколько они поощряют ток, а препятствуют току, я полагаю), добавляя проводимости в параллельная ветвь, а затем снова обратное преобразование в сопротивление. Конвертировать в любом случае легко: \$G_R=\frac{1}{R}\$ и \$R=\frac{1}{G_R}\$. Итак, здесь вы должны сделать следующее:
$$\begin{align*} R_{экв} &= \frac{1}{G_{экв}}\\\\ &= \frac{1}{G_{3\:\Omega}+G_{6\:\Omega}}\\\\ &= \frac{1}{\frac{1}{3\:\Omega}+\frac{1}{6\:\Omega}}\\\\ &= 2\:\Омега \end{выравнивание*}$$
Теперь вы можете легко вычислить падение напряжения, как и на первом шаге, как \$6\:\textrm{A}\cdot 2\:\Omega=12\:\textrm{V}\ $. И зная это, вы можете легко вернуться назад и вычислить токи в каждом из двух резисторов, поскольку теперь вы знаете падение напряжения на них.
Вы можете даже упростить описанный выше процесс для случая всего двух параллельных резисторов:
$$R_{эквив} = \frac{R_1\cdot R_2}{R_1+R_2}$$ проводимости носит более общий характер и может обрабатывать три, четыре и более резистора параллельно. Но два резистора встречаются достаточно часто, поэтому приведенную выше формулу стоит запомнить.
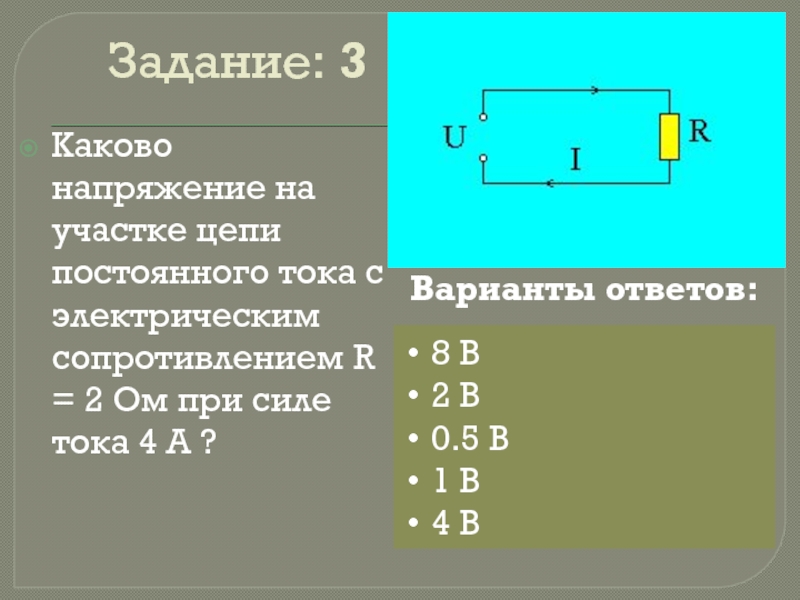
Объяснение закона Ома и электрического сопротивления проводной схемы, используемой для измерения тока и напряжения для расчета сопротивления I = V/R V=IR R = V/I. сопротивление напряжению для омического проводника Примечания к пересмотру IGCSE/GCSE Physics для экзаменов AQA Edexcel OCR
Возраст уровня GCSE в Великобритании ~ 14–16 лет, ~ 9–10 классы в США Примечания к редакции ФИЗИКИ редакция 27.05.2023 [ПОИСК]
Электричество Раздел 3: 3.1 Закон Ома и электрическое сопротивление провода — схема для измерения силы тока и напряжения на рассчитать сопротивление — что такое омический проводник? Примечания к пересмотру исследования доктора Брауна по физике Есть различные разделы для проработки, после 1 их можно читать и изучать в любом порядке. ИНДЕКС по физике электричества раздел 3 примечания по току, напряжению, сопротивлению, энергии и заряду передача в цепях 3,1 А Ом Закон (и упоминание других единиц, рассматриваемых в других разделах)
3.1B Простой Эксперимент по измерению сопротивления одного компонента с несколькими вольтамперные показания
3.1С Расследование ток — напряжение характеристики провода
Схема 31 показано, как исследовать, как I зависит от V для сопротивления
3.1D Электрическое сопротивление — эксперименты по исследовать ВАХ различных сопротивлений и достоверность, или в противном случае по закону Ома
ЧТО ДАЛЬШЕ? НАЧАЛО страницы ИНДЕКС по физике электричества раздел 3 примечания по току, напряжению, сопротивлению, энергии и заряду передача в цепях электронный документ коричневый — комментарии — запрос? ИНДЕКС всех моих ЗАПИСОК ПО ФИЗИКЕ БОЛЬШОЙ веб-сайт и с помощью [ПОИСК BOX] ниже, возможно, быстрее, чем навигация по много субиндексов UK KS3 Научные викторины для Учащиеся естественных наук KS3 в возрасте ~ 11-14 лет, ~ 6, 7 и 8 классы США Биология * Химия * Физика Великобритания Учащиеся GCSE/IGCSE в возрасте ~14-16 лет, ~9-10 классы в США Химия продвинутого уровня для довузовской школы ~16-18 ~11-12 классы США, K12 с отличием Найдите свой GCSE/IGCSE научный курс для получения дополнительной помощи, ссылки на все примечания к научным изменениям Используй свой
мобильный телефон или ipad и т. |
|


 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия

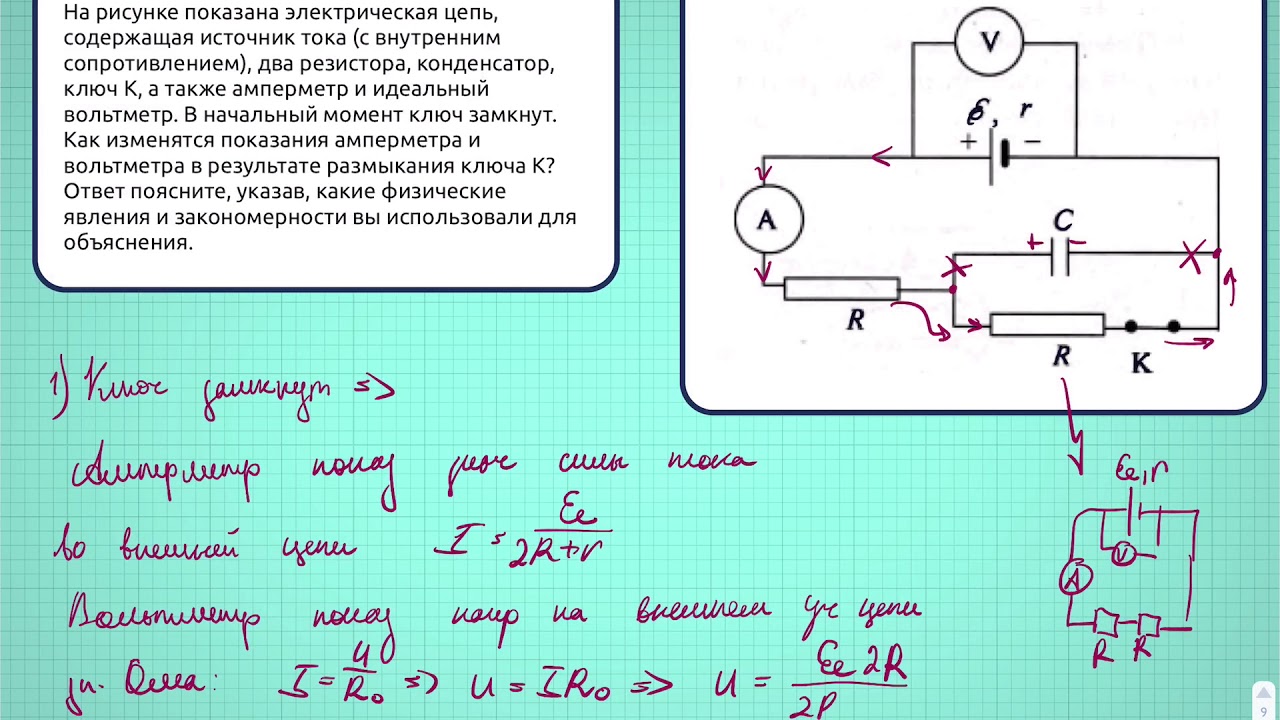
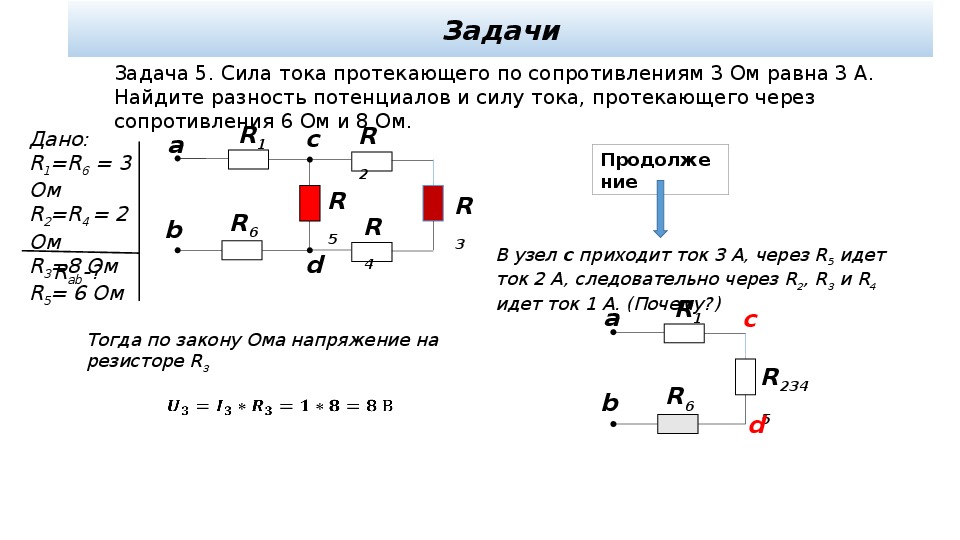







 2 по 3.4 описывает и поясняет несколько примеров
графиков ВАХ, которые можно исследовать с помощью схемы 31 (справа)
2 по 3.4 описывает и поясняет несколько примеров
графиков ВАХ, которые можно исследовать с помощью схемы 31 (справа)  д. в «ландшафтном» режиме?
д. в «ландшафтном» режиме?