Напряжение на участке цепи.

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.

На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b.

Рис. 13. Участок электрической цепи

На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки b на величину, равную произведению тока на сопротивление :

.

В соответствии с определением, напряжение между точками a и b

. (8)

Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.

В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.

Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.

На рис. 14 а и б показаны участки некоторых цепей, по которым протекает ток .. Найдем напряжение между точками a и c для этих участков.

а) б)

Рис. 14. Участки электрической цепи

По определению

. (9)

Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 14,а) идем встречно ЭДС , поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС , т. е.

. (10)

На рис. 14,б при перемещении от точки c к точке b идем согласно ЭДС

и потому потенциал точки b оказывается больше, чем потенциал точки c на величину ЭДС , т.е.

. (11)

Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением :

. (12)

Таким образом, для рис. 14,а имеем

, или

. (13)

И для рис. 14,

б имеем

, или

. (14)

Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения изобразится стрелкой, направленной от a к c.

Из самого определения напряжения следует также, что . Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.

6. Закон Ома для участка цепи, не содержащего эдс.

Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи, изображенному на рис. 13 имеем

или

. (15)

7. Закон Ома для участка цепи, содержащего эдс.

Закон Ома для участка цепи, содержащего ЭДС, позволяет найти ток этого участка по известной разности потенциалов на концах этого участка и имеющейся на этом участке ЭДС . Так из уравнения (13) имеем для схемы рис. 14,

а

. (16)

Аналогично из уравнения (14) для схемы рис. 14, б следует

. (17)

Уравнения (16) и (17) выражают собой закон Ома для участка цепи, содержащего ЭДС, для разных случаев включения ЭДС .

Закон Ома онлайн — формулы и калькулятор

На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн

Закон Ома — один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.

Содержание:

1. калькулятор закона Ома
2. закон Ома для участка цепи
3. формула силы тока
4. формула напряжения
5. формула сопротивления
6. примеры задач

Закон Ома для участка цепи

Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= \dfrac{U}{R}

Формула силы тока

Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.

{I = \dfrac{U}{R}}

I — сила тока

U — напряжение

R — сопротивление

Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).

Формула напряжения

Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.

{U = I \cdot R}

U — напряжение

I — сила тока

R — сопротивление

Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.

Формула сопротивления

Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.

{R = \dfrac{U}{I}}

R — сопротивление

U — напряжение

I — сила тока

Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.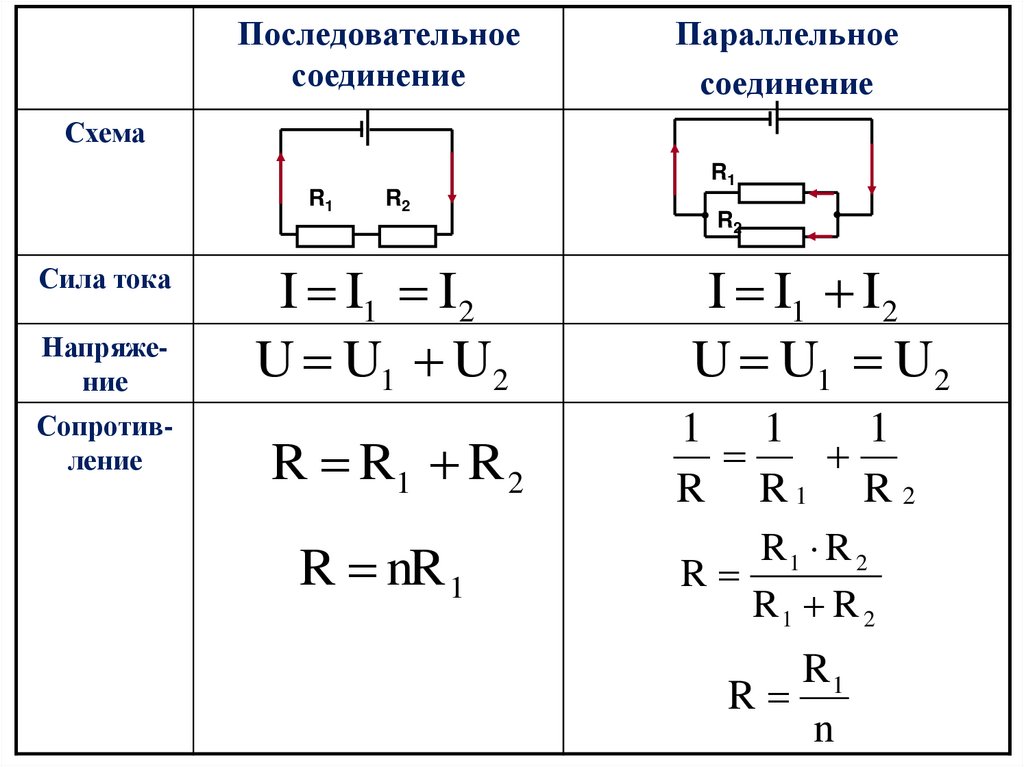

Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома

Задача 1

Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.

Решение

Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.

I = \dfrac{U}{R} = \dfrac{4}{40} = 0.1 А

Ответ: 0.1 А

На этой странице есть калькулятор, который поможет проверить полученный ответ.

Задача 2

Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.

Решение

Для решения этой задачи нам пригодится формула напряжения.

U = I \cdot R = 2 \cdot 40 = 80 В

Ответ: 80 В

Проверим получившийся результат с помощью калькулятора .

Задача 3

Найдите сопротивление спирали, сила тока в которой 0. 5 А, а напряжение на ее концах 120 В.

Решение

Чтобы найти сопротивление спирали нам потребуется формула сопротивления.

R = \dfrac{U}{I} = \dfrac{120}{0.5} = 240 Ом

Ответ: 240 Ом

Проверка .

Закон

Ом — Нахождение напряжения в цепи, состоящей из последовательной и параллельной?

Как вы правильно сделали, вы начинаете с узла , на котором есть \$60\:\textrm{V}\$, а затем замечаете, что они указывают точный ток, выходящий из этого узла (\$6\:\textrm{A }\$) и по какому маршруту (резистор \$5\:\Omega\$.) Поскольку весь этот ток должен «проходить» через этот резистор, отсюда следует, что должно быть \$6\:\textrm{A}\ cdot 5\:\Omega = 30\:\textrm{V} \$ через резистор. Единственная проблема на данный момент — спросить себя, означает ли это, что пункт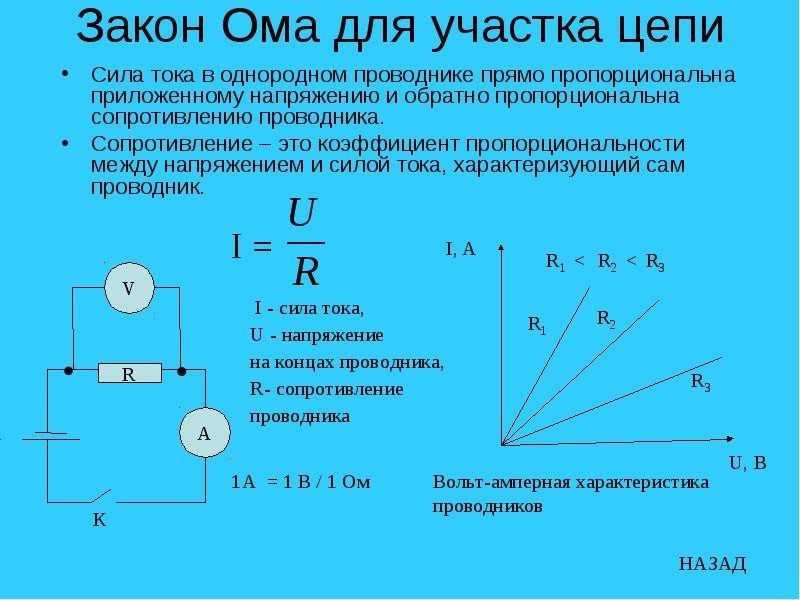

A равно \$V_A=60\:\textrm{V}+30\:\textrm{V}=90\:\textrm{V}\$ или, если это \$V_A=60\: \textrm{V}-30\:\textrm{V}=30\:\textrm{V}\$. По соглашению ток считается «положительным», поэтому ток течет от более положительного конца к более отрицательному концу. Стрелка показывает это и означает, что \$V_A=60\:\textrm{V}-30\:\textrm{V}=30\:\textrm{V}\$.

Хорошая работа!

Хорошо. Итак, теперь вы столкнулись с параллельно расположенной парой резисторов. Что здесь происходит? Ну, ток делит. Кто-то идет в одном направлении, а кто-то в другом. Сумма, конечно, по-прежнему \$6\:\textrm{A}\$. Вы начинаете решать эту проблему, признавая, что напряжение на этих двух резисторах должно быть одинаковым, поскольку они подключены с обоих концов. Узел A может иметь некоторое напряжение \$V_A\$, а узел B может иметь некоторое напряжение \$V_B\$. Но узел

B не может иметь два разных напряжения. Так же как и узел A . У узла может быть только одно напряжение. Таким образом, напряжение на резисторе \$3\:\Omega\$ должно быть точно таким же, как и на резисторе \$6\:\Omega\$. Однако дело в том, что ток делится (и пока единственное, что вы знаете, это то, что сумма должна быть \$6\:\textrm{A}\$), должно быть так, что напряжение, развивающееся на верхнем резисторе должно быть таким же, как напряжение, развиваемое на нижнем резисторе. Это напряжение будет \$V_B — V_A\$. Это простой факт.

Итак, давайте запишем это:

$$\begin{align*} V_B — V_A &= I_{3\:\Omega}\cdot 3\:\Omega\\\\ V_B — V_A &= I_{6\:\Omega}\cdot 6\:\Omega\\\\ &\поэтому ~~~~~I_{3\:\Omega}\cdot 3\:\Omega = I_{6\:\Omega}\cdot 6\:\Omega \end{align*}$$

Но, конечно, вы также знаете:

$$I_{3\:\Omega}+I_{6\:\Omega} = 6\:\textrm{A}$$

Вы можете решить эти два уравнения, чтобы найти это:

$$\begin{align*} I_{3\:\Omega} &= 4\:\textrm{A}\\\\ I_{6\:\Omega} &= 2\:\textrm{A} \end{выравнивание*}$$

Отсюда вы знаете, что падение напряжения должно быть \$12\:\textrm{V}\$, чтобы \$V_B=V_A-12\:\textrm{V}=18\:\textrm{V}\ $.

Теперь, как и все, есть ярлыки, разработанные, когда одно и то же делается снова и снова. Никому не нравится решать два одновременных уравнения каждый раз, когда они встречаются с такой парой параллельных резисторов. Поэтому они придумали полезные правила, которым нужно следовать . (Это то же самое, что изучение таблицы умножения и умножение от руки — это избавляет вас от сложения, когда вы сталкиваетесь с проблемой умножения.)

Одно правило, которое следует усвоить, состоит в том, что вы можете заменить параллельную пару резисторов одним эквивалентным резистором, преобразовав их в проводимости (насколько они поощряют ток, а препятствуют току, я полагаю), добавляя проводимости в параллельная ветвь, а затем снова обратное преобразование в сопротивление. Конвертировать в любом случае легко: \$G_R=\frac{1}{R}\$ и \$R=\frac{1}{G_R}\$. Итак, здесь вы должны сделать следующее:

$$\begin{align*} R_{экв} &= \frac{1}{G_{экв}}\\\\ &= \frac{1}{G_{3\:\Omega}+G_{6\:\Omega}}\\\\ &= \frac{1}{\frac{1}{3\:\Omega}+\frac{1}{6\:\Omega}}\\\\ &= 2\:\Омега \end{выравнивание*}$$

Теперь вы можете легко вычислить падение напряжения, как и на первом шаге, как \$6\:\textrm{A}\cdot 2\:\Omega=12\:\textrm{V}\ $. И зная это, вы можете легко вернуться назад и вычислить токи в каждом из двух резисторов, поскольку теперь вы знаете падение напряжения на них.

Вы можете даже упростить описанный выше процесс для случая всего двух параллельных резисторов:

$$R_{экв} = \frac{R_1\cdot R_2}{R_1+R_2}$$ проводимости носит более общий характер и может обрабатывать три, четыре и более резистора параллельно. Но два резистора встречаются достаточно часто, поэтому приведенную выше формулу стоит запомнить.

Калькулятор падения напряжения переменного/постоянного тока и формула

 

Как рассчитывается формула падения напряжения?

Формула падения напряжения рассчитывается путем умножения тока цепи на общее сопротивление проводника. Наш калькулятор падения напряжения постоянного тока позволяет вам выбрать проводящий материал (медь или алюминий), выбрать размер американского провода (AWG), ввести одностороннюю цепь (длина в футах) и величину нагрузки (в амперах). Это рассчитает падение напряжения, напряжение на конце нагрузки цепи, падение напряжения в процентах и ​​CMA проводника.

Наш калькулятор падения напряжения постоянного тока использует K = 12,9 мил Ом на фут для меди или K = 21,2 мил Ом на фут для алюминия. Эти значения предполагают рабочую температуру проводника 75 градусов C. Для других значений K, основанных на температуре проводника, используйте расширенный калькулятор падения напряжения постоянного тока.

 

Калькулятор падения напряжения постоянного тока

Выбрать материалМедьАлюминий	Выберите размер18 AWG16 AWG14 AWG12 AWG10 AWG8 AWG6 AWG4 AWG3 AWG2 AWG1 AWG1/0 AWG2/0 AWG3/0 AWG4/0 AWG250 kcmil300 kcmil350 kcmil400 kcmil500 kcmil600 kcmil700 kcmil750 kcmil800 kcmil900 тыс.смил1000 тыс.кмил1250 тыс.кмил1500 тыс.кмил1750 тыс.кмил2000 тыс.кмил
Выберите напряжение и фазу 120 В 1-фазный 240 В 1-фазный 208 В 3-фазный 3-проводной 120/208 В 3-фазный 4-проводной 277 В 1-фазный 480 В 3-фазный 277/480 3-фазный 4-проводной 600 В 3-фазный 24 постоянного тока или 1-фазный AC48 DC или 1-фазный AC124 DC или 1-фазный AC
Введите одностороннюю цепь (длина в футах)	Введите нагрузку (в амперах)
Падение напряжения	Напряжение на стороне нагрузки цепи
Падение напряжения в процентах	смa проводника

 

Запросить цену     Промышленные продукты      Подпишитесь на электронную почту

Что такое падение напряжения?

Падение напряжения — это величина потери напряжения, возникающая в любой части или во всей цепи из-за импеданса. Слишком низкие перепады напряжения могут привести к снижению производительности продукта и даже к повреждению электрооборудования, если оно достаточно сильное. Хотя Национальный электрический кодекс (NEC) не признает падение напряжения проблемой безопасности, они рекомендуют ограничить падение напряжения от коробки выключателя до самой дальней розетки для освещения, обогрева и питания до 3% от напряжения цепи. Это стало возможным благодаря правильному выбору сечения проволоки. Использование формулы падения напряжения или калькулятора падения напряжения может помочь вам избежать хлопот и головной боли, вызванных выбором неправильного материала проводки и размеров для ваших потребностей в питании.

Насколько допустимо падение напряжения?

Национальные электротехнические нормы и правила утверждают, что падение напряжения на 5 % в самой дальней розетке ответвленной электропроводки допустимо для нормальной эффективности. Для 120-вольтовой 15-амперной цепи это означает, что падение напряжения на самом дальнем выходе не должно превышать 6 вольт, когда цепь полностью загружена.