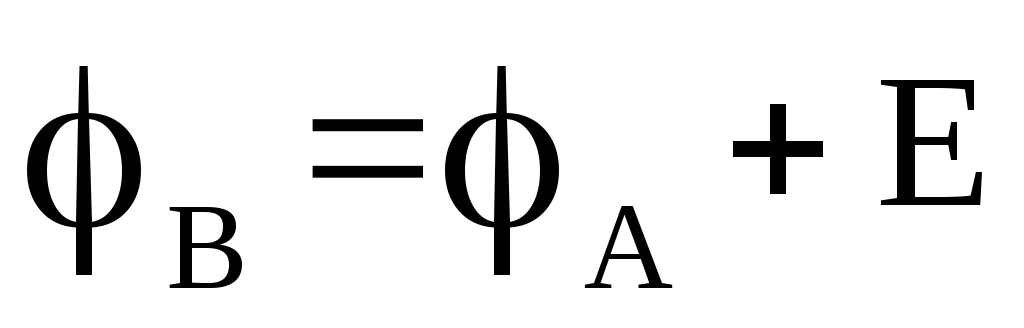
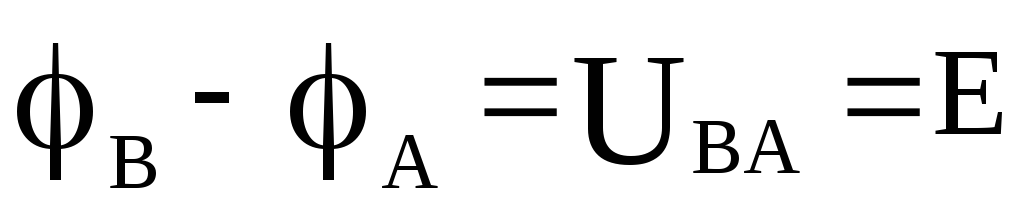В чем разница между ЭДС, разностью потенциалов и падением напряжения?

Первичное понятие здесь – потенциал. Электрический потенциал – это работа, которую необходимо совершить, чтобы увести заряд 1 Кл из данной точки в точку с нулевым потенциалом, то есть в точку, которая считается началом отсчёта. В электростатике за точку отсчёта обычно принимают бесконечно удалённую точку, в электронике – минусовой вывод источника питания, хотя в принципе точку отсчёта можно выбрать любую, исходя из соображений удобства. Разность потенциалов – это разность между величинами электрических потенциалов в двух точках независимо от природы того явления, которое создаёт эту разность. Она равна работе по перемещению заряда 1 Кл из одной точки в другую. ЭДС – это характеристика источника электрической энергии (гальванического элемента, батареи, генератора) . Она численно равна разности потенциалов между плюсовым и минусовым выводами источника питания на холостом ходу, то есть при отсутствии тока. Например, когда батарейка не включена в электрическую цепь. Напряжение – это разность потенциалов между выводами источника электрической энергии в рабочем режиме, т. е. когда течёт ток. Обычно оно меньше, чем ЭДС, хотя возможны исключения. Падение напряжения – это разность потенциалов, которая возникает на выводах сопротивления, когда через него течёт электрический ток. Резюме: ЭДС, напряжение, падение напряжения – это одно и то же явление, в общем случае называемое разностью потенциалов. Разница только в том, какой физический процесс порождает эту разность потенциалов.

ЭДС — физ. величина, характеризует работу сторонних сил (некулоновских) по перемещению заряда. Напряжение — характеризует работу тока по перемещению заряда. Разность потенциалов — характеризует работу сил поля по перемещению заряда из точки с одним потенциалом в точку с другим потенциалом. (Потенциал — энергетическая характеристика поля) . Падение напряжения — это произведение силы тока на сопротивление участка цепи. Всё измеряется в Вольтах.

Как истолковать обратную пропорциональную зависимость емкости конденсатора от расстояния между пластинами? Ведь емкость — заряд, который обеспечивает единичную разность потенциалов между пластинами конденсатора. При этом получается, что при раздвигании пластин необходим все меньший и меньший заряд для создания одной и той же разности потенциалов. — Перестаю понимать не только что такое емкость но и разность потенциалов. Ландсберг пишет о невозможности конструирования с этой связи простых аналогий и каких-то объяснений. Тарелька пишется без мягкого знака. Это нельзя понять. Это надо запомнить.

На вопрос отвечает Новая концепция электричества Твердохлебова Г. А. <img src=»//otvet.imgsmail.ru/download/265070448_52cea8b10a0f24d0f8bc2b3f9ae53ae2_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/265070448_52cea8b10a0f24d0f8bc2b3f9ae53ae2_120x120.jpg» data-big=»1″>

Лекция №1 электрическое пoлe

1.1. Напряжение. Потенциал. Разность потенциалов

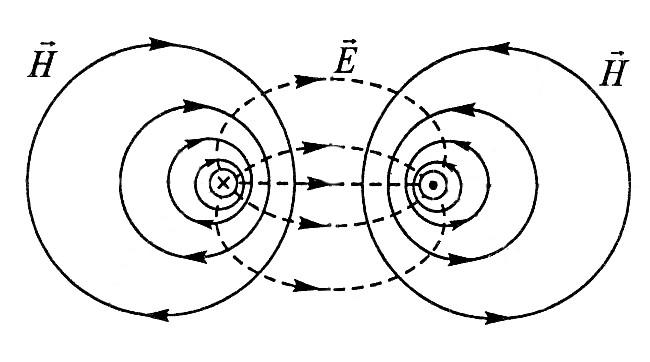
Электромагнитное поле состоит из электрического поля (Е) и магнитного поля (Н) (рис. 1.1).

Заряженные частицы создают электрическое поле. Под действием электрического поля заряды движутся, образуя электрический ток. Электрический ток создает магнитное поле.

Н

Рис. 1.1

апряженность электрического поля(Е) — векторная величина, характеризующая электрическое поле в каждой его точке (рис. 1.1).

Электрическое напряжение между двумя точками(

U) равно работе сил поля по перемещению единичного положительного заряда из одной точки поля в другую. Напряжение измеряется в вольтах.

Потенциал( ) – это напряжение между какой-либо точкой электрического поля и землей, потенциал которой условно принят равным нулю.Потенциал изме­ряется в вольтах.

Напряжение между двумя точками электрического поля (например, точкой Аи точкойВ на рис. 1.2) равно разности потенциалов между этими точками:

U_АВ = _А — 

В

_З = 0 – потенциал земли

U_АЗ =_А — _З = _А

U_ВЗ =_В — _З = _В

U_АВ =_А — _В

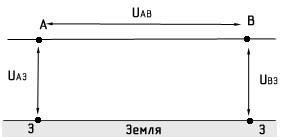
Рис. 1.2

1.2. Электрическая емкость. Конденсаторы

Конденсатор – это система из двух проводников (обкладок), разде­ленных диэлектриком, то есть, материалом, не проводящим электрический ток (рис. 1.2). Условное обозначение конденсатора показано на рисунке 1.3, а – конденсатор постоянной емкости, б – переменной емкости.

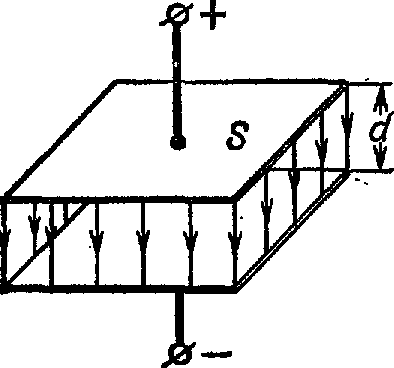
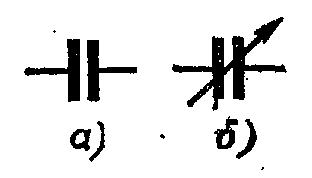
Рис. 1.2 Конденсатор Рис. 1.3 Условное обозначение Рис. 1.4 Бумажный конденсатор

конденсаторов на схемах

Конденсаторы обладают свойством накапливать на своих обкладках равные по величине и разные по знаку электрические заряды Q:

Q = CU  

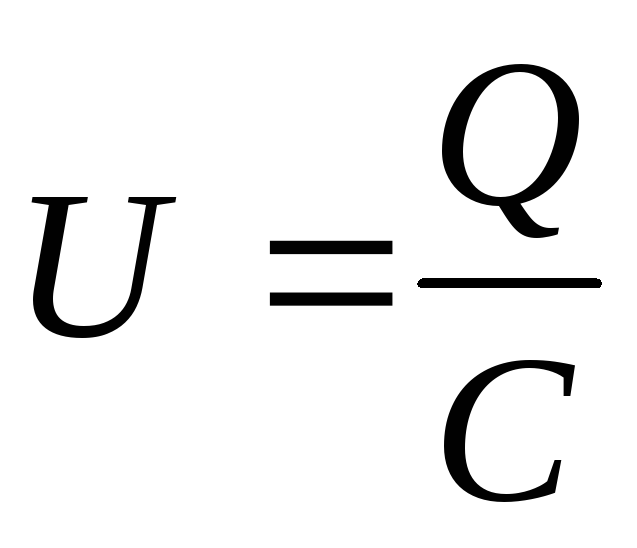
где Q — Заряд каждой из обкладок конденсатора, Кл;

U — напряжение между обкладками, В;

С — емкость конденсатора, Ф (Фарада).

Емкость конденсатора (С) зависит от формы и размеров его обкла­док (S – рис. 1.2), расстояния между ними (d – рис. 1.2) и свойств диэлек­трика, разделяющего обкладки. Конденсаторы бывают бумажные, слюдяные, керамические и др. Бумажные конденсаторы (рис. 1.4) состоят из двух длин­ных лент алюминиевой фольги, изолированных лентами парафинированной бумаги.

1.3. Соединение конденсаторов

При последовательном соединении конденсаторы соединяются один за другим (например, на рис. 1.5 — C₁ и C₂).

Эквивалентная(общая) емкость последовательно соединен­ных конденсаторов(С) определяется по формуле

. Для двух конденсаторов.

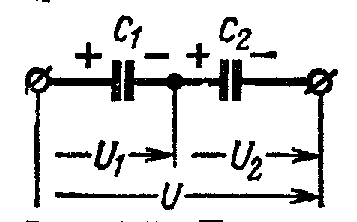
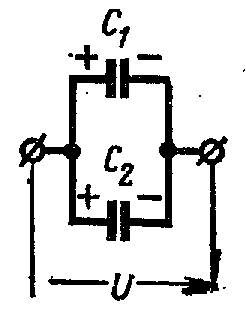
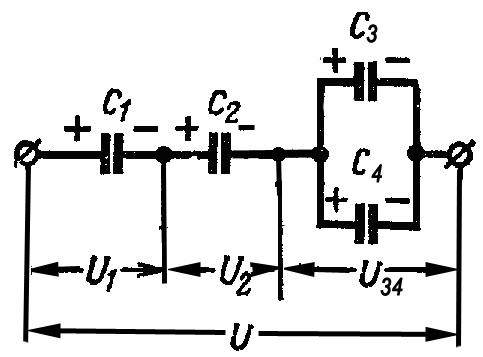
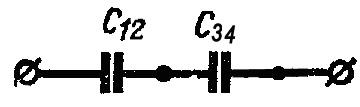
Рис. 1.5 Последовательное Рис. 1.6 Параллельное Рис. 1.7 Смешанное

соединение конденсаторов соединение конденсаторов соединение конденсаторов

При параллельном соединении все положительно заряженные пластины конденсаторов присоединяются к одной точке цепи, а отрицательно заряженные – к другой точке (рис. 1.6). Эквивалентная емкость при параллельном соединении конденсаторов определяется по формуле:

С = C₁ + C₂ + C₃ …

Смешанное соединение конденсаторов– это соединение, при котором часть конденсаторов соединены последовательно, а часть – параллельно (рис. 1.7).Эквивалентная емкость последовательно соединенных кон­денсаторов C₁ и C₂: 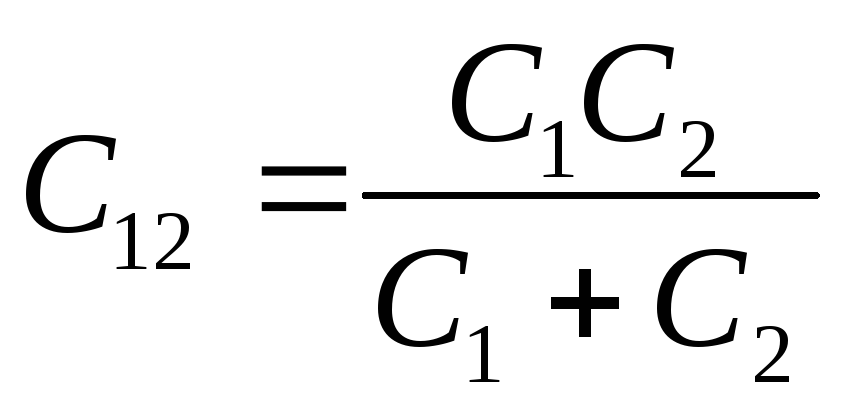.Эквивалентная емкость параллельно соединенных конденса­торов С₃ и С₄: С₃₄ = С₃ + С₄ . Эквивалентная емкость смешанного соединения .

1.2. Электрическое напряжение. Электрический потенциал. Разность потенциалов. Изменение потенциала вдоль участка цепи

Рассмотрим область пространства, в котором существует электрическое поле. Это может быть поле неподвижных зарядов или поле постоянных токов, протекающих по неподвижным проводникам, при условии, что поле исследуется вне области действия источников электродвижущих сил.

При перемещении какого-либо заряда из одной точки в другую силы поля, действующие на заряд, совершают работу. Отношение этой работы к переносимому заряду называется электрическим напряжением между рассматриваемыми точками.

Иногда вместо термина «напряжение между точками» употребляют термин «падение напряжения между точками».Если конечная точка для всех перемещений рассматриваемого пространства задана, то величина совершаемой работы при перемещении заряда из произвольной точки А в конечную точку N будет функцией только координат точки А. Отношение величины работы к величине заряда называют потенциалом точки А.

Следует отметить: что путь перемещения заряда может проходить в средах, различающихся друг от друга своими свойствами (например, в диэлектриках, в проводниках и т. д.).

Величина работы, совершаемой силами поля, определяется только положением начальной и конечной точек пути перемещения заряда. В соответствии со сказанным можно определить напряжение между точками А и В как разность потенциалов между этими точками:

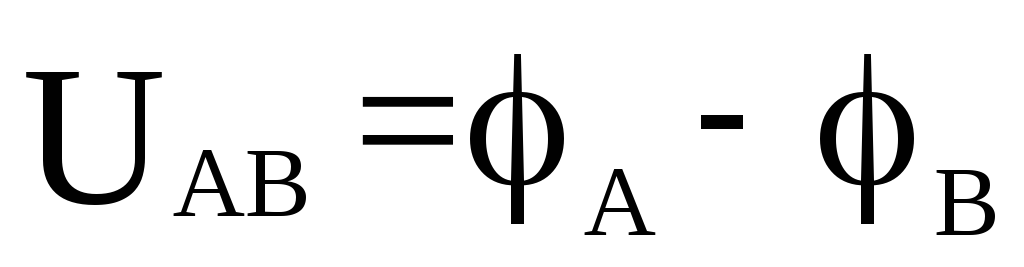
Потенциал заданной конечной точки можно считать равным нулю.

Под воздействием электрического поля, созданного источниками электрической энергии внутри проводников, в них начинается упорядоченное движение зарядов – электрический ток.

Проследим изменение потенциала вдоль участка электрической цепи. Это позволит установить общие правила, которыми мы будем пользоваться в дальнейшем.

Рассмотрим участок электрической цепи, содержащий только резистор R, по которому протекает ток I (рис. 1.4). Ток протекает от точки А с более высоким потенциалом к точке В с более низким потенциалом. Пусть известен потенциал точки А. Определим потенциал точки В.

Пусть известен потенциал точки А. Определим потенциал точки В. Он будет меньше потенциа

ла точки А на величину падения напряжения на резисторе R:

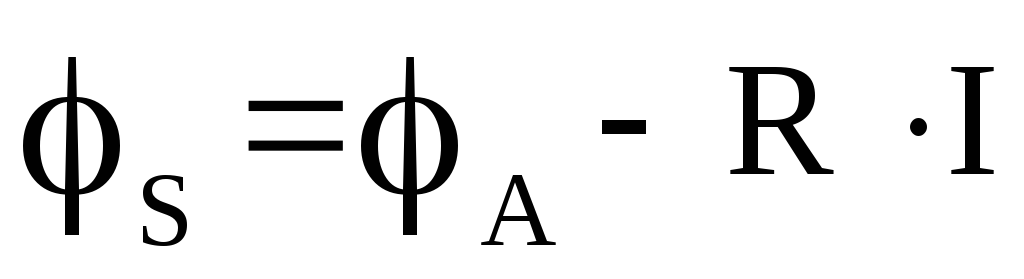
Разность потенциалов между точками А и В – есть напряжение между этими точками

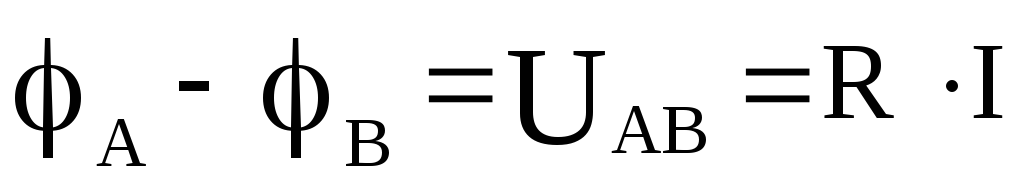(1.1)

Если же известен потенциал точки В, то потенциал точки А при заданном направлении тока

будет выше потенциала точки В на величину падения напряжения на резисторе R:

и напряжение определяется аналогично предыдущем

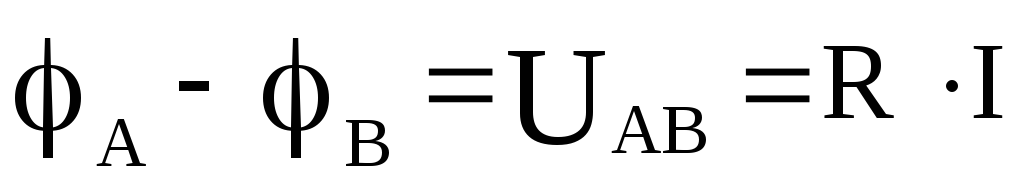
Очевидно, что (см. рис. 1.4).

Рассмотрим участок цепи, содержащий только ЭДС Е (см. рис. 1.5). Пусть известен потенциал точки А. При переходе через источник ЭДС (по стрелке) потенциал повышается на величину ЭДС Е. Поэтому для потенциала точки В следует записать и разность потенциалов

Если же известен потенциал точки В, то потенциал точки A меньше на величину ЭДС Е

(переход через источник осуществляется против стрелки).

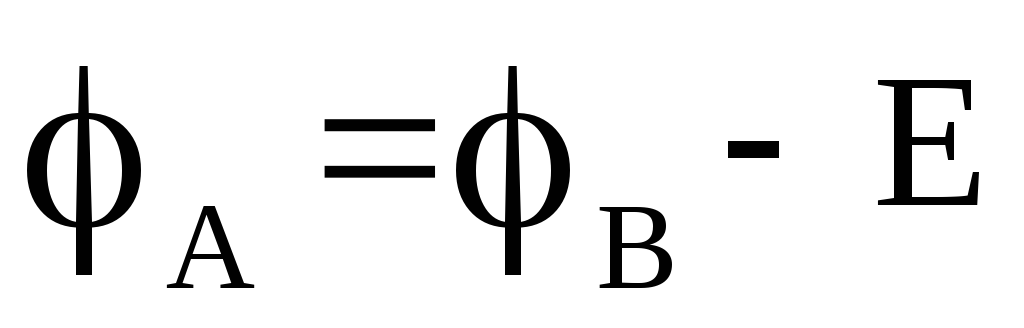
Разность потенциалов получается такой же

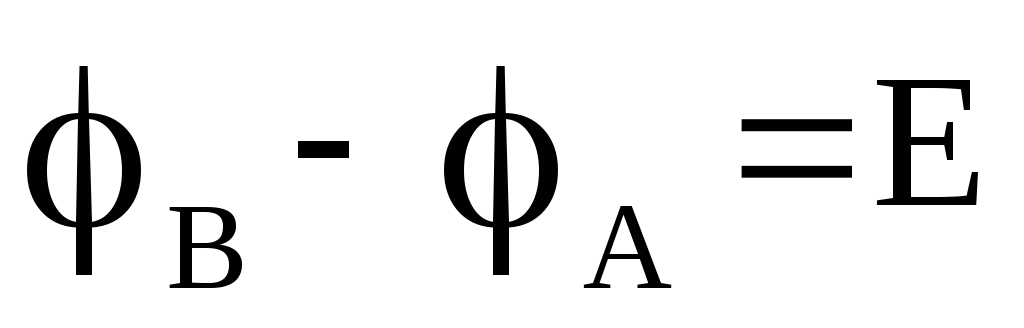
Очевидно, что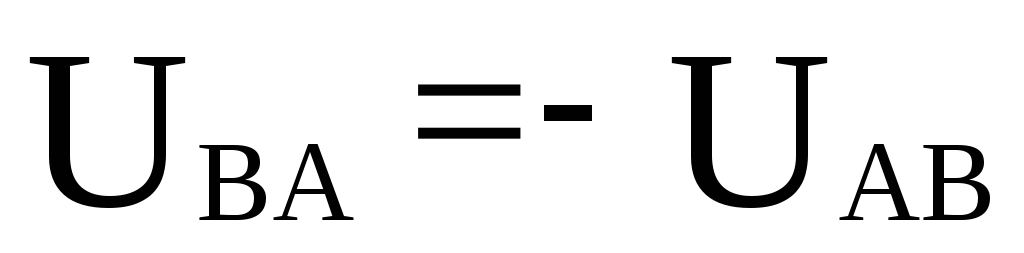 (см. рис. 1.5).

Работа сил электрического поля. Потенциал и разность потенциалов. Эквипотенциальные поверхности. Связь между напряжённостью и напряжением.

⇐ ПредыдущаяСтр 14 из 15Следующая ⇒

2. Модель строения атомного ядра. Ядерные силы. Энергия связи. Ядерные реакции.
В 1932г. после открытия протона и нейтрона учеными Д.Д. Иваненко (СССР) и В. Гейзенберг (Германия) была выдвинута протонно-нейтронная модель ядра атома.

Согласно этой модели:
— ядра всех химических элементов состоят из нуклонов: протонов и нейтронов
— заряд ядра обусловлен только протонами
— число протонов в ядре равно порядковому номеру элемента
— число нейтронов равно разности между массовым числом и числом протонов (N=A-Z)

Условное обозначение ядра атома химического элемента:

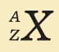
X – символ химического элемента
А – массовое число, которое показывает :
— массу ядра в целых атомных единицах массы (а.е.м.)
(1а.е.м. = 1/12 массы атома углерода)
— число нуклонов в ядре (A = N + Z) , где N – число нейтронов в ядре атома
Z – зарядовое число, которое показывает:
— заряд ядра в элементарных электрических зарядах (э.э.з.)
( 1э.э.з. = заряду электрона = 1,6 х 10^-19 Кл)
— число протонов
— число электронов в атоме
— порядковый номер в таблице Менделеева
Ядерные силы — силы притяжения, связывающие протоны и нейтроны в ядре.

Свойства:

1.На расстояниях порядка 10^-13см сильные взаимодействия соответствуют притяжению, при уменьшении расстояния – отталкиванию.

2.Независимы от наличия электрического заряда (свойство зарядовой независимости) Одинаковая сила действует и на протон и на нейтрон.

3.Взаимодействуют с ограниченным числом нуклонов (свойство насыщения).

4.Короткодействующие: быстро убывают, начиная с r ≈ 2,2^.10^-15 м.

Энергия, которая необходима для полного расщепления ядра на отдельные нуклоны, называется энергией связи. Энергия связи очень велика. При синтезе 4 г гелия выделяется такое же количество энергии, как при сжигании двух вагонов каменного угля.

Масса ядра всегда меньше суммы масс покоя свободных протонов и нейтронов, его составляющих.
Разность между массой ядра и суммой масс протонов и нейтронов называется дефектом масс.

Формула для вычисления энергии связи:

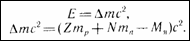
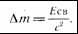— дефект массы.

m_{p –}масса покоя протона_; m_{n –} масса покоя нейтрона. М_я — масса ядра атома.

В атомной физике массу удобно выражать в атомных единицах массы:

1 а.е.м.=1,67·10^-27 кг. Коэффициент связи энергии и массы (равный с²): с²= 931,5 МэВ/а·е·м.

Ядерные реакции — превращения атомных ядер, вызванные их взаимодействиями с различными частицами или друг с другом.

Символическая запись: А + а = В + b. При написании ядерных реакций используются законы сохранения заряда и массового числа (числа нуклонов).

Примеры:

 

Энергетический выход ядерной реакции — разность между суммарной энергией связи частиц, участвующих в реакции и продуктов реакции.

Реакции, происходящие с выделением энергии, наз. экзотермическими, с поглощением — эндотермическими.

 

Билет 23.

Рекомендуемые страницы: