Векторы в пространстве
Векторы в пространстве
вход
Содержание
I . Понятие вектора в пространстве
II . Коллинеарные векторы
III . Компланарные векторы
IV . Действия с векторами
V. Разложение вектора
VI . Базисные задачи
Проверь себя
Помощь в управлении презентацией
Выход
Понятие вектора в пространстве
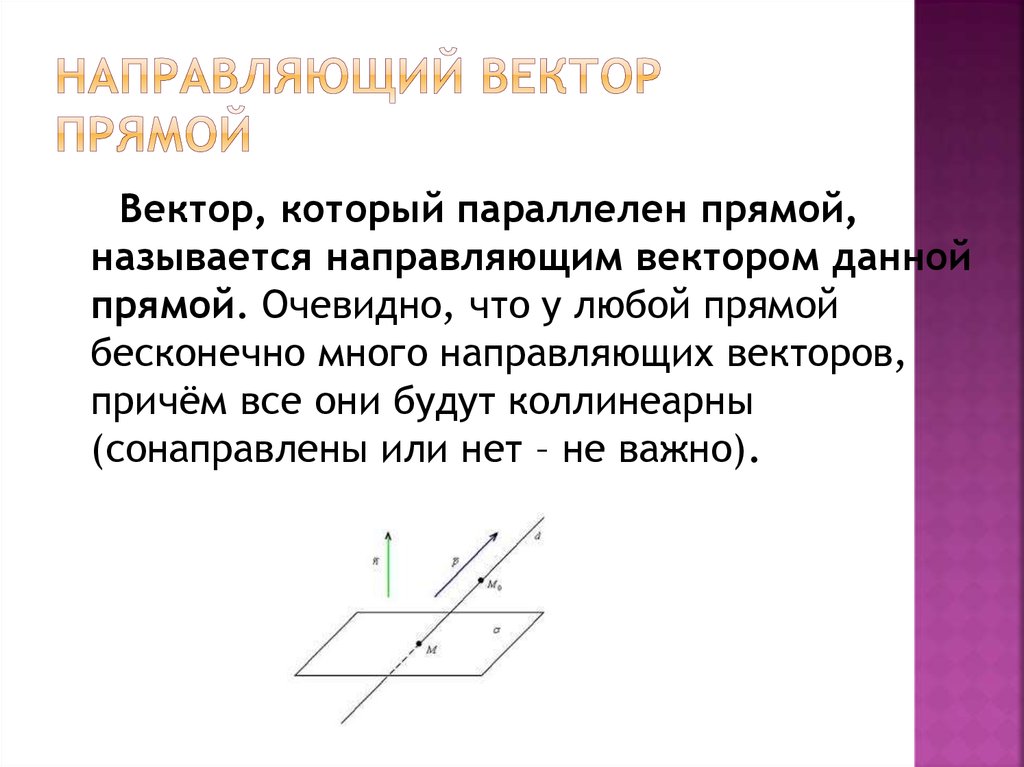
Вектор(направленный отрезок) –
отрезок, для которого указано какой из его концов считается началом, а какой – концом.
Длина вектора – длина отрезка AB.
В
M
А
Коллинеарные векторы
Два ненулевых вектора называются коллинеарными , если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
- Сонаправленные векторы
- Противоположно направленные векторы
Сонаправленные векторы
Сонаправленные векторы — векторы, лежащие
по одну сторону от прямой, проходящей через их начала.
Нулевой вектор считается сонаправленным с любым вектором.
- Равные векторы
Равные векторы
Равные векторы — сонаправленные векторы,
длины которых равны.
От любой точки можно отложить вектор,
равный данному, и притом только один.
Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала.
- Противоположные векторы
Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны.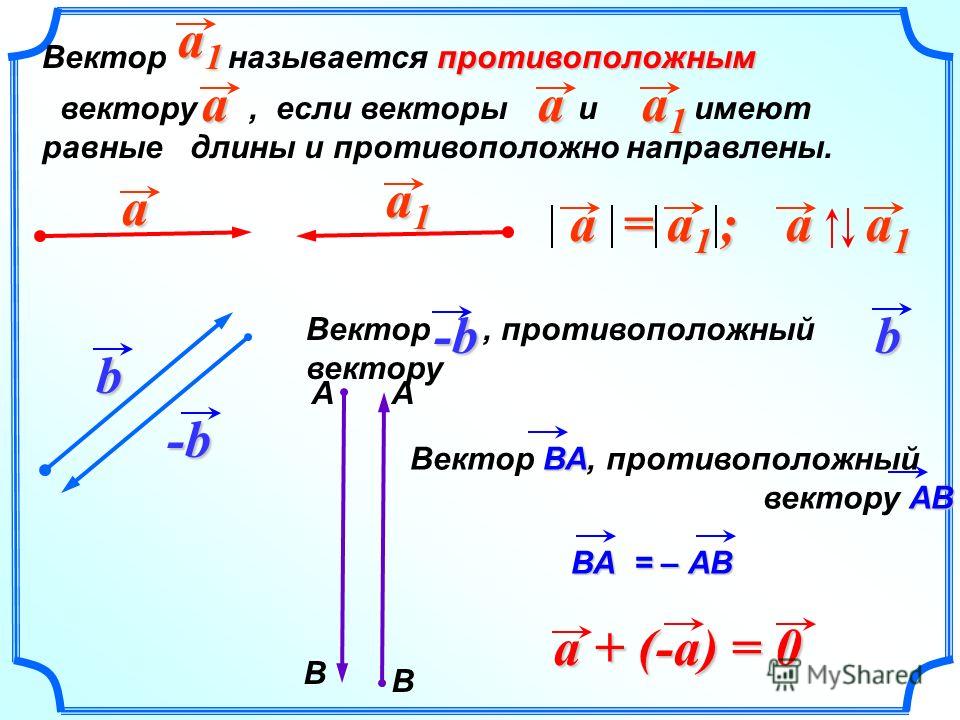
Вектором, противоположным нулевому,
считается нулевой вектор.
Признак коллинеарности
Доказательство
Доказательство признака коллинеарности
Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости.
Пример:
B 1
C 1
A 1
D 1
B
C
А
D
О компланарных векторах
Любые два вектора всегда компланарны.
Три вектора, среди которых имеются два коллинеарных, компланарны.
α
если
Признак компланарности
Доказательство
Задачи
Задачи на компланарность
- Компланарны ли векторы:
а)
б)
Справка Решение
- Известно, что векторы , и компланарны.
 Компланарны ли векторы:
Компланарны ли векторы:
а)
б)
Справка Решение
Решение
Решение
Решение
Доказательство признака компланарности
B 1
С
B
A
A 1
O
Свойство компланарных векторов
Действия с векторами
- Сложение
- Вычитание
- Умножение вектора на число
- Скалярное произведение
Сложение векторов
- Правило треугольника
- Правило параллелограмма
- Правило многоугольника
- Правило параллелепипеда
- Свойства сложения
Правило треугольника
B
А
C
Правило треугольника
B
А
C
Для любых трех точек А, В и С справедливо равенство:
Правило параллелограмма
B
А
C
Свойства сложения
Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при последовательном откладывании).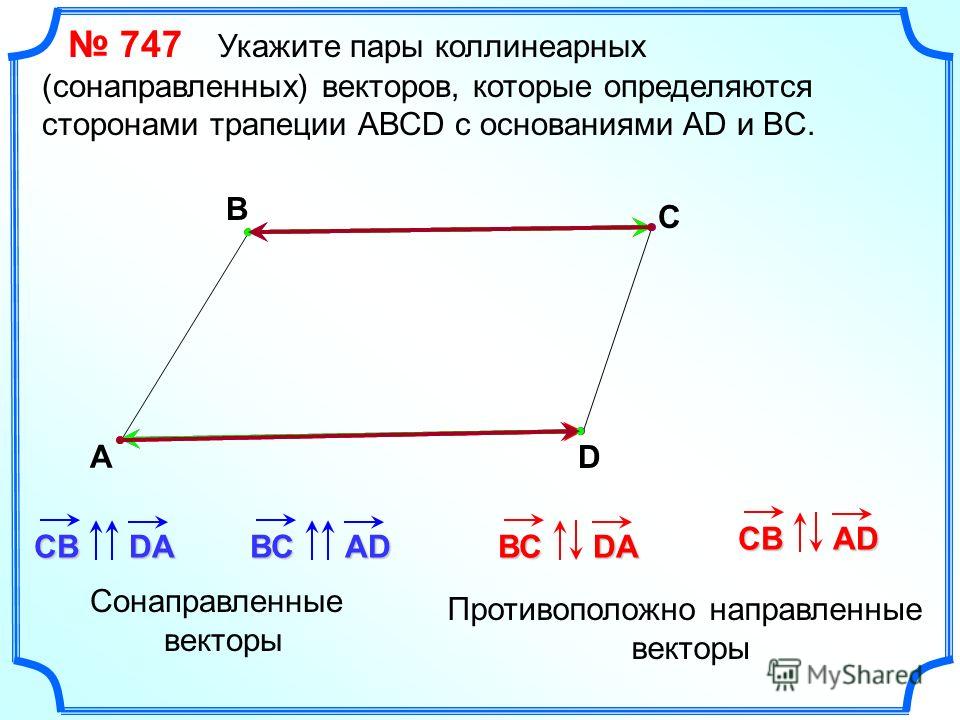
B
C
A
Пример
E
D
Пример
B 1
C 1
A 1
D 1
B
C
A
D
Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
B 1
C 1
A 1
D 1
B
C
А
D
Свойства
B 1
C 1
A 1
D
B
C
А
D
Вычитание векторов
- Вычитание
- Сложение с противоположным
Вычитание
Разностью векторов и называется такой
вектор, сумма которого с вектором равна
вектору .
Вычитание
B
A
Правило трех точек
C
Правило трех точек
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
B
А
K
Сложение с противоположным
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору .
А
B
O
Умножение вектора на число
Свойства
- Произведением нулевого вектора на любое число считается нулевой вектор.
- Произведение любого вектора на число нуль есть нулевой вектор.
Свойства
Скалярное произведение
Скалярным произведением

Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения
Справедливые утверждения
- скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти векторы перпендикулярны
- скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату
его длины
Вычисление скалярного произведения в координатах
Доказательство
Доказательство формулы скалярного произведения
B
α
O
A
A
B
O
O
B
A
Доказательство формулы скалярного произведения
Свойства скалярного произведения
1 0 .
2 0 .
3 0 .
4 0 .
(переместительный закон)
(распределительный закон)
(сочетательный закон)
Разложение вектора
- По двум неколлинеарным векторам
- По трем некомпланарным векторам
Разложение вектора по двум неколлинеарным векторам
Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство
Доказательство теоремы
- Пусть коллинеарен .
Тогда , где y – некоторое число. Следовательно,
т.е. разложен по векторам и .
P
B
O
A
A 1
Доказательство теоремы
- не коллинеарен ни вектору , ни вектору .

Отметим О – произвольную точку.
Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом.
Допустим:
Тогда:
—
Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в виде
где x, y, z – некоторые числа, то говорят, что вектор
разложен по векторам , и .
Числа x, y , z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство
Доказательство теоремы
P
С
B
P 1
P 2
O
A
Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом.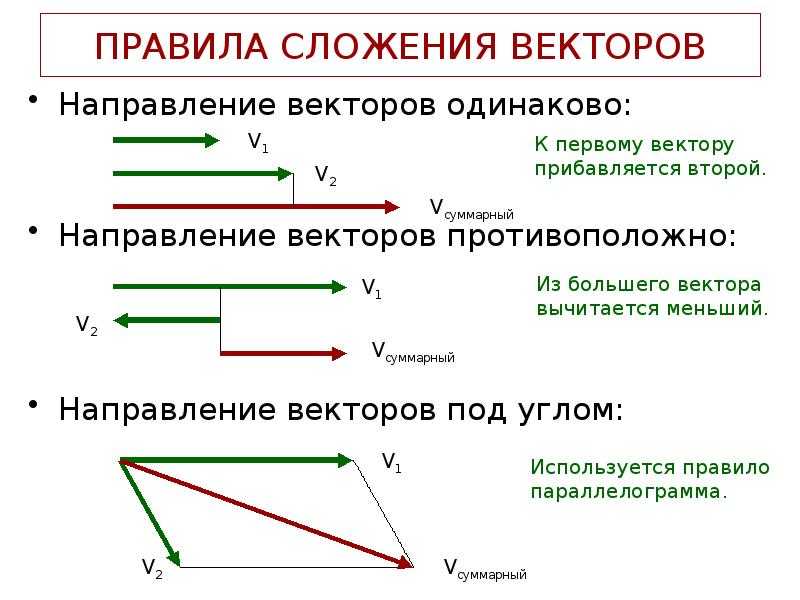
Допустим:
Тогда:
—
Базисные задачи
Вектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения
диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда
Вектор, проведенный в середину отрезка,
равен полусумме векторов, проведенных из той же точки в его концы.
С
A
B
O
Доказательство
Доказательство
С
A
B
O
Вектор, проведенный в точку отрезка
Точка С делит отрезок АВ в отношении т : п .
С
A
m
n
B
O
Доказательство
Доказательство
С
A
m
n
B
O
Вектор, соединяющий середины двух отрезков,
равен полусумме векторов, соединяющих их концы.
N
С
N
D
С
D
B
B
M
M
A
A
Доказательство
Доказательство
N
С
D
B
M
A
Вектор, проведенный в центроид треугольника,
равен одной трети суммы векторов, проведенных из этой точки в вершины треугольника.
Центроид – точка пересечения медиан треугольника.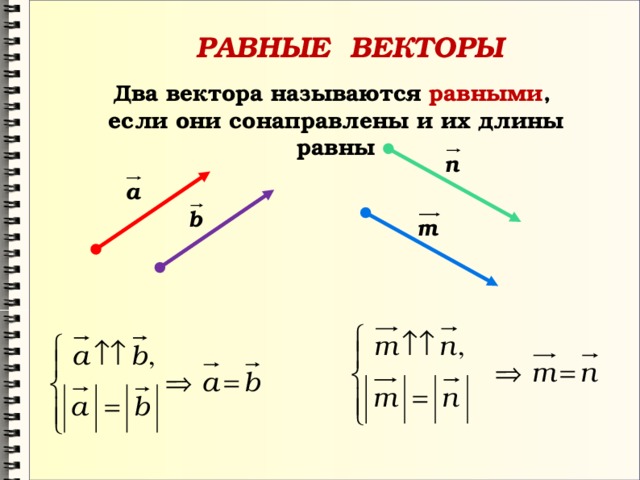
O
С
M
A
B
Доказательство
Доказательство
O
С
M
K
A
B
Вектор, проведенный в точку пересечения диагоналей параллелограмма,
равен одной четверти суммы векторов, проведенных из этой точки в вершины параллелограмма.
O
C
B
M
A
D
Доказательство
O
Доказательство
C
B
M
A
D
Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.
C 1
B 1
A 1
D 1
B
C
A
D
Доказательство
Доказательство
B 1
C 1
A 1
D 1
B
C
A
D
Помощь в управлении презентацией
- управление презентацией осуществляется с помощью левой клавиши мыши
- переход от одного слайда к другому и на гиперссылки по одиночному щелчку
- завершение презентации при нажатии кнопки выход
переход к следующему слайду
возврат к содержанию
возврат к подтеме
возврат с гиперссылок
Проверь себя
- Устные вопросы
- Задача 1 .
 Задача на доказательство
Задача на доказательство - Задача 2. Разложение векторов
- Задача 3. Сложение и вычитание векторов
- Задача 4. Скалярное произведение
Устные вопросы
Справедливо ли утверждение:
а) любые два противоположно направленных вектора коллинеарны?
б) любые два коллинеарных вектора сонаправлены?
в) любые два равных вектора коллинеарны?
г) любые два сонаправленных вектора равны?
д)
е) существуют векторы , и такие, что
и не коллинеарны, и не коллинеарны, а
и коллинеарны?
Ответы
Ответы
а) ДА
б) НЕТ (могут быть и противоположно направленными)
в) ДА
г) НЕТ (могут иметь разную длину)
д) ДА
е) ДА
Задача 1.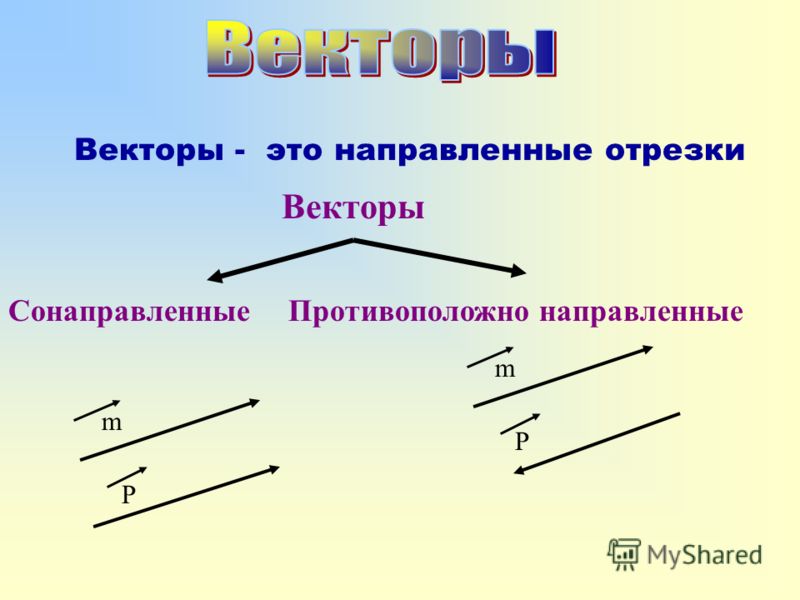 Задача на доказательство
Задача на доказательство
B 1
C 1
A 1
D 1
M 2
M 1
B
C
А
D
Решение
Решение
B 1
C 1
A 1
D 1
M 2
M 1
B
C
А
D
Задача 2. Разложение векторов
Разложите вектор по , и :
а)
б)
в)
г)
Решение
D
B
A
N
C
Решение
а)
б)
в)
г)
Задача 3. Сложение и вычитание
Упростите выражения:
а)
б)
в)
г)
д)
е)
Решение
Решение
а)
б)
в)
г)
д)
е)
Задача 4.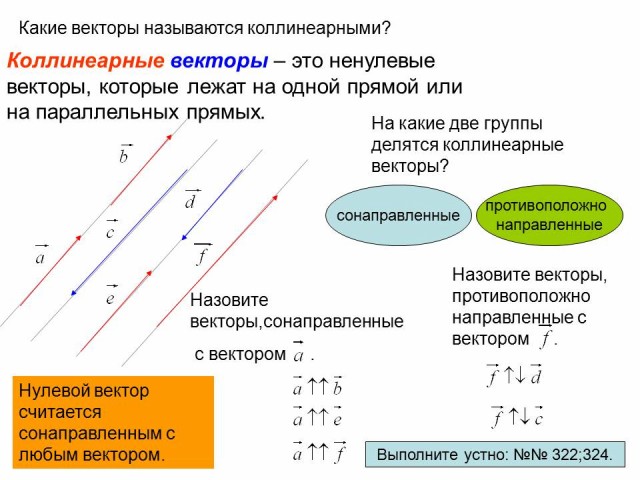 Скалярное произведение
Скалярное произведение
Вычислить скалярное произведение векторов:
C 1
B 1
A 1
D 1
B
C
A
D
Решение
Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
B 1
C 1
O 1
A 1
D 1
B
C
A
D
Решение
Решение
Решение
Решение
B 1
C 1
O 1
A 1
D 1
B
C
A
D
Векторы на плоскости — презентация онлайн
Похожие презентации:
Векторы.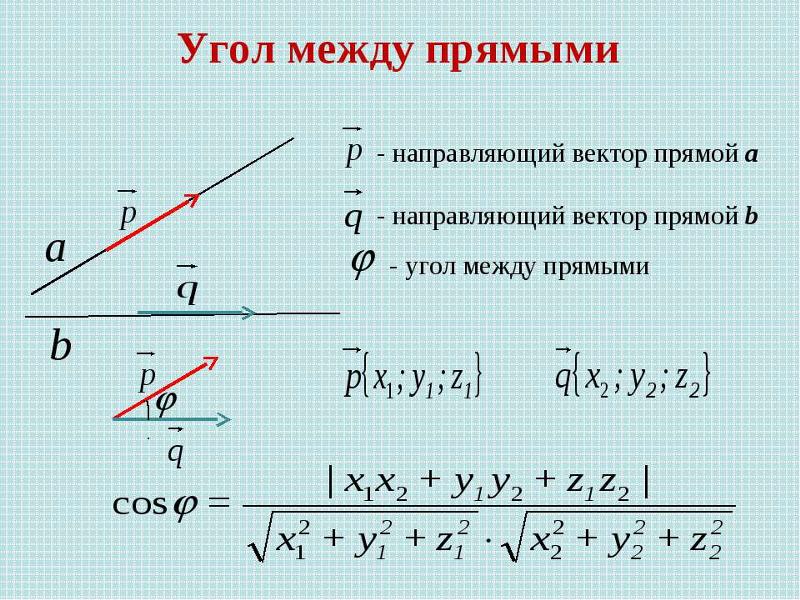 Понятие вектора
Понятие вектора
Векторы на плоскости
Векторы на плоскости и в пространстве. Основные понятия
Координаты и векторы
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
Векторы в пространстве
Понятие вектора в пространстве
Векторы. Модуль вектора. Равенство векторов. Сложение векторов
Векторы в пространстве
Векторы. Равенство векторов
1. Тема урока:
2. План.
1.Историческая справка.
2.Определение вектора.
3.Нулевой вектор.
4.Длина вектора.
5.Коллинеарные векторы.
6.Виды коллинеарных векторов.
7.Противоположные векторы.
8.Равные векторы.
9.Откладывание вектора от данной точки.
3. Историческая справка
• Термин вектор (от лат. Vector –“ несущий “) впервые появился
в 1845 г. у ирландского
математика Уильяма
Гамильтона (1805 – 1865) в
работах по построению
числовых систем.
4. Что такое вектор?
Понятие вектора возникает там, гдеприходится иметь дело с объектами, которые
характеризуются величиной и направлением:
например, скорость, сила, давление. Такие
величины называются векторными
величинами или векторами.
5. Геометрическое понятие вектора
• ОПР: Отрезок, для которого указано ,какой из его концов считается
началом , а какой – концом,
называется направленным отрезком
или вектором.
6. Геометрическое понятие вектора
• Направление вектора указывается стрелкой. Точка Aназывается началом вектора, а точка B – концом.
• Векторы обозначаются латинскими буквами a, b, c,
…, а также AB, CD, … (на первом месте ставится
начало вектора).
В
Конец
вектора
a
C
c
А
b
Начало
вектора
D
7. Нулевой вектор
• Любую точку плоскостиможно считать вектором.
Такой вектор называется
нулевым.
• Начало нулевого вектора
совпадает с его концом.
• Нулевой вектор
обозначается 0 или СС.
М
MM — нулевой вектор
С
CC — нулевой вектор
8. Длина (модуль) вектора.
• ОПР: Расстояние между началом и концом вектораназывается длиной или модулем вектора.
• Обозначение: |а| или |АВ|.
• Длина нулевого вектора равна нулю.
|0| =0
Задание 1.
Каждая клетка на рисунке имеет сторону,
равную единице измерения отрезков.
A
B
C
a
D
N
|AB| = 5
|CD| = 4
|a| = 5
|NN| = 0
АВ 6
Задание 2.
А
CD 5
C
EF 2,5
F
MM 0
E
B
M
a 13
b 4,5
c 3
D
a
b
c
11. Коллинеарные векторы
ОПР: Два ненулевых вектораназываются коллинеарными, если они
лежат на параллельных прямых или на
одной прямой.
b
Нулевой вектор считается коллинеарным
любому вектору.
a
b
a
12. Задание: укажите коллинеарные векторы
Ob
CD, KF, O, a, b –
коллинеарные
N
D
a
K
O, a – коллинеарные
O, NP – коллинеарные
P
C
m
F
NP, m – не коллинеарные
13.
 Коллинеарные векторы• Сонаправленные
Коллинеарные векторы• Сонаправленные• Противоположно
направленные
Сонаправленные векторы
a
b
АА
а в
Два вектора называются сонаправленными,
если они коллинеарные и направлены одинаково.
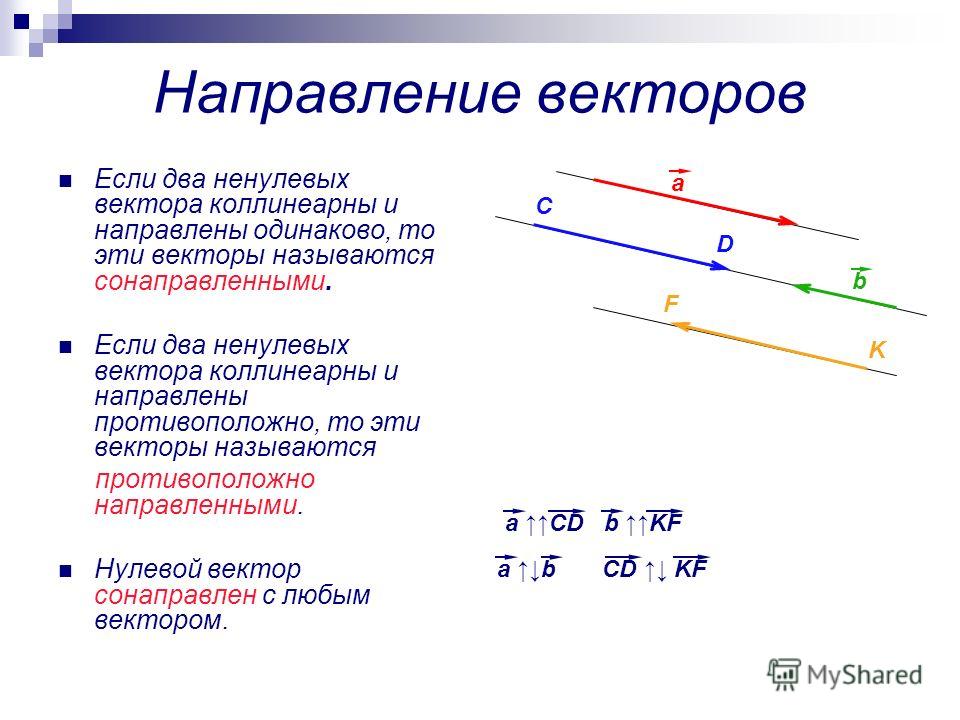
Противоположно направленные векторы
a
а в
b
Два вектора называются противоположно направленными,
если они коллинеарны и противоположно направлены
Свойства коллинеарных векторов.
b
a
c
b
a
c 0 ,
то a b
если a с, b с,
то a b
c
b
c
если a с, b с,
a
если a с, b с,
то a b
18. Противоположные векторы
Длины равныДва вектора называются противоположными,
если они противоположно направлены и их длины равны.
19. Равные векторы
aa
a
a
a
20. ОПР: Ненулевые векторы называются равными, если они сонаправлены и их модули равны. Все нулевые векторы равны друг другу.
a b, если1.a b
2. a b
Свойство равных векторов.
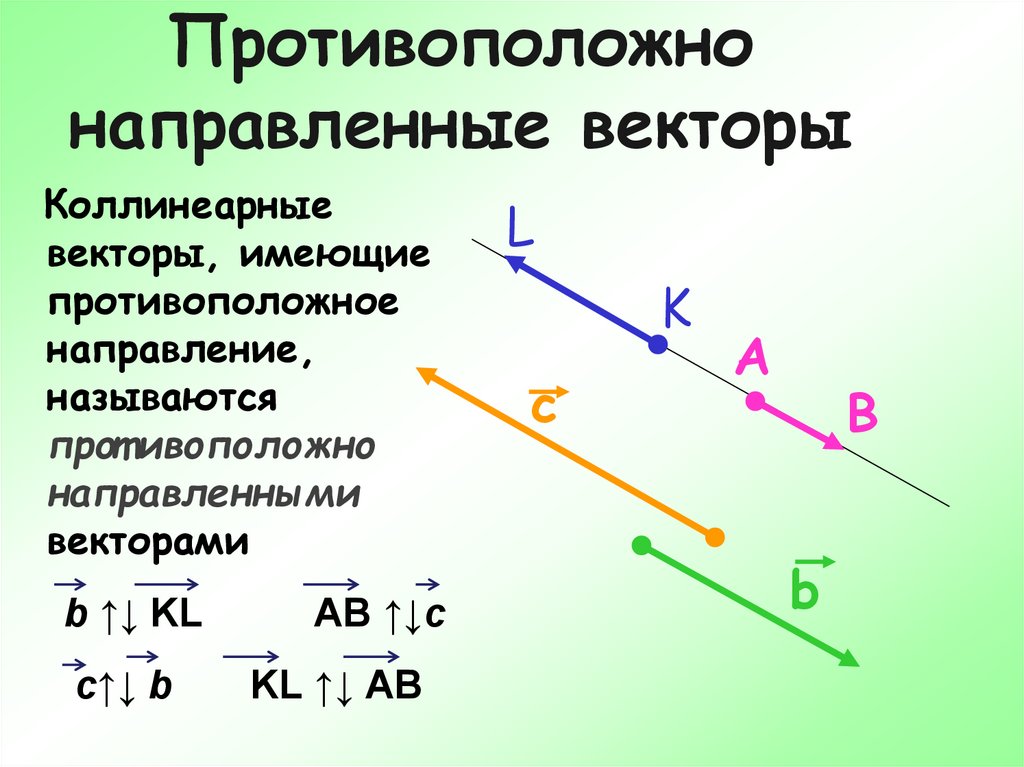
Задание: найдите равные векторы.
В
a
2
a
С
О
А
1
b
=
b
D
АВСD – параллелограмм.
ВA = CD;
AВ = DC;
CВ = DA;
Найдите еще пары равных векторов.
О – точка пересечения диагоналей.
AD = BC.
22. Откладывание вектора от данной точки
• От любой точки можно отложить вектор, равныйданному вектору, и притом только один.
N
В
а
М
А
M p
N’
p II AB
MN = AB
MN’ = AB
p
MN = a
23. Упражнение
На рисунке 1 изображён параллелепипедABCDA B C D
Точки М и К – середины рёбер В С и А D .
Укажите все пары:
1
1
1
1.
1
1
1
1
А) сонаправленных векторов
Б) противоположно направленных векторов
В) равных векторов.
(1)
С1
М
В1
К
D1
А1
В
А
С
D
25. Ответы.
• А)KD и MC ,BC и B C , A D и BC ,AD и BC
1
1
1
1
1
1
1
1.
• Б)DC и AB , AD и BC , AD и B C ,
AD и A D
1
1
1
1.
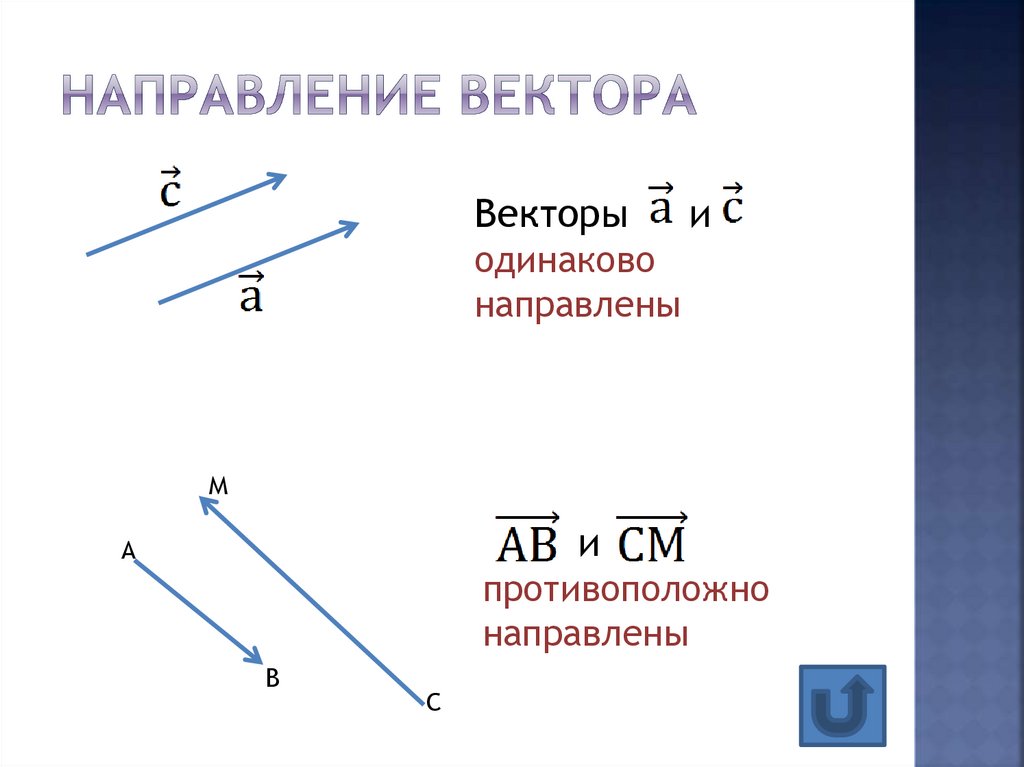
• В)DK и MC , AB и CD , AB и AC , B C и BC ,
AD и B C
1
1
1.
1
1
26. Задача 1
Какие из векторов,
изображенных на
рисунке:
1) коллинеарны;
2) сонаправлены;
3) противоположно
направлены;
4) имеют равные длины?
Отложите эти векторы
от одной точки.
d
c
a
b
Задача 2. В прямоугольнике АВСD АВ=3см, ВС=4см,
точка М – середина стороны АВ. Найдите длины векторов.
АВ = 3
В
4
С
ВC = 4
DС = 3
MА = 1,5
3
M
5
СВ = 4
АС = 5
А
D
МC =
Задача 3. В параллелограмме АВСD диагонали
пересекаются в точке О. Равны ли векторы. Обоснуйте
ответ.
С
В
О
А
AВ = DC;
D
ВС = DА;
AО = ОC;
AС = ВD.
29. Задача 4
• На рисунке изображена равнобедренная трапецияKLMN.
а) Укажите сонаправленные, противоположно
направленные, равные вектора.
б) Укажите векторы, длины которых равны. Равны ли
при этом сами векторы?
L
K
M
N
English Русский Правила
Поиск вектора направления по двум точкам
Все ресурсы предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Найдите вектор направления по двум точкам
Найдите вектор направления если точки A и B равны и , соответственно.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор, точка A является конечной точкой, а точка B — начальной точкой.
Вектор направления можно определить путем вычитания начала из конечной точки.
Сообщить об ошибке
Найти вектор через точки
и .
Возможные ответы:
Правильный ответ:
Объяснение:
Правильный вектор получается вычитанием двух точек: .
Так как вычитание здесь покомпонентное, то оно дается формулой: .
В результате получается вектор .
Вектор тоже правильный, так как он является скалярным множителем вектора, помеченного как правильный. Он находится путем вычитания двух точек в обратном порядке.
Он находится путем вычитания двух точек в обратном порядке.
Сообщить об ошибке
Найдите вектор, у которого есть начальная и конечная точки.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
Найдите вектор направления с начальной точкой и конечной точкой.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
Найти если и .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, идущий из в , вычтите координаты x и y из .
Сообщить об ошибке
Найти если и .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления от к , вычтите координаты x и y из .
Сообщить об ошибке
Найдите вектор направления, который имеет начальную точку в и конечную точку .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
Найдите вектор направления, который имеет начальную точку в и конечную точку в .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
Найдите вектор направления с начальной точкой и конечной точкой .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
Найдите вектор направления, который имеет начальную точку в и конечную точку в .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.
Сообщить об ошибке
← Предыдущий 1 2 Следующий →
Уведомление об авторских правах
Все ресурсы Precalculus
12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept
Вектор направления можно определить по разности положений двух векторов.

Задать вопрос
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 284 раза
$\begingroup$
Я изучаю векторное уравнение, и у меня есть сомнения относительно этого утверждения:
Вектор направления можно определить по разности двух положение векторов.
Определенный вектор направления является исходным вектором направления или преобразованным вектором направления?
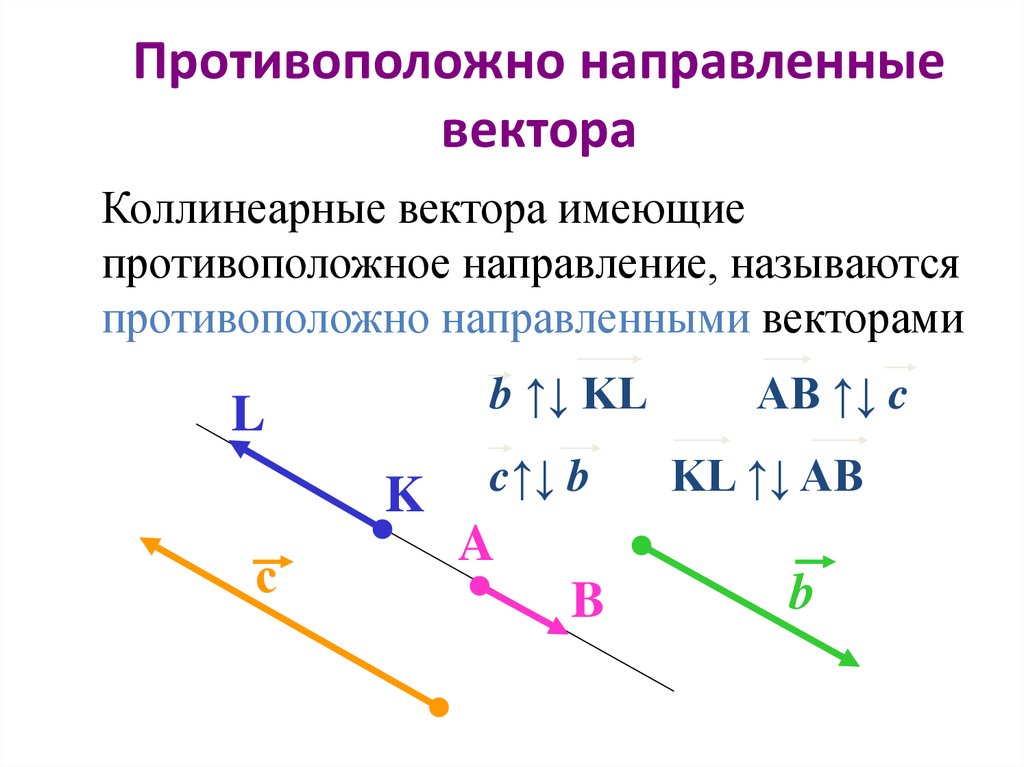
Под «транслированным вектором направления» я подразумеваю: ( на двух изображениях красный сегмент — это вектор направления)
А под «исходным вектором направления» я подразумеваю:
И, что является доказательством этого утверждения?
Приветствуются любые советы, чтобы лучше понять эту тему, заранее спасибо.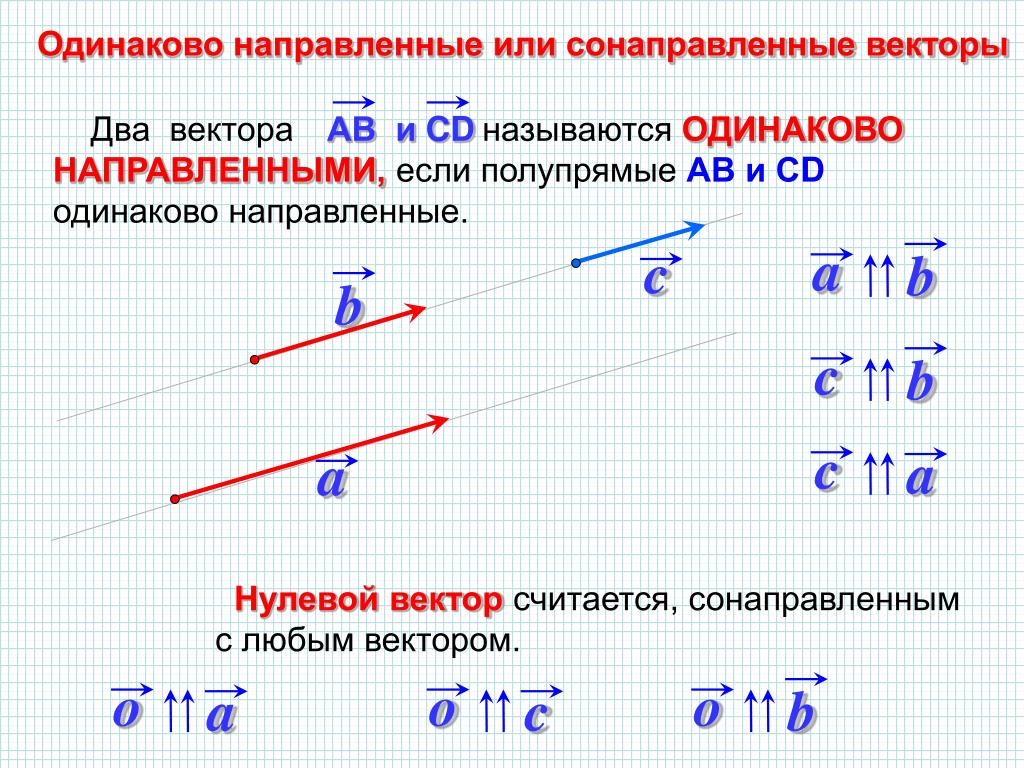
- векторов
$\endgroup$
$\begingroup$
Линия параметризуется, зная некоторые точек на нем (задаются вектором $\vec x_0$ из начала координат) и вектором направления $\vec v$. Тогда вектор из начала координат в произвольную точку прямой можно записать в виде $$\vec x = \vec x_0 + t\vec v \quad\text{для некоторого значения скаляра } t.$$
Обратите внимание, что если вы знаете две точки на прямой, это соответствует таким выражениям для двух различные значения $t$, поэтому вы восстанавливаете вектор направления (или его ненулевое скалярное число), вычитая два вектора: Если $\vec x_1 = \vec x_0 + t\vec v$ и $\vec x_2 = \vec x_0 + s\vec v$ (где $s$ и $t$ — разные скаляры), тогда $$\vec x_2 — \vec x_1 = (\vec x_0 + s\vec v) — (\vec x_0 + t\vec v) = (s-t)\vec v,$$ по желанию.
$\endgroup$
3
$\begingroup$
Вы определяете исходный вектор направления.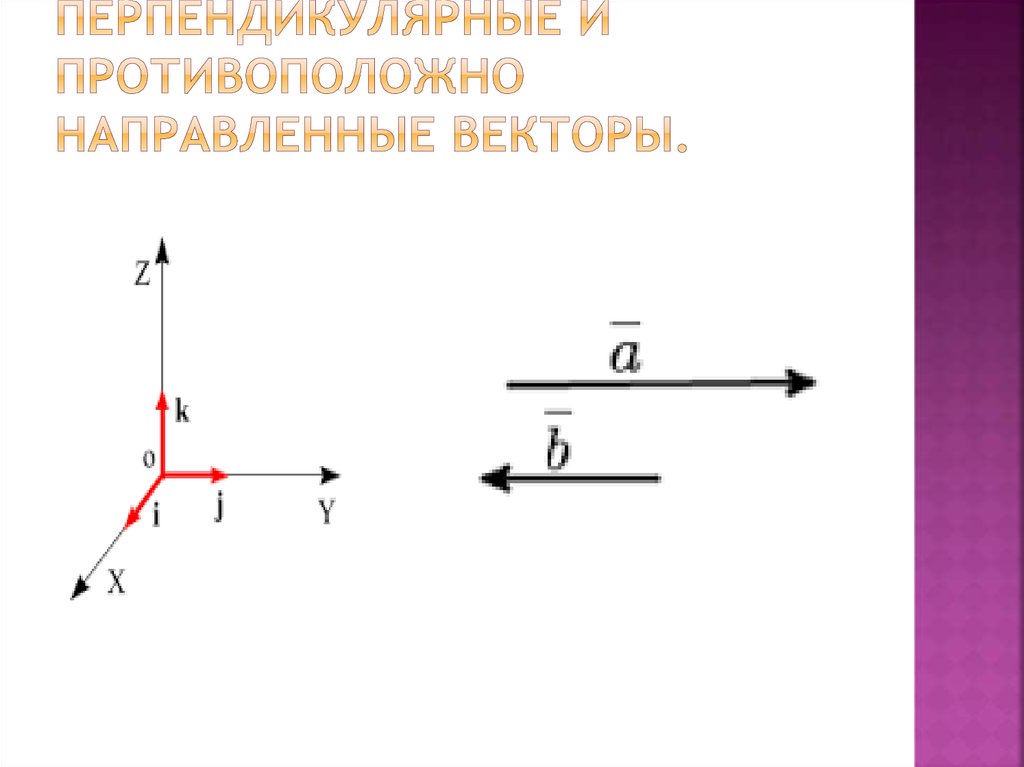


 Компланарны ли векторы:
Компланарны ли векторы: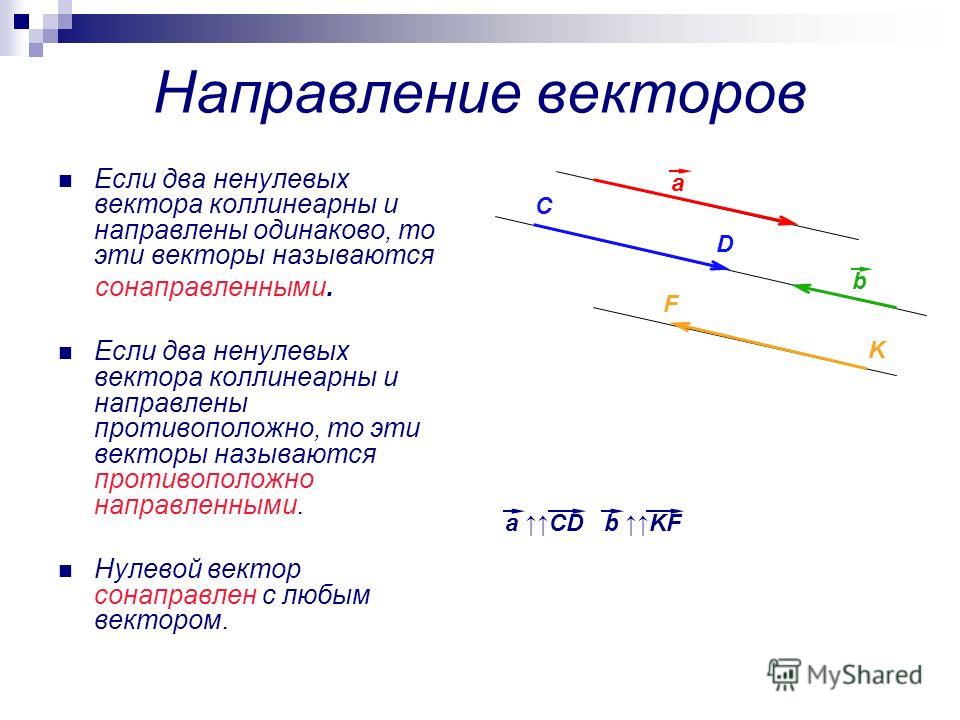
 Задача на доказательство
Задача на доказательство