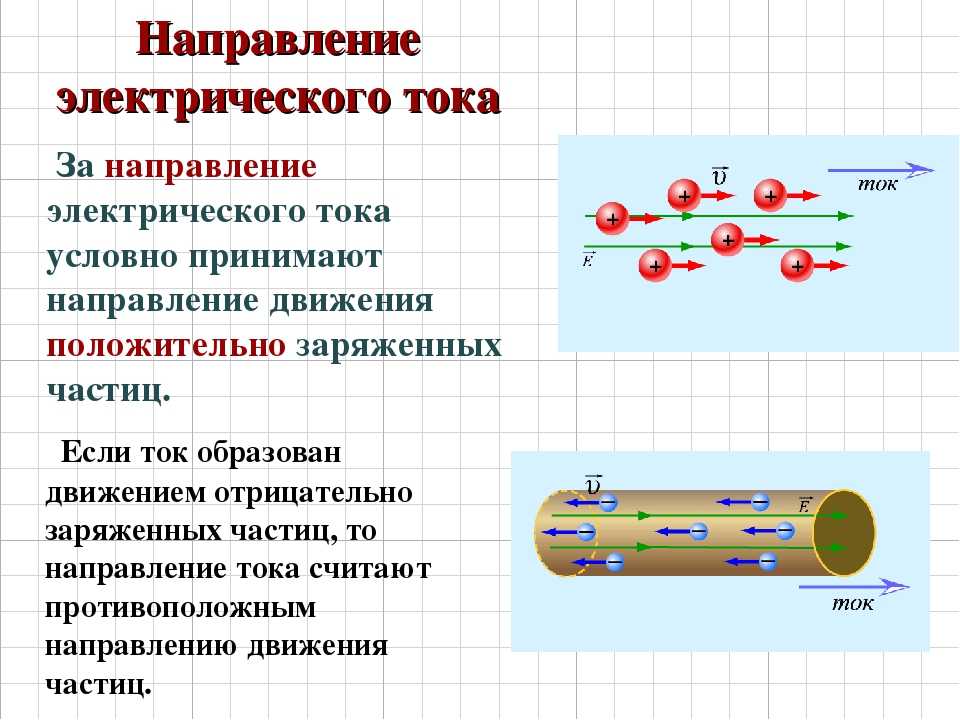
электрический ток | это… Что такое электрический ток?
электри́ческий токнаправленное (упорядоченное) движение заряженных частиц: электронов, ионов и др. Условно за направление электрического тока принимают направление движения положительных зарядов.
* * *
ЭЛЕКТРИЧЕСКИЙ ТОКЭЛЕКТРИ́ЧЕСКИЙ ТОК, направленное (упорядоченное) движение заряженных частиц: электронов (см. ЭЛЕКТРОН (частица)), ионов (см. ИОНЫ) и др. За направление тока принимают направление движения положительно заряженных частиц; если ток создается отрицательно заряженными частицами (например, электронами), то направление тока считают противоположным направлению движения частиц.
Различают электрический ток проводимости, связанный с движением заряженных частиц относительно той или иной среды (т. е. внутри макроскопических тел), и конвекционный ток (см. КОНВЕКЦИОННЫЙ ТОК) — движение макроскопических заряженных тел как целого (например, заряженных капель дождя).
Если в цепи устанавливается электрический ток, то это означает, что через поперечное сечение проводника ( ПРОВОДНИКИ) все время переносится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной характеристикой тока, называемой силой тока (см. СИЛА ТОКА). Сила тока равна отношению величины заряда, переносимого через поперечное сечение проводника за определенный интервал времени, к продолжительности этого интервала. Если сила тока и его направление со временем не меняется, то ток называют постоянным током (см. ПОСТОЯННЫЙ ТОК).
ПРОВОДНИКИ) все время переносится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной характеристикой тока, называемой силой тока (см. СИЛА ТОКА). Сила тока равна отношению величины заряда, переносимого через поперечное сечение проводника за определенный интервал времени, к продолжительности этого интервала. Если сила тока и его направление со временем не меняется, то ток называют постоянным током (см. ПОСТОЯННЫЙ ТОК).
Для возникновения и существования электрического тока необходимо наличие свободных положительно или отрицательно заряженных частиц, не связанных в единую электрически нейтральную систему, и силы, создающей и поддерживающей их упорядоченное движение. Обычно силой, вызывающей такое движение, является сила со стороны электрического поля внутри проводника, которая определяется электрическим напряжением (
Важнейшей характеристикой проводника является зависимость силы тока от напряжения — вольт-амперная характеристика (см.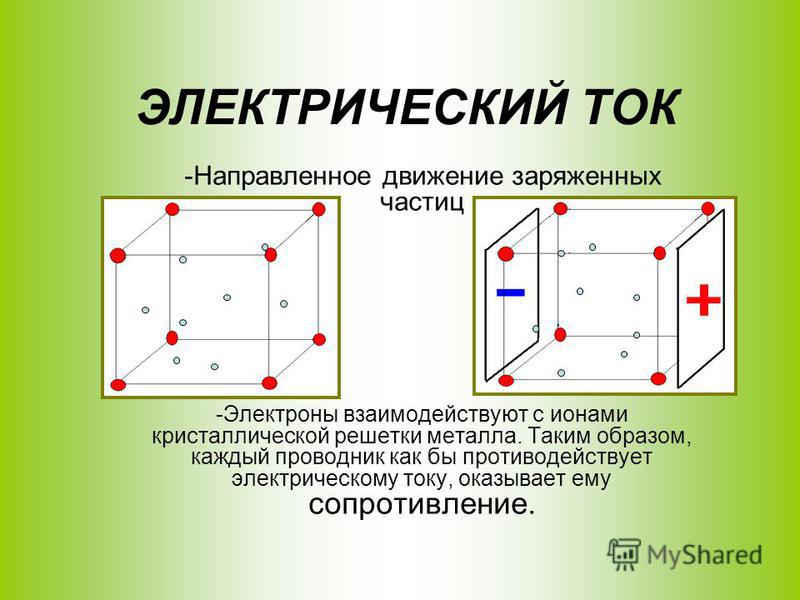 ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА). Она имеет простейший вид для металлических проводников и электролитов: сила тока прямо пропорциональна напряжению (Ома закон (см. ОМА ЗАКОН)).
ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА). Она имеет простейший вид для металлических проводников и электролитов: сила тока прямо пропорциональна напряжению (Ома закон (см. ОМА ЗАКОН)).
Протекая по веществу, электрический ток может оказывать магнитное, тепловое, химическое воздействие. Магнитное действие заключается в возникновении магнитного поля, это действие является всеобщим, проявляется у всех без исключения проводников. Тепловое действие электрического тока заключается в нагреве вещества, через которое протекает ток (исключение — сверхпроводники (
Максвеллом введено понятие полного тока, который, в соответствии с его теорией всегда замкнут: на концах проводника обрывается лишь ток проводимости, а в диэлектрике ( ДИЭЛЕКТРИКИ) (вакууме) между концами проводника имеется ток смещения (см. ТОК СМЕЩЕНИЯ), который замыкает ток проводимости. Поэтому плотность полного электрического тока jполн равна сумме плотности тока проводимости j и плотности тока смещения jсм, и определяет создаваемое им магнитное поле.
ДИЭЛЕКТРИКИ) (вакууме) между концами проводника имеется ток смещения (см. ТОК СМЕЩЕНИЯ), который замыкает ток проводимости. Поэтому плотность полного электрического тока jполн равна сумме плотности тока проводимости j и плотности тока смещения jсм, и определяет создаваемое им магнитное поле.
Jполн = j + ?D/?t
Способность веществ проводить электрический ток очень сильно различается для разных материалов и характеризуется электропроводностью ( В электролитах (
В электролитах (
Газы из нейтральных молекул являются диэлектриками. Электрический ток проводят лишь ионизованные газы — плазма (см. ПЛАЗМА). Носителями тока в плазме служат положительные и отрицательные ионы (как в электролитах) и свободные электроны (как в металлах).
определение, краткая характеристика, физические свойства и использование
Что собой представляет направленное движение заряженных частиц? Для многих это непонятная сфера, но на самом деле все очень просто. Так, когда говорят про направленное движение заряженных частиц, то подразумевают ток. Давайте разберемся в его основных характеристиках и формулировках, а также рассмотрим вопросы безопасности при работе с ним.
Общая информация
Начать следует с определения. Под электрическим током всегда подразумевается упорядоченное (направленное) движение заряженных частиц, что осуществляется под действием электрического поля. Какие именно объекты могут рассматриваться в данном случае? Под частицами подразумевают электроны, ионы, протоны, дырки. Важно также знать, что собой являет сила тока. Так обозначается количество заряженных частиц, которые протекают через поперечное сечение проводника за единицу времени.
Какие именно объекты могут рассматриваться в данном случае? Под частицами подразумевают электроны, ионы, протоны, дырки. Важно также знать, что собой являет сила тока. Так обозначается количество заряженных частиц, которые протекают через поперечное сечение проводника за единицу времени.
Сановник – это влиятельная персона в масштабах государства
Один человек никогда не сможет направлять развитие государства. И даже если публике демонстрируют…
Природа явления
Все физические вещества состоят из молекул, которые формируются из атомов. Они также не являются конечным материалом, потому что имеют в себе элементы (ядро и вращающиеся вокруг него электроны). Все химические реакции сопровождаются движением частиц. Например, при участии электронов одни атомы будут испытывать их недостаток, а другие – избыток. В таком случае вещества обладают разноименными зарядами. Если произойдет их контакт, то электроны из одного будут стремиться перейти в другое.
Такая физическая природа элементарных частиц объясняет суть электрического тока. Это направленное движение заряженных частиц будет происходить до тех пор, пока не произойдет выравнивание значений. При этом реакция изменений является цепной. Иными словами, вместо ушедшего электрона на его место приходит другой. Для замены используются частицы соседнего атома. Но и на этом цепочка не заканчивается. К крайнему атому также может прийти электрон, например, от отрицательного полюса источника протекающего тока.
Это направленное движение заряженных частиц будет происходить до тех пор, пока не произойдет выравнивание значений. При этом реакция изменений является цепной. Иными словами, вместо ушедшего электрона на его место приходит другой. Для замены используются частицы соседнего атома. Но и на этом цепочка не заканчивается. К крайнему атому также может прийти электрон, например, от отрицательного полюса источника протекающего тока.
Кордегардия — это помещение для караула: краткое описание и…
Большинству жителей Северной столицы известно здание кордегардии у Петербургской заставы. Однако…
В качестве примера такой ситуации можно привести батарейку. С отрицательной части проводника электроны перемещаются на положительный полюс источника. Когда все частицы в отрицательно зараженном компоненте заканчиваются, то ток прекращается. В таком случае говорят, что батарейка «села». Какова скорость направленного движения заряженных частиц, перемещающихся таким образом? Дать ответ на этот вопрос не так легко, как может показаться на первый взгляд.
Роль напряжения
Для чего используется данное понятие? Напряжением называют характеристику электрического поля, которая является разностью потенциалов двух точек, что находятся в нем внутри. Многим это может показаться не очень понятным. Когда речь заходит про направленное (упорядоченное) движение заряженных частиц, то разбираться в напряжении нужно.
Восход и заход Солнца. Время восхода и захода Солнца
Восход и заход Солнца — ежедневные явления, которыми можно наслаждаться вечно. Воспринимая как…
Представим, что у нас есть простейший проводник. Таковым может быть проволока, сделанная из металла, например, меди или алюминия. В нашем случае это не столь важно. Масса электрона составляет 9,10938215(45)×10-31кг. Это означает, что он является вполне материальным. Но ведь металл проводника твердый. Как же в таком случае по нему могут протекать электроны?
Почему в металлических изделиях может быть ток
Давайте обратимся к основам химии, которые каждый из нас имел возможность изучать в школе. Если число электронов равно в веществе количеству протонов, то обеспечивается нейтральность элемента. Основываясь на периодическом законе Менделеева определяется то, с каким веществом приходится иметь дело. Это зависит от количества протонов и нейтронов. Нельзя обойти вниманием и большую разницу между массами ядра и электронов. Если их убрать, то вес атома практически не измениться.
Если число электронов равно в веществе количеству протонов, то обеспечивается нейтральность элемента. Основываясь на периодическом законе Менделеева определяется то, с каким веществом приходится иметь дело. Это зависит от количества протонов и нейтронов. Нельзя обойти вниманием и большую разницу между массами ядра и электронов. Если их убрать, то вес атома практически не измениться.
К примеру, масса протона примерно в 1836 больше, нежели значение электрона. Но эти микроскопические частицы очень важны, ведь они могут легко покидать одни атомы и присоединяться к другим. При этом уменьшение или увеличение их числа приводит к изменению заряда атома. Если рассматривать отдельно взятый атом, то у него количество электронов всегда будет переменным. Они постоянно его покидают и возвращаются обратно. Это происходит вследствие теплового движения и потери энергии.
Химическая специфика физического явления
Когда происходит направленное движение электрически заряженных частиц, то не теряется ли атомарная масса? Не меняется ли состав проводника? Это очень важное заблуждение, которое сбивает с толку многих. Ответ в этом случае только отрицательный. Связано это с тем, что химические элементы определяются не своей атомарной массой, а количеством протонов, которые есть в ядре. Наличие или отсутствие электронов/нейтронов в этом случае роли не играет. На практике это выглядит таким образом:
Ответ в этом случае только отрицательный. Связано это с тем, что химические элементы определяются не своей атомарной массой, а количеством протонов, которые есть в ядре. Наличие или отсутствие электронов/нейтронов в этом случае роли не играет. На практике это выглядит таким образом:
- Добавляем или убавляем электроны. Получается ион.
- Добавляем или убавляем нейтроны. Получается изотоп.
Химический элемент при этом не меняется. Но с протонами ситуация другая. Если он всего один, значит, перед нами водород. Два протона – и речь идет уже о гелии. Три частицы – это литий. И так далее. Кого заинтересовало продолжение, тот может посмотреть таблицу Менделеева. Запомните: хоть тысячу раз ток будут пропускать через проводник, его химический состав меняться не будет. Но возможно иное.
Электролиты и другие интересные моменты
Особенность электролитов состоит в том, что меняется именно их химический состав. Тогда под воздействием тока из раствора выделяются элементы электролита. Когда их потенциал исчерпается, направленное движение заряженных частиц прекратится. Такая ситуация связана с тем, что носителями зарядов в электролитах являются ионы.
Когда их потенциал исчерпается, направленное движение заряженных частиц прекратится. Такая ситуация связана с тем, что носителями зарядов в электролитах являются ионы.
Восход и заход Солнца. Время восхода и захода Солнца
Восход и заход Солнца — ежедневные явления, которыми можно наслаждаться вечно. Воспринимая как…
Кроме того, встречаются химические элементы вообще без электронов. В качестве примера можно привести следующее:
- Атомарный космический водород.
- Все вещества, пребывающие в состоянии плазмы.
- Газы в верхних слоях атмосферы (не только Земли, но и других планет, где есть массы воздуха).
- Содержимое ускорителей и коллайдеров.
Также следует отметить, что под действием электрического тока некоторые химические вещества могут буквально рассыпаться. В качестве известного примера можно назвать плавкий предохранитель. Как это выглядит на микроуровне? Движущиеся электроны расталкивают атомы на своем пути. Если ток очень сильный, то кристаллическая решетка проводника не выдерживает и разрушается, а вещество расплавляется.
Возвращаемся к скорости
Ранее этот момент поверхностно был затронут. Теперь давайте уделим ему более пристальное внимание. Следует отметить, что понятия скорости направленного движения заряженных частиц в виде электрического тока не существует. Это связано с тем, что переплетаются разные величины. Так, по проводнику распространяется электрическое поле со скоростью, которая близка к движению света, то есть около 300 000 километров в секунду.
Под его воздействием начинают движение все электроны. Но их скорость очень мала. Она составляет примерно 0,007 миллиметров в секунду. При этом они еще и хаотически мечутся в тепловом движении. В случае с протонами и нейтронами ситуация иная. Они слишком крупные, чтобы с ними происходили такие же события. Как правило, говорить об их скорости, как близкой к значению света, не приходится.
Физические параметры
Теперь давайте рассмотрим, что собой представляет движение заряженных частиц в электрическом поле с физической точки зрения. Для этого представим, что у нас есть картонная коробка, в которой помещается 12 бутылок газированного напитка. При этом есть попытка поместить туда еще одну емкость. Предположим, это удалось. Но коробка еле выдержала. При попытке засунуть еще одну бутылку она разрывается, а все емкости вываливаются.
Для этого представим, что у нас есть картонная коробка, в которой помещается 12 бутылок газированного напитка. При этом есть попытка поместить туда еще одну емкость. Предположим, это удалось. Но коробка еле выдержала. При попытке засунуть еще одну бутылку она разрывается, а все емкости вываливаются.
Рассматриваемую коробку можно сравнить с поперечным сечением проводника. Чем этот параметр выше (толще провод), тем большую силу тока может обеспечить. Это определяет то, какой объем может иметь направленное движение заряженных частиц. В нашем случае коробка, в которой находится от одной до двенадцати бутылок, может спокойно выполнять свое прямое предназначение (не разорвется). По аналогии можно сказать, что проводник не сгорит.
Если превысить обозначенную величину, то объект выйдет из строя. В случае с проводником вступит в действие сопротивление. Очень хорошо описывает направленное движение электрически заряженных частиц закон Ома.
Взаимосвязь разных физических параметров
На коробку из нашего примера можно поставить еще одну. В таком случае на единице площади можно будет разместить уже не 12, а целых 24 бутылки. Добавляем еще одну – и их уже тридцать шесть. Одна из коробок может рассматриваться в качестве физической единицы, аналогичной напряжению тока.
В таком случае на единице площади можно будет разместить уже не 12, а целых 24 бутылки. Добавляем еще одну – и их уже тридцать шесть. Одна из коробок может рассматриваться в качестве физической единицы, аналогичной напряжению тока.
Чем она шире (при этом уменьшается сопротивление), тем больше количество бутылок (которые в нашем примере заменяют силу тока) можно разместить. Увеличивая штабель коробок, можно размещать на единице площади дополнительные емкости. В таком случае растет мощность. При этом не разрушается коробка (проводник). Вот что вкратце выходит по этой аналогии:
- Общее количество бутылок увеличивает мощность.
- Число емкостей в коробке отображает силу тока.
- Количество ящиков в высоту позволяет судить о напряжении.
- Ширина коробки дает представление о сопротивлении.
Возможные опасности
Мы уже разобрали, что направленное движение заряженных частиц называется током. Следует отметить, что данное явление может быть опасным для здоровья и даже жизни человека. Вот краткий перечень свойств электрического тока:
Вот краткий перечень свойств электрического тока:
- Обеспечивает нагревание проводника, по которому он протекает. Если бытовая электрическая сеть перегружается, то изоляция будет постепенно обугливаться и осыпаться. Вследствие этого возникает вероятность короткого замыкания, которое является очень опасным.
- Электрический ток, когда он протекает по бытовым приборам и проводам, встречает сопротивление элементов, формирующих материалы. Поэтому он выбирает путь, у которого значение этого параметра является минимальным.
- Если произошло короткое замыкание, то сила тока резко растет. При этом выделяется существенное количество тепла. Оно может расплавить металл.
- Короткое замыкание может произойти из-за попадания влаги. В рассмотренных ранее случаях загораются расположенные рядом предметы, но в этом варианте всегда страдают люди.
- Удар электричеством несет в себе существенную опасность. Вполне вероятен даже смертельный исход. Когда электрический ток протекает через организм человека, то сильно уменьшается сопротивление тканей.
 Они начинают нагреваться. При этом разрушаются клетки и отмирают нервные окончания.
Они начинают нагреваться. При этом разрушаются клетки и отмирают нервные окончания.
Вопросы безопасности
Чтобы избежать воздействия электрического тока, необходимо использовать специальные средства защиты. Работу следует вести в резиновых перчатках с использованием коврика из этого же материала, разрядных штанг, а также устройств заземления рабочих мест и аппаратуры.
Автоматические выключатели с различной защитой показали себя хорошо в качестве устройства, которое способно сохранить жизнь человека.
Также не следует забывать о элементарной технике безопасности при работе. Если возникло возгорание с участием электрооборудования, можно использовать только углекислотные и порошковые огнетушители. Вторые показывают в борьбе с огнем лучший результат, но аппаратуру, засыпанную пылью, не всегда можно восстановить.
Заключение
На понятных каждому читателю примерах мы выяснили, что упорядоченное направленное движение заряженных частиц называется электрическим током. Это очень интересное явление, важное с позиций как физики, так и химии. Электрический ток является неутомимым помощником человека. Однако обращаться с ним нужно осторожно. В статье рассмотрены вопросы безопасности, на которые следует обращать внимание, если нет желания погибнуть.
Это очень интересное явление, важное с позиций как физики, так и химии. Электрический ток является неутомимым помощником человека. Однако обращаться с ним нужно осторожно. В статье рассмотрены вопросы безопасности, на которые следует обращать внимание, если нет желания погибнуть.
15.3: Движение заряженных частиц — Бесплатные тексты по физике
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 32836
- Дэвид Дж. Рэймонд
- Технологический институт Нью-Мексико через The New Mexico Tech Press
Теперь рассмотрим некоторые примеры движения заряженных частиц под действием электрического и магнитного полей.
Частица в постоянном электрическом поле
Предположим, что частица с зарядом q подвергается воздействию постоянного электрического поля \(\mathrm{E}_{\mathrm{x}}\) в направлении \(x\). Компонент \(x\) силы, действующей на частицу, равен \(\mathrm{F}_{\mathrm{x}}=\mathrm{q} \mathrm{E}_{\mathrm{x}}\ ). Следовательно, согласно второму закону Ньютона ускорение в направлении \(x\) равно \(a_{x}=F_{x}/m=q E_{x}/m\), где \(m\) — масса частица. Поведение частицы такое же, как если бы она находилась в постоянном гравитационном поле, равном \(\mathrm{qE}_{\mathrm{x}} / \mathrm{m}\).
Частица в консервативном электрическом поле
Если \(\partial \mathbf{A} / \partial \mathrm{t}=0\), то электрическая сила, действующая на заряженную частицу, равна
\[\mathbf{F} _{\text {электрический}}=-q\left(\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi} {\ partial z} \ right), \ quad \ frac {\ partial \ mathbf {A}} {\ partial t} = 0 \ label {15,7} \]
Эта сила консервативна, с потенциальной энергией \(\ mathrm {U}=\mathrm{q} \phi . \). Вспоминая, что полная энергия \(\mathrm{E}=\mathrm{K}+\mathrm{U},\) частицы под действием консервативной силы остается постоянной во времени, мы можем заключить, что изменение в кинетической энергии с положением частицы как раз минус изменение потенциальной энергии: \(\Delta \mathrm{K}=-\Delta \mathrm{U}\). Обратите внимание, в частности, что если частица возвращается в исходное положение, изменение потенциальной энергии равно нулю, а кинетическая энергия восстанавливает свое начальное значение.
\). Вспоминая, что полная энергия \(\mathrm{E}=\mathrm{K}+\mathrm{U},\) частицы под действием консервативной силы остается постоянной во времени, мы можем заключить, что изменение в кинетической энергии с положением частицы как раз минус изменение потенциальной энергии: \(\Delta \mathrm{K}=-\Delta \mathrm{U}\). Обратите внимание, в частности, что если частица возвращается в исходное положение, изменение потенциальной энергии равно нулю, а кинетическая энергия восстанавливает свое начальное значение.
Если \(\partial \mathbf{A} / \partial \mathrm{t} \neq 0\), то есть вероятность, что электрическая сила не является консервативной. Напомним, что магнитное поле получается из A . Интересно, что необходимым и достаточным критерием неконсервативной электрической силы является изменение магнитного поля со временем. Этот результат был впервые получен экспериментально английским физиком Майклом Фарадеем в 1831 году и почти в то же время американским физиком Джозефом Генри. Далее в этой главе он будет рассмотрен подробнее.
Далее в этой главе он будет рассмотрен подробнее.
Крутящий момент на электрическом диполе
Теперь представим себе «гантель», состоящую из положительных и отрицательных зарядов одинаковой величины q, разделенных расстоянием d, как показано на рис. 15.1. Если имеется однородное электрическое поле E , положительный заряд испытывает силу \(\text { qE }\), а отрицательный заряд испытывает силу \(\text {-qE }\). Таким образом, результирующая сила, действующая на гантель, равна нулю.
Рисунок 15.1: Эскиз определения электрического диполя. Два заряда q и -q соединены незаряженным стержнем длины \(d\). Векторы \(\text { d / } 2\) и \(\text {-d / } 2\) задают положения двух зарядов относительно центральной точки между ними. Две силы обусловлены электрическим полем E.Крутящий момент, действующий на гантель, не равен нулю. Полный крутящий момент, действующий вокруг начала координат на рисунке 15.1, представляет собой сумму крутящих моментов, действующих на два заряда:
\[\boldsymbol{\tau}=(-q)(-\mathbf{d} / 2) \times \ mathbf{E}+(q)(\mathbf{d} / 2) \times(\mathbf{E})=q \mathbf{d} \times \mathbf{E}\label{15.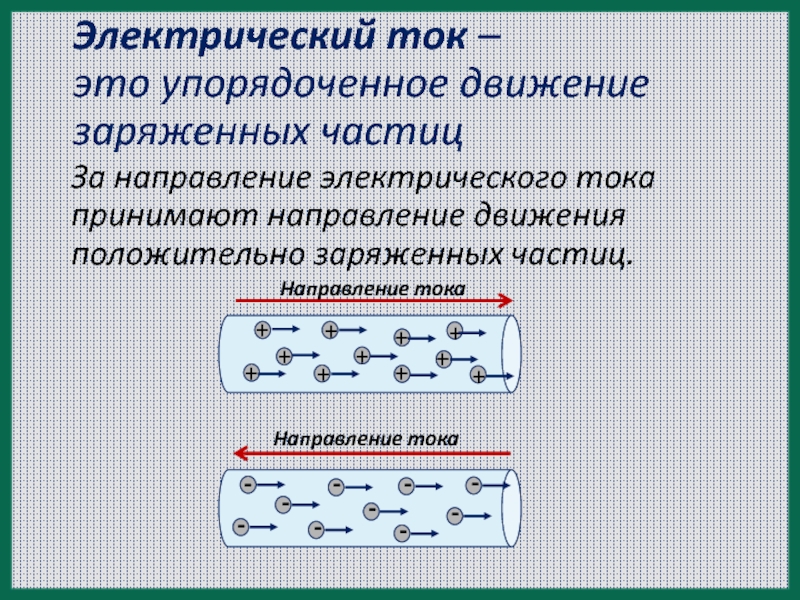 8}\]
8}\]
вектор d можно рассматривать как имеющий длину, равную расстоянию между двумя зарядами, и направление, идущее от отрицательного заряда к положительному.
Величина \(\mathbf{p}=q \mathbf{d}\) называется электрическим дипольным моментом . (Не путайте с импульсом!) Крутящий момент равен
\[\boldsymbol{\tau}=\mathbf{p} \times \mathbf{E}\label{15.9}\]
Это показывает, что крутящий момент зависит от дипольного момента или произведения заряда и расстояния. Таким образом, уменьшение расстояния вдвое и удвоение заряда приводит к тому же самому дипольному моменту.
Тенденция крутящего момента состоит в том, чтобы повернуть диполь так, чтобы дипольный момент p параллельно электрическому полю E . Величина крутящего момента определяется как
\[\tau=p E \sin (\theta)\label{15.10}\]
, где угол θ определен на рисунке 15.1 и \(p=|\ mathbf{p}|\) — величина электрического дипольного момента.
Потенциальная энергия диполя рассчитывается следующим образом: Скалярный потенциал, связанный с электрическим полем, равен \(\phi=-E z\), где E — величина поля, предполагаемая точкой в направлении +z. Таким образом, потенциальная энергия одиночной частицы с зарядом q равна \(U=q \phi=-\mathrm{q} \mathrm{Ez}\). Полная потенциальная энергия диполя равна сумме потенциальных энергий отдельных зарядов:
\[\begin{align}
U &=(+q)\left(-E z_{+}\right)+(-q)\left(-E z_{-}\right)=-q E \left(z_{+}-z_{-}\right) \\
&=-q E d \cos (\theta)=-p E \cos (\theta)=-\mathbf{p} \cdot \ mathbf{E}
\end{aligned}\label{15.11}\]
где z + и z — — позиции z положительных и отрицательных зарядов. Приравнивание z + — z — к \(\mathrm{d} \cos (\theta)\) можно проверить, исследуя геометрию рисунка 15.1.
Тенденция электрического поля выравнивать дипольный момент с самим собой подтверждается формулой потенциальной энергии.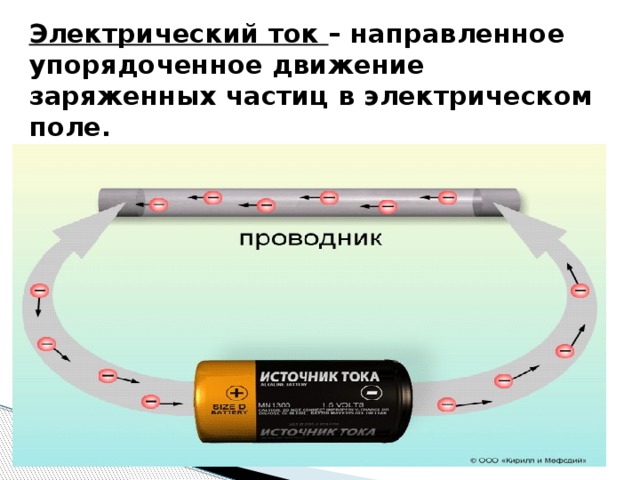 Потенциальная энергия самая низкая, когда дипольный момент выровнен с полем, и самая высокая, когда они выровнены в противоположных направлениях.
Потенциальная энергия самая низкая, когда дипольный момент выровнен с полем, и самая высокая, когда они выровнены в противоположных направлениях.
Частица в постоянном магнитном поле
Магнитная сила, действующая на частицу с зарядом \(q\), движущуюся со скоростью v , равна \(\mathbf{F}_{\text {магнитный}}=\mathrm{q} \mathbf{v} \times \mathbf{B}\), где \(B\) — магнитное поле. Магнитная сила направлена перпендикулярно как магнитному полю, так и скорости частицы. Из-за последнего момента магнитное поле не совершает никакой работы над частицей. Таким образом, сама по себе магнитная сила не может изменить величину скорости частицы, хотя и может изменить ее направление.
Рис. 15.2: Спиралевидное движение заряженной частицы в направлении магнитного поля. Он состоит из кругового движения вокруг вектора поля и переноса вдоль поля. Если магнитное поле постоянно, величина магнитной силы, действующей на частицу, также постоянна и имеет значение \(F_{\text {магнитный}}=\operatorname{gvB} \sin (\theta)\), где \ (v=|\mathbf{v}|, \mathrm{B}=|\mathbf{B}|\), а \(\theta\) — угол между v и B . Если начальная скорость перпендикулярна магнитному полю, то \(\sin (\theta)=1\) и сила равна \(\mathrm{F}_{\text{магнитный}}=\mathrm{qvB} \). Частица просто движется по кругу с магнитной силой, направленной к центру круга. Эта сила, деленная на массу m, должна равняться центростремительному ускорению частицы: } / \mathrm{m}=\mathrm{qvB} / \mathrm{m}\) в нерелятивистском случае, где \(R\) — радиус окружности. Решение для \(R\) дает
Если начальная скорость перпендикулярна магнитному полю, то \(\sin (\theta)=1\) и сила равна \(\mathrm{F}_{\text{магнитный}}=\mathrm{qvB} \). Частица просто движется по кругу с магнитной силой, направленной к центру круга. Эта сила, деленная на массу m, должна равняться центростремительному ускорению частицы: } / \mathrm{m}=\mathrm{qvB} / \mathrm{m}\) в нерелятивистском случае, где \(R\) — радиус окружности. Решение для \(R\) дает
\[R=m v /(q B)\label{15.12}\]
Угловая частота вращения
\[\omega=v / R=q B / m \quad \text { (циклотронная частота ). }\label{15.13}\]
Обратите внимание, что эта частота является константой, не зависящей от радиуса орбиты частицы или ее скорости. Это называется циклотронной частотой.
Если начальная скорость не перпендикулярна магнитному полю, то частица по-прежнему имеет круговую составляющую движения в плоскости, нормальной к полю, но также дрейфует с постоянной скоростью в направлении поля. Конечным результатом является спиральное движение в направлении магнитного поля, как показано на рис. 15.2. Радиус окружности в этом случае равен \(\mathrm{R}=\mathrm{mv}_{\mathrm{p}} /(\mathrm{qB})\), где \(\mathrm{v}_ {\mathrm{p}}\) — составляющая \(v\), перпендикулярная магнитному полю.
15.2. Радиус окружности в этом случае равен \(\mathrm{R}=\mathrm{mv}_{\mathrm{p}} /(\mathrm{qB})\), где \(\mathrm{v}_ {\mathrm{p}}\) — составляющая \(v\), перпендикулярная магнитному полю.
Скрещенные электрические и магнитные поля
Если у нас есть перпендикулярные электрические и магнитные поля, как показано на рис. 15.3, то заряженная частица может двигаться так, что электрические и магнитные силы просто компенсируют друг друга. Согласно уравнению силы Лоренца (15.2.3), условием для этого является \(\mathbf{E}+\mathbf{v} \times \mathbf{B}=0\). Если
 е. полях, перпендикулярных друг другу) заряженная частица может двигаться с постоянной скоростью v с величиной, равной \(v=|E | /|B|\) и направление, перпендикулярное как \(E\), так и \(B\). Это связано с тем, что электрические и магнитные силы, \(F _ {\ text {электрические}} = q \ mathrm {E} \ text {и} F _ {\ text {магнитные}} = q v \ times B \), уравновешивают друг друга. в таком случае.
е. полях, перпендикулярных друг другу) заряженная частица может двигаться с постоянной скоростью v с величиной, равной \(v=|E | /|B|\) и направление, перпендикулярное как \(E\), так и \(B\). Это связано с тем, что электрические и магнитные силы, \(F _ {\ text {электрические}} = q \ mathrm {E} \ text {и} F _ {\ text {магнитные}} = q v \ times B \), уравновешивают друг друга. в таком случае.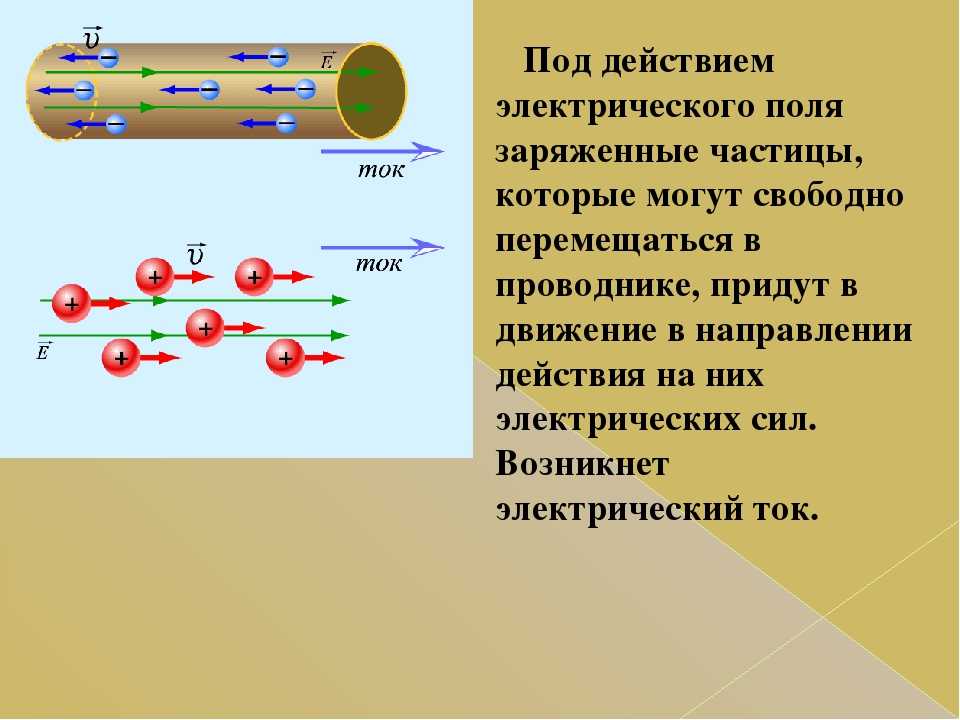 Четырёхпотенциальные точки вдоль оси \(х\).
Четырёхпотенциальные точки вдоль оси \(х\). Этот аргумент показывает, что электрическое поле, воспринимаемое в одной системе отсчета, не обязательно совпадает с электрическим полем, воспринимаемым в другой системе отсчета. На рис. 15.4 показано, почему это так. На левой панели показана ситуация в системе отсчета, движущейся вправо, которая является незаштрихованной рамкой на этом изображении. Заряженная частица неподвижна в этой системе отсчета. Четырехпотенциал является чисто пространственноподобным, не имеющим временной компоненты \(\phi / \mathrm{c} .\). Предполагая, что 
Эта страница под названием 15.3: Charged Particle Motion распространяется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Дэвидом Дж. Рэймондом (The New Mexico Tech Press) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Дж. Рэймонд
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать оглавление
- нет
- Теги
- source@http://kestrel.
 nmt.edu/~raymond/books/radphys/book2/book2.html
nmt.edu/~raymond/books/radphys/book2/book2.html
- source@http://kestrel.
Движение заряженных частиц в магнитных полях
Движение заряженных частиц в магнитных полях
Сравнение движений двух разных частиц в одном магнитное поле
|


 Они начинают нагреваться. При этом разрушаются клетки и отмирают нервные окончания.
Они начинают нагреваться. При этом разрушаются клетки и отмирают нервные окончания.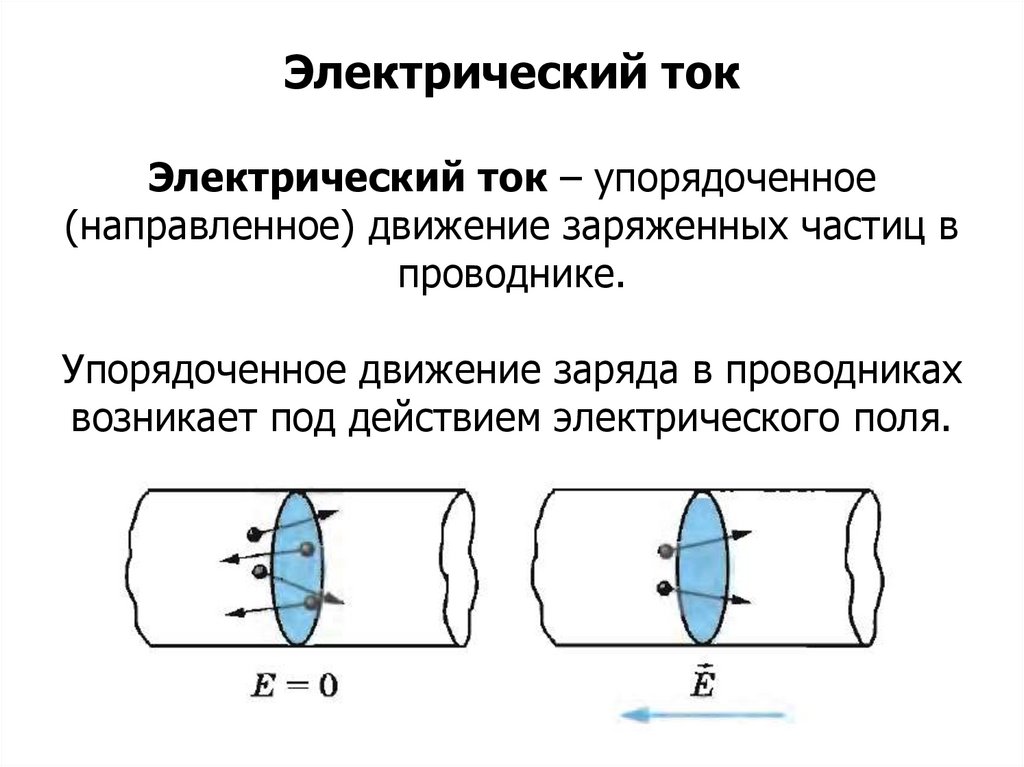 nmt.edu/~raymond/books/radphys/book2/book2.html
nmt.edu/~raymond/books/radphys/book2/book2.html Электрон попадает в однородный магнитный
поле B направлен за пределы страницы, отмечен пунктирными линиями
как показано
Электрон попадает в однородный магнитный
поле B направлен за пределы страницы, отмечен пунктирными линиями
как показано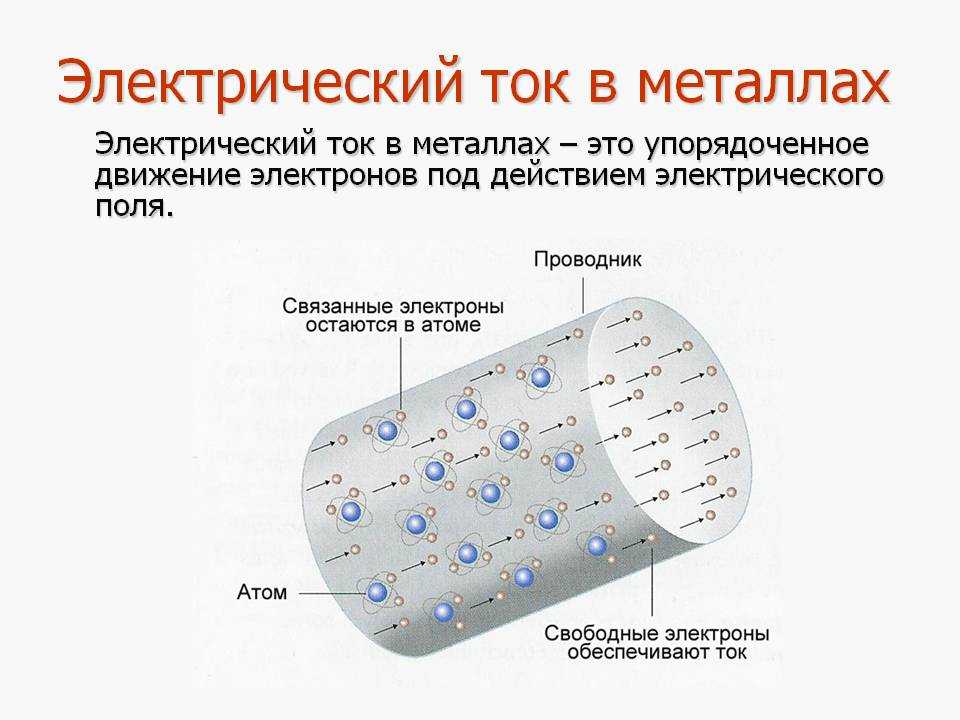 Ион водорода (протон; показан слева как +q) и альфа
частица (два протона плюс два нейтрона; вы можете нарисовать ее) введите
поле с той же скоростью. Предположим, что поле большое
достаточно, чтобы частицы могли совершать полные круговые траектории
внутри поля.
Ион водорода (протон; показан слева как +q) и альфа
частица (два протона плюс два нейтрона; вы можете нарисовать ее) введите
поле с той же скоростью. Предположим, что поле большое
достаточно, чтобы частицы могли совершать полные круговые траектории
внутри поля.