Предложения со словосочетанием ВЕКТОР НАПРАВЛЕНИЯ

Когда же мы формулируем цель позитивно, мы обозначаем вектор направления движения, смотрим вперёд и выстраиваем путь. Судмедэксперт может по характеру раны определить вектор направления травмирующего предмета, положение пострадавшего в момент травмы, а также выяснить возможность причинения ранения собственноручно пострадавшим. Для этого был лишь необходим более точный вектор направления поиска артефактов из текущего положения. Но нет, резко меняется вектор направления опасности. Вот он начинает смещаться в мою сторону. Однако я уже на месте. Как вы скоро увидите – это законы квантовой физики, в которых сознание и вектор направления напрямую связаны с энергетическими затратами.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова плюха (существительное):

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

Проследил за вектором направления интереса и сам впал в ступор. Мечта задаёт вектор направления, без которого не горят глаза и отсутствует желание активно жить и светить в этом мире. Условно говоря, естествознание было призвано решить ряд загадок или так называемых вечных вопросов: о происхождении мира и человека, об уровнях устройства мира, о преобразовании мёртвого в живое и, наоборот, о векторе направления времени, о возможности сверхдальних путешествий в пространстве и т. п. – Создав заклинание «ураган» и придав ему нужный вектор направления, я полетел в сторону пытающегося улизнуть кораблика, поднимая вокруг себя на воде огромные волны. Тем самым, находим вектор направления. Вектор направления луча – зенит. Чувствительный медицинский сканер выявил главный вектор направления развития болезни. Атака не замедлила себя ждать, и первый выпад я пропустил мимо, сделав шаг в сторону, одновременно захватывая и меняя вектор направления силы удара противника. Караван двигался, меняя вектор направления три или четыре раза, чтобы в случае обнаружения не было возможности однозначно вычислить конечную точку маршрута, поэтому его поиск не был задачей тривиальной. По-моему, возрастная психология пытается изучать те изменения, которые происходят в психической реальности, ориентируясь как на главный вектор направления изменения – физическое время жизни человека. Именно от них зависит его мировосприятие, определяющее жизненные ценности, которые в свою очередь задают вектор направления жизни. Но иногда, чтобы сделать первый шаг, ему нужна помощь, толчок, который поможет преодолеть инерционное движение по жизни и перенаправит вектор направления в другую сторону. Это признаки распада политического пространства, социума, идейно-информационной сферы и утрата вектора направления движения. В этих, как вы их назвали, духовных поисках очень важен вектор направления, а у алхимии он был изначально несколько сомнительный. Всего-то и надо было, что убрать из плетения

вектор направления, сделать разряд расфокусированным и определить границы его распространения. Может показаться, что малюсенькие шажочки ничего не меняют, но именно они в итоге формируют вектор направления нашей жизни, и, как следствие, составляют то, что мы называем судьбой. Движения носят фазовый, возвратно-поступательный характер и эти перемещения ограничены вектором направления – слог однонаправленности но. После того как мы вышли из ангара, получили вектор направления для прыжка. Поравнявшись с идущими мне навстречу парнем и девушкой, я на автопилоте делаю шаг-под-шаг, и моё тело, чуть изменив вектор направления, как-то легко обходит молодую парочку. Потребность в новом поколении юристов была вызвана рядом причин: советская модель образования постепенно изжила себя, и по инерции просуществовала 20 лет, юриспруденция того периода была основана на общественно-экономической формации тех времён, тем самым современное российское образование, как и юриспруденция нуждается во внесении изменений и новшеств; уровень правосознания и правой культуры среди граждан уже на протяжении многих лет не имеет определённого вектора направления, большинству гражданского населения свойственна склонность к заблуждению относительно своих прав и обязанностей; правоохранительная система государства также нуждается в пресыщении новыми достойными кадрами, а правоприменительная практика в возвращении к эстетическому и подлинному своему выражению. Для всех остальных надо знать вектор направления. Второе важное условие – вектор направления взгляда. Вы чувствуете? – вектор направления совсем другой. Он не изменял массу, скорость, вектор направления движущегося объекта или другие его характеристики. Органы судебной власти являются самыми активными и ответственными участниками применения законодательных и иных нормативных правовых актов, что обуславливает их роль в определении вектора направления правоприменительной практики. Дочь с претендентом на секунду замерли, осознавая, что манёвр не удался, и сменили вектор направления. В любом случае вектор направлений поисков меняется. – Сила и вектор направления желания Здесь заметно соответствие вектора направления перемены деградации жизни и уменьшение количества свободы. Жизненный статус определяет вектор направления рабочего состояния каждого. Так как в структуре атома всегда присутствует вращение электронов вокруг своей оси, то всегда присутствует вектор направления движения, собственный момент вращения, не связанный с перемещением самой частицы. Накануне засиделась допоздна над теорией вектора направления силы, а потом решила буквально пять минуточек перед сном почитать, всего пару страничек древнеэльфийских сказаний и мифов. Человек уясняет

вектор направления и действует по строгим правилам. Вырвав с него крышку и выворотив само устройство из металлического пола, я присоединил к нему всё тяги, управляющие вектором направления и подачи топлива. Стань «генеральным директором» своих мыслей, задавая им правильный вектор направления, своевременно награждая мозг и предоставляя ему достойный отдых после выполненных задач. Вектор направления сменялся настолько быстро, что я порой не успевал опомниться: «Как это произошло?» Животный страх, часто сохраняет нам жизнь, но в этой ситуации, наоборот, важно не сдрейфить. Вектор направления массажа ноги – вверх: от стопы – к колену, от колена – к паховой области и ягодице. – Не то чтобы сформировал, но он мог всего несколькими словами задать целый вектор направления жизненных принципов. И, если обстоятельства благоприятствуют, то можно задать вектор направления развития определённого сектора экономики или бизнеса на ближайшее время. Стрела судьбы – вектор направления движения. Ему нужно только активировать энергию с накопителей и задать вектор направления силы. Только познав и изучив информацию, можно надеяться на изменения и способ поменять вектор направления.

Векторная Направленность Радиокомпонентов — Back To Music

Vector

В статье собрана и структуирована информация о Векторной Направленнности радиокомпонентов, даны ее определения и свойства, методика определения Векторов проводников и диэлектриков, способы формирования необходимого Направления у компонентов в момент их перехода из жидкого состояния в твердое, рекомендации по использованию радиокомпонентов с известной Векторной Направленностью.

Антон Степичев

---

Векторные свойства направленности радиокомпонентов были обнаружены во время серии экспериментов по формированию направленности в проводниках (припое) и диэлектриках (воске, которым пропитана конденсаторная бумага) [1] и являются развитием и уточнением свойств Линейной Направленности компонентов. Учет векторной направленности позволяет создавать аудиосистемы с принципиально новыми свойствами, такие как — тестовый аудиотракт и активная двухполосная АС с экстраординарной музыкальной ясностью звучания. Ясное звучание музыки снижает процент ошибок во время тестирований, позволяя всесторонне оценивать качество звучания, как отдельных компонентов, так и всей системы в целом.

Определения:

Вектор направленности радиокомпонента — это условный, направленный отрезок прямой, проходящей сквозь тело компонента, начинающийся в определенной точке входа на поверхости компонента и заканчивающийся в определенной точке выхода на противоположной поверхности компонента. Вектор описывает трехмерное направление наилучшего звучания радиокомпонента и выраженность (силу) его направленности.
Векторные потери — ухудшение ясности звучания аудиотракта, связанное с не точным соблюдением векторной направленности его радиокомпонентов.
Векторное поле — направленное (несимметричное, полярное) поле неизвестной природы, формирующее векторную направленность у металлов и диэлектриков в момент их перехода из жидкого состояния в твердое. Наличие Векторного поля выведено гипотетически, только по косвенным признакам.

свойства векторов обнаруженные экспериментально

1. Точное совпадение вектора фабрично изготовленного компонента с его продольной осью – редкий, частный случай. Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено, вектор у произвольно взятого компонента может быть направлен в любую, заранее не предсказуемую сторону, которую можно определить только экспериментально.
2. При прочих равных, коллинеарные и компланарные векторы звучат одинаково, таким образом, в каждом компоненте мы имеем совокупность пар входных и выходных точек касания, с нулевыми векторными потерями.
3. Во всех направлениях, перпендикулярных вектору, направленность у компонента отсутствует, при этом звучание компонента становится усредненным по отношению к его звучанию вдоль и против вектора.
4. Векторы не меняют свою ориентацию относительно геометрической формы радиокомпонентов, ни под действием постоянного электрического тока, ни под действием магнитного поля.
   Установлено, что у старых трансформаторов, кондесаторов, в проводке различных электроприборов, как постоянного, так и переменного тока, других бывших в употреблении радиокомпонентов, десятилетиями проработавших в одинаковых «электро-магнитных условиях», составляющие их проводники и диэлектрики, с точки зрения направленности, остались соединены без какой-либо системы, например: направление выводов трансформаторов не совпадает с направлением их обмоток в 50% случаев, а монтаж проводки никогда не соответствует Электрическим Контурам и содержит в своих цепях, как прямые, так и встречные включения проводников.
5. Механическая обработка поверхности компонентов (пиление, строгание, шлифовка, етс.) вызывает временные коррекции направления и силы вектора. Механическая обработка, при этом, оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонетов. (подробнее)
6. При изгибе или скручивании моножильного провода, металлических пластин и т.п., их вектор изгибается и скручивается точно повторяя искаженную форму компонента, при этом, если затем восстановить форму компонента, направление его вектора через какое-то непродолжительное время так-же полностью восстанавливается.
7. Результирующее направление и сила вектора цепей компонентов и параллельного соединения компонентов определяется по математическим правилам сложения векторов отдельных компонентов, входящих в цепи и соединения.

Определение направления вектора

Определение вектора плоского проводника — направление вектора определяется по его трем ортогональным проекциям на взаимно перпендикулярных поверхностях исследуемого компонента. На поверхности исследуемого проводника (условно — в плоскости, образованной осями Х и Y), например, на поверхности отрезка фольги, определяется воображаемая окружность, щупы тестового аудиотракта устанавливаются в диаметрально противоположных точках на этой воображаемой окружности и замыкают сигнальную цепь тестового тракта. Затем, оставаясь в диаметрально противоположных точках, оба щупа одновременно смещаются вдоль окружности без отрыва от поверхности и во время их перемещения оценивается изменения в звучании тестового тракта. По прошествии каждым из щупов полного круга и их возвращения в свои исходные точки, на поверхности фольги рисуется стрелка проекции «XY» вектора направленности, начало которой определят точка касания выходного щупа тестового тракта, а конец – точка касания входного щупа в тот момент, когда ясность звучания тракта оказывается наилучшей. Затем определяется проекция вектора вдоль оси «Z», то-есть, определяется входная и выходная поверхности тестируемого проводника. Щупы во время тестирования должны касаться поверхностей компонента в точках, расположенных точно друг напротив друга. При последующей переполюсовке щупов в этих точках, оценивается изменения в звучании тестового аудиотракта, по результатам оценки определяются и маркируются входная и выходная поверхности фольги. По полученным двум проекциям мысленно строится результирующий, трехмерный вектор направленности, который используется впоследствии при сборке электрических частей тракта в соответствии со схемой контуров.

Определение вектора проводника круглого сечения — для определения вектора провода, один его конец зажимается между щупами тестового тракта, замыкая собой сигнальную цепь тракта, затем он медленно проворачиваятся на 360 градусов. Во время вращения проводника определяется такое его положение относительно щупов, когда ясность звучания тракта окажется наилучшей. Таким образом определяются входная и выходная точки проекции «XY» вектора одного конца провода. Затем ту же операцию проделывают на другом конце провода. После определения входных и выходных точек на боковых поверхностях концов проводов, определяется продольная направленность с касанием соответствующими щупами тестового тракта найденных, боковых входных и выходных точек проводника. Метить провода удобно загибанием их кончика в нужную сторону, пайка проводов при этом производится касанием найденными боковыми поверхностями в соответствии со схемой контуров, то-есть так, чтобы выходная, боковая поверхность «исходящего» провода соприкасалась с входной боковой поверхностью следующего (по ходу направления контура) проводника в цепи.

Определение вектора диэлектриков — вектор диэлектриков определяется так-же, как и у проводников, но после смачивания его поверхности какой-нибудь токопроводящей жидкостью, например водопроводной водой. (подробнее)

! —Во всех вышеперечисленных методиках во избежание ошибок необходимо учитывать вектор щупов тестового Аудиотракта, это означает, что во время векторного тестирования компонентов, входная боковая поверхность входного щупа должна быть обращена в сторону выходного щупа, а выходная боковая поверхность выходного щупа должна, соответственно, быть обращена в сторону входного щупа.

Формирование вектора с заданным направлением

В домашних условиях Вектор необходимого для тех или иных целей Направления можно сформировать у легкоплавких металлов (свинец, олово, алюминий), а так-же у диэлектриков (восках, смолах, лаках и красках). На данный момент известно, что:

1. Устойчивая, векторная направленность у металлов и диэлектриков формируется в момент их перехода из жидкого состояния в твердое, предположительно — под действием некого, направленного поля, названного мной «Векторным Полем», при этом компонент во время своего перехода из расплавленного состояния в твердое «запоминает» то состояние поля, которое его пересекало (окружало) в данный момент и «помнит» его до тех пор, пока его снова не расплавить.
2. Векторная направленность свойственна всем твердым предметам, как созданных человеком, так и необработанным, природным материалам. Пока остается загадкой, как это необычное свойство предметов проявляет себя вне аудио.
3. У растений вектор направлен в соответствии с изменениями их размеров во время их роста, то-есть — от корней к кроне и от сердцевины к поверхности. Здесь, похоже, отслеживается наличие некой причинно следственной связи, о которой писал в одной из своих статей С.Куниловский [2].
4. У человека (лично у меня) выявлены два сильных источника векторного поля — это руки и точка между бровями (третий глаз). Степень влияния моего поля на формирование вектора предметов варьируется под действием различных, плохо предсказуемых обстоятельств. Что-либо говорить о сознательном и целенаправленном применении тонких полей человека в аудио пока не представляется возможным, точно установлено только то, что человек оказывает ощутимое влияние на звучание конструкции, которую он изготавливает не зависимо от того, хочет он этого, или нет.
5. Векторное поле каждого предмета, как и векторное поле человека, оказывает влияние на формирование направленности у находящихся рядом с ним предметов, которые в этот момент переходят из расплавленного состояния в твердое. Таким образом, можно говорить о наличии тонких, векторных полей разной силы и конфигурации у всех, окружающих нас предметов. Влияние полей человека и полей всех твердых предметов на формирование векторов у затвердевающих жидкостей, пропорционально их текущей силе и обратно пропорционально растоянию между ними.
6. Существует, по крайней мере, один источник векторного поля, влияние которого не зависит от расстояния до какого либо объекта в помещении, включая пол и потолок. Данное поле, в случае, когда ему не оказывает противодействие поля посторонних, близко расположенных предметов и/или человека, формирует у затвердевающих предметов вектор с направлением «снизу-вверх». Наличие этого поля было выведено логически, когда стало ясно, что во время экспериментов по формированию направленности у радиокомпонентов, каждый раз отслеживается некая, устойчивая коррекция вектора в направлении «снизу-вверх». Скомпенсировать это влияние «снизу-вверх» (то-есть отклонить его в сторону или изменить на противоположное направление) оказалось возможным только при помощи практически прямого контакта рук с застывающим припоем (через тонкую бумагу) или при застывании припоя или воска на массивной, металлической или деревянной плите, вектор которой направлен вверх. Я предположил, что данное влияние «снизу-вверх» — это влияние векторного поля Земли, поскольку его влияние имеет наибольшую силу. Человек, находящийся даже на небольшом удалении, влияет на затвердевающие компоненты в меньшей степени, а предметы, как созданные человеком, так и самой природой — влияют еще меньше, даже при прямом контакте с испытуемым, застывающим компонентом.

Использование векторной направленности в радиолюбительских конструкциях

Учет векторной направленности компонентов требует от сборщика радиоаппаратуры таланта и навыков аудиоэксперта. Проще всего начать с формирования необходимой направленности припоя, для чего можно использовать влияние векторного поля Земли: во время пайки, ориентируясь на схему контуров, необходимо стараться распологать выход одного из спаиваемых компонентов над входом другого и давать пайке застыть не изменяя положения выводов компонентов. После застывания припоя, полученная цепочка «выход компонента-пайка-вход следующего компонента» будет иметь минимально возможные векторные потери. В случае использования такого метода и старого припоя (например оловянно-свинцовой посуды 18-19 веков, оловянных солдатиков тех-же лет, свинцовых мушкетных пуль и подобных предметов с подходящей для пайки пропорцией свинца и олова), звучание пайки будет максимально приближено к звучанию скрутки, которая, с моей точки зрения, является эталонным соединением. Напомню, что эталонная скрутка — это скрутка двух проводников «внахлест» (не «бантиком»), когда конец одного провода последовательно переходит в начало другого. Завивка пары при этом производится по часовой стрелке [3] так, чтобы угол между проводами во время скрутки был равен 90 градусам.

Пользоваться влиянием векторного поля Земли так-же можно для формирования необходимого вектора направленности воска при производстве конденсаторов, угольного лака в сопротивлениях, во время сушки лакокрасочных покрытий, клеев и других, подобных материалов.

Антон Степичев, 16 августа 2013.

---

Примечания

[1] — см. мое интернет сообщение от 7 марта 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:

…Правильное паправление имеет три независимые координаты по отношению к продольной оси у ЛЮБОГО проводника т.е. у полоски фольги есть входная и выходная сторона а циллиндрический проводник необходимо соединять определенным боком. Таким образом Вектор правильного направления стал трехмерным и счас исследуются способы минимизации векторных потерь…

[2] — Ссылка на источник не найдена.

[3] — см. мое интернет сообщение от 6 декабря 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:

…Есть еще немаловажные тонкости. Эти, найденные мной эзотерические правила, действуют и в головках и в трансформаторах и в рулонах конденсаторов и в динамиках — в любых радиокомпонентах, где есть спирали:
Катушка должна быть расположена вертикально (отверстие смотрит вниз),
Провод, если смотреть на катушку сверху, намотан по часовой стрелке.
«начало» провода должно быть внутри и сверху катушки. Заземляется именно начало провода. Конец провода становится сигнальным и он должен выходить из катушки внизу…

---

Другие статьи по теме

Длина и направление вектора — Студопедия

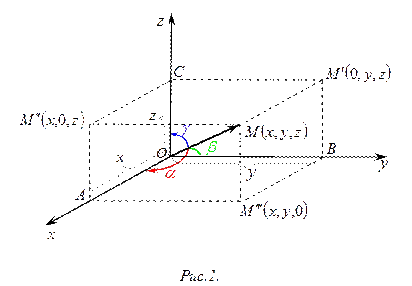
Пусть 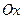, , 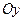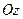‑ три взаимно перпендикулярные оси в трёхмерном пространстве (оси координат), исходящие из общей точки 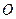(начало координат), образуют правую тройку (т.е. для наблюдателя, находящегося по направлению оси 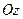, кратчайший поворот 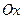оси к оси 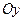происходит против часовой стрелки).

Для каждой точки 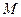пространства существует её радиус-вектор .

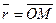Определение 1. Под декартовыми прямоугольными координатам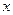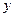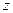и , , точки 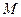понимаются проекции её радиус вектора 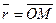на соответствующие оси координат, т.е. 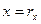, , 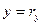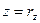. Точка 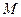с координатами 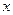, , 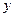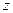обозначается 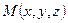, где 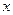‑ абсцисса, 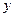‑ ордината, 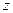‑ аппликата.

Для нахождения координат, через точку 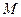проводятся три плоскости перпендикулярные осям 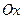, , 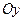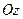. Тогда на этих осях получатся направленные отрезки (рис.1)

, , ,

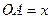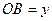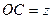численно равные координатам точки .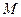

Радиус-вектор 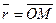‑ диагональ параллепипеда, поэтому

.

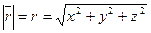Если обозначить , , 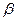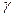( 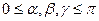) углы, образованные радиус-вектором 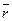с координатными осями 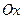, , 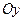, 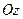то

, , .

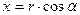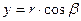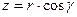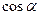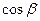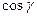, , называются направляющими косинусами радиус-вектора .

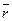Так как

,

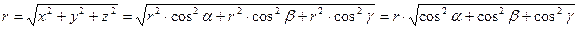то 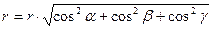и 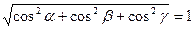. Следовательно,

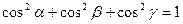
сумма квадратов направляющих косинусов радиус-вектора точки пространства равна 1.

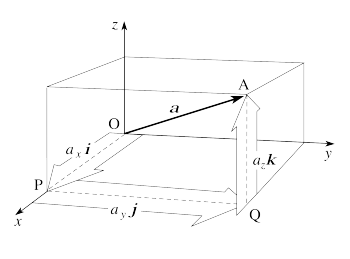
Определение 2. Если в пространстве 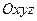задан вектор 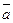, то проекции этого вектора на оси координат

, ,

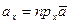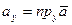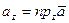
называются координатами вектора 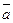. При этом вектор записывается так: .

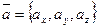Так как вектор 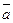свободный, то его можно рассматривать как радиус-вектор точки 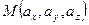. Отсюда получаем длину вектора

,

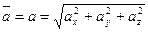т.е. модуль вектора равен корню квадратному из суммы квадратов его координат.

Направляющие косинусы вектора 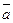определяются из уравнений

, , ,

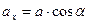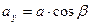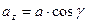т.е.

, , .

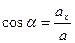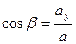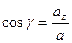Пример. Найти длину и направление вектора .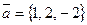

Решение. , , , .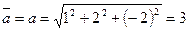

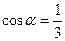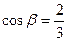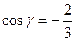Предложения со словосочетанием НАПРАВЛЕНИЕ ВЕКТОРА

Направление приобретённой намагниченности будет совпадать с направлением вектора напряжённости магнитного поля данного времени в данной точке. При анализе вектора доминирующего развития личности длина вектора не играет особой роли, гораздо важнее направление вектора. Кроме того, это чувство прививает оператору способность прислушиваться к общему окружающему фону и улавливать направление векторов опасности, угрозы, интереса или тревоги, исходящие от мыслящих существ, обитающих вокруг. У него изменение направления векторов тяги осуществляется благодаря изменению направления воздушного потока после винтов, сами же винты сохраняют своё положение в пространстве. Поэтому ему достаточно рулей на кожухах воздушных винтов, изменяющих направление вектора тяги в некоторых пределах и позволяющих управляться на очень малых скоростях.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова пришпиливать (глагол), пришпиливает:

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

Это, безусловно, люди, одарённые силой лидерства и принявшие этот дар. Вопрос в направлении вектора этой силы. При решении задач методом проб и ошибок решения идут в направлении вектора психологической инерции. Сброшенные с «горизонтального» бомбардировщика бомбы рассеиваются в виде эллипса, сильно вытянутого по одной из своих осей, в направлении вектора скорости самолёта; устройство бомбосбрасывателя позволяло, задавая интервал времени при т.н. «сбросе серией», ещё более вытянуть в длину полосу падения бомб. Форма лопаток подбирается так, чтобы направление вектора абсолютной скорости за ступенью соответствовало направлению вектора абсолютной скорости на входе в рабочее колесо. Правило для найма: вектор врождённого занятия должен иметь направление, близкое к направлению вектора цели компании. Противоположное направление векторов движения дефинитивной и акмеологической зрелости, в конце концов, приводит к тому, что физически беспомощный человек преклонного возраста нередко являет собой образец одухотворённой, просветлённой личности (индивидуальности, субъекта). При этом следует учитывать, что в первой четверти фазы направления векторов скорости и цели совпадают, во второй же части вектор скорости будет направлен преимущественно вперед-вверх. Нет смысла начинать собеседование с кандидатом, если направление вектора его врождённого занятия не сходно с направлением вектора цели компании. Следует отметить, что центростремительное ускорение меняет только направление вектора скорости, не влияя на его величину; ускорение ac направлено по радиусу окружности к её центру. Гравитационное поле небесных тел формируется за счёт того, что колебания всего множества массообразующих квантов небесного тела в виде атомных ядер химических элементов, из которых состоит это небесное тело, синхронизируются не только по частоте, образуя резонансный колебательный контур, но упорядочивают направление векторов колебаний, благодаря чему каждый материальный квант атомарной или молекулярной структуры совершает свои колебания строго вдоль множества сходящихся линий, направленных от поверхности планетного тела к его физическому центру тяжести. Когда я говорю о направлении вектора деятельности компании, то имею в виду вектор всей компании, а не вектор подразделения или должности. На первый взгляд довольно странный ход инженерной мысли, но, как показывает анализ, соединяющая вершину пирамиды и нижнюю излучающую камеру линия, как раз и будет задавать основное направление вектора распространения волны. Указанные вращательно-поступательные движения магнитного и гравитационного зарядов и определяют направление вектора спина, спиновый магнитный момент и собственный механический момент электрона, а их магнитомеханическое отношение есть величина постоянная для стабильных микрочастиц – это основной закон природы. Година, однозначно указывает на возможность технической индукциисобственного гравитационного монополя со значением его величины соизмеримой с вращающейся массой системы, направлением вектора которого можно управлять путём вращения магнитного кластера по часовой или против часовой стрелки. Центростремительное ускорение показывает, как меняется направление вектора скорости, оно всегда направлено к центру. Если система – это автоматически неотработанная задача на эмоциональном уровне – она становится самой сильной мотивацией в любую сторону, а направление вектора задаёте вы – всё направлено на отработку. Кроме того, динамическая конструкция из отдельных элементов позволит создавать некоторую асимметрию паруса и корректировать направление вектора тяги. Если сотрудник ценный, но направления векторов не близки, то ценность такого сотрудника можно увеличить, предоставив человеку возможность получать дополнительную энергию от врождённого занятия. Итак, при обратном направлении вектора времени из настоящего в прошлое одномерная и не имеющая обрывов нить протона, опутывающая вроде змеи центральную сингулярность, ускоренно вращается, сжимается и сосредоточивается подобно сжатой пружине. Это самое центростремительное ускорение и показывает, насколько сильно меняется направление твоего движения (по-умному – направление вектора скорости). Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси. Если направление вектора врождённого занятия ценного сотрудника сходно с направлением вектора цели компании, то вкладывайте в этого человека (обучайте, уделяйте внимание, заботьтесь). Направление вектора равнодействующей определяется углами. При вращении по часовой стрелке критический режим наступает в районе 550 об/мин и создаётся тягапротив направления вектора гравитации, а при вращении против часовой стрелки, критический режим наступает в районе 600 об/мин и создаётся тяга по направлению вектора гравитации. Направление вектора магнитного поля в этих стенах совпадало с направлением вектора магнитного поля роликов. Кроме того, преобладание суммы неспецифических звеньев факторов воздействия само по себе уже может изменять направление вектора суммы их специфических звеньев (даже в случае применения однонаправленных по специфичности воздействий) при значительном превышении первыми пороговых значений. Касательное ускорение характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости; при замедлении оно направлено противоположно направлению вектора скорости. Это является основой для формирования направления вектора качественного развития общества, в том числе профессионального. Например, машина, которая поворачивает налево, испытывает ускорение, даже если её скорость (50 км/ч) не меняется: зато меняется направление вектора скорости. Лопатки рабочего колеса должны быть установлены таким образом, чтобы передние кромки их были направлены по направлению вектора «w» или под небольшим углом к нему. Если выражаться образно, двигатель прогибает пространство в направлении вектора движения. Вектор всегда задаёт направление, а кто даёт направление вектору? Очевидно тот, кто управляет этим вектором. Благая весть, вечность, весна, завет… Кроме того, величины возникающих в различных точках тела напряжений напрямую зависят как от формы тела, так и от направления вектора приложенной силы. – Секрет в том, чтобы повернуть прогресс вспять, развернуть направление вектора. Направление вектора тяги – два-десять-десять от нормальной сетки… Пренебрежение мнением и стремлением всех слоёв общества порождает мировоззренческий хаос в мыслях и действиях, туманность в направлении вектора дальнейшего развития общества, разброд и шатание в идеологических вопросах. Проведённый пунктиром в обратном направлении вектор 3–2 изображает движение мысли от понятия к конкретному явлению. Эта книга обо всех трёх направлениях векторов жизни. Т.е. мозг – это сосуд, задающий направление вектора сна: содержание сна, или сновидение. Важно было одно: сделать возможным изменение направления вектора лагеря русских. Значит гены определяют направление вектора, нашу основную дорогу, а наша свобода воли – это свобода метаться от одной обочины к другой? Иными словами, тут становится понятным само направление вектора развития эволюции жизни – в сторону всё большей адаптации всех свойств пустоты на природе человека, а именно абсолютного ноля. Направление вектора не имеет смысла, если вектор бессилен. Огонь меняет уклад жизни человека, способствует изменению его внешнего облика, становится важным фактором изменения направления вектора развития от биологических изменений в сторону развития социума. Представители коренных народностей воспринимают указания направления, исходящие от земли; я называю эти направления векторами.

Предложения со словосочетанием ЗАДАТЬ ВЕКТОР

Всем главным героям нужно задать вектор развития характера, который будет прослеживаться в любом эпизоде. Намного проще держать в руке округлый предмет, чем пытаться одним пальцем задать вектор движения указателя по экрану. Но на самом деле он необходим для создания определённой турбулентности и чтобы задать вектор физической силе, кинетической энергии, если угодно. Эта книга задала вектор моего поиска: я стал поглощать религиозную литературу в огромном количестве и днём, и ночью, где бы ни находился. Этот подход на несколько столетий задал вектор исследования в категориях «объективного» познания.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова гомогенность (существительное):

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

Это поможет ощутимо сузить круг подозреваемых, задаст вектор поисков. Любой мастер реальности должен уметь задать вектор, чтобы направить эволюцию туда, куда ему необходимо… – К комбату, – лаконично задал вектор посыльный. – Уже вообще-то. И, если обстоятельства благоприятствуют, то можно задать вектор направления развития определённого сектора экономики или бизнеса на ближайшее время. В общем, лучше сразу задать вектор общения поспокойней, а то ещё вообразит, что раз я «вспомнил», то надо меня того… этого. Эти аспекты управления принципиально важны в деятельности и малой технологической компании, выводящей на рынок свой первый продукт, и крупной корпорации, долгие годы работающей в своей отрасли, и государства, которое стремится задать вектор и обеспечить темпы инновационного развития страны. События 2014—15 гг. задали вектор внутреннего политического и идеологического развития страны. – Тогда взяли спирта и к кому-нибудь домой в гости, чтобы немедленно набухаться и задать вектор настроения на время, которое быстро пролетит до следующего похода… Задача правильного вуза – дать студентам необходимые теоретические знания и базовые практические навыки работы в выбранном направлении, помочь им реализовать свой творческий и научный потенциал, испытать свои силы в общественной деятельности, задать вектор трудоустройства и дальнейшего построения образовательной и карьерной траектории. Но главное – он задал вектор развития города на много лет вперёд. Для активации достаточно мысленно его представить, затем конструкцию опять же мысленно перенести в область магического зрения, напитать энергией из ауры и задать вектор движения. Ему нужно только активировать энергию с накопителей и задать вектор направления силы. Тем самым я задал вектор развития людей.

Векторы, графическое изображение векторов, величина вектора, направление вектора

Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.

Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.

Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,
        
В контексте векторов мы применяем = чтобы обозначить их равность.

Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.

Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.

Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √[2 — (-1)]² + (4 — 3)² = √9 + 1 = √10,
|| = √[0 — (-3)]² + [0 — (-1)]² = √9 + 1 = √10,
|w| = √(4 — 1)² + [-1 — (-2)]² = √9 + 1 = √10.
Отсюда
|u| = | = |w|.
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u, , и w имеют равные величины и одно и то же напраывление,
u = = w.

Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.

Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.

В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.

Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =

Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.

Если две силы F₁ и F₂ действуют на один объект, результирующая сила есть сумма F₁ + F₂ этих двух отдельных сил.

Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.

Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v|² = 15² + 25²          Здесь |v| обозначает длину или величину v.
|v| = √15² + 25²
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя к

{\ displaystyle {\ hat {\ mathbf {v}}}} (произносится как «в-шляпа»). ^{[1] [2]}

Термин вектор направления используется для описания единичного вектора, используемого для представления пространственного направления, и такие величины обычно обозначаются как d ; Представленные таким образом двумерные пространственные направления численно эквивалентны точкам на единичной окружности. Та же конструкция используется для указания пространственных направлений в 3D, которые эквивалентны точке на единичной сфере.знак равно ты | ты | {\ displaystyle \ mathbf {\ hat {u}} = {\ frac {\ mathbf {u}} {| \ mathbf {u} |}}}

где | u | — норма (или длина) и . ^{[3] [4]} Термин нормализованный вектор иногда используется как синоним единичного вектора .

Единичные векторы часто выбираются для формирования основы векторного пространства, и каждый вектор в пространстве может быть записан как линейная комбинация единичных векторов.

По определению, скалярное произведение двух единичных векторов в евклидовом пространстве является скалярным значением, равным косинусу меньшего подведенного угла.В трехмерном евклидовом пространстве перекрестное произведение двух произвольных единичных векторов является третьим вектором, ортогональным им обоим, длина которого равна синусу меньшего вложенного угла. Нормализованное перекрестное произведение корректирует эту изменяющуюся длину и дает взаимно ортогональный единичный вектор для двух входов, применяя правило правой руки для разрешения одного из двух возможных направлений.

Энциклопедия YouTube

• 1/5

  Просмотры:

  435045

  28 267

  453 304

  429 819

  211 193

• ✪ Обозначение единичного вектора | Векторы и пространства | Линейная алгебра | Хан Академия

• ✪ Как найти единичный вектор (3d)

• ✪ Единичные векторы | Векторы | Precalculus | Хан Академия

• ✪ Нормальный вектор из уравнения плоскости | Векторы и пространства | Линейная алгебра | Хан Академия

• ✪ Нахождение единичного вектора, Пример 1

Мы уже видели что вы можете визуально представить вектор в виде стрелки, где длина стрелки величина вектора и направление стрелки — направление вектора.И если мы хотим представить это математически, мы могли просто думать о, ну, начиная из хвоста вектор, как далеко прочь — голова вектора в горизонтальном направлении? И как далеко это в вертикальное направление? Так, например, в горизонтальное направление, тебе придется пройти это расстояние. А потом в вертикальное направление, тебе придется пройти это расстояние. Позвольте мне сделать это в другой цвет. Вам придется пойти на это расстояние прямо здесь. Итак, давайте просто скажем что это расстояние 2 и что это расстояние равно 3.Мы могли бы представлять этот вектор — и давайте назовем этот вектор v. может представлять вектор v как упорядоченный список или 2-кортеж из — так что мы можем сказать, что мы переместить 2 в горизонтальное направление и 3 в вертикальном направлении. Итак, вы могли бы представить это так. Вы могли бы представлять вектор v вот так, где это 2 запятая 3, вот так. И что я сейчас хочу чтобы познакомить вас с … и мы могли придумать другие способы представления этот кортеж — это другое обозначение. И это действительно выходит из идеи о том, что это значит складывать и масштабировать векторы.И для этого мы собираемся определить то, что мы называем единичными векторами. И если мы в два измерения, мы определить единичный вектор для каждый из размеров мы работаем. Если мы в трех измерениях, мы бы определяли единичный вектор для каждого из трех измерений в котором мы работаем. Итак, давайте сделаем это. Итак, давайте определим единичный вектор i. И способ, которым мы обозначаем это единичный вектор вместо того, чтобы ставить стрелка сверху, мы надеваем на него эту шляпу. Итак, единичный вектор я, если бы мы хотели написать это в этом обозначение прямо здесь, мы бы сказали, что идет только 1 единица в горизонтальном направлении, и это вообще не идет в вертикальном направлении.Так бы выглядело что-то вроде этого. Это единичный вектор i. И тогда мы можем определить другой единичный вектор. И давай позвоним этот единичный вектор — или это обычно называется j, который пойдет только в вертикальное направление, а не в горизонтальном направлении. И не в горизонтальное направление, и идет 1 единица в вертикальное направление. Так пошла 1 единица по горизонтали. И теперь Джей собирается пойти 1 единица по вертикали. Так что … вот так. Теперь любой вектор, любой двумерный вектор, теперь мы можем представить в виде суммы увеличенные версии i и j.И вы говорите, ну Как мы это делаем? Ну вы могли представить вектор v прямо здесь это сумма вектора это движется чисто в горизонтальном направлении имеющий длину 2, и вектор, который движется чисто в вертикальном направлении, что имеет длину 3. Итак, мы могли сказать этот вектор v— пусть я делаю это в этом того же синего цвета — равно — так что если мы хотим вектор длиной 2 и он движется чисто в горизонтальное направление, ну, мы могли бы просто масштабировать вверх по единичному вектору i. Мы могли бы просто умножить 2 раза i.Итак, давайте сделаем это — равно в 2 раза больше нашего единичного вектора i. Итак, 2i собирается быть всем этим прямо здесь или весь этот вектор. Позволь мне сделать это этот желтый цвет. Этот вектор прямо над здесь вы можете рассматривать как 2i. И затем мы собираемся прибавить 3 раза j — итого плюс 3 раза j. Позвольте мне написать это так. Позвольте мне получить этот цвет. Еще раз 3 раза J будет этот вектор прямо здесь. И если вы добавите этот желтый вектор прямо здесь к пурпурному вектору, вы получите … заметьте, мы ставим хвост пурпурного вектора во главе желтый вектор.И если вы начнете с хвост желтого вектора и вы идете до самого голова пурпурного вектора, вы сейчас построили вектор v. Итак, вектор v, вы могли бы представить это как вектор-столбец, как этот, 2 3. Вы могли бы представлять это как 2 запятая 3, или вы могли бы представить это как 2 раза я в этой маленькой шляпе над ним плюс 3 раза j, в этой маленькой шляпе. i — единичный вектор в горизонтальное направление, в положительном горизонтальное направление. Если ты хочешь идти наоборот, ты умножил бы его на отрицательный.И j — единичный вектор в вертикальном направлении. Как мы увидим в будущем видео, как только вы перейти в три измерения, вы представите k. Но это очень естественно переводить между этими двумя вещи. Уведомление, 2, 3—2, 3. Итак, давайте на самом деле выполнить некоторые векторные операции используя это обозначение. Итак, скажем, что я определить другой вектор. Допустим, это вектор b. Я просто придумаю некоторые цифры здесь. Вектор b равен отрицательному 1 умножить на i — умножить на единичный вектор i — плюс 4-кратный единичный вектор в горизонтальном направлении.Итак, учитывая эти два определения векторов, что было бы вектор v плюс b быть равен? И я призываю вас сделать паузу видео и подумайте над этим. Ну еще раз, мы просто буквально нужно добавить соответствующие компоненты. Мы могли бы сказать, хорошо, ну давай подумаем о том, что мы делаем в горизонтальное направление. Мы идем 2 в горизонтальное направление здесь, и теперь мы идем на отрицательный 1. Итак, наша горизонтальная компонент собирается быть 2 плюс отрицательный 1-2 плюс минус 1 в горизонтальном направлении.И мы будем размножаться что умножает единичный вектор i. И это однажды снова просто возвращается добавить соответствующие компоненты вектора. И тогда у нас будет плюс 4 или плюс 3 плюс 4 — И позвольте мне написать это так — умножить на единичный вектор j в вертикальном направлении. И так это происходит дать нам — я сделай все это одним цветом — 2 плюс отрицательная 1 равно 1i. И мы могли буквально напишите это так же, как я. Собственно, давайте так и сделаем. Давайте просто напишем это как i. Но мы получили это от 2 плюс отрицательный 1 равен 1.1 раз вектор просто будет этим вектором, плюс 3 плюс 4 это 7-7j. И вы видите, это точно как мы видели сложение векторов в прошлом, это то, что мы может также представлять вектор б вот так. Мы могли бы это представить вот так — отрицательные 1, 4. И так, если бы ты был добавить v к b, вы добавляете соответствующие термины. Итак, если бы мы добавили соответствующие условия, ищем у них как столб векторов, то есть будет равно 2 плюс отрицательный 1, который равен 1. 3 плюс 4 равно 7. Так это то же самое представление как это.знак равно [ 0 0 1 ] {\ displaystyle \ mathbf {\ hat {i}} = {\ begin {bmatrix} 1 \\ 0 \\ 0 \ end {bmatrix}}, \, \, \ mathbf {\ hat {j}} = {\ begin {bmatrix} 0 \\ 1 \\ 0 \ end {bmatrix}}, \, \, \ mathbf {\ hat {k}} = {\ begin {bmatrix} 0 \\ 0 \\ 1 \ end {bmatrix}} }

Они образуют набор взаимно ортогональных единичных векторов, обычно называемых стандартным базисом в линейной алгебре.

Они часто обозначаются с использованием общих векторных обозначений (например, i или я → {\ Displaystyle {\ vec {\ imath}}} ), а не стандартную запись единичного вектора (например,3 ) {\ Displaystyle (\ mathbf {\ шляпа {е}} _ {1}, \ mathbf {\ шляпа {е}} _ {2}, \ mathbf {\ шляпа {е}} _ {3})} , со шляпкой или без нее, также используются, ^[3] , особенно в контекстах, где i , j , k может привести к путанице с другой величиной (например, с индексными символами, такими как i , j , k , которые используются для идентификации элемента набора или массива или последовательности переменных).

Когда единичный вектор в пространстве выражается в декартовой системе счисления как линейная комбинация i , j , k , его три скалярных компонента можно называть направляющими косинусами.{\ displaystyle \ mathbf {\ hat {\ rho}}} и

.Вектор

, их величина и направление. Определяется с примерами и вопросами викторины.

Вектор — это то, что имеет две и только две определяющие характеристики.

• Величина: величина означает «размер» или «количество»
• Направление: значение направления не требует пояснений. Это просто означает, что вектор направлен из одного места в другое.

Значение «направления» можно увидеть в различии между скорость и скорость.В физике скорость — это чистый скаляр, или что-то с величиной, но без направления, например 5 м / с. 5 метров в секунду не говорят нам, в какую сторону движется объект. Это не дает нам подсказки о направлении. Все, что мы знаем по скорости, — это величина движения. С другой стороны, Скорость в физике должна быть выражена как вектор с величиной и направлением. Например, скорость 5 м / с на восток — это скорость, потому что она сообщает вам величину движения, 5 метров в секунду, а также направление на восток.

Величина: размер

Чтобы проиллюстрировать идею величины, посмотрите на два красных кружка ниже. Круг А имеет величина больше, чем у круга B.

Практика Проблемы

Задача 1

В каком направлении изображен вектор?

Направление

Направление вектора — северо-восток или по диагонали вверх и вправо (за исключением измерения угла с помощью транспортира, мы не можем быть более точными с этим изображением)

Проблема 2

Какова величина и направление вектора ниже?

Покажи ответ

Направление вектора — 55 ° к северу от востока, величина вектора — 2.3.

Задача 3

Найдите величину и направление вектора на диаграмме ниже.

Покажи ответ

Направление вектора 47 ° к северу от запада, величина вектора равна 2.

Задача 4

Найдите величину и направление вектора на диаграмме ниже.

Покажи ответ

Направление вектора — 43 ° к востоку от юга, величина вектора — 3. Также можно описать направление этого вектора как 47.К югу от востока.

Задача 5

В чем разница между вектором, который находится на 55 ° к северу от запада, и вектором, который находится на 35 ° к западу от севера?

Покажи ответ

С точки зрения направления, нет никакой разницы между 55 ° к северу от запада и 35 ° к западу от севера.

.

Углы направления векторов

На рисунке 1 показан единичный вектор u, образующий угол θ с положительной осью x. Угол θ называется направленным углом вектора u.

Конечная точка вектора u лежит на единичной окружности, поэтому u можно обозначить как:

u = 〈x, y〉 = 〈cosθ, sinθ〉 = (cosθ) i + (sinθ) j

Любой вектор, образующий угол θ с положительной осью x, может быть записан как единичный вектор, умноженный на величину вектора.

v = v∥ (cosθ) i + ∥v∥ (sinθ) j

v = ai + bj

Следовательно, угол направления θ любого вектора можно рассчитать следующим образом:

УГОЛ НАПРАВЛЕНИЯ:

загар θ = грех θ cosθ знак равно ∥в∥син θ ∥v∥cosθ знак равно б а

Давайте рассмотрим несколько примеров.

Для работы этих примеров требуется использование различных векторных правил.Если вы не знакомы с правилом, перейдите к соответствующей теме для обзора.

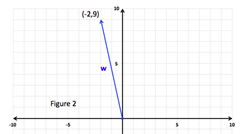
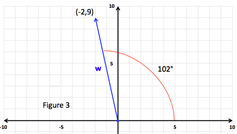
Пример 1. Найдите угол направления w = -2i + 9j.

Шаг 1: Определите значения для a и b и вычислите θ. загар θ = б а	а = -2, б = 9 tanθ = б а знак равно 9 −2 θ = загар −1 | 9 −2 | θ≈78 °
Шаг 2: Определите квадрант, в котором находится вектор.	Поскольку конец вектора равен (-2, 9), он попадет в квадрант II, как и θ.
Шаг 3: Внесите необходимые корректировки, чтобы найти направленный угол θ от положительной оси x.	Поскольку исходный угол равен 78 °, направленный угол от положительной оси x составляет 180 ° — 78 ° = 102 °.

Пример 2: Найдите угол направления v = 3 ( cos60 ° i + sin60 ° j ) .

Шаг 1. Упростите вектор v с помощью скалярного умножения. kv = k v 1 , v 2 = k v 1 , k v 2 → Скалярное умножение	v = 3 ( cos60 ° i + sin60 ° j ) v = 3 · cos60 ° i + 3 · sin60 ° j v = 3 · 1 2 я + 3 · 3 2 j v = 3 2 я + 3 3 2
Шаг 2: Определите значения для a и b и вычислите θ.	а = 3 2 , B = 3 3 2 tanθ = б а знак равно 3 3 2 3 2 знак равно 3 3 2 · 2 3 знак равно 3 θ = загар −1 | 3 | θ = 60 °
Шаг 3: Определите квадрант вектора, в котором лежит.

.

Как найти величину и направление вектора

2. Образование
3. Наука
4. Физика
5. Как найти величину и направление вектора

Стивен Хольцнер

Если вам заданы компоненты вектора, такие как (3, 4), вы можете легко преобразовать их в способ выражения векторов по величине / углу с помощью тригонометрии.

Например, взгляните на вектор на изображении.

Предположим, вам даны координаты конца вектора и вы хотите найти его величину, v , и угол, theta. Благодаря вашим знаниям тригонометрии вы знаете

Где tan theta — тангенс угла. Это означает, что

тета = загар ^–1 ( y / x )

Предположим, что координаты вектора равны (3, 4). Вы можете найти угол тета как загар ^–1 (4/3) = 53 градуса.

Вы можете использовать теорему Пифагора, чтобы найти гипотенузу — величину, v — треугольника, образованного x, y, и v:

Подставьте числа для этого примера, чтобы получить

Итак, если у вас есть вектор, заданный координатами (3, 4), его величина равна 5, а угол — 53 градуса.

Пример вопроса

1. Преобразуйте вектор, заданный координатами (1.0, 5.0) в формате величины / угла.

   Правильный ответ — величина 5,1, угол 79 градусов.

   1. Примените теорему Пифагора, чтобы найти величину. Подставьте числа, чтобы получить 5.1.

   2. Примените уравнение theta = tan ^–1 ( y / x ), чтобы найти угол. Подставьте числа, чтобы получить загар ^–1 (5,0 / 1,0) = 79 градусов.

Практические вопросы

1. Преобразуйте вектор (5.0, 7.0) в виде величины / угла.

2. Преобразуйте вектор (13.0, 13.0) в форму величины / угла.

3. Преобразуйте вектор (–1,0, 1,0) в форму величины / угла.

4. Преобразует вектор (–5.0, –7.0) в форму величины / угла.

Ниже приведены ответы на вопросы практики:

1. Величина 8,6, угол 54 градуса

   1. Примените уравнение

   , чтобы найти звездную величину, равную 8.6.

   1. Примените уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (7,0 / 5,0) = 54 градуса.

2. Величина 18,4, угол 45 градусов

   1. Примените уравнение

      , чтобы найти звездную величину, равную 18,4.

   2. Примените уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (13.0 / 13,0) = 45 градусов.

3. Величина 1,4, угол 135 градусов

   1. Примените уравнение

      , чтобы найти звездную величину, равную 1,4.

   2. Примените уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (1.0 / –1.0) = –45 градусов.

      Однако обратите внимание, что угол на самом деле должен быть между 90 и 180 градусами, потому что первая компонента вектора отрицательна, а вторая положительна.Это означает, что вы должны добавить 180 градусов к –45 градусов, что даст вам 135 градусов (тангенс 135 градусов также равен 1,0 / –1,0 = –1,0).

4. Величина 8,6, угол 234 градуса

   1. Примените уравнение

      , чтобы найти звездную величину, равную 8,6.

   2. Примените уравнение theta = tan – 1 (y / x), чтобы найти угол: tan – 1 (–7,0 / –5,0) = 54 градуса.

      Однако обратите внимание, что угол на самом деле должен составлять от 180 до 270 градусов, потому что обе компоненты вектора отрицательны.Это означает, что вы должны добавить 180 градусов к 54 градусам, что даст вам 234 градуса (тангенс 234 градусов также составляет –7,0 / –5,0 = 7,0 / 5,0).

Об авторе книги

Стивен Хольцнер, доктор философии, был преподавателем и редактором журнала PC Magazine .

.