Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Андронов В.В. Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика: Учебное пособие для студентов очного и заочного обучения. Спец. 260100 и 260200. 2-е изд., доп. и испр. — М: МГУЛ, 2003.- 137 с. Книга содержит материал лекций, которые автор читает в Московском государственном университете леса студентам технологических специальностей. Настоящая, первая часть книги, включает статику и кинематику. Для лучшего усвоения материала в конце каждой лекции приводятся вопросы для самопроверки и упражнения. В интересах студентов заочных форм обучения в книге большое внимание уделяется поясняющим примерам и решению задач. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Момент силы относительно точки Алгебраический момент силы Основные типы связей и их реакции Упражнения ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ Сходящиеся силы. Приведение сходящихся сил к простейшему виду Вычисление и построение равнодействующей Условия равновесия сходящихся сил Теорема о трех силах Теорема Вариньона Пара сил и ее момент Приведение системы пар сил к простейшему виду или сложение пар сил Упражнения ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ Момент силы относительно оси Аналитический способ вычисления момента Геометрический способ вычисления момента Преобразование пространственной произвольной системы сил Приведение пространственной произвольной системы сил к данному центру. 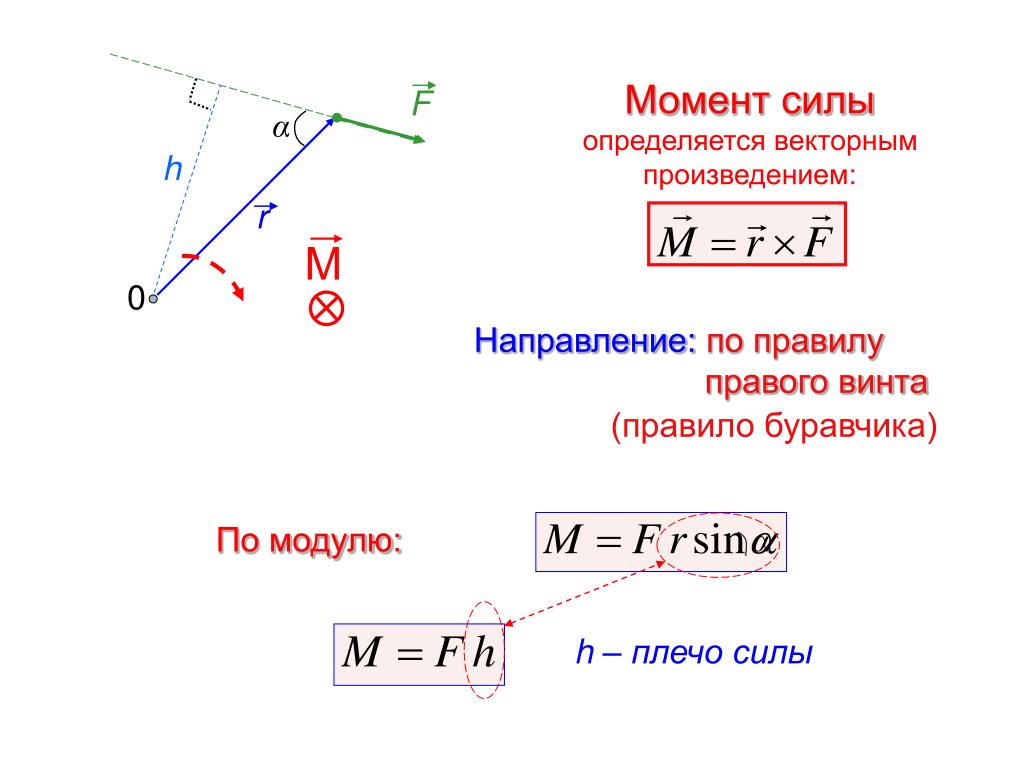Главный вектор и главный момент. Основная теорема статики Вычисление и построение главного вектора и главного момента Перемена центра приведения ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ Случаи приведения к простейшему виду Условия (уравнения) равновесия пространственной произвольной системы сил Частные случаи системы сил Плоская система сил Система параллельных сил Равновесие системы тел Вопросы для самопроверки ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ Центр параллельных сил Распределенные силы Центр тяжести Интегральные формулы для координат центра тяжести Метод разбиения Вопросы для самопроверки ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ Трение покоя и трение скольжения Трение качения Решение задач статики при учете сил трения Заклинивание Упражнения КИНЕМАТИКА ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ Способы задания движения точки Определение траектории, скорости и ускорения точки при векторном способе задания движения Определение траектории, скорости и ускорения точки при координатном способе задания движения Определение скорости и ускорения точки при естественном способе задания движения Естественные координатные оси и их орты Определение скорости Определение ускорения Вопросы для самопроверки ЛЕКЦИЯ 8. 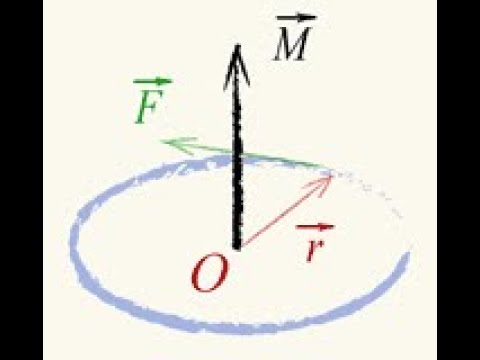ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение Вращательное движение Уравнение вращательного движения. Угловая скорость и угловое ускорение тела Траектории, скорости и ускорения точек тела Векторы угловой скорости и углового ускорения тела Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела Вопросы для самопроверки ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Уравнения движения Угловая скорость и угловое ускорение тела при плоскопараллельном движении Определение скоростей точек тела. Метод полюса Мгновенный центр скоростей Определение скоростей точек плоской фигуры через мгновенный центр скоростей Различные случаи определения положения мгновенного центра скоростей Определение ускорений точек тела Вопросы для самопроверки ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Теорема сложения скоростей Теорема сложения ускорений Причины появления ускорения Кориолиса Вычисление и построение ускорения Кориолиса Вопросы для самопроверки ДОБАВЛЕНИЕ. 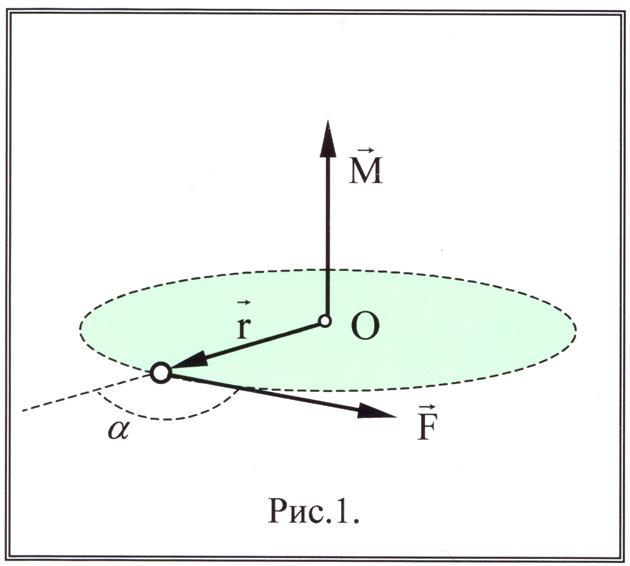КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ Схема и расчетная модель процесса фугования Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке Геометрические характеристики поверхности в случае многоножевой головки РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

определение, формула расчета, пример решения задачи

Типичными задачами раздела физики «Статика» являются проблемы равновесия тел. В этом случае равенство нулю суммы внешних сил является недостаточной информацией для определения состояния рассматриваемого тела, поэтому используют другую величину, которая называется моментом силы. Чему равен он и как его использовать для решения задач на равновесие, рассматривается в этой статье.

Значение понятия

Определение момента силы или кручения, как его часто принято называть, можно дать следующее: это физическая величина, равная произведению действующей силы, приложенной к некоторой точке тела P, на плечо силы, равное расстоянию от оси крепления этого тела O до точки P. Для явного представления данного определения приведем иллюстрацию.

Момент сил относительно оси вращения: основные понятия,…

Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными…

Здесь мы видим, что воздействие силы F на ключ длиною d (плечо) приведет к закручиванию гайки, которая играет роль оси O для данной системы.

В итоге можно записать, что модуль момента силы равен следующему выражению: M = d * F. Откуда видно, чем больше плечо d, тем потребуется меньшая сила F для создания определенного момента кручения M. Единица измерения в СИ для рассматриваемой величины — это ньютоны на метр (Н*м).

M¯ — это вектор

Мы рассмотрели не полностью вопрос, чему равен момент силы относительно оси. Дело в том, что воздействующая сила может быть приложена к рычагу под некоторым углом. И для этого случая не была приведена формула вычисления величины M. На самом деле последняя является вектором, а не скаляром. Она определяется через векторное произведение.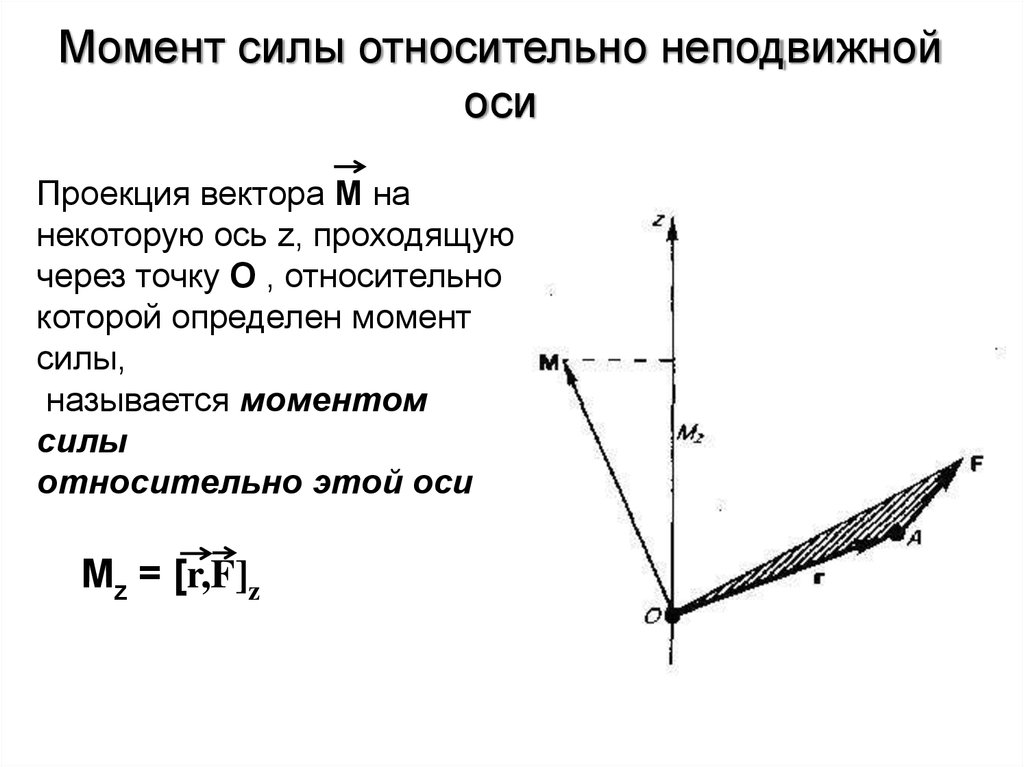 Один вектор известен — это внешняя сила F¯. Другим направленным отрезком является OP¯ (в соответствии с точками, введенными в предыдущем пункте). Чему равен силы момент в этом случае? Он может быть записан в виде следующего выражения: M¯ = OP¯ * F¯ (черта над каждым множителем — это значок вектора).

Момент инерции маятника: определение, специфические…

При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать…

Модуль произведения двух векторов равен абсолютной длине каждого из них на синус угла между ними. Поскольку в пункте выше между силой и плечом угол равен 90^o, то векторная формула переводится в скалярный вид путем простого опускания значка вектора. Если же отмеченный угол не является прямым, тогда следует произведение модулей векторов домножить на синус соответствующего угла. Эта ситуация приведена на рисунке ниже.

Здесь видно, что сила F направлена под углом Φ, а это значит, что абсолютное значение момента силы можно рассчитать так:

M = L * F * sin(Φ).

Здесь L уже не является рычагом силы, однако, L * sin(Φ) = d (это равенство следует из определения синуса угла Φ), и скалярное выражение для момента снова можно записать в форме, приведенной в первом пункте статьи.

Направление вектора M¯

Итак, мы научились вычислять, чему момент силы равен относительно оси, но поскольку он является еще и вектором, то следует познакомиться с вопросом, как определять его направление. Конечно, для этого можно воспользоваться правилом правой руки, которое справедливо для любого векторного произведения, однако результирующий вектор зависит от направления умножаемых отрезков и от порядка их следования в произведении, то есть результатом OP¯ * F¯ и F¯ * OP¯ будут векторы с противоположным направлением.

Уравнение моментов: моменты силы, импульса и инерции

Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то…

Поэтому рекомендуется запомнить следующее правило: если представить, что результирующая сила F привела к вращению тела вокруг его оси против часовой стрелки, значит, наблюдатель смотрит на систему с вершины вектора M¯, который в этом случае считается положительным. Наоборот, если сила F должна вызвать вращение тела по часовой стрелке, то наблюдатель смотрит на момент силы вдоль направления его действия, здесь модуль M¯ — это отрицательная величина.

Выше приведен рисунок, на котором показан вектор M¯ с учетом направления вращения в системе. Его модуль, согласно вышесказанному, является положительным, то есть +M.

Системы с несколькими действующими силами

До настоящего времени приводились примеры, в которых вращение осуществляет лишь единственная сила. В общем случае таких сил может быть несколько. Как вычислять результирующий момент кручения? Величина M является аддитивной, то есть для ее вычисления можно суммировать момент от каждой силы, но при этом следует соблюдать знак (+M или -M).

Решение задачи на равновесие двух тел

Теперь решим простую задачу. Ниже приведен рисунок, где изображено два человека, находящихся в равновесии. Необходимо определить, во сколько раз желтый человек сидит дальше от оси вращения, чем зеленый, зная, что его вес в 1,5 раза меньше веса его напарника.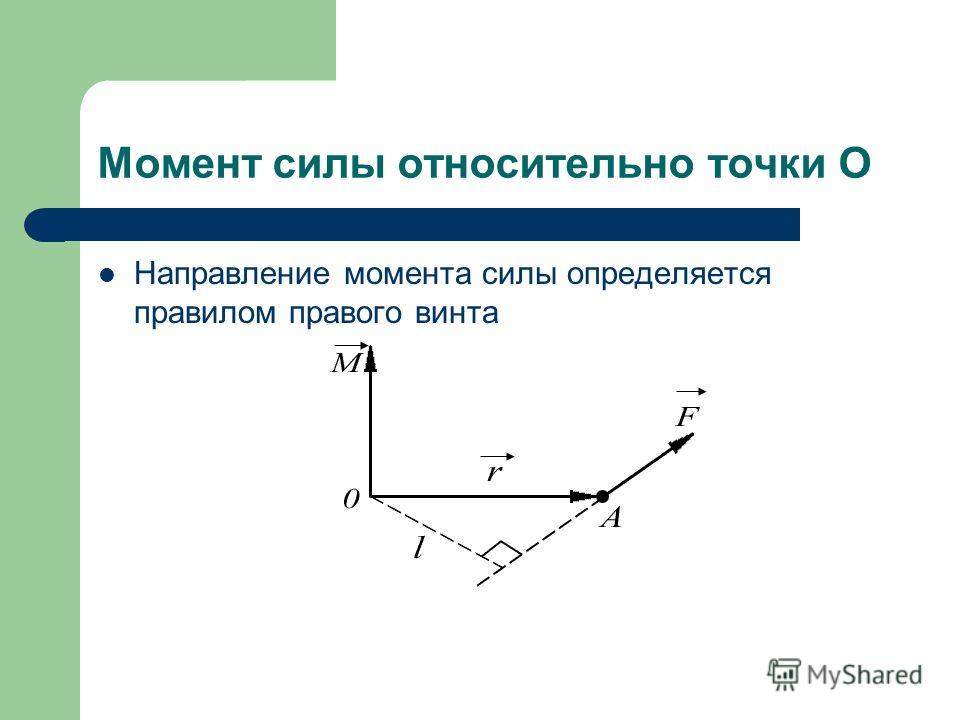

В первую очередь следует определить, какие силы действуют в системе. Их три: две силы тяжести каждого человека и сила реакции опоры оси. Поскольку плечо для последней равно нулю, то момента кручения она не создает. Остается рассмотреть две силы тяжести.

Так как система находится в равновесии, то общий момент силы тяжести равен нулю. Обозначим P₁, P₂ и x₁, x₂ — веса и расстояния от оси для желтого и зеленого человека, соответственно. Вес желтого человека создает вращение против часовой стрелки, значит, его момент кручения является положительным. Для зеленого человека эта величина будет отрицательной. Тогда имеем: P₁ * x₁ — P₂ * x₂ = 0. Откуда получаем: P₂ / P₁ = x₁ / x₂ = 1,5.

Таким образом, желтый человек сидит в 1,5 раза дальше от оси, чем зеленый.

Карта механики — Момент относительно точки

Для любой точки протяженного тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент относительно этой точки.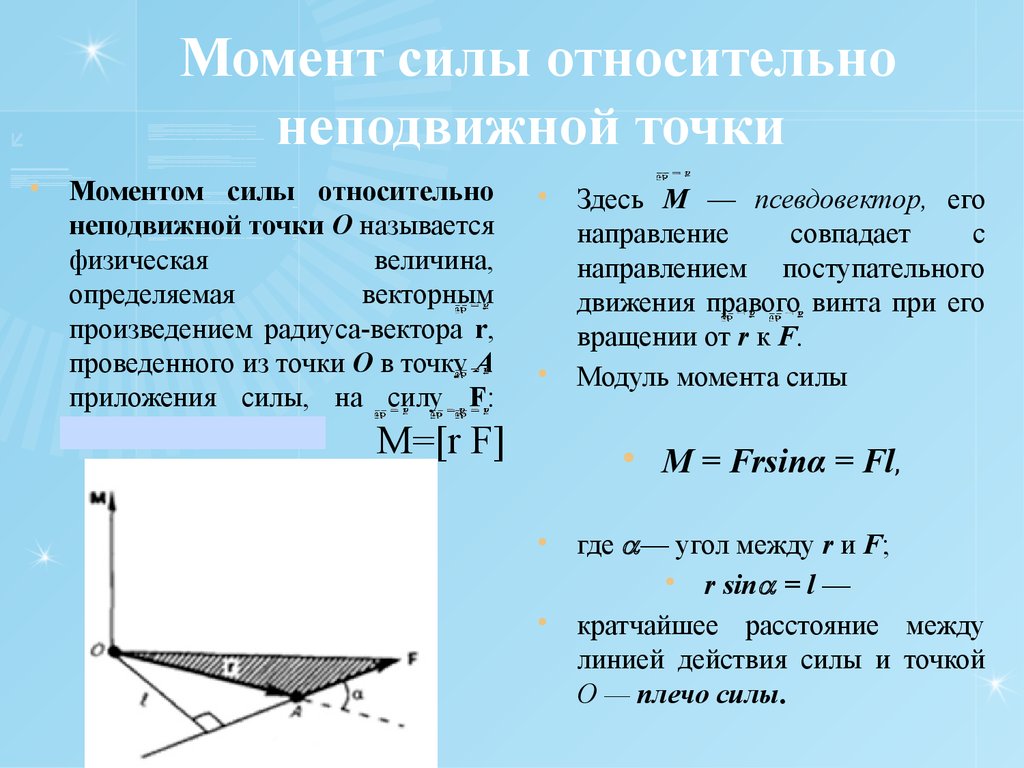

Как обсуждалось на странице моментов, момент — это тенденция силы вызывать вращение.

Альтернативой расчету момента через скалярные величины является использование векторного метода или метода векторного произведения . Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод векторного произведения. Метод векторного произведения для вычисления моментов говорит, что вектор момента силы относительно точки будет равен векторному произведению вектора r

из точки в любую точку на линии действия силы и самого вектора силы.

\[\vec{M}=\vec{r}\times \vec{F}\]

Большое преимущество этого метода в том, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от точки до любой части линии действия. Для любой задачи существует много возможных векторов r , хотя из-за того, как работает перекрестное произведение, все они должны в конце концов давать один и тот же вектор моментов.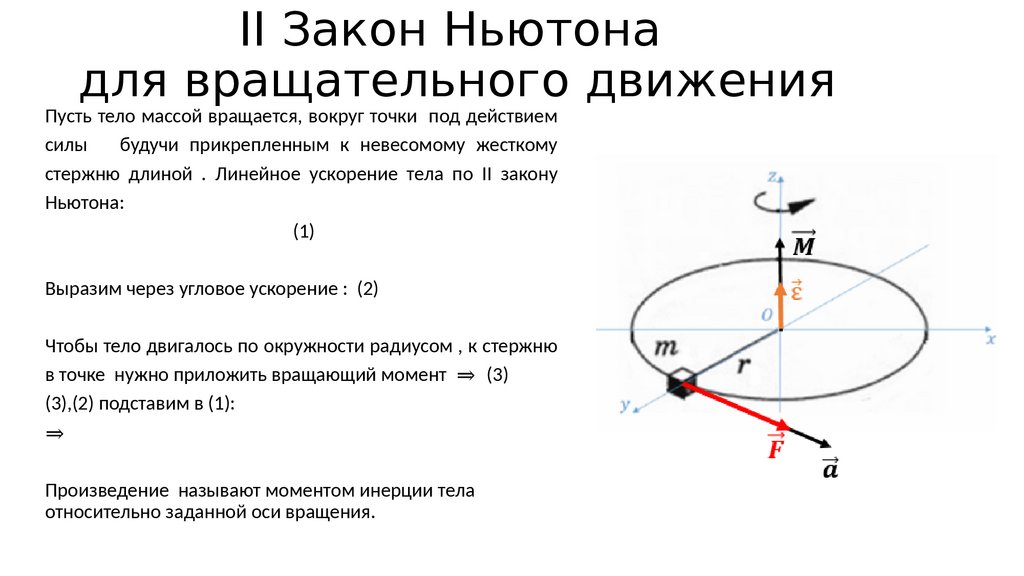

Вектор момента силы F относительно точки A будет равен векторному произведению вектора r и вектора силы. Вектор r — это вектор из точки А в любую точку на линии действия силы.

Здесь важно отметить, что все величины ( r , F и M ) являются векторами. Прежде чем вы сможете найти векторное произведение, вам нужно будет записать r и F в векторной компонентной форме. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента r и F векторы. Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для расчетов.

Полученный вектор момента совпадет с осью вращения для данного момента, где вы можете использовать правило правой руки, чтобы определить, движется ли момент по часовой стрелке или против часовой стрелки вокруг этой оси.

Результат пересечения r F даст нам вектор момента. Для этой двумерной задачи вектор момента указывает в положительном направлении z. Мы можем использовать правило правой руки, чтобы определить направление вращения с момента (выровняйте большой палец правой руки с вектором момента, и наши согнутые пальцы будут указывать в направлении вращения с момента).

Наконец, также важно отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным. Это означает, что порядок векторов имеет значение, и r пересечение F не будет таким же, как F пересечение r . Важно всегда использовать r крест F при расчете моментов.

Видео-вопрос: Определение величины момента вектора силы, действующей в точке в трех измерениях

Стенограмма видео

Если в точке 𝐴 пять, минус восемь, 11 действует сила 𝐅, равная шести 𝐢 минус семь 𝐣 минус восемь 𝐤, найти модуль составляющей момента 𝐅 относительно оси 𝑦.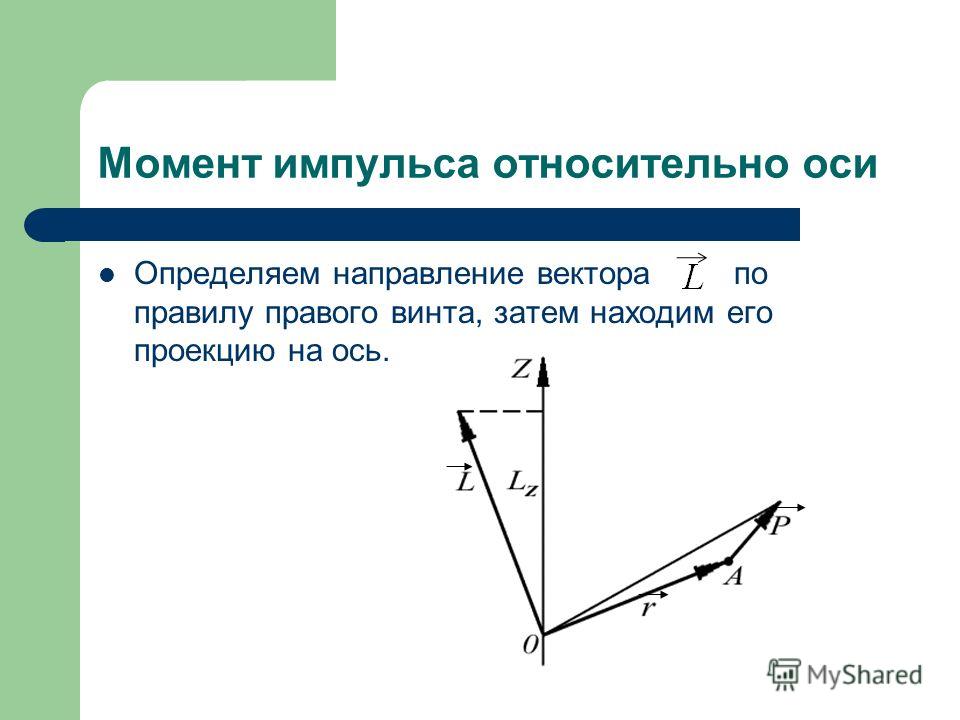

Начнем с того, что нарисуем схему ситуации. Нам говорят, что точка 𝐴 имеет 𝑥-координату пять, 𝑦-координату минус восемь и 𝑧-координату 11. Примерно так. Нам говорят, что в этой точке действует вектор силы 𝐅, равный шести 𝐢 минус семь 𝐣 минус восемь 𝐤. Таким образом, мы можем нарисовать этот вектор силы в виде стрелки на нашей диаграмме. Теперь нас просят найти величину составляющей момента 𝐅 относительно оси 𝑦. Давайте разберем это шаг за шагом, чтобы мы могли точно увидеть, о чем здесь идет речь.

Во-первых, можно вспомнить, что момент, то есть вращательная сила, может быть представлен вектором. Как правило, мы можем назвать этот вектор 𝐌. Теперь мы можем вычислить этот вектор 𝐌, найдя векторное перекрестное произведение вектора положения, в котором действует сила, относительно точки, относительно которой мы вычисляем моменты, и самого вектора силы. Таким образом, вычисление этого перекрестного произведения говорит нам о моменте, создаваемом силой 𝐅. Другими словами, он сообщает нам момент 𝐅.

Теперь, когда мы вычисляем векторное произведение двух трехмерных векторов, таких как 𝐑 и 𝐅, результатом является вектор с одинаковым количеством измерений. Это означает, что когда мы вычисляем вектор моментов 𝐌, мы получаем трехмерный вектор. И мы можем записать компоненты как 𝐌 𝑥 раз 𝐢 шляпа плюс 𝐌 𝑦 раз 𝐣 шляпа плюс 𝐌 𝑧 раз 𝐤 шляпа. Каждое из этих условий является одной из составляющих момента.

Мы видим, что вопрос требует от нас величины одного из компонентов. В частности, это после величины компонента относительно оси 𝑦. Чтобы понять, что это значит, вспомним, что направление вектора момента параллельно оси вращения момента. Это означает, что 𝑥-компонента вектора момента описывает компонент этого момента, который вращается вокруг оси, указывающей в 𝑥-направлении. 𝑦-компонента вектора момента описывает компонент этого момента, который вращается вокруг оси, указывающей в 𝑦-направлении. А 𝑧-компонента этого вектора момента описывает компонент момента, который вращается вокруг оси, указывающей в 𝑧-направлении.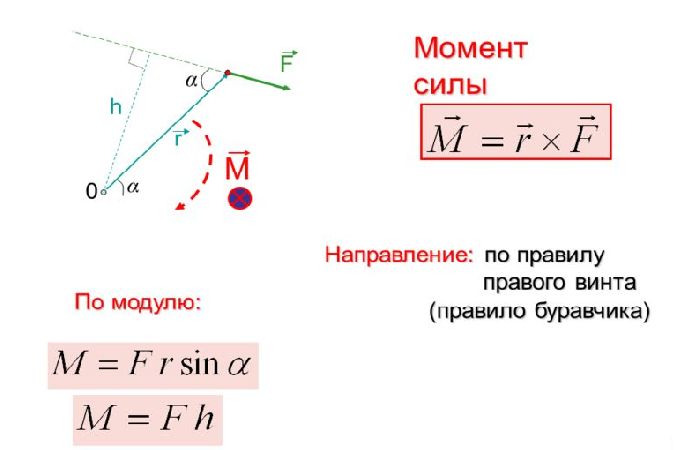

Это означает, что если мы вычисляем момент относительно начала координат, то, например, 𝑥-компонента вектора момента описывает компонент момента, который вызывает вращение вокруг самой 𝑥-оси. Точно так же 𝑦-компонента вектора момента описывает компонент момента, который вызывает вращение вокруг 𝑦-оси, о чем нас и спрашивает вопрос.

Наконец, тот факт, что в вопросе просто указывается величина этого компонента, просто означает, что нам нужно указать размер этого векторного компонента, не записывая его как вектор. Этот бит довольно прост. Если 𝑦-компонента 𝐌 𝑦 умножить на 𝐣 шляпу, то единичный вектор 𝐣 шляпа просто говорит нам направление этого вектора. Он указывает в 𝑦-направлении. А величина вектора просто задается 𝐌 𝑦. Итак, чтобы найти то, что ищет этот вопрос, нам нужно рассчитать момент, создаваемый силой 𝐅 относительно начала координат. А для этого нам нужно найти векторное произведение этих двух векторов.

Помните, что вектор 𝐑 — это вектор положения точки, в которой действует сила, в данном случае 𝐴, относительно точки, относительно которой мы вычисляем моменты.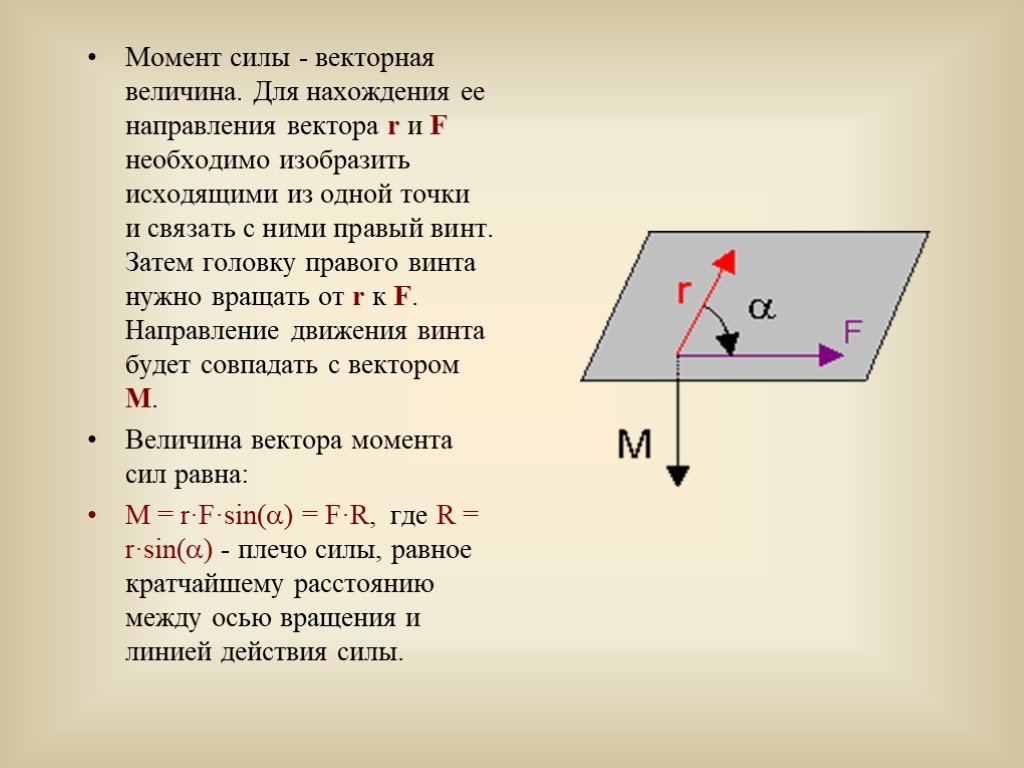 В данном случае это происхождение. Таким образом, вектор 𝐑 — это вектор положения, идущий от начала координат к точке 𝐴. Это означает, что 𝐑, записанное как сумма его компонентов, эффективно задается координатами точки 𝐴, умноженными на соответствующие единичные векторы. Таким образом, мы можем сказать, что 𝐑 равно пятикратному 𝐢 шляпе минус восьмикратному 𝐣 шляпе плюс 11𝐤 шляпе.

Чтобы вычислить перекрестное произведение 𝐑 и 𝐅, нам нужно найти определитель этой матрицы три на три, где элементы в верхней строке матрицы — это три используемых нами базисных вектора. Элементы в средней строке матрицы — это три компонента первого вектора, который мы перемножаем. В данном случае это 𝐑. А элементы в нижней строке — это компоненты второго вектора, который мы перемножаем, в данном случае 𝐅. Обратите внимание, что здесь важен порядок 𝐑 и 𝐅. Перекрестное произведение 𝐑 и 𝐅 не совпадает с перекрестным произведением 𝐅 и 𝐑.

Эффективно вычисление определителя этой матрицы состоит из трех частей.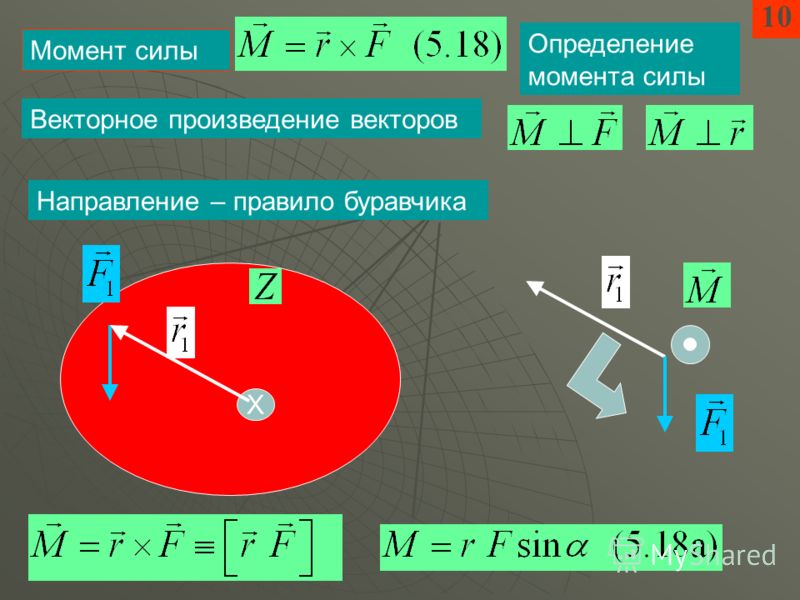 Во-первых, у нас есть единичный вектор 𝐢 шляпа, умноженный на 𝐑 𝑦 раз 𝐅 𝑧 минус 𝐑 𝑧 раз 𝐅 𝑦. Затем мы вычитаем единичный вектор 𝐣 шляпу, умноженный на 𝐑 𝑥 раз 𝐅 𝑧 минус 𝐑 𝑧 раз 𝐅 𝑥. И, наконец, у нас есть единичный вектор 𝐤 шляпа, умноженный на 𝐑 𝑥 раз 𝐅 𝑦 минус 𝐑 𝑦 раз 𝐅 𝑥. Эти три члена являются 𝑥-, 𝑦- и 𝑧-компонентами вектора момента 𝐌. Однако, поскольку нас интересует только величина компонента этого вектора момента, который проходит вокруг оси 𝑦, это означает, что нас интересует только этот средний член. Величина этого компонента задается отрицательным числом 𝐑 𝑥, умноженным на 𝐅 𝑧 минус 𝐑 𝑧, умноженным на 𝐅 𝑥.

𝐑 𝑥 — величина 𝑥-компоненты вектора смещения 𝐑. В данном случае это пять. А 𝐅 𝑧 — величина 𝑧-компоненты вектора силы 𝐅. Это минус восемь. 𝐑 𝑧 — величина 𝑧-компоненты 𝐑, равной 11. А 𝐅 𝑥 — величина 𝑥-компоненты 𝐅, равной шести. В целом, это дает нам минус пять раз минус восемь минус 11 раз шесть. Пять раз минус восемь — это минус 40, а 11 раз шесть — это 66. Минус 40 минус 66 — это минус 106.