Правило левой руки для силы Ампера – примеры и формулировка определения кратко
4
Средняя оценка: 4
Всего получено оценок: 63.
Обновлено 12 Января, 2021
4
Средняя оценка: 4
Всего получено оценок: 63.
Обновлено 12 Января, 2021
Из курса физики известно, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Для определения направления этой силы используется специальное правило, называемое правилом левой руки. Поговорим кратко об этом правиле.
Сила и закон Ампера
На заряд, движущийся в магнитном поле, действует со стороны этого поля сила, называемая силой Лоренца.
Рис. 1. Сила Лоренца.Если в магнитное поле помещен проводник с током, то силы Лоренца, действующие на движущиеся носители заряда в этом проводнике, складываются в силу, называемую силой Ампера.
Модуль силы Ампера рассчитывается по закону Ампера:
$$F= I |\overrightarrow B| Δl sin \alpha,$$
где:
- $F$ — модуль силы Ампера;
- $I$ — величина тока в проводнике;
- $Δl$ — длина проводника;
- $\alpha$ — угол между линиями магнитного поля и направлением тока в проводнике.

Направление силы Ампера
Обычно действие сил совпадает с направлением движения тел или с направлением на источник силы. В случае с силой Ампера ситуация иная.
Направление действия силы Ампера не совпадает ни с направлением движения тока, ни с направлением вектора магнитной индукции. Сила Ампера направлена перпендикулярно обоим этим направлениям. То есть, если линии магнитного поля направлены по вертикали, а проводник расположен горизонтально слева направо, то сила Ампера будет направлена вдоль линии «вперед-назад». Причем ее направление также будет зависеть от направлений магнитной индукции и электрического тока в проводнике. «Просто запомнить» все направления невозможно. Поэтому для силы Ампера установили специальное мнемоническое правило левой руки.
Правило левой руки
Формулировка правила левой руки для силы ампера звучит так:
Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения тока в проводнике, а перпендикулярная составляющая индукции $B_{\perp}$ входила в ладонь, то отставленный большой палец покажет направление силы Ампера.
Как пользоваться этим правилом? Разберем примеры.
- Допустим, проводник расположен горизонтально, и ток по нему идет вперед. Следовательно, четыре пальца левой руки надо вытянуть вперед по этому направлению.
- Теперь допустим, что линии магнитного поля направлены сверху вниз (сверху «север» подковообразного магнита, снизу — «юг»). Следовательно, левую руку надо повернуть ладонью вверх, чтобы линии магнитного поля входили в ладонь и «прокалывали» ее (четыре пальца по-прежнему должны быть вытянуты вперед).
- Отставленный большой палец левой руки будет направлен влево. Это и есть направление силы Ампера для данной ситуации.
Другой пример.
- Пусть проводник расположен вертикально. А магнитное поле направлено справа налево (справа «север» магнита, слева — «юг»).
- Располагаем левую руку четырьмя пальцами вверх. Ладонь открытой стороной должна «смотреть вправо», чтобы магнитные линии входили и «прокалывали» ее.

- Отставленный большой палец покажет назад. Именно так и будет направлена сила Ампера в данном случае.
Обратите внимание, что силу Ампера порождает только перпендикулярная составляющая магнитного поля. А значит, руку надо располагать так, чтобы линии магнитного поля всегда входили в нее под углом, максимально близким к прямому.
Особым случаем является ситуация, когда направление тока и магнитной индукции совпадает. В этом случае руку невозможно расположить так, чтобы линии магнитной индукции входили в нее. Следовательно, силы Ампера здесь не возникнет. В самом деле, если линии магнитной индукции параллельны направлению тока, то перпендикулярная составляющая этих линий равна нулю, и значение силы Ампера в вышеприведенной формуле также равно нулю.
Рис. 3. Различные случаи применения правила левой руки.Что мы узнали?
Для определения направления силы Ампера используется специальное мнемоническое правило левой руки. С помощью этого правила можно не только определить направление силы Ампера, но и обнаружить случай, когда сила Ампера равна нулю.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 63.
А какая ваша оценка?
|
Заглавная страница
КАТЕГОРИИ: Археология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
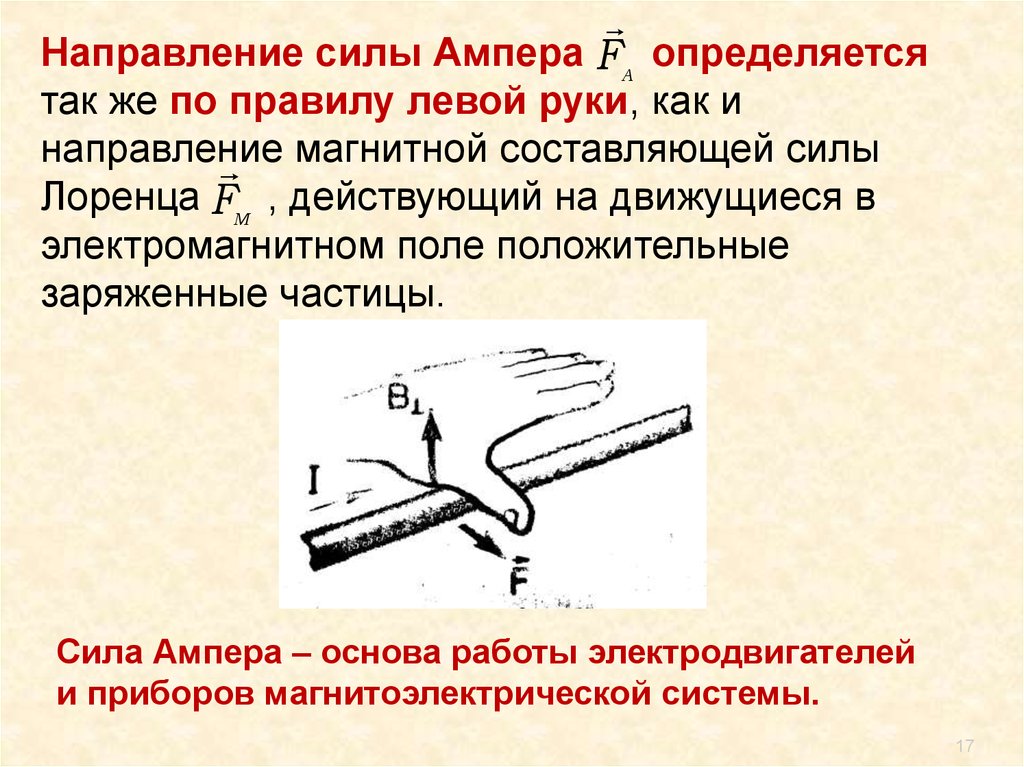
⇐ ПредыдущаяСтр 5 из 5 Правило левой руки :если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90°большой палец, укажет направление силы Ампера.
27.Геометрическая оптика.Показатель преломления. Законы отражения и преломления света . Полное внутреннее отражение . Преломление– изменение направления света при переходе из одной прозрачной среды в другую.АО – падающий луч, ОВ – преломленный луч ОС — к границе раздела двух сред, α — угол падения, β – угол преломления, n12 [1] – относительный показатель преломления, n1, n2 [1]- абсолютные показатели преломления 1-й и 2-й среды,v1, v2[м/с] – скорость света в 1-й и 2-й среде, с = 3*108 – скорость света вакууме Рассмотрим переход света из воздуха в стекло α >β. Законы преломления.1) n= n12= При изменении угла падения меняется угол преломления, но отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных 2-х сред и называется относительным показателем преломления второй среды(стекло) по отношению к первой(воздух), следствие: падающий и преломленный лучи обратимы.2). Падающий, преломленный лучи и перпендикуляр, к границе 2-х сред, восстановленный в точке падения луча, лежат в одной плоскости.  Полное отражение.Рассмотрим переход света из плотной среды (стекло) в менее плотную (воздух). Тогда = = α <βЕсли α < αпр., то β <900, В основе геометрической оптики лежат след.утверждения 28.Поглащение света . Законы Бугера и Бера Где a(альфа) — натуральный показатель поглощения. Зако́н Бугера — Ламберта — Бера — физический закон, определяющий ослабление параллельногомонохроматического пучка света при распространении его в поглощающей среде. Закон выражается следующей формулой: , где — интенсивность входящего пучка, — толщина слоя вещества, через которое проходит свет, —показатель поглощения
29.Тепловое излучение . Законы Стефана-Больцмана и Вина Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимостьмощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
где ε — степень черноты (для всех веществ ε < 1, для абсолютно черного тела ε = 1). При помощи законаПланка для излучения, постоянную σ можно определелить как
Фотоэлектрический эффект Фотоэффектомназывается явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передается электронам вещества. ⇐ Предыдущая12345 Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
22.9: Магнитные поля, создаваемые токами – Закон Ампера
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2703
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Вычислять ток, создающий магнитное поле.
- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.
Какой ток необходим для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.
Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.
Магнитное поле, создаваемое длинным прямым проводом с током: правило правой руки 2
Магнитные поля имеют как направление, так и величину. Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рисунке \(\PageIndex{1}\). Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Правило правой руки 2 (RHR-2) вытекает из этого исследования и действительно для любого текущего сегмента — указывают большим пальцем в направлении тока, а пальцы скручиваются в направлении создаваемых им петель магнитного поля .
Правило правой руки 2 (RHR-2) вытекает из этого исследования и действительно для любого текущего сегмента — указывают большим пальцем в направлении тока, а пальцы скручиваются в направлении создаваемых им петель магнитного поля .

Пример \(\PageIndex{1}\): расчет силы тока, создающего магнитное поле провод. 9{-7} T \cdot m / A} \\[5pt] &= 25 A. \end{align*} \]
Обсуждение:
Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см из длинной прямой проволоки. Обратите внимание, что ответ указан только с двумя цифрами, поскольку в этом примере поле Земли указано только с двумя цифрами.
Закон Ампера и др.
Магнитное поле длинного прямого провода имеет больше значений, чем вы можете предположить на первый взгляд. Каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком. Формальная формулировка направления и величины поля, создаваемого каждым сегментом, называется Законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому Законом Ампера , который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в 22.
Это приводит к более полному закону, называемому Законом Ампера , который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в 22. 4, концентрируясь на полях, создаваемых в некоторых важных ситуациях.
4, концентрируясь на полях, создаваемых в некоторых важных ситуациях.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ОТНОСИТЕЛЬНОСТЬ:
Слушая все, что мы делаем об Эйнштейне, иногда создается впечатление, что он изобрел теорию относительности из ничего. Напротив, одним из мотивов Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле, создаваемое круглой петлей с током
Магнитное поле вблизи проволочной петли с током показано на рисунке \(\PageIndex{2}\). Как направление, так и величина магнитного поля, создаваемого петлей с током, сложны. RHR-2 можно использовать для указания направления поля вблизи петли, но для более подробной информации необходимо картографирование с помощью компаса и правил относительно линий поля, приведенных в разделе 22.4. Есть простая формула для напряженность магнитного поля в центре круглой петли . Это
\[B = \frac{\mu_{0}I}{2R}\left(в \quad center \quad of \quad loop\right),\label{22. 10.3}\]
10.3}\]
, где \(R\) — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но оно действительно только в центре круглой петли из проволоки. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре контура. Один из способов получить большее поле — это иметь \(N\) петель; тогда поле равно \(B = N \mu_{0} I / \left(2R\right)\). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, поскольку ток проходит дальше.
Рисунок \(\PageIndex{2}\): (a) RHR-2 показывает направление магнитного поля внутри и снаружи контура с током. (b) Более детальное картографирование с помощью компаса или зонда Холла дополняет картину. Поле похоже на поле стержневого магнита.Магнитное поле, создаваемое токопроводящим соленоидом
Соленоид представляет собой длинную катушку провода (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. На рисунке \(\PageIndex{3}\) показано, как выглядит поле и как его направление задается RHR-2.
Поле сразу за катушками почти равно нулю. На рисунке \(\PageIndex{3}\) показано, как выглядит поле и как его направление задается RHR-2.
Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Лишь ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет такую же сложность, как и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто \[B = \mu_{0}nI \left(внутри \quad a \quad соленоида\right),\label{10.22.4}\], где \(n\) количество петель на единицу длины соленоида (\(n = N/l\), где \(N\) — количество петель, а \(l\) — длина). Обратите внимание, что \(B\) — это напряженность поля в любом месте однородной внутренней области, а не только в центре. Большие однородные поля, распределенные по большому объему, возможны с соленоидами, как следует из примера.
Большие однородные поля, распределенные по большому объему, возможны с соленоидами, как следует из примера.
Обсуждение
Это большая напряженность поля, которую можно установить над соленоидом большого диаметра, например, при медицинском использовании магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, согнутый в окружность. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
ИССЛЕДОВАНИЯ PHET: ГЕНЕРАТОР
Генерируйте электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.
Резюме
- Сила магнитного поля, создаваемого током в длинном прямом проводе, определяется выражением \[B = \frac{\mu_{0}I}{2 \pi r} \left(long \quad Straight \quad wire\right), \nonumber\] где \(I\) — ток, \(r\) — кратчайшее расстояние до провода, а константа \(\mu_{0} = 4\pi \times 10^{-7} T \cdot m/a\) — проницаемость свободного пространства.

- Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а остальные пальцы согните в направлении магнитного поля. петли поля , созданные им.
- Магнитное поле, создаваемое током, следующим по любому пути, представляет собой сумму (или интеграл) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общей зависимости между током и полем, известной как закон Ампера. .
- Напряженность магнитного поля в центре круглой петли определяется выражением \[B = \frac{\mu_{0}I}{2R} \left(в \quad center \quad of \quad loop\right), \ nonumber\] где \(R\) — радиус петли. Это уравнение принимает вид \(B = \mu_{0}nI/\left(2R\right)\) для плоской катушки из \(N\) петель. РХР-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
- Напряженность магнитного поля внутри соленоида равна \[B = \mu_{0}nI \left(внутри \quad a \quad solenoid\right), \nonnumber\], где \(n\) — количество витков на единицу длина соленоида.
 Поле внутри очень однородно по величине и направлению.
Поле внутри очень однородно по величине и направлению.
Глоссарий
- Правило правой руки 2 (RHR-2)
- правило для определения направления магнитного поля, создаваемого проводом с током: направьте большой палец правой руки в направлении тока, а пальцы согните в направлении петель магнитного поля
- напряженность магнитного поля (величина), создаваемая длинным прямым проводом с током
- определяется как \(B=\frac{μ_0I}{2πr}\), где I — сила тока, \(r\) — кратчайшее расстояние до провода, а \(μ_0\) — проницаемость свободного пространства 9{−7}Тл⋅м/А\)
- напряженность магнитного поля в центре круглой петли
- определяется как \(B=\frac{μ_0I}{2R}\), где \(R\) — радиус петли
- соленоид
- тонкая проволока, намотанная в катушку, которая создает магнитное поле при пропускании через нее электрического тока
- напряженность магнитного поля внутри соленоида
- определяется как \(B=µ0nI\), где \(n\) — количество витков на единицу длины соленоида (\(n=N/l\), где \(N\) — количество витков и \(l\) длина)
- Закон Био-Савара
- физический закон, описывающий магнитное поле, создаваемое электрическим током, с помощью определенного уравнения
- Закон Ампера
- физический закон, утверждающий, что магнитное поле вокруг электрического тока пропорционально току; каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком
- Уравнения Максвелла
- набор из четырех уравнений, описывающих электромагнитные явления
Эта страница под названием 22. 9: Магнитные поля, создаваемые токами — Закон Ампера распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
9: Магнитные поля, создаваемые токами — Закон Ампера распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Закон Амепера
- Закон Био-Савара
- Напряженность магнитного поля
- напряженность магнитного поля в центре круглой петли
- напряженность магнитного поля внутри соленоида
- Уравнения Максвелла
- проницаемость свободного пространства
- правило правой руки
- соленоид
- источник@https://openstax.
 org/details/books/college-physics
org/details/books/college-physics
Три правых правила электромагнетизма – Arbor Scientific
Джеймс ЛинкольнНажмите здесь, чтобы подписаться на нашу рассылку новостей CoolStuff и получать уведомления о выпуске следующего блога.
Преподавание электричества и магнетизма осложняется тем, что магнитные силы перпендикулярны движению частиц и токов. Для этого требуется трехмерная перспектива, которая может ввести переменную «неправильного» направления. Чтобы избежать ошибок, будем «правы» и воспользуемся правилом правой руки.
Кто-то скажет, что существует только одно правило правой руки, но я считаю, что соглашение о трех отдельных правилах для наиболее распространенных ситуаций очень удобно.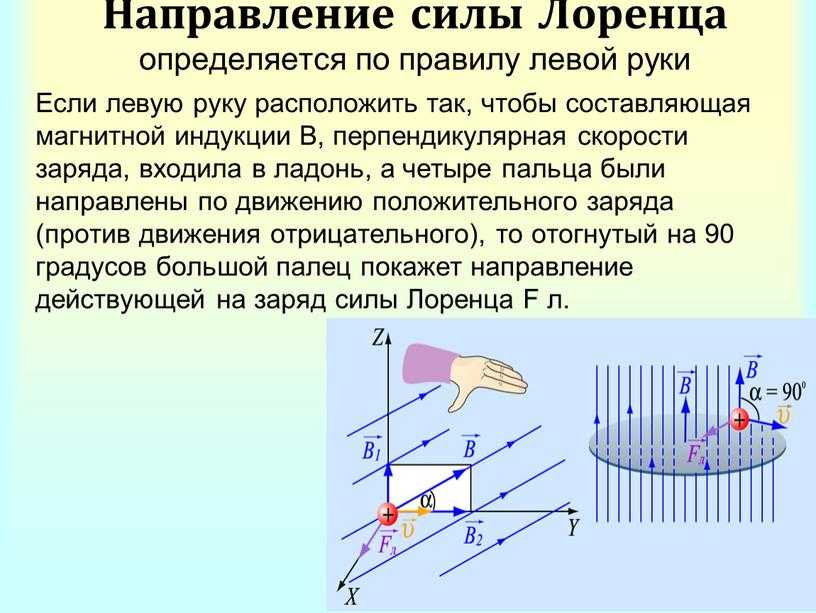 Это для (1) длинных прямых проводов, (2) свободно движущихся зарядов в магнитных полях и (3) правила соленоида, которые представляют собой петли тока. Назвать эти правила правильнее. Это не законы природы, а условности человечества. Мы используем правила, чтобы помочь нам решить проблемы, законы должны быть основной причиной того, почему правила работают.
Это для (1) длинных прямых проводов, (2) свободно движущихся зарядов в магнитных полях и (3) правила соленоида, которые представляют собой петли тока. Назвать эти правила правильнее. Это не законы природы, а условности человечества. Мы используем правила, чтобы помочь нам решить проблемы, законы должны быть основной причиной того, почему правила работают.
Электричество и Магнетизм — связанные явления, но под прямым углом друг к другу. Таким образом, мы используем соглашение правой руки, чтобы предсказать направление полей относительно друг друга.
Правило №1 – Закон Эрстеда
Наш рассказ начинается с демонстрации Эрстеда, которая впервые была проведена во время лекции в 1821 году. Что Эрстед впервые показал, что при прохождении провода с током стрелка компаса – которая является магнитом – стрелка отклоняется. Когда он находится под магнитом, он отклоняется в другую сторону. Направление, на которое указывает магнит, параллельно магнитному полю вокруг провода.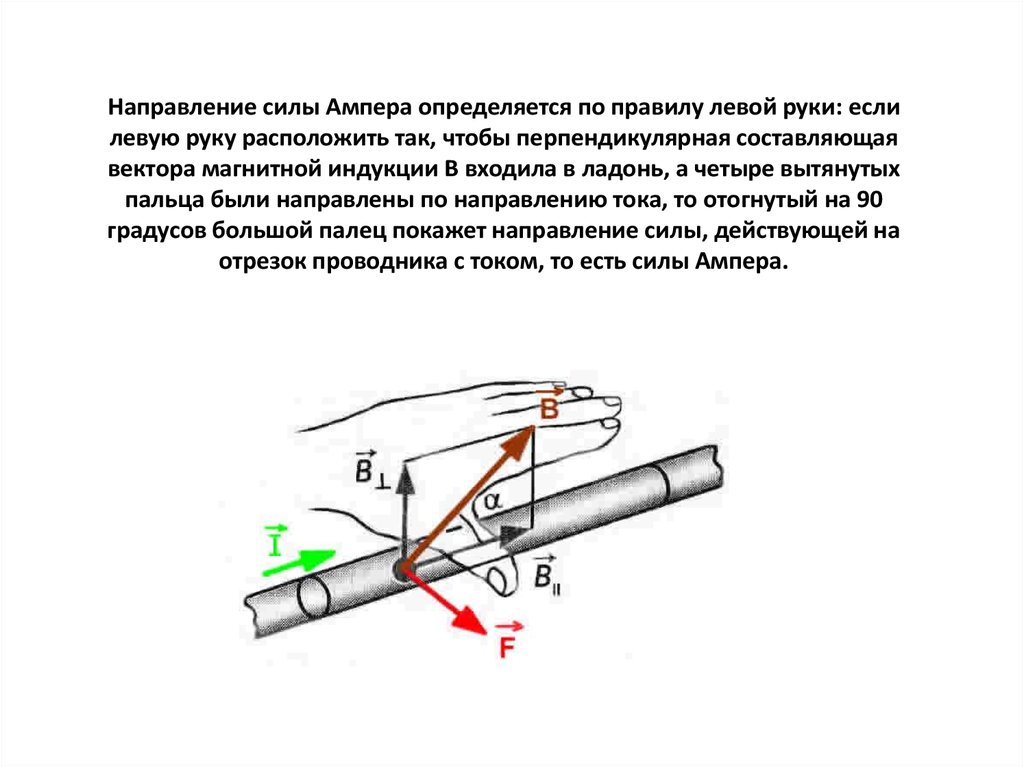 И вы можете предсказать это с вашей правой рукой!
И вы можете предсказать это с вашей правой рукой!
Датский физик и химик Ханс Кристиан Эрстед
Направьте большой палец правой руки вдоль потока тока, определяемого как поток положительного заряда. Теперь согните пальцы, как будто они обвивают проволоку. Направление, на которое указывают ваши пальцы, — это направление магнитного поля, создаваемого током. Иногда мне нравится называть это ПРАВОСТОРОННИМ ИЗОБРАЖЕНИЕМ или законом Ампера. Сам Ампер описал это как циферблат часов: если ток течет по циферблату часов, то магнитное поле будет вращаться по часовой стрелке.
Хороший способ продемонстрировать это явление — использовать набор маленьких прозрачных компасов. Когда они намотаны на вертикальный провод без тока, все они изначально будут указывать на север. Но, если ток включен, компасы будут выравниваться по петле вокруг тока. Важно отметить, что компасы влияют друг на друга, поэтому определение правильного расстояния между ними может помочь сделать демонстрацию более драматичной.
Воспроизвести демонстрацию Эрстеда довольно легко. Я использую около 5 ампер.
По мере того, как ток течет вверх, магнитное поле закручивается.
Обычно они просто указывают на север, но когда я включаю ток, мы видим, что все они указывают вокруг него, точно так же, как мы предсказываем правой рукой.
Правило № 2. Сила Лоренца
Это второе правило правой руки обычно применяется к свободно движущимся зарядам, называемым катодными лучами, или к другим видам электрического тока.
Экран компьютера с электронно-лучевой трубкой — один из ярких способов продемонстрировать силу Лоренца. Экран освещается движущимися электронами, а движущиеся заряды толкаются магнитными полями. Это неожиданно для многих людей, которые думают, что магниты воздействуют только на такие металлы, как железо и никель. (После использования ЭЛТ просто оставьте его отключенным на несколько минут, и это почти полностью восстановит исходный цвет экрана.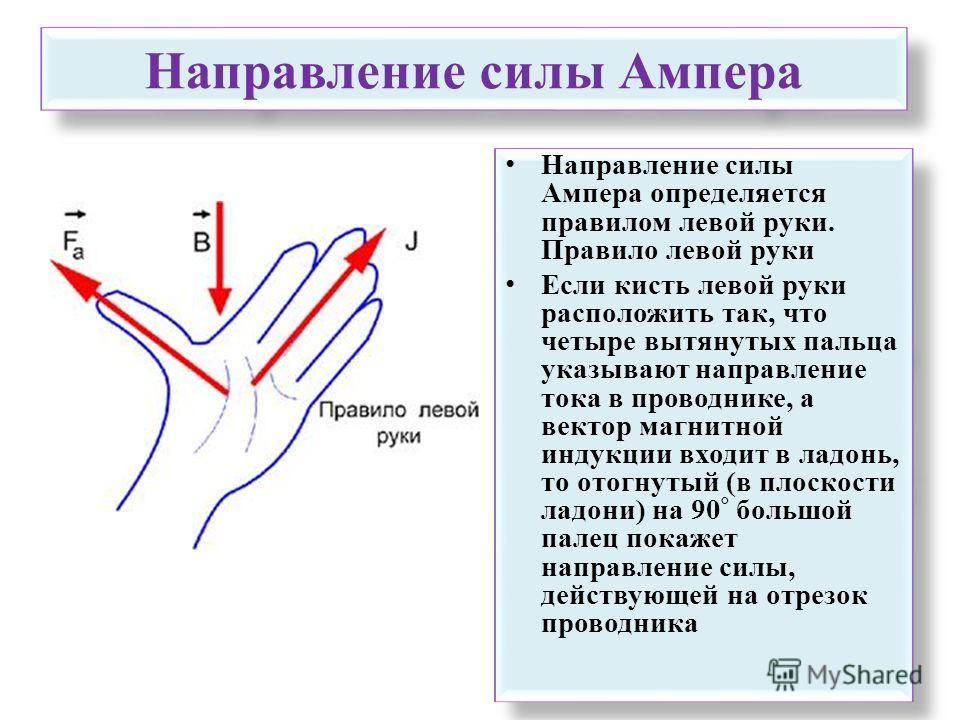 )
)
Этот экран компьютера с электронно-лучевой трубкой изначально был полностью красным. Но эти магниты отклонили электроны от приземления на их правильные пиксели.
Поскольку электрический ток состоит из движущихся зарядов, мы также можем перемещать его с помощью магнитов. Один из способов показать это — с помощью электрического качающегося аппарата. Это подчеркнет, что ток, поле и сила находятся под прямым углом.
Используя правую руку, ток течет от плюса к минусу – большой палец. Магнитное поле – указательный палец – направлено с севера на юг (обычно это означает от красного к синему). Сила тока перпендикулярна обоим из них и определяется вашим средним пальцем 9.0032
Это правило 2 nd обычно называют силой Лоренца по имени Г. А. Лоренца, современника Эйнштейна, хотя его действие было известно еще во времена Майкла Фарадея.
Теперь некоторые люди и некоторые книги предпочитают использовать ладонь для представления силы, которая будет текущей силой поля (открытая ладонь).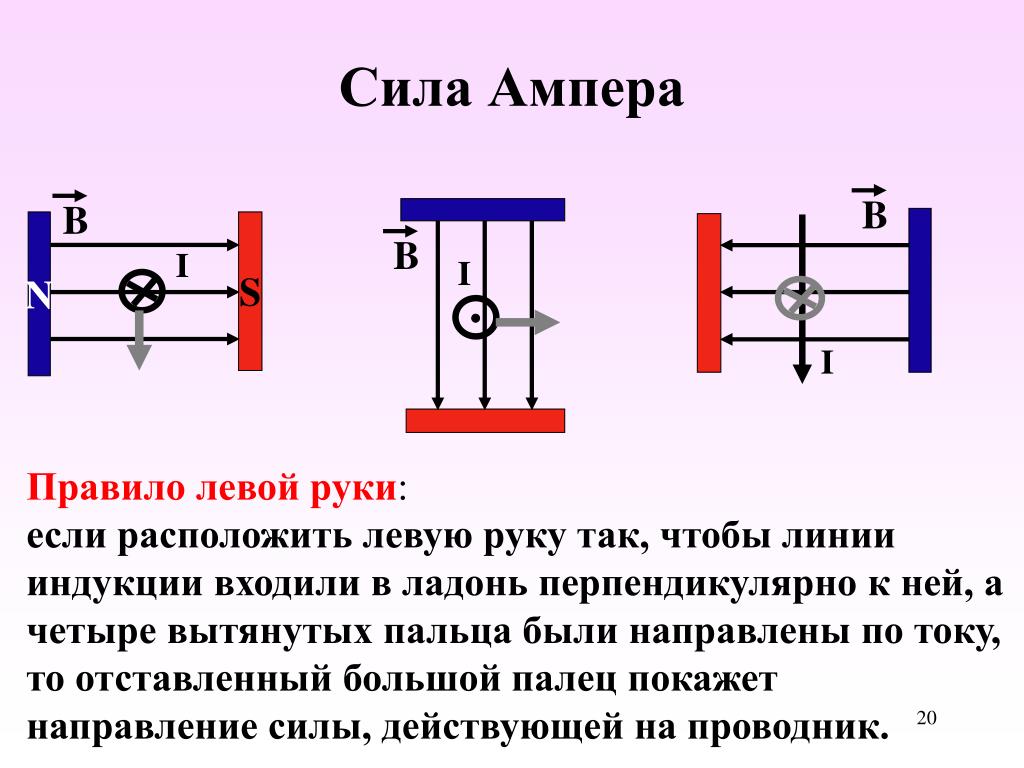
Магнитное поле действует на ток в 3D.
Пальцы направлены по векторам правой рукой.
Еще один способ продемонстрировать это — демонстрация лампочки «Электричество и магнетизм». Когда есть переменный ток, провод вибрирует, но когда это постоянный ток, мы можем приложить усилие в определенном направлении. Используя правую руку, можно предсказать направление течения.
Нити накала лампы Эдисона отклоняются.
Для течения токов, представляющих собой воображаемый поток положительного заряда, уместно использовать правую руку. Но когда дело доходит до отрицательных токов, таких как электроны, уместно использовать левую руку, что дает результат, противоположный положительному заряду. Если кто-то хочет продемонстрировать силу Лоренца на ЭЛТ, полезно знать, чтобы подчеркнуть «использовать правило левой руки для отрицательных зарядов».
Правило №3 – Правило соленоида
Соленоид с воздушным сердечником может действовать как стержневой магнит. Отталкивая север и притягивая юг. На самом деле, если вы проследите магнитное поле с помощью компаса, вы увидите, что оно идеально соответствует поведению стержневого магнита.
Отталкивая север и притягивая юг. На самом деле, если вы проследите магнитное поле с помощью компаса, вы увидите, что оно идеально соответствует поведению стержневого магнита.
Используя третье правило правой руки, мы можем предсказать, какая сторона катушки находится на севере.
Пусть ваши скрученные пальцы будут направлением течения. Он зацикливается. Тогда ваш большой палец будет СЕВЕРНЫМ концом электромагнита.
Соленоид ведет себя точно так же, как стержневой магнит с четко определенными северным и южным полюсами.
Северный конец соленоида отталкивает северный конец этого стержневого магнита.
Правило левой руки
Правило правой руки предполагает условный ток , то есть… ток течет от положительного к отрицательному. Все курсы в колледже соответствуют этой концепции. НЕ ВСЕ курсы физики в старших классах используют эту концепцию. Например, в некоторых средних школах используются правила «левой руки», потому что они имеют дело с ПОТОКОМ ЭЛЕКТРОНОВ, то есть… потоком тока от отрицательного к положительному (например, направление, в котором электроны текут от батареи).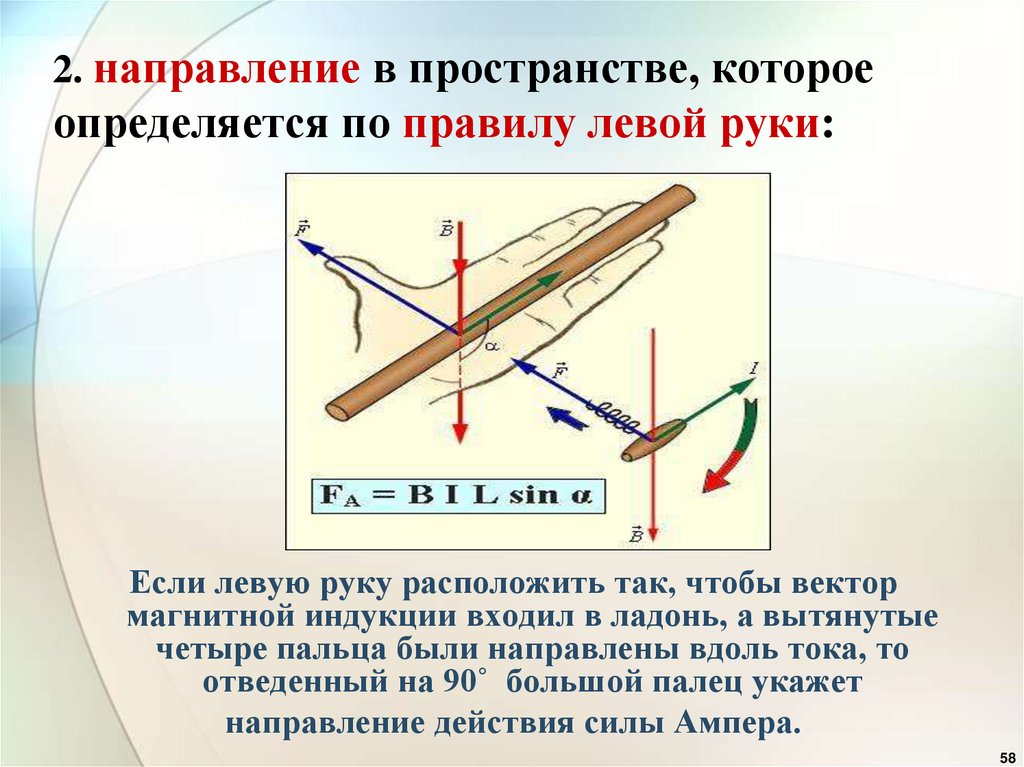




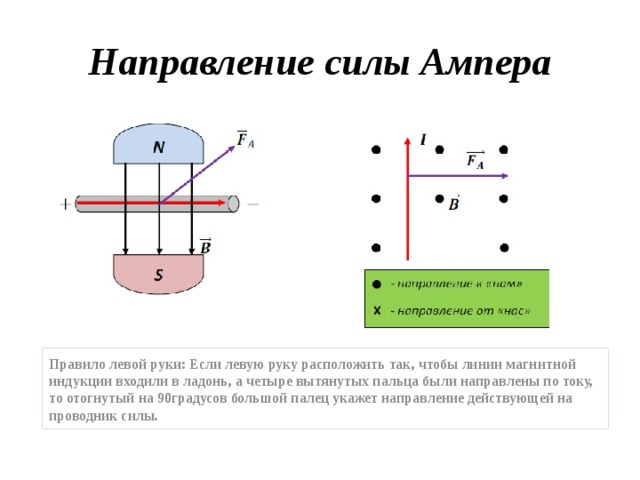
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

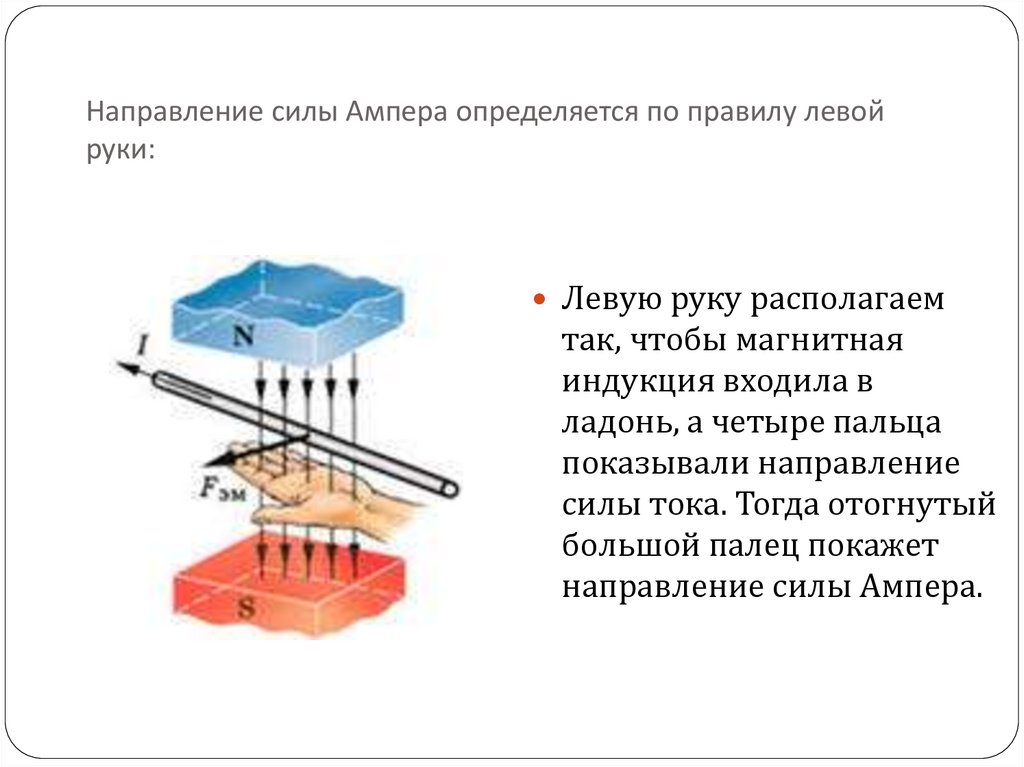 , то β >900 — полное отражение, αпр [град] – предельный угол
, то β >900 — полное отражение, αпр [град] – предельный угол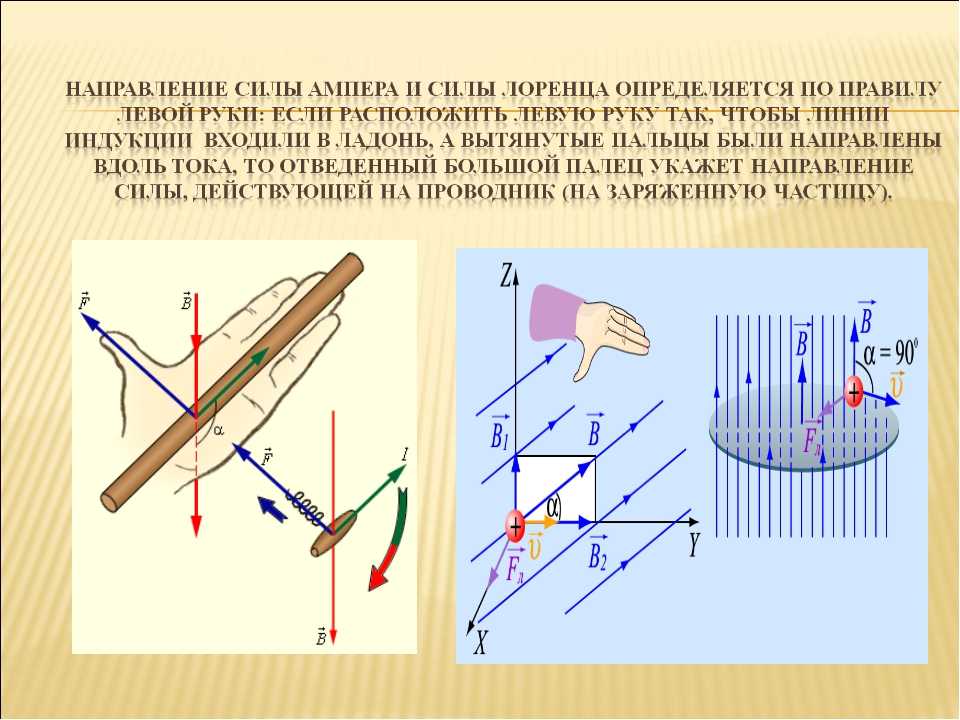 Натуральный показатель поглощения зависит от природы и состояния вещества, а также от частоты (длины волны) света.
Натуральный показатель поглощения зависит от природы и состояния вещества, а также от частоты (длины волны) света. (−3)м ⋅ К . Закон Вина – закон смещения т.к. он показывает смещение положения максимума функции по мере возрастания температуры в область коротких длин волн. Он объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение.
(−3)м ⋅ К . Закон Вина – закон смещения т.к. он показывает смещение положения максимума функции по мере возрастания температуры в область коротких длин волн. Он объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение.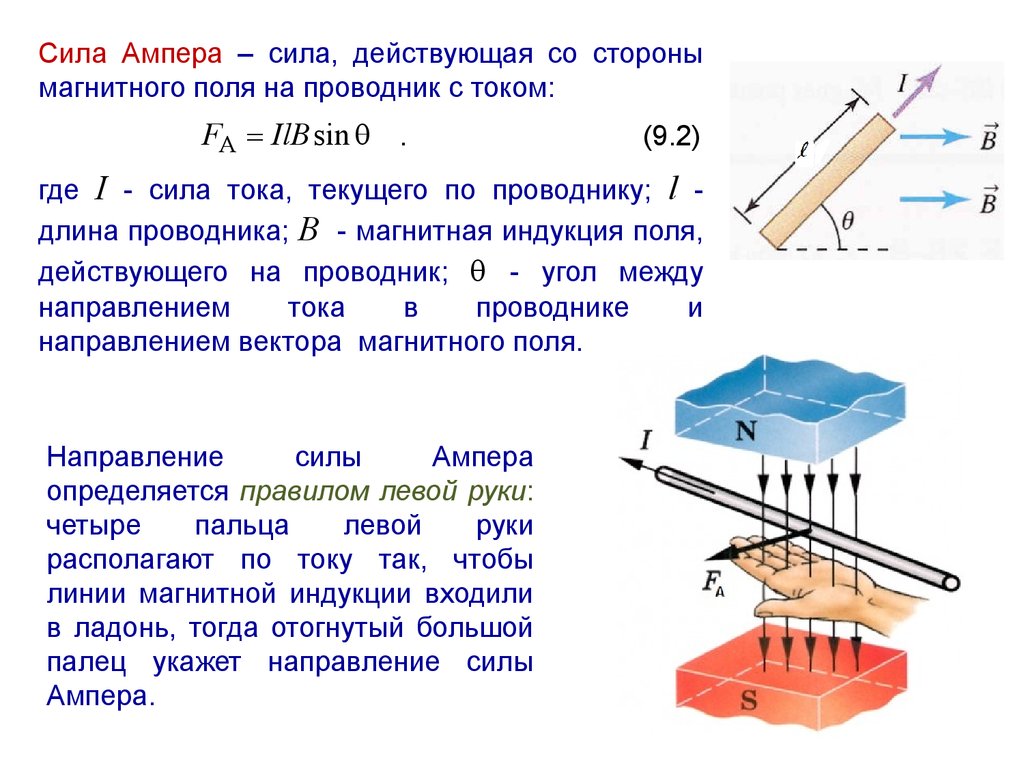 Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.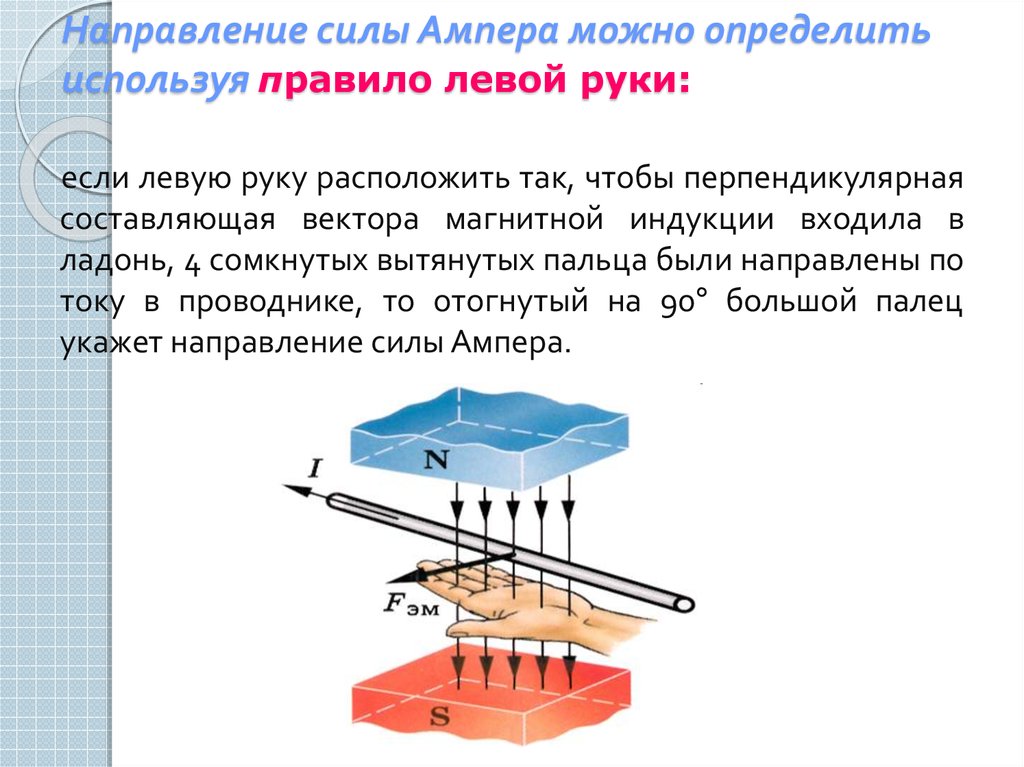 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
 Поле внутри очень однородно по величине и направлению.
Поле внутри очень однородно по величине и направлению. org/details/books/college-physics
org/details/books/college-physics