Метод наложения токов. Пример решения
Наряду с методом контурных токов для анализа электрических цепей используется другой метод – метод наложения. Этот метод основан на принципе наложения, который применяется только к линейным системам.
Метод наложения относительно прост, и в основном применяется для не сложных электрических цепей.
Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником).
Порядок расчета
1 – Составление частных схем, с одним источником ЭДС, остальные источники исключаются, от них остаются только их внутренние сопротивления.
2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой.
Пример решения методом наложения
1. Для начала произвольно выберем направление токов, если в итоге какой либо ток получится со знаком минус, значит нужно изменить направление данного тока на противоположное.
2. Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник. Для удобства частичные токи будем обозначать штрихами.
Свернем схему к одному контуру, с сопротивлением источника и эквивалентным сопротивлением цепи для нахождения тока источника I1. Для тех, у кого возникают затруднения с нахождением эквивалентного сопротивления рекомендуем прочесть статью виды соединения проводников.
Найдем ток по закону Ома для полной цепи
Найдем напряжение на R2345
Тогда ток I3 равен
А ток I4
Определим напряжение на R25
Найдем токи I2 и I5
3. Составим частную схему со вторым источником ЭДС
Аналогичным образом вычислим все частичные токи от второй ЭДС
4. Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус.
5. Проверим с правильность решения с помощью баланса мощностей.
Небольшая погрешность связана с округлениями промежуточных значений в ходе выполнения вычислений.
Читайте также — Метод узловых потенциалов
Метод наложения — chipenable.ru
В этом посте мы поговорим о простом методе расчета электрических цепей, известном как метод наложения или суперпозиции. Его можно применять для анализа электрических схем с несколькими источниками напряжения. Новичку может показаться, что он не использует такие схемы, но это не совсем так.
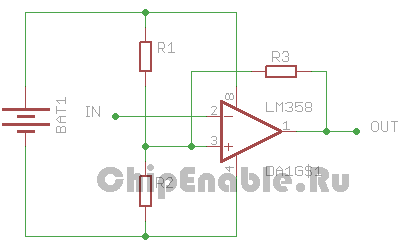
Допустим, нам нужно рассчитать напряжение на положительном входе операционного усилителя при максимальном напряжении на выходе. Чтобы это сделать, нужно перерисовать часть исходной схемы в ее эквивалент.
Входной ток операционного усилителя очень мал (для идеального операционного усилителя он вообще принимается равным нулю), поэтому можно считать, что он представляет собой высокоомное сопротивление, не влияющее на наши расчеты, и пренебречь им в эквивалентной схеме.
На выходе усилителя у нас максимальные выходное напряжение, так называемое напряжение насыщения. Для операционного усилителя общего назначения оно обычно меньше напряжения питания на 1-2 В. Выход усилителя мы можем заменить источником напряжения. Выходным сопротивлением операционного усилителя (омы) мы опустим, допустив что оно на порядок меньше сопротивлений наших резисторов и не оказывает влияния на расчеты.
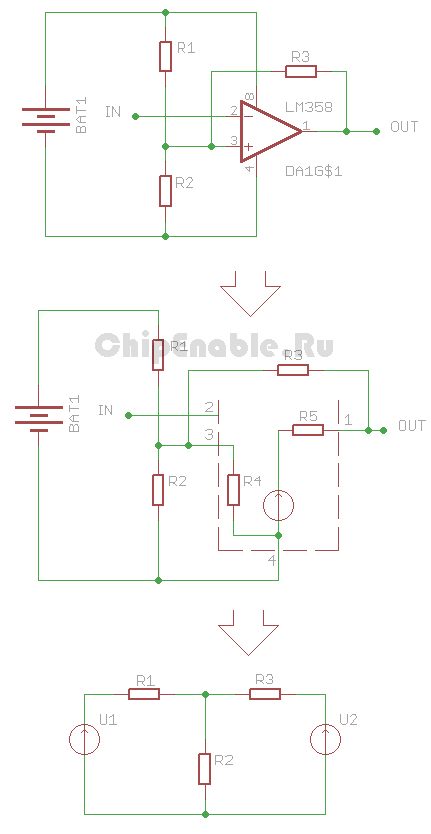
А теперь к нашим баранам. Суть метода наложения заключается в следующем. Каждый источник напряжения вызывает в схеме протекание определенных токов. Когда источников напряжения несколько, грубо говоря, создаваемые ими токи «накладываются» друг на друга. Чтобы рассчитать результирующий ток методом наложения, нужно определить токи в электрической цепи отдельно для каждого источника, а затем просуммировать их, учитывая знак.
Применять этот метод можно по такому алгоритму.
1. Обозначаем в исходной схеме произвольные направления токов. Это нужно сделать для каждой ветви.
2. Из одной схемы с N источниками напряжения делаем N схем с одним источником напряжения. При этом остальные источники в этих схемах заменяются внутренним сопротивлением источника или перемычкой (если мы пренебрегаем внутренним сопротивлением источника).
3. Рассчитываем частичные токи в каждой из схем с одним источником. В этих схемах направления токов будут четко определены полярностью источника напряжения.
4. Складываем частичные токи или напряжения в одинаковых ветвях цепи с учетом знака. Частичный ток, совпадающий по направлению с искомым, считаем положительным, а который не совпадает — отрицательным. Если результирующий ток будет иметь положительный знак, то его направление совпадает с тем, который мы выбрали на первом шаге. Если он будет иметь отрицательный знак, то его направление противоположно выбранному.
Рассчитаем токи в расположенной ниже схеме, следуя описанному алгоритму.
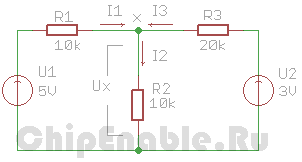
1. Задаем произвольные направления токов во всех ветвях цепи.
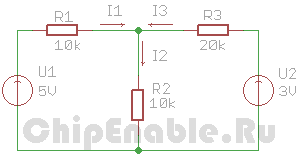
2. Рисуем для каждого источника напряжения отдельную схему и указываем сразу направления протекания токов. Ток течет от большего потенциала к меньшому, короче от плюса к минусу.
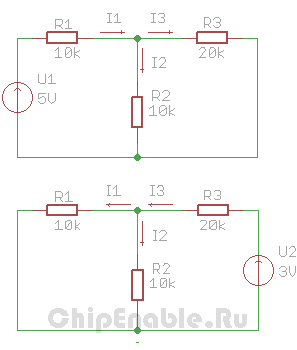
3. Рассчитываем частичные токи в каждой из схем с одним источником. Номиналы резисторов и значения напряжений указаны в схемах. В этих расчетах используется только закон Ома, Кирхгофа и формула для вычисления сопротивления параллельно соединенных резисторов.
Первая схема
I1 = I2 + I3
I1 = U1/(R1 + R2||R3)
R2||R3 = (R2 * R3)/(R2 + R3) = (10 * 20)/(10 + 20) = 6.7 кОм
I1 = 5/(10 + 6.7) = 0.3 мА
Ux = U1 — Ur1 = U1 — I1*R1 = 5 — 0.3*10 = 2 В
I1 = Ux/R2 = 2/10 = 0.2 мА
I3 = Ux/R3 = 2/20 = 0.1 мА
Вторая схема
I3 = I2 + I1
I3 = U2/(R3 + R1||R2)
R1||R2 = (R1 * R2)/(R1 + R2) = (10*10)/(10 + 10) = 5 кОм
I3 = 3/(20 + 5) = 0.12 мА
Ux = U2 — Ur3 = U2 — I3*R3 = 3 — 0.12*20 = 0.6 В
I1 = Ux/R1 = 0.6/10 = 0.06 мА
I2 = Ux/R2 = 0.6/10 = 0.06 мА
4. Складываем частичные токи, соблюдая знак.
Частичные токи для первой схемы
I1_1 = 0.3 мА
I2_1 = 0.2 мА
I3_1 = 0.1 мА
I1_2 = 0.06 мА
I2_2 = 0.06 мА
I3_2 = 0.12 мА
Результирующие токи
Направление I1_1 совпадает с I1 — берем его со знаком плюс. Направление I1_2 не совпадает с I1 — берем его со знаком минус.
I1 = I1_1 — I1_2 = 0.3 — 0.06 = 0.24 мА
Аналогично рассчитываем токи I2 и I3.
I2 = I2_1 + I2_2 = 0.2 + 0.06 = 0.26 мА
I3 =- I3_1 + I3_2 = -0.1 + 0.12 = 0.02 мА
Все рассчитанные токи имеют положительный знак, значит выбранные на первом шаге направления токов оказались правильными.
Ну и напоследок проверим результат.
I2 = I1 + I3
0.26 = 0.24 + 0.02
Все совпадает.
Чтобы рассчитать напряжение Ux в разобранной схеме, не обязательно рассчитывать все токи, можно выполнить вычисления быстрее.

Запишем напряжение Ux для двух схем. Это будет формула обычного делителя напряжения, где в качестве одного из членов будет параллельное сопротивление двух резисторов.
Ux1 = U1* (R2||R3)/(R1 + R2||R3) = 5 * (6.7)/(10 + 6.7) = 2 В
Ux2 = U2 *(R2||R1)/(R3 + R2||R1) = 3 * (5)/(20 + 5) = 0.6 В
Тогда Ux будет равно сумме этих напряжений.
Ux = Ux1 + Ux2 = 2 + 0.6 = 2.6 В
На этом все. Жми на кнопку «Поделиться», если тебе понравилась эта статья.
Частичный ток — Большая Энциклопедия Нефти и Газа, статья, страница 3
Частичный ток
Вытекающие ив точек К токи поступают на выходное сопротивление в качестве частичных токов, соответствующих двоичному коду. [31]
Таким образом, получается, что в каждой ветви существует столько же частичных токов, сколько источников в цепи. Реальный ток в каждой ветви определяется как алгебраическая сумма частичных токов этой ветви. [32]
Существенным недостатком метода наложения является необходимость повышенной точности расчета в том случае, когда частичные токи имеют противоположное направление и близки по значениям. Повышенная точность необходима из-за того, что относительно небольшая погрешность при расчете частичного тока может привести к большой погрешности в окончательном результате. [33]
Влияние нагрузки на величину 2 или на собственную коррозию протектора обусловлено тем, что катодный частичный ток / к зависит от потенциала или тока. Коррозия с кислородной деполяризацией не зависит от материала и потенциала, а выделение водорода с увеличением токовой нагрузки уменьшается. Кроме того, выделение водорода существенно зависит от материала, причем более благородные элементы сплава стимулируют собственную коррозию протектора. Однако в противоположность этому при анодной реакции по уравнению ( 7.5 а) эквивалентная реакция по уравнению (7.56) с повышением потенциала или нагрузки тоже усиливается. В таком случае I к IK получаются пропорциональными между собой, и коэффициент а2 становится независимым от нагрузки. Другое объяснение этой величины а2 основывается на механизме, по которому на поверхности протектора имеется активный участок, пропорциональный току, на котором вследствие гидролиза происходят коррозия с кислородной деполяризацией и выделение водорода [3, 4] 1 В этом случае понятны и значения, отличающиеся от а20 5, в том числе и меньшие. Оба механизма практически уже нельзя различить, если места протекания частичных реакций по уравнениям ( 7.5 а) и (7.56) очень близки между собой. [34]
Для пассивации благоприятно не только уменьшение плотности тока пассивации, но и увеличение плотности катодного частичного тока. По этой причине пассивирующие ингибиторы являются также окислителями. [35]
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 3 — 22, б ив) с выбранным положительным направлением тока в ветви ( рис. 3 — 22, о) или противоположно ему. [36]
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 2 — 21, б и в) с выбранным положительным направлением тока в ветви ( рис. 2 — 21, а) или противоположно ему. [37]
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 2.21 6 и в) с выбранным положительным направлением тока в ветви ( рис. 2.21, а) или противоположно ему. [38]
Из этих уравнений видно, что ток каждой ветви п-лучевой звезды можно представить в виде суммы п — 1 частичных токов, пропорциональных напряжениям между соответствующими точками звезды. [39]
Применяя к заданной линейной цепи метод наложения, можно рассматривать для любого момента времени ток в цепи как результат наложения частичных токов, созданных каждой гармоникой напряжения в отдельности. [40]
ЭДС остальных источников равны нулю; gki lEi / Ef — взаимная проводимость ветвей k и i, равная отношению частичного тока ветви k к ЭДС источника ветви i при условии, что ЭДС остальных источников равны нулю. [41]
Из этих уравнений видно, что ток каждой ветви л-лучевой звезды легко представить в виде суммы ( п — 1) частичных токов, пропорциональных напряжениям между соответствующими точками рассматриваемой схемы. [42]
Из этих уравнений видно, что ток каждой ветви я — лучевой звезды можно представить в виде суммы ( п — 1) частичных токов, пропорциональных напряжениям между соответствующими точками рассматриваемой схемы. [43]
Частичный ток — Большая Энциклопедия Нефти и Газа, статья, страница 2
Частичный ток
Cтраница 2
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 2.21 6 и в) с выбранным положительным направлением тока в ветви ( рис. 2.21, а) или противоположно ему. [16]
Применяя метод наложения, можно определять частичные токи не отдельно от каждого источника, а от источников, разделенных на группы. [17]
В схемах замещения с источниками тока частичные токи ветвей определяются от каждого из них при исключении остальных источников тока в результате разрыва содержащих их ветвей. [18]
В схемах замещения с источниками тока частичные токи ветвей определяются от каждого из них при исключении остальных источников тока в результате разрьша содержащих их ветвей. [19]
В схемах замещения с источниками тока частичные токи ветвей определяются от каждого из них при исключении остальных источников тока в результате разрыва содержащих их ветвей. [20]
При больших токах в коррозионном элементе катодным частичным током на аноде можно пренебречь, так что согласно рис. 2.5 можно принять 1л а. В выражение для плотности тока обмена (2.43) наряду с отношением площадей и разностью потенциалов входит также эффективность катода. [21]
Недостатком метода наложения является то, что частичные токи, имеющие в какой-либо ветви различные направления, могут быть очень большими по сравнению с величиной результирующего тока, вследствие чего небольшая неточность в определении частичных токов может привести к большой погрешности при подсчете результирующего тока в ветви. [22]
Таким образом, для каждой ветви получается столько частичных токов, сколько источников содержит цепь. [24]
Таким образом, для каждой ветви получается столько частичных токов, сколько источников содержит цепь. [25]
На рис. 2.5 схематически показаны суммарный ток и частичные токи для смешанного электрода. [27]
В результате расчета каждой из этих преобразованных цепей определяются частичные токи от действия данного источника. Значение действительных токов ветвей определяется алгебраическим суммированием частичных токов в этих ветвях. [28]
Реальный ток в каждой ветви определяется как алгебраическая сумма частичных токов этой ветви. [30]
Страницы: 1 2 3 4
Применение метода наложения к расчету электрических цепей с двумя и более источниками энергии. Метод узловых потенциалов (узловых напряжений) (главы 3-5 учебного пособия «Теоретические основы электротехники в примерах и задачах»)
3. ПРИМЕНЕНИЕ МЕТОДА НАЛОЖЕНИЯ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ДВУМЯ И БОЛЕЕ ИСТОЧНИКАМИ ЭНЕРГИИ
Если цепь имеет несколько источников энергии, то для расчета цепи можно применить метод наложения. Этот метод использует принцип независимости действия источников. Использование принципа наложения дает возможность заменить вычисления сложных цепей несколькими относительно простыми цепями, в каждой из которых действует один источник энергии.
Задача 3.1.
Методом наложения определить токи во всех ветвях цепи,
схема которой приведена на рис. 3.1, если задано  ,
,  ,
, 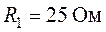 ,
, 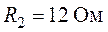 ,
, 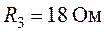 .
.
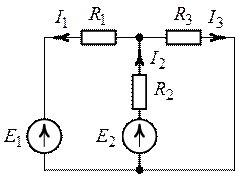
Рис. 3.1.
Решение.
1. Произвольно выбираем положительные направления токов в ветвях цепи (рис. 3.1). Определяем частичные токи от действия каждого источника в отдельности.
2. Частичные токи 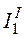 ,
,  и
и 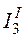 от
действия источника
от
действия источника  , при
, при  (рис. 3.2).
(рис. 3.2).
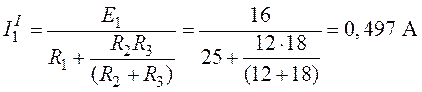 ,
,
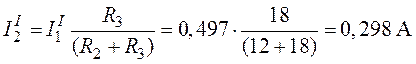 ,
,
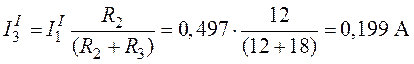 .
.
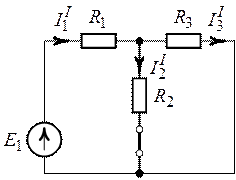
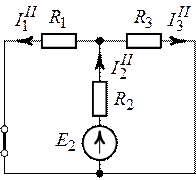
Рис. 3.2. Рис. 3.3.
3. Частичные токи 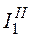 ,
, 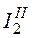 и
и 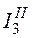 от
действия источника
от
действия источника  , при
, при 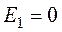 (рис. 3.3).
(рис. 3.3).
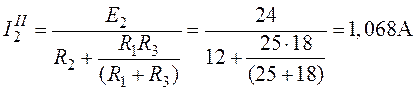 ,
,
 ,
,
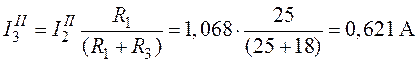 .
.
4. Токи от действия обоих источников в исходной схеме (рис. 3.1) определятся как алгебраическая сумма частичных токов от действия каждого источника в отдельности (см. рис. 3.2 и рис. 3.3):
 ;
;
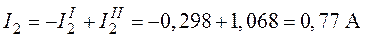 ;
;
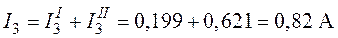 .
.
П р и м е ч а н и е: частичный ток, совпадающий по направлению с искомым
(рис. 3.1), считается положительным, а несовпадающий – отрицательным. Отрицательное
значение тока 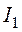 указывает на то, что
направление тока противоположно указанному на рис. 3.1.
указывает на то, что
направление тока противоположно указанному на рис. 3.1.
Задача 3.2.
Используя метод наложения определить токи во всех
ветвях цепи , рис. 3.4, если задано  ,
,  ,
, 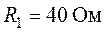 ,
,  ,
, 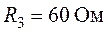 ,
,  .
.
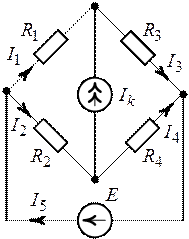

Рис. 3.4. Рис. 3.5.
Решение.
1. Принимаем за положительные направления токов в ветвях цепи направления, указанные на рис. 3.4.
2. Определяем частичные токи 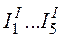 от
действия источника ЭДС
от
действия источника ЭДС  , при
, при 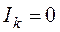 (рис. 3.5):
(рис. 3.5):
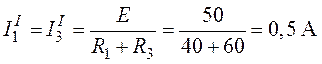 ;
;
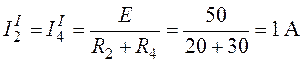 ;
;
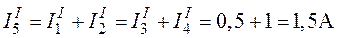 .
.
3. Определяем частичные токи  от
действия источника тока
от
действия источника тока 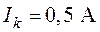 , при
, при 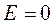 (рис. 3.6). Приведем схему (рис. 3.6)
к более удобному для расчета виду (рис. 3.7).
(рис. 3.6). Приведем схему (рис. 3.6)
к более удобному для расчета виду (рис. 3.7).


Рис. 3.6. Рис. 3.7.
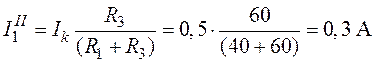 ;
;
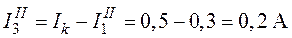 ;
;
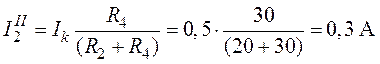 ;
;
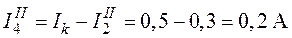 ;
;
 .
.
4. Токи в исходной схеме (рис. 3.4) от действия обоих источников определим, как алгебраическую сумму частичных токов (см. рис. 3.5 и рис. 3.6)
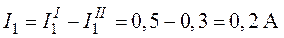 ;
;
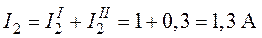 ;
;
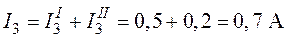 ;
;
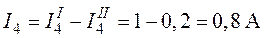 ;
;
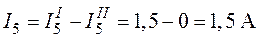 .
.
Задачи для самостоятельного решения
Задача 3.3. Методом
наложения определить токи в цепи (рис. 3.8), если задано  ,
, 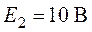 ,
, 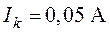 ,
, 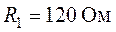 ,
, 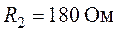 .
.
О т
в е т: 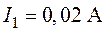 ,
, 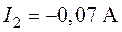 .
.
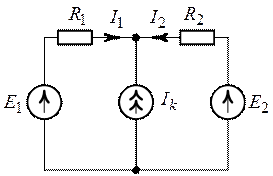
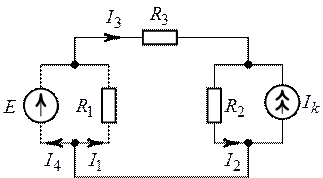
Рис. 3.8. Рис. 3.9.
Задача 3.4. Методом
наложения определить все токи в цепи, схема которой приведена на рис. 3.9.
Параметры элементов цепи заданы 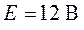 ,
, 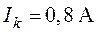 ,
, 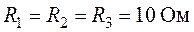 .
.
О т
в е т: 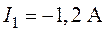 ,
, 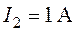 ,
, 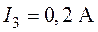 ,
, 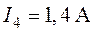 .
.
Задача 3.5. В
схеме (рис. 3.10) методом наложения определить все токи, если 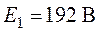 ,
, 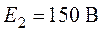 ,
, 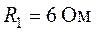 ,
, 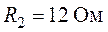 ,
, 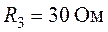 ,
, 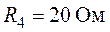 .
.
О т в е т: 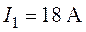 ,
, 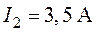 ,
, 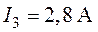 ,
, 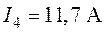 ,
, 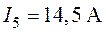 ,
,
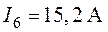 .
.
Задача 3.6.
Для схемы цепи рис. 3.11 используя метод наложения определить все токи, если 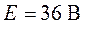 ,
, 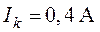 ,
, 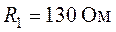 ,
, 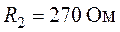 ,
, 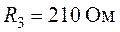 ,
, 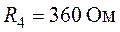 .
.
О т
в е т: 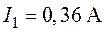 ,
, 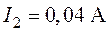 ,
, 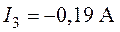 ,
,  ,
,
 .
.
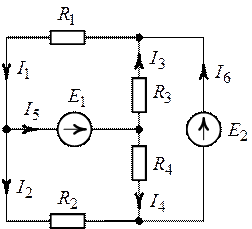
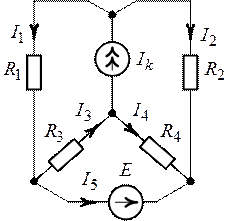
Рис. 3.10. Рис. 3.11.
Задача 3.7.
Используя метод наложения рассчитать токи в схеме цепи рис. 3.12, если 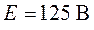 ,
, 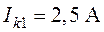 ,
, 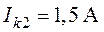 ,
, 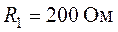 ,
,  ,
, 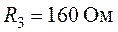 ,
, 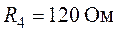 .
.
О т
в е т: 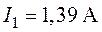 ,
, 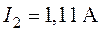 ,
, 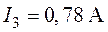 ,
, 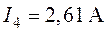 ,
,
 .
.
Задача 3.8. Методом
наложения определить токи в ветвях цепи (рис. 3.13) содержащих резистивные
сопротивления. Дано 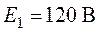 ,
, 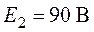 ,
, 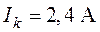 ,
, 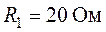 ,
, 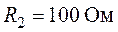 ,
, 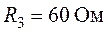 .
.
О т
в е т: 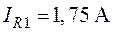 ,
, 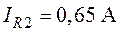 ,
, 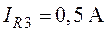 .
.
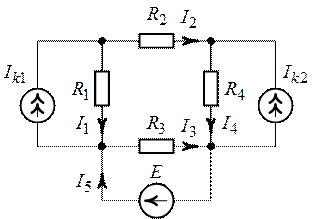
Рис. 3.12. Рис. 3.13.
4. МЕТОД КОНТУРНЫХ ТОКОВ
Задачу расчета разветвленных цепей можно значительно упростить, если воспользоваться специальными методами расчета сложных цепей. Одним из этих методов является метод контурных токов. Метод контурных токов можно определить как метод расчета, в котором за неизвестные принимаются токи контуров. Использование метода позволяет сократить количество составляемых уравнений по отношению к расчету при непосредственном применении законов Кирхгофа.
Задача 4.1.
Методом контурных токов рассчитать все токи в ветвях
схемы (рис. 4.1). Даны: 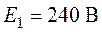 ,
,  ,
,  ,
, 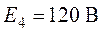 ,
, 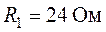 ,
, 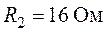 ,
, 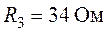 ,
, 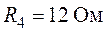 ,
, 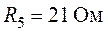 ,
, 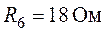 . Выполнить проверку решения по
второму закону Кирхгофа.
. Выполнить проверку решения по
второму закону Кирхгофа.
Решение.
1. Цепь (рис. 4.1) содержит шесть ветвей (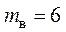 ), четыре узла (
), четыре узла (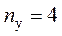 ), источники тока в цепи отсутствуют (
), источники тока в цепи отсутствуют (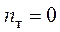 ).
).
Зададим произвольное положительное направление токов в ветвях схемы и обозначим их как указано на рис. 4.2.
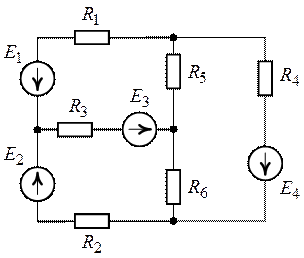
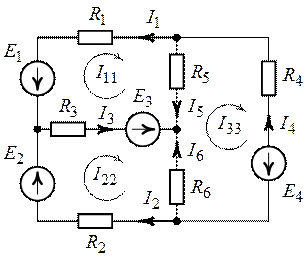
Рис. 4.1. Рис. 4.2.
2. Определим достаточное количество уравнений для расчета цепи по методу контурных токов:
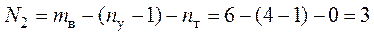 .
.
Достаточное
количество контурных уравнений равно трем. Выделим в схеме три независимых
контура, по которым замкнем контурные токи  ,
,  и
и 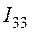 (рис.
4.2). Направление действия контурных токов выберем по часовой стрелке. Положительное
направление обхода контура совместим с направлением контурного тока.
(рис.
4.2). Направление действия контурных токов выберем по часовой стрелке. Положительное
направление обхода контура совместим с направлением контурного тока.
3. Система контурных уравнений (уравнений по второму закону Кирхгофа) имеет вид (рис. 4.2):
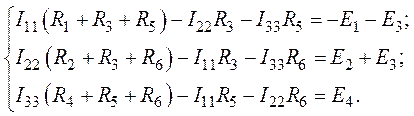
4. Выполним подстановку числовых значений
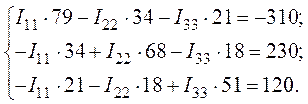
5. Решение полученной системы уравнений выполним с помощью определителей по методу Крамера:
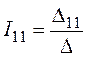 ,
, 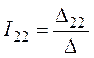 ,
,  .
.
Главный определитель системы:
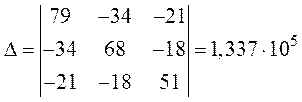 .
.
Дополнительные определители:
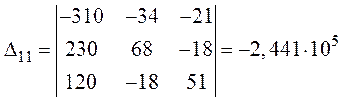 ,
,
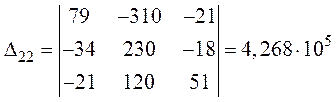 ,
,
 .
.
6. Контурные токи
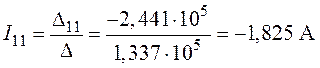 ,
,
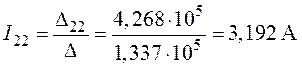 ,
,
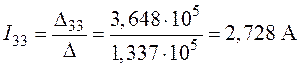 .
.
7. Действительные токи в ветвях схемы (рис. 4.2) определим как алгебраическую сумму контурных токов смежных контуров:
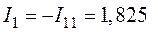 ;
;
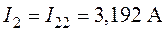 ;
;
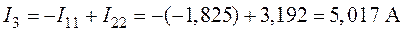 ;
;
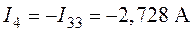 ;
;
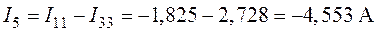 ,
,
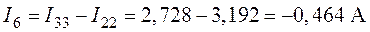
8. Проверку расчета выполним, составив уравнение по второму закону Кирхгофа, например, для внешнего контура (рис. 4.2). Направление обхода контура по часовой стрелке
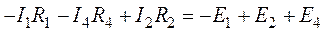 .
.
Подставляя в уравнение числовые значения, получим:
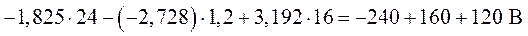 ,
,
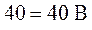 .
.
Задача 4.2.
Для схемы, рис. 4.3, пользуясь методом контурных
токов, определить все токи, если 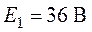 ,
, 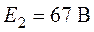 ,
, 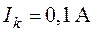 ,
, 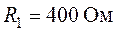
 ,
,  ,
, 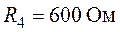 ,
, 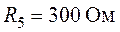 .
.
Решение.
1. Схема (рис. 4.3) содержит шесть ветвей (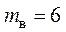 ), четыре узла (
), четыре узла (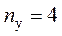 ), один источник тока
), один источник тока 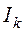 (
(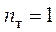 ).
).
Положительные направления токов в ветвях схемы обозначим в соответствии с рис. 4.4.
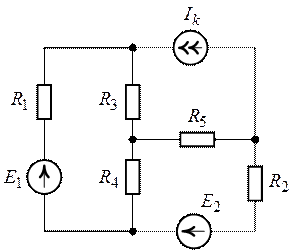

Рис. 4.3. Рис. 4.4.
2. Достаточное количество уравнений для расчета цепи по методу контурных токов равно двум:
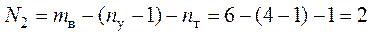 .
.
Независимые контура и направления протекания контурных
токов ,
,  обозначены
на рис. 4.4.
обозначены
на рис. 4.4.
Для ветви с источником тока 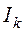 создадим
третий контур с контурным током
создадим
третий контур с контурным током 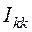 по направлению,
совпадающему с направлением источника (рис. 4.4).
по направлению,
совпадающему с направлением источника (рис. 4.4).
Считаем, что 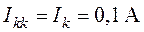 является
известным контурным током, который будем учитывать только при составлении
уравнений независимых контуров.
является
известным контурным током, который будем учитывать только при составлении
уравнений независимых контуров.
3. Система уравнений, составленная по методу контурных токов, будет иметь вид:
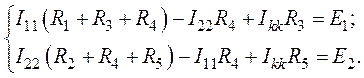
4. После подстановки числовых значений параметров цепи получим:
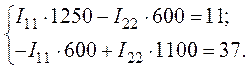
5. Решение системы позволяет получить значения контурных токов
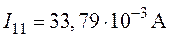 ,
, 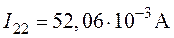 .
.
6. Действительные токи в ветвях (рис.4.4) находим как алгебраическую сумму контурных токов смежных контуров
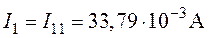 ;
;
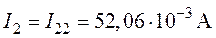 ;
;
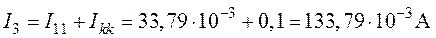 ;
;
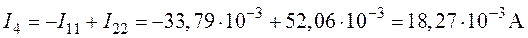 ;
;
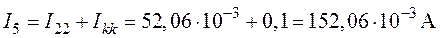 .
.
Задача 4.3.
Требуется рассчитать токи в ветвях цепи (рис. 4.5),
если 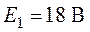 ,
,  ,
,  ,
, 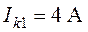 ,
, 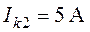 ,
, 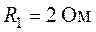 ,
, 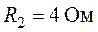 ,
, 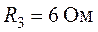 ,
, 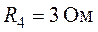 ,
, ,
, 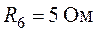 . Расчеты выполнить методом контурных
токов.
. Расчеты выполнить методом контурных
токов.

Рис. 4.5.
Решение.
1. Преобразуем цепь (рис. 4.5) к виду более удобному для расчета, объединив в один узел узлы равного потенциала (рис. 4.6).
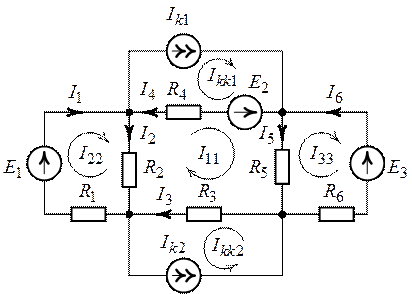
Рис. 4.6.
Цепь (рис. 4.6) содержит восемь ветвей (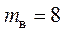 ), четыре узла (
), четыре узла (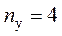 ), два источника тока
), два источника тока 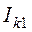 ,
, 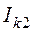 (
(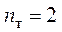 ).
).
Зададимся произвольным положительным направлением токов в ветвях схемы и обозначим их как указано на рис. 4.6.
2. Определим достаточное количество уравнений, которое равно трем
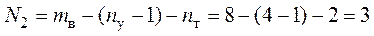 .
.
Выделим в схеме три независимых контура, по которым
замкнем контурные токи  ,
,  и
и 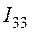 .
.
Направление контурных токов выберем по часовой
стрелке. Для ветвей с источниками тока создадим два дополнительных контура с
контурным током 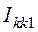 ,
, 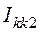 .
Направления дополнительных контурных токов выберем так, чтобы они совпадали с
направлениями действия источников тока
.
Направления дополнительных контурных токов выберем так, чтобы они совпадали с
направлениями действия источников тока 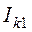 и
и 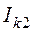 .
.
3. Система контурных уравнений, записанных по второму закону Кирхгофа относительно неизвестных контурных токов, имеет вид
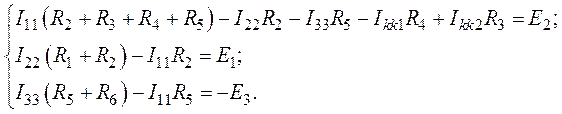
4. Приведем систему к матричной форме
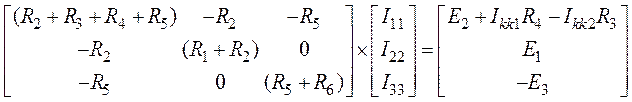 .
.
5. Подставив числовые значения параметров элементов цепи, получим
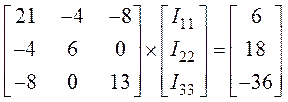 .
.
6. Решение матричной системы позволяет определить контурные токи
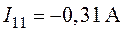 ,
,  ,
, 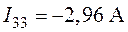 .
.
7. Определяем действительные токи в ветвях схемы (рис. 4.6)
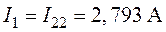 ;
;
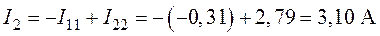 ;
;
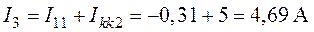 ;
;
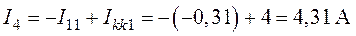 ;
;
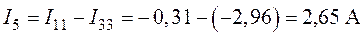 ;
;
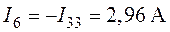 .
.
Задачи для самостоятельного решения
Задача 4.4. Для
цепи изображенной на рис. 4.7, требуется определить контурные токи, указные на
схеме, если 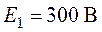 ,
, 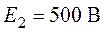 ,
, 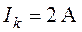 ,
, 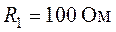 ,
, 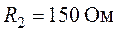 ,
, 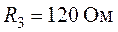 ,
, 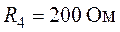 ,
, 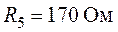 .
.
О т в е т: 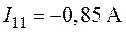 ,
, 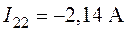 .
.
Задача 4.5. Требуется
рассчитать контурные токи, указные на схеме (рис.4.8), если 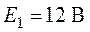 ,
,  ,
, 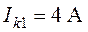 ,
, 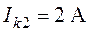 ,
, 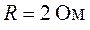 .
.
Для составления системы необходимо выбрать направления токов в ветвях
⇐ ПредыдущаяСтр 4 из 17Следующая ⇒
Система уравнений решается и находятся неизвестные токи.
Доп. уравнение: 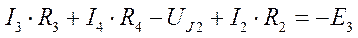 . Из него находят UJ2.
. Из него находят UJ2.
1.6. Принцип и метод наложения в теории цепей.
Принцип наложения или суперпозиции – это физический принцип, который говорит, что результирующее действие, возникающее от воздействия нескольких сил, может быть в линейной системе найдено как алгебраическая сумма от действий каждой силы в отдельности. В теории цепей под силой рассматривается воздействие каждого источника. Тогда можно заключить, что ток, который возникает на участке цепи под действием нескольких источников, работающих одновременно, можно определить как алгебраическую сумму частичных токов, каждый из которых возникает под действием своего источника, работающего отдельно от остальных источников. Это применимо только для линейных цепей (систем). К линейным относят цепи, свойства и параметры которых не зависят от величин, направлений токов и напряжений в элементах цепи.
Частичные токи рассчитываются каждый в своей схеме замещения, в которой оставляют один источник, а остальные заменяют следующим образом: идеальный источник тока – разрывом (J=0), идеальный источник напряжения – перемычкой, проводником (E=0), реальные источники энергии – внутренними сопротивлениями.
К полученным схемам применяют законы Кирхгофа, законы Ома. На основе этих положений возникает метод наложения для расчетов токов и напряжений. Особенно он необходим, когда в цепи действует несколько разнотипных источников (например, с разными частотами, с разными видами действия, с разной формой воздействия).
Рассмотрим на примере.
Пример 1
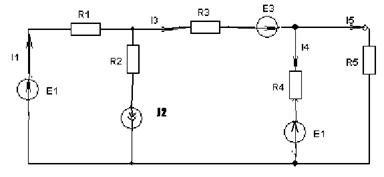 К данной схеме можно применить как метод наложения, так и метод токов ветвей.
К данной схеме можно применить как метод наложения, так и метод токов ветвей.
Составим четыре схемы замещения, в каждой из которых будет действовать только один источник энергии и протекать частичные токи от этого источника.
1)
При этом надо учитывать направления частичных токов источников.
2)
3)
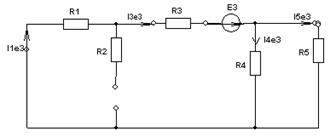
4)
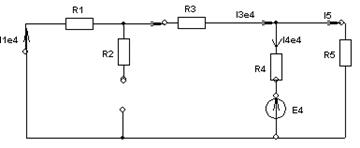
В итоге определяют токи от всех источников , например, I1=I1E1+I1J2+I1E3+I1E4
Как мы видим, в данном примере решение было бы легче при применении метода токов ветвей.
1.7. Метод контурных токов
1. Недостатки МТВ
Основной недостаток – довольно большое количество уравнений и соответственно трудоемкость работы. Поэтому были разработаны другие методы, в частности метод контурных токов (МКТ) и метод узловых напряжений или потенциалов (МУН), где получается меньше уравнений.
2. Основы МКТ
В качестве неизвестных здесь используются так называемые контурные токи. Это некоторые условные мысленные токи, протекающие по выбранным независимым контурам. В качестве дополнительных неизвестных берутся напряжения на идеальных источниках тока. Система уравнений составляется только на основе второго закона Кирхгофа с применением закона Ома. Конкретные токи ветвей (действительные токи) определяются как алгебраическая сумма соответствующих контурных токов, протекающих через ветвь.
3. Определение числа уравнений и выбор контуров для МКТ
Количество уравнений определяется по формуле:
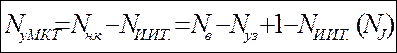
Контуры выбираются так, чтобы в них не входили идеальные источники тока (основные контуры). Дополнительные контуры выбираются с одним источником тока. Их уравнения в систему не включаются, но их влияние учитывается при решении системы.
4. Пример использования
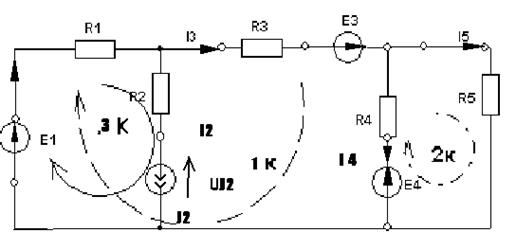
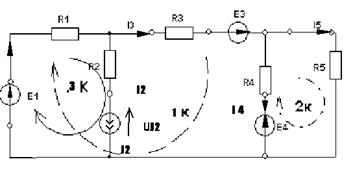
NB=5, NУЗ=3, NHK=3, NИИТ(J)=1.
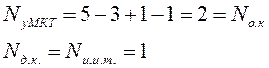 Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I1К,I2К, причем I3К=J2.
Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I1К,I2К, причем I3К=J2.

Решив данную систему и определив контурные токи, найдем токи ветвей следующим образом:
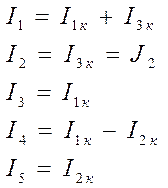
Для определения напряжения на источнике тока составляется вспомогательное уравнение по закону Кирхгофа для дополнительного (3) контура: 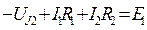 . Отсюда определяется UJ2.
. Отсюда определяется UJ2.
Можно выделить алгоритм расчета:
Определение количества уравнений
Выбор основных и дополнительных контуров
Составление системы уравнений для контурных токов
Решение системы уравнений
Определение токов ветвей
Частичный ток — Большая Энциклопедия Нефти и Газа, статья, страница 1
Частичный ток
Cтраница 1
Частичный ток г может быть найден, если положить все задающие напряжения и токи активного двухполюсника равными нулю. Получившийся при этом пассивный двухполюсник полностью характеризуется своим эквивалентным сопротивлением R3 относительно выделенных зажимов. [1]
Частичный ток i1 может быть найден, если положить все задающие напряжения и токи активного двухполюсника равными нулю. Получившийся при этом пассивный двухполюсник полностью характеризуется своим эквивалентным сопротивлением R3 относительно выделенных зажимов. [2]
Какие частичные токи считаются положительными, а какие, отрицательными при расчете реальных токов. [3]
Измерить первые и вторые частичные токи. [4]
Для каждой ветви получается столько частичных токов, сколько источников содержит цепь. [5]
Это справедливо, если все частичные токи / j равны или, что то же самое, если все положения новых цепочек равновероятны. [6]
Он представляет собой именно тот частичный ток, который относится к переходу находящихся в определенном положении пластинок Ю, I в пластинки ш, ( 1 1) путем отложения на них новой цепочки на определенном ребре. [7]
При расчете этих цепей определяются частичные токи во всех ветвях. [8]
На рис. 20.11 показана кривая анодный частичный ток — потенциал ( а) для пассивируемого металла в среде с током пассивации 1р и соответствующая кривая катодный частичный ток — потенциал ( б) для водорода. Ввиду высокого перенапряжения водорода ток пассивации не достигается. При свободной коррозии устанавливается стационарный потенциал UKa в активном состоянии. Если этот материал привести в контакт с металлом, имеющим меньшее перенапряжение водорода в соответствии с кривой катодный частичный ток — потенциал ( см. рис. 20.11, в), то такой катодный частичный ток будет достаточен для пассивации. [10]
Сущность метода заключается в нахождении частичных токов в ветвях при поочередном действии источников тока и последующем определении действительных токов путем наложения ( алгебраического суммирования) частичных токов. [12]
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 3 — 22, б ив) с выбранным положительным направлением тока в ветви ( рис. 3 — 22, о) или противоположно ему. [13]
Знак, который ставится перед частичным током, зависит от того, совпадает ли направление частичного тока ( рис. 2 — 21, б и в) с выбранным положительным направлением тока в ветви ( рис. 2 — 21, а) или противоположно ему. [14]
Страницы: 1 2 3 4

