Учебное пособие для самостоятельной работы студентов, страница 13
Электротехника \ Теоретические основы электротехники
Найти: Rаb, I1, I2, I3, I4, I5.
Ответ. Rаb = 10 Ом, I1 = 4 A, I2 = 2 A, I3 = 2 A,
I4 = 1 A, I5 = 1 A.
Рис. 2.25. Расчетная схема к задаче 4
Задача 5. На рис.2.26 R1 = 3 Ом, R2 = 3 Ом, R3 = 3 Ом,
R4 = 1 Ом, R5 = 1 Ом.
Найти Rаb.
Ответ. Rаb = 2 Ом.
Рис. 2.26. Расчетная схема к задаче 5
Задача 6. На рис. 2.27
Е = 10 В, R1 = 10 Ом, R2 = 20 Ом,
Найти I.
Ответ. I = 1 A.
Рис. 2.27. Расчетная схема к задаче 6
Задача 7. На рис.2.28 I = 1 A, Е = 10 В, R1 = 3 Ом, R2 = 7 Ом.
Найти Uаb.
Ответ. Uаb. = 20 В.
Рис. 2.28. Расчетная схема к задаче 7
Задача 8. На рис. 2.29 R1 = 3 Ом, R2 = 1 Ом, R3 = 1 Ом, Е1 = 10 В, Е2 = 5 В.
Найти Uаb.
Ответ. Uаb = 6 В.
Рис.2.29. Расчетная схема к задаче 8
Задача 9.
Найти Uаb.
Ответ. Uаb = 6 В.
Рис. 2.30. Расчетная схема к задаче 9
Задача 10.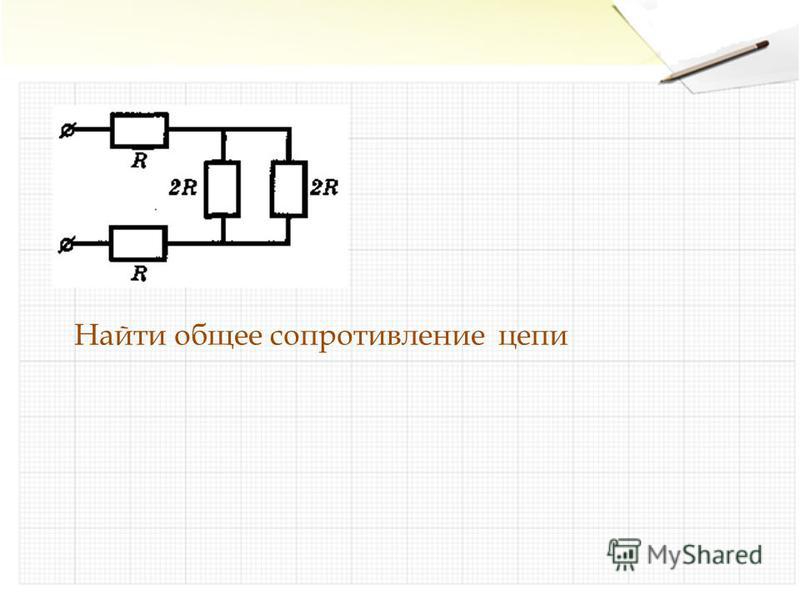 При одном значении сопротивления нагрузки RН (см. рис.2.31) показания амперметра – 1 А, вольтметра
– 9,9 В; при другом значении – 2 А и 9,9 В. Измерительные приборы считаем
идеальными (RA = 0; RV = ).
При одном значении сопротивления нагрузки RН (см. рис.2.31) показания амперметра – 1 А, вольтметра
– 9,9 В; при другом значении – 2 А и 9,9 В. Измерительные приборы считаем
идеальными (RA = 0; RV = ).
Найти: ЕЭ, RЭ.
Ответ. ЕЭ = 10 В, R
Рис. 2.31. Расчетная схема к задаче 10
Задача 11. При сопротивлении нагрузки RН1 = 9 Ом (см. рис.2.32) амперметр показал ток I1 = 1 A; при RН2 = 4 Ом, ток I2 = 2 A, RA = 0,9 Ом.
Найти: ЕЭ, RЭ.
Ответ. ЕЭ = 10 В, RЭ = 0,1 Ом.
Рис. 2.32. Расчетная схема к задаче 11
Задача 12. При сопротивлении нагрузки RН1 = 10 Ом (см. рис.2.33) вольтметр показал напряжение U1 = 9,9 B; при RН2 = 4,92 Ом, напряжение U2

Найти: ЕЭ, RЭ.
Ответ. ЕЭ = 10 В, RЭ = 0,1 Ом.
Рис. 2.33. Расчетная схема к задаче 12
2.8.2. Определение входного сопротивления
Условие задачи. Определить входное сопротивление цепи (рис.2.34, схемы 1-20). Параметры сопротивлений заданы в омах. Ответ приведен под схемой.
Знаком обозначена общая точка схемы.
Рис. 2.34 лист 1. Расчётные схемы
Рис. 2.34 лист 2. Расчётные схемы
Рис.2.34 лист 3. Расчетные схемы
Пример. Определить
входное сопротивление Rab цепи, приведенной на рис.2.35 а, если R1 = R5 = R8 = R9 = 30 Ом,
R2 = 20 Ом,
R3 = R4 = 8 Ом, R6 = 2 Ом, R7 = 10 Ом.
Точки, отмеченные , можно объединить
в одну точку общим проводом (показан штриховой линией). Тогда расчетная схема
примет вид схемы на рис.2.35,б, на которой резистор R
; Ом;
Поскольку R3 = R4, R5 = R8 =R5 , то
; Ом; ; Ом.
В результате получим схему, приведенную на рис.2.35,в, в которой R589 и R6 соединены последовательно:
; Ом.
Между точками 1 и b – параллельное соединение из RЭ1 и R12:
Окончательно входное сопротивление цепи относительно точек а и b:
;
Ом.
Рис. 2.35. Преобразование электрической схемы для определения Rab
2. 8.3. Определение напряжения участка цепи
8.3. Определение напряжения участка цепи
Условие задачи. В заданной цепи (рис.2.36, схемы 1-20) действует источник постоянной ЭДС Е. Определить токи ветвей и напряжение Uав. Составить баланс мощностей. ЭДС задана в вольтах, сопротивления – в омах.
Ответ приведен под схемой.
Рис. 2.36 лист 1. Расчётные схемы
Рис. 2.36 лист 2. Расчётные схемы
Рис. 2.36 лист 3. Расчётные схемы
Пример. В расчетной схеме, приведенной на рис. 2.37, заданы Е = 120 В, R1 = R4 = 40 Ом, R2 = R3 = 60 Ом, R5 = 50 Ом.
Определить все токи и напряжение Uав. Составить баланс мощностей.
Рис.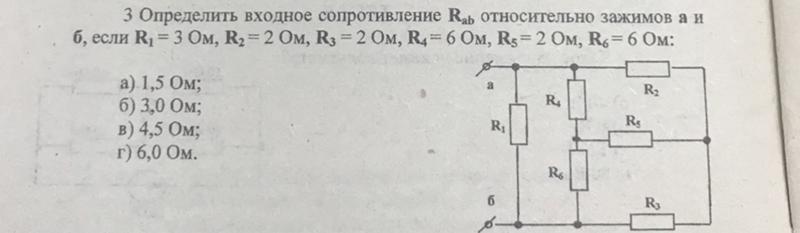
Решение.
; Ом;
; Ом;
; Ом;
;
; А;
; В;
; В;
; А;
; А;
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Сопротивление входное — что это такое?
Сопротивление – это физическая электротехническая величина, отражающая противодействие движению электрического тока в проводнике или в цепи. Впервые она была обоснована и закреплена в фундаментальной связи с напряжением и силой тока в законе Ома – немецкого физика, который изучал эту взаимосвязь. В честь него и названа единица измерения сопротивления – Ом. Часто при выполнении монтажа какой-либо электросети необходимо найти общее сопротивление цепи при различных способах подключения. О том, как это правильно сделать и расскажет этот материал.
Что такое общее сопротивление цепи
Если говорить простыми словами, общее сопротивление электрической цепи – это такое R, которое она оказывает на напряжение в ее проводниках и приборах. Существует два типа напряжения (исходя из силы тока) – постоянное и переменное. Так же и сопротивление делится на активное и реактивное, которое, в свою очередь, подразделяется на индуктивное и емкостное. Активный тип не зависит от частот сети. Также для него абсолютно не важно, какой ток протекает по проводникам. Реактивный же, наоборот, зависит от частоты, причем емкостная характеристика в конденсаторах и индуктивная в трансформаторах ведут себя по-разному.
Существует два типа напряжения (исходя из силы тока) – постоянное и переменное. Так же и сопротивление делится на активное и реактивное, которое, в свою очередь, подразделяется на индуктивное и емкостное. Активный тип не зависит от частот сети. Также для него абсолютно не важно, какой ток протекает по проводникам. Реактивный же, наоборот, зависит от частоты, причем емкостная характеристика в конденсаторах и индуктивная в трансформаторах ведут себя по-разному.
Закон Ома
Помимо сопротивления подключенных в сеть электроприборов, на общее состояние оказывают влияние даже промежуточные провода, также имеющие сопротивляемость напряжению.
Резистор – основной элемент сопротивляемости цепи
Закон Ома для полной цепи
Закон Ома для полной цепи
гласит, что
сила тока
в цепи пропорциональна действующей в цепи электродвижущей силе (
ЭДС
) и обратно пропорциональна сумме
сопротивлений цепи
и
внутреннего сопротивления источника
.
Онлайн калькулятор
Найти силу тока
ЭДС: ε = В Сопротивление всех внешних элементов цепи: R = Ом Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока
I = 12 /4+2 = 2 А
Найти ЭДС
Сила тока: I = А Сопротивление всех внешних элементов цепи: R = Ом Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС
ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I = А ЭДС: ε = В Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r =
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Как правильно найти и посчитать формулой сопротивление цепи
Сперва следует разобрать понятия и формулы. Индуктивный тип считается так: XL= ωL, где L – индуктивность цепи, а ω – круговая частота переменного тока, равная 2πf (f – частота переменного тока). Чем больше частота сети, тем большим R для нее становится какая-либо катушка индуктивности.
Индуктивный тип считается так: XL= ωL, где L – индуктивность цепи, а ω – круговая частота переменного тока, равная 2πf (f – частота переменного тока). Чем больше частота сети, тем большим R для нее становится какая-либо катушка индуктивности.
Вам это будет интересно Определение резонанса
Емкостный тип можно рассчитать по формуле: Xc = 1/ ωC, где С – емкость радиоэлемента. Здесь все наоборот. Если происходит увеличение частоты, то сопротивляемость конденсатора напряжению уменьшается. Из этого исходит то, что для сети постоянного тока конденсатор – бесконечно большое R.
Высчитать характеристику можно и с помощи других величин
Но не только вид сопротивления и радиоэлементы, обеспечивающие его, влияют на общее значение цепи. Особую роль играет также и способ соединения элементов в электроцепь. Существует два варианта:
- Последовательный;
- Параллельный.
В последовательном подключении
Это самый простой тип для практического и теоретического рассмотрения. В нем элементы резисторного типа соединяются, очевидно, последовательно, образуя подобие «змейки» после чего электрическая цепь замыкается. Посчитать общее значение в таком случае довольно просто: требуется последовательно сложить все значения, выдаваемые каждым из резисторов. Например, если подключено 5 резисторов по 5 Ом каждый, то общий параметр будет равен 5 на 5 – 25 Ом.
В нем элементы резисторного типа соединяются, очевидно, последовательно, образуя подобие «змейки» после чего электрическая цепь замыкается. Посчитать общее значение в таком случае довольно просто: требуется последовательно сложить все значения, выдаваемые каждым из резисторов. Например, если подключено 5 резисторов по 5 Ом каждый, то общий параметр будет равен 5 на 5 – 25 Ом.
Формула последовательной сети
В параллельном подключении
Немного сложнее все устроено в параллельных сетях. Если при последовательном способе току нужно пройти все резисторы, то тут он вправе выбрать любой. На самом деле он просто будет разделен между ними. Суть в том, что есть характеристика, схожая для всех радиоэлементов, например, величина в 5 Ом означает, что для нахождения общего R необходимо разделить его на количество всех подключенных резисторов: 5/5 = 1 Ом.
Важно! Из-за того, что напряжение на параллельных участках одинаково, а токи складываются, то есть сумма токов в участках равна неразветвленному току, то Rобщ будет высчитываться формуле: 1/R = 1/R1 + 1/R2 + … + 1/Rn.
Формула параллельной сети
Параметры резисторного элемента
- Для резисторов применяется понятие мощности. При прохождении через них электротока происходит выделение тепловой энергии, рассеиваемой в окружающее пространство. Мощность детали является параметром, который показывает, сколько энергии она может выделить в виде тепла, оставаясь работоспособной. Мощность зависит от габаритов детали, поэтому у маленьких зарубежных резисторов ее определяют на глаз, сравнивая с российскими, технические характеристики которых известны;
Ряд сопротивления резистора Е24
Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю.
На схеме мощность показана следующим образом.
Условное обозначение мощности
- Второй параметр – сопротивление элемента. На российских деталях типа МЛТ и крупных импортных образцах оба параметра указываются на корпусе (мощность – Вт, сопротивление – Ом, кОм, мОм).
 Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;
Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;
Цветовая маркировка резисторов
- Допуски. Невозможно изготовить деталь с номинальным сопротивлением, в точности соответствующим заявленному значению. Поэтому всегда указываются границы погрешности, называемые допуском. Его величина – 0,5-20%;
- ТКС – коэффициент температуры. Показывает, как варьируется сопротивление при изменении внешней температуры на 1°С. Желательно, но не обязательно подбирать элементы с близким или идентичным значением этого показателя для одной цепи.
Как определить формулой общее сопротивление цепи
Из закона Ома исходит то, что общее сопротивление равно общему напряжению, деленному на общую силу тока в цепи. При параллельном подключении напряжение, как уже было сказано, равно везде, поэтому необходимо узнать его значение на любом участке цепи. С током все сложнее, так как на каждой ветке его значение свое и зависит от конкретного R.
Вам это будет интересно WAGO соединители
Также необходимо помнить, что могут быть параллельные подключения с нулевым значением R. Если в какой-либо ветке нет резистора или другого подобного элемента, но весь ток будет течь через нее и все общее значение для цепи станет нулевым. На практике это случается при выходе резистора из строя или при замыкании. Такая ситуация может навредить другим элементам из-за большой силы тока.
Таблица удельной величины для различных проводников
Закон Ома для участка цепи
Закон Ома для участка цепи
гласит, что
сила тока
(I) на участке электрической цепи прямо пропорциональна
напряжению
(U) на концах участка цепи и обратно пропорциональна его
сопротивлению
(R).
Онлайн калькулятор
Найти силу тока
Напряжение: U = В Сопротивление: R = Ом
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока
на этом участке I = 12 /2= 6 А
Найти напряжение
Сила тока: I = A Сопротивление: R = Ом
Формула
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение
на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U = В Сила тока: I = A
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление
на этом участке R = 12 /6 = 2 Ом
Онлайн-калькулятор расчета сопротивление цепи
Для того чтобы сэкономить свое время и не заниматься скучными пересчетами, рекомендуется пользоваться калькуляторами по расчету сопротивления и многих других величин в режиме онлайн. Большинство из них бесплатные:
Большинство из них бесплатные:
- Сalc.ru (https://www.calc.ru/raschet-elektricheskikh-tsepey.html). Возможен расчет закона Ома для участка цепи, реактивного и активного сопротивления при последовательном и параллельном соединении резисторов;
- Asutpp.ru (https://www.asutpp.ru/kalkulyator-rascheta-parallelnogo-soedineniya-rezistorov.html). Калькулятор для параллельного соединения. Достаточно указать количество элементов и Ом-характеристику каждого из них;
- Cxem.net (https://cxem.net/calc/calc.php). Обладает таким же количеством калькуляторов, как и первый вариант, что позволяет радиолюбителю выполнить вычисление любых интересующих параметров сети.
Интерфейс одного из калькуляторов
В статье подробно рассказано, как вычислить общее сопротивление цепи. При разных типах подключения элементов она считается по-разному, но благодаря давно выведенным формулам в любом случае нет ничего сложного.
Параллельное соединение резисторов
При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.
Расчет эквивалентного сопротивления элементов цепи
Токи Фуко — понятие и применение на практике
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.
Общее сопротивление электрической цепи, чему оно равно и как найти по формуле.
Как известно во всем нужна своя мера, которая позволяет делать точные системы, устройства, механизмы, схемы. Мера множественная, имеет свои конкретные величины. В сфере электротехники основными величинами являются напряжение, ток, сопротивление, мощность, частота (для переменного и импульсного тока). Величины между собой связаны определенными формулами. Самой важной формулой, наиболее используемой электриками, электронщиками является закон Ома ( I = U/R, то есть — сила тока равна напряжению деленному на сопротивление). Зная любые две величины из этой формулы всегда можно найти третью.
Зная любые две величины из этой формулы всегда можно найти третью.
От сопротивления электрической цепи зависит силы тока при наличии определенного напряжения. Если меняется сопротивление в цепях схемы, то и меняться режимы ее работы в отдельных ее участках или во всей цепи. Знание величины сопротивления могут помочь выявить неисправность, узнать (вычислить из формулы) другие электрические величины в схеме, зависящие от этого сопротивления.
Теперь давайте посмотрим от чего зависит общее сопротивление электрической цепи. Общее — это сумма частных. Любая электрическая цепь и схема содержит в себе электрические компоненты, которые обладают внутренним сопротивлением. Даже обычный конденсатор (две пластины проводника, разделенные диэлектриком, что позволяет накапливать электрический заряд между этими пластинами, не пропуская постоянный ток), который, казалось бы, по сути своей его не должен иметь (точнее оно бесконечно большое) обладает реактивным сопротивлением.
Самая простая электрическая цепь состоит из источника питания и нагрузки. К примеру это будет обычная батарейка и маленькая лампочка накаливания. И батарейка и лампочка имеют свои сопротивления, которые суммируются, что определяет силу тока, текущему по этой простейшей цепи (при определенной величине напряжения). Допустим к нашей цепи мы добавим еще один элемент нагрузки (вторую такую же лампочку). Ее можно подключить к этой простейшей цепи двумя способами либо параллельно первой лампочки, либо же последовательно ей
К примеру это будет обычная батарейка и маленькая лампочка накаливания. И батарейка и лампочка имеют свои сопротивления, которые суммируются, что определяет силу тока, текущему по этой простейшей цепи (при определенной величине напряжения). Допустим к нашей цепи мы добавим еще один элемент нагрузки (вторую такую же лампочку). Ее можно подключить к этой простейшей цепи двумя способами либо параллельно первой лампочки, либо же последовательно ей
При последовательном подключении сопротивление будет суммироваться:
При параллельном подключении общее сопротивление можно найти по таким формулам:
То есть, большинство схем будут иметь в себе либо параллельное подключение сопротивлений, либо последовательное или же смешанное. В случае сложной электрической цепи определение общего электрического сопротивления происходит по частям (группам), состоящим, опять же, из параллельных и последовательных подключений элементов, обладающими сопротивлением. Правильнее начинать с той части цепи, схемы, которая имеет наибольшую удаленность от двух конечных выводов, рассматриваемых как контакты общего сопротивления.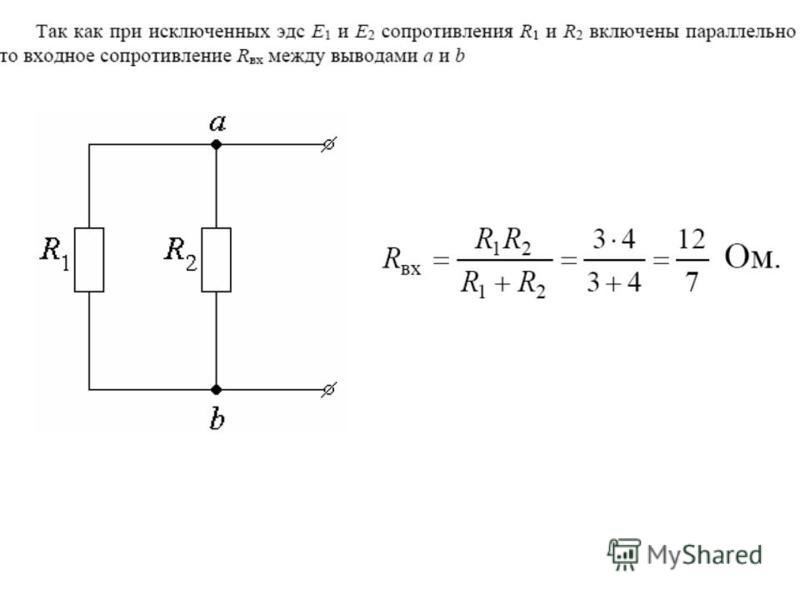 На рисунке ниже приведен пример последовательности вычисления общего сопротивления сложной цепи, схемы.
На рисунке ниже приведен пример последовательности вычисления общего сопротивления сложной цепи, схемы.
Но ведь существуют электрические цепи, в которых общее сопротивление может постоянно меняться, к примеру схема стабилизированного регулятора частоты вращения постоянного электродвигателя, подключенная к самому двигателю. При изменении нагрузки на валу двигателя будет меняться его внутреннее сопротивление, следовательно меняться будет и режимы работы схемы (поддерживающая нужную частоту вращения вала). В таких цепях электрическое сопротивление является динамическим, изменяющемся. Можно лишь рассчитать усредненное сопротивление, которое не будет абсолютно точным.
Помимо этого, как было подмечено ранее, существует еще реактивное сопротивление, которое бывает у индуктивных и емкостных элементов цепи. Оно явно себя проявляет в схемах, что работают с переменным, импульсным током. Если в цепях постоянного тока конденсатор (стоящий последовательно) не будет проводить через себя ток, то в цепи переменного тока будет все иначе. Причем его реактивное сопротивление будет зависеть от частоты (при одной и той же емкости). Вот формулы для нахождения реактивного емкостного и индуктивного сопротивления:
Причем его реактивное сопротивление будет зависеть от частоты (при одной и той же емкости). Вот формулы для нахождения реактивного емкостного и индуктивного сопротивления:
P.S. общее сопротивление можно находить и через использование закона Ома, который гласит, что сопротивление равно напряжение деленное на силу тока. Следовательно, берем мультиметр, измеряем ток и напряжение в том месте цепи, где хотим узнать сопротивление. Воспользовавшись формулой Ома находим (определяем) электрическое сопротивление нужного участка цепи. Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.
ac — Расчет входного сопротивления в простой цепи
спросил
Изменено 5 лет, 6 месяцев назад
Просмотрено 2к раз
\$\начало группы\$
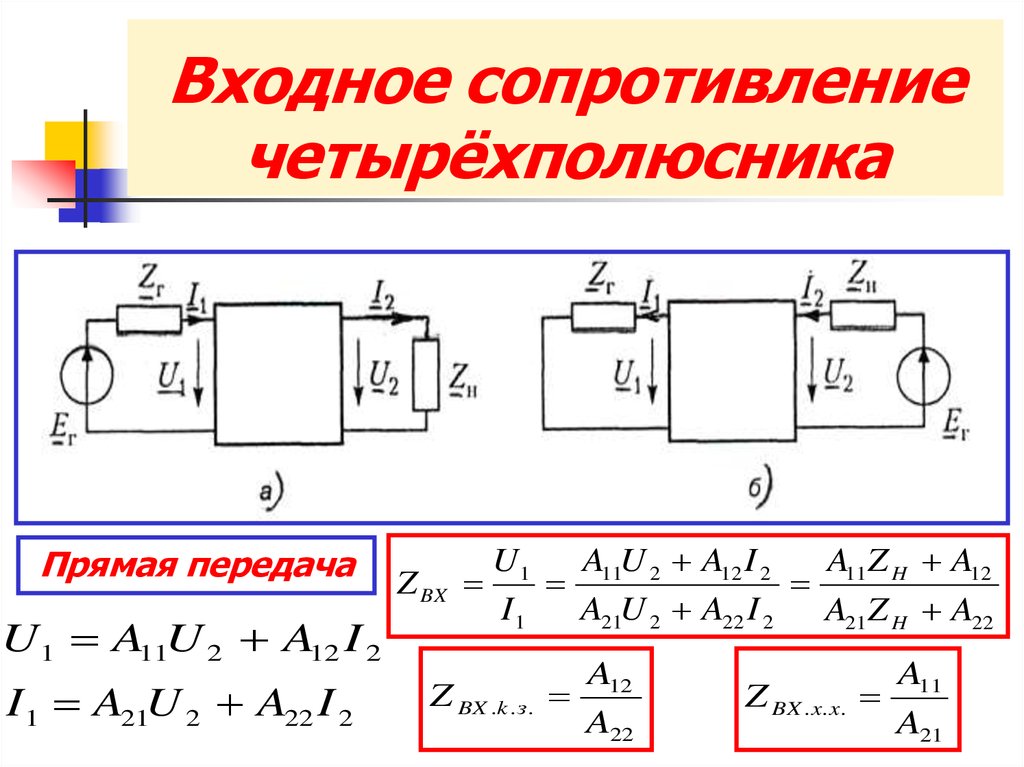
Я хочу рассчитать входное сопротивление в следующей схеме:
смоделируйте эту схему — Схема создана с помощью CircuitLab
Из крайнего левого контура у меня есть этот
$$U_{in}+I_{in}R=V_1$$
, так что, кажется, мне нужно выразить V1 через Uin, но я не могу этого сделать. Как мне подойти к этой проблеме?
Как мне подойти к этой проблеме?
Можно ли заменить управляемый источник тока эквивалентным источником напряжения, включенным последовательно с резистором? А потом добавить два источника напряжения, которые тогда будут последовательно?
- переменный ток
- входное сопротивление
\$\конечная группа\$
3
\$\начало группы\$
В вашем уравнении ошибка со знаком.
Применяя KCL в узле \$U_{in}\$, видим, что ток через \$R\$ идет от справа налево , что подразумевает
$$U_{in} — I_{in} R = V_1$$
На самом деле, и в более общем смысле, признайте, что параллельный резистор и управляемый источник тока можно заменить резистором с сопротивлением \$-R\$.
Чтобы убедиться в этом, посмотрите на аналогичную пару, изолированно управляемую текущим тестовым источником:
смоделируйте эту схему — схема, созданная с помощью CircuitLab
Тестовый источник «видит», в данном случае, \$ -1\Омега\$ сопротивления.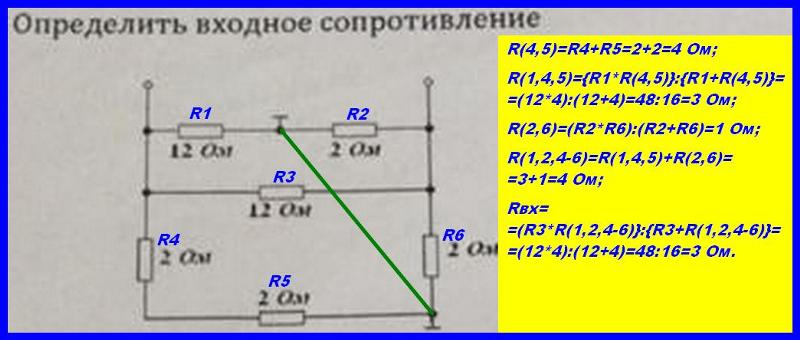
Чтобы найти входной импеданс, используйте аналогичный подход, чтобы найти эквивалентный импеданс цепи справа от отрицательного резистора, и тогда вы уменьшите схему до простой цепи с двумя последовательными импедансами. Тогда входное сопротивление будет очевидным.
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Операционный усилитель
Операционный усилитель— Как найти входное сопротивление этой схемы OPAMP?
спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 1к раз
\$\начало группы\$
Предположим, что операционный усилитель является идеальным с бесконечным усилением (a) и бесконечным входным сопротивлением Я ясно вижу, что входное сопротивление этой схемы равно R1 (поправьте меня, если я ошибаюсь), но я не могу решить, используя анализ обратной связи на OPAMP.
У меня есть два вопроса относительно этой схемы
Q1. Поскольку операционный усилитель считается идеальным, входное сопротивление базового усилителя становится бесконечным.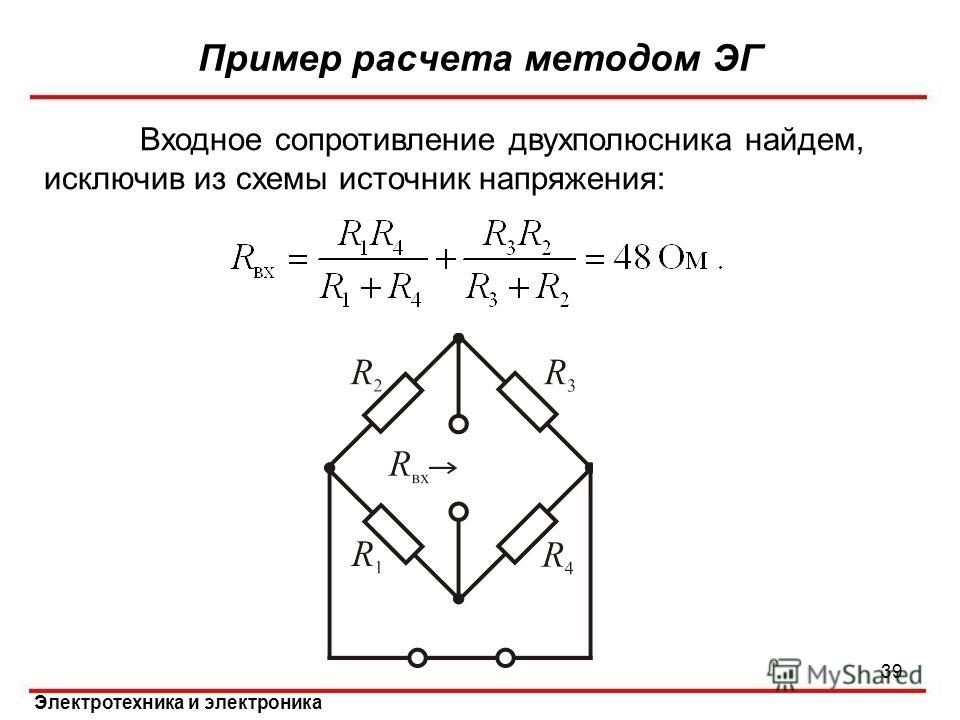
Таким образом, импеданс обратной связи должен быть бесконечен/контур усиления, который получается бесконечным
Q2. Если мне дана вторая схема, представляющая собой принципиальную схему с источником тока на входе в ОУ, показанную на рисунке выше, то могу ли я найти входное сопротивление без использования преобразования источника и преобразования неидеального источника в неидеальный источник напряжения
Если да, то так как напряжение на сопротивлении R1 в цепи с источником тока равно нулю, то сопротивление становится равным нулю \$\конечная группа\$
2
\$\начало группы\$
Поскольку операционный усилитель считается идеальным, входное сопротивление базового усилителя становится бесконечным.
Я не уверен, что вы подразумеваете под «базовым усилителем». Возможно, вы имеете в виду: операционный усилитель имеет входы с бесконечным входным сопротивлением. Это просто означает, что на входы операционного усилителя ток не поступает. Это ничего не говорит о схеме, которая представляет собой операционный усилитель + цепь обратной связи.
Это просто означает, что на входы операционного усилителя ток не поступает. Это ничего не говорит о схеме, которая представляет собой операционный усилитель + цепь обратной связи.
Таким образом, импеданс обратной связи должен быть равен бесконечности * усиление обратной связи, которое получается бесконечным
Что вы подразумеваете под «импедансом обратной связи»? Я также не понимаю, почему вы умножаете входное сопротивление операционного усилителя на «усиление обратной связи». Может быть, вы запутались с отношениями относительно выходное сопротивление операционного усилителя в конфигурации с обратной связью?
Тот факт, что операционный усилитель считается идеальным, делает это понятным. Так как на выходе будет определенное напряжение, то разность напряжений на входе ОУ составит
\$V_{in} = V_{out} / A = V_{out} / \infty= 0 \$
As вход + операционного усилителя заземлен, это означает, что вход — также будет на уровне земли. Тогда это означает, что входное сопротивление равно \$R_1\$
Тогда это означает, что входное сопротивление равно \$R_1\$
Преобразование \$V_1\$ и \$R_1\$ в \$I_1\$ и \$R_1\$ выполняется простым применением Thevenin.
Но выполнение этого изменяет входную цепь так, что вы не можете считать, что \$V_N\$ ведет себя так же!
Для управления левой схемой требуется источник напряжения (и \$Z_{in} = R_1\$), в то время как для схемы справа требуется источник тока и входной импеданс (как видно из источник тока) равен \$Z_{in} = 0\$
=> Две цепи не имеют одинаковых входных импедансов.
\$\конечная группа\$
1
\$\начало группы\$
При расчете обратной связи необходимо выполнить расчет усилителя с обратной связью . Это означает, что входное сопротивление, которое вы используете, является входным сопротивлением усилителя с добавленной цепью обратной связи. Таким образом, усилитель raw имеет бесконечный входной импеданс и нулевой выходной импеданс, но поскольку он используется в схеме, усилитель имеет входное усиление R2, потому что есть путь от входного вывода к выходу.
Таким образом, усилитель raw имеет бесконечный входной импеданс и нулевой выходной импеданс, но поскольку он используется в схеме, усилитель имеет входное усиление R2, потому что есть путь от входного вывода к выходу.
Тогда входное сопротивление усилителя + обратная связь равно \$\lim_{a \to \infty} \frac{R2}{a}\$, и все это имеет смысл.
\$\конечная группа\$
9
\$\начало группы\$
Другая логическая перспектива — когда на инвертирующий выход подается противоположное напряжение, так что дифференциальное напряжение всегда равно нулю (независимо от коэффициента усиления по напряжению).
Вы можете видеть Vin+=0V, поэтому Vin/Rin=Zin вы вводите импеданс. Даже если бы был сдвиг уровня на входе на Vcc/2 и то же самое с сигналом! Зин — это та же «виртуальная земля» на Вине.
Это применимо только к линейной работе и нарушению допущений, когда выход насыщен.


 Даля 166
Даля 166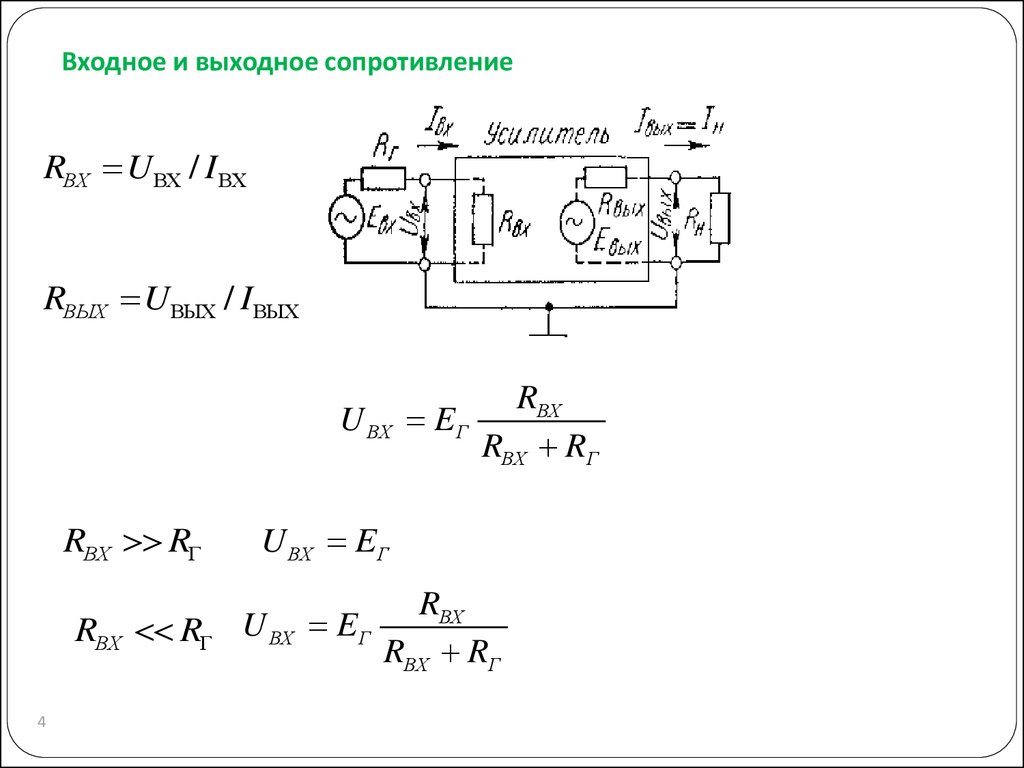 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123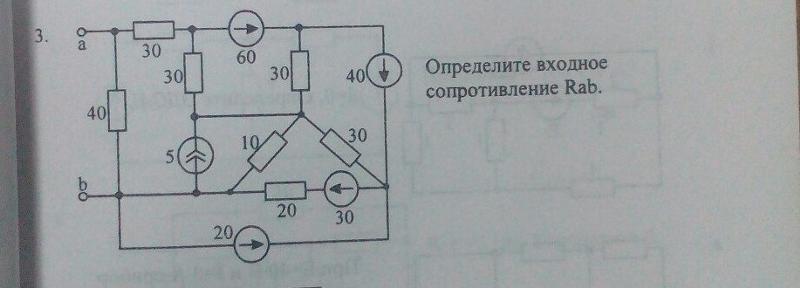 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;
Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;