Вынужденные колебания в контуре. Резонанс
Уравнение вынужденных колебаний
Вынужденными колебаниями называют периодические изменения параметров, которые описывают систему под влиянием внешней силы. Для реализации вынужденных электрических колебаний в $RLC$ контуре в него включают переменную ЭДС (рис.1).
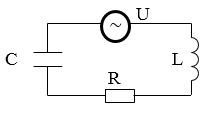
Рисунок 1.
В общем случае вынужденные колебания в таком контуре можно записать как:
где $L$ — индуктивность, $R$ — сопротивление, $C$ — емкость, $U\left(t\right)$ — внешнее воздействие.
Рассмотрим случай, когда в контур подается переменное напряжение ($U$) изменяющееся по гармоническому закону:
Тогда уравнение колебаний запишется в виде:
где ${\omega }_0=\frac{1}{\sqrt{LC}}$- собственная частота колебаний контура, $\beta =\frac{R}{2L}.$ По аналогии с механическими колебаниями можно записать частное решение данного уравнения как:
где $q_m=\frac{U_m}{\omega \sqrt{{R^2+\left(\omega L-1/\omega C\right)}^2}},\ tg\Psi=\frac{R}{\frac{1}{\omega C}-\omega L}$.
Как известно, общее решение неоднородного уравнения получают как сумму частного решения данного уравнения (в нашем случае это (4)) и общего решения соответствующего однородного уравнения. Так для уравнения:
общим решением является выражение:
Так как выражение (6) содержит множитель $e^{\left(-\beta t\right)}$, то при $t\to \infty ,\ $ $e^{\left(-\beta t\right)}\to 0,$ поэтому для установившихся колебаний решением уравнения (3) считают функцию (4).
Сила тока для установившихся вынужденных колебаний может быть записана как:
где $I_m={\omega q}_m$, $\varphi =\Psi-\frac{\pi }{2}$ — сдвиг фаз между тока и приложенного напряжения. Соответственно:
Надо отметить, что выполняется равенство:
Выражение (9) означает, что сумма напряжений на каждом из элементов цепи в момент времени $t$ равна приложенному напряжению.
Резонанс
Появление сильных колебаний при частоте внешней силы равной (или почти равной) собственной частоте колебательного контура, называют резонансом. Суть явления заключается в том, что как бы одиночные «толчки» усиливают друг друга. В таком случае получается, что энергия, которая вкладывается в систему, является максимальной. Амплитуда колебаний нарастает до тех пор, пока увеличивающиеся силы трения (в среднем) за период толчка не станут компенсировать действие каждого «толчка». В этот момент устанавливается максимум энергии и максимум амплитуды.
Резонансной частотой для заряда (${\omega }_{qr}$) и напряжения (${\omega }_{Cr}$) на конденсаторе являются частоты, заданные уравнениями:
Резонансные кривые для заряда и напряжения на конденсаторе имеют одинаковый вид (рис.2).

Рисунок 2.
Если $\omega =0$ кривые (рис.2) сходятся в одной точке, при этом напряжение на конденсаторе равно напряжению, которое возникает на нем при подключении источника:
Максимум резонансной кривой выше и острее, чем меньше коэффициент затухания (меньше $R$, больше $L$).
Кривые для силы тока изображены на рис. 3. Амплитудное значение силы тока максимально, если $\omega L-\frac{1}{\omega C}=0.\ $Частота силы тока при резонансе (${\omega }_{Ir}$):

Рисунок 3.
Пример 1
Задание: Получите функции $U_R(t),U_C(t),U_L(t)$ в $RCL$ контуре, если приложенное напряжение задано уравнением: $U=U_m{cos \left(\omega t\right)\ }.$
Решение:
В качестве основы для решения задачи используем выражение:
\[I\left(t\right)={I_m cos\ }\left(\omega t-\varphi \right)\left(1.1\right).\]Исходя из (1.1) для напряжения на сопротивлении ($U_R$) в соответствии с законом Ома для участка цепи можно записать, что:
Используя закон изменения заряда в контуре, заданном в условии:
\[q=q_m{cos \left(\omega t-\Psi\right)\ }(1.3)\]найдем $U_C\left(t\right)$ как:
\[U_C\left(t\right)=\frac{q}{C}=\frac{q_m{cos \left(\omega t-\Psi\right)\ }}{C}=U_{mC}{cos \left(\omega t-\varphi -\frac{\pi }{2}\right)\ }\left(1.4\right),\]где $U_{mC}=\frac{q_m}{C}=\frac{I_m}{С\omega }.$ Напряжение на катушке индуктивности найдем как:
\[U_L=L\frac{dI}{dt}=-L\omega {I_m sin\ }\left(\omega t-\varphi \right)=U_{Lm}{cos \left(\omega t-\varphi +\frac{\pi }{2}\right)\ }\left(1.5\right).\]Пример 2
Задание: Определите, во сколько раз напряжение на конденсаторе может превышать напряжение, которое приложено к $RLC$ контуру, если добротность контура равна $O$. Считать, что внешнее напряжение подчиняется гармоническому закону, затухание в контуре мало.
Решение:
Условие малости затухания для контура означает, что:
\[\beta \ll {\omega }_0(2.1)\]Напряжение на конденсаторе можно выразить как:
\[U_{mC}=\frac{q_m}{C}=\frac{U_m}{\omega C\sqrt{{R^2+\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(2.2\right)\]где $q_m=\frac{U_m}{\omega \sqrt{{R^2+\left(\omega L-1/\omega C\right)}^2}}$. Если при резонансе в нашем случае $\omega \approx {\omega }_0$, то максимальное напряжение на конденсаторе при резонансе равно ($U_{mCr}$):
\[U_{mCr}=\frac{U_m}{{\omega }_0C\sqrt{{R^2+\left({\omega }_0L-\frac{1}{{\omega }_0C}\right)}^2}}\ \approx \frac{U_m}{{\omega }_0RC}\left(2.3\right),\]где при малом затухании можно считать, что ${\omega }_0L-\frac{1}{{\omega }_0C}\approx 0$
Найдем отношение $\frac{U_{mCr}}{U_m}$, получим:
\[\frac{U_{mCr}}{U_m}=\frac{1}{{\omega }_0RC}=O\left(2.4\right),\]где $O=\frac{1}{R}\sqrt{\frac{L}{C}}$, ${\omega }_0=\frac{1}{\sqrt{LC}}$.
Ответ: $\frac{U_{mCr}}{U_m}=O.$
1.5.3. Вынужденные электрические колебания. Резонанс в последовательном контуре
Чтобы
вызвать вынужденные колебания, нужно
оказывать на систему внешнее периодически
изменяющееся воздействие. В случае
электрических колебаний это можно
осуществить, если включить последовательно
с элементами контура переменную ЭДС
или подать на контур переменное напряжение  (рис.1.5.5).
(рис.1.5.5).
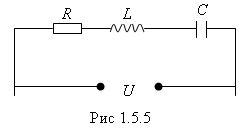 Цепь,
в которой последовательно с ЭДС включены
сопротивлениеR,
индуктивность L и конденсатор С, называется
последовательным колебательным контуром.
Рассмотрим процессы в этом контуре.
Цепь,
в которой последовательно с ЭДС включены
сопротивлениеR,
индуктивность L и конденсатор С, называется
последовательным колебательным контуром.
Рассмотрим процессы в этом контуре.
По
второму правилу Кирхгофа 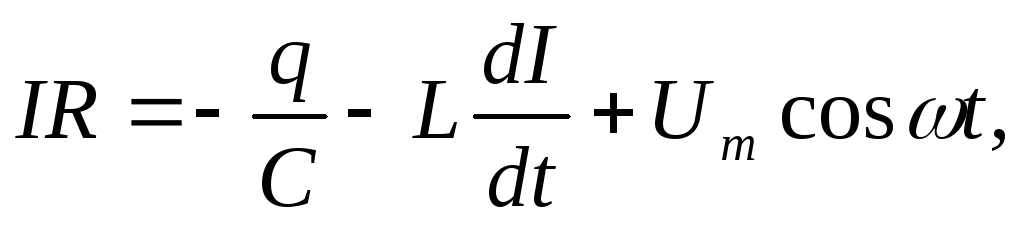 или
или  . Разделив на L,
получаем уравнение вынужденных колебаний
. Разделив на L,
получаем уравнение вынужденных колебаний
 (1.5.2)
(1.5.2)
Частное решение этого уравнения
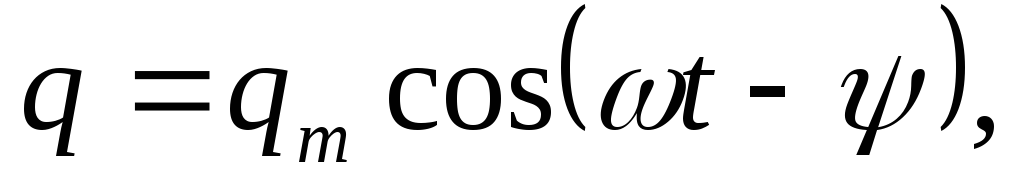 (1.5.3)
(1.5.3)
где 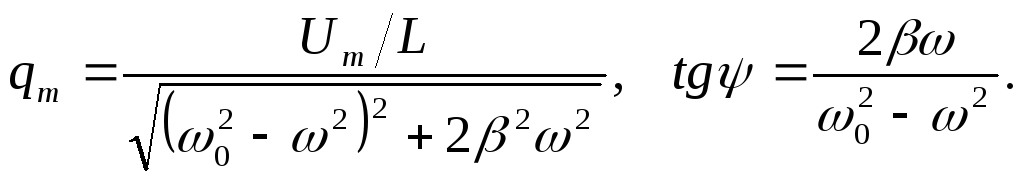 Подставим
Подставим 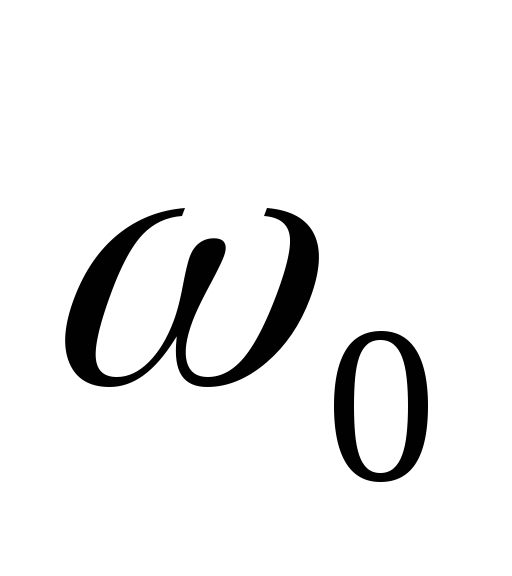 и
и  :
:
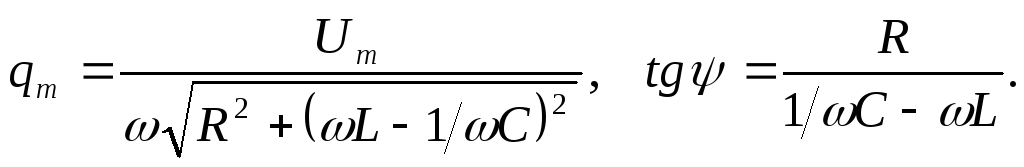
Общее
решение получится, если к частному
решению (1.5.3) прибавить общее решение
однородного дифференциального уравнения,
которое было получено в предыдущем
параграфе. Оно содержит множитель 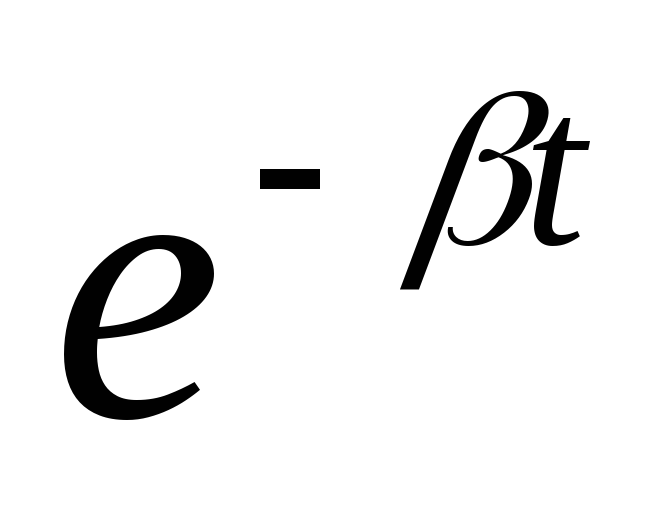 ,
который очень быстро убывает, и при
прошествии достаточно большого времени
,
который очень быстро убывает, и при
прошествии достаточно большого времени 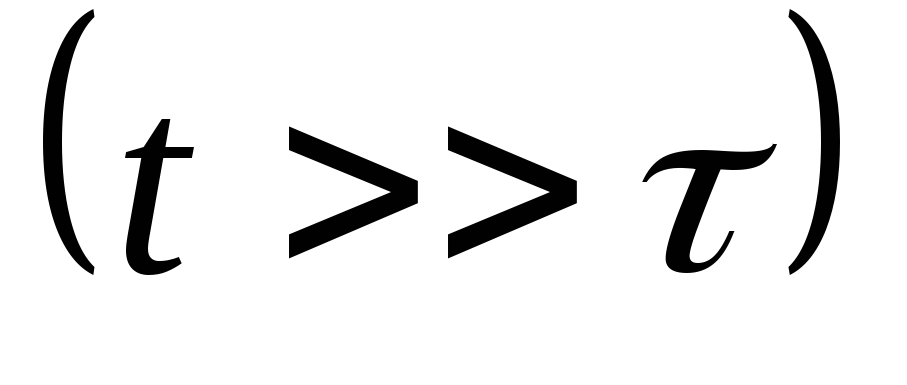 им можно пренебречь. Таким образом,
установившиеся вынужденные электромагнитные
колебания в контуре описываются
уравнением (1.5.3).
им можно пренебречь. Таким образом,
установившиеся вынужденные электромагнитные
колебания в контуре описываются
уравнением (1.5.3).
Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (1.5.3) по времени:
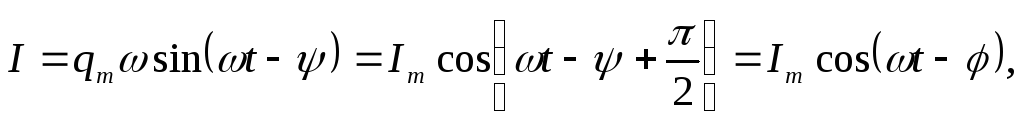
где 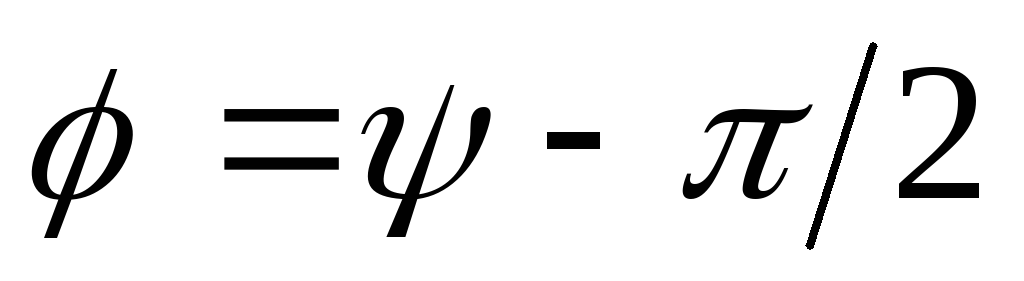 — сдвиг фаз между током и приложенным
напряжением. Тогда
— сдвиг фаз между током и приложенным
напряжением. Тогда
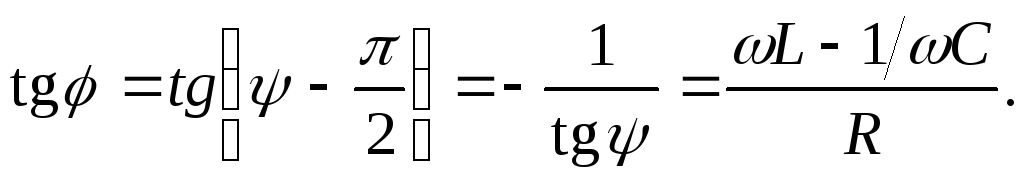
Из
этого выражения следует, что ток отстает
по фазе от напряжения (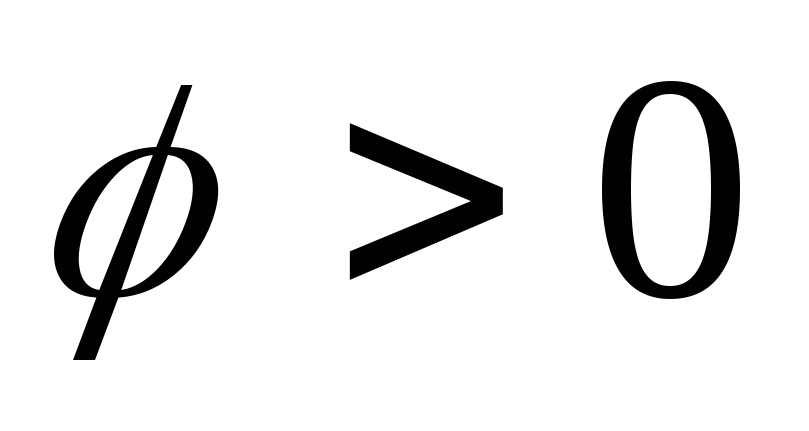 )при
)при 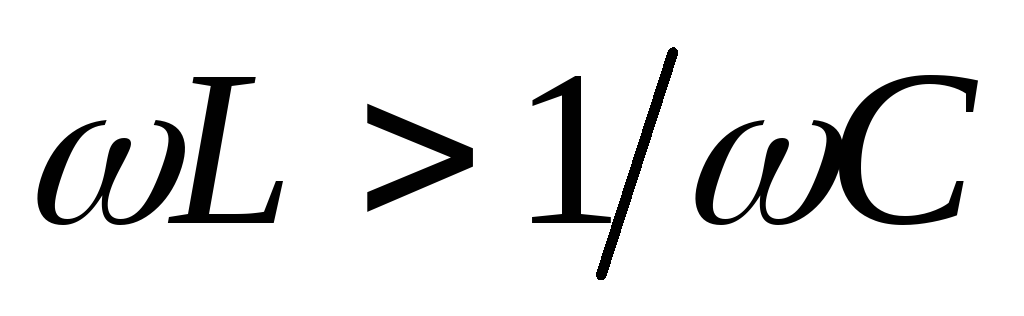 .
И опережает напряжение (
.
И опережает напряжение (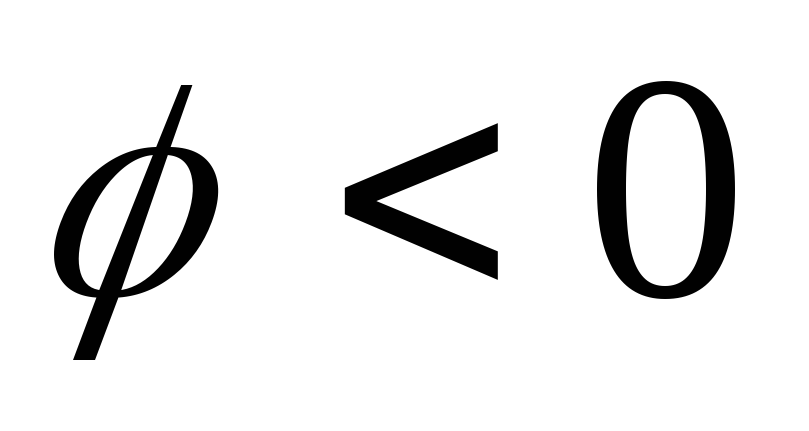 )
при
)
при 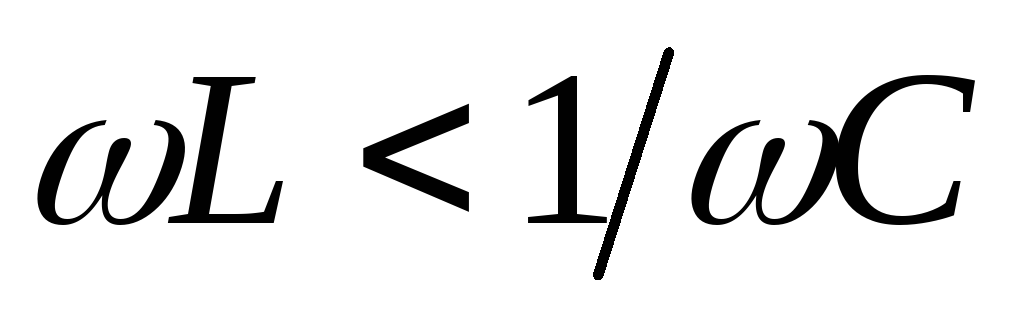 .
Для силы тока можно записать
.
Для силы тока можно записать
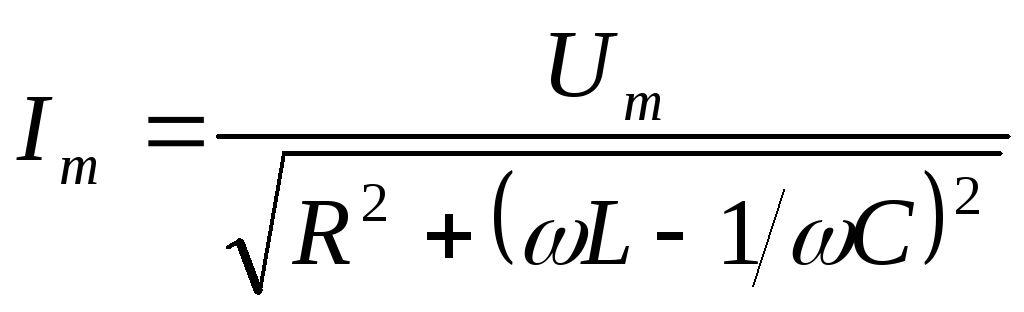 .
(1.5.4)
.
(1.5.4)
Представим
соотношение (1.5.2) в виде: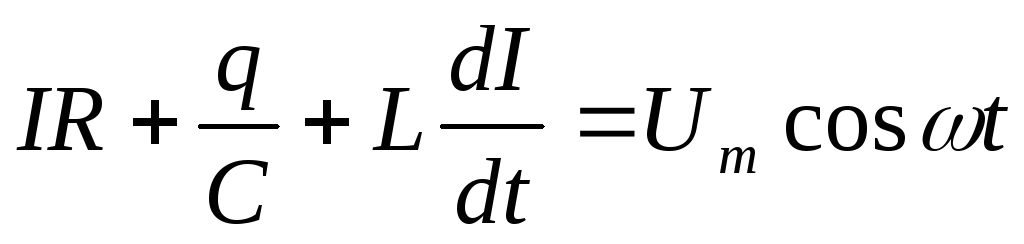 .
Произведение
.
Произведение 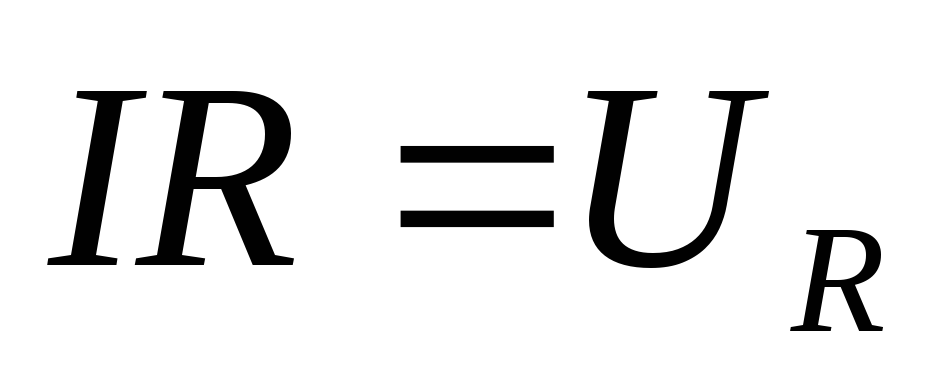 — падение напряжения на активном
сопротивлении;
— падение напряжения на активном
сопротивлении; 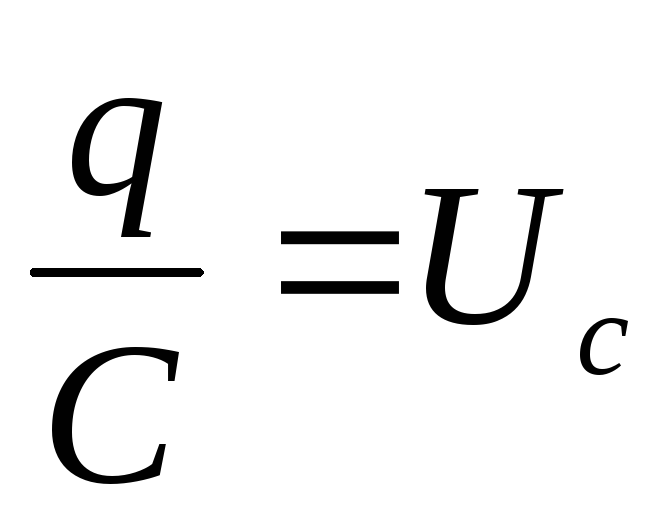 — падение напряжения на конденсаторе;
— падение напряжения на конденсаторе; 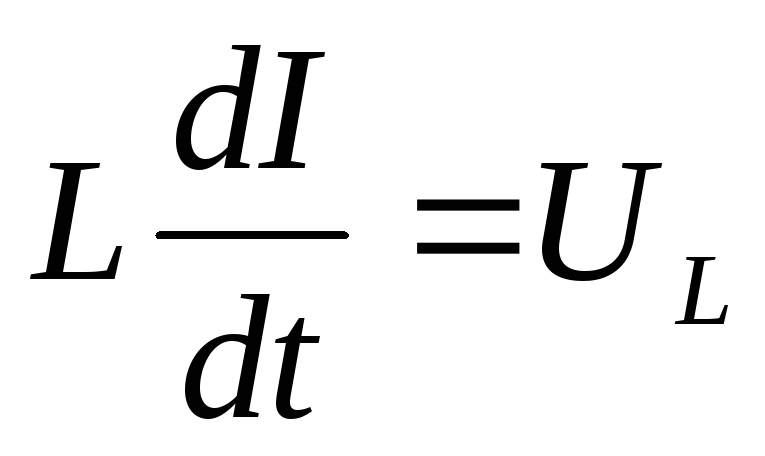 – напряжение на индуктивности; тогда
можно записать
– напряжение на индуктивности; тогда
можно записать
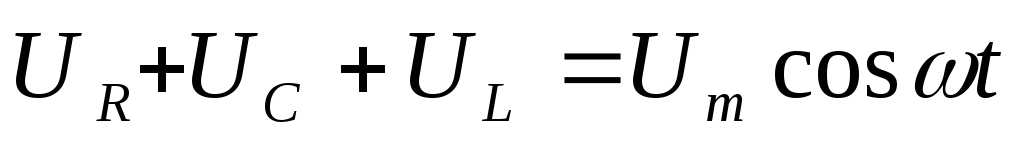 .
(1.5.5)
.
(1.5.5)
Таким образом, сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.
 Согласно
(1.5.4)
Согласно
(1.5.4)  — напряжение на активном сопротивлении
совпадает по фазе с током в контуре.
— напряжение на активном сопротивлении
совпадает по фазе с током в контуре.
Для
напряжения на конденсаторе, подставив
(1.5.3), имеем 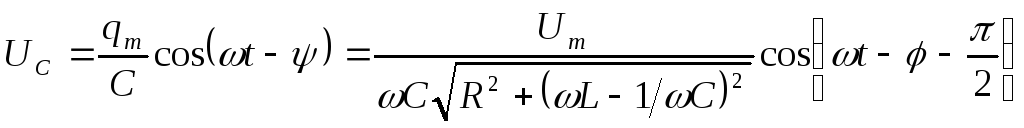
Напряжение на
индуктивности 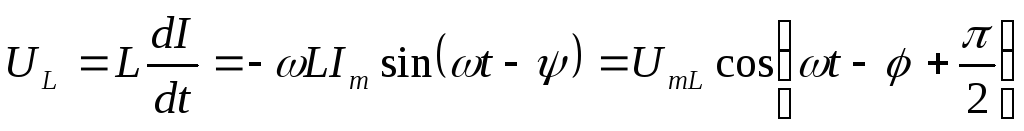 ,
где
,
где 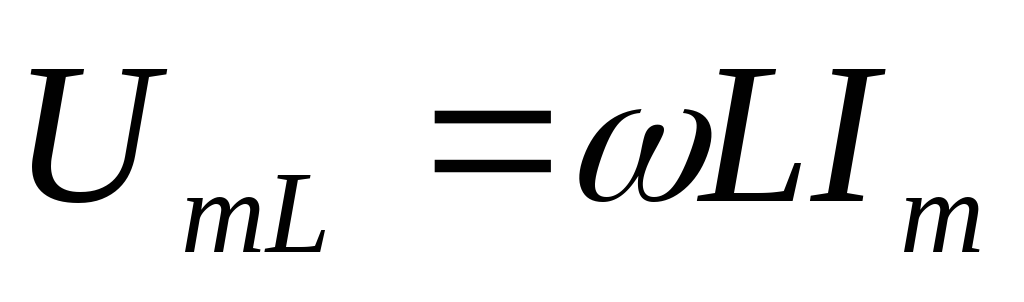 ,– напряжение на индуктивности
опережает ток на π/2.
,– напряжение на индуктивности
опережает ток на π/2.
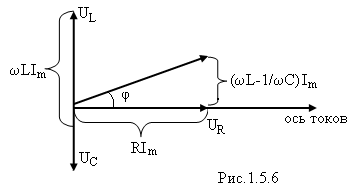
Фазовые соотношения можно представить наглядно с помощью векторной диаграммы. Действительно, гармонические колебания можно задать с помощью вектора, длина которого равна амплитуде колебаний , а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 1.5.6).
 совпадает по фазе
с током,
совпадает по фазе
с током, 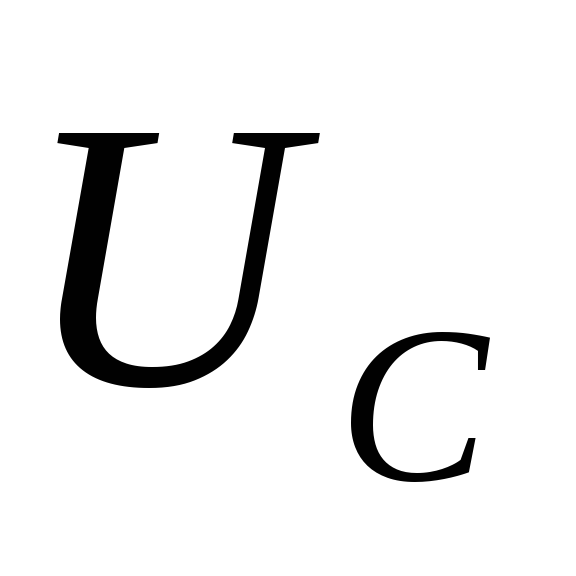 – отстаёт на π/2),
– отстаёт на π/2), 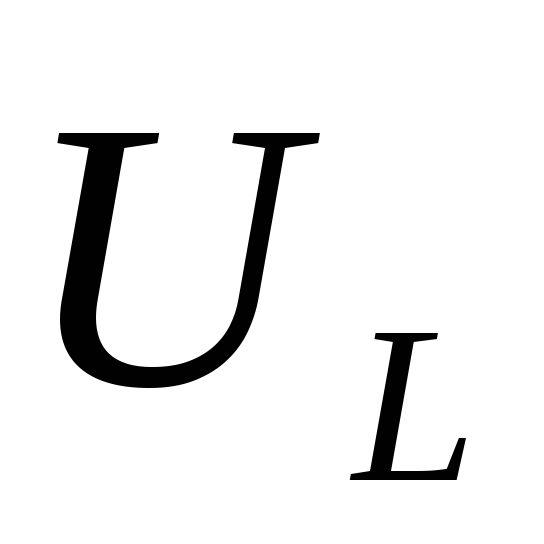 – опережает на π/2.
Векторы
– опережает на π/2.
Векторы 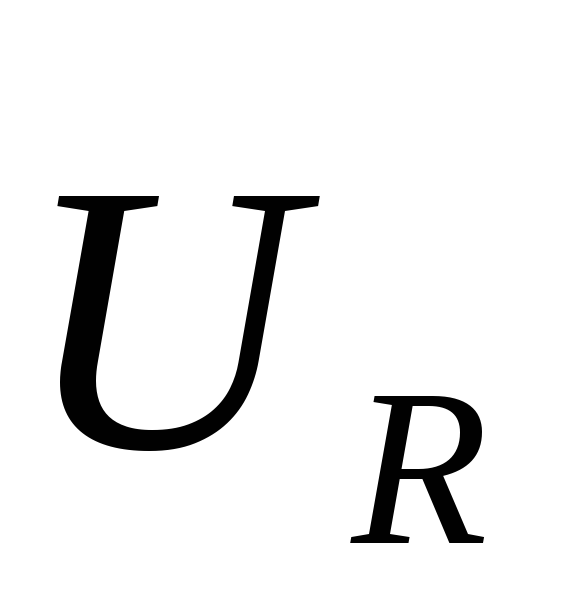
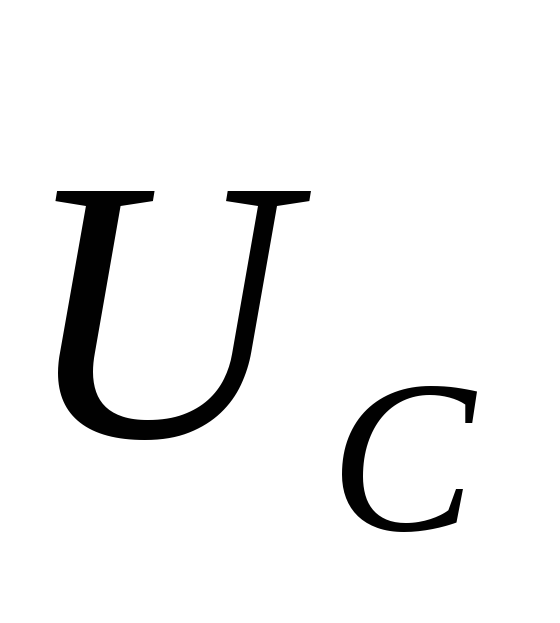 ,
, 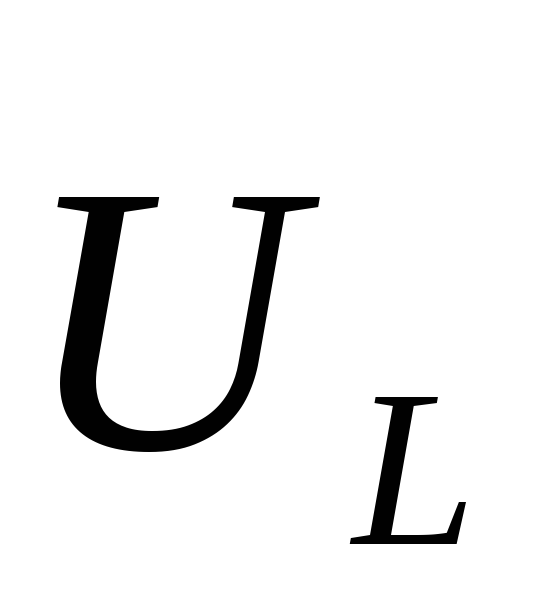 в сумме дают
в сумме дают 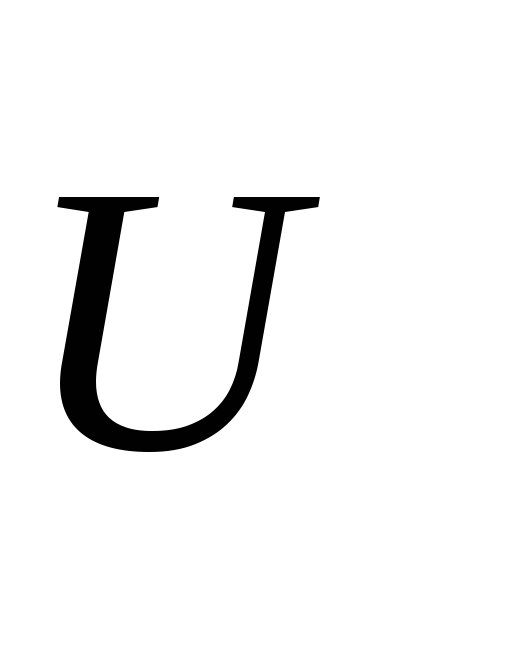 ,
причём U определяется выражением (1.5.5).
,
причём U определяется выражением (1.5.5). При
определенной частоте внешнего воздействия
в контуре наступает резонанс. Резонансная
частота для напряжения на конденсаторе 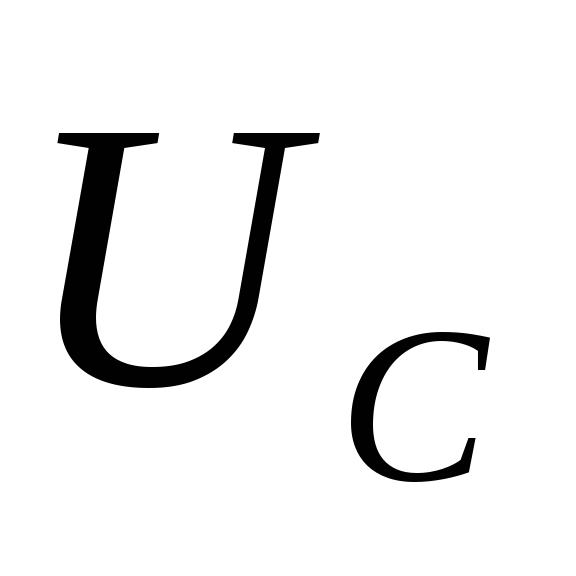
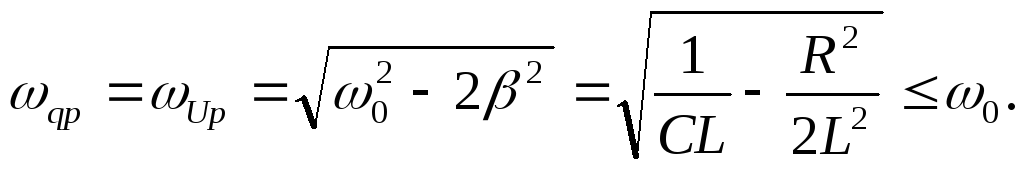 Резонансные кривые для
Резонансные кривые для 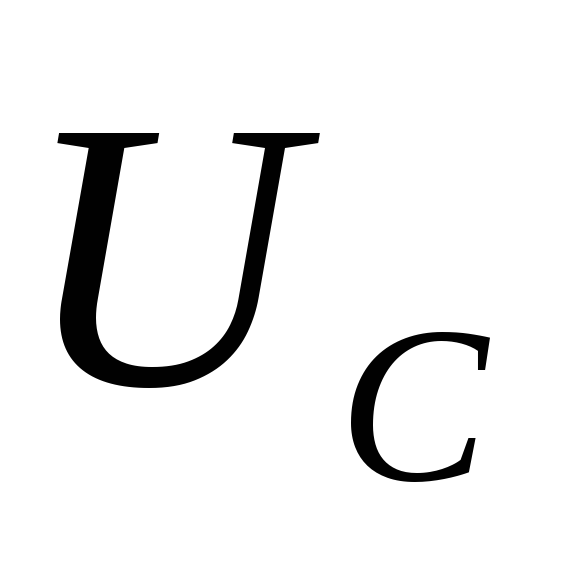 имеют вид, представленный на рис.1.5.7.
имеют вид, представленный на рис.1.5.7.
Все
резонансные частоты 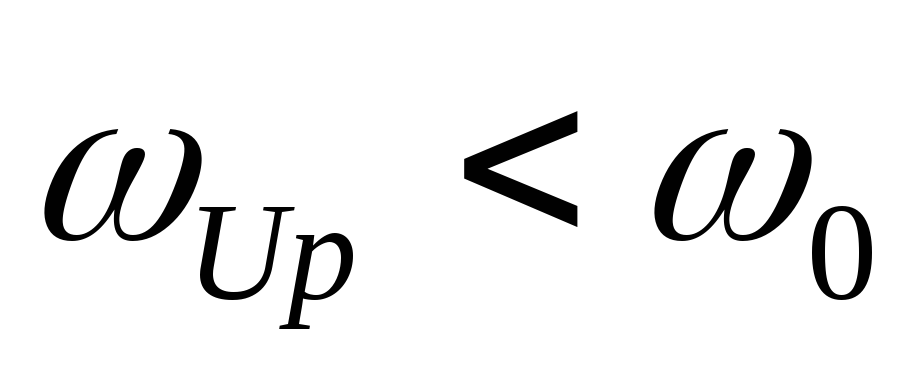 .
При ω→0 резонансные кривые сходятся в
одной точке
.
При ω→0 резонансные кривые сходятся в
одной точке 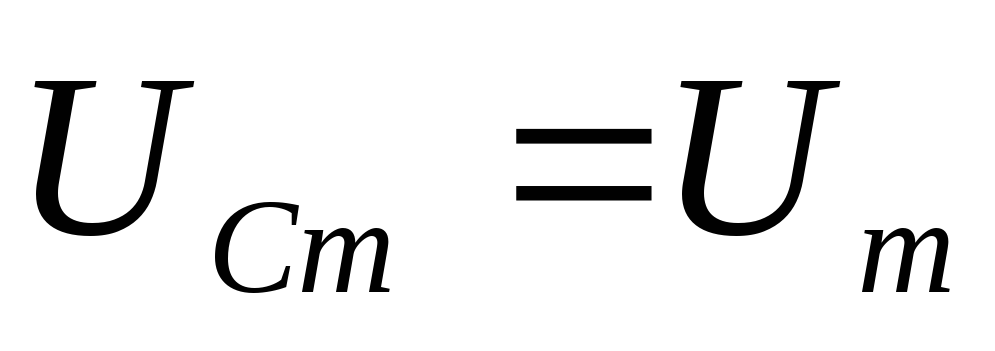
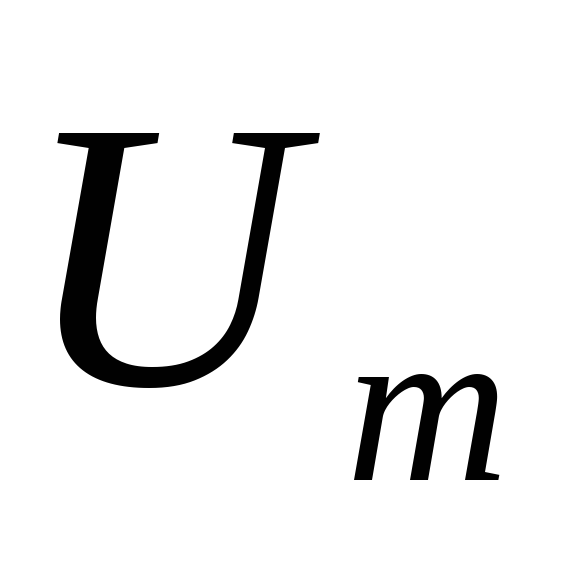 .
Максимум при резонансе тем острее и
выше, чем меньше затухание β=R/2L,
то есть чем меньше R и больше L.
Ход резонансной кривой аналогичен
резонансной кривой при механических
колебаниях.
.
Максимум при резонансе тем острее и
выше, чем меньше затухание β=R/2L,
то есть чем меньше R и больше L.
Ход резонансной кривой аналогичен
резонансной кривой при механических
колебаниях.Резонансные кривые для тока приведены на рис.1.5.8.
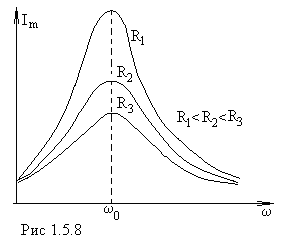
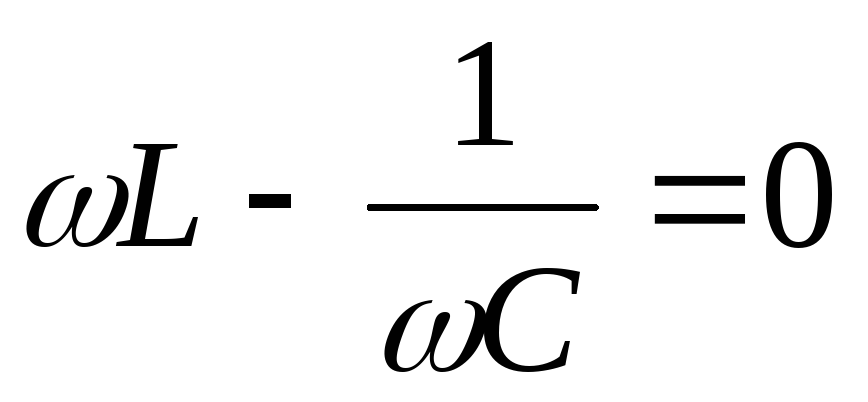 ,
то есть резонансная частота для силы
тока совпадает с собственной частотой
колебаний контура:
,
то есть резонансная частота для силы
тока совпадает с собственной частотой
колебаний контура:
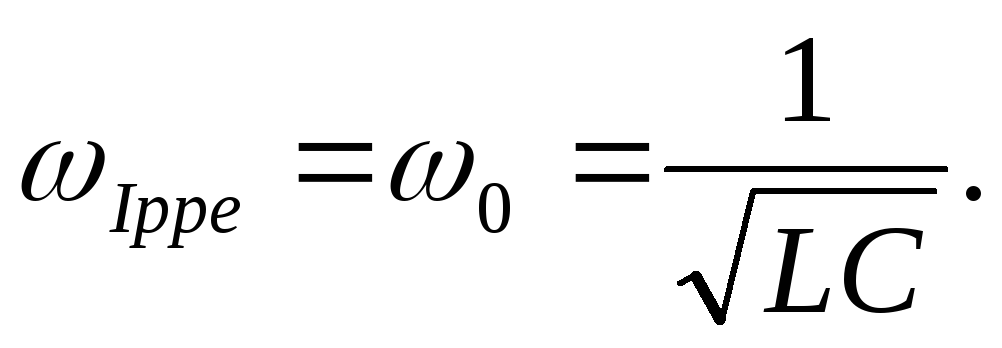
При ω→0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.
При
малом затухании (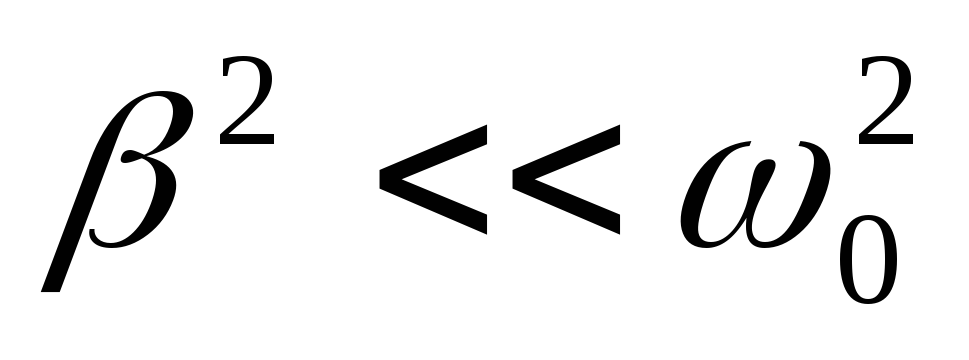
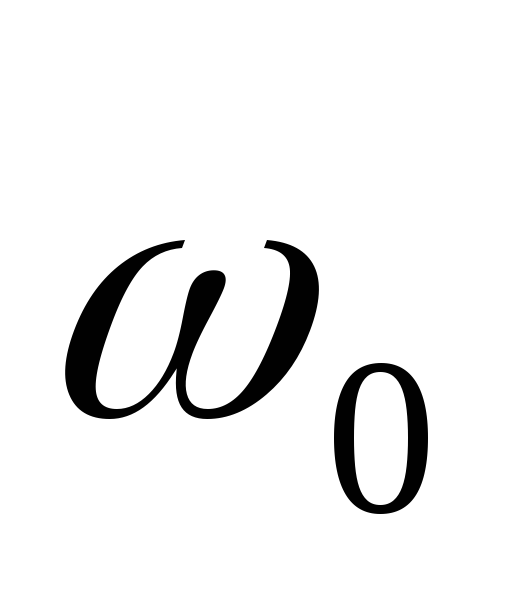 .
Тогда отношение амплитуды напряжения
на конденсаторе при резонансе к амплитуде
внешнего напряжения равно:
.
Тогда отношение амплитуды напряжения
на конденсаторе при резонансе к амплитуде
внешнего напряжения равно: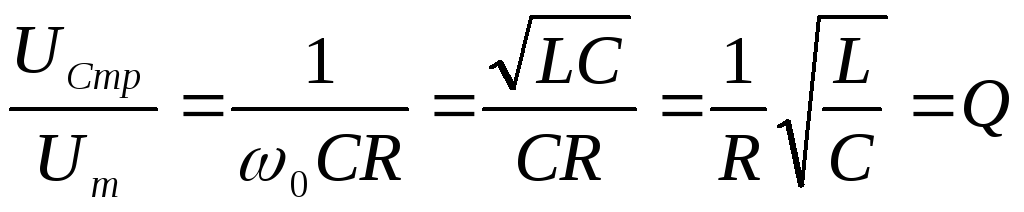
— то есть добротность контура показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.
Итак,
при резонансе причём 
 поэтому
поэтому 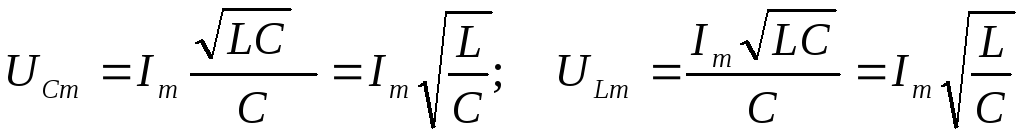 — амплитуды напряжений на ёмкости
и индуктивности равны между собой, но
противоположны по фазе. Поэтому напряжения
на ёмкости и индуктивности компенсируют
друг друга, и цепь ведёт себя цепь только
с активным сопротивлением. Вся энергия,
приложенная к контуру, идёт на
Ленц-Джоулево тепло. Ток в цепи достигает
максимального значения. Это резонанс
напряжений – индуктивногои емкостного
— амплитуды напряжений на ёмкости
и индуктивности равны между собой, но
противоположны по фазе. Поэтому напряжения
на ёмкости и индуктивности компенсируют
друг друга, и цепь ведёт себя цепь только
с активным сопротивлением. Вся энергия,
приложенная к контуру, идёт на
Ленц-Джоулево тепло. Ток в цепи достигает
максимального значения. Это резонанс
напряжений – индуктивногои емкостного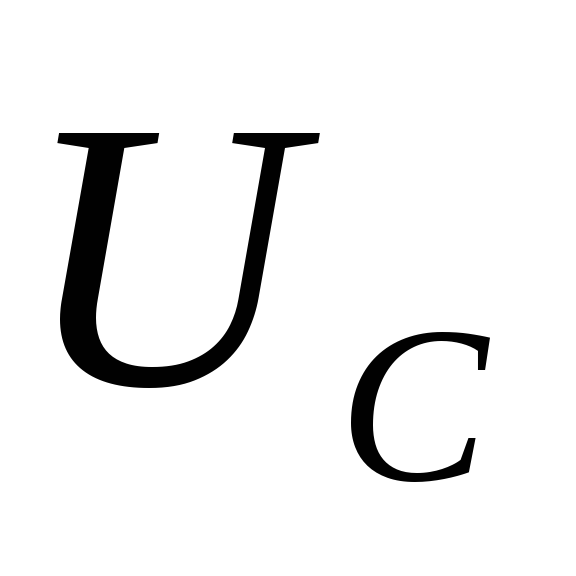 .
.
Изучение колебательного контура
Подборка по базе: 17.03 Изучение эмоциональной сферы дошкольников.docx, 1. Содержание программы Углублённое изучение биологии.odt, Яшкова А.Н. Изучение ученических групп.doc, Лабораторная работа 5. Изучение свободных и вынужденных колебани, Заявление на изучение факультативных или элективных дисциплин.rt, Лабараторная №1 Изучение и поверка цифровых измерителей температ, Лабараторная №1 Изучение и поверка цифровых измерителей температ, 7-Лабораторная работа (Физика) (Внешний фотоэффект. Изучение зак, Лабораторная работа № 4.02 — Изучение оптических характеристик р, Лабораторная работа №4.03 — Изучение дифракции света.docx.
Лабораторная работа 231
ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО КОНТУРА
Общие сведения
К
олебательный контур (рис.1) представляет собой замкнутую электрическую цепь, состоящую из катушки индуктивности L и конденсатора С, в которой могут возбуждаться электрические колебания.
Свойства колебательного контура во многом аналогичны свойствам механических колебательных систем. В частности, электрические колебания также сопровождаются попеременным превращением энергии одного вида в энергию другого вида, свободные электрические колебания затухают со временем, а в случае вынужденных электрических колебаний наблюдается явление резонанса.
Благодаря своим свойствам, колебательный контур широко используется на практике – он является одним из основных элементов радиотехнических устройств.
Возникновение колебаний в контуре
Если разомкнуть цепь колебательного контура и от внешнего источника зарядить конденсатор, то на его обкладках возникнут разноименные заряды  и
и  , а между обкладками – электрическое поле, энергия которого равна
, а между обкладками – электрическое поле, энергия которого равна
 , (1)
, (1)
где  – разность потенциалов (напряжение) между обкладками.
– разность потенциалов (напряжение) между обкладками.
При замыкании цепи контура конденсатор начинает разряжаться через катушку индуктивности и его заряд уменьшается (рис.2). При этом сила тока в контуре нарастает (по абсолютной величине) постепенно из-за возникновения в катушке э.д.с. самоиндукции  , которая (согласно правилу Ленца) препятствует изменению тока:
, которая (согласно правилу Ленца) препятствует изменению тока:
 . (2)
. (2)

Рис. 2
В момент времени  (Т — период колебаний), когда конденсатор разрядится полностью (q = 0), сила тока достигнет своего максимального значения —
(Т — период колебаний), когда конденсатор разрядится полностью (q = 0), сила тока достигнет своего максимального значения — , и энергия электрического поля полностью превратится в энергию магнитного поля катушки:
, и энергия электрического поля полностью превратится в энергию магнитного поля катушки:
 (3)
(3)
Хотя разность потенциалов между обкладками конденсатора в этот момент будет равна нулю, ток в цепи не прекратится мгновенно, так как его уменьшение приведет к возникновению э.д.с. самоиндукции, поддерживающей движение зарядов в прежнем направлении.
В момент времени  заряды на обкладках конденсатора достигнут прежней максимальной величины, но поменяются знаками. В этот момент
заряды на обкладках конденсатора достигнут прежней максимальной величины, но поменяются знаками. В этот момент  , и энергия магнитного поля полностью превратится в энергию электрического поля. Затем снова начнется разряд конденсатора, но ток в контуре будет иметь обратное направление. В момент
, и энергия магнитного поля полностью превратится в энергию электрического поля. Затем снова начнется разряд конденсатора, но ток в контуре будет иметь обратное направление. В момент  конденсатор разрядится, и вновь из-за э.д.с. самоиндукции, возникающей в катушке, начнется его перезарядка. В момент времени
конденсатор разрядится, и вновь из-за э.д.с. самоиндукции, возникающей в катушке, начнется его перезарядка. В момент времени  заряд конденсатора станет равным по величине и знаку своему первоначальному значению (при t = 0), после чего описанные выше процессы будут периодически повторяться – в контуре возникнут непрерывные периодические изменения величин заряда и тока, т.е. электрические колебания. Так как внешнее напряжение к контуру не приложено, то имеют место так называемые свободные (или собственные) колебания.
заряд конденсатора станет равным по величине и знаку своему первоначальному значению (при t = 0), после чего описанные выше процессы будут периодически повторяться – в контуре возникнут непрерывные периодические изменения величин заряда и тока, т.е. электрические колебания. Так как внешнее напряжение к контуру не приложено, то имеют место так называемые свободные (или собственные) колебания.
Дифференциальное уравнение свободных незатухающих колебаний
Уравнение, описывающее процессы в колебательном контуре при отсутствии потерь энергии, известно из курса физики средней школы, где оно было получено на основе закона сохранения энергии. Получим это уравнение с помощью второго правила Кирхгофа, согласно которому алгебраическая сумма падений напряжений на каждом из элементов замкнутого контура равна алгебраической сумме э.д.с., действующих в этом контуре.
На основании второго правила Кирхгофа для рассматриваемого колебательного контура можно записать:
 (4)
(4)
или
 . (4а)
. (4а)
Поделим это равенство на  и, учитывая, что
и, учитывая, что  , получим дифференциальное уравнение, описывающее изменение заряда конденсатора во времени:
, получим дифференциальное уравнение, описывающее изменение заряда конденсатора во времени:
 . (4б)
. (4б)
Если обозначить  как
как  , уравнение (4б) примет вид
, уравнение (4б) примет вид
 . (4в)
. (4в)
Решением этого уравнения является функция
 , (5)
, (5)
показывающая, что заряд на обкладках конденсатора изменяется по гармоническому закону с циклической (угловой) частотой 
 , (6)
, (6)
называемой собственной частотой колебательного контура.
Период колебаний равен (формула Томсона)
 . (7)
. (7)
Напряжение на конденсаторе и ток в контуре также изменяются по гармоническому закону:
 , (8)
, (8)
 . (9)
. (9)
Из формул (5), (8), (9) видно, что колебания заряда (или напряжения) и тока сдвинуты по фазе на  ; ток достигает максимального значения, когда заряд и напряжение равны нулю, и наоборот (см. рис.2).
; ток достигает максимального значения, когда заряд и напряжение равны нулю, и наоборот (см. рис.2).
Затухание свободных колебаний в реальном контуре
Формулы (5), (8) и (9) описывают незатухающие колебания в идеальном контуре без потерь энергии. Однако, всякий реальный колебательный контур, кроме емкости и индуктивности, обладает еще и активным сопротивлением R . Величина этого сопротивления определяется, в основном, сопротивлением провода, которым намотана катушка. Энергия расходуется на нагревание этого провода, и колебания постепенно затухают.
Для реального контура (рис.3), согласно второму правилу Кирхгофа, можно записать:
 , (10)
, (10)
где  – падение напряжения на активном сопротивлении. Учитывая, что
– падение напряжения на активном сопротивлении. Учитывая, что  ,
,  ,
,  , а также
, а также  и
и  , уравнение (10) можно записать в виде
, уравнение (10) можно записать в виде
 . (10а)
. (10а)
Поделив все члены уравнения на  и введя обозначения
и введя обозначения  и
и  , получим
, получим
 (10б)
(10б)
Решением уравнения (10б) является функция
 , (11)
, (11)
к оторая отличается от функции (5) тем, что амплитуда колебаний зависит от времени:
оторая отличается от функции (5) тем, что амплитуда колебаний зависит от времени:  (рис.4). Колебания затухают тем быстрее, чем больше величина параметра
(рис.4). Колебания затухают тем быстрее, чем больше величина параметра  , называемого коэффициентом затухания.
, называемого коэффициентом затухания.

Наличие активного сопротивления приводит к уменьшению частоты колебаний
 . (12)
. (12)
Кроме коэффициента затухания  , используется еще один параметр – логарифмический декремент затухания
, используется еще один параметр – логарифмический декремент затухания  , характеризующий изменение амплитуды колебаний за время, равное одному периоду:
, характеризующий изменение амплитуды колебаний за время, равное одному периоду:
 . (13)
. (13)
Получение незатухающих колебаний. Резонанс
Наиболее важными для практического применения являются незатухающие (вынужденные) колебания, получаемые при включении в контур э. д. с. (см. рис.5), которая изменяется по гармоническому закону:
 . (14)
. (14)
В этом случае, пользуясь вторым правилом Кирхгофа, можно получить уравнение
 (15)
(15)
Решение этого уравнения дает функцию, описывающую вынужденные колебания заряда с частотой, равной частоте переменной э. д. с.,  :
:
 , (16)
, (16)
где
 . (17)
. (17)
Соответственно,
 (18)
(18)
и
 . (19)
. (19)
Здесь
 (20)
(20)
Как видно из (20), амплитудное значение силы тока (Im) можно определить по закону Ома через амплитуду э.д.с. и полное сопротивление контура (импеданс) Z. Величина Z зависит от активного сопротивления R, емкостного  и индуктивного
и индуктивного  сопротивлений:
сопротивлений:  . (21)
. (21)
Величина  называется реактивным сопротивлением контура.
называется реактивным сопротивлением контура.
Из равенства (21) видно, что полное сопротивление контура принимает минимальное значение  при
при  , что имеет место, если
, что имеет место, если
 . (22)
. (22)
Согласно (20) амплитудное значение силы тока  при этом достигает максимума
при этом достигает максимума
 (23)
(23)
Явление резкого возрастания амплитуды колебаний силы тока, (или напряжения), наблюдаемое при  , называется явлением резонанса. Частота
, называется явлением резонанса. Частота  называется резонансной частотой для тока. Отметим, что резонансная частота для напряжения на конденсаторе равна
называется резонансной частотой для тока. Отметим, что резонансная частота для напряжения на конденсаторе равна  .
.
График зависимости  (или
(или  ) от частоты внешней э.д.с.,
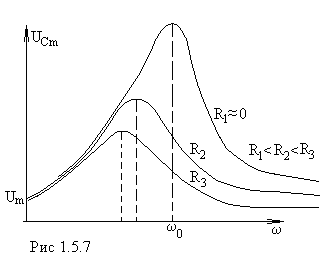
) от частоты внешней э.д.с.,  называется резонансной кривой. Форма резонансной кривой зависит от величины активного сопротивления: чем меньше R, тем выше и острее максимум резонансной кривой (рис. 6).
называется резонансной кривой. Форма резонансной кривой зависит от величины активного сопротивления: чем меньше R, тем выше и острее максимум резонансной кривой (рис. 6).


Параметры, имеющие важное значение для практики
С точки зрения практики важнейшими параметрами колебательного контура, наряду с резонансной частотой, являются его добротность и полоса пропускания.
Добротностью Q называется величина, обратно пропорциональная логарифмическому декременту затухания:
 . (24)
. (24)
Если затухание мало, т.е.  , то, как следует из (12),
, то, как следует из (12),  и
и
 . (25)
. (25)
Величина  называется характеристическим или волновым сопротивлением контура. Таким образом, добротность контура зависит от соотношения между активным R и волновым
называется характеристическим или волновым сопротивлением контура. Таким образом, добротность контура зависит от соотношения между активным R и волновым  сопротивлениями: чем меньше R, тем выше Q.
сопротивлениями: чем меньше R, тем выше Q.
Добротность контура показывает, во сколько раз напряжение на конденсаторе (или катушке индуктивности) в момент резонанса может превысить напряжение внешнего источника  . Действительно, согласно закону Ома, резонансное напряжение на конденсаторе равно
. Действительно, согласно закону Ома, резонансное напряжение на конденсаторе равно
 , (26)
, (26)
или с учетом равенств (23), (22), (6) и (25) . (26а)
. (26а)
Отсюда
 . (27)
. (27)
О т величины добротности зависит так называемая избирательность приемного устройства, т.е. его способность выделять сигнал только одной из нескольких радиостанций, работающих на близких частотах. Сказанное иллюстрирует рис.7.
т величины добротности зависит так называемая избирательность приемного устройства, т.е. его способность выделять сигнал только одной из нескольких радиостанций, работающих на близких частотах. Сказанное иллюстрирует рис.7.
Рис.7а Рис.7б
При высокой добротности контура (рис.7а) амплитуда сигнала  от радиостанции, работающей на частоте
от радиостанции, работающей на частоте  , на которую настроен контур, значительно больше амплитуды сигнала
, на которую настроен контур, значительно больше амплитуды сигнала  от радиостанции, работающей на нерезонансной частоте
от радиостанции, работающей на нерезонансной частоте  . При низкой добротности (рис.76) сигналы
. При низкой добротности (рис.76) сигналы  и
и  сравнимы по величине; при любой настройке контура (на
сравнимы по величине; при любой настройке контура (на  или на
или на  ) обе радиостанции будут слышны одновременно.
) обе радиостанции будут слышны одновременно.
Добротность контура зависит от его активного сопротивления и, прежде всего, от активного сопротивления катушки индуктивности. Следовательно, основным путем увеличения добротности контура является уменьшение активного сопротивления катушки индуктивности. Это достигается следующими способами:
Хорошие колебательные контуры имеют добротность, равную нескольким сотням. Отметим, что согласно (25) уже при
 активное сопротивление
активное сопротивление  и в обычных радиотехнических контурах (
и в обычных радиотехнических контурах ( от 50 до 150) влияние активного сопротивления на частоту колебаний ничтожно мало. Это позволяет использовать формулу (6) для расчета резонансной частоты реального контура.
от 50 до 150) влияние активного сопротивления на частоту колебаний ничтожно мало. Это позволяет использовать формулу (6) для расчета резонансной частоты реального контура.Чрезмерно высокие значения  приводят к тому, что резко сужается полоса пропускания
приводят к тому, что резко сужается полоса пропускания  . За
. За  принимают ширину резонансной кривой, измеренную на уровне
принимают ширину резонансной кривой, измеренную на уровне  (рис. 8).
(рис. 8).

Рис.8
Вопрос о полосе пропускания контура имеет большое значение, т.к. для неискаженной передачи и приема сигналов необходимо, чтобы все частоты, входящие в состав сигнала, в одинаковой степени излучались передающим устройством или усиливались приемным устройством.
Между резонансной частотой, полосой пропускания и добротностью существует следующая связь:
 . (28)
. (28)
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Описание установки
Установка (рис. 9) состоит из генератора высокочастотных гармонических колебаний ГЗ-7А, с выхода которого переменное напряжение подается через сопротивление  на колебательный контур. Напряжение на колебательном контуре регистрируется о помощью осциллографа С1-54. В контур поочередно могут включаться конденсаторы
на колебательный контур. Напряжение на колебательном контуре регистрируется о помощью осциллографа С1-54. В контур поочередно могут включаться конденсаторы  (переключателем
(переключателем  ) и сопротивления
) и сопротивления  (переключателем
(переключателем  ).
).
Рис.9
Порядок выполнения работы
Шнуры питания генератора ГЗ-7А и осциллографа С1-54 включить всеть напряжением 220 В. Перевести тумблеры включения на панели генератора (2 тумблера) в положение «вкл», нажать кнопку «СЕТЬ» на панели осциллографа. Поставить указатель диапазонов частот на генераторе в положение «Д 1,4 ÷ 4 МГц». Это соответствует тому, что частота генерируемых колебаний будет находиться в диапазоне от 1,4 до 4 МГц (1 МГц = 106 Гц). Измерения можно производить спустя 5 минут после включения приборов.
УПРАЖНЕНИЕ I. Измерение индуктивности катушки колебательного контура
Для изготовления колебательных контуров чаще всего используют конденсаторы известной емкости, широкий набор которых выпускается промышленностью. В то же время катушки индуктивности рассчитывают и изготовляют специально для каждого конкретного случая. В связи с этим часто возникает задача измерения величины индуктивности изготовленной катушки. Обычно она решается путем подключения к катушке конденсатора известной емкости и измерения частоты образовавшегося колебательного контура. Индуктивность катушки при этом рассчитывается по формуле:
 (29)
(29)
где  – резонансная частота, измеряемая в герцах.
– резонансная частота, измеряемая в герцах.
В нашем случае имеются два конденсатора известной емкости: С1 = 430 пФ и С2 = 220 пФ (1 пФ = 10–12Ф), с помощью которых можно определить индуктивность катушки. Для этого необходимо:
Установить ручку «частота» на генераторе Г3-7А вращением по часовой стрелке в крайнее положение.
Установить на вольтметре генератора ручкой «Регулировка выхода плавно» напряжение 8 В (по средней шкале).
Переключатель П2 на стенде поставить в положение I.
Переключатель П1 на стенде поставить в положение I, что соответствует включению в контур конденсатора С1.
Определить резонансную частоту , для чего:
, для чего:
плавно поворачивая ручку «Частота» на генераторе, добиться максимальной амплитуды сигнала на экране осциллографа;
снять показания (в МГц) со шкалы частот генератора, соответствующей интервалу 1,4 – 4 МГц (шкала Д).
Включить в контур конденсатор С2 (переключатель П1 поставить в положение II) и вновь определить резонансную частоту , выполнив пункт 5.
, выполнив пункт 5.
По формуле (29) вычислить индуктивность катушки для обоих случаев.
Вычислить среднее значение индуктивности .
.
Заполнить таблицу I
Сделать вывод о зависимости резонансной частоты контура от емкости конденсатора С.
Таблица I
| Положение переключателя ПI | С, пФ | 0, МГц | L, Гн |  , Гн , Гн |
| I | ||||
| П |
УПРАЖНЕНИЕ 2. Измерение емкости конденсатора
Если индуктивность контура известна, то, измерив резонансную частоту, можно определить емкость конденсатора, включенного в контур. Определим неизвестную емкость конденсатора С3.
1. Переключатель ПI на стенде поставить в положение III.
2. Найти резонансную частоту  , выполнив пункт 5 упр. I.
, выполнив пункт 5 упр. I.
3. Вычислить емкость конденсатора по формуле
 (30)
(30)
УПРАЖНЕНИЕ 3. Изучение влияния сердечника на величину индуктивности катушки
В тех случаях, когда необходимо изменять резонансную частоту колебательного контура, обычно используются конденсаторы переменной емкости. Однако иногда удобнее изменять величину индуктивности катушки. Это достигается с помощью сердечников, которые могут перемещаться внутри каркаса, на котором намотана катушка,
В вашем распоряжении имеются латунный и ферритовый сердечники. Выясним, как влияют на индуктивность катушки и на резонансную частоту контура сердечники, изготовленные из различных материалов:
I. Введите латунный сердечник внутрь каркаса катушки.
2. Выполните пункты 4 и 5 упражнения I и определите  .
.
3. Поменяйте латунный сердечник на ферритовый и вновь найдите  , выполнив пункт 5 упражнения I.
, выполнив пункт 5 упражнения I.
4. Вычислите индуктивность катушки с латунным и ферритовым сердечниками по формуле
 (31)
(31)
(за  взять значение
взять значение  из первой строки таблицы I).
из первой строки таблицы I).
5. Заполните таблицу 2.
6. Сделайте выводы о влиянии материала сердечника на величину индуктивности катушки и на резонансную частоту контура.
Таблица 2
| Сердечник |  , МГц , МГц | L, Гн |
УПРАЖНЕНИЕ 4. Снятие резонансных кривых
Переключатель ПI поставить в положение I.
Переключатель П2 поставить в положение I.
Ручкой «частота» установить на шкале генератора резонансную частоту .
.
Ручкой «регулировка выхода» плавно установить на вольтметре напряжение, равное 8В.
Ручкой «усиление» на осциллографе установить на экране размер изображения 2А (см. рис.10), равный 50 мм.

Рис.10
Ручкой «Частота» генератора устанавливать поочередно значения частоты на шкале Д, приведенные в табл.3, и снимать с экрана осциллографа соответствующие значения величины 2А в мм. Заполнить табл.3.
ПРИМЕЧАНИЕ: При изменении частоты напряжение на выходе генератора также меняется, поэтому после каждой установки частоты следует выставлять напряжение, равное 8 В.
Таблица 3
Поставить переключатель П2 в положение II. При этом в контур включается сопротивление R2.
Заполнить табл.4, выполняя действия, описанные в пункте 6 данного упражнения.
Таблица 4
9. По данным табл. 3 и 4 построить графики зависимости величины 2А от частоты для обоих случаев: 1) R= RI, 2) R = R2.
10. По полученным графикам, используя формулу (28) и рис. 8, определить добротность контура для обоих случаев. Сделать вывод, какое из сопротивлений (R1 или R2 больше).
МАТЕРИАЛ ДЛЯ САМОКОНТРОЛЯ
ФОРМУЛЫ
УРАВНЕНИЯ
| 1 | Уравнение, описывающее идеальный контур (свободные незатухающие колебания) |  |
| 2 | Уравнение, описывающее реальный контур (свободные затухающие колебания) |  |
| 3 | Уравнение, описывающее реальный контур, в котором действует э.д.с. (вынужденные колебания) |  |
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что представляет собой колебательный контур?
Что необходимо сделать, чтобы вызвать свободные колебания в контуре?
Каким способом, кроме рассмотренного в описании, можно возбудить свободные колебания в контуре?
Что называется амплитудой, частотой, фазой и периодом колебаний?
Какие превращения энергии происходят в колебательном контуре?
Почему свободные колебания затухают?
Как формулируется закон Джоуля-Ленца? Какое отношение он имеет к колебательному контуру?
Что характеризуют коэффициент затухания и логарифмический декремент затухания?
Как получить незатухающие колебания? Как еще называют такие колебания?
Что такое резонанс? Когда он наблюдается?
Чем отличаются резонансные кривые для напряжения от резонансных кривых для тока? (Укажите два различия).
Как зависит форма резонансной кривой от добротности контура?
Какой элемент контура определяет, в основном, его добротность?
Как связаны добротность и полоса пропускания контура?
Как формулируется второе правило Кирхгофа?
Как согласуется со вторым правилом Кирхгофа тот факт, что в момент резонанса напряжение на конденсаторе (и катушке индуктивности) в Q раз больше величины внешней э.д.с.?
Назовите единицы измерения следующих величин: I, U, R, Z, C, L, q, W, , T, , , Q, .
Индекс «С» указывает, что индексируемый параметр (в данном случае – напряжение) относится к конденсатору, индекс «m» обозначает максимальное значение этого параметра.
Положительным будем считать ток, при котором заряд конденсатора (q) увеличивается.
Индексы «Сmp» означают: «С» — относящийся к конденсатору; «m» — максимальный; «p» — резонансный.
При изменении емкости конденсатора на 100 пФ резонансная частота
Условие задачи:
При изменении емкости конденсатора на 100 пФ резонансная частота колебательного контура увеличилась от 0,2 до 0,25 МГц. Какой индуктивностью обладает контур?
Задача №9.12.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\Delta C = 100\) пФ, \(\nu_1=0,2\) МГц, \(\nu_2=0,25\) МГц, \(L-?\)
Решение задачи:
Резонансная частота равна собственной частоте колебаний этого колебательного контура, поэтому её можно определить по формуле:
\[\nu = \frac{1}{{2\pi \sqrt {LC} }}\;\;\;\;(1)\]
В этой формуле \(L\) – индуктивность катушки, \(C\) – электроемкость конденсатора.
Из формулы (1) мы видим, что зависимость между электроемкостью контура и резонансной частотой контура обратно пропорциональная. Учитывая это, запишем две формулы для определения частот \(\nu_1\) и \(\nu_2\):
\[\left\{ \begin{gathered}
{\nu _1} = \frac{1}{{2\pi \sqrt {LC} }} \;\;\;\;(2)\hfill \\
{\nu _2} = \frac{1}{{2\pi \sqrt {L\left( {C – \Delta C} \right)} }} \hfill \\
\end{gathered} \right.\]
Возведем в квадрат обе части (2), тогда:
\[\nu _1^2 = \frac{1}{{4{\pi ^2}LC}}\]
Откуда индуктивность контура \(L\) можно будет определить по следующей формуле:
\[L = \frac{1}{{4{\pi ^2}\nu _1^2C}}\;\;\;\;(3)\]
Также разделим верхнее равенство системы на нижнее, тогда мы получим:
\[\frac{{{\nu _1}}}{{{\nu _2}}} = \sqrt {\frac{{C – \Delta C}}{C}} \]
Возведем в квадрат обе части полученного равенства, тогда:
\[\frac{{\nu _1^2}}{{\nu _2^2}} = \frac{{C – \Delta C}}{C}\]
Перемножим “крест-накрест”, а потом раскроем скобки в левой части:
\[\nu _2^2\left( {C – \Delta C} \right) = \nu _1^2C\]
\[\nu _2^2C – \nu _2^2\Delta C = \nu _1^2C\]
В левую часть перенесем все слагаемые с множителем \(C\), остальное перенесем в правую сторону:
\[\nu _2^2C – \nu _1^2C = \nu _2^2\Delta C\]
\[C\left( {\nu _2^2 – \nu _1^2} \right) = \nu _2^2\Delta C\]
Отсюда выразим начальную емкость \(C\):
\[C = \frac{{\nu _2^2\Delta C}}{{\nu _2^2 – \nu _1^2}}\]
Это выражение нам нужно подставить в формулу (3), так мы получим решение задачи в общем виде:
\[L = \frac{{\nu _2^2 – \nu _1^2}}{{4{\pi ^2}\nu _1^2\nu _2^2\Delta C}}\]
Посчитаем численный ответ:
\[L = \frac{{{{0,25}^2} \cdot {{10}^{12}} – {{0,2}^2} \cdot {{10}^{12}}}}{{4 \cdot {{3,14}^2} \cdot {{0,2}^2} \cdot {{10}^{12}} \cdot {{0,25}^2} \cdot {{10}^{12}} \cdot 100 \cdot {{10}^{ – 12}}}} = 2,3 \cdot {10^{ – 3}}\;Гн = 2,3\;мГн\]
Ответ: 2,3 мГн.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
1.3. Вынужденные электрические колебания. Резонанс в последовательном контуре
Чтобы
вызвать вынужденные колебания, нужно
оказывать на систему внешнее периодически
изменяющееся воздействие. В случае
электрических колебаний это можно
осуществить, если включить последовательно
с элементами контура переменную ЭДС
или подать на контур переменное напряжение 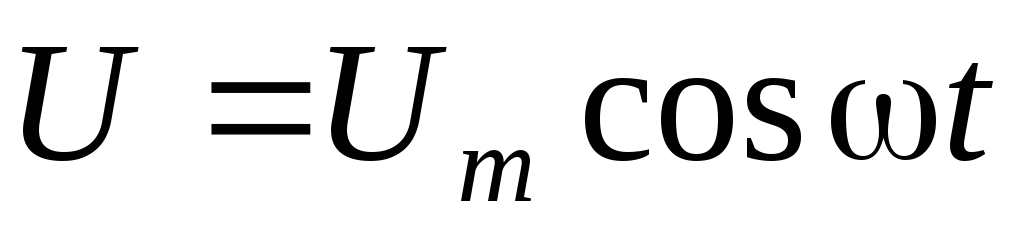 (рис.5).
(рис.5).
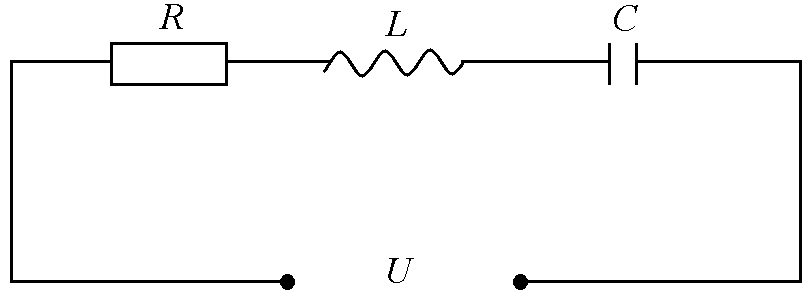
Рис. 5
Цепь, в которой последовательно с ЭДС включены сопротивление R, индуктивность L и конденсатор С, называется последовательным колебательным контуром. Рассмотрим процессы в этом контуре.По второму
правилу Кирхгофа 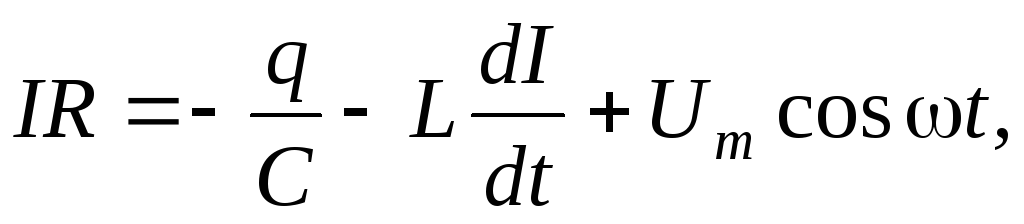
или 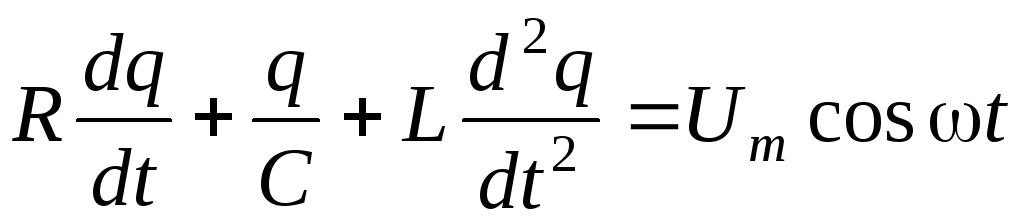 . Разделив на L,
получаем уравнение вынужденных колебаний
. Разделив на L,
получаем уравнение вынужденных колебаний
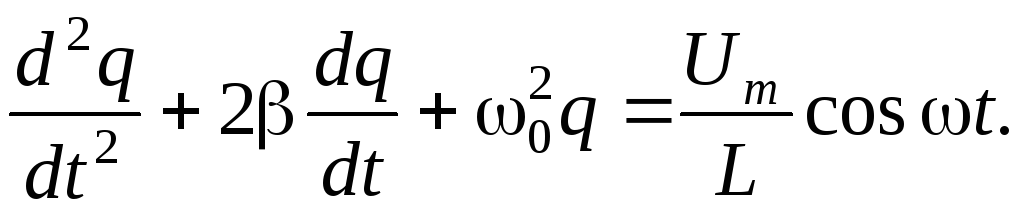 (2)
(2)
Частное решение этого уравнения
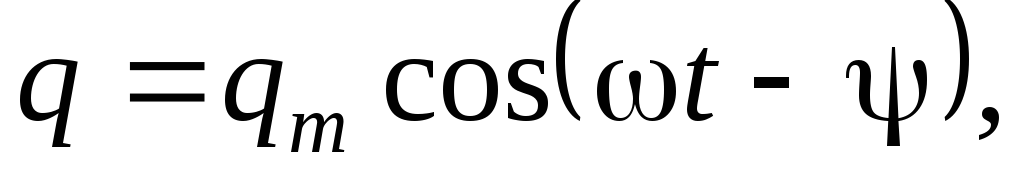 (3)
(3)
где 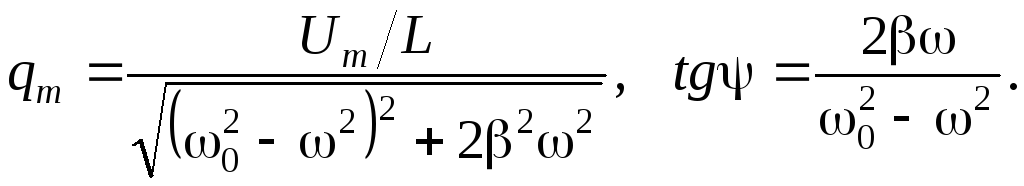 Подставим
Подставим  и
и  :
:
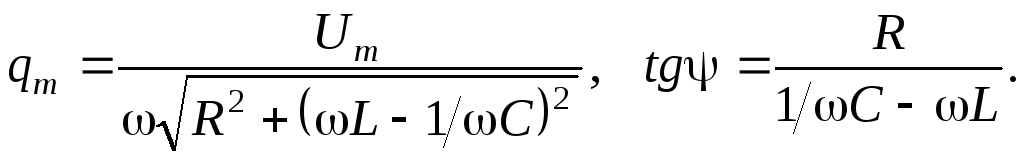
Общее решение получится, если к
частному решению (3) прибавить общее
решение однородного дифференциального
уравнения, которое было получено в
предыдущем параграфе. Оно содержит
множитель 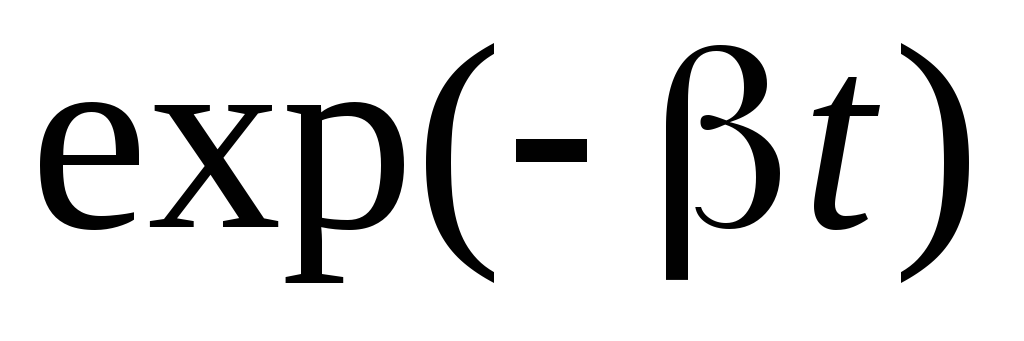 ,
который очень быстро убывает, и при
прошествии достаточно большого времени
,
который очень быстро убывает, и при
прошествии достаточно большого времени  им можно пренебречь. Таким образом,
установившиеся вынужденные электромагнитные
колебания в контуре описываются
уравнением (3).
им можно пренебречь. Таким образом,
установившиеся вынужденные электромагнитные
колебания в контуре описываются
уравнением (3).
Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (3) по времени:
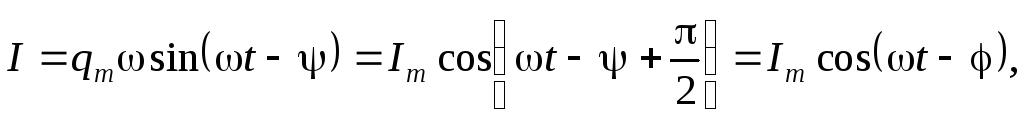
где 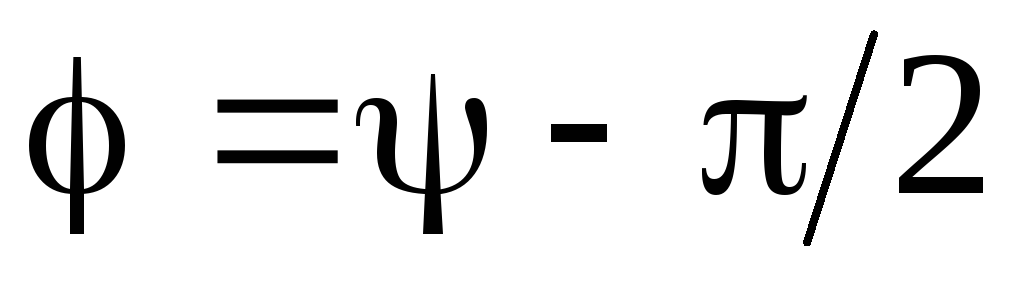 — сдвиг фаз между током и приложенным
напряжением. Тогда
— сдвиг фаз между током и приложенным
напряжением. Тогда
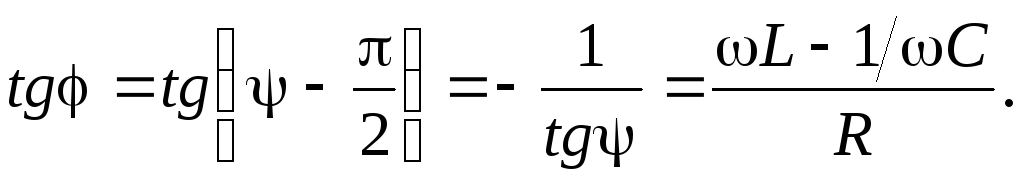
Из этого
выражения следует, что ток отстает по
фазе от напряжения ( )при
)при 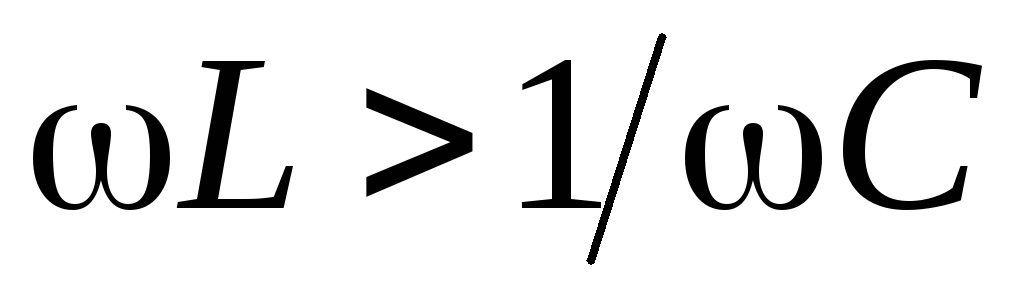 .
И опережает напряжение (
.
И опережает напряжение (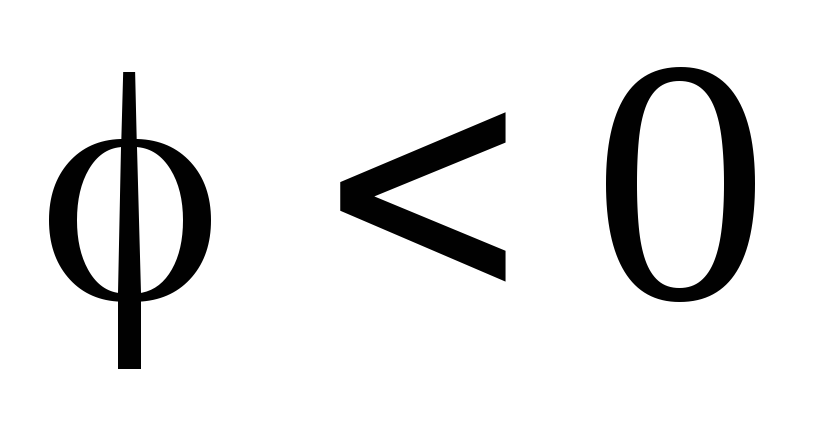 )
при
)
при 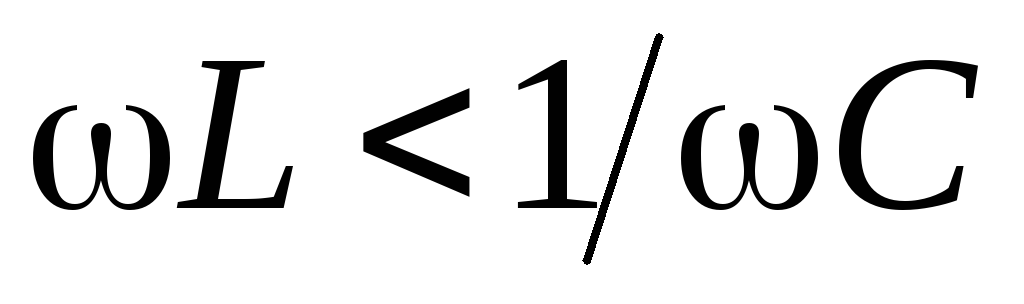 .
Для силы тока можно записать
.
Для силы тока можно записать
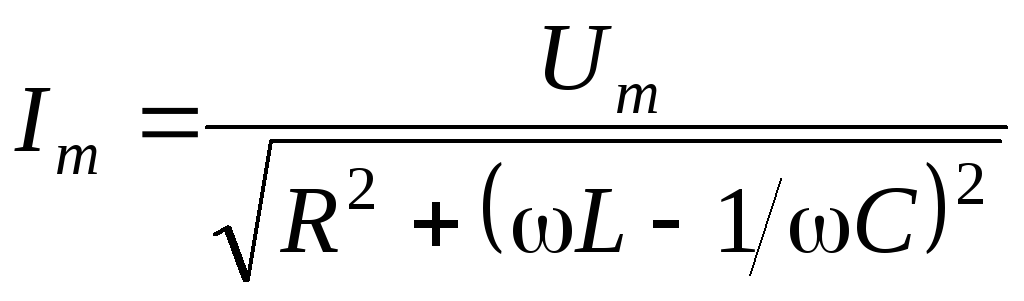 .
(4)
.
(4)
Представим
соотношение (2) в виде: .
Произведение
.
Произведение 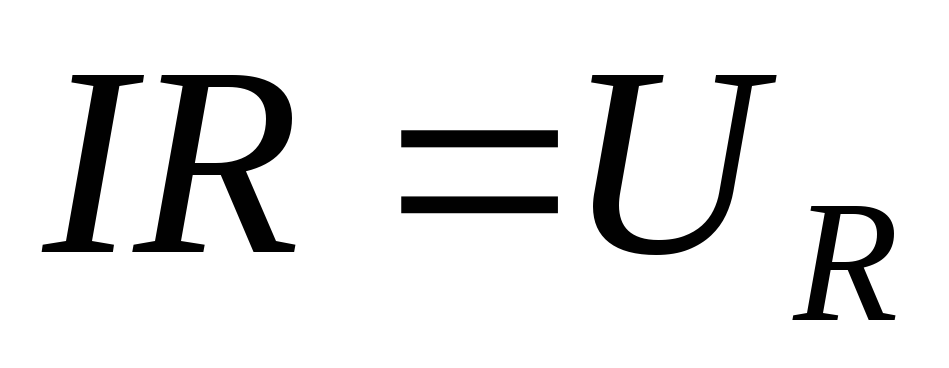 — падение напряжения на активном
сопротивлении; — падение напряжения на конденсаторе;
— падение напряжения на активном
сопротивлении; — падение напряжения на конденсаторе; 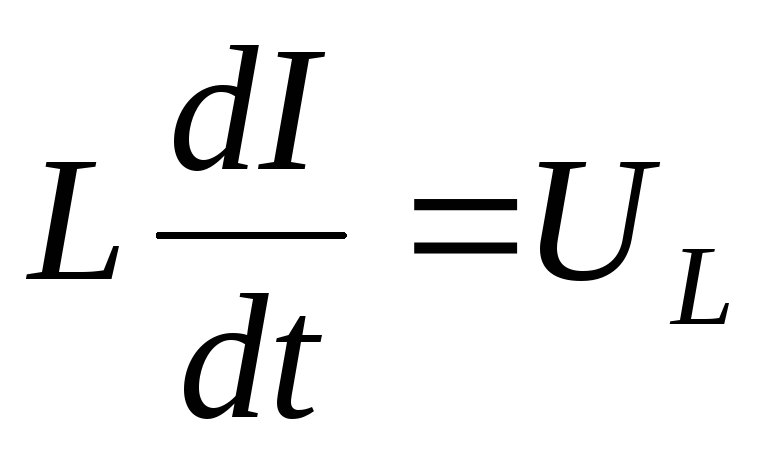 – напряжение на индуктивности; тогда
можно записать
– напряжение на индуктивности; тогда
можно записать
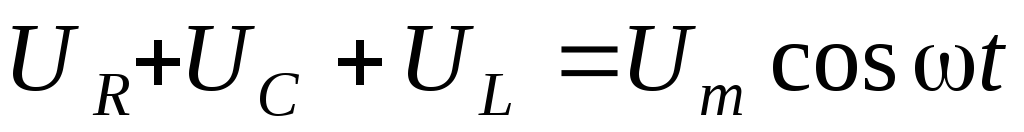 .
(5)
.
(5)
Таким образом, сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.
Согласно (4) 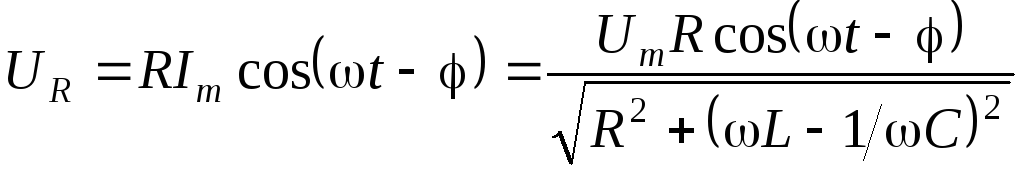 — напряжение на активном сопротивлении
совпадает по фазе с током в контуре.
— напряжение на активном сопротивлении
совпадает по фазе с током в контуре.
Для
напряжения на конденсаторе, подставив
(3), имеем 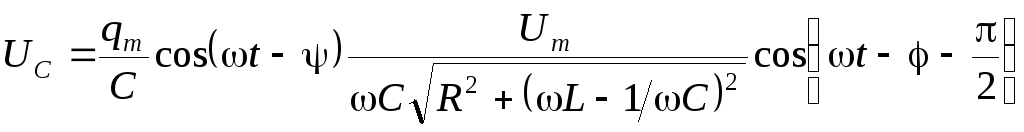 –
напряжение на ёмкости отстаёт от силы
тока на π/2.
–
напряжение на ёмкости отстаёт от силы
тока на π/2.
Напряжение на индуктивности
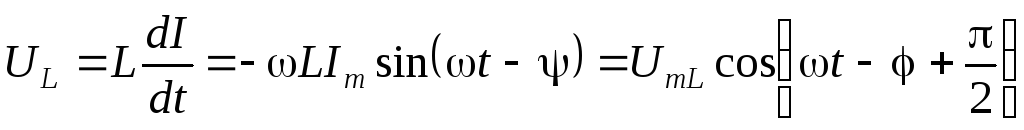 ,
,
где 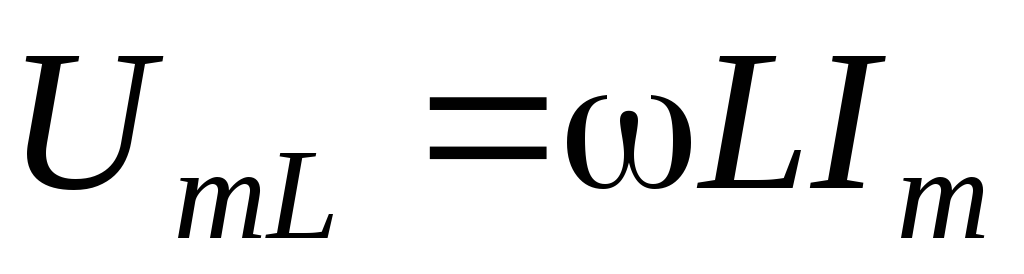 ,– напряжение на индуктивности
опережает ток на π/2.
,– напряжение на индуктивности
опережает ток на π/2.
Фазовые соотношения можно представить наглядно с помощью векторной диаграммы. Действительно, гармонические колебания можно задать с помощью вектора, длина которого равна амплитуде колебаний , а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 6).
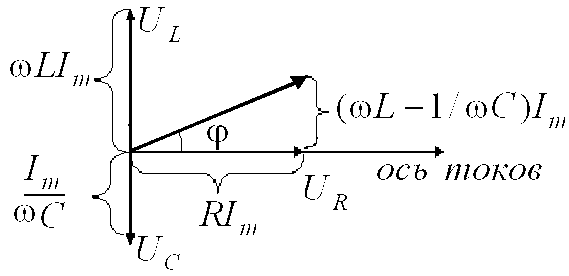
Рис. 6
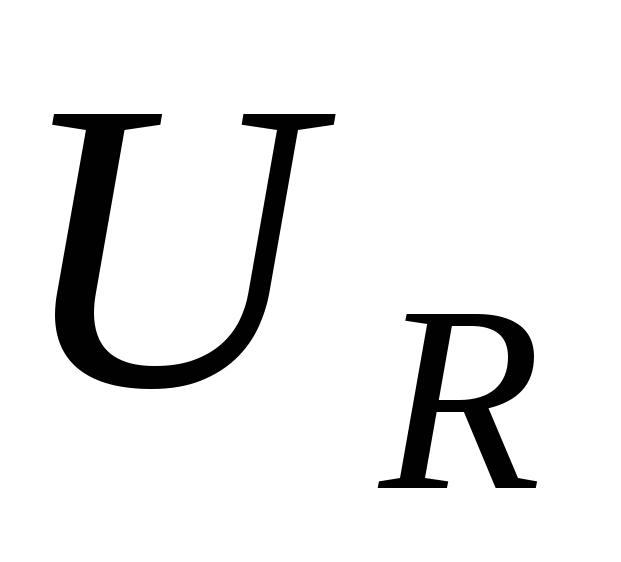 совпадает по фазе с током,
совпадает по фазе с током, 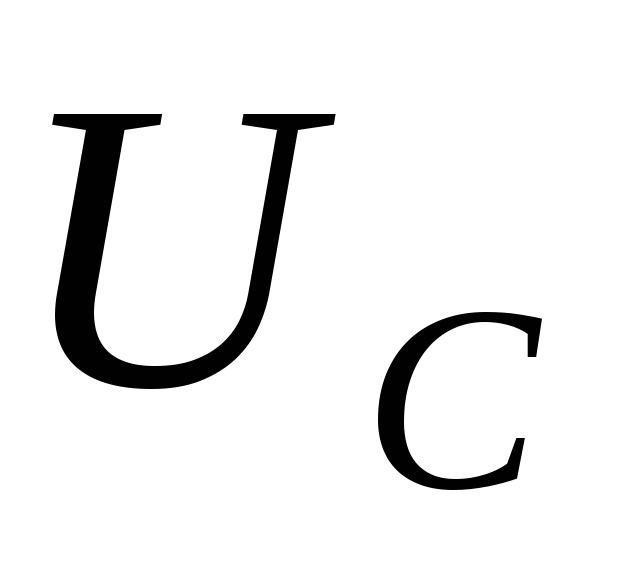 – отстаёт на π/2),
– отстаёт на π/2), 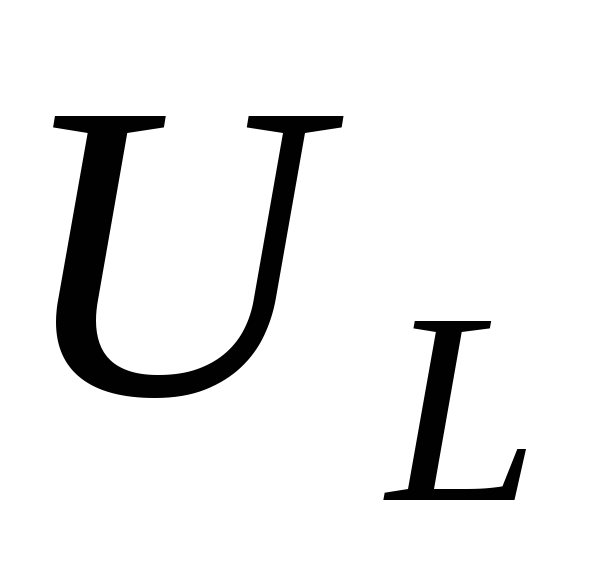 – опережает на π/2. Векторы
– опережает на π/2. Векторы 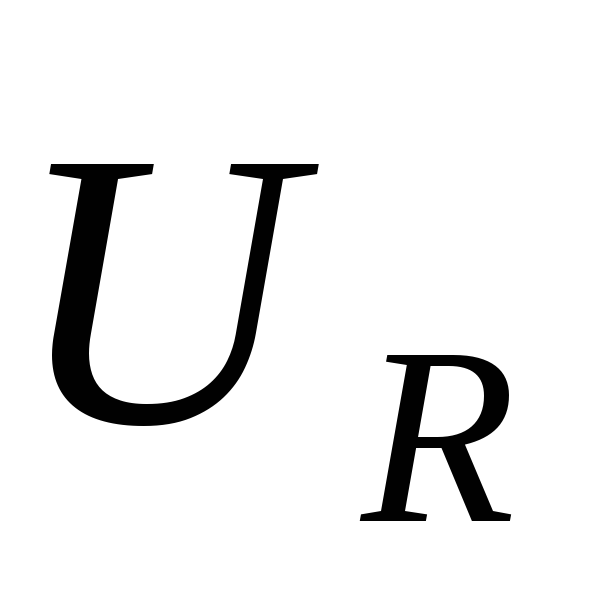 ,
, 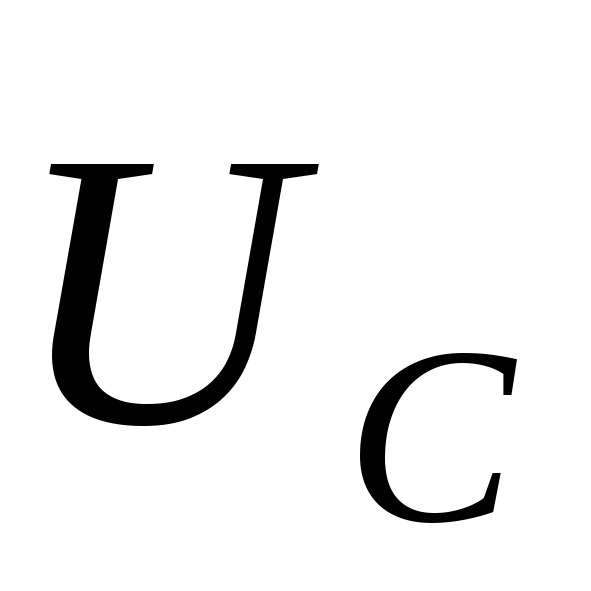 ,
, 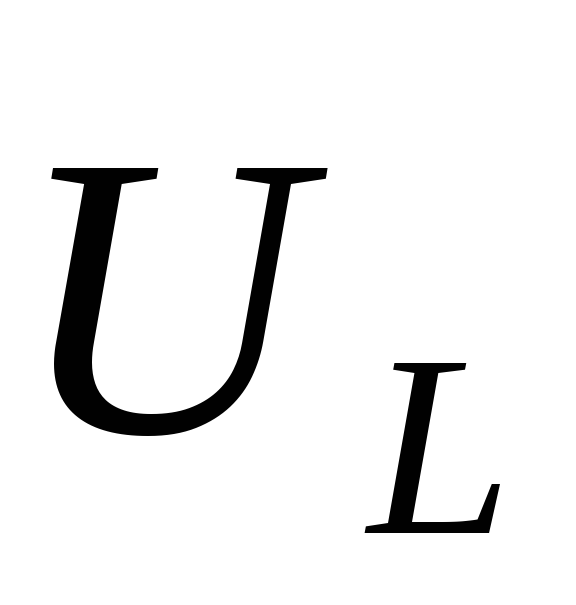 в сумме дают
в сумме дают  ,
причём U определяется выражением (5).
,
причём U определяется выражением (5). При
определенной частоте внешнего воздействия
в контуре наступает резонанс. Резонансная
частота для напряжения на конденсаторе 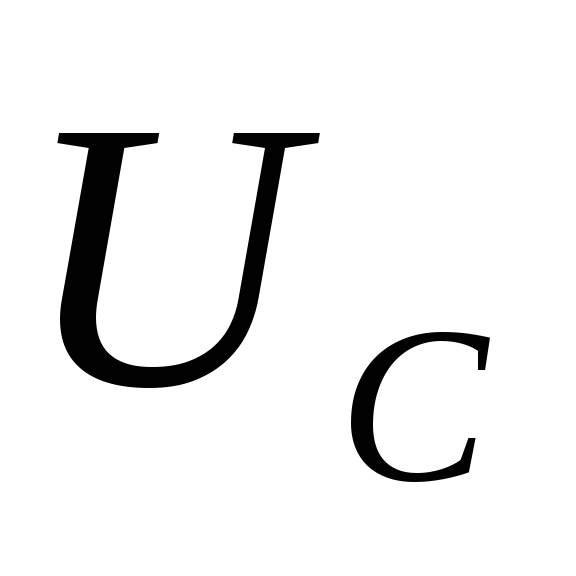 и для заряда q равна:
и для заряда q равна:
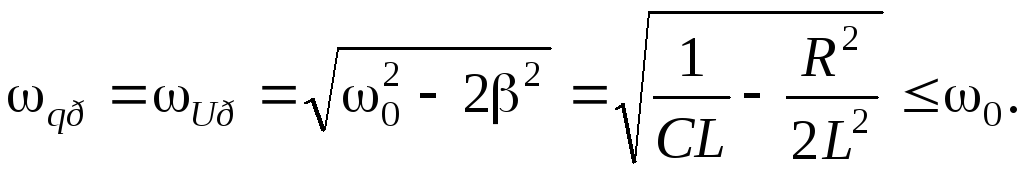 Резонансные кривые для
Резонансные кривые для 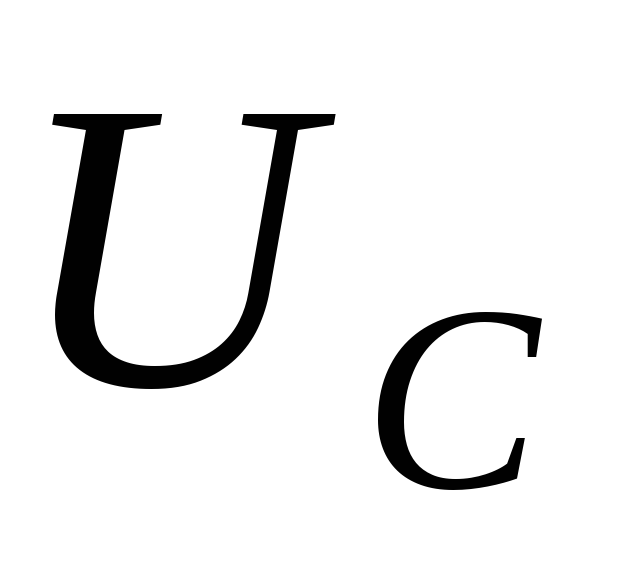 имеют вид, представленный на рис.7. Все
резонансные частоты
имеют вид, представленный на рис.7. Все
резонансные частоты 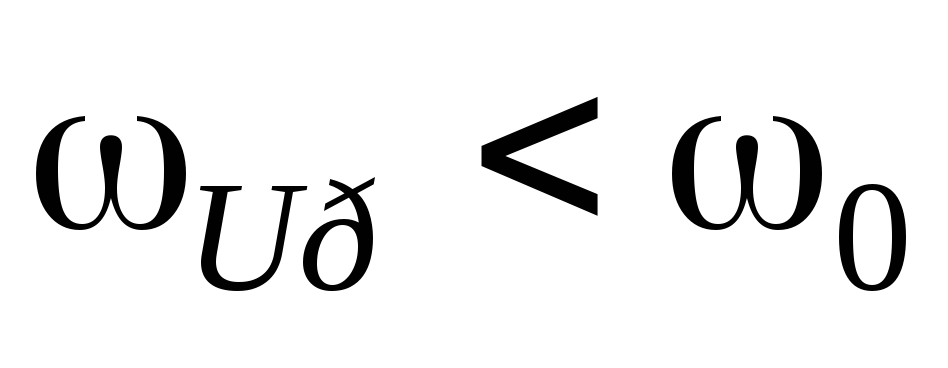 .
При ω→0 резонансные кривые сходятся в
одной точке
.
При ω→0 резонансные кривые сходятся в
одной точке 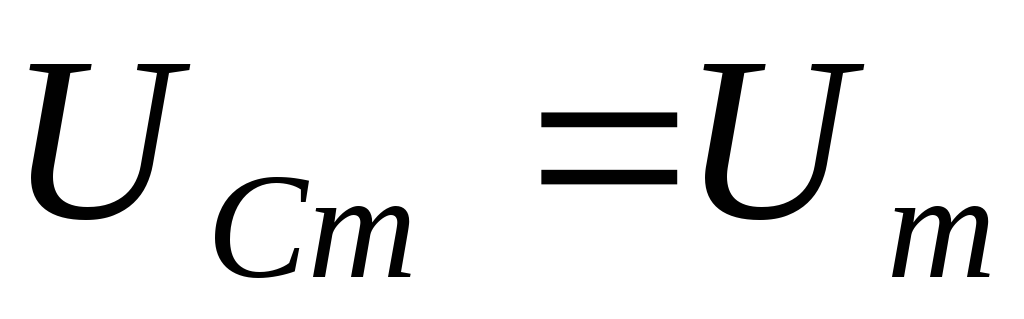 – это напряжение на конденсаторе при
подключении его к источнику постоянного
напряжения
– это напряжение на конденсаторе при
подключении его к источнику постоянного
напряжения 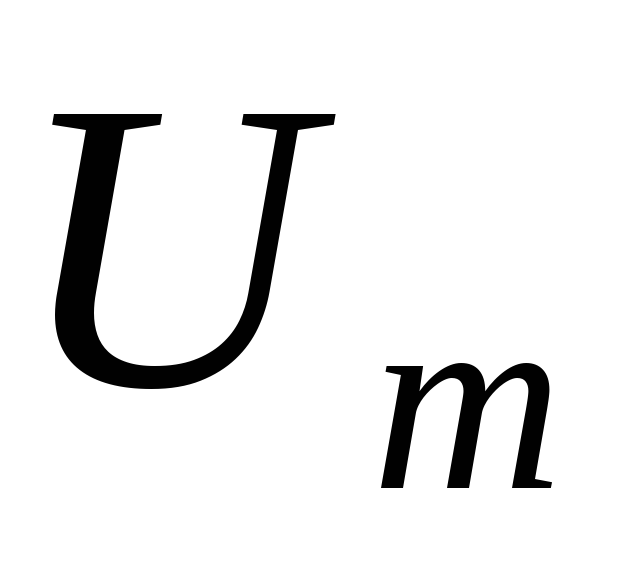 .
Максимум при резонансе тем острее и
выше, чем меньше затухание β=R/2L,
то есть чем меньше R и больше L.
Ход резонансной кривой аналогичен
резонансной кривой при механических
колебаниях.
.
Максимум при резонансе тем острее и
выше, чем меньше затухание β=R/2L,
то есть чем меньше R и больше L.
Ход резонансной кривой аналогичен
резонансной кривой при механических
колебаниях.
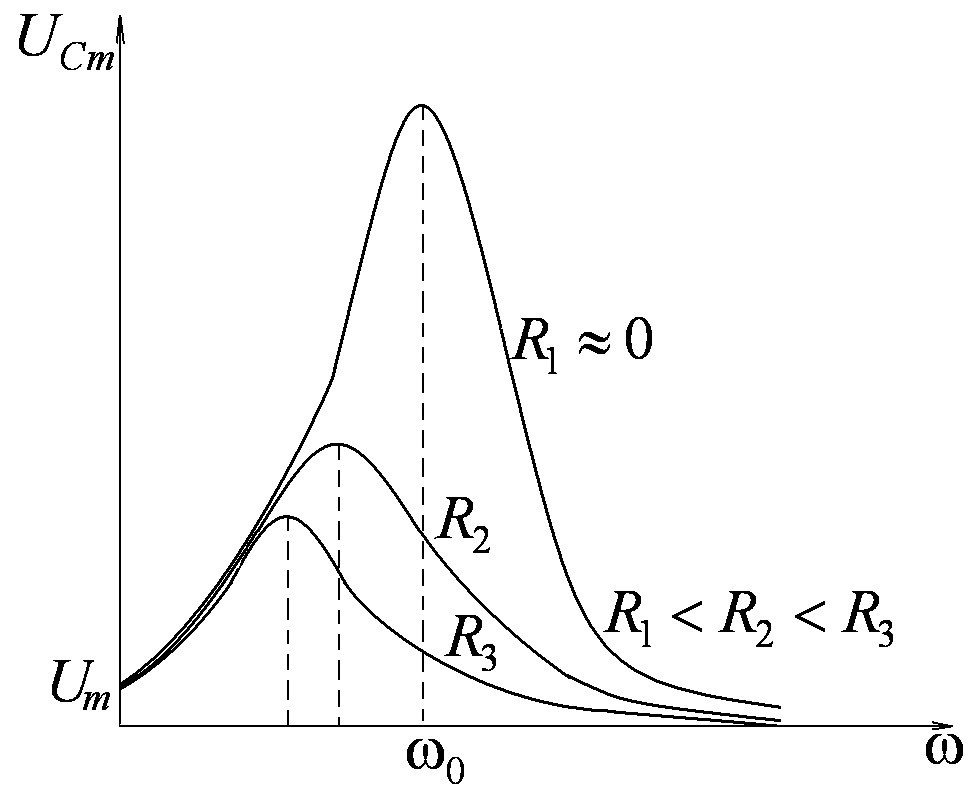
Рис. 7
Резонансные кривые для тока приведены на рис. 8. Амплитуда
силы тока имеет максимальные значения,
когда 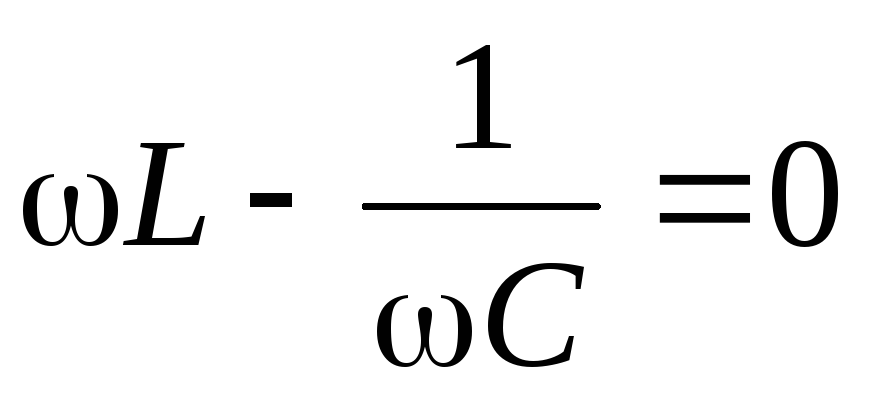 ,
то есть резонансная частота для силы
тока совпадает с собственной частотой
колебаний контура:
,
то есть резонансная частота для силы
тока совпадает с собственной частотой
колебаний контура:

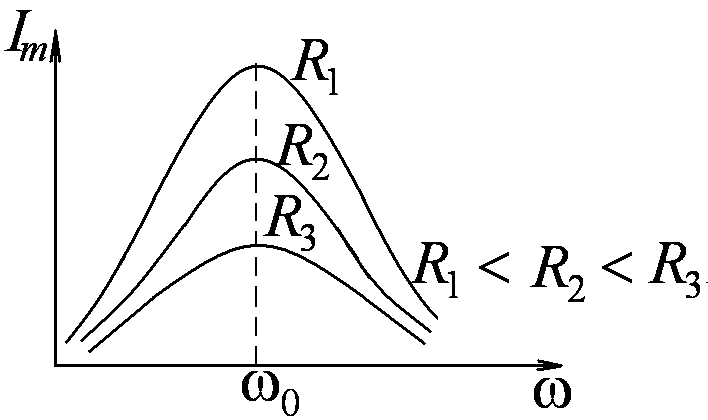
Рис. 8
При ω→0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может. При малом
затухании (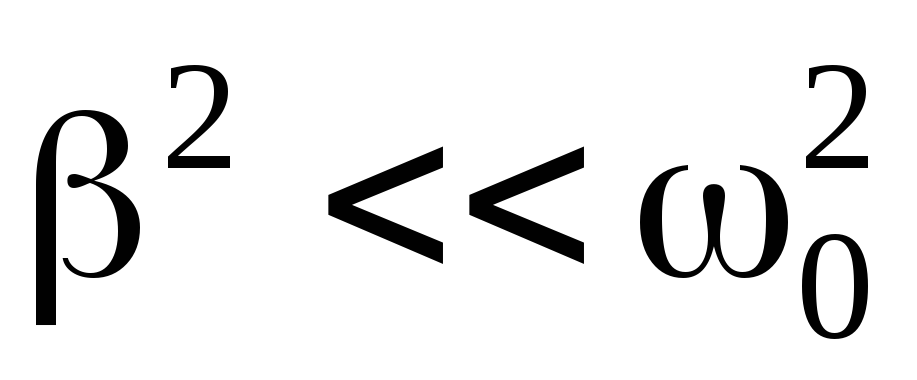 )
резонансную частоту для напряжения
можно считать равной
)
резонансную частоту для напряжения
можно считать равной 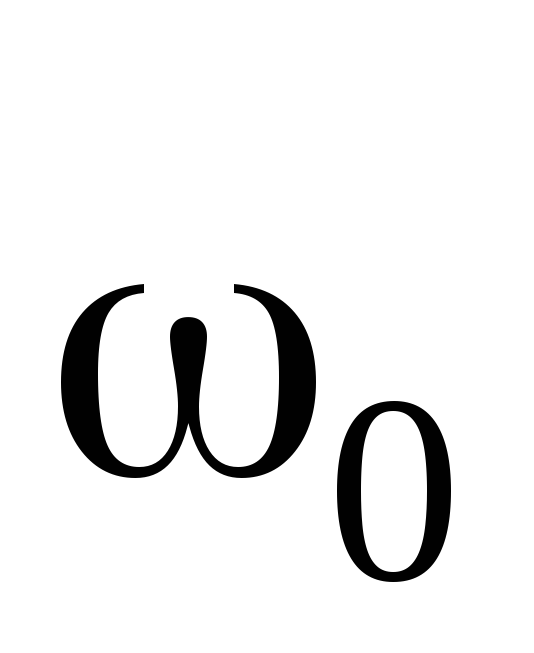 .
Тогда отношение амплитуды напряжения
на конденсаторе при резонансе к амплитуде
внешнего напряжения равно:
.
Тогда отношение амплитуды напряжения
на конденсаторе при резонансе к амплитуде
внешнего напряжения равно:
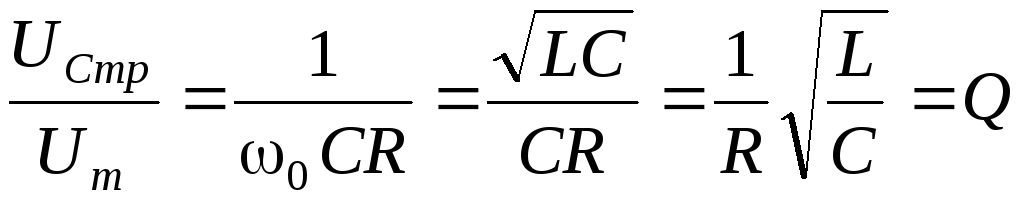
– то есть добротность контура показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.
Итак, при
резонансе 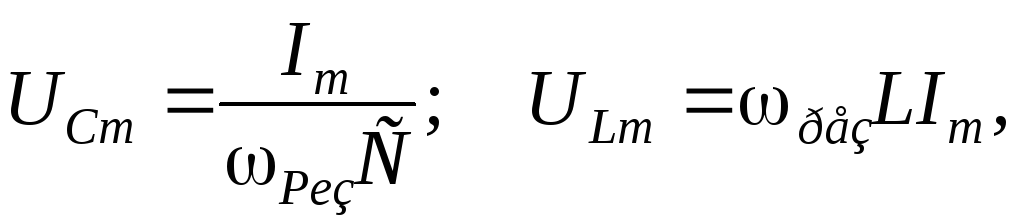 причём
причём 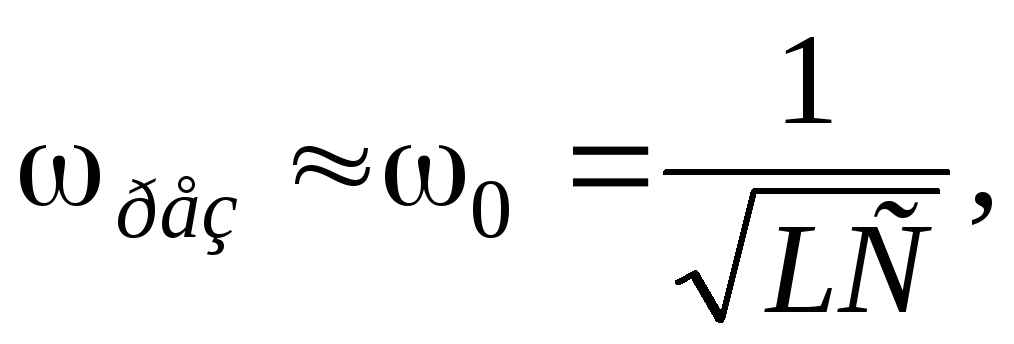 поэтому
поэтому
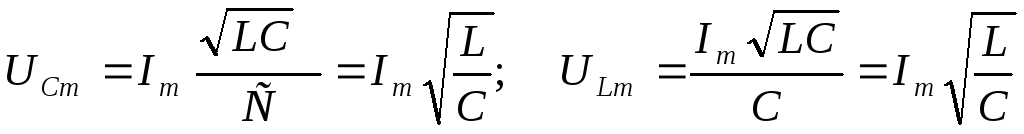
– амплитуды
напряжений на ёмкости и индуктивности
равны между собой, но противоположны
по фазе. Поэтому напряжения на ёмкости
и индуктивности компенсируют друг
друга, и цепь ведёт себя как цепь только
с активным сопротивлением. Вся энергия,
приложенная к контуру идёт, на Ленц-Джоулево
тепло. Ток в цепи достигает максимального
значения. Это резонанс напряжений –
индуктивного  и емкостного
и емкостного .
.
45. Вынужденные электрические колебания
Установившиеся колебания. Вернемся к уравнениям колебательного контура:
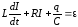 или с учетом
или с учетом 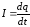
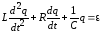 .
.
Рассмотрим случай, когда в контур включена внешняя переменная ЭДС зависящая от времени по гармоническому закону
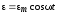 .
.
Колебания, возникающие под действием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями.
В данном случае уравнение колебательного контура записывается как
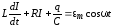 или
или 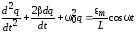 ,
,
где введены обозначения:
 ;
; 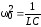 ,
,
где 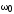 — собственная частота контура;
— коэффициент затухания.
— собственная частота контура;
— коэффициент затухания.
Решение этого уравнения, как известно из математики, представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения.
Нас будут интересовать только установившиеся колебания, т.е. частное решение этого уравнения (общее решение однородного уравнения экспоненциально затухает, и по прошествии некоторого времени оно практически исчезает, обращается в нуль).
Это решение имеет вид
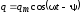 ,
,
где 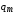 — амплитуда заряда на конденсаторе;
— разность фаз между колебаниями заряда
и внешней ЭДС
— амплитуда заряда на конденсаторе;
— разность фаз между колебаниями заряда
и внешней ЭДС 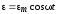 .
.
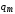 и
определяются только свойствами самого
контура и вынуждающей ЭДС ,
причем оказывается, что
и
определяются только свойствами самого
контура и вынуждающей ЭДС ,
причем оказывается, что 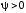 ,
поэтомуq всегда отстает по фазе от .
,
поэтомуq всегда отстает по фазе от .
Чтобы определить
постоянные 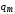 и,
надо подставить
и,
надо подставить 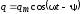 в исходное уравнение
в исходное уравнение
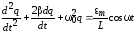
и преобразовать полученное выражение. В целях достижения большей простоты сначала найдем ток I и затем его выражение подставим в исходное уравнение
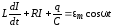 .
.
Попутно
будет решен и вопрос с постоянными 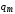 и.
и.
Продифференцируем
выражение 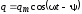 поt и найдем:
поt и найдем:
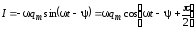 .
.
Запишем это выражение так:
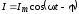 ,
,
где 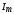 — амплитуда тока;
— сдвиг по фазе между током и внешней
ЭДС :
— амплитуда тока;
— сдвиг по фазе между током и внешней
ЭДС :
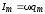 ;
; 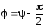 .
.
Для того, чтобы
найти 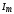 и
представим исходное уравнение
и
представим исходное уравнение  в виде:
в виде:
,
где слева записана сумма напряжений на индуктивности L, сопротивления R и емкости С.
Таким образом, мы видим, что сумма этих напряжений равна в каждый момент времени внешней ЭДС . Учитывая соотношения
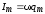 и
и 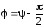
запишем:
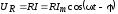 ;
;
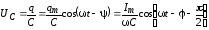 ;
;
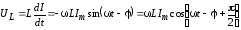 .
.
Векторная
диаграмма.
Из последних трех формул видно, что  находится в
фазе с током I,
находится в
фазе с током I,  отстает по фазе от тока на
отстает по фазе от тока на 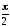 ,
а
,
а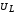 опережает на
опережает на 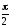 .
Все это можно наглядно представить с
помощью векторной диаграммы, изобразив
амплитуды напряжений
.
Все это можно наглядно представить с
помощью векторной диаграммы, изобразив
амплитуды напряжений
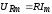 ;
;  ;
;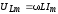
и их векторную сумму, равную, согласно
 ,
,
вектору
величины 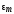 (рис. 16.4)
(рис. 16.4)

Рис. 16.4
Из прямоугольного
треугольника этой диаграммы легко
получить следующие выражения для 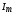 и
в уравнении
и
в уравнении 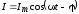 :
:
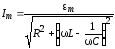 ;
; 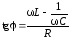 .
.
46. Электрический резонанс. Резонансные кривые
Электрическим
резонансом называется явление резкого возрастания
амплитуды вынужденных колебаний при
приближении частоты вынуждающей силы
(частоты вынуждающего переменного
напряжения или внешней переменной ЭДС
)
к частоте, равной или близкой собственной
частоте колебательной системы. Графики
зависимостей амплитуд тока I,
заряда Q на конденсаторе и напряжений 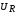 ,
,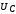 ,
,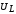 от частоты
внешней ЭДС
называются резонансными кривыми.
Резонансные кривые для силы тока
от частоты
внешней ЭДС
называются резонансными кривыми.
Резонансные кривые для силы тока 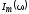 показаны на рис. 16.5.
показаны на рис. 16.5.
Как видно из
выражения 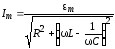 ,
амплитуда силы тока имеет максимальное
значение при
,
амплитуда силы тока имеет максимальное
значение при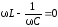 .
.
Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура:
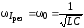 .
.
Максимум при
резонансе оказывается тем выше и острее,
чем меньше коэффициент затухания 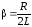 .
.

Рис. 16.5
Резонансные кривые
для заряда на конденсаторе 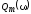 показаны на рис. 16.6 (резонансные кривые
для напряжения
показаны на рис. 16.6 (резонансные кривые
для напряжения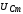 на конденсаторе имеют такой же вид).
Максимум амплитуды заряда достигается
при резонансной частоте
на конденсаторе имеют такой же вид).
Максимум амплитуды заряда достигается
при резонансной частоте
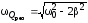 ,
,
которая
по мере уменьшения
все больше приближается к  .
Для получения этого выражения надо
представить
.
Для получения этого выражения надо
представить ,
согласно
,
согласно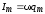 ,
как
,
как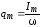 ,
где
,
где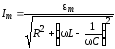 ,
тогда
,
тогда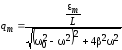 .
.
Максимум этой функции, или, что то же самое, минимум подкоренного выражения, найдем, приравняв производную по от подкоренного выражения к нулю
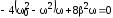 .
.
Это равенство
выполняется при  ,
,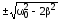 ,
у которых только положительное значение
имеет физический смысл. Следовательно,
резонансная частота
,
у которых только положительное значение
имеет физический смысл. Следовательно,
резонансная частота
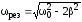 .
.
Рис. 16.6
На рис. 16.7 изображено
перераспределение амплитуд напряжений 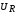 ,
,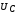 ,
,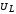 в зависимости от частоты
внешней ЭДС.
в зависимости от частоты
внешней ЭДС.

Рис. 16.7
Резонансные частоты
для 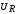 ,
,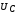 ,
, определяются следующими формулами:
определяются следующими формулами:
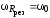 ;
; 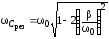 ;
;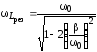 .
.
Чем меньше ,
тем ближе резонансные частоты всех
величин к значению  .
.
Резонансные
кривые и добротность.
Форма резонансных кривых определенным
образом связана с добротностью Q контура. Особенно простой эта связь
оказывается для случая слабого затухания,
т.е. при 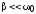 .
.
В этом случае
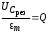 ,
,
где Q – добротность.
Действительно,
при 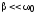 ,
величина
,
величина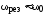 и
и
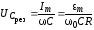 или
или 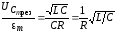 ,
,
а это и есть добротность Q контура.
Таким образом,
добротность контура (при 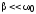 )
показывает во сколько раз максимальное
значение амплитуды напряжения на
конденсаторе (и на индуктивности)
превышает амплитуду внешней ЭДС.
)
показывает во сколько раз максимальное
значение амплитуды напряжения на
конденсаторе (и на индуктивности)
превышает амплитуду внешней ЭДС.
Добротность контура
связана с другой важной характеристикой
резонансной кривой – ее шириной. При 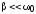
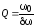 ,
,
где 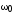 — резонансная частота;
— резонансная частота;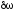 — ширина резонансной кривой на «высоте»,
равной 0,7 от максимальной, т.е. в резонансе.
— ширина резонансной кривой на «высоте»,
равной 0,7 от максимальной, т.е. в резонансе.
Резонанс. Таким образом, явление резонанса в случае электромагнитных колебаний – это возбуждение сильных колебаний при частоте внешней ЭДС или напряжения, равной или близкой к собственной частоте колебательного контура. Резонанс используют для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того, чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т.е. изменением емкости С и индуктивности L колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.

