Военно-техническая подготовка
1.4. Колебательный контур.
1.4.1. Свободные колебания в контуре.
Свободные (или собственные) колебания — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие).
Пусть конденсатор ёмкостью C заряжен до напряжения U0 . Энергия, запасённая в конденсаторе составляет
,
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток I , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
,
где L — индуктивность катушки, I0
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения — U0 .
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
Рис 1. Пример: Осциллограмма LC контура во время замыкания заряженного конденсатора на катушку индуктивности.
С = 240нФ(заряженный), L = 360нГн, F0 ≈ 542кГц.
1.4.2. Вынужденные колебания в контуре.
Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:
.
Консервативный гармонический осциллятор
Второй закон Ньютона для такого осциллятора запишется в виде:
.
Если ввести обозначения:
,
и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:
,
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
,
где A , φ — произвольные постоянные, которые определяются из начальных условий.
Найдём частное решение.
,
и получим значение для константы:
,
Тогда окончательное решение запишется в виде:
.
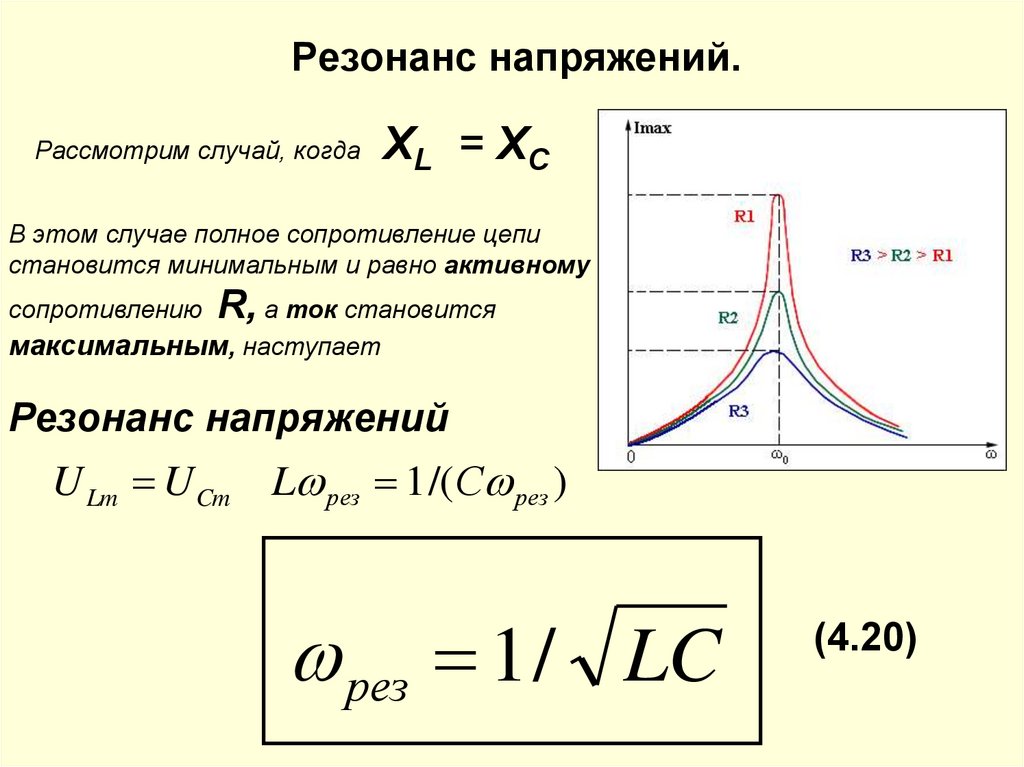
1.4.3. Резонанс в колебательном контуре.
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы.
В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
При достижении резонанса, импеданс (комплексное сопротивление двухполюсника (электрической цепи, содержащей две точки для соединения с другими цепями) для гармонического сигнала) последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения
,
где ω = 2πf ;
f — резонансная частота в герцах;
L — индуктивность в генри;
C — ёмкость в фарадах.
Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте.
Рис 2. Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания.
1.4.4. Связанные цепи.
Если изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе, то эти два элемента индуктивно связаны, а возникающая э.д.с. называется э.д.с. взаимной индукции.
Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи
,
где М – взаимная индуктивность элементов цепи,
L 1 и L 2 – индуктивности элементов.
При расчете цепей с взаимной индуктивностью следует на схеме отметить стрелками выбираемые положительные направления токов в ветвях (или контурных токов). Кроме того, одинаковыми условными значками (звездочками, точками, буквами и т.п.) обозначить одноименные зажимы каждой пары индуктивно связанных катушек.
Одноименными называются такие зажимы, при одинаковом положительном направлении токов относительно которых, магнитные потоки самоиндукции и взаимной индукции складываются.
1.4.5. Кварцевый резонатор.
Кварцевый резонатор — прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы.
На пластинку, кольцо или брусок, вырезанные из кристалла кварца определённым образом, нанесены 2 и более электродов — проводящие полоски.
Пластинка закреплена и имеет собственную резонансную частоту механических колебаний.
При подаче напряжения на электроды благодаря пьезоэлектрическому эффекту происходит изгибание, сжатие или сдвиг в зависимости от того, каким образом вырезан кусок кристалла.
Однако колеблющаяся пластинка в результате того же пьезоэлектрического эффекта создаёт во внешней цепи противо-ЭДС, что можно рассматривать как явление, эквивалентное работе катушки индуктивности в колебательном контуре.
Если частота подаваемого напряжения равна или близка к частоте собственных механических колебаний пластинки, затраты энергии на поддержание колебаний пластинки оказываются намного ниже, нежели при большом отличии частоты. Это тоже соответствует поведению колебательного контура.
Рис 3. Эквивалентная схема.
Условное обозначение кварцевого резонатора (сверху) и его эквивалентная схема (снизу)
C0 — собственная ёмкость кристалла, образуемая кристаллодержателем и/или обкладками резонатора.
C1, L1 — эквивалентная ёмкость и индуктивность механической колебательной системы резонатора.
R1 — эквивалентное сопротивление потерь механической колебательной системы.
Колебательный контур — что это такое? Формулы и схемы
Покажем, как применять знание физики в жизни
Начать учиться
Сегодня нас ждёт увлекательный эксперимент: мы перейдём от этапа «вообще не понимаю, что это» к «надо же, как всё просто и логично» всего за одну статью. Не верите? Мы вам обещаем! Мы поговорим о колебательных контурах, электромагнитных волнах и том, как мы встречаемся с этими понятиями в обычной жизни.
Колебания
Начнём обсуждение этой темы с колебаний. В обычной жизни мы часто слышим это слово: «цветок колеблется на ветру», «я не могу принять решение, колеблюсь», «температура воздуха колеблется в диапазоне…».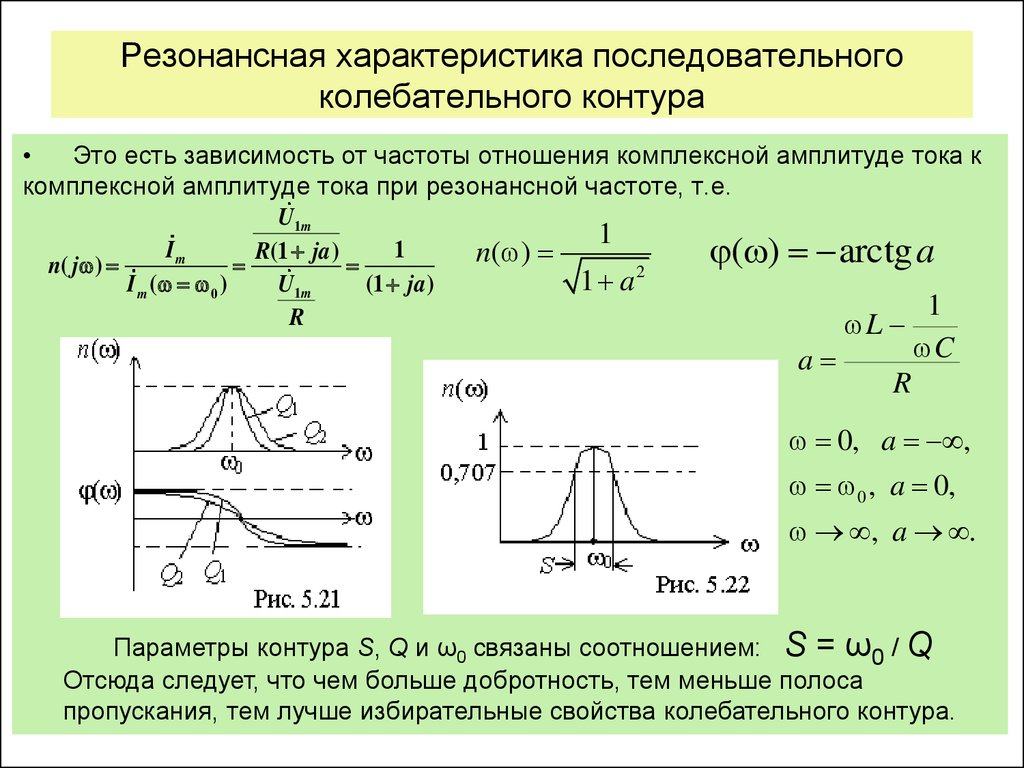
Но что такое колебания в физике?
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
Попробуйте привести несколько примеров такого движения. Верно, к колебаниям можно отнести движение стрелки, вращение качели, качание маятника часов.
Колебания бывают вынужденными и свободными.
Вынужденные колебания — это колебания, происходящие под действием внешней периодически меняющейся силы.
Посадите свою маленькую сестрёнку или братишку на качели: раскачивая их, вы станете той самой внешней силой, под действием которой качели движутся, совершая при этом вынужденные колебания.
Свободные колебания — это колебания, происходящие под действием внутренних сил в колебательной системе.
Груз колеблется на нити или пружине — вот самый распространённый пример свободных колебаний. Такие колебания всегда затухающие, потому что ни у одной системы нет бесконечного запаса энергии для такого движения: рано или поздно колебание прекратится.
Что может совершать свободные колебания? Математический (груз + нить) и пружинный (груз + пружина) маятники, а также электромагнитные волны.
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Электромагнитные волны
В курсе школьной физики 8-го класса вы изучали отдельно главы про электричество и магнетизм, и только в 9–10-х классах узнали, что такое разделение не совсем верно. Дело в том, что электричество и магнетизм — две стороны одной монеты, они не могут существовать друг без друга. Движущееся электрическое поле порождает магнитное, а движущееся магнитное поле порождает электрическое.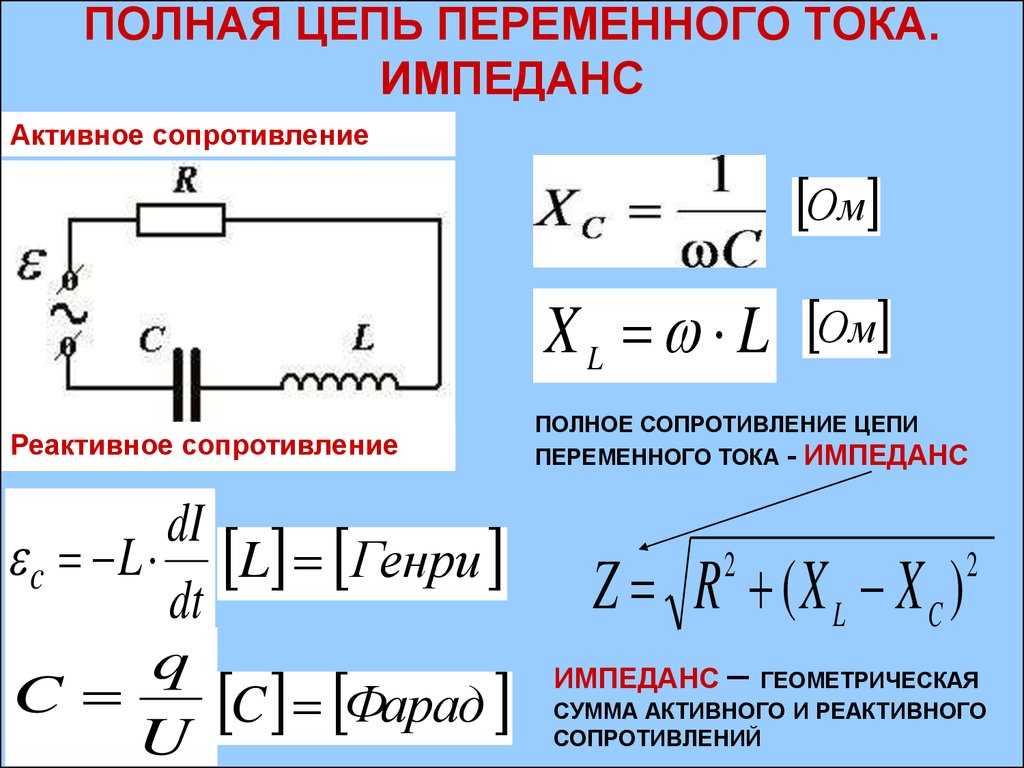
Эти поля распространяются в пространстве одновременно и, что удивительно, в разных плоскостях. Взгляните на рисунок!
Электромагнитные волны — это распространение в пространстве с течением времени переменных (вихревых) электрических и магнитных полей.
Вихревым электрическим полем называется поле, силовые линии которого представляют собой замкнутые линии.
В разрезе этой темы стоит запомнить две фамилии: Максвелл и Герц. Вот увидите, как сойдёт с ума от счастья учитель физики, когда вы их назовёте. 😅 Джеймс Максвелл описал основные положения электромагнитной теории, а Генрих Герц доказал существование электромагнитных волн опытным путём.
К электромагнитным волнам относятся радио, Wi-Fi и даже свет. Более подробно об этом можно прочесть в нашей статье.
Что такое колебательный контур?
Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.
Также можно сказать, что колебательный контур — это электрическая цепь, работа которой порождает электромагнитное поле.
Но зачем кому-то создавать такие колебания?
Колебательные контуры — неотъемлемая часть многих производственных процессов. С их помощью изготавливают радиоприёмники, генераторы сигналов, блоки измерения частоты, контроллеры частоты напряжения на двигателях.
Возможно, вам может показаться, что это устройство давно устарело и используется в каких-то непонятных вещах, но стоит понимать, что без них не было бы возможно создание домофона, электромагнитов, различных датчиков, с которыми мы встречаемся ежедневно.
Колебательный контур состоит из двух компонентов: катушки и конденсатора, и выглядит вот так:
Катушка индуктивности (или соленоид) — это стержень с несколькими слоями обмотки медной проволокой.
Именно он создаёт колебания в колебательном контуре. Стержень, находящийся в середине катушки, называется дроссель, или сердечник.
Катушка способна создавать колебания, только если есть электрический заряд. Она обладает низким сопротивлением.
Конденсатор — это элемент, способный накопить в себе большое количество электрического заряда. Он состоит из двух обкладок, между которыми находится диэлектрик (вещество, не проводящее электрический ток).
В чём его отличие от обычного аккумулятора? В аккумуляторе происходит превращение механической, химической, световой и других энергий в электрическую, в конденсаторе же накапливается заряд, который он может отдать весь сразу.
Часто в электрическую цепь колебательного контура подключают ещё один элемент — резистор, который обладает сопротивлением и контролирует силу тока и напряжение в цепи.
Виды колебательных контуров
По типу соединения колебательные контуры можно разделить на последовательный и параллельный.
Также физики выделяют особый тип контура — идеальный.
Идеальный колебательный контур — контур, сопротивление которого отсутствует, порождая при этом незатухающие свободные электромагнитные колебания.
Как вы думаете, можно ли создать такой контур и работать с ним на практике? К сожалению, такое маловероятно. Идеальный колебательный контур — всего лишь математическая модель, допущение, с помощью которого можно вывести формулы, ускорить расчёты и оценить характеристики контура в производстве.
Характеристики колебательного контура
Главные характеристики как параллельного, так и последовательного колебательного контура:
L — индуктивность катушки;
С — электроёмкость конденсатора.
Индуктивность катушки — это показатель, который численно равен электродвижущей силе (в вольтах), возникающей в цепи при изменении силы тока на 1 А за 1 секунду. Измеряется в генри (Гн).
Когда катушка подключена к цепи постоянного тока, то её индуктивность описывает энергию магнитного поля, которое создается этим током по формуле:
, где W — энергия магнитного поля, L — индуктивность, I — сила тока в цепи.
Индуктивность зависит от геометрических размеров контура и магнитных свойств среды (сердечника).
Электроёмкость — характеристика конденсатора, равная отношению заряда конденсатора к напряжению, под которым он находится. Измеряется в фарадах (Ф).
Электроёмкость можно вычислить по следующим формулам:
- , где e0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.
- , где q — заряд, U — напряжение в цепи.
Кстати, 1 фарад — весьма большая величина, поэтому электроёмкость конденсатора чаще всего выражается в пико- или нанофарадах.
Принцип действия колебательного контура
Итак, каким же образом работает колебательный контур? Разделим процесс на два этапа.
| Процесс происходит в обратном порядке:
|
Цикл повторяется до тех пор, пока на конденсаторе будет заряд. В идеальном колебательном контуре этот процесс происходил бы бесконечно, а в реальном неизбежны потери энергии, и колебания затухают.
Формула Томпсона
Характеристики L и С колебательного контура связаны между собой с помощью формулы Томпсона, которая описывает период свободных колебаний в LC-контуре:
, где T — период электромагнитных колебаний, L — индуктивность катушки колебательного контура, C — ёмкость конденсатора, π — число пи.
Эта формула для колебательного контура является одной из основных, обратите на неё особенное внимание!
Закон сохранения энергии в колебательном контуре
В колебаниях, как и в любом другом движении, работают законы сохранения энергии. Как именно это выражается?
Принцип работы контура основан на трансформации энергии, превращении электрической энергии в магнитную и наоборот. Тогда энергию колебательного контура можно описать так:
W = WC(t) + WL(t) = const
Когда энергия электрического поля становится максимальной, энергия магнитного поля равна нулю, что работает и в обратном направлении.
1 | Максимальна при q max: | 0 |
2 | 0 | Максимальна при I max:: |
Так как энергии достигают своего максимума с равным числовым значением, сделаем вывод:
Резонанс в LC-контуре
Обещаем, последнее на сегодня!
Помимо вышеперечисленных характеристик, есть ещё одна величина, которая описывает колебания в контуре, и это резонансная частота.
Ну, здесь всё просто. Помним, что частота колебаний и период — взаимно обратные величины, а значит:
«Ну хорошо», — скажете вы, «и в чём вообще суть?».
А вот в чём: в электрическом колебательном контуре резонанс (резкое увеличение амплитуды колебаний) происходит на определённой частоте, когда индуктивность L и ёмкость C уравновешены. Благодаря этому энергии могут свободно циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Наше сегодняшнее путешествие в мир физики было весьма увлекательным, хоть и непростым, согласны? На онлайн-курсе физики в школе Skysmart вы сможете ещё больше утвердиться в мысли, что физика — наука для жизни, а ещё подготовитесь к экзаменам и научитесь уверенно и без затруднений делать лабораторные работы.
Дарья Вишнякова
К предыдущей статье
Оптическая сила линзы
К следующей статье
Явление резонанса
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Саморезонансная частота и целостность сигнала | Блог Advanced PCB Design
Любой из этих конденсаторов может выступать в качестве резонатора благодаря собственной резонансной частоте конденсатора
Многие конструкторы небрежно относятся к выбору конденсаторов для своих печатных плат.
Иногда конденсаторы имеют неправильный размер для соответствующего напряжения питания, что может привести к выходу из строя конденсатора, если потенциал на конденсаторе превысит номинальное значение. В других случаях разработчики учитывают напряжение питания, но не учитывают общий заряд, который должен удерживать конденсатор, чтобы компенсировать колебания тока в определенных частях цепи.
Поскольку все больше систем работает на все более высоких частотах и скоростях переключения, конструкция и выбор конденсаторов становятся все более важными. Собственная резонансная частота конденсатора приводит к тому, что ваш конденсатор перестает вести себя как настоящий конденсатор и начинает вести себя больше как индуктор на высокой частоте. Этот важный эффект незаметен на низких частотах, но становится серьезной проблемой, связанной с целостностью сигнала, целостностью мощности и согласованием импеданса на высоких частотах.
Идеальные и реальные конденсаторы
Идеальная модель конденсатора может быть получена из уравнений Максвелла путем определения модели с двумя бесконечно большими идеальными проводящими пластинами.
Плотность заряда определена на одной пластине, с равной и противоположной плотностью заряда, индуцированной на противоположной пластине. Две пластины разделены диэлектриком с известной диэлектрической проницаемостью, и вы можете рассчитать электрическое поле между двумя пластинами по закону Гаусса. Затем вы можете легко вычислить разность потенциалов, которая должна существовать между двумя пластинами путем интегрирования. Это позволяет определить простое уравнение Q=CV. Вы также можете сделать это, используя метод изображений.
Для более сложных конденсаторов, таких как конденсаторы с круглыми пластинами, используемые в печатных платах, можно рассчитать идеальное значение емкости вручную, используя метод изображений. Хотя эти два основных метода могут быть использованы для определения идеальной емкости, они полностью игнорируют поведение конденсатора в реальной цепи, в том числе в печатной плате.
Из-за сопротивления выводов конденсатора последовательно с идеальным конденсатором возникает небольшое сопротивление, известное как эффективное последовательное сопротивление (ESR).
Геометрия проводников внутри конденсатора также обеспечивает некоторую небольшую индуктивность последовательно с идеальным конденсатором, известную как эффективная последовательная индуктивность (ESL). Наконец, существует очень большое сопротивление утечки между двумя пластинами внутри конденсатора, поскольку диэлектрик не является идеальным изолятором. В результате этих трех паразитных эффектов реальный конденсатор фактически представляет собой сеть RLC, как показано на схеме ниже.
Модель RLC для определения собственной резонансной частоты конденсатора
Значение C можно принять за емкость, указанную в техническом описании компонента. Сопротивление утечки учитывает кратковременную утечку, которая возникает в любом конденсаторе после того, как он был заряжен и впоследствии удален из цепи. Это значение обычно достаточно велико, чтобы им можно было пренебречь в схемах с непрерывным приводом.
Очень важно отметить, что частота собственного резонанса не равна обратному квадратному корню из ESL*C, что справедливо только при отсутствии демпфирования.
Хотя ESL и ESR имеют тенденцию быть довольно малыми, постоянная демпфирования в реальном конденсаторе равна ESR/(2*ESL), что означает, что демпфирование может быть заметным, особенно в плоских конденсаторах с большей площадью. Это необходимо учитывать при моделировании с использованием реальных моделей конденсаторов, и это определяет реакцию конденсатора на компенсацию звона на шине питания.
Определение собственной резонансной частоты конденсатора
Поскольку реальный конденсатор на самом деле представляет собой последовательную RLC-цепь, вы можете легко определить собственную резонансную частоту конденсатора с помощью модели SPICE, если вы знаете сопротивление утечки, ESR и ESL. Значение емкости, указанное в таблицах данных, может использоваться как C в сети RLC. Сопротивление утечки обычно достаточно велико, чтобы им можно было пренебречь в активно управляемых цепях, и им можно безопасно пренебречь, когда конденсатор заряжен до достаточно высокого напряжения постоянного тока.
Собственная резонансная частота конденсатора может варьироваться от низких значений МГц до значений ГГц.
При измерениях вы можете легко определить спектр импеданса конкретного конденсатора, используя развертку частоты и измерение выходного сигнала с помощью осциллографа. Вы также можете легко сделать это с помощью векторного анализатора цепей. Затем вы можете рассчитать значения ESL и ESR, измерив скорость затухания переходного процесса и резонансную частоту конденсатора в простой тестовой схеме.
Аналоговое моделирование с реальными конденсаторами и катушками индуктивности
Точно так же, как конденсаторы имеют собственную резонансную частоту, катушки индуктивности также имеют собственную резонансную частоту. Это означает, что реальные катушки индуктивности также должны быть смоделированы как их собственная сеть RLC. На определенной частоте вы обнаружите, что ваш индуктор будет иметь пик в своем спектре импеданса при значении высокой частоты, которое зависит от паразитной емкости, паразитной проводимости подложки и ESR в эквивалентной модели индуктора.
В качестве примера того, как эти факторы влияют на целостность сигнала, рассмотрим использование схемы незатухающего LC-генератора для согласования импеданса в высокочастотной аналоговой схеме (например, однодиапазонной антенне). Как правило, вы проектируете сеть так, чтобы она имела определенное значение импеданса на резонансной частоте LC-генератора (равное собственной частоте LC), которая равна частоте возбуждения элемента схемы. Реальное поведение конденсатора и катушки индуктивности может привести к тому, что фактическая резонансная частота LC-генератора отклонится от идеального расчетного значения. В спектре импеданса сети могут быть даже множественные резонансные или антирезонансные пики. Это также влияет на пропускную способность соответствующей сети.
Собственный резонанс двух разных конденсаторов. (Слева) собственная резонансная частота конденсатора, генерируемая каждым конденсатором при изолированном испытании.
(Справа) пики резонанса и антирезонанса в реальной схеме из-за собственного резонанса конденсатора.
При использовании таких элементов схемы, как ВЧ-усилители или антенны, требующих согласования определенного импеданса, следует позаботиться о том, чтобы нежелательные высокочастотные резонансы и антирезонансы не попадали в полосу пропускания антенны или усилителя. Пропускная способность сети также должна быть больше, чем пропускная способность элемента схемы. В общем, вы не можете избежать создания этих резонансов/антирезонансов более высокого порядка с помощью схемы согласования LC, но вы можете тщательно выбирать компоненты и проектировать схему так, чтобы эти нежелательные резонансы/антирезонансы не находились в пределах полосы пропускания элемента схемы.
В рамках согласования импеданса с силовыми цепями, работающими на очень высокой частоте в нелинейном режиме, и с другими нелинейными цепями в целом, вы можете определить правильное значение импеданса, которое вам нужно, используя анализ нагрузки-тяги на нескольких частотах, охватывающих всю полосу пропускания цепи.
. Это позволяет вам определить правильное согласование импеданса для заданного значения входной мощности на нескольких частотах по всей полосе пропускания схемы. Для линейных цепей, таких как антенны и активные цепи, работающие в линейном режиме, вы можете использовать развертку частоты переменного тока для определения спектра импеданса согласующей цепи, не беспокоясь о входной мощности.
Некоторые разработчики могут попытаться компенсировать собственную резонансную частоту шунтирующего или развязывающего конденсатора путем параллельного размещения двух конденсаторов с разными собственными резонансными частотами. На самом деле это не рекомендуется, так как вы непреднамеренно создадите резонансный генератор, который может сильно излучать на высоких частотах и влиять на согласование импеданса в рассматриваемой схеме. Это также может нанести ущерб, если вы сделаете это, чтобы попытаться обеспечить развязку на шине питания, поскольку можно вызвать мощный звон на шине питания, когда несколько цепей управляются одновременно.
Обязательно учитывайте собственную резонансную частоту конденсатора при выборе шунтирующих/развязывающих конденсаторов.
Если вам нужно изучить, как собственная резонансная частота конденсатора влияет на реальные схемы, программное обеспечение для проектирования и анализа печатных плат от Cadence включает в себя ряд моделей, которые вы можете использовать для проверки целостности питания и сигнала в ваших проектах. Интегрированное решение SI/PI Analysis для проектирования печатных плат, входящее в состав Allegro PCB Designer, и полный набор инструментов анализа Cadence упрощают выполнение важных расчетов мощности и целостности сигналов непосредственно на основе проектных данных, предлагая всестороннее представление о поведении ваших схем. .
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты.
Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions
УЗНАТЬ БОЛЬШЕ15.5 Резонанс в цепи переменного тока — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Определение пиковой резонансной угловой частоты переменного тока для цепи RLC
- Объясните ширину кривой зависимости средней мощности от угловой частоты и ее значение, используя такие термины, как полоса пропускания и добротность.0003
I0=V0R2+(ωL-1/ωC)2.I0=V0R2+(ωL-1/ωC)2.
15,15
Если мы можем изменять частоту генератора переменного тока, сохраняя неизменной амплитуду его выходного напряжения, то соответственно изменяется и ток.
График зависимости I0I0 от ωω показан на рис. 15.17.Рисунок 15.17 При резонансной частоте контура RLC , ω0=1/LC, ω0=1/LC, амплитуда тока достигает своего максимального значения.
В «Колебаниях» мы столкнулись с аналогичным графиком, на котором амплитуда затухающего гармонического осциллятора была построена в зависимости от угловой частоты синусоидальной движущей силы (см. «Вынужденные колебания»). Это сходство — больше, чем просто совпадение, как было показано ранее применением правила цикла Кирхгофа к схеме на рис. 15.11. Это дает
Ldidt+iR+qC=V0sinωt,Ldidt+iR+qC=V0sinωt,
15.16
or
Ld2qdt2+Rdqdt+1Cq=V0sinωt,Ld2qdt2+Rdqdt+1Cq=V0sinωt,
where we substituted dq (т)/ дт для и (т). Сравнение Уравнения 15.16 и из Колебания, Затухающие колебания для затухающего гармонического движения ясно показывает, что управляемая цепь серии RLC является электрическим аналогом управляемого затухающего гармонического генератора.
Резонансная частота f0f0 Цепь RLC — это частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения. При проверке это соответствует угловой частоте ω0=2πf0ω0=2πf0, при которой импеданс Z в уравнении 15.15 является минимальным, или когда
ω0L=1ω0Cω0L=1ω0C
и
ω0=1LC.
15.17
Это резонансная угловая частота контура. Подставляя ω0ω0 в уравнение 15.9, уравнение 15.10 и уравнение 15.11, мы находим, что при резонансе
ϕ=tan−1(0)=0, I0=V0/R, и Z=R.ϕ=tan−1(0)=0, I0 =V0/R, и Z=R.
Следовательно, при резонансе цепь RLC является чисто резистивной, с приложенными ЭДС и током в фазе.
Что происходит с мощностью при резонансе? Уравнение 15.14 показывает нам, как средняя мощность, передаваемая от генератора переменного тока к комбинации RLC , зависит от частоты.
Кроме того, PavePave достигает максимума, когда Z , зависящее от частоты, является минимумом, то есть когда XL=XCиZ=R.XL=XCиZ=R. Таким образом, при резонансе средняя выходная мощность источника в цепи серии RLC максимальна. Из уравнения 15.14 этот максимум равен Vrms2/R.Vrms2/R.На рис. 15.18 представлен типичный график зависимости PavePave от ωω в области максимальной выходной мощности. Ширина полосы ΔωΔω резонансного пика определяется как диапазон угловых частот ωω, в котором средняя мощность PavePave превышает половину максимального значения Pave.Pave. Острота пика описывается безразмерной величиной, известной как добротность Q цепи. По определению
Q=ω0Δω, Q=ω0Δω,
15,18
, где ω0ω0 — резонансная угловая частота. Высокое значение Q указывает на острый резонансный пик. Мы можем дать Q с точки зрения параметров схемы как
Q=ω0LR.
Q=ω0LR.15.19
Рисунок 15.18 Как и ток, средняя мощность, передаваемая от генератора переменного тока к цепи RLC , имеет пик на резонансной частоте.
Резонансные контуры обычно используются для передачи или подавления выбранных частотных диапазонов. Это делается путем регулировки значения одного из элементов и, следовательно, «настройки» схемы на определенную резонансную частоту. Например, в радиоприемниках приемник настраивается на нужную станцию путем регулировки резонансной частоты его схемы в соответствии с частотой станции. Если схема настройки имеет высокий уровень Q , он будет иметь небольшую полосу пропускания, поэтому сигналы от других станций на частотах, даже немного отличающихся от резонансной, встречают высокое сопротивление и не проходят по цепи. Сотовые телефоны работают аналогичным образом, обмениваясь сигналами с частотой около 1 ГГц, которые настраиваются схемой индуктор-конденсатор.
Одним из наиболее распространенных применений конденсаторов является их использование в цепях синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов (рис. 15.19).).Рисунок 15.19 Когда металлоискатель приближается к металлическому предмету, изменяется собственная индуктивность одной из его катушек. Это вызывает сдвиг резонансной частоты цепи, содержащей катушку. Этот сдвиг определяется схемой и передается дайверу через наушники. (кредит: модификация работы Эрика Липпманна, ВМС США)
Пример 15,4
Резонанс в цепи серии
RLC(a) Какова резонансная частота цепи с использованием последовательно соединенных значений напряжения и LRC из примера 15.2? б) Если генератор переменного тока настроен на эту частоту без изменения амплитуды выходного напряжения, какова будет амплитуда тока?
Стратегия
Резонансная частота для схемы RLC рассчитывается по уравнению 15.
17, которое получается из баланса реактивных сопротивлений конденсатора и катушки индуктивности. Поскольку цепь находится в резонансе, полное сопротивление равно резистору. Затем пиковый ток рассчитывается делением напряжения на сопротивление.Решение
- Резонансная частота находится из уравнения 15.17:
f0=12π1LC=12π1(3,00×10-3H)(8,00×10-4F)=1,03×102Гц. f0=12π1LC=12π1(3,00×10-3H)(8,00×10-4F)=1,03×102Гц.
- При резонансе импеданс цепи чисто резистивный, а амплитуда тока равна
I0 = 0,100 В 4,00 Ом = 2,50 × 10–2 А. I0 = 0,100 В 4,00 Ом = 2,50 × 10–2 А.
Значение
Если бы цепь не была настроена на резонансную частоту, нам понадобился бы импеданс всей цепи для расчета тока.
Пример 15,5
Передача мощности в цепи
RLC серии при резонансеа) Чему равна резонансная угловая частота Цепь RLC с R=0,200 Ом, R=0,200 Ом, L=4,00×10-3H, L=4,00×10-3H и C=2,00×10-6F?C=2,00×10-6F? (b) Если источник переменного тока с постоянной амплитудой 4,00 В настроен на эту частоту, какова средняя мощность, передаваемая в цепь? (c) Определите Q и пропускную способность этой цепи.
Стратегия
Резонансная угловая частота рассчитывается по уравнению 15.17. Средняя мощность рассчитывается по среднеквадратичному напряжению и сопротивлению в цепи. Коэффициент качества рассчитывается по уравнению 15.19.и зная резонансную частоту. Полоса пропускания рассчитывается по уравнению 15.18 и зная коэффициент качества.
Решение
- Резонансная угловая частота
ω0=1LC=1(4,00×10-3H)(2,00×10-6F)=1,12×104рад/с /с.
- На этой частоте средняя мощность, передаваемая в цепь, максимальна. Это
Pave=Vrms2R=[(1/2)(4,00 В)]20,200 Ом=40,0 Вт. Pave=Vrms2R=[(1/2)(4,00 В)]20,200 Ом=40,0 Вт.
- Добротность цепи составляет
Q=ω0LR=(1,12×104 рад/с)(4,00×10-3H)0,200 Ом=224.
Затем мы находим для полосы пропускания
Δω=ω0Q=1,12×104рад/с224=50,0рад/с. Δω=ω0Q=1,12×104рад/с224=50,0рад/с.
Значение
Если требуется более узкая полоса пропускания, поможет более низкое сопротивление или более высокая индуктивность.
Однако более низкое сопротивление увеличивает мощность, передаваемую в цепь, что может быть нежелательно, в зависимости от максимальной мощности, которая может быть передана.Проверьте свое понимание 15,6
В схеме на рис. 15.11 L=2,0×10-3H, L=2,0×10-3H, C=5,0×10-4F, C=5,0×10-4F и R=40 Ом. R=40 Ом. а) Чему равна резонансная частота? б) Каково сопротивление цепи в резонансе? в) Чему равно i ( t ) при резонансе, если амплитуда напряжения равна 10 В? (d) Частота генератора переменного тока изменена на 200 Гц. Вычислите разность фаз между током и ЭДС генератора.
Проверьте свое понимание 15,7
Что произойдет с резонансной частотой цепи серии RLC , если следующие величины увеличить в 4 раза: (а) емкость, (б) собственную индуктивность и (в) сопротивление?
Проверьте свое понимание 15,8
Резонансная угловая частота цепи серии RLC составляет 4,0×102 рад/с.
- Резонансная частота находится из уравнения 15.17:
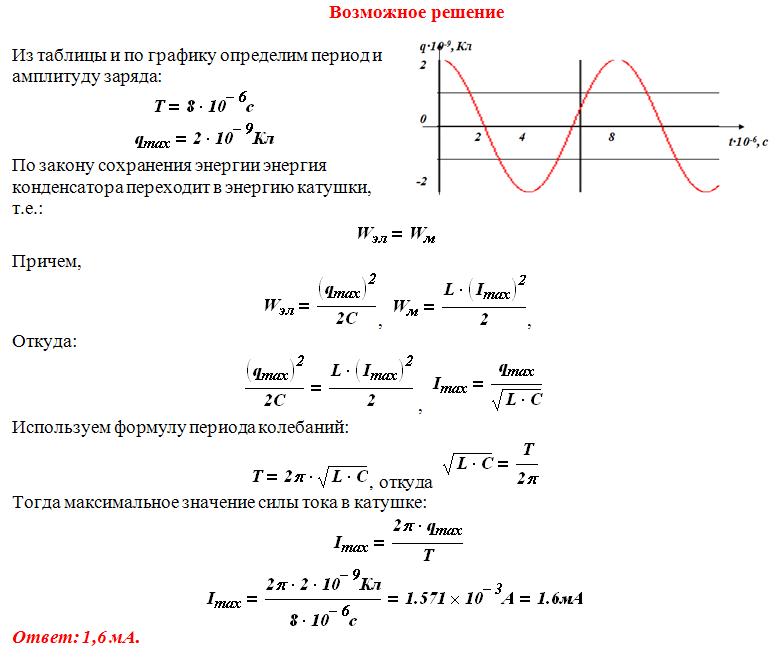
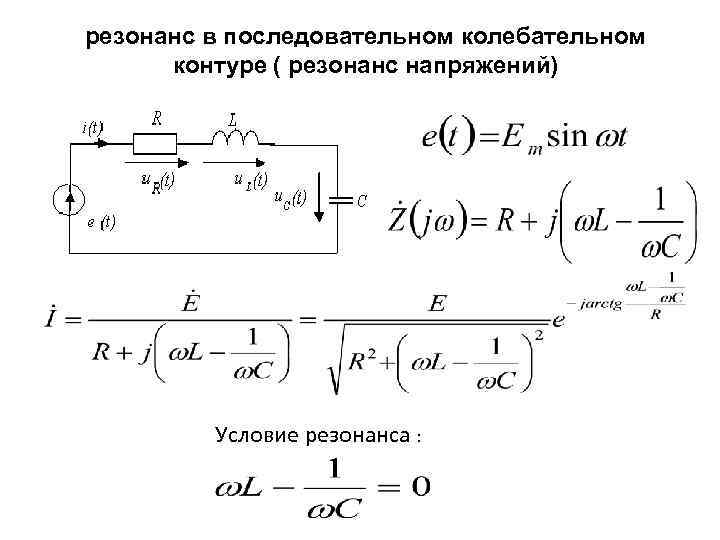График зависимости I0I0 от ωω показан на рис. 15.17.
Кроме того, PavePave достигает максимума, когда Z , зависящее от частоты, является минимумом, то есть когда XL=XCиZ=R.XL=XCиZ=R. Таким образом, при резонансе средняя выходная мощность источника в цепи серии RLC максимальна. Из уравнения 15.14 этот максимум равен Vrms2/R.Vrms2/R.
Q=ω0LR.
Одним из наиболее распространенных применений конденсаторов является их использование в цепях синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов (рис. 15.19).).
17, которое получается из баланса реактивных сопротивлений конденсатора и катушки индуктивности. Поскольку цепь находится в резонансе, полное сопротивление равно резистору. Затем пиковый ток рассчитывается делением напряжения на сопротивление.
Однако более низкое сопротивление увеличивает мощность, передаваемую в цепь, что может быть нежелательно, в зависимости от максимальной мощности, которая может быть передана.
