Онлайн калькуляторы векторов
Данный раздел содержит калькуляторы, позволяющие выполнять все основные действия над векторами. В частности, с помощью данных калькуляторов можно вычислять скалярное, векторное и смешанное произведения векторов, раскладывать вектора по базису, проверять их ортогональность, компланарность и др. Всего представлено 19 калькуляторов и для каждого предусмотрено подробное решение соответствующей задачи.
Операции над векторами 19
Сложение векторов Калькулятор позволяет складывать вектора, заданные в координатной форме.
Разность векторов Калькулятор позволяет вычитать вектора, заданные в координатной форме.
Модуль (длина) вектора Калькулятор находит модуль (длину) вектора с описанием подробного решения на русском языке.
Угол между векторами Калькулятор позволяет найти угол между векторами. Подробное решение также имеется.
Проекция вектора Калькулятор вычисляет проекцию вектора на ось или на другой вектор.
Как найти векторное произведение векторов онлайн? · Как пользоваться Контрольная Работа РУ
Сервис на сайте Контрольная работа Ру «Векторное произведение» позволяет получить не только теоретическое определение векторного произведения векторов, но ещё и по данным вам векторам вычислить итоговый вектор векторного произведения с подробным решением.
Приведём пример, как использовать данный калькулятор онлайн.
Допустим, нам даны векторы a = (1, 2, 3) и b = (4, 5, 6) и нужно вычислить [a, b] — их векторное произведение.
Для этого используйте следующие несколько шагов:
1. Перейдите на страницу сервиса онлайн тут
2. Введите первый вектор, который входит в векторное произведение, как показано на рис:
3. После того, как вы нажали кнопку «Далее», то введите второй вектор, который входит в векторное произведение, как на рис.:
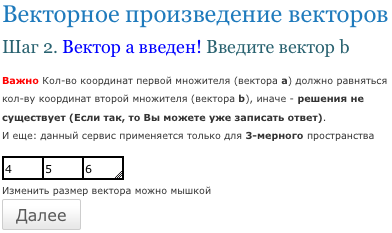
4. Опять нажмите кнопку «Далее» и вы получите результат:
| Даны вектора a = |
[1 2 3] |
и b = |
[4 5 6] |
Найдем векторное произведение векторов [a * b]
Векторное произведение легко найти (равно такому определителю):
| [a * b] = |
| i j k | | a1 a2 a3 | | b1 b2 b3 | |
, |
где i, j и k — единичные векторы, направленные соотв. вдоль оси x, y, z
Находим:
| [a * b] = |
| i j k | | 1 2 3 | | 4 5 6 | |
= |
= ((2) * (6) — (3) * (5))i + ((3) * (4) — (1) * (6))j + ((1) * (5) — (2) * (4))k = -3i + 6j + -3k,
т.е. векторное произведение равно [a * b] = [-3 6 -3]
Вычислить векторное произведение векторов онлайн
Как известно, в результате скалярного произведения векторов получается число. Итогом векторного произведения векторов является вектор.
Итак, векторным произведением двух неколлинеарных векторов (а и b) называется третий вектор ©, имеющий следующие свойства:
1. длина его численно равняется площади параллелограмма, построенного на векторах а и b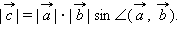
2. вектор с перпендикулярный плоскости векторов а и b.
3. направление вектора с таково, что кратчайший поворот от вектора а к вектору b происходит против часовой стрелки, если посмотреть с конца вектора с.
В зависимости от направления вектора с тройка векторов а, b, с называется правой или левой. В данном случае тройка векторов а, b, с — правая.
Геометрический смысл произведения.
Модуль произведения двух векторов равняется площади параллелограмма, построенного на этих векторах: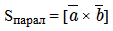
Половина модуля векторного произведения двух векторов (a и b) равняется площади треугольника, построенного на этих векторах:
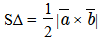Векторное произведение можно представить в координатной форме через координаты векторов а и b. Пусть а = {ах;ау;az} и b = {bх;bу;bz}, тогда произведение двух векторов можно рассчитать по формуле:
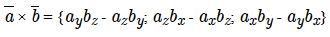Свойства векторного произведения векторов: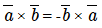
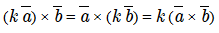
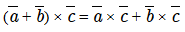Векторное произведение двух параллельных между собой не нулевых векторов равняется нулевому вектору.Векторное произведение произвольного вектора на нулевой равняется нулевому вектору. Быстро рассчитать векторное произведение векторов вам поможет онлайн калькулятор. Вводим координаты каждого из векторов. Жмем Вычислить.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Смешанное произведение векторов. Онлайн калькулятор.
Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4), для записи произведения двух чисел используйте знак «*» (например, 5*6), для возведения числа в целую степень (не более 100 и не меньше -100) используйте знак «^» (например, 5^-12 или 6^3), для умножения числа на число в целой степени используйте запись типа, 5*10^2 или 2.3*10^-4 или (1/2)*4^6 или 17*3^-12 и т.д.
Как найти смешанное произведения векторов
Пример №1Найдем смешанное произведение векторов пространства. Координаты векторов заданны точками.
Координаты точки А вектора AB: (7; 9 ; -7)
Координаты точки B вектора AB: (-1 ; 0 ; 16)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Координаты точки E вектора CD: (14 ; -1 ; 2)
Координаты точки F вектора CD: (6 ; -3 ; -4)
Решение:
Вычислим координаты первого вектора по двум точкам A и B:
AB = {xB — xA ; yB — yA; zB — zA} = {-1 — 7 ; 0 — 9 ; 16 — (-7)} = {-8 ; -9 ; 23}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {xD — xC ; yD — yC; zD — zC} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
Вычислим координаты третьего вектора по двум точкам E и F:
EF = {xF — xE ; yF — yE; zF — zE} = {6 — 14 ; -3 — (-1) ; -4 — 2} = {-8 ; -2 ; -6}
Смешанное произведение векторов — это число, равное значению определителя матрицы третьего порядка, строками которой являются координаты умножаемых векторов. Найдем значение определителя: AB ⋅ CD ⋅ EF =| ABx | ABy | ABz |
| CDx | CDy | CDz |
| EFx | EFy | EFz |
ABy = -9
ABz = 23
CDx = 7
CDy = 6
CDz = 7
EFx = -8
EFy = -2
EFz = -6
AB ⋅ CD ⋅ EF =
| (-8) | (-9) | 23 |
| 7 | 6 | 7 |
| (-8) | (-2) | (-6) |
Пример №2
Найдем смешанное произведение векторов пространства.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)
Координаты вектора c: (3 ; 8 ; 9)
Решение:
Смешанное произведение векторов — это число, равное значению определителя матрицы третьего порядка, строками которой являются координаты умножаемых векторов. Найдем значение определителя: a ⋅ b ⋅ c = = ax — ay + az = axbycz — axbzcy — aybxcz + aybzcx + azbxcy — azbycxax = 5ay = 1
az = 7
bx = 2
by = 4
bz = 6
cx = 3
cy = 8
cz = 9
a ⋅ b ⋅ c = = 5 — 1 + 7 = (5 ⋅ 4 ⋅ 9) — (5 ⋅ 6 ⋅ 8) — (1 ⋅ 2 ⋅ 9) + (1 ⋅ 6 ⋅ 3) + (7 ⋅ 2 ⋅ 8) — (7 ⋅ 4 ⋅ 3) = 180 — 240 — 18 + 18 + 112 — 84 = -32
Механика
Электричество и магнетизм
Конденсаторы
Как найти векторные компоненты
- Образование
- Наука
- Физика
- Как найти векторные компоненты
Стивен Хольцнер
В физике, когда вы разбиваете вектор на части, эти части называются его компонентами . Например, в векторе (4, 1) компонент оси x (горизонтальный) равен 4, а компонент оси y (вертикальный) равен 1.Обычно физическая задача дает вам угол и величину для определения вектора; вы должны сами найти компоненты, используя небольшую тригонометрию.
Предположим, вы знаете, что мяч катится по плоскому столу под углом 15 градусов от направления, параллельного нижнему краю, со скоростью 7,0 м / сек. Вы можете узнать, сколько времени потребуется мячу, чтобы скатиться с края на 1,0 метр вправо.
Определите свои оси так, чтобы шар изначально находился в начале координат, а ось x была параллельна нижнему краю стола (см. Рисунок).Таким образом, проблема сводится к выяснению того, сколько времени потребуется мячу, чтобы катиться на 1,0 метр в направлении x . Чтобы узнать время, вам сначала нужно знать, насколько быстро мяч движется в направлении x .
Проблема говорит вам, что мяч катится со скоростью 7,0 м / сек под углом 15 градусов к горизонтали (вдоль положительной оси x ), что является вектором: 7,0 м / сек при 15 градусах дает вам обоим. величина и направление. У вас есть скорость — векторная версия скорости.Скорость мяча — это величина его вектора скорости, и когда вы включаете направление этой скорости, вы получаете вектор скорости v .
Чтобы узнать, с какой скоростью мяч движется к краю стола, вам нужна не общая скорость мяча, а составляющая его скорости x . Компонент x — это скаляр (число, а не вектор), и вы пишете его так: v x . Компонент y вектора скорости мяча равен v y .Таким образом, можно сказать, что
v = ( v x , v y )
Вот как можно выразить разбиение вектора на составляющие. Так что здесь v x ? И если на то пошло, что такое v y , составляющая скорости y ? Вектор имеет длину (7,0 м / сек) и направление
И вы знаете, что край таблицы равен 1.0 метров вправо.
Как вы можете видеть на рисунке, вам нужно использовать некоторую тригонометрию, чтобы разделить этот вектор на его компоненты. Нет пота. Триггер легко сделать после того, как вы опустите углы, которые вы видите на рисунке.
Величина вектора v выражается как v , и из рисунка видно, что верно следующее:
Два уравнения векторных компонент стоит знать, потому что вы часто видите их в любом начальном курсе физики.Убедитесь, что вы знаете, как они работают, и всегда держите их под рукой.
Конечно, если вы забудете эти уравнения, вы всегда сможете получить их из базовой тригонометрии. Возможно, вы помните, что синус и косинус угла в прямоугольном треугольнике определяются как отношение противоположной стороны и смежной стороны к гипотенузе, например:
Умножив обе части этих уравнений на v , можно выразить компоненты вектора x и y как
Вы можете пойти дальше, связав каждую сторону треугольника друг с другом (и если вы знаете, что
, вы можете вывести все это из двух предыдущих уравнений по мере необходимости; не нужно все это запоминать):
Вы знаете, что
, чтобы вы могли найти составляющую скорости мяча x , v x , таким образом:
Вставка цифр дает
Теперь вы знаете, что мяч летит на 6.8 метров в секунду вправо. А поскольку вы также знаете, что край стола находится на расстоянии 1 метра, вы можете разделить расстояние на скорость, чтобы получить время:
Поскольку вы знаете, насколько быстро мяч движется в направлении x , теперь вы знаете ответ на проблему: мячу потребуется 0,15 секунды, чтобы упасть с края стола. А как насчет компоненты скорости y ? Это тоже легко найти:
Об авторе книги
Стивен Хольцнер, доктор философии, работал редактором журнала PC Magazine и работал на факультете Массачусетского технологического института и Корнельского университета.Он написал Physics II For Dummies , Physics Essentials for Dummies и Quantum Physics for Dummies .
,Как найти векторное произведение или кросс-произведение двух векторов
О «Как найти векторное произведение или кросс-произведение двух векторов»
Как найти векторное произведение или перекрестное произведение двух векторов:
Здесь мы увидим, как найти векторное произведение или векторное произведение двух векторов.
Рабочее правило для поиска перекрестного произведения
Пусть
Нахождение взаимного произведения двух векторов — Примеры
Вопрос 1:
Найдите величину вектора x b, если вектор = 2i вектор + j вектор + 3k вектор и b вектор = 3i вектор + 5j вектор — 2k вектор
Решение:
= вектор i [-2-15] — вектор j [-4-9] + вектор k [10-3]
= вектор i [-17] — вектор j [-13] + вектор k [7]
axb = -17 i вектор + 13 j вектор + 7 k вектор
Чтобы найти его величину, мы должны извлечь квадратный корень и найти сумму коэффициентов при i, j и k.
| a x b | = √ (-17) 2 + 13 2 + 7 2
= √ (289 + 169 + 49)
= √507
Вопрос 2:
Покажите, что
Решение:
ax (b + c) = axb + axc — (1)
bx (c + a) = bxc + bxa — (2)
cx (a + b) = cxa + cxb — (3)
(1) + (2) + (3)
ax (b + c) + bx (c + a) + cx (a + b)
= axb + axc + bxc + bxa + cxa + cxb
Поскольку коммутативность не применима в смешанном произведении,
= axb + axc + bxc — axb — axc — bxc
= 0
Следовательно, это доказано.
Вопрос 3:
Найдите векторы величины 10√3, перпендикулярные плоскости, которая содержит вектор i + 2j вектор + вектор k и вектор i + вектор 3j + вектор 4k
Решение:
Пусть a вектор = i вектор + 2j вектор + k вектор
b вектор = i вектор + 3j вектор + 4k вектор
требуемый вектор, перпендикулярный заданным векторам
= ± μ [(axb) / | axb |]
= i [8-3] — j [4-1] + k [3-2]
a x b = 5i — 3j + k
| a x b | = √5 2 + (-3) 2 + 1 2
= √ (25 + 9 + 1)
= √35
Требуемый вектор = ± (10√3 / √35) ( 5i — 3j + k)
= ± (10√3 / √35) (5i — 3j + k)
После того, как мы изучили все вышеперечисленное, мы надеемся, что студенты поняли «Свойства скалярного произведения или точечного произведения».
Помимо материалов, приведенных в разделе «Свойства скалярного произведения или точечного произведения», если они вам понадобятся другие вопросы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами при цене за единицу
Проблемы со словом при скорости единицы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
ЗадачиЗадачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Теорема Пифагора Задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
L.Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
,Точечное произведение двух векторов
Линейная алгебра — Векторы: (урок 2 из 3)
Точечный продукт
Определение:
Скалярное произведение (также называемое внутренним произведением или скалярным произведением) двух векторов определяется как:
Где | A | и | B | представляет величины векторов A и B, — угол между векторами A и Б.
Расчет точечного произведения
Точечное или скалярное произведение векторов и может быть записано как:
Пример (расчет в двух измерениях):
Векторы A и B предоставлены и ,Найдите точечный продукт двух векторов.
Решение:
Пример (расчет в трех измерениях):
Векторы A и B предоставлены и , Найдите точечный продукт двух векторов.
Решение:
Расчет длины вектора
Длина вектора равна:
Пример:
Vector A выдается.Найдите | A | .
Решение:
Угол между двумя векторами
Угол между двумя ненулевыми векторами A, и B равен
.Пример: (угол между векторами в двух измерениях):
Определите угол между и ,
Решение:
Нам понадобятся величины каждого вектора, а также скалярное произведение.
Угол,
Пример: (угол между векторами в трех измерениях):
Определите угол между и ,
Решение:
Опять же, нам нужны величины, а также скалярное произведение.
Угол,
Ортогональные векторы
Если два вектора ортогональны , то: ,
Пример:
Определите, являются ли следующие векторы ортогональными :
Решение:
Скалярное произведение —
Итак, два вектора ортогональны.
,c ++ — Как узнать, присутствует ли элемент в std :: vector?
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
- реклама Обратитесь к разработчикам по всему миру
Загрузка…
